Sinai’s Work on Markov Partitions and SRB Measures

Abstract

Some principal contributions of Ya. Sinai to hyperbolic theory of dynamical systems, focusing mainly on constructions of Markov partitions and of Sinai–Ruelle–Bowen measures, are discussed. Some further developments in these directions stemming from Sinai’s work, are described.

The author was partially supported by NSF grant DMS–1400027.

1 Introduction

In this article I discuss some of the many principal contributions of Ya. Sinai to the hyperbolic theory of smooth dynamical systems. I focus on two related topics: (1) Markov partitions and (2) Sinai–Ruelle–Bowen (SRB) measures. Dynamical systems that admit Markov partitions with finite or countable number of partition elements allow symbolic representations by topological Markov shifts with finite or respectively countable alphabet. As a result these systems exhibit high level of chaotic behavior of trajectories. SRB-measures serve as natural invariant measures with rich collection of ergodic properties. Various constructions of Markov partitions as well as of SRB-measures represent an important and still quite active area of research in dynamics that utilizes Sinai’s original ideas and develops them further to cover many other classes of dynamical systems. Therefore, along with describing results by Ya. Sinai, I briefly survey some of the latest developments in this area.

I stress that hyperbolic theory of dynamical systems provides a rigorous mathematical foundation for studying models in science that exhibit chaotic motions. For reader’s convenience, I begin with an informal discussion of the role that the hyperbolic theory plays in studying various chaotic phenomena.

1.1 From Scientific Determinism to Deterministic Chaos

In the nineteenth century the prevailing view in dynamics was causal or scientific determinism best expressed by Laplace as follows:

We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes.

It took about a century to shake up this view with the discovery by Poincaré—in his work on the three-body problem—of the existence of homoclinic tangles formed by intersections of stable and unstable separatrices of a hyperbolic fixed point.

Poincaré wrote:

When we try to represent the figure formed by these two curves and their infinitely many intersections… one must be struck by the complexity of this shape, which I do not even attempt to illustrate. Nothing can give us a better idea of the complication of the three-body problem, and in general of all problems of dynamics for which there is no uniform integral.

In 1963, in his talk at the International Conference on Nonlinear Oscillations (Kiev, Ukraine), Smale [66] made the crucial observation that the homoclinic tangle contains a horseshoe, i.e., a fractal set that is locally the product of two Cantor sets. One obtains this set by taking the closure of the set of intersections of stable and unstable separatrices near the fixed point. The horseshoe provided the first example of a differential map with infinitely many hyperbolic periodic points.

Smale’s discovery was an important step in shaping up a new area of research in dynamical systems—the hyperbolicity theory—that studies relations between chaotic motions, instability of trajectories and fractal structure of invariant sets. The foundation of this new area was built in the 1960s–1970s in seminal works of Anosov, Sinai, and Smale, see [5, 6, 59,60,61,62, 66, 67]. I would like also to emphasize an important role for the development of the theory of dynamical systems that was played during this time by two Moscow seminars, one run by Alekseev and Sinai¹ and another one by Anosov and Katok (see [19, 37, 38]) as well as by Smale’s school at Berkeley.

The current view on dynamics draws a much richer picture allowing a variety of motions ranging from regular to intermittently chaotic to all-time chaotic. Moreover, a dynamical system, which is typical in a sense, should possess an invariant fractal set of complicated self-similar geometric structure, and the trajectories that start on or in a vicinity of this set are unstable (hyperbolic). The combination of fractality of the set and instability of trajectories causes these trajectories to behave unpredictably; such a chaotic behavior can persist all the time or can be intermittent.

Furthermore, one should typically expect to have infinitely many such fractal sets, which are mixed together in one invariant multi-fractal set. These fractal sets can occupy either the whole phase space, or a part of it, in which case the dynamics on its complement can be quite regular—the highly non-trivial phenomenon known as the essential coexistence, see [25, 26, 35] for a detailed description of the phenomenon and recent examples of systems with discrete and continuous time that exhibit it.

To describe the phenomenon of the appearance of “chaotic” motions in purely deterministic dynamical systems, one uses the controversial but expressive term deterministic chaos.² Its crucial feature is that the chaotic behavior is not caused by an external random force such as white noise, but by the system itself. The source of the deterministic chaotic behavior is instability along typical trajectories of the system, which drives orbits apart. On the other hand, compactness of the phase space forces them back together; the consequent unending dispersal and return of nearby trajectories is one of the hallmarks of chaos.

After Poincaré, the fact that instability can cause some complicated chaotic behavior was further observed and advanced in works of Birkhoff, Hadamard, Hopf, and Morse. Many years later some systems with chaotic behavior were found and studied numerically by Lorenz, Chirikov, Ford, Zaslavsky, etc. I refer the reader to Sinai’s articles [63,64,65] for a more detailed discussion of the chaos theory, its earlier development and relations between chaotic behavior and instability of trajectories as well as for relevant references. In these papers Sinai also demonstrates how ideas and methods of statistical physics can be used to explain various chaotic phenomena in dynamics.

1.2 Markov Partitions and Symbolic Representations of Chaotic Dynamics

To explain what it means for deterministic trajectories to exhibit chaotic behavior, consider a map f acting on a phase space M and a point x ∈ M. Let us divide the phase space into two parts A and B. Given an orbit {f ⁿ(x)}, we write 0 if f ⁿ(x) lies in A and 1 otherwise. This way we obtain a coding of every trajectory by a two-sided infinite sequence of symbols 0 and 1 that is

$$\displaystyle \begin{aligned} x\to\omega = \{\dots,\omega_{-2},\omega_{-1},\omega_0,\omega_1,\omega_2, \dots\}, \text{ where } \omega_i=0 \text{ or } 1. \end{aligned}$$

The principal question is:

Given a symbolic sequence of 0 and 1, can we find a point x whose trajectory is coded by this sequence?

If so, starting with a random symbolic sequence that is obtained, for example, by flipping a dime, one gets a random orbit of the system whose location in either A or B can only be predicted with a certain probability.

Another way to look at this is to say that the system under consideration is modeled by (or equivalent to) the classical Bernoulli process in probability theory.

Smale’s horseshoe is a classical example which allows the above coding and hence, a symbolic representation by the full shift on 2 symbols. In many “practical” situations however, one may need more sophisticated partitions of the phase space called Markov partitions (the term coined by Sinai). In general, elements of Markov partitions may have very complicated fractal structure. These partitions allow one to model the systems by more general Markov (not necessarily Bernoulli) processes with finite or even countable set of states. From the probability theory point of view such processes are chaotic in the strongest possible sense.

The first construction of Markov partitions was obtained by Adler and Weiss [1] in the particular case of hyperbolic automorphisms of the 2-torus (see also Berg, [12] whose work is independent of [1]). As a crucial corollary they observed that the map allowed a symbolic representation by a subshift of finite type and that this can be used to study its ergodic properties.

Sinai’s groundbreaking contribution was to realize that existence of Markov partitions is a rather general phenomenon and in [59] he designed a method of successive approximations to construct Markov partitions for general Anosov diffeomorphisms (see Sect. 3 below for more details). Furthermore, in [62] Sinai showed how Markov partitions can be used to study ergodic properties of hyperbolic dynamical systems and he was also the first to observe the analogy between the symbolic models of Anosov diffeomorphisms and lattice gas models in physics—the starting point in developing the thermodynamic formalism.

Using a different approach, Bowen constructed Markov partitions with finitely many elements for Axiom A diffeomorphisms, see [15]. The construction for hyperbolic flows was carried out independently by Bowen [16] and Ratner [54] (see also [15, 17]). Recently, Sarig [57] constructed Markov partitions with a countable number of elements for surface diffeomorphisms with positive topological entropy. Symbolic dynamics associated with hyperbolic systems was also studied by Alekseev [2].

Aside from smooth dynamical systems, Markov partitions with countable number of partition elements were constructed for a particular class of hyperbolic billiards by Bunimovich and Sinai [20] and by Bunimovich, Sinai, and Chernov [21] (see also the article by Szasz [68]).

1.3 Entropy

Introduced by Kolmogorov and Sinai, the metric entropy is one of the most important invariants of dynamics, and this manifests itself in the famous isomorphism problem. Given a transformation T : X → X preserving a measure μ, we say that (T, μ) is a Bernoulli automorphism if it is metrically isomorphic to the Bernoulli shift (σ, κ) associated to some Lebesgue space (Y, ν), so that ν is metrically isomorphic to Lebesgue measure on an interval together with at most countably many atoms and κ is given as the direct product of $\mathbb {Z}$ copies of ν on $Y^{\mathbb {Z}}$. Bernoulli systems exhibit the highest level of chaotic behavior and entropy is a complete invariant that distinguishes one Bernoulli map from another. This statement is known as the isomorphism problem for Bernoulli systems. I refer the reader to the article by Gurevich [32] for a more detailed discussion of this problem, its history, and relevant references, but I would like to emphasize the important role of Sinai’s work on weak isomorphism [58] that laid the ground for the famous Ornstein solution of the isomorphism problem for Bernoulli systems, [46, 47].

Since in this paper we are mostly interested in smooth hyperbolic dynamical systems, we will present a formula for the entropy of these systems with respect to smooth or SRB measures. This formula connects the entropy with the Lyapunov exponents (see Theorem 3 below); the latter are asymptotic characteristics of instability of trajectories of the system. We will also discuss the Bernoulli property; establishing it for smooth hyperbolic systems is based on verifying Ornstein’s criterium for Bernoullicity.

1.4 Hyperbolicity

Intuitively, hyperbolicity means that the behavior of orbits that start in a small neighborhood of a given one resembles that of the orbits in a small neighborhood of a hyperbolic fixed point. In other words, the tangent space along the orbit {f ⁿ(x)} should admit an invariant splitting

$$\displaystyle \begin{aligned} T_{f^n(x)}M=E^s(f^n(x))\oplus E^u(f^n(x)) \end{aligned} $$

(1)

into the stable subspace E ^s along which the differential of the system contracts and the unstable subspace E ^u along which the differential of the system expands.

One should distinguish between two types of hyperbolicity: uniform and nonuniform. In the former case every trajectory is hyperbolic and the contraction and expansion rates are uniform in x. More generally, one can consider a compact invariant subset Λ ⊂ M and require that f acts uniformly hyperbolic on Λ. Such a set Λ is called uniformly hyperbolic. In the case of nonuniform hyperbolicity the set of hyperbolic trajectories has positive (in particular, full) measure with respect to an invariant measure and the contraction and expansion rates depend on x. Thus, nonuniform hyperbolicity is a property of the system as well as of its invariant measure (called hyperbolic).

One can extend the notion of hyperbolicity by replacing the splitting (1) along the orbit {f ⁿ(x)} with the splitting

$$\displaystyle \begin{aligned} T_{f^n(x)}M=E^s(f^n(x))\oplus E^c(f^n(x))\oplus E^u(f^n(x)) \end{aligned} $$

(2)

into the stable E ^s, unstable E ^u and central E ^c subspaces with the rates of contraction and/or expansion along the central subspace being slower than the corresponding rates along the stable and unstable subspaces. This is the case of partial hyperbolicity.

2 An Overview of Hyperbolicity Theory

In this section I formally introduce three major types of hyperbolicity and briefly discuss some of their basic properties.

2.1 Uniform Hyperbolicity

It originated in the work of Anosov and Sinai [5, 6]; see also the book [39] for the state of the art exposition of the uniform hyperbolicity theory.

A diffeomorphism f of a compact Riemannian manifold M is called uniformly hyperbolic or Anosov if for each x ∈ M there is a continuous df-invariant decomposition of the tangent space T _x M = E ^s(x) ⊕ E ^u(x) and constants c > 0, λ ∈ (0, 1) such that for each x ∈ M:

• 1. ∥d _x f ⁿ v∥≤ cλ ⁿ∥v∥ for v ∈ E ^s(x) and n ≥ 0;

• 2. ∥d _x f ⁻ⁿ v∥≤ cλ ⁿ∥v∥ for v ∈ E ^u(x) and n ≥ 0.

The distributions E ^s and E ^u are called stable and unstable, respectively. One can show that they depend Hölder continuously in x. Clearly, the angle between stable and unstable subspaces is bounded away from zero in x.

Using the classical Hadamard–Perron theorem, for each x ∈ M one can construct a local stable manifold V ^s(x) and a local unstable manifold V ^u(x) such that

(L1):

x ∈ V ^{s, u}(x) and T _x V ^{s, u}(x) = E ^{s, u}(x);

(L2):

f(V ^s(x)) ⊂ V ^s(f(x)) and f ⁻¹(V ^u(x)) ⊂ V ^u(f ⁻¹(x)).

Furthermore, define the global stable manifold W ^s(x) and the global unstable manifold W ^u(x) by

$$\displaystyle \begin{aligned} W^s(x)=\bigcup_{n\ge 0}f^{-n}(V^s(f^n(x))), \quad W^u(x)=\bigcup_{n\ge 0}f^n(V^u(f^{-n}(x))). \end{aligned}$$

These sets have the following properties:

(G1):

they are smooth submanifolds;

(G2):

they are invariant under f, that is, f(W ^{s, u}(x)) = W ^{s, u}(f(x));

(G3):

they are characterized as follows:

$$\displaystyle \begin{aligned} \begin{aligned} W^s(x)&=\{y\in M: d(f^n(y),f^n(x))\to 0, \, n\to\infty\},\\ W^u(x)&=\{y\in M: d(f^n(y),f^n(x))\to0, \, n\to-\infty \}; \end{aligned} \end{aligned}$$

(G4):

they integrate the stable and unstable distributions, that is, E ^{u, s}(x) = T _x W ^{u, s}(x).

It follows that W ^s(x) and W ^u(x) form two uniformly transverse f-invariant continuous stable and unstable foliations W ^s and W ^u with smooth leaves. In general, the leaves of these foliations depend only continuously on x.³

Any sufficiently small perturbation in the C ¹ topology of an Anosov diffeomorphism is again an Anosov diffeomorphism. Hence, Anosov diffeomorphisms form an open set in the space of C ¹ diffeomorphisms of M.

There are very few particular examples of Anosov diffeomorphisms, namely

• 1. A linear hyperbolic automorphism of the n-torus given by an n × n-matrix A = (a _ij) whose entries a _ij are integers, $\det A=1$ or − 1, and all eigenvalues |λ|≠1;

• 2. The Smale automorphism of a compact factor of some nilpotent Lie group (see [67] and also [39]).

A topologically transitive C ² Anosov diffeomorphism f preserving a smooth measure μ is ergodic, and if f is topologically mixing, then it is a Bernoulli diffeomorphisms with respect to μ. The Bernoulli property was established by Bowen [15], and a much more general result is given by Statement 4 of Theorem 2.

A compact invariant subset Λ ⊂ M is called hyperbolic if for every x ∈ Λ the tangent space at x admits an invariant splitting as described above. For each x ∈ Λ one can construct local stable V ^s(x) and unstable V ^u(x) manifolds which have Properties (L1) and (L2).

A hyperbolic set Λ is called locally maximal if there exists a neighborhood U of Λ with the property that given a compact invariant set Λ ^′⊂ U, we have that Λ ^′⊂ Λ. In this case

$$\displaystyle \begin{aligned} \varLambda=\bigcap_{n\in\mathbb{Z}}\,f^n(U). \end{aligned}$$

Locally maximal hyperbolic sets can be characterized as having local direct product structure, that is, given two points x, y ∈ Λ, which are sufficiently close to each other, the intersection [x, y] = V ^s(x) ∩ V ^u(y) lies in Λ. If g is a small perturbation in the C ¹ topology of a diffeomorphism f with a locally maximal hyperbolic set Λ _f, then g possesses a locally maximal hyperbolic set Λ _g that lies in a small neighborhood of Λ _f.

A diffeomorphism f is called an Axiom A diffeomorphism if its non-wandering set Ω(f) is a locally maximal hyperbolic set.

The Spectral Decomposition Theorem claims (see [39]) that the set Ω(f) of an Axiom A diffeomorphism f can be decomposed into finitely many disjoint closed f-invariant locally maximal hyperbolic sets, Ω(f) = Λ ₁ ∪⋯ ∪ Λ _m such that f|Λ _i is topologically transitive. Moreover, for each i there exists a number n _i and a set A _i ⊂ Λ _i such that the sets f ^k(A _i) are disjoint for 0 ≤ k < n _i, their union is the set $\varLambda _i,\, f^{n_i}(A_i)=A_i$, and the map $f^{n_i}|A_i$ is topologically mixing.

2.2 Nonuniform Hyperbolicity

It originated in the work of Pesin [49,50,51]; see also the books [7, 8] for a sufficiently complete description of the modern state of the theory.

A diffeomorphism f of a compact Riemannian manifold M is non-uniformly hyperbolic if there are a measurable df-invariant decomposition of the tangent space T _x M = E ^s(x) ⊕ E ^u(x) and measurable positive functions ε(x), c(x), k(x) and λ(x) < 1 such that for almost every x ∈ M (here $\angle (S_1,S_2)$ denotes the angle between subspaces S _j):

• 1. ∥df ⁿ v∥≤ c(x)λ(x)ⁿ∥v∥ for v ∈ E ^s(x), n ≥ 0;

• 2. ∥df ⁻ⁿ v∥≤ c(x)λ(x)ⁿ∥v∥ for v ∈ E ^u(x), n ≥ 0;

• 3. $\angle (E^s(x),E^u(x))\ge k(x)$;

• 4. c(f ^m(x)) ≤ e ^ε(x)|m| c(x), k(f ^m(x)) ≥ e ^−ε(x)|m| k(x), λ(f ^m(x)) = λ(x), $m\in \mathbb {Z}$.

The last property means that the rates of contraction and expansion (given by λ(x)) are constant along the trajectory and the estimates in (1) and (2) can deteriorate with a rate which, while exponential, has a sufficiently small exponent.

Non-uniform hyperbolicity can also be expressed in more “practical” terms using the Lyapunov exponent of μ:

$$\displaystyle \begin{aligned} \chi(x,v)=\limsup_{n\to\infty}\frac 1n\log\|df^n_xv\|, \, x\in M, \, v\in T_xM. \end{aligned}$$

This means that for all sufficiently large n and a sufficiently small ε,

$$\displaystyle \begin{aligned} \|df^n_xv\|\sim\exp (\chi(x,v)\pm\varepsilon)n. \end{aligned}$$

If χ(x, v) > 0, the differential asymptotically expands v with some exponential rate, and if χ(x, v) < 0, the differential asymptotically contracts v with some exponential rate.

Therefore, f is non-uniformly hyperbolic if for almost every trajectory with respect to μ, the Lyapunov exponent χ(x, v) is not equal to zero for every vector v; in this case the measure μ is called hyperbolic. In other words,

$$\displaystyle \begin{aligned} E^s(x)=E^s_f(x)=\{v\in T_xM:\chi(x,v)<0\}, \quad E^u(x)=E^u_f(x)=E^s_{f^{-1}}(x). \end{aligned}$$

Nonuniform hyperbolicity is equivalent to the fact that Lyapunov exponents of f are nonzero almost everywhere in M (i.e., the smooth invariant measure for f is hyperbolic)—the phenomenon known as the Anosov rigidity. One can show that f is an Anosov diffeomorphism if:

• 1. the Lyapunov exponents for f are nonzero at every point x ∈ M, see [33, 45];

• 2. the Lyapunov exponents for f are nonzero on a set of total measure one, i.e., on a set that has full measure with respect to any invariant measure, see [23, 24].

If μ is a hyperbolic measure, then for almost every x ∈ M one can construct local stable and unstable manifolds V ^s(x) and V ^u(x). They depend measurably on x, in particular, their sizes can be arbitrarily small.

An example of a diffeomorphism with nonzero Lyapunov exponents was constructed by Katok [36]. Starting with a hyperbolic automorphism of the 2-torus, he used the slow-down procedure in a neighborhood of a hyperbolic fixed point p to turn p into an indifferent fixed point. In particular, the Lyapunov exponents at p are all zero. Katok used this example as a starting point in his construction of area preserving C ^∞ diffeomorphisms with nonzero Lyapunov exponents on compact surfaces. This result was extended by Dolgopyat and Pesin [31] who showed that any compact manifold of dimension ≥2 admits a volume preserving C ^∞ diffeomorphism with nonzero Lyapunov exponents.

2.3 Partial Hyperbolicity

It originated in the work of Brin and Pesin [18] and of Pugh and Shub [34]; see also the book [52] for a sufficiently complete exposition of the core of the theory.

A diffeomorphism f of a compact Riemannian manifold M is called partially hyperbolic if for each x ∈ M there is a continuous df-invariant decomposition of the tangent space T _x M = E ^s(x) ⊕ E ^c(x) ⊕ E ^u(x) and constants c ₁, c ₂, c ₃, c ₄ > 0, λ ₁ < μ ₁ ≤ μ ₂ < λ ₂, μ ₁ ≤ 1 such that for each x ∈ M and n ≥ 0:

• 1. $\| d_xf^nv\|\le c_1\lambda _1^n\|v\|$ for v ∈ E ^s(x);

• 2. $\| d_xf^nv\|\ge c_2\lambda _2^n\|v\|$ for v ∈ E ^u(x);

• 3. $c_4\mu _1^n\|v\|\le \| d_xf^nv\|\le c_3\mu _2^n\|v\|$ for v ∈ E ^c(x).

The distributions E ^s, E ^u, and E ^c are called stable, unstable and central, respectively. They depend continuously in x.⁴ Clearly, the angle between any two subspaces E ^s(x), E ^u(x) and E ^c(x) is bounded away from zero uniformly in x.

Any sufficiently small perturbation in the C ¹ topology of a partially hyperbolic diffeomorphism is again a partially hyperbolic diffeomorphism. Hence, partially hyperbolic diffeomorphisms form an open set in the space of C ¹ diffeomorphisms of M.

The stable and unstable distributions E ^s and E ^u can be integrated to continuous foliations W ^s and W ^u, respectively, with smooth leaves. The central distribution may or may not be integrable.

Some well-known examples of partially hyperbolic diffeomorphisms are (1) a direct product of an Anosov diffeomorphism with the identity map of a manifold; (2) a group extension over an Anosov diffeomorphism; (3) the time-1 map of an Anosov flow.

A compact invariant subset Λ ⊂ M is called partially hyperbolic if the restriction f|Λ is partially hyperbolic in the above sense. For each x ∈ Λ, one can construct local stable V ^s(x) and unstable V ^u(x) manifolds.

3 Markov Partitions

3.1 Definition of Markov Partitions

Let Λ be a locally maximal hyperbolic set for a diffeomorphism f of a compact smooth Riemannian manifold M. From now on we assume that f|Λ is topologically mixing. The general case can be easily reduced to this one by using the Spectral Decomposition Theorem.

A non-empty closed set R ⊂ Λ is called a rectangle if

• $\operatorname {\mathrm {diam}} R\le \delta$ (where δ > 0 is sufficiently small);

• $R=\overline {\text{int}\, R}$ where int R is defined in the relative topology in R;

• [x, y] ∈ R whenever x, y ∈ R.⁵

A rectangle R has direct product structure that is given x ∈ R, there exists a homeomorphism ⁶

$$\displaystyle \begin{aligned} \theta\colon R\to R\cap V^{(s)}(x)\times R\cap V^{(u)}(x). \end{aligned}$$

One can show that both θ and θ ⁻¹ are Hölder continuous. A finite cover $\mathcal {R}=\{R_1,\dots , R_p\}$ of Λ by rectangles R _i, i = 1, …, p is called a Markov partition for f if

• 1. int R _i ∩int R _j = ∅ unless i = j;

• 2. for each x ∈int R _i ∩ f ⁻¹(int R _j) we have

  $$\displaystyle \begin{aligned} f (V^s(x)\cap R_i)\subset V^s(f(x))\cap R_j, \quad f (V^u(x)\cap R_i)\supset V^u(f(x))\cap R_j. \end{aligned}$$

These relations are called the Markov property of the Markov partition. We stress that despite the name a Markov partition $\mathcal {R}$ is a cover of Λ which is almost a partition: any two elements of the cover can intersect only along their boundaries.

3.2 Symbolic Models

A Markov partition $\mathcal {R} =\{R_1,\dots , R_p\}$ generates a symbolic model of f|Λ by a finite Markov shift or a subshift of finite type (Σ _A, σ), where Σ _A is the set of two-sided infinite sequences of numbers {1, …, p}, which are admissible with respect to the transfer matrix of the Markov partition A = (a _ij) (i.e., a _ij = 1 if int R _i ∩ f ⁻¹(int R _j)≠∅, and a _ij = 0 otherwise). Namely, define

$$\displaystyle \begin{aligned} R^{(u)}_{i_{0}\dots i_n}=\bigcap_{j=0}^nf^{-j}(R_{i_j}),\quad R^{(s)}_{i_{-n}\dots i_{-1}}=\bigcap_{j=-1}^{-n}f^{-j} (R_{i_j}), \end{aligned}$$

$$\displaystyle \begin{aligned} R_{i_{-n}\dots i_n}=R^{(s)}_{i_{-n}\dots i_{-1}}\cap R^{(u)}_{i_{0}\dots i_n}. \end{aligned}$$

Now we define the coding map χ: Σ _A → Λ by

$$\displaystyle \begin{aligned} \chi (\dots, i_{-n}, \dots, i_{0}, \dots i_n ,\dots) =\bigcap_ {n\ge 0}R_{i_{-n}\dots i_n}. \end{aligned}$$

Note that the maps f and σ are conjugate via the coding map χ, i.e., f ∘ χ = χ ∘ σ. The map χ is Hölder continuous and injective on the set of points whose trajectories never hit the boundary of any element of the Markov partition.

For any points ω = (…, i ₋₁, i ₀, i ₁, … ) ∈ Σ _A and $\omega ^{\prime } =(\dots , i^{\prime }_{-1},i^{\prime }_0,i^{\prime }_1,\dots )\in \varSigma _A$ with the same past (i.e., $i^{\prime }_j=i_j$ for any j ≤ 0) we have that χ(ω ^′) ∈ V ^(u)(x) ∩ R(x), where x = χ(ω) and R(x) is the element of a Markov partition containing x. Similarly, for any point $\omega ^{\prime \prime }=(\dots , i^{\prime \prime }_{-1}, i^{\prime \prime }_0, i^{\prime \prime }_1,\dots )\in \varSigma _A$ with the same future as ω (i.e., $i^{\prime \prime }_j=i_j$ for any j ≥ 0) we have that χ(ω ^′′) ∈ V ^(s)(x) ∩ R(x). Thus, the set V ^(u)(x) ∩ R(x) can be identified via the coding map χ with the cylinder $C_{i_{0}}^+$ in the space $\varSigma _A^+$ of “positive” one-sided infinite sequences of numbers {1, …, p} and the set V ^(s)(x) ∩ R(x) can be identified via the coding map χ with the cylinder $C_{i_{0}}^-$ in the space $\varSigma _A^-$ of “negative” one-sided infinite sequences of numbers {1, …, p}.

3.3 Sinai’s Construction of Markov Partitions

I outline here a construction of Markov partition from [59] (see also [27]). For simplicity, I only consider Anosov diffeomorphisms of the two-dimensional torus, in which case the geometry of the construction is rather simple and it produces a partition whose elements are connected subsets with non-empty interior. In the multi-dimensional case the requirement that partition elements are connected cannot be ensured unless one allows partitions with countable number of elements. For the construction of Markov partitions for general Axiom A maps I refer the reader to the works of Bowen [14, 15].⁷

Let f be an Anosov diffeomorphism of the two dimensional torus $\mathbb {T}^2$. Fix ε > 0. We shall construct a Markov partition with diameter of elements ≤ ε. It suffices to do so for some power n of f. Indeed, if $\mathcal {R}$ is a Markov partition for f ⁿ, then $\bigcap _{k=-n}^nf^k\mathcal {R}$ is a Markov partition for f.

For points in the torus, local stable and unstable manifolds are smooth curves which are called stable and unstable curves. In the course of our construction every rectangle R is a closed connected subset of the torus. Its boundary ∂R is the union of four curves, two of which are stable and the other two are unstable. The union of stable curves forms the stable boundary ∂ ^s R of R while the union of unstable curves forms the unstable boundary ∂ ^u R of R. For every x ∈ R we denote by $\gamma ^s_R(x)$ (respectively, $\gamma ^u_R(x)$) the full length stable (respectively, unstable) curve through x, i.e., the segment of stable (unstable) curve whose endpoints lie on the unstable (stable) boundary of R.

Let us now fix δ > 0, n > 0, and let λ ∈ (0, 1) be the constant in the definition of Anosov diffeomorphisms. A collection of rectangles $\tilde {\mathcal {R}}=\{\tilde {R}_1,\dots ,\tilde {R}_p\}$ is called a sufficient (n, δ)-collection if

• 1. $\bigcup _{j=1}^p\tilde {R}_j=\mathbb {T}^2$;

• 2. $\operatorname {\mathrm {diam}}\tilde {R}_j\le \delta$, j = 1, …, p;

• 3. given a rectangle $\tilde {R}_j$, one can find two subcollections of rectangles $\{\tilde {R}_{i_1},\dots ,\tilde {R}_{i_k}\}$ and $\{\tilde {R}_{s_1},\dots ,\tilde {R}_{s_t}\}$ such that

  • (a) $f^n(\tilde {R}_j)\subset \bigcup _{\ell =1}^k\tilde {R}_{i_\ell }$ and $f^{-n}(\tilde {R}_j)\subset \bigcup _{\ell =1}^t\tilde {R}_{s_\ell }$;

  • (b) for every $x\in \tilde {R}_j$, if f ⁿ(x) lies in some rectangle $\tilde {R}_{i_\ell }$ from the first subcollection, then $f^n(\gamma ^s_{\tilde {R}_j}(x))\subset \gamma ^s_{\tilde {R}_{i_\ell }}(f^n(x))$;

  • (c) for every $x\in \tilde {R}_j$, if f ⁻ⁿ(x) lies in some rectangle $\tilde {R}_{s_\ell }$ from the second subcollection, then $f^{-n}(\gamma ^u_{\tilde {R}_j}(x))\subset \gamma ^u_{\tilde {R}_{s_\ell }}(f^{-n}(x))$.

It is not difficult to show that given δ > 0 and a large enough n > 0, there is a sufficient (n, δ)-collection $\tilde {\mathcal {R}}$.

Our goal is to slightly “extend” each rectangle of a given sufficient (n, δ)-collection $\tilde {\mathcal {R}}$ in both the stable and unstable directions to ensure the Markov property in these directions. This will produce a cover of the torus by rectangles, which is a Markov cover.

To this end fix a rectangle $\tilde {R}_j\in \tilde {\mathcal {R}}$ and consider two subcollections $\{\tilde {R}_{i_1},\dots ,\tilde {R}_{i_k}\}$ and $\{\tilde {R}_{s_1},\dots ,\tilde {R}_{s_t}\}$, which have the properties with respect to $\tilde {R}_j$ mentioned above. We refer to the union of the (un)stable boundaries of all rectangles in the subcollection as the (un)stable boundary of the subcollection.

Consider the set $f^n(\partial ^u\tilde {R}_j)$. It consists of two unstable curves $\gamma ^u_1=f^n(\tilde {\gamma }^u_1)$ and $\gamma ^u_2=f^n(\tilde {\gamma }^u_2)$ where the curves $\tilde {\gamma }^u_1$ and $\tilde {\gamma }^u_2$ form the unstable boundary of $\tilde {R}_j$. Denote by A ₁, B ₁ and A ₂, B ₂ the endpoints of these curves. We refer to A ₁ and A ₂ as the left endpoints of $\gamma ^u_1$ and $\gamma ^u_2$, respectively, and to B ₁ and B ₂ as the right endpoints of $\gamma ^u_1$ and $\gamma ^u_2$, respectively. If $\tilde {R}_m$ is a rectangle from the subcollection that contains A ₁, then it also contains A ₂.

Consider now the full length unstable curve $\gamma ^u_{\tilde {R}_m}(A_1)$. It intersects the stable boundary of $\tilde {R}_m$ at two points, C ₁ and D ₁. One of them, say C ₁, lies on the “left” of A ₁ and does not belong to the curve $\gamma ^u_1$ (while the other one does). We now extend the curve $\tilde {\gamma }^u_1$ to the left by adding the segment f ⁻ⁿ(A ₁ C ₁) to its left point f ⁻ⁿ(A ₁). It is easy to see that the length of this segment does not exceed δλ ⁻ⁿ. Similarly, the full length unstable curve $\gamma ^u_{\tilde {R}_m}(A_2)$ intersects the stable boundary of $\tilde {R}_m$ at two points, C ₂ and D ₂ of which C ₂ lies on the “left” of A ₂ and does not belong to the curve $\gamma ^u_2$. We again extend the curve $\tilde {\gamma }^u_2$ to the left by adding the segment f ⁻ⁿ(A ₂ C ₂) to its left point f ⁻ⁿ(A ₂). The length of this segment does not exceed δλ ⁻ⁿ. As a result we obtain a new rectangle $\tilde {R}_j^l$, which is a left extension of the rectangle $\tilde {R}_j$. The left stable boundary of this new rectangle is the stable curve f ⁻ⁿ(C ₁ C ₂).

In a similar manner we can extend the rectangle $\tilde {R}_j$ to the right and obtain a new rectangle which has the Markov property in the unstable direction with respect to the subcollection associated to $\tilde {R}_j$. Continuing in this way, we obtain a new cover $\tilde {\mathcal {R}}^{(1)}=\{\tilde {R}_1^{(1)},\dots ,\tilde {R}_p^{(1)}\}$ which has the Markov property in the unstable direction with respect to the cover $\tilde {R}$. Note that the diameter of each rectangle in the new cover in the unstable direction does not exceed δ + δλ ⁿ, while the diameter in the stable direction does not exceed δ. Proceeding by induction we obtain a sequence of covers $\tilde {\mathcal {R}}^{(q)}=\{\tilde {R}_1^{(q)},\dots ,\tilde {R}_p^{(q)}\}$ such that

• 1. rectangles in the cover $\tilde {\mathcal {R}}^{(q)}$ have the Markov property in the unstable direction with respect to the rectangles in the cover $\tilde {\mathcal {R}}^{(q-1)}$;

• 2. the diameter of each rectangle in the cover $\tilde {\mathcal {R}}^{(q)}$ in the unstable direction does not exceed

  $$\displaystyle \begin{aligned} \frac{1-\lambda^{-(q+1)n}}{1-\lambda^{-n}}2\delta, \end{aligned}$$

  while the diameter in the stable direction does not exceed δ;

• 3. for each q > 0 and j = 1, …, p we have that $\tilde {R}_j^{(q)}\subset \tilde {R}_j^{(q-1)}$ and the rectangle $\tilde {R}_j^{(q)}$ is a connected subset.

One can show that the sets $R_j^+=\bigcup _{q>0}\tilde {R}_j^{(q)}$ forms a cover $\mathcal {R}^+$, which has the Markov property in the unstable direction and whose diameter in the unstable direction does not exceed $\frac {1}{1-\lambda ^{-n}}2\delta$, while the diameter in the stable direction does not exceed δ. Furthermore each rectangle in this cover is a connected subset. Replacing f ⁿ with f ⁻ⁿ and repeating the above argument, we can slightly extend each element of the cover $\mathcal {R}^+$ in the stable direction to obtain a new cover $\mathcal {R}=(\mathcal {R}^+)^-$ which has the Markov property in both the unstable and stable directions and whose diameter does not exceed $\frac {1}{1-\lambda ^{-n}}2\delta$. Moreover, each rectangle in this cover is a connected subset. One can now subdivide the rectangles of the cover to obtain the desired Markov partition.

4 SRB Measures I: Hyperbolic Attractors

4.1 Topological Attractors

Let f be a diffeomorphism of a compact smooth Riemannian manifold M. A compact invariant subset Λ ⊂ M is called a topological attractor for f if there is an open neighborhood U of Λ such that $\overline {f(U)}\subset U$ and

$$\displaystyle \begin{aligned} {\varLambda}=\bigcap_{n\ge 0}f^n(U). \end{aligned}$$

The set U is said to be a trapping region or a basin of attraction for Λ. The maximal open set with this property is called the topological basin of attraction for Λ. It follows immediately from the definition of the attractor that Λ is locally maximal, i.e., is the largest invariant set in U.

4.2 Natural and Physical Measures

Starting with the volume m in U, consider its evolution under the dynamics, i.e., the sequence of measures

$$\displaystyle \begin{aligned} m_n=\frac 1n\sum_{k=0}^{n-1}\,f_*^km. \end{aligned} $$

(3)

This sequence is compact in the week^∗ topology, and hence has a convergent subsequence $m_{n_k}$. Clearly, the limit of $m_{n_k}$ is supported on Λ and by the Bogolubov–Krylov theorem, it is an f-invariant measure called a natural measure for f. In general, the measure μ may be quite trivial—just consider the point mass at an attracting fixed point.

Given a measure μ on an attractor Λ, define its basin of attraction B(μ) as the set of μ-generic points x ∈ U, i.e., points such that for every continuous function φ on Λ,

$$\displaystyle \begin{aligned} \lim_{n\to\infty}\,\frac 1n\sum_{k=0}^{n-1}\varphi(f^k(x))=\int_\varLambda\, \varphi\,d\mu. \end{aligned} $$

(4)

A natural measure μ on the attractor Λ is a physical measure if its basin of attraction B(μ) has positive volume. An attractor with a physical measure is called a Milnor attractor.

4.3 SRB Measures

Let μ be a hyperbolic invariant measure supported on Λ. Using results of nonuniform hyperbolicity theory one can construct for almost every x ∈ Λ a local stable V ^s(x) manifold and a local unstable V ^u(x) manifold. It is easy to show that for such points x we have V ^u(x) ⊂ Λ and consequently, W ^u(x) ⊂ Λ (recall that W ^u(x) is the global unstable manifold through x). On the other hand, the intersection of Λ with stable manifolds of its points is a Cantor set.

There is a collection {Λ _ℓ}_ℓ≥1 of nested subsets of Λ that exhaust Λ (mod 0) such that local stable V ^s(x) and unstable V ^u(x) manifolds depend continuously on x ∈ Λ _ℓ. In particular, their “sizes” are bounded uniformly from below. Given x ∈ Λ _ℓ, set

$$\displaystyle \begin{aligned} Q_\ell(x)=\bigcup_{y\in B(x,r_\ell)\cap\varLambda_\ell}\, V^u(y), \end{aligned}$$

where r _ℓ > 0 is sufficiently small, and let ξ _ℓ be the partition of Q _ℓ(x) by local unstable leaves V ^u(y), y ∈ B(x, r _ℓ) ∩ Λ _ℓ. Denote by μ ^u(y) the conditional measure on V ^u(y) generated by μ with respect to the partition ξ _ℓ and by m ^u(y) the leaf-volume on V ^u(y) generated by the Riemannian metric.⁸

A hyperbolic invariant measure μ on Λ is called an SRB measure (after Sinai, Ruelle and Bowen) if for every ℓ with μ(Λ _ℓ) > 0, almost every x ∈ Λ _ℓ and almost every y ∈ B(x, r _ℓ) ∩ Λ _ℓ the measures μ ^u(y) and m ^u(y) are equivalent. The idea of describing an invariant measure by its conditional probabilities on the elements of a continuous partition goes back to the classical work of Kolmogorov and later work of Dobrushin on random fields, [30] (see also [62]).

The following result describes the density d ^u(x, y) of the conditional measure μ ^u(x) with respect to the leaf-volume m ^u(x).

Theorem 1 (Sinai [62], Pesin and Sinai [53], Ledrappier [41])

For almost every x the density d ^u(x, y) is given by d ^u(x, y) = ρ ^u(x)⁻¹ ρ ^u(x, y) where for y ∈ V ^u(x)

$$\displaystyle \begin{aligned} \rho^u(x,y)=\prod_{k=0}^\infty \frac{\mathit{\text{Jac}}(df|E^u(f^{-k}(y)))}{\mathit{\text{Jac}}(df|E^u(f^{-k}(x)))} \end{aligned} $$

(5)

and

$$\displaystyle \begin{aligned} \rho^u(x)=\int_{V^u(x)}\rho^u(x,y)\,dm^u(x)(y) \end{aligned} $$

(6)

is the normalizing factor.

The Eq. (5) can be viewed as an analog of the famous Dobrushin–Lanford–Ruelle equation in statistical physics, see [40] and [62].

Using results of nonuniform hyperbolicity theory one can obtain a sufficiently complete description of ergodic properties of SRB measures.

Theorem 2

Let f be a C ^{1+ 𝜖} diffeomorphism of a compact smooth manifold M with an attractor Λ and let μ be an SRB measure on Λ. Then

• 1. Λ =⋃_i≥0 Λ _i , Λ _i ∩ Λ _j = ∅;

• 2. μ(Λ ₀) = 0 and μ(Λ _i) > 0 for i > 0;

• 3. f|Λ _i is ergodic for i > 0;

• 4. for each i > 0 there is n _i > 0 such that $\varLambda _i=\bigcup _{j=1}^{n_i}\varLambda _{ij}$ where f(Λ _ij) = Λ _{i j+1} , $f(\varLambda _{n_i1})=\varLambda _{i1}$ and $f^{n_i}|\varLambda _{i1}$ is Bernoulli.

For smooth measures this theorem was proved by Pesin in [50] and its extension to SRB measures was obtained by Ledrappier in [41] (see also [7, 8]). We note that the proof of the Bernoulli property in Statement 4 of the theorem is based on the work of Ornstein and Weiss who established the Bernoulli property for geodesic flows on compact manifolds of negative curvature, [48].

SRB measures admit the following characterization.

Theorem 3

Let μ be a measure on Λ of positive entropy. Then μ is an SRB measure if and only if its entropy is given by the entropy formula :

$$\displaystyle \begin{aligned} h_\mu(f)=\int_\varLambda\,\sum_{\chi_i(x)>0}\,\chi_i(x)\,d\mu(x). \end{aligned}$$

For smooth measures (which are particular cases of SRB measures) the entropy formula was proved by Pesin [50] (see also [7]) and its extension to SRB measures was obtained by Ledrappier and Strelcyn [42]. The fact that a hyperbolic measure satisfying the entropy formula is an SRB measure was shown by Ledrappier [41].⁹

It follows from Theorem 3 that any ergodic SRB measure is a physical measure (any ergodic component of an SRB measure is an ergodic SRB measure). In particular, if an attractor supports an ergodic SRB measure then it is a Milnor attractor.

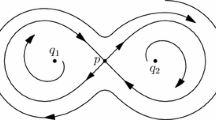
The limit measures for the sequence of measures (3) are natural candidates for SRB measures. The classical eight figure map ¹⁰ is an example of a diffeomorphism f with an attractor Λ such that the sequence of measures (3) converges to a hyperbolic measure μ whose basin of attraction has full volume, however μ is not an SRB measure for f.

4.4 Uniformly Hyperbolic Attractors

An attractor Λ is hyperbolic if it is a uniformly hyperbolic set for f.¹¹ The unstable subspace E ^u is integrable: given x ∈ Λ, the global unstable manifold W ^u(x) lies in Λ, and hence the attractor is the union of the global unstable manifolds of its points, which form a lamination of Λ. On the other hand the intersection of Λ with stable manifolds of its points may be a Cantor set.

Theorem 4

Assume that the map f|Λ is topologically transitive. Then the sequence of measures (3) converges to a unique SRB measure on Λ and so does the sequence of measures (7) (independently of the starting point x).

This theorem was proved by Sinai, [60] for the case of Anosov diffeomorphisms, Bowen [15], and Ruelle [56] extended this result to hyperbolic attractors, and Bowen and Ruelle [17] constructed SRB measures for Anosov flows.

Well-known examples of hyperbolic attractors are the DA (derived from Anosov) attractor and the Smale–Williams solenoid (see [39] for definitions and details).

In the following two subsections I will outline two different approaches to prove Theorem 4. The first approach was developed by Sinai in [60] and uses Markov partitions, while the second one deals with the sequence of measures (3) in a straightforward way and hence, is more general. In particular, it can be used to construct some special measures for partially hyperbolic attractors which do not allow Markov partitions; these are so called u-measures which are natural analog of SRB measures in this case, see [53] and Sect. 6. For simplicity of the exposition I only consider the case of Anosov diffeomorphisms, extension to hyperbolic attractors is not difficult.

4.5 First Proof of Theorem 4 (Sinai [60])

Let $\mathcal {R}$ be a Markov partition of sufficiently small diameter and let $\mathcal {R}^-=\bigvee _{n=0}^\infty f^{-n}\mathcal {R}$. One can show that the partition $\mathcal {R}^-$ has the following properties:

• 1. $f\mathcal {R}^-\ge \mathcal {R}^-$;

• 2. $\bigvee _{k=0}^\infty f^k\mathcal {R}^-$ is the trivial partition;

• 3. there is an r > 0 such that every element of the partition $\mathcal {R}^-$ is contained in a local stable manifold and contains a ball in this manifold of radius r.

Given x ∈ Λ, denote by $C_{\mathcal {R}^-}(x)$ the element of the partition $\mathcal {R}^-$ containing x. For every n > 0 we have that $f^n(C_{\mathcal {R}^-}(x))=C_{f^n(\mathcal {R}^-)}(f^n(x))$ and that f ⁿ is a bijection between $C_{\mathcal {R}^-}(x)$ and $C_{f^n(\mathcal {R}^-)}(f^n(x))$. Therefore, f ⁻ⁿ transfers the normalized leaf-volume on $C_{f^n(\mathcal {R}^-)}(f^n(x))$ to a measure on $C_{\mathcal {R}^-}(x)$ which we denote by μ _n. This measure is equivalent to the leaf-volume on $C_{\mathcal {R}^-}(x)$ and we denote by ρ _n(y) the corresponding density function, which is continuous. One can show that the sequence of functions ρ _n converges uniformly to a continuous function $\tilde \rho (y)=\tilde \rho _{C_{\mathcal {R}^-}(x)}(y)$, which can be viewed as the density function for a normalized measure $\tilde \mu _{C_{\mathcal {R}^-}(x)}$ on $C_{\mathcal {R}^-}(x)$. These measures have the following properties:

• 1. $\tilde \mu _{C_{\mathcal {R}^-}(x)}$ is equivalent to the leaf-volume on $C_{\mathcal {R}^-}(x)$;

• 2. for every measurable set $A\subset C^{\prime }_{\mathcal {R}^-}\subset C_{f^{-1}(\mathcal {R}^-)}$ the following Chapman–Kolmogorov relation holds:

  $$\displaystyle \begin{aligned} \tilde\mu(A|C_{f^{-1}(\mathcal{R}^-)})=\tilde\mu(A|C^{\prime}_{\mathcal{R}^-}) \tilde\mu(C^{\prime}_{\mathcal{R}^-}|C_{f^{-1}(\mathcal{R}^-)}); \end{aligned}$$

• 3. the measures $\tilde \mu$ are determined by Properties 1 and 2 uniquely.

One can now show that for any x ∈ M and any measurable subset A ⊂ M there is a limit

$$\displaystyle \begin{aligned} \mu(A) = \lim_{n\to\infty}\tilde\mu(A|C_{f^{-n}(\mathcal{R}^-)}(x)), \end{aligned}$$

which does not depend on x. The number μ(A) determines an invariant measure for f which is the desired SRB measure.

4.6 Second Proof of Theorem 4 (Pesin and Sinai, [53])

The way of constructing SRB measures on Λ based on the sequence of measures (3) can be viewed as being “from outside of the attractor”. There is another way to construct SRB measures “from within the attractor”. Fix x ∈ Λ and consider a local unstable leaf V = V ^u(x) at x. One can view the leaf-volume m ^u(x) on V ^u(x) as a measure on the whole of Λ. Consider the sequence of measures on Λ

$$\displaystyle \begin{aligned} \nu_n(x)=\frac 1n\sum_{k=0}^{n-1}\,f_*^km^u(x). \end{aligned} $$

(7)

We shall show that every limit measure for the sequence of measures (7) is an SRB-measure. In fact, every SRB-measure μ can be constructed in this way, i.e., it can be obtained as the limit measure for a subsequence of measures ν _n. Furthermore, if f|Λ is topologically transitive, then the sequence of measures (7) converges to μ and so does the sequence of measures (3).

We stress that in the definition of the sequence of measures (7) one can replace the local unstable manifold V ^u(x) with any admissible manifold, i.e., a local manifold passing through x and sufficiently close to V ^u(x) in the C ¹ topology.

Let μ be a limit measure of the sequence of measures (7) and let z be such that μ(B(z, r)) > 0 for every r > 0. Consider a rectangle R of size r > 0 containing z and its partition ξ into unstable local manifolds V ^u(y), y ∈ R. We identify the factor space R∕ξ with W = V ^s(z) ∩ Λ and we denote by U _n = f ⁿ(V ). Set

$$\displaystyle \begin{aligned} \begin{aligned} A_n&=\{y\in W\colon V^u(y)\cap U_n\ne\emptyset\}, \\ B_n&=\{y\in W\colon V^u(y)\cap \partial U_n\ne\emptyset\}, \\ C_n&=A_n\setminus B_n. \end{aligned} \end{aligned}$$

Note that C _n is a finite set, and we denote by δ _n the measure on W, which is the uniformly distributed point mass on C _n. If h is a continuous function on Λ with support in R, then

$$\displaystyle \begin{aligned} \begin{aligned} \int_\varLambda\,h\,d\nu_n&=\int_R\,h\,d\nu_n\\ &=\sum_{y\in A_n}\,\int_{V^u(z)\cap U_n}\,h\,d\nu_n\\ &=\sum_{y\in C_n}\,\int_{V^u(z)\cap U_n}\,h\,d\nu_n +\sum_{y\in B_n}\,\int_{V^u(z)\cap U_n}\,h\,d\nu_n\\ &=I^{(1)}_n+I^{(2)}_n. \end{aligned} \end{aligned}$$

One can show that $I^{(2)}_n\le \frac {C}{n}$ where C > 0 is a constant. One can further show that

$$\displaystyle \begin{aligned} \begin{aligned} I^{(1)}_n&=c_n\sum_{y\in C_n}\rho^u(f^n(x),y) \int_{V^u(y)}\,h(w)\rho^u(y,w)\,d\mu^u(w)\\ &=\int_Wc_n\rho^u(f^n(x),y)\rho^u(y)\,d\delta_n(y) \int_{V^u(y)}\,h(w)\frac{\rho^u(y,w)}{\rho^u(y)}\,d\mu^u(w), \end{aligned} \end{aligned}$$

where

$$\displaystyle \begin{aligned} c_n=\Bigl[\prod_{k=0}^{n-1}\text{Jac}(df|E^u(f^k(x)))\Bigr]^{-1} \end{aligned}$$

and ρ ^u(y) is given by (6).

It follows that for any subsequence n _ℓ →∞ for which the sequence of measures $\nu _{n_\ell }(x)$ converges to a measure μ on Λ, one has that μ is an SRB measure.

The above argument implies that μ(int R) > 0 and hence, the set

$$\displaystyle \begin{aligned} E=\bigcup_{n\in\mathbb{Z}}\,f^n(\text{int}\, R) \end{aligned}$$

is open and is an ergodic component of μ of positive measure (i.e., f|E is ergodic). In fact, every ergodic component of μ can be obtained in this way and hence, is open (mod 0). One can derive from here that there are at most finitely many SRB measures and if f|Λ is topological transitive, then there is only one SRB measure.

5 SRB Measures II: Chaotic Attractors

5.1 Chaotic Attractors: The Concept

An attractor Λ for a diffeomorphism f is chaotic if there is a natural measure that is hyperbolic, i.e., a measure with nonzero Lyapunov exponents (with some being positive and some being negative). In this case using results of nonuniform hyperbolicity theory one can show that for almost every x ∈ Λ there are a local stable V ^s(x) and unstable V ^u(x) manifolds. It is easy to see that for such points x we have V ^u(x) ⊂ Λ, so that the attractor contains all the unstable manifolds of its points.

5.2 Chaotic Attractors: Some Open Problems

• 1. Construct an example of a diffeomorphism f with an attractor Λ such that the volume m is a non-invariant hyperbolic measure for f (i.e., for almost every x ∈ U with respect to m and for every nonzero vector v ∈ T _x M the Lyapunov exponent χ(x, v)≠0) but the sequence of measures (3) converges to a measure μ on Λ for which the Lyapunov exponent χ(x, v) = 0 for almost every x ∈ U with respect to μ and for every nonzero vector v ∈ T _x M;

• 2. Construct an example of a diffeomorphism f with an attractor Λ such that for almost every x ∈ U with respect to volume m and for every nonzero vector v ∈ T _x M the Lyapunov exponent χ(x, v) = 0 but the sequence of measures (3) converges to a hyperbolic measure μ on Λ.

5.3 The Hénon Attractor

Consider the Hénon family of maps given by

$$\displaystyle \begin{aligned} H_{a,b}(x,y)=(1-ax^2+by,x). \end{aligned} $$

(8)

For a ∈ (0, 2) and sufficiently small b there is a rectangle in the plane, which is mapped by H _a,b into itself. It follows that H _a,b has an attractor—the Hénon attractor.

Benedicks and Carleson [9] developed a highly sophisticated techniques to describe the dynamics near the attractor. Building on this analysis, Benedicks and Young [10] established existence of SRB measures for the Hénon attractors.

Theorem 5

There exist ε > 0 and b ₀ > 0 such that for every 0 < b ≤ b ₀ one can find a set A _b ∈ (2 − ε, 2) of positive Lebesgue measure with the property that for each a ∈ A _b , the map H _a,b admits a unique SRB measure μ _a,b.

Wang and Young [71] introduced and studied some more general 2-parameter families of maps with one unstable direction to which the above result extends.

The underlying mechanism of constructing SRB measures in these systems is the work of Young [72] where she introduced a class of non-unformly hyperbolic diffeomorphisms f admitting a symbolic representation via a tower whose base A is a hyperbolic set with direct product structure and the induced map on the base admits a Markov extension. Assuming that the return time R to the base is integrable, one can show that there is an SRB measure.

As in the case of uniformly hyperbolic systems, the real power of a symbolic representation is not just to help prove existence of SRB-measures but to show the exponential decay of correlations, the Central Limit Theorem, etc. For the Hénon attractor, Benedicks and Young [11] showed that if for all T > 0 we have $\int R\,dm\le C\lambda ^T$ where C > 0, 0 < λ < 1 and the integral is taken over the set of points x ∈ A with R(x) > T, then f has the exponential decay of correlations for the class of Hölder continuous functions.

5.4 Chaotic Attractors: An Example

Let f be a diffeomorphism with an attractor Λ to be the Smale–Williams solenoid. f has an SRB measure on Λ. In a small ball B(p, r) around a fixed point p, the map f is the time-1 map of the linear system $\dot x = Ax$ of ODEs.¹² We wish to perturb f locally by slowing down trajectories near p. Define a map g to be the time-1 map for the following nonlinear system of ODEs inside B(p, r)

$$\displaystyle \begin{aligned} \dot x = \psi(x)Ax \end{aligned}$$

and set g = f outside of B(p, r). Here ψ(x) = ∥x∥^α for ∥x∥ < 2 and ψ(x) = 1 for $\|x\|\geqslant 2$.

Theorem 6 (Climenhaga, Dolgopyat, Pesin, [28])

The map g has an SRB-measure.

5.5 Chaotic Attractors: Constructing SRB-Measures

Consider the set S ⊂ U (U is a neighborhood of the attractor Λ) of points such that

• f(S) ⊂ S, i.e., S is forward invariant;

• there are two measurable cone families K ^s(x) = K ^s(x, E ₁(x), θ(x)) and K ^u(x) = K ^u(x, E ₂(x), θ(x)),¹³ which are invariant,¹⁴ i.e.,

  $$\displaystyle \begin{aligned} \overline{Df(K^u(x))}\subset K^u(f(x)), \quad \overline{Df^{-1}(K^s(f(x)))}\subset K^s(x) \end{aligned}$$

  and transverse, i.e., T _x X = E ₁(x) ⊕ E ₂(x).

Define

• $\lambda ^s(x)=\sup \{\log \|Df(v)\|\colon v\in K^s(x),\|v\|=1\}$—coefficient of contraction;

• $\lambda ^u(x)=\inf \{\log \|Df(v)\|\colon v\in K^u(x),\|v\|=1\}$—coefficient of expansion;

• $d(x)=\max \left (0, (\lambda ^s(x)-\lambda ^u(x)\right )$—defect of hyperbolicity;

• λ(x) = λ ^u(x) − d(x)—coefficient of effective hyperbolicity;

• $\alpha (x)=\angle (K^s(x),K^u(x))>0$—angle between the cones;

• $\rho _{\hat \alpha }(x)=\lim _{n\to \infty }\frac 1n\#\{0\le k<n\colon \alpha (f^k(x))<\hat \alpha \}$—average time the angle between the cones is below a given threshold $\hat \alpha >0$.

We further assume that for every x ∈ S,

(S1):

$\underline {\lim }_{n\to \infty }\frac 1n \sum _{k=0}^{n-1} \lambda (f^k(x)) > 0$;

(S2):

$\lim _{\bar \alpha \to 0}\rho _{\bar \alpha }(x) = 0$;

(S3):

$\overline {\lim }_{n\to \infty } \frac 1n \sum _{k=0}^{n-1} \lambda ^s(f^k(x)) < 0$.

Theorem 7 (Climenhaga, Dolgopyat, Pesin, [28])

Assume that the set S has positive volume. Then f possesses an SRB-measure.

In [70], Viana conjectured that if the set of all points with non-zero Lyapunov exponents for a C ^1+α diffeomorphism f has positive (in particular, full) volume (which is not necessarily invariant), then f admits an SRB measure. The above theorem provides some stronger conditions under which the conclusion of Viana’a conjecture holds. An affirmative solution of this conjecture for surface diffeomorphisms, under some general additional assumptions, is obtained in a recent work by Climenhaga, Luzzatto and Pesin [29]. It is conjectured that if Requirement (S1) is replaced with a stronger requirement that

$$\displaystyle \begin{aligned} \underline{\lim}_{n\to\infty}\frac 1n \sum_{k=0}^{n-1} \lambda(f^k(x))\ge\lambda \end{aligned}$$

for some λ > 0, then f possesses at most finitely many SRB-measures. In [55], F. Rodriguez Hertz, J. Rodriguez Hertz, Tahzibi and Ures showed that any topologically transitive surface diffeomorphism possesses at most one SRB measure.

6 SRB-Measures III: Partially Hyperbolic Attractors

6.1 Partially Hyperbolic Attractors

An attractor Λ is partially hyperbolic if f|Λ is uniformly partially hyperbolic, i.e., if the tangent space TΛ admits an invariant splitting

$$\displaystyle \begin{aligned} T\varLambda=E^s\oplus E^c\oplus E^u \end{aligned}$$

into strongly stable, central and strongly unstable subspaces, respectively, which satisfy conditions (1)–(3) in Sect. 2.3. The subspace E ^u is integrable: given x ∈ Λ, a local unstable leaf V ^u(x) lies in Λ, and hence so does the global strongly unstable manifolds W ^u. It follows that the attractor is the union of the global strongly unstable manifolds of its points, which form a lamination of Λ.

One can obtain an example of a partially hyperbolic attractor by considering the product map F = f ₁ × f ₂ where f ₁: M → M is a map possessing a uniformly hyperbolic attractor and f ₂: S ¹ → S ¹ is an isometry.

If f is a diffeomorphism possessing a uniformly (partially) hyperbolic attractor Λ = Λ _f then any sufficiently small perturbation g of f in the C ¹ topology possesses a uniformly (partially) hyperbolic attractor Λ _g that lies in a small neighborhood of Λ _f. This provides an open set of uniformly (partially) hyperbolic attractors in the spaces of C ¹ diffeomorphisms.

6.2 SRB-Measures on Partially Hyperbolic Attractors

Let Λ be a partially hyperbolic attractor for a diffeomorphisms f. A measure μ on Λ is a u-measure if for almost every x ∈ Λ, the conditional measure μ ^u(x) generated by μ on the global strongly unstable leaf W ^u(x) is absolutely continuous with respect to the leaf-volume m ^u(x). One can show that the Jacobian of the u-measure in the unstable direction is given by the formula (5). The following result shows that every partially hyperbolic attractor carries a u-measure. Its proof can be obtained by adjusting the argument in the second proof of Theorem 4 to the partial hyperbolicity setting.

Theorem 8 (Pesin, Sinai, [53])

The following statements hold:

• 1. Any limit measure μ of the sequence of measures (3) is a u-measure on Λ;

• 2. Any limit measure μ of the sequence of measures (7) is a u-measure on Λ.

Unlike the case of hyperbolic attractors, the topological transitivity of f|Λ (or even topological mixing) does not guarantee uniqueness of u-measures.¹⁵

Every SRB-measure on a partially hyperbolic attractor Λ is a u-measure but not every u-measure is an SRB-measure. We say that a u-measure ν has negative (positive) central exponents if there is an invariant subset A ⊂ Λ with ν(A) > 0 such that the Lyapunov exponents χ(x, v) < 0 (respectively, χ(x, v) > 0) for every x ∈ A and every nonzero vector v ∈ E ^c(x). A u-measure with negative (positive) central exponents is an SRB-measure.

Below is a result that guarantees existence and uniqueness of SRB-measures for partially hyperbolic attractors with negative central exponents. It requires existence of at least one u-measure with negative central exponents and a strong transitive condition. A detailed discussion of these requirements can be found in [22].

Theorem 9 (Bonatti, Viana, [13]; Burns, Dolgopyat, Pollicott, Pesin, [22])

Let f be a C ^{1+ 𝜖} diffeomorphism of a compact smooth manifold M with a partially hyperbolic attractor Λ. Assume that:

• 1. there exists a u-measure ν with negative central exponents;

• 2. for every x ∈ Λ the global strongly unstable manifold W ^u(x) is dense in Λ.

Then ν is the unique u-measure for f and is the unique hyperbolic SRB-measure for f whose basin of attraction B(ν) has full volume in the topological basin of attraction of Λ.

The case of positive central exponents is more difficult and existence of SRB-measures can be established under the stronger requirements that (see [69]):

• 1. there is a unique u-measure ν with positive central exponents on a subset A ⊂ Λ of full measure;

• 2. for every x ∈ Λ the global strongly unstable manifold W ^u(x) is dense in Λ.

6.3 Dominated Splitting and SRB-Measures

The key tool in constructing SRB-measures in the uniform hyperbolic setting is presence of a dominated splitting, i.e., a decomposition of the tangent bundle T _x M = E ₁(x) ⊕ E ₂(x) for every x ∈ Λ such that

• 1. E ₁(x) and E ₂(x) depend continuously on x;

• 2. $\measuredangle (E_1(x),E_2(x))$ is bounded away from 0;

• 3. there is 0 < λ < 1 such that

  $$\displaystyle \begin{aligned} \|Df|E_1(x)\|<\lambda, \quad \|Df|E_1(x)\|\cdot \|Df^{-1}|E_2(f(x))\|<\lambda. \end{aligned}$$

Construction of SRB measures for systems with dominated splitting was effected in various situations. Here is an (incomplete) list:

• (Alves, Bonatti, Viana, [3]) there is a subset S ⊂ U of positive volume and ε > 0 such that for every x ∈ S,

  $$\displaystyle \begin{aligned} \lim\sup_{n\to\infty}\frac 1n\sum_{j=1}^n\,\log\|df^{-1}|E_2(f^j(x))\|<-\varepsilon. \end{aligned}$$

  In this case, in addition one can have no more than finitely many distinct SRB measures.

• (Alves, Dias, Luzzatto, Pinheiro, [4]) there is a subset S ⊂ U of positive volume and ε > 0 such that for every x ∈ S,

  $$\displaystyle \begin{aligned} \lim\inf_{n\to\infty}\frac 1n\sum_{j=1}^n\,\log\|df^{-1}|E_2(f^j(x))\|<-\varepsilon. \end{aligned}$$

  In this case, in addition one can have no more than finitely many distinct SRB measures. In fact, if f is topologically transitive and m(S) = 1, then the SRB measure is unique.

We stress that for non-uniformly hyperbolic f, the splitting of the tangent space does not have to be dominated.