Keywords

Introduction

Many parents, teachers, and members of the public at large believe that learning mathematics is primarily focused on remembering arithmetic facts. This is despite a general push from professional mathematics organizations and advisory committees, like the National Council of Teachers of Mathematics , arguing that mathematics instruction should incorporate more spatial thinking, with less focus on the solving routine number problems and less teaching largely rote skills (e.g., CCSSI, 2010; NCTM, 2000; NRC, 2005). Teachers’ spatial skills are correlated with their motivation and interest in teaching mathematics and students’ spatial skills are correlated with their persistence in learning mathematics (Edens & Potter, 2013). Moreover, teachers are amenable to teaching spatial skills when they are informed about their importance (Krakowski, Ratliff, Gomez, & Levine, 2010). A recent meta-analysis shows that spatial skills can be improved via a variety of interventions (e.g., Uttal et al., 2013). Improving spatial skills pays off in the longer term; an individual’s spatial skill predicts the likelihood he or she will enter a Science, Technology, Engineering and Mathematics (STEM) field beyond both verbal and mathematical abilities (Casey, Nuttall, & Pezaris, 2001; Casey, Nuttall, Pezaris, & Benbow, 1995; Wai, Lubinski, & Benbow, 2009). Adding spatial skills to our conventionally number-focused mathematics instruction may be a way to increase students’ mathematics understanding, and prompting teachers to support students’ spatial thinking may be an attainable and effective way to improve mathematics achievement.

In this chapter, we describe how spatial thinking relates to mathematical thinking. To do so we will need to address several questions along the way. First, what are spatial and mathematical abilities, and which skills comprise them? Second, what are the strengths and limitations of the factor analytic approach used to describe the interconnected structures of spatial skills and of mathematical skills? Third, how can cognitive science help us to understand the connections between spatial skill and mathematics? Finally, what are the educational implications of these connections? In answering these questions, we will illustrate a pathway for future research and provide guiding principles for the design of future studies and implementation of effective educational practices that leverage the connection between spatial skills and mathematics instruction.

What Are Spatial and Mathematical Abilities and What Skills Comprise Them?

We begin by briefly discussing the methods psychologists have used to analyze the relations among cognitive abilities. Early psychologists first attempted to define “intelligence” by analyzing the “structure of the intellect,” specifically whether certain cognitive components were irreducible and unique (Spearman, 1927; Thurstone, 1938; Guilford, 1967). This work relied on factor analysis, a procedure that identifies “latent” factors that can account for co-variation in many tasks. This method provides a simple, quantitative solution to the question we, and earlier theorists, ask: what are the fewest and most important skills needed to describe an ability?

In the next section, we describe past efforts to describe and analyze spatial and mathematical abilities. There have been multiple attempts to isolate independent skills in each ability, as well as meta-analyses that have looked across many studies in order to validate the strongest theories about the nature of those skills. Understanding the constellation of unique skills and how they relate to one another is a critical first step to understanding how spatial thinking may be advantageous when thinking of mathematics problems. Specifically, these relations may guide hypotheses about the best candidate spatial skills to strengthen in order to improve specific aspects of mathematical thinking.

Skills Making Up the Spatial Domain

Spatial skill is most broadly defined as “how individuals deal with materials presented in space-whether in one, two or three dimensions, or how individuals orient themselves” (Carroll, 1993). More concretely, “spatial ability” has been defined as the “ability to generate, retain, retrieve, and transform well-structured visual images” (Lohman, 1994). The NSF Spatial Intelligence and Learning Center proposed a 2 × 2 framework that categorized spatial skills by whether the transformation was dynamic or static and whether it occurs within an object or between multiple objects (e.g., a dynamic-within object spatial problem is imagining an image turning clockwise and a static-between object spatial problem is reading a map, Newcombe & Shipley, 2015). Spatial skills vary widely in terms of the stimuli that they operate on and the type of transformation that is performed, leading to the widely held belief that there are multiple, distinct spatial processes (Linn & Petersen, 1985; Voyer, Voyer & Bryden, 1995; Hegarty & Waller, 2005). In many cases, similar spatial tasks vary in the spatial skills they require (e.g., the dissociation in imagining a different perspective vs. imagining an object rotating, Hegarty & Waller, 2004) and as abilities change throughout development they take on different characteristics (e.g., sex differences in two-dimensional but not three-dimensional mental rotation, Neubauer, Bergner, & Schatz, 2010). In short, spatial ability is a broad domain and relating spatial skills to mathematical ones is a complicated task (for a more thorough review of a variety of spatial skills and mathematical skills, see Mix & Cheng, 2011).

Multiple large-scale factor analyses were conducted over the twentieth century with the aim of differentiating specific intelligences from “g” or general intelligence. L.L. Thurstone investigated the issue primarily by factor analyzing a battery of cognitive tasks. He described the resulting factors as “primary mental abilities,” two of which were “spatial visualization” and “number facility” (Thurstone, 1933; Thurstone, 1938). Following his efforts, theorists began to assume that spatial intelligence exists, and attempted to better describe its characteristics, and how spatial skills might further explain variance across a variety of spatial measures.

Of four large-scale factor analyses in the latter part of the twentieth century that included a wide range of spatial measures, all four found evidence for a spatial visualization factor, generally dealing with imagistic transformations (Carroll, 1993; Lohman, 1988; McGee, 1979; Michael, Guilford, Fruchter, & Zimmerman, 1957). This factor consistently included tasks such as paper folding, a task measuring the ability to predict the result of a series of folds to a piece of paper and a hole punch, and form board, which measured the ability to pick the shapes needed to assemble a larger shape (Carroll, 1993; Lohman, 1988; McGee, 1979; Michael et al., 1957). Another task, cube comparisons, which measured the ability to determine whether a set of drawings of dice-like stimuli are two different views of the same object, loaded on the spatial visualization factor in two of the four studies, but in earlier studies loaded on separate spatial relations and orientation factor, which generally captured tasks that required perceiving the relative positions and angle of nearby objects. The other factors that were extracted across these studies were interpreted as various forms of specialized perceptual and motoric factors (kinesthetic imagery, Michael et al., 1957; closure speed, flexibility of closure, perceptual speed, and visual memory, Carroll, 1993). Thus, these initial studies all found a similar spatial visualization factor, but differed in terms of other factors they extracted, likely because they included different tasks in the analysis.

More recent factor analytic research has investigated how spatial skills relate to other cognitive abilities. For instance, Miyake, Friedman, Rettinger, Shah, and Hegarty (2001) examined the connection of spatial skills to working memory, the ability to remember and manipulate information, and executive functioning, the ability to monitor one’s own behavior and to select among choices to achieve specific goals. The three spatial skills tested were spatial visualization, which involves complex mental manipulations of objects, spatial relations, which involve simpler, speeded two-dimensional transformations, and visuospatial perceptual speed, which involves quickly perceiving and making judgments about stimuli, such as whether a particular shape is present in a complex image. Each of these skills differ in the time-scale they act on and the type of transformations they require, rather than being defined by content or whether they rely on visual or kinesthetic information. These skills not only loaded on separate factors, but each also related differentially to working memory and executive function (i.e., both spatial visualization and spatial relations were significantly related to executive functioning, while visuospatial perceptual speed alone was significantly related to working memory, Miyake et al., 2001).

Evidence that each of the spatial skills have divergent connections to other skills provides external validation that they are in fact separate. It is also useful to contextualize the different kinds of spatial skill with respect to their potential roles in mathematics problems; some skills seem to be more basic and could have important role in imagining the transformations signified by arithmetic operations, while others might be more related to choosing an effective, spatially grounded strategy to solve problems involving numbers. Thus, developing an accurate understanding of our primary spatial abilities is critical if we hope to improve our understanding and use of the pathway from spatial skill to mathematics achievement. In the next section, we look at characteristics of mathematical skills, as a way of identifying potential skill to skill connections between spatial and mathematical thinking.

Skills Making Up Mathematical Domain

Mathematical ability , like spatial ability, is highly complex and multifaceted; humans must learn and use a variety of concepts, from how to differentiate and represent approximate magnitudes (Feigenson, Dehaene & Spelke, 2004) to a basic understanding of what a “natural number” is and how it relates to fundamental principles of arithmetic, such as commutativity (Rips, Bloomfield & Asmuth, 2008). Mathematical problems also vary widely in the property of numerical magnitudes involved in the problem (e.g., parity, rationality, size) and the operation applied to these magnitudes. In addition, even for specific magnitudes and operations, there are marked differences in the efficiency of the strategies used to solve these problems (Siegler, 1999). Further, different numerical skills take on greater importance in schooling across development, and in some cases the connection of basic skills to applied, mathematical reasoning depends on the exact way a mathematical problem is framed (Libertus, Feigenson, & Halberda, 2013; Landy, Brookes, & Smout, 2011).

The effort to extract primary mental abilities that was applied to spatial abilities was also applied to mathematical skills, resulting in a factor that was dubbed “facility with numbers” (Thurstone, 1938). Follow-up factor analyses carried out on purely mathematical measures over various ages during development extracted factors that seemed to be less-than-pure mathematical factors (e.g., deductive reasoning and adaptability to a new task, in a study of tenth grade students understanding of algebra, Kline, 1960; abstraction, analysis, application, in a study of elementary school students mathematical reasoning, Rusch, 1957). These early results are also notable in that many theorists found evidence of a spatial factor in mathematics (e.g., Kline, 1960; Werdelin, 1966) or else argued that there was a spatial sensorimotor intelligence factor important to mathematical reasoning (Aiken Jr, 1970; Coleman, 1960; Skemp, 1961).

Few studies have examined mathematical measures broadly enough to reveal separate skills. Yet this examination is vital because mathematics is frequently divided by differences in content rather than skills. For instance, the recently adopted Common Core State Standards for Mathematics (CCSS-M , 2010) in first grade creates a domain called “Counting and Cardinality,” which includes performance standards that are nominally connected but that actually require a variety of different skills and conceptual understandings. Memorizing and reciting the count list is quite different from an active process of “counting on” from a number besides one. Further, understanding that the count list is used to determine the exact the number of items in a set requires more than knowledge of the count list, and is achieved well after young children can count fluently from 1 to 10 or higher (e.g., Sarnecka & Carey, 2008). These three skills are also distinct from the ability to identify and interpret numerals, yet these are placed in the same domain (CCSS-M, 2010).

On the whole, the factor analytic approach has not identified the kinds of distinct mathematical skills that have emerged from cognitive science research, which makes it difficult to identify skill-to-skill connections between spatial skill and particular aspects of mathematics. As summarized above, factor analytic studies of spatial tasks researchers have found evidence of multiple spatial skills, albeit with some inconsistency from study to study. Attempts to identify the structure of mathematical skills have been less successful, with some studies revealing factors that are related to solving mathematics problems, like deductive reasoning, and others revealing factors related to generic cognitive functions, like adaptability to a new task (Kline, 1960). In addition, in both the spatial and mathematical domains, researchers have sometimes found evidence of only a single, domain-wide factor (Mix et al., 2016; Mix et al., 2017). The absence of strong evidence of distinct skills and ambiguity of the results highlights the limitations of the factor analytic approach. Nonetheless, this approach does have some strengths—in particular providing a way to delimit hypotheses about how skills within and across domains relate to each other. In the next section, we further explore these strengths and limitations.

Strengths and Limitations of the Factor Analytic Approach

As we have seen, researchers have relied on factor analysis to define precisely what we mean by spatial skills, mathematical skills, and their overlap. This information is potentially important for educators as it could guide the development of effective approaches to improving mathematics learning, but can we trust the results these analyses yield?

The central strength of the factor analytic approach is that it explains the covariance in scores from a large set of correlated tasks, omitting random error and variance associated with each task, unlike correlational and regression approaches (Bollen, 1989). Factor analysis also has a built-in method of rejecting unnecessary skills (e.g., the Kaiser rule, only skills that explain significant covariation are kept, Kaiser, 2016). It also provides a way to decide among competing theories about the nature of factors (comparing models with different skills statistically is implicit in any factor analysis; Tomarken & Waller, 2005).

A second strength of factor analysis is that it allows a researcher to choose whether the skills can be related to one another not. Specifically, one can choose whether skills are allowed to be correlated rather than totally distinct to each other (geomin rotation, e.g., in a case where skills are thought to rely on common cognitive resources) or that tasks should only load strongly on one factor and not others (varimax rotation, e.g., in a case where skills are thought to be wholly distinct, Browne, 2010). While the number and overall strength of each skill will not change, rotation may cause a change in which tasks will be related to each skill. This strength requires that the researcher make a principled choice about the domain being considered because multiple rotation methods will fit the data equally well, and each will lead to different interpretations.

A third strength of the approach is the simplicity of checking preliminary exploratory factor analysis (EFA) with a confirmatory factor analysis (CFA). While many other methods could be used to replicate a finding, the use of an initial EFA, to identify a pattern of loadings, followed by CFA, where that specific pattern is tested, has a proven track record (e.g., Gerbing & Hamilton, 1996). This well-worked path of substantiating claims about the structure of skills is particularly useful given that investigating the large number of tasks that measure spatial and numerical reasoning is a costly effort, and a variety of different, and at times conflicting, factor structures emerged from earlier studies that did not use this approach (e.g., three broad factors in Michael et al., 1957 versus seven specific factors in Carroll, 1993).

Despite these benefits, the factor analytic approach also has limitations—practical, statistical, and interpretive. Practically, researchers must select enough tasks to cover the domain of interest, but also be selective about those tasks to ensure that they are reliable. Oversampling tasks that are closely related is problematic because it may cause a spurious skill to be extracted because of the similarities in the tasks, or even lead to multiple skills being extracted when absent oversampling there would be only one (as noted by Hegarty & Waller, 2005). Conversely, including tasks that are multidimensional (e.g., that rely on both spatial and non-spatial reasoning), will make loadings more difficult to interpret. Similarly, selecting tasks that are strongly affected by the way participants respond, such as those that include multiple choice questions, may result in extracting “methods” factors that capture variance not as a result of similar underlying processes but rather as a result of using the same test format (e.g., Maul, 2013).

Factor analyses are also limited by statistical power and sample considerations. Researchers must collect data concurrently on a large number of participants, as smaller sample factor analyses on few participants do not always recover stable factor structure in empirical studies (MacCallum, Widaman, Zhang, & Hong, 1999) or true factors in simulation studies (Preacher & MacCallum, 2002). Approximately 20 observations per task are needed to achieve adequate power (Hair Jr, Anderson, Tatham, & Black, 1995). Missing data in any one task requires more complicated statistical procedures, like imputation (Little & Rubin, 1989) or relying on the remaining data to reveal the factor structure through maximum likelihood estimation (Tucker & Lewis, 1973). Even a stable factor structure may arise from random sampling error, which would lead to the same pattern of loadings not being found in a second sample (Cliff & Pennell, 1967). In short, factor analysis reveals true skills only when a large sample of representative and complete data is collected.

Finally, the interpretation of a factor analysis is a complicated issue. The nature of each factor in a solution is decided by the researcher based on the tasks that load on that factor as well as based on the tasks that do not load on that factor (Rummel, 1970). These types of decisions are highly subjective and the researcher’s biases may lead them to interpret random patterns as meaningful (Armstrong & Soelberg, 1968). The researcher must decide how and why the tasks that load on a skill could be logically connected and in most cases the data are correlational and cannot reveal a causal relation. In the next section, we discuss how factor analysis can be used in concert with a cognitive science informed and process-oriented view of spatial and numerical ability to better understand their connection.

How Can Cognitive Science Help Us to Understand the Connections Between Spatial Skill and Mathematics?

An alternative to an approach that relies solely on the measurement of skills through factor analysis is a multi-faceted cognitive science approach that focuses on mental processes. This approach asks more specific questions using a variety of tools. “Which theories explain differences within spatial and mathematical skills?” can be addressed through meta-analysis of many studies. “What skills are used in both spatial and mathematical problems?” can be answered by a cross-domain factor analysis. “What components of a spatial skill allows a child to solve a mathematics problem?” can be addressed with process models of skills.

We apply this approach to the present question, first by examining theoretical distinctions among characteristics of skills through meta-analytic studies. We will then discuss a recent analysis of the connection between spatial and mathematical tasks using factor analysis, and the kinds of process models that follow from this analysis. Finally, we examine how the components of spatial skills might influence mathematical reasoning by training spatial skills and examining the benefits to mathematical problem solving.

Which Theories Explain Differences Among Spatial and Mathematical Skills?

Meta-analysis and Divisions Among Skills

Although factor analytic studies have provided insights into the relations of various skills, there are considerations that factor analysis can miss because it is a primarily data-driven approach. Cognitive science counters this deficiency by incorporating more theory-driven research that takes into account the expertise of content experts as well as consistent findings in the field to articulate theories about the nature of skills and then makes predictions and tests critical assumptions. These assumptions are best tested with as much evidence as possible, which requires aggregating multiple studies, even some that were not conducted to explicitly test the theory in question, in a meta-analysis. With regard to examining the relation of spatial and numerical skills, one important way in which this theory testing has taken place is in the form of resolving factor analysis with frequently reported differences associated with gender (e.g., Casey et al., 1995) and with prevailing theories about the structure of each domain.

Gender differences in spatial skills.

Linn and Petersen (1985) tested differences in three spatial skills that were chosen to test the theory that there were gender differences in particular kinds of spatial thinking: spatial perception, in which subjects must determine spatial relations in spite of distractors, mental rotation, the ability to quickly rotate two- or three-dimensional objects, and spatial visualization, which included multistep, complex spatial transformations, excluding mental rotation. Linn and Petersen’s categorization schema was validated by their analysis of age and gender-based differences between categories: while mental rotation showed sex differences across the lifespan, spatial perception never did, and spatial visualization showed differences only in samples older than 18 years (Linn & Petersen, 1985). Similarly, Voyer, Voyer, and Bryden (1995) organized spatial skills in the same way and found that both mental rotation and spatial perception showed much more frequent, and larger, effect sizes based on gender than did spatial perception. These results suggest that there may be gender differences in spatial skills, from genetic and/or environmental causes (Levine, Foley, Lourenco, Ehrlich, & Ratliff, 2016), which may be relevant to the design of effective interventions that address gender gaps in mathematics achievement (Casey et al., 1995).

Differentiating spatial skills: Static or dynamic? Within or between objects?.

Uttal and colleagues (2016) conducted a theory-driven meta-analysis , beginning with a process-oriented account reflected by a typology with orthogonal dimensions that had support from behavioral (Newcombe & Shipley, 2015) and neurological evidence (e.g., Chatterjee, 2008). Specifically, Uttal et al. (2016) argued that spatial relations between objects are processed differently than processing the spatial properties of the objects themselves, known as the intrinsic-extrinsic division. Further, they argued that spatial information that is accessible from stationary frames is processed differently than spatial information that involves movement and change, the static-dynamic division. This theoretical frame relies on direct evidence of dissociations, such as occurs based on whether tasks are large or small scale (e.g., Hegarty, Montello, Richardson, Ishikawa, & Lovelace, 2006) or imagining movement of an object versus changing perspective in relation to a scene containing multiple objects (Hegarty & Waller, 2004; Huttenlocher & Presson, 1973). The results of the meta-analysis showed that spatial training leads to unique transfer both within each cell of the typology (e.g., from mental to rotation training to other dynamic, intrinsic measures), but also transfer between cells (e.g., from mental rotation training to perspective taking), suggesting that the underlying processes in the various cells are not entirely distinct.

While the typology’s clear dimensions might be intuitively useful as they are clearer than highly interpreted factors, they may miss the mark in terms of empirical support. For instance, a line of research regarding the cognitive styles of children and adults has provided evidence that the extrinsic-intrinsic dimension is useful for understanding how individuals process spatial information, but also adds to it an algorithmic, verbal form of processing spatial information, and does not distinguish between dynamic and static imagery (e.g., Kozhevnikov, Kozhevnikov, Yu, & Blazhenkova, 2013). A direct test of the typology seems to confirm this, with evidence for the extrinsic/intrinsic continuum but not the static/dynamic one (Mix, Hambrick, Satyam, Burgoyne, & Levine, 2018). Similarly, Atit, Shipley, and Tikoff (2013) tested the dimensions in the typology by measuring adults on a variety of mental transformation tasks, including mental rotation, paper folding, and a “breaking” test, and found that an additional orthogonal axis, between rigid and non-rigid transformations was needed to explain their results. Thus, there appear to be a variety of competitors to the original 2 × 2 typology of spatial skill categories, and it seems that neither the factor-analytical nor the theory-driven approach has arrived at a final solution about the number and types of spatial skills. The addition of this theoretical framing to the original data-driven factor analysis provides new ways to describe and explain differences spatial reasoning skill, which we can probe using both experiments and modeling.

Theoretical approach to mathematical skills.

While the factor analytic approach applied to mathematics resulted in multiple skills , different studies contradicted one another regarding the nature of those skills. Several theoretically motivated lines of research have used other methods to determine how understanding of mathematical concepts and basic representation of numerical magnitude interact with each other, effectively providing more process-oriented dimensions and a more detailed hierarchy of basic and composite numerical skills. This work focuses our attention on skills that are likely to have the greatest effect on mathematical achievement over time. We review this literature by highlighting a few illustrative studies that will help us to focus our efforts.

Mathematics as concepts vs. procedures.

Researchers have for years debated whether teaching students to be fluent in mathematical procedures is helpful for improving their understanding of mathematics or if it merely causes children to demonstrate rote-learning skills (Schoenfeld, 2014). While some research suggests that promoting a conceptual grounding of mathematics is of greatest important (e.g., Star, 2005) others argue for a more measured approach, wherein concepts and procedures are more mutually supportive (e.g., Baroody, 2003; Rittle-Johnson, Siegler, & Alibali, 2001). Recent research suggests that certain mathematical concepts that are often overlooked early on might have an outsized role in later mathematics achievement, e.g., patterning skill in early elementary school predicts mathematics achievement later, above and beyond more procedural acts, like counting (Rittle-Johnson, Fyfe, Hofer, & Farran, 2016). The relative importance of teaching concepts versus procedures to mathematical achievement is an important issue to raise because certain spatial skills might be more important when learning numerical concepts than for learning numerical procedures, and vice versa (e.g., certain gestures highlight conceptual groupings for young children’s addition, Goldin-Meadow, Cook, & Mitchell, 2009, while undergrads benefit more from abstract than concrete examples when learning modulo Kaminski, Sloutsky, & Heckler, 2009).

Thinking symbolically vs. non-symbolically.

Recent debate has also focused on how mathematics achievement relates to our basic sense of numerical magnitude, frequently indexed by non-symbolic magnitude comparisons and ordering (e.g., Barth, Beckmann, & Spelke, 2008; Mazzocco, Feigenson, & Halberda, 2011; Mundy & Gilmore, 2009; Rousselle & Noël, 2007). While some argue that this number sense is strongly related to our ability to represent number in more complex number skills (Mazzocco et al., 2011), recent large-scale studies have also shown that our symbolic sense of number is the strongest predictor of mathematics achievement across the elementary school years (comparing in first grade, ordering in sixth grade, Lyons, Price, Vaessen, Blomert, & Ansari, 2014). Meta-analysis confirmed a significantly larger relation of our symbolic number sense to our ability to understand more complex mathematics subject areas non-symbolic number sense (Schneider et al., 2016) and thus may be a better target for training. However, the question of whether spatial skills training can be used to train symbolic and/or non-symbolic number sense remains open, particularly if certain mathematical skills, like understanding fractional magnitude depend on earlier developing non-symbolic ratio or proportional reasoning (Matthews, Lewis, & Hubbard, 2016; Möhring, Newcombe, & Frick, 2015).

These strands of research together suggest that there are many important divisions in spatial and mathematical skills that have not been detected by the basic factor analyses of each domain, but nevertheless could play a role in the relation between spatial and mathematical thinking. In the next section, we consider what can be learned from studies that examine the connection of spatial and mathematical skills. Specifically, we look at recent studies that use factor analysis on both mathematical and spatial domains, to determine whether there is evidence for hybrid spatial-mathematical skills and/or evidence for specific spatial skills that are closely related to general mathematical skills. We then outline how process models of spatial skills can help build out theories about how spatial skills may support mathematical achievement.

What Skills Are Used in Both Spatial and Mathematical Problems?

A number of studies have examined the relation between specific spatial skills and mathematical achievement (for a review, see Mix & Cheng, 2012: Visuospatial working memory, Raghubar, Barnes, & Hecht, 2010; Mental Rotation, Kyttälä, et al., 2003; Block Design, Markey, 2009; Patterning, Rittle-Johnson et al., 2016). Some other spatial skills, often those less researched, have not shown the same connection to mathematics, despite in some cases clear areas where it seems like there might be overlap. For instance, we might expect interpreting maps or solving problems of scale (e.g., DeLoache, Uttal, & Pierroutsakos, 1998; Huttenlocher, Newcombe, & Vasilyeva, 1999), which both involve symbolic thinking, to be useful for understanding numerical symbols. We might also expect that those individuals skilled in disembedding shapes from visual scenes might be better able at analyzing charts and graphs (Clark III, 1988). However, such connections have not been frequently reported.

An obstacle to identifying mechanisms that connect specific mathematical and spatial skills is the high degree of interrelation among skills. Even in rare cases where multiple measures of spatial skills are included in studies with mathematical outcomes, it can be difficult to interpret the result because all spatial skills are correlated with mathematical outcomes. This type of evidence fails to provide support for the theory that certain specific spatial skills are important for mathematics achievement nor how they enable better performance and learning of mathematical skills.

Cross-Domain Factor Analysis of Spatial Reasoning and Mathematical Reasoning

In this section, we focus on two questions central to the goal of this chapter: first, are the spatial and mathematically domains connected generally or by specific skills, and second, is there evidence for shared processes used in both domains? We highlight a pair of studies conducted by the authors that addressed these questions by using factor analysis to determine whether skills in the spatial and mathematical domain load on a single or multiple factors across children’s kindergarten to sixth grade education. To our knowledge, there have not been studies that have systematically examined how spatial and mathematical skills, and their interconnections, change over developmental time.

Surveying the field of spatial and mathematical connections.

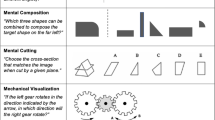
Mix and colleagues conducted a two-stage , exploratory and confirmatory factor analysis of data collected over the 2012–2013 and 2013–2014 school years (Mix et al., 2016; Mix et al., 2017). The goal of the studies was to examine what latent factors explain covariation in age-appropriate mathematics measures and spatial measures. In each study, tasks that had the greatest likelihood of showing spatial-mathematical connections based on the existing literature were included, e.g., between spatial visualization and complex mathematical relations, between form perception and symbolic reasoning, and between spatial scaling and a number line representations (Thompson, Nuerk, Moeller, & Kadosh, 2013; Landy & Goldstone, 2010; Slusser, Santiago & Barth, 2013, respectively). As shown in Fig. 5.1, by design these spatial skills fall into different places along the dimensions described by the spatial typology (e.g., Uttal, et al., 2016), which should allow us to pick up on differential connections between, for instance, extrinsic versus intrinsic spatial skills and mathematical skills.

Fig. 5.1
figure 1

Measures included in EFA/CFA within Spatial Typology (Uttal et al., 2013)

Full size image

Selection of measures of spatial and mathematical skill.

Each task , with some grade appropriate modifications, was administered to kindergarten, third and sixth grade children, which allowed for the possibility of detecting developmental shifts in the relation of spatial and mathematical skills. In addition, the data were collected from students across a wide variety of school settings to ensure the results were generalizable. The specific tasks and their sources are shown in Table 5.1.

Table 5.1 Skills measured in Mix et al. (2016)
Full size table

Separate but correlated spatial and mathematical factors.

In both studies spatial and mathematical processing , as measured by their latent factors, were found to be separate but highly correlated from kindergarten through sixth grade, controlling for general cognitive ability as measured by a vocabulary test. The processes that are accessed when performing a broad range of spatial tasks are highly related to those accessed when performing a broad range of mathematical tasks across development. It was perhaps surprising that separate, domain-specific factors were obtained, given that the covariance among tasks might have been based on one of many other shared task characteristics. For instance, factors may have instead tracked to the way in which children responded to tasks (e.g., productive vs. receptive), or to form of stimuli (symbolic vs. non-symbolic), or to the cognitive resources required (high vs. low executive function), or, as some have previously theorized, we might have found no differentiation between spatial and mathematical skills at all (e.g., a single factor that all measures loaded on). These results show that spatial and mathematical domains are separate, but closely related, and this appears to be the case across the entire elementary school age period.

Cross-loading tasks.

We also found that a few specific spatial tasks cross-loaded on the mathematical factor beyond the general connection, which changed over the course of the three grades. In kindergarten, mental rotation was significantly related to the mathematical factor, whereas in sixth grade, visuospatial working memory and visuo-motor integration took on a significant relation. These tasks in particular may have special significance in mathematics education at their respective years, should these relationships prove to be causal when tested in training studies. The relative loadings of each task to the general factor in each grade appear remarkably stable across development, which suggests that each task continues to rely on the same resources and processes over the course of development. The few spatial tasks that do show cross-loadings draw at first from dynamic processes (mental rotation) and later from more static processes (visuo-spatial working memory and visuo-motor integration), and in terms of previously identified spatial factors, from spatial visualization to those more associated with perception and working memory.

Open questions.

While these factor analyses provided greater certainty of finding shared processing when we examine spatial or mathematical tasks in the same factor analysis, they raised many important questions that remain to be answered. One key question is how spatial skills can influence mathematical reasoning, by what processes or components? While we did find a few cross-loadings between the numeric and spatial factors on spatial and mathematical skills, most spatial skills did not cross-load to mathematical ability, except through the general factor relation. Still, measures like mental rotation in kindergarten, and visuospatial working memory and visuo-motor integration in sixth grade may be the best candidates for training, even taking the instability of the cross-loadings into account. By focusing our training efforts on those specific measures, we can begin to flesh out more causal models that provide a mechanism to the results observed in the correlational factor analysis (see Mix, Levine, Cheng, & Stockton, under review). In the next section, we focus on process models, which can help to identify what components of spatial skills could be important for mathematical reasoning.

Spatial Processes in Mathematics Achievement

The cross-loadings revealed by the factor analyses indicate that there is a link between mental rotation and mathematics in kindergarteners. Other research corroborates this relation as a fruitful connection to explore. For example, Gunderson, Ramirez, Levine, and Beilock (2012) showed that performance on a number line estimation task mediated the relation between performance on a spatial transformation task and an approximate calculation task. However, this finding leads to the questions about the specific processes involved in each of the tasks (number line estimation, spatial transformation, and approximate calculation). Which processes explain the connections seen in these studies? For example, spatial transformation relies on both being able to rotate objects mentally and to match features, either of which might explain its relation to number line estimation, which is itself multifaceted, requiring both an ordinal awareness of numerical magnitude and a mapping from numerical magnitude to spatial extent. Clarifying the specific relations between these measures is important because a well-specified mechanism is key to a well-designed and effective educational intervention.

There is also reason to move beyond the results of both the factor analyses and other previous studies that only analyze summary scores in order to build a theory about spatial-mathematical connections. Each of the measures tested in the previously described factor analyses was comprised of a complicated set of underlying processes and may have relied on integrating multiple orthogonal dimensions of difficulty (e.g., see Cheng, Mix, Reckase, Levine, & Freer, under review, regarding the automatic and deliberate elements of visuospatial working memory). Theorists often tend to assume that specific processes elicit a single, specific type of process, for instance that a mental rotation task reflects dynamic spatial visualization and not static, form perception, but is this actually the case? Moreover, even if it is, which of these processes is also important for young children’s mathematical skills? Despite this, we know that we should take care not to reify the processes we measure with tasks. By modeling the underlying processes involved in a task we are better able to understand what proficiency on a task actually indicates. Our ultimate goal when examining spatial tasks for their underlying processes is to answer basic questions asked in developmental research : which spatial processes are causally related to the development of mathematical reasoning (Overton & Reese, 1973)?

Models of cognitive processes break down tasks into interacting components. These models have been used to understand performance and growth on a wide range of tasks, from remembering lists (Henson, 1998) to analogical reasoning (Doumas, Hummel, & Sandhofer, 2008), to simple arithmetic (Ashcraft, 1987). For example, Thompson, Ratcliff, and Mckoon (2016) used a diffusion model to compare children’s and adults’ symbolic and non-symbolic number discrimination. The model parameters showed differences in how adults and children, beyond simple performance differences between groups. That is, the diffusion model indicated that the reason adults could respond faster than children was because adults acquired enough information to decide whether magnitudes were different more quickly than children, regardless of whether those magnitudes were dots or numerals.

Mental rotation.

The question of whether young children connect the dynamic transformation process used in a mental rotation to numerical tasks has been asked since at least since the 1970s. Marmor (1977) asked whether children who are better at mental rotation perform better on number conservation and Davidson (1987) asked whether children who are better at rotational displacement problems perform better on arithmetic problems. While correlations have been observed between tasks requiring mental rotation and a variety of mathematical tasks, it is not clear why this is the case. Below, we will use models of mental rotation to describe potential connections to mathematical concepts and procedures. We also review recent studies that attempt to determine whether training processes that underlie mental rotation performance are beneficial to mathematical reasoning.

A process view of mental rotation. It is useful to first describe the process typically assumed during mental rotation. Imagining the rotation of an object may feel intuitive but it is not so simple to verbally describe how it is done. Even the most general definition of the process involved, e.g., “MR involves transforming a representation held in visual short-term memory” (Provost & Heathcote, 2015) is not wholly uncontroversial, in that the speed, automaticity, and number of transformations are not specified. Mental rotation was hypothesized as a cognitive construct after Shepard and Metzler (1971) reported that the speed with which participants could determine if a three-dimensional block stimulus matched a target was a function of the angular disparity between the presented object and the target. Evidence suggests that participants intuitively rotate the object in the direction that requires the least amount of angle to match its target (Cooper & Shepard, 1973), which shows that participants can quickly identify their target in its typical orientation, and that they are not confused by similar objects (Corballis, 1988). Mental rotation tasks are often treated as if they reflect a “pure” ability to imagine rotations, but cognitive models reveal that mental rotation involves diverse subcomponents, which are relevant to our understanding of why mental rotation is related to mathematics.

Angular disparity. The best-fitting process model of behavioral data suggests participants actually engage in multiple, small but variable rotations in succession, almost as if they were grasping and turning an object until the participant reaches his or her limit of manual flexibility, then repeats (Provost & Heathcote, 2015). The analogy to actual manual rotation is supported by neuroimaging work that shows that the pattern of activation when participants enact mental rotation is similar to activity when participants actually move objects (Thayer & Johnson, 2006; Zacks, 2008). Models also suggest participants need increasing evidence as a function of the angle of disparity in order to make a decision (i.e., when the stimulus is rotated far from the target, participants need to gradually accumulate evidence about the stimuli’s angle, causing them to take longer to be certain of their choice, Provost & Heathcote, 2015).

Different processes for complex and simple stimuli. There are also important differences among mental rotation tasks that reveal different processes at work beyond a purely “rotational” process. When comparisons must be made between stimuli that are more complex, reaction times are slower than between simple stimuli (Bethell-Fox & Shepard, 1988; Shepard & Metzler, 1988). Similarly, studies that include MR tasks with distractors find the most frequent incorrect choice in MR tasks is the choice of the mirror image of the correct choice rotated to the same degree as the correct choice (e.g., Kelley, Lee, & Wiley, 2000). Cognitive models account for this with a component that allows for confusability between the target and its mirror (e.g., confusing a “d” for a “b”), particularly when the stimuli are complex. These results and models suggest that all mental rotation stimuli are not equal, and that a separate process of “abstraction” of complex stimuli might need to occur within some mental rotation trials (Lovett & Schultheis, 2014). Thus, it is possible that abstraction, and not angular disparity, could be the source of connection between performance on mental rotation tasks and mathematics rather than the rotation process per se.

Not mental rotation at all. Participants’ own descriptions of their strategies in mental rotation more frequently involve description of matching features of targets and choices, rather than mental rotation (Shepard, 1978). It is also clear that for a non-trivial number of trials of a mental rotation task, choices are made without engaging in mental rotation, particularly for 2D objects for which participants may use a fast flipping transformation (Cooper & Shepard, 1973; Kung & Hamm, 2010; Searle & Hamm, 2012). This suggests that the overall performance curve reflects a mixture of slower, rotational trials, and faster, non-rotational trials, overall resulting in the canonical bowed out curve that relates angular disparity to rotation speed (Searle & Hamm, 2017). Perhaps it is the quicker type of transformation, or the ability to pull out relevant feature of a spatial stimuli, which actually relate to mathematics, and not the angle-specific transformation.

Influence of mental rotation on mathematical reasoning.

When we consider the form of the mental rotation task that was administered to children in kindergarten through third grade in the factor analytic studies (Mix et al., 2016), a number of potential processing models need to be considered. Participants were presented two-dimensional, scrambled alpha-numeric characters and were instructed to choose two of four stimuli that matched a target. The angles of rotation of the choices included both small and large angular disparities. Thus, it seems likely that non-rotational strategies might be available to children who engaged in the task, but also that both complexity of stimuli and angle might be critical to the relation to mathematical skill. Sixth grade children completed a three-dimensional mental rotation task with cube stimuli, which are potentially less solvable by non-rotational processes, and neither they nor third graders showed any specific cross-loading between mental rotation and mathematical ability.

In thinking about how mental rotation related process might more generally relate to early numeric processes and tasks, it is useful to examine where these connections have been observed. The majority of studies where mental rotation has been connected to mathematics skills were conducted with adults or older children—more comparable to the older children in our studies (third and sixth graders), who performed three-dimensional cube rotations. These other studies reported relations of performance on such mental rotation tasks to performance in broad areas of mathematics such as geometry (Battista, 1990; Delgado & Prieto, 2004; Kyttälä & Lehto, 2008), mental arithmetic (Kyttälä & Lehto, 2008; Reuhkala, 2001), problem solving (Hegarty & Kozhevnikov, 1999), and even to number sense in adults (Thompson et al., 2013). In addition, most of those studies included multiple other spatial measures and many of them were correlated with mathematical and verbal measures. Perhaps these correlations actually represent variation not specific to mental rotation skill or even solely related to spatial skill, rather reflecting a relation of mathematics performance to general intelligence or other domain general cognitive skills.

In the few studies that have focused on relations between mental rotation and mathematics in younger children or that have attempted to train mental rotation in order to improve mathematics, only a few have shown a connection (Kyttälä, Aunio, Lehto, Van Luit, & Hautamäki, 2003; Cheng & Mix, 2014; Lowrie, et al., 2017). It is interesting to note that the study that found a null relation (Carr, Steiner, Kyser, & Biddlecomb, 2008) used a 3-D measure of mental rotation, which models suggest would decrease the incidence of non-rotational responding such as the use feature matching strategies (Hawes, Moss, Caswell, & Poliszczuk, 2015; Xu & LeFevre, 2016). However, it is also possible that a 3D mental rotation task is too difficult for young children, and therefore suppresses individual differences (Neuburger, Jansen, Heil, & Quaiser-Pohl, 2011).

One possible explanation for the kindergarten connection between mental rotation and mathematics is that it reflects the ability to detect form or imagine transformations that could be useful for early mathematics concepts (e.g., better discriminating and encoding of numerical symbols; better imagining of transformations of quantities involved in arithmetic problems; a more easily visualized “mental number line” representation). This last connection was recently substantiated directly; adults who performed better at mental rotation had stronger spatial-numeric associations (Thompson et al., 2013). The subcomponents of mental rotation, both the recognition of parts of objects (affected by the complexity of those objects, as in a computational model of mental rotation, Lovett & Schultheis, 2014) and the process of mentally rotating those objects could be differently engaged throughout mathematical activities. Some processes involved in mental rotation and other spatial visualization type skills, whether they are the processes used in slow rotations or fast transformations, may be more important than others for mathematical reasoning, and this could vary depending on the particular mathematics problems being examined and the ages of the participants—a rich set of questions in need of further study.

Visuospatial working memory.

Working memory is a construct that was initially proposed to address gaps in previous theories of memory (Baddeley & Hitch, 1974). Previous theories had suggested that for very recently activated information, short-term memory provided a place to hold in mind a small amount of information without rehearsal, but with considerable loss due to decay of information, before it was consolidated in long-term memory (Broadbent, 2018). In contrast, working memory models proposed buffer areas that come into play as a sort of way-station between perception and processing where information is selectively acted upon. A shared feature of models of working memory was the central executive function, which essentially coordinates all of the different functions that must be carried out (shifting attention, processing, storing, updating, and maintaining information) and some have characterized this model as requiring a sort homunculus rather than providing a real mechanism by which all of these functions are carried out (Wingfield, 2016).

Modality specificity of visuospatial working memory. Competing theories have contested how much of the processing of visuospatial working memory is just re-presentation of sensory modality information that will become important later in processing. They have also questioned when and how information is retained, culled, and transformed, in what is generally described as executive function (Miyake et al., 2001; Smith & Jonides, 1999). Experimental evidence suggests that age has disparate effects on different working memory functions; shifting focus shows age-related improvement, whereas the number of errors due to interference or substitution of information does not change over development (Carriedo, Corral, Montoro, Herrero, & Rucián, 2016; Lendínez, Pelegrina, & Lechuga, 2015). A more detailed understanding of how working memory carries out processing of complex spatial stimuli is needed, particularly in how it handles uniquely spatial information, to fully explain its relation to mathematical processing, and how mathematical tasks impose spatial processing demands.

Insights from visuospatial working memory process models. Working memory is necessary for basic attentional processes, such as keeping the perceptual representation of a recent stimulus activated, and localized processing of different types of stimuli (e.g., verbal vs spatial, comprising movement and location information, vs object, comprising static images; Johnson et al., 2005). Meta-analysis of brain imaging studies showed working memory activation for spatial “where” content was handled by specific brain regions, as was verbal content, while object related activation was not consistently tied to particular brain regions (Nee et al., 2013), suggesting it is handled by many brain regions. Further, areas that are activated for spatial content tend to have differentiated functional roles, with one, the superior frontal sulcus, activating most strongly to refresh a location in memory rather than when perceiving location (Johnson et al., 2005). This suggests that different processing may occur more readily for certain spatial content, which further suggests that how one thinks about mathematical problems may depend on its spatial characteristics (e.g., the size of symbols in a mathematics problem affects an individual’s answers and errors to that problem, Landy & Goldstone, 2010).

Visusospatial working memory as a measure of discarding irrelevant information. Models of working memory have shown that the function of visuospatial working memory is more dedicated to active maintenance, particularly removal of unneeded information, than to processing novel information (Ecker, Lewandowsky, & Oberauer, 2014). Further, while the efficiency and overall strength of memory is often measured by the number of items one can keep in mind, the model reveals that how many items we remember is unrelated to how quickly we can remove items from memory. This conforms with other models that suggest the removal of unwanted information, and visuospatial processing more generally, relates directly to “fluid intelligence,” not because of shared processing but rather because both systems must update continuously to what are described as “top-down processing goals” (e.g., inferential reasoning, Shipstead, Harrison, & Engle, 2016). It is possible that VSWM is related to mathematics because, particularly for mathematics problems given to older children, information must be changed and relations among numerical variables are fluid (e.g., the identity of “x” in algebra , whether an operation involving a fraction represents an increase or decrease in magnitude).

Influence of visuospatial working memory on mathematics.

In contrast to the specific relation of mental rotation and mathematics in kindergarteners, in sixth graders VSWM is specifically related to mathematics. As with mental rotation there are some basic implications that process models might make for the results of the cross-domain factor analysis. First, one limitation of our visuospatial working memory task was that it plausibly involved both spatial storage and processing and central executive functions associated with working memory or fluid intelligence. Our primary measure of working memory was a measure of the location of stimuli, which makes it likely that children were responding with the “where” pathway of working memory rather than the “what,” object focused form of working memory. The iterative nature of the task, wherein children were required to respond to many trials of increasingly populated arrays, also suggests that we were not purely measuring the capacity of children’s memory, and their ability to maintain items in memory, but also their ability to “actively forget” information from previous trials.

Among the studies that have connected working memory to specific numerical skills, a variety have found general connections to mathematical skills (Reuhkala, 2001; Szűcs, Devine, Soltesz, Nobes, & Gabriel, 2014; Kyttälä & Lehto, 2008; Bull, Espy, & Wiebe, 2008; Casey et al., 1995; Primi, Ferrão, & Almeida, 2010). Fortunately , several of these studies have specifically probed verbal and visuospatial memory, as well as some form of executive functioning, and have shown that VSWM is the construct at work. Studies that provide an account of which function(s) of working memory (e.g., attending, storage capacity, etc.) actually connect to numerical skills are rare (but see Dulaney, Vasilyeva, & O'Dwyer, 2015, showing storage and attention are related to mathematics achievement). One clue to a functional role to analysis and manipulation of specifically spatial information comes from a recent study; fourth graders who specifically fared poorly on mathematical problem-solving had poor spatial working memory, and could not access or envision spatial relations, but performed normally on visual working memory tasks (Passolunghi & Mammarella, 2010). One important venue of future research should look at what about mathematical problem solving in fourth through sixth grades relies on this VSWM.

Several theorists have posited that visuospatial processes facilitate learning numerical skills through specific routes. One suggests that VSWM enables more abstract or conceptual thought (e.g., Nath & Szücs, 2014) while another suggests it provides a resource that allows for more complex and useful numerical strategies (Foley, Vasilyeva, & Laski, 2017). By these accounts the additional storage and visuospatial analysis resources work over time to facilitate learning and improved performance. One possibility is that these resources allow one to first form mental models or to imagine more useful mental models of mathematical problems.

Other longitudinal work examining the relational between several components of working memory and mathematics achievement is consistent with our finding of a significant relation of VSWM to mathematics in sixth graders but not in kindergarteners or third graders. Specifically, Li and Geary (2013) observed no relation between any component of working memory and mathematics ability in first grade, but that those children who increased the most in their visuospatial memory from first to fifth grade scored significantly higher than their peers on measures of numerical operations, while other spatial measures were not significant predictors. These results provide longitudinal evidence of the increasing importance of visuospatial working memory, mirroring the cross-sectional findings that emerged through confirmatory factor analysis (Mix et al., 2017).

What Are the Educational Implications of Relations Between Mathematical and Spatial Skills?

Several studies have investigated whether training spatial skills can improve numeracy or, more generally, mathematical achievement. In this section, we review recent efforts to include spatial skills in educational settings and interventions to improve mathematical outcomes. We then describe general principles to improve mathematical education by incorporating spatial skill instruction.

Spatializing the Mathematics Curriculum

As shown by a meta-analysis carried out by Uttal et al. (2013), spatial skills are malleable. Moreover, training a particular spatial skill leads not only to improvement in that spatial skill but also to spatial skills more generally. However, training of specific spatial skills in order to improve specific mathematical skills sometimes works (e.g., Cheng & Mix, 2014; Nath & Szücs, 2014; Foley et al., 2017; Lowrie, Logan, and Ramful, 2017) and sometimes does not (e.g., Hawes, et al., 2013; Simons, et al., 2016; Xu & LeFevre, 2016). Further, teaching-specific spatial skills to students may present a tall order in actual educational settings, both because these skills are generally outside the bounds of required curricula, and because existing research does not support clear prescriptions about when specific kinds of spatial training would be beneficial.

A more recent effort to improve mathematics education is a more kitchen sink approach, where spatial skills are focused on more generally in their own right. This approach has proven successful at attenuating the effects of low spatial reasoning on mathematics performance in undergraduate students (Sorby, Casey, Veurink, & Dulaney, 2013) as well as providing a core of spatial skills that appear to be generally advantageous for success in the STEM disciplines (Sorby, 2009; Miller & Halpern, 2013). Another effective method of promoting spatial skills quickly and early has been to infuse this kind of thinking into play activities like block play (Casey et al., 2008). Evidence suggests that children’s experience with basic spatial play activities like puzzles and blocks has early connections to performance on spatial tasks such as mental rotation (Levine, Ratliff, Huttenlocher, & Cannon, 2012) and to foundational mathematics concepts and practices (Verdine, Irwin, Golinkoff, & Hirsh-Pasek, 2014).

Classroom interventions that incorporate spatial skills training more generally have had some success in early education. Students in one school program that was provided with spatial training activities over the course of the school year showed substantial growth in spatial and mathematical domains (Bruce & Hawes, 2015). Providing 9- to 10-year-old students with weekly lessons that emphasized different aspects of working memory, including VSWM , was also effective in increasing students’ visual perception abilities, span, and addition accuracy (Witt, 2011). A more integrated approach to including spatial skills in the classroom focuses on providing teachers with formative assessments, feedback, and professional development geared at making pre-kindergarten teachers aware of spatial skills and their connection to mathematical achievement, with promising preliminary results (Young, Raudenbush, Fraumeni, & Levine, 2017). We believe that these forms of early intervention, which help to get children’s spatial and numerical skills on track early, are especially important to closing later gaps in achievement across STEM areas.

General Principles for Leveraging Spatial Skills to Improve Education

A number of studies provide evidence that spatial training is particularly useful when learning new content, as in the case when college students begin visualization intensive organic chemistry (Stieff, 2013). This was born out by the results of regressions analyses conducted after the exploratory factor analysis of space and mathematics. In all three grade levels the authors studied (K, 3rd, and 6th), the results suggested that spatial skills were more closely related to novel mathematical content (Mix et al., 2016). In addition, teaching using spatial tools, such as gesture, rich spatial language, diagrams, and spatial analogies, (Newcombe, 2010), as well as 3D manipulatives (Mix, 2010) has been shown to be helpful to student mathematics learning (e.g., Richland, Stigler, & Holyoak, 2012; Levine, Goldin-Meadow, Carlson & Hemani-Lopez, 2018). Further, those tools appear to be particularly effective in helping students understand difficult concepts and procedures when they are combined (e.g., spatial language and gesture, Congdon, Novack, Brooks, Hemani-Lopez, O’Keefe, Goldin-Meadow, 2017). By providing rich spatial information in multiple ways, educators can help students create a lexicon of spatial relations, terms, and connections to mathematics , which can be utilized again and again as the child encounters novel problems.

Conclusions

In this chapter, we have provided a review of the literature suggesting that spatial skills can be organized into factors and also divided along several meaningful dimensions. We argue that these divisions can help us to understand a set of skills that widely differ and should motivate further exploration of spatial processing. We also believe that more attention should be paid to the way that spatial skills differ in their connection to other cognitive abilities and in how malleable and easily trained they are. We have shown that children’s numerical and spatial abilities are related at the level of shared underlying processes across development, yet remain functionally distinct at each time. We have argued for a more fine-grained, process oriented view of spatial numeric relations which does not reify cognitive constructs but breaks them down to search for mechanism. We argue that combining information gained from factor analyses (in this case showing the correlated, overlapping structure of spatial and mathematical skills) with methods and models from cognitive science highlights a way to uncover mechanisms and causal connections between basic processes and achievement. We also believe that these process accounts can be leveraged for educational gains. The research we have reviewed suggests that spatial skills hold promise as pathways by which numerical skills can be improved and mathematics achievement can be maximized.