Topology Optimization for Compliance Minimization and Actuator Layout to Vibration Suppress

Abstract

This article addresses the compliance problem along with the piezoelectric actuator design for active vibration control. The structure layout is obtained by solving a compliance minimization problem while the actuators topology is found by the maximization of a controllability index written in terms of the controllability Gramian, which is a measure that describes the ability of the actuators input to move the system state from an initial condition to a desired final state, at rest for instance, in a finite time interval. Also, the polarization direction of each actuator is defined according to the distribution of an additional design variable. Therefore, it is possible to produce both tensile and compressive fields in different points of the structure using the same applied control voltage. In order to achieve this goal, a material interpolation scheme based on the Piezoelectric Material with Penalization and Polarization (PEMAP-P) model is employed and both the optimum structure/actuator layout and polarization profile are obtained simultaneously. The sensitivities with respect to the polarization and design variables are calculated analytically. Numerical examples are presented considering the control of bending vibration modes for a cantilever beam and a simply supported beam in order to show the efficiency of the proposed formulation. The control performance of the designed structures are analyzed by means of a Linear-Quadratic Regulator (LQR) simulation and these results are compared to the ones obtained by a formulation that does not take into account the actuator polarity in the optimization problem, i.e., the polarization profile is stated a priori.

1 Introduction

An active vibration control (AVC) strategy requires the use of sensors to collect information related to the structural motion and actuators to apply an active damping which reduces the vibration effects. Moreover, a control law is also required to calculate the input signal, which is applied to the actuators, with appropriate magnitude, frequency and phase, based on the output signal from the sensors [1]. Piezoelectric materials are frequently employed in AVC applications due to their fast response, easy implementation, and possibility to be used either as sensor or actuator due to the direct and inverse piezoelectric effects [2]. Several authors have proposed efficient strategies for the design of structures with piezoelectric sensors and actuators since the control performance depends on the geometrical parameters of these transducers. A detailed technical review on the optimal placement of piezoelectric transducers can be found in Gupta et al. [3]. Topology optimization problems based on controllability and observability were used to design piezoelectric actuators [4, 5] and sensors [6].

In this work, a simultaneous optimization approach is employed to design flexible structures with embedded in-plane piezoelectric actuators. The compliance minimization with volume constraint is carried out along with the actuator design. A controllability measure is maximized in order to define the optimized actuator layout [7] and its polarization [8]. Thus, each part of the piezoelectric domain can have different poling directions, which allows the actuators to create tensile and compressive strain fields at different points of the structure when a single-input control voltage is applied. The topology optimization method based on the SIMP [9] and PEMAP-P [10] models is employed in this work to find topologies that result in a minimum compliance structure and piezoelectric actuators with improved control performance. Numerical examples are presented considering the application of a Linear Quadratic Regulator (LQR) scheme in order to verify the influence of the optimized polarization profile on the controller gains and displacement responses.

2 Problem Description

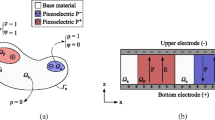
The structure topology is characterized by the distribution of the design variable $\chi$ that indicates the presence of material ($\varOmega - \varOmega _v$) and void regions ($\varOmega _v$), as represented in Fig. 1.

Fig. 1.

General problem for the structure with multi-polarized piezoelectric actuators.

A second design variable $\rho$ indicates the presence of base material ($\varOmega _b$) or piezoelectric material ($\varOmega _a = \varOmega _n \cup \varOmega _p$), with its polarization direction described by $\varphi$. Thus, $\varOmega _n$ and $\varOmega _p$ represent, respectively, negative and positive polarization for the piezoelectric media.

The linear piezoelectric constitutive model is used to relate the mechanical stresses ($\sigma _i$) and the electric displacements ($D_i$) with the mechanical strain field ($\varepsilon _i$) and the electric field ($E_i$), written as:

$$\begin{aligned} \sigma _i = c_{ij}\varepsilon _j - d_{ki}E_k, \end{aligned}$$

(1)

$$\begin{aligned} D_i = d_{ij}\varepsilon _j + e_{ik}E_k \end{aligned}$$

(2)

where $c_{ij} = c_{ij}\left( \chi ,\rho \right)$, $d_{ij} = d_{ij}\left( \chi ,\rho ,\varphi \right)$ and $e_{ij} = e_{ij}\left( \chi ,\rho ,\varphi \right)$ are, respectively, the elastic, piezoelectric and dielectric constants which make Eq. (1) becomes the Hooke’s law when $\chi = 1$ and $\rho = 0$.

The equation of motion can be written in terms of modal coordinates $\mathbf {r}$, as:

$$\begin{aligned} \varvec{\ddot{\mathrm{r}}} + 2\mathbf {Z}\varvec{\varOmega } \varvec{\dot{\mathrm{r}}} + \varvec{\varOmega }^2 \mathbf {r} + \varvec{\varPsi }^{\mathrm {T}} \mathbf {K}_{up}\mathbf {v} = \varvec{\varPsi }^{\mathrm {T}}\mathbf {f} \end{aligned}$$

(3)

where $\mathbf {Z}$ is the diagonal matrix of modal damping ratios, $\varvec{\varOmega }$ is the diagonal matrix of natural frequencies, $\varvec{\varPsi }$ is the modal matrix, $\mathbf {K}_{up}$ is the piezoelectric coupling matrix, $\mathbf {v}$ is the vector of nodal voltages, $\mathbf {f}$ is the vector of nodal mechanical forces, and the upper dot denotes time derivative.

3 Topology Optimization Problem

The design variables are penalized in order to push intermediate values toward either 0 or 1, and, consequently, the elastic properties and density for the k-th finite element are written as [9]:

$$\begin{aligned} c_{ij} = {\chi _k}^{p_0} \left[ {\rho _k}^{p_1} c_{ij}^{pzt} + (1 - {\rho _k}^{p_1} )c_{ij}^{base} \right] \end{aligned}$$

(4)

$$\begin{aligned} \gamma = {\chi _k}\left[ {\rho _k} {\gamma }^{pzt} + (1 - {\rho _k} ){\gamma }^{base} \right] \end{aligned}$$

(5)

where $c_{ij}^{base}$ and $c_{ij}^{pzt}$ are, respectively, the elastic properties of base and piezoelectric material; $\gamma ^{base}$ and $\gamma ^{pzt}$ are the density of base and piezoelectric material, respectively; $p_0$ and $p_1$ are the SIMP penalization factors. The Piezoelectric Material with Penalization and Polarization (PEMAP-P) takes into account the possibility of define either positive or negative polarization. Then, the coupling piezoelectric and dielectric properties for the k-th element are interpolated as [10]:

$$\begin{aligned} d_{ij} = {\chi _k}^{p_0} {\rho _k}^{p_2} \left( 2\varphi _k - 1 \right) ^{p_3} d_{ij}^{pzt} \end{aligned}$$

(6)

$$\begin{aligned} e_{ij} = {\chi _k}^{p_0} {\rho _k}^{p_2} \left( 2\varphi _k - 1 \right) ^{p_4} e_{ij}^{pzt} \end{aligned}$$

(7)

where $d_{ij}^{pzt}$ and $e_{ij}^{pzt}$ are, respectively, the electromechanical coupling and dielectric properties of the piezoelectric material; $p_2$, $p_3$ and $p_4$ are the PEMAP-P penalization factors.

The structure topology problem is written as:

$$\begin{aligned} \begin{aligned} \underset{ \varvec{\chi }}{\mathrm {minimize}}:&\quad f_s= \mathbf {f}^{\mathrm {T}} \mathbf {u}\\ \mathrm {subject \ to} :&\quad g_s = \frac{\sum _{i=1}^{n}\chi _i}{\sum _{i=1}^{n}V_i} \le C_V \\ :&\quad 0 < \chi _i \le 1 \quad i=1,2,\ldots , n \\ \end{aligned} \end{aligned}$$

(8)

where $\chi _i$ is the design variable associated with the i-th element, $V_i$ is the volume of the i-th element, $C_V$ is a threshold for the structure volume and n is the number of elements.

The actuator design is defined by the maximization of the controllability measure $\lambda _1$, which is proportional to the energy transmitted from the actuator to the first vibration mode [11]. Thus, the actuator topology problem is written as [8]:

$$\begin{aligned} \begin{aligned} \underset{ \varvec{\rho }, \varvec{\varphi } }{\mathrm {maximize}}:&\quad f_c= \lambda _1\\ \mathrm {subject \ to}:&\quad g_c = \frac{\sum _{i=1}^{n}\rho _i}{\sum _{i=1}^{n} V_i} \le C_P \\ :&\quad 0 \le \rho _i \le 1 \quad i=1,2,\ldots , n \\ :&\quad 0 \le \varphi _i \le 1 \quad i=1,2,\ldots , n\\ \end{aligned} \end{aligned}$$

(9)

where $\rho _i$ and $\varphi _i$ are the design variables related to the i-th element, $V_i$ is the volume of the i-th element and $C_P$ is a threshold for the actuators volume. The controllability measure $\lambda _1$ is the first eigenvalue of the controllability Gramian $\mathbf {W}$, which is obtained by solving the Lyapunov equation [12]:

$$\begin{aligned} \mathbf {A}\mathbf {W} + \mathbf {W}\mathbf {A}^{\mathrm {T}}+ \mathbf {B}\mathbf {B}^{\mathrm {T}} = \mathbf {0} \end{aligned}$$

(10)

where $\mathbf {A}$ and $\mathbf {B}$ are the system and control input matrices given by:

$$\begin{aligned} \mathbf {A}= \left[ \begin{array}{cc} \mathbf {0} &{} \mathbf {I}\\ -\varvec{\varOmega }^2 &{} -2\mathbf {Z}\varvec{\varOmega }\\ \end{array} \right] \qquad \mathbf {B}= \left[ \begin{array}{c} \mathbf {0} \\ -\varvec{\varPsi }^{\mathrm {T}}{} \mathbf K _{u\phi } \\ \end{array} \right] \end{aligned}$$

(11)

where $\mathbf {0}$ and $\mathbf {I}$ are the zero and identity matrices, respectively.

4 Numerical Results

In this section, the proposed formulation is examined by means of two numerical examples, as represented in Fig. 2. The base material is defined as an isotropic elastic material with aluminum constitutive properties ($E = 71\cdot 10^{9}$ $\mathrm {N/m^2}$, $\nu = 0.33$, and $\gamma = 2700$ $\mathrm {kg/m^3}$), and a piezoelectric ceramic PZT-5A is considered as the active material. The elastic, piezoelectric and dielectric constants for a PZT-5A can be found in Gonçalves et al. [8].

Fig. 2.

Description of the analyzed examples (all dimensions in millimeters).

Both structures are modeled using 1600 finite elements. For the volume constraints, $C_V$ and $C_P$ are set, respectively, as 0.5 and 0.2. The penalization exponents of the material model are set as $p_0 = p_1 = p_2 = 3$ and $p_3 = p_4 = 1$. Uniform initial distribution is employed for the design variables as $\chi _i = C_V$, $\rho _i = C_P$, and $\varphi _i - 0.5$. For the compliance problem, an unit static force (1N) is considered for all examples.

Figures 3 and 4 present the interpreted designs for examples A and B, respectively, considering uniform and optimized polarization. Design variables greater than or equal to 0.5 are lead to 1 while the remaining variables are lead to 0 (except for $\chi$ where a lower bound 0.001 is considered to avoid ill-conditioning problems). In these figures, blue and red represent piezoelectric domains with negative and positive polarizations, respectively, while white represents base material elements. Void domains, i.e., elements with $\chi = 0.001$, are removed from the mesh to better represent the interpreted structures.

Fig. 3.

Interpreted design for the example A with: (a) uniform and (b) optimized polarization.

Fig. 4.

Interpreted design for the example B with: (a) uniform and (b) optimized polarization.

For both examples, the controllability measure $f_c$ is improved when the polarization is taken into account in the optimization problem.

A Linear-Quadratic Regulator (LQR) scheme is employed to compare the control performance of the designed structures and actuators. For this controller, the optimal feedback gain matrix is chosen to minimize the quadratic cost function [13]:

$$\begin{aligned} J=\frac{1}{2}\int _{0}^{t_f} \left( \mathbf {x}^\mathrm {T} \mathbf {Q} \mathbf {x} + {\phi }^2 \right) \ dt \end{aligned}$$

(12)

where $\mathbf {x}$ is the state vector containing the modal displacements ($\mathbf {r}$) and velocities ($\mathbf {\dot{r}}$), ${\phi }$ is the single-input control voltage, and $\mathbf {Q}$ is a semi-positive definite weighting matrix for the state variables $\mathbf {x}$, defined as:

$$\begin{aligned} \mathbf {Q}= \left[ \begin{array}{ccc} q \mathbf {I} &{} &{} \mathbf {0} \\ &{}&{}\\ \mathbf {0} &{} &{} \mathbf {I}\\ \end{array}\right] \end{aligned}$$

(13)

where q is a scalar weighting factor.

Assuming that all states are known during the analyzed time interval, the gain matrix is:

$$\begin{aligned} \mathbf {G} = \mathbf {R}^{-1} \mathbf {B}^\mathrm {T} \mathbf {P} \end{aligned}$$

(14)

where ${\mathbf {P}}$ is the solution of the algebraic Riccati equation [13]:

$$\begin{aligned} {\mathbf {A}}^\mathrm {T} {\mathbf {P}} + {\mathbf {P}} \mathbf {A} - {\mathbf {P}}{{\mathbf {B}}}{{\mathbf {B}}}^\mathrm {T} {\mathbf {P}} + \mathbf {Q} = \mathbf {0} \end{aligned}$$

(15)

The structure is considered at rest initially, i.e., $\mathbf {x}(0) = \mathbf {0}$, and then an unit impulsive load f(t) is applied at the input point represented in Fig. 2. Displacement responses u(t) are evaluated at the same point. The LQR weighing factor q was chosen as the maximum value that satisfies the condition $-250\ \mathrm {V}< \phi (t) < 250\ \mathrm {V}$ for any $t \in \left[ 0, t_f \right]$, as presented in Fig. 5.

Fig. 5.

Maximum absolute control voltage as a function of the LQR weighing factor q.

An overview of the simulated control models is presented in Table 1 for both examples in terms of the LQR weighing factor (q), RMS displacement ($u_{RMS}$), and RMS control voltage ($\phi _{RMS}$).

Table 1. Displacements and input voltages when applying the LQR controller.

Solutions with optimized polarization resulted in piezoelectric actuators with improved control performances. For both cases, higher control gains can be applied without exceeding a maximum voltage condition. This operating condition is a suitable way to define the control gains since exceeding the maximum voltage may cause depolarization and irreversible damage to the piezoelectric material.

5 Concluding Remarks

A simultaneous approach for the design of flexible structures with minimal compliance and optimized piezoelectric actuators was studied. One can observe that there is no significant differences in the topologies. It is explained by the assumption of computing only the design variables $\varphi$ when minimizing the compliance objective function ($f_s$). The solver would distribute the piezoelectric material aiming at maximizing the structural stiffness if the design variables $\rho$ were calculated in this optimization problem and, therefore, it could depreciate the controllability objective function ($f_c$). Related to the AVC problem, the optimized structures were analyzed by means of an LQR controller and the piezoelectric actuators with optimized polarization presented improved controllability measure and control performance. An important feature of this approach is that, for the studied examples, higher control gains can be applied to the actuators with optimized polarization without exceeding a control voltage limit.