A Boundary Auto-Location Algorithm for the Prediction of Milling Stability Lobe Diagram

Abstract

Chatter is known as a main factor that limits the machining quality and efficiency, and one universal solution is to predict occurrences of chatter via calculating the stability lobe diagram (SLD), such as time-domain methods, which are relatively time-consuming. Thus, based on time-domain methods, a boundary auto-location algorithm for the prediction of SLD in milling is proposed. In the proposed method, by setting a series of judgements based on the state of the transition matrix of the dynamic system, the calculation trajectory automatically surrounds the stability boundary line except isolated islands. Only the points on and around the stability boundary were calculated to draw SLD. The contrast simulations were conducted to verify the calculation efficiency of the given algorithm. And the results show that the computational time of the proposed method was cut down significantly than that of the traditional method.

1 Introduction

Prediction of stability lobe diagram is a vital method to avoid chatter that limits the quality and efficiency of manufacturing. However, the calculation of the stability prediction relate to plenty of parameters, such as modal parameters, cutting parameters and so on. It is time-consuming to calculate all of the points’ stability of the parameters space, like the robotic milling. Therefore, a boundary auto-location algorithm is proposed to solve this issue in the prediction of SLD.

With respect to the prediction of cutting stability, so far there are two major methods: one is the frequency-domain method [1, 2], which is characterized by high-computational-efficiency and relatively low prediction accuracy [3]; another is time-domain method [4, 5], which is time-consuming and has higher prediction accuracy than the former. For the cutting system, the stability can be predicted by solving its feature equation in the former method and the time-periodic delayed-differential equation in the later method. Many efforts have been devoted to improving the prediction accuracy and efficiency in the previous literatures.

Altintas and Budak [1] proposed zero-order method that used the average of the Fourier series of the dynamic milling force to approximate the milling force variation, but is not capable in low radial immersion milling. Merdol and Altintas [2] solved this issue via developing multi-frequency method considering the harmonics of the tooth-passing frequencies. Insperger et al. [4] firstly proposed semi-discretization method (SDM), in which the time-delayed term is discretized. And it is widely adopted to predict the stability of linear-variant time-delayed milling system in time domain. Then, some novel and improved algorithms were proposed to improve the computational efficiency, like full-discretization method (FDM) presented by Ding et al. [5], numerical integration method (NIM) [7], linear approximation of acceleration method (LAAM) [8], Runge-Kutta-based complete discretization method(RKCDM) presented by Li et al. [9], and so on [10, 11]. Also, Li et al. [12] proposed a fast-straight forward method to plot SLD using modal parameters of milling system, but with a relatively low accuracy. In this paper, based on the time-domain methods, a fast algorithm of SLD prediction was developed without consideration of the special SLD contour that called stability isolated islands mentioned in Ref. [13].

All of the time-domain methods focus on the stability calculation of certain cutting parameters, like revolution speed and cut depth which are generally used to represent two-dimension SLD. Therefore, in the traditional method, SLD is given by calculating stabilities of all the points in the discretized cutting parameters space. It is a huge work and time-consuming. In this paper, by setting a series of judgements based on the state of the transition matrix of the dynamic system, only the points on and around the stability boundary were automatically calculated to draw SLD.

The remaining part of this paper is organized as follows: Sect. 2 proposes the boundary auto-location algorithm for prediction of the SLD; Sect. 3 gives the comparisons of computational efficiency between the proposed method and traditional methods. And in Sect. 3 this paper is concluded.

2 The Proposed Algorithm

2.1 The Stability Prediction Model in Milling Process

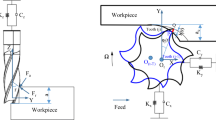
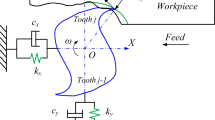
The milling system can be simplified as a two-DOF dynamic system, as shown in Fig. 1, the dynamic model is a time-periodic delayed-differential equation and can be expressed in the form of Eq. (1), as follow:

Fig. 1.

The two-DOF dynamic model of milling system

$$ \varvec{M}\left[ {\begin{array}{*{20}c} {\ddot{x}\left( t \right)} \\ {\ddot{y}\left( t \right)} \\ \end{array} } \right] + \varvec{C}\left[ {\begin{array}{*{20}c} {\dot{x}\left( t \right)} \\ {\dot{y}\left( t \right)} \\ \end{array} } \right] + \varvec{K}\left[ {\begin{array}{*{20}c} {x\left( t \right)} \\ {y\left( t \right)} \\ \end{array} } \right] = \varvec{K}_{{\mathbf{c}}} \left( t \right)\left[ {\begin{array}{*{20}c} {x\left( t \right) - x\left( {t - T} \right)} \\ {y\left( t \right) - y\left( {t - T} \right)} \\ \end{array} } \right] $$

(1)

where $M,\,C,\,K,K_{c} \left( t \right)$ is the mass, damping, stiffness matrices and the cutting force coefficient matrix of dynamic system respectively. $x\left( t \right) - x\left( {t - T} \right)$, $y\left( t \right) - y\left( {t - T} \right)$ represent the dynamic displacement of the cutter between the previous and current revolution on the $X,Y$ direction. $T$ is the tooth-passing period.

By using one of the time-domain methods in the references, the Eq. (1) can be solved and the transition matrix $\varPhi$ of the dynamic system can be obtained. And then according to the Floquet theory, the system is judged as stable when the maximum absolute value of the eigenvalues of the transition matrix $\varPhi$ is less than 1. The following deduction process is developed based on this criterion.

2.2 The Algorithm for Locating the Original Point on the Stability Boundary

Firstly, it is necessary to evenly discretize the cutting parameters space of SLD. Here, the revolution speed and cut depth are used to configure the two-dimension SLD. The revolution speed and cut depth interval are divided into m and n discrete values as follows:

$$ \left\{ {\begin{array}{*{20}c} {S_{i} = \frac{i}{m}(S_{\hbox{max} } - S_{\hbox{min} } ),\text{i} = 1,2, \ldots ,\text{m}} \\ {d_{j} = \frac{j}{n}(d_{\hbox{max} } - d_{\hbox{min} } ),\text{j} = 1,2, \ldots ,\text{n}} \\ \end{array} } \right. $$

(2)

where $S,d$ respectively represent the revolution speed and cut depth.

Then, along the revolution speed incremental direction $i = 1 \to m$, the limitation value of cut depth $d_{chatter}$ related to each discrete revolution speed $S_{i}$ can be sequentially obtained via the algorithm in this paper.

For the proposed boundary auto-location algorithm, there is an initial condition: the original point on the stability boundary should be determined, like the point A shown in the Fig. 2. To locate this original point, the Algorithm I is also developed based on the bisection method.

Fig. 2.

The original point A on the stability boundary

As shown in the Fig. 2, SLD is divided into stable and unstable zone by the stability boundary, and this discrimination method could be formulated as the follow:

$$ \left\{ {\begin{array}{*{20}c} {E_{\phi } \left( {S_{i} ,d_{j} } \right) \ge 1,\quad system\,\,is\,\,unstable} \\ {E_{\phi } \left( {S_{i} ,d_{j} } \right) < 1,{\kern 1pt} \quad system{\kern 1pt} \,\,is\,\,{\kern 1pt} stable} \\ \end{array} } \right. $$

(3)

where $E_{\varPhi } \left( {S_{i} ,d_{j} } \right)$ refers to the maximum absolute value of the eigenvalues of the transition matrix $\varPhi$ under the cutting parameters of $\left( {S_{i} ,d_{j} } \right)$.

Note that $E_{\varPhi } \left( {S_{i} ,d_{j} } \right)$ of all the points on the stability boundary are equal to 1. Therefore, the boundary point $\left( {S_{i} ,d_{chatter} } \right)$ of current discrete revolution speed $S_{i}$ can be located rapidly based on the bisection method.

This bisection method iterates from $i = 1$ to $i = m$ until finding the first boundary point, which one would be identified as the original point A for the next algorithm. Each iteration start with an initial subscript interval of cut depth $\left[ {a,b} \right] = \left[ {1, n} \right]$, and then $a\,and\,b$ would be updated corresponding to the value of $E_{\varPhi } \left( {S_{i} ,d_{j} } \right)$ as follow:

$$ \left\{ {\begin{array}{*{20}c} {b = j,\quad E_{\phi } \left( {S_{i} ,d_{j} } \right) > 1{\kern 1pt} {\kern 1pt} {\kern 1pt} } \\ {a = j,\quad E_{\phi } \left( {S_{i} ,d_{j} } \right) < 1} \\ \end{array} } \right. $$

(4)

Where $\text{j} = \left[ {\left( {a + b} \right)/2} \right]$, and the bracket [ ] is a sign operator which means rounding down the number.

There exist the boundary point among interval $\left[ {a,b} \right]$ when $(E_{\varPhi } \left( {S_{i} ,d_{a} } \right) - 1) \,\cdot\,$$(E_{\varPhi } \left( {S_{i} ,d_{b} } \right) - 1) \le 0$. And then the cutting parameter $\left( {S_{i} ,d_{chatter} } \right)$ of the boundary point can be approximated by some interpolation methods, such as Lagrange Approximation. Here, the boundary point is given by Eq. (5) as follow:

$$ \begin{aligned} & d_{chatter} = d_{a} + \left( {1 - E_{\phi } \left( {S_{i} ,d_{a} } \right)} \right) \cdot \left( {d_{b} - d_{a} } \right)/\left( {E_{\phi } \left( {S_{i} ,d_{b} } \right) - E_{\phi } \left( {S_{i} ,d_{a} } \right)} \right), \\ & if\left( {E_{\phi } \left( {S_{i} ,d_{a} } \right) - 1} \right) \cdot \left( {E_{\phi } \left( {S_{i} ,d_{b} } \right) - 1} \right) \le 0 \\ \end{aligned} $$

(5)

The detailed algorithm can be summarized as Algorithm I. Meanwhile, it is worthy to be mentioned, in general, if there exist one boundary point among subscript interval $\left[ {a,b} \right]$, the relationship that $b = a + 1$ is satisfied. This attribute would be useful for the boundary auto-location algorithm.

2.3 The Boundary Auto-Location Algorithm

As can be seen in Fig. 2, generally, the stability boundary is a contour line, which is known for its continuity and equivalence. Therefore, once one boundary point has been founded, like the aforementioned point A $\left( {S_{i} ,d_{chatter} } \right)$, the next boundary point $\left( {S_{i + 1} ,d_{chatter} } \right)$ can be determined in the neighborhood of it. Based on this it is unnecessary to calculate all the points among $\left[ {d_{1} ,d_{n} } \right]$ to determine the next $d_{chatter}$, only the points on and around the latest stability boundary point are needed.

Assume that, under the current discrete revolution speed $S_{i}$, the $d_{chatter }$ locate in the subscript interval $\left[ {a,b} \right]$ with $b = a + 1$, such as point A. And the next iteration should start from $j = b$ or $j = a$ under the next discrete revolution speed $S_{i + 1}$, in other words, directly calculating the value of the $E_{\varPhi } \left( {S_{i + 1} ,d_{b} } \right)$ or $E_{\varPhi } \left( {S_{i + 1} ,d_{a} } \right)$. Then same as the Algorithm I above, the Eq. (5) also can be used to determine the stability boundary point. But different from the update forms of the parameters $a,b\,and\,j$ that used in Eq. (4), here, those parameters are updated in the form of Eq. (6).

$$ \left\{ {\begin{array}{*{20}c} {b = j,\quad E_{\phi } \left( {S_{i} ,d_{j} } \right) > 1{\kern 1pt} {\kern 1pt} {\kern 1pt} } \\ {a = j,\quad E_{\phi } \left( {S_{i} ,d_{j} } \right) < 1} \\ \end{array} } \right. $$

(6)

In this method, the calculation process would been proceeding along the incremental direction of cut depth when the current point $\left( {S_{i} ,d_{j} } \right)$ is judged as stable and along the decremental direction in the unstable zone. Only a few steps are performed for this process to locate the new stability point, because the attributes of continuity and equivalence of the contour line. The whole trajectory of the calculation process closely surround the stability boundary, just like automatically keep following the tangential direction of the boundary line as can be seen in Fig. 3. The method of this part can be summarized as Algorithm II. Note that, in a special case where the system is stable in whole given cut depth interval $\left( {d_{min} ,d_{max} } \right)$ under current revolution speed, the algorithm would proceed along $d_{max}$ until entering into the unstable zone.

Fig. 3.

Diagram of calculation process of the boundary auto-location algorithm

3 Simulations

The experimental platform is Intel(R) Core(TM) i5-4460, CPU@3.20 GHz, RAM 8 GB, and all of the algorithms are written and executed in MATLAB R2012a. The transition matrix $\varPhi$ of the dynamic system is calculated via using the 2nd-FDM, NIM, and LAAM in the literatures [6], [7], and [8], respectively. The computational efficiency of the proposed method is studied and compared with that of the traditional method. Besides, the SDM in literature [4] is used as a criterion-reference to validate the accuracy of the calculation results.

Here, SLD of single-DOF milling model is represented by parameters space with cut depth and revolution speed under $0\,{\text{mm}} \le d \le 4\,{\text{mm}}$ and $5000\,{\text{rpm}} \le S \,\le$ 10000 rpm. The quantity of discretization are $m = 160$ and $n = 80$. Besides, the tooth-passing period T, which is also an important parameter and proportional to the prediction accuracy in time-domain method to solve Eq. (1), is divided into 40 time intervals in the first three methods. And the tooth-passing period T in the last method is divided into 200 time intervals as a criterion-reference.

The other cutting parameters, including tool, cutting force coefficients, etc., and dynamic parameters, including modal mass, natural frequency, etc., are same as the benchmark data adopted in the references [4, 6,7,8], as can be seen in Table 1.

Table 1. The cutting and dynamic parameters for single-DOF milling model.

The calculation results and comparisons of SLD for single-DOF milling model based on different time-domain methods are shown as Fig. 4. Because the transition matrix $\varPhi$ of every point of SLD is same in each case, there is minimal difference of the stability boundary between the proposed fast algorithm and the traditional algorithm. And the tiny difference here is caused by the calculation method of contour line in MATLAB, which is used in later. The boundary point of the former is determined by Eq. (5), while the interpolation method, like Eq. (5), is also used in revolution speed interval to determine the boundary point of the later.

Fig. 4.

SLD of the fast algorithm based on: (a) 2nd-FDM (b) NIM (c) LAAM

Meanwhile, in the terms of prediction accuracy the LAAM has the highest agreement with the criterion-referenced lobe in Fig. 4(c). The 2nd FDM in Fig. 4(a) is inferior to the former, and the NIM in Fig. 4(b) is lowest.

The comparisons of the computational time of the fast algorithm based on different method are shown in Table 2. There are three results of each case are given on account of the fluctuations of computer performance. And the computational efficiency is represented by the average of those three times. Compared with the traditional method that calculates all the points of SLD, the proposed algorithm enhance the computational time by 18.7 times in the 2nd-FDM-based case, 17.4 times in the NIM-based case and 19.5 times in the NIM-based case.

Table 2. The comparisons of the computational time.

Therefore, the proposed boundary auto-location algorithm significantly improved the computational efficiency of the SLD prediction with same accuracy as the time-domain methods.

4 Conclusions

This paper proposes a boundary auto-location algorithm for the prediction of milling stability lobe diagram without consideration of stability isolated islands. In the proposed method, the calculation trajectory automatically follows the tangential direction of the stability boundary line via setting the judgements based on the state of the transition matrix of the dynamic system and Floquet theory. Only the points on and around the stability boundary were calculated, thereby avoiding to calculate all of the points on SLD. The high-computational-efficiency of the proposed algorithm is validated by the simulations, in which the computational time is enhanced significantly than that of the traditional method.