Keywords

1 Governing Equations and Numerical Implementation

When ice rich frozen soil is involved, the large strain consolidation theory is usually employed to describe soil skeleton mechanical behavior and fluid flow in post-thawed domain [1]. Generally, the consolidation theory includes four parts (i.e., kinematic equation, constitutive equation, Darcy’s law and fluid mass conservation equation), where the three dimensional linear constitutive theory us expressed as,

$$ \mathop {\sigma_{ij} }\limits^{ \bullet } = \frac{E}{(1 + v)} \mathop {\varepsilon_{ij}}\limits^{\bullet} + \frac{vE}{(1 - 2v)(1 + v)} \mathop {\varepsilon_{ij}}\limits^{\bullet} \delta_{ij} - \delta_{ij} u $$
(1)

In which, \( \sigma_{ij} \) is total stress tensor, E is Young’s modulus, v is Poisson’s ratio, δij is the Kronecker symbol, and \( \dot{\varepsilon }_{ij} \) is symmetric deformation tensor.

The thermal conductive equations are implemented to detect the post-thawed domain as following,

$$ \left\{ {\begin{array}{*{20}l} { - h_{{i^{\prime}i}}^{{}} + h_{v} = \rho c\frac{\partial T}{\partial t}} \\ {h_{i} = - \xi T_{{i^{\prime}}} } \\ \end{array} } \right. $$
(2)

In Eq. (2), T is temperature (°C), hv (W/m3) is volumetric heat source intensity; c (J/kg·°C) and ξ (W/m·°C) are specific heat and thermal conductivity, respectively; ρ is the media density (kg/m3). Both of the thermal parameters are temperature dependent, and the details can be referred to literatures [2, 3].

As it can be seen in Eq. (2), the linear stress-strain relationship was used in previous three dimensional analysis of frozen soil thaw consolidation [4, 5]. For ice rich frozen soil, the compressibility of which shows strong nonlinearity, and the nonlinear stress-strain relationship must be used to describe the soil skeleton mechanical behaviours. In the following, a nonlinear relationship between void ratio (e) and compression modulus (Es) is used to modify the original linear thaw consolidation theory, i.e.,

$$ E_{s} = \frac{{1 + e_{0} }}{\lambda }\exp (\frac{{e_{0} - e}}{\lambda }) $$
(3)

where, λ is the slope of K0 compression e-log (stress) curve. The Young’s modulus (E) can be further expressed as,

$$ E = \left( {1 - \frac{{2v^{2} }}{1 - v}} \right)E_{s} $$
(4)

In numerical analysis, a linear interpolation function Eq. (3) for fitting the nonlinear relationship between void ratio and compression modulus is proposed for guaranteeing calculation accuracy and efficiency as,

$$ E_{s(t + t\Delta )} = (1 - \frac{{e_{t + t\Delta } - e_{m} }}{{e_{m + 1} - e_{m} }})E_{s(m)} + \frac{{e_{t + t\Delta } - e_{m} }}{{e_{m + 1} - e_{m} }}E_{s(m + 1)} (e_{m} \le e_{t + t\Delta } \le e_{m + 1} ,m = 0,2,3,{ \ldots },4) $$
(5)

where, Es(m) and em are the data points obtained from the K0 compression e-log (stress) curve.

2 Verification and Results Discussion

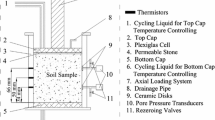
To verify the applicability of the proposed linear interpolation function for fitting the nonlinear relationship between void ratio and compression modulus, a series of 1-D thaw consolidation tests under different dry unit weight and surcharge loads were conducted, and the corresponding parameters for consolidation calculation are obtained in Table 1.

Table 1. Parameters for consolidation calculation.
Full size table

As the two main indexes representing the thaw consolidation behavior of frozen soil, thaw consolidation degree (TD) and the pore water pressure at thawing front (PPTF) are closely related thaw consolidation ratio (TCR) [2, 6], which is defined as,

$$ TCR = \frac{\alpha }{{2(c_{v} )^{1/2} }} $$
(6)

where, α is the thawing rate of soil sample, which is related to the thermal properties and boundaries; cv is the consolidation coefficient and defined as,

$$ c_{v} = \frac{{kE_{s0} }}{{\rho_{w} }} $$
(7)

where, the secant compression modulus (Es0) is used for ease of analyzing the difference between linear and nonlinear relationships.

Figures 1 and 2 show the relationships between thaw consolidation degree (TD), normalized pore water pressure at thawing front (NPPTF) and TCR, where TD and NPPTF are defined as,

Fig. 1.
figure 1

Changes in NPPTF vs. TCR (top)

Full size image
Fig. 2.
figure 2

Changes in TD with TCR (bottom).

Full size image
$$ TD = \frac{{h({\text{t}})}}{{h_{\hbox{max} } ({\text{t}})}} $$
(8)
$$ N_{PPTF} = \frac{u}{{p_{0} }} $$
(9)

where, h(t) is the thaw displacement, \( h_{\hbox{max} } (t) = \frac{{E_{s0} }}{{P_{0} }}x(t) \) and x(t) is the thaw depth at time t. It can be seen that for the calculated results of both stress-strain relationships, NPPTF is proportionally related to TCR, while it is opposite for TD. This indicates that with increase of TCR, more post-thawed pore water is generated, while the rate of drainage (cv) is relatively decreased. Subsequently, the TCD decreases and NPPTF increases. By comparing the calculated results of both relationships (linear and nonlinear), it can be found that for both of the indexes, the linear results are lower than that of nonlinear results, which is due to the calculated differences of both stress-strain relationships on thaw displacement and pore water pressure. In addition, the nonlinear stress-strain relationship shows a higher accuracy on of the TCD and NPPTF (Figs. 1 and 2) than the linear relationship, which indicates the applicability of the proposed linear interpolation function in cold regions engineering when ice rich permafrost is involved.