Relativistic Flows in Astrophysics

Abstract

Most of the matter accreting onto a compact object, or emanating from its vicinity, can be satisfactorily modeled as a fluid. These fluids are different from terrestrial versions. The temperature can range from relativistic values to non-relativistic ones and at high temperature, the fluid is composed of charges and not neutral particles as is the case in the terrestrial version.

We use relativistic equation of state to describe trans-relativistic fluid, around compact objects and at regions far from it. For steady state investigation we took the help of generalized Bernoulli parameter which acts as a constant of motion. We also exploited the fact that the global solution should be of higher entropy and correct boundary conditions. This approach is considered for dissipative accretion flow in curved geometry around black holes, magnetosphere around neutron stars or white dwarfs, and also for magnetically driven outflows. We show that the flow geometry close to a black hole is quite different from a neutron star because of the strong magnetic field around the latter, which has implication on the radiative processes dominant nearby. We also obtained shock solutions for lepton dominated accretion flow around neutron stars, but not around black holes, this is again due to the different flow geometry around the two different types of compact objects. Magnetically driven flows in the special relativistic domain, are able to produce flows which connect both the Alfven and fast sonic points. Numerical simulation of the fluid with relativistic equation of state, shows distinct differences depending on the composition of the flow.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Examples of relativistic flows in astrophysics are invariably linked to matter flow into or out of a compact object. Generally a flow is called relativistic when the fluid moves from one spatial position to the other with a speed (i.e., bulk speed) close to the speed of light. Such insane speed can be achieved by accreting matter close to a black hole (BH) [37], or, when matter around a compact object like BH or neutron star (NS) is violently ejected in the form of astrophysical jets [38]. Since, an accretion disk around a compact object has never been directly observed, but jets have been observed, majority of investigations on relativistic fluid were applied to the studies of jets [2, 5,6,7,8, 13, 33]. By relativistic fluid mechanics, the general trend had been to either use relativistic equations of motion or, use Newtonian equations of motion with pseudo potentials, and use the adiabatic index to be Γ = 4∕3 in the equation of state of the fluid. However, the thermal speed of the particles that constitute an astrophysical fluid, may also approach the speed of light at some regions of the flow but non-relativistic elsewhere, and thereby make the fluid thermally trans-relativistic. In such cases Γ is no more constant, but a function of temperature and composition of the fluid [1, 31, 32].

The exact equation of state (EoS) for relativistic gas has been used in relativistic hydrodynamics tentatively [18, 19]. The major stumbling block is that the perfect EoS is expressed as the ratio of modified Bessel’s function of the second kind of order one, two and three, or two and three, or one and two [1, 15, 31], which depends on the recurrence relation used and are equivalent to each other [36]. An extremely close but algebraic approximation of the perfect EoS was proposed [3, 12, 27] and was used to study relativistic jets in flat metric and jets and accretion flow near a BH and NS in strong gravity.

In the next section, we introduce the relativistic EoS and its properties. In Sect. 3, we discuss application of this equation of state on the dynamics of relativistic outflows in flat metric as well as, curved metric. In Sect. 4.1, we discuss the accretion flow onto magnetized compact objects with hard surface. In Sect. 4.2 we discuss accretion on to black holes, and possible precursor of jets. In the last section we summarize and point out to some future direction and issues.

2 Equation of State

The closure relation between the thermodynamic quantities like the internal energy, pressure and mass density, is called equation of state (EoS) of a fluid, and it helps to solve the equations of hydrodynamics. If the thermal speed of constituent particles are non-relativistic then the internal energy can be computed by obtaining the expression of average energy of the particles in the momentum or configuration space and is given by e _th = p∕(Γ − 1), where p is the isotropic pressure [30]. However, if the constituent particles are identical and executing relativistic motion, then the EoS obtained independently by [1, 15, 31] was shown to be equivalent by [36], and are given by

$$\displaystyle \begin{aligned}e=\rho c^2\frac{3K_3(1/\varTheta)+K_1(1/\varTheta)}{4K_2(1/\varTheta)}=\rho c^2\frac{K_3(1/\varTheta)}{K_2(1/\varTheta)}-p =\rho c^2 \left(3\varTheta +\frac{K_1(1/\varTheta)}{K_2(1/\varTheta)}\right). \end{aligned}$$

Here Θ is proportional to temperature and c is the speed of light in vacuum. We may use the acronym RP (relativistic perfect) to represent the above EoS. The problem is the presence of the ratios of modified Bessel’s function, which are difficult to implement in numerical schemes. Primarily motivated by this fact, we proposed a new EoS which was an extremely close approximate of the exact relativistic EoS, in addition it also satisfies the fundamental Taub’s inequality [32] and is given by [3, 12, 27],

$$\displaystyle \begin{aligned} e=n_{e^-}m_ec^2f; ~~f=(2-\xi)\left[1+\varTheta\left(\frac{9\varTheta+3}{3\varTheta+2}\right)\right] +\xi\left[\frac{1}{\eta}+\varTheta\left(\frac{9\varTheta+3/\eta}{3\varTheta+2/\eta}\right)\right] {} \end{aligned} $$

(1)

where, $\xi =n_{p^+}/n_{e^-}$ is the relative proportion of protons w.r.t electrons, η = m _e∕m _p is the ratio of electron to proton rest mass and Θ = kT∕m _ec ², where k is the Boltzmann constant. We may use the acronym CR to represent the EoS represented by Eq. (1), from the initials of the original proposers. Figure 1 shows how closely CR mimics RP, even for fluids with different composition. The temperatures corresponding to the electron and proton rest mass are marked on the T axis. It is clear if the flow temperature is higher than the proton temperature then Γ → 4∕3. However, for purely leptonic flow, Γ → 4∕3 at temperatures greater than electron rest mass.

Fig. 1

Comparison of Γ as a function of T, between that computed from RP (solid/black, long-dashed/magenta) and CR (dashed/red, dotted/blue) EoS. The two different distributions are for electron-proton flow (ξ = 1) and electron-positron flow (ξ = 0) (Ref: Fig. C1 a of [36]) (Color figure online)

3 Relativistic Fluids: Outflows

The energy-momentum tensor of a fluid is given by

$$\displaystyle \begin{aligned} T^{\mu \nu}=T^{\mu \nu}_{\mathrm{M}}+T^{\mu \nu}_{\mathrm{R}}+T^{\mu \nu}_{\mathrm{EM}}, {} \end{aligned} $$

(2)

where, the suffix M, R and EM represent the three components for matter, radiation and electro-magnetic field of the energy-momentum tensor, that describes a relativistic fluid. The composite form of the equation of motion of the fluid is given by,

$$\displaystyle \begin{aligned} T^{\mu \nu}_{; \nu}=0 {} \end{aligned} $$

(3)

and the particle number (of matter) conservation equation

$$\displaystyle \begin{aligned} (nu^\nu)_{;\nu}=0. {} \end{aligned} $$

(4)

In the above, the Greek alphabets signify space-time components in four space, u ^μ components of four velocity, and n the number density measured in fluid rest frame. One needs to solve Eqs. (3), (4) in a given space-time metric, whose general form is ds ² = g _μνdx ^μdx ^ν.

3.1 Time Dependent Relativistic Hydrodynamics

We developed a relativistic hydrodynamic code ($T^{\mu \nu }_{\mathrm {R}}=T^{\mu \nu }_{\mathrm {EM}}=0$) in special relativity (i.e., g _μμ = (−1, 1, 1, 1), g _μν|_{μ ≠ ν} = 0). The energy momentum tensor of the matter is given by $T^{\mu \nu }_{\mathrm {M}}=(e+p)u^\mu u^\nu + p g^{\mu \nu }$. The fluxes were calculated by using Eq. (1). In Fig. 2, we plot density contour and velocity vectors of relativistic jet launched with Lorentz factor γ _inj = 10. In the computational set up we assumed c = 1. We showed the jet profile and shock positions differ if we change the composition parameter [4, 14].

Fig. 2

Density contour and velocity vector of an astrophysical jet launched with γ _inj = 10, ρ _inj = 0.1 pressure p = 0.01 and ambient density ρ _amb = 100. The jet is composed of electron-proton plasma

3.2 Radiatively Driven Stationary Jets in Curved Space Time

If we consider $T^{\mu \nu }_{\mathrm {EM}}=0$, g _tt = −(1 − 2GM∕rc ²) = −1∕g _rr;g _θθ = r ², g _ϕϕ = r ²sin²θ;g _μν|_{μ ≠ ν} = 0, and ∂∕∂t = ∂∕∂ϕ = 0, we are in the realm of radiatively driven axisymmetric, stationary flow. For u ^r > 0 therefore we are in the regime of radiatively driven jets. The radiative stress tensor is given by $T^{\mu \nu }_{\mathrm {R}}=\int I l^\mu l^\nu d\varOmega$. The momentum balance equation becomes,

$$\displaystyle \begin{aligned} u^r\frac{du^r}{dr}+\frac{1}{r^2}=-\left(1-\frac{2}{r}+u^ru^r\right) \frac{1}{e+p}\frac{dp}{dr}+{\rho}_e\frac{{\sigma\sqrt{g^{rr}}\gamma^3} }{m_e(e+p)}{\Im}^r {} \end{aligned} $$

(5)

$$\displaystyle \begin{aligned} \sigma= \chi_c\sigma_T=\left[\frac{1}{1+\left(\frac{T_e}{4.5 \times 10^8}\right)^{0.86}}\right]\sigma_T {} \end{aligned} $$

(6)

σ _T is Thomson scattering cross section, for χ _c = 1 it is the Thomson scattering cross section. ℑ ^r is a function of radiation moments, and T _e is the electron temperature. The entropy equation is given by

$$\displaystyle \begin{aligned} \frac{de}{dr}-\frac{e+p} {\rho}\frac{d\rho}{dr}=-\frac{\gamma \rho_e(1-\chi_c)R_t}{\sqrt{g^{rr}}}. {} \end{aligned} $$

(7)

Here R _t is radiative contribution representing energy exchange between radiation and fluid:

$$\displaystyle \begin{aligned}R_t=\frac{\sigma}{m_e}\left[\frac{g^{rr} {\mathscr{R}}_0}{v}+\frac{v {\mathscr{R}}_2}{g^{rr}}-2{\mathscr{R}}_1\right] \end{aligned}$$

where, ${\mathscr {R}}_0,~{\mathscr {R}}_1,~{\mathscr {R}}_2$ are the zeroth, first and second moments of radiation field.

Integrating Eqs. (5) and (7) we obtain the generalised Bernoulli parameter

$$\displaystyle \begin{aligned} E=-h u_te^{-X_f}, {} \end{aligned} $$

(8)

where

$$\displaystyle \begin{aligned}X_f=\int dr \frac{\gamma (2-\xi)}{(f+2 \varTheta )\sqrt{g^{rr}}}\left[\Im-(1-\chi_c)R_t\right]. \end{aligned}$$

It is to be remembered that E is a constant of motion, even if radiation imparts momentum and energy to the jet. It was shown that a jet can suffer from stationary internal shocks due to the change in flow geometry, and also due to the radiation field from a moderately thick accretion disk [34, 35]. However, in the Compton scattering regime because a part of the radiation energy is absorbed by the matter, it increases the thermal energy of the jet and produces faster jets. In Fig. 3a, c, d we plot the jet three-velocity v with radial distance r for the disk with same disk luminosity. The jet generalized Bernoulli parameter E is reduced from 1.2 to 1.07 to 1.04. In Fig. 3a, b we compare the three velocity and temperature of the jet with E = 1.2, and show that both the velocity and temperature of the jet is more in the Compton regime than the Thomson scattering regime by about 20%. Figure 3c shows the existence of an internal shock in the jet.

Fig. 3

Comparison of radiatively driven jet for (a), (b) E = 1.2, (c) E = 1.07 and (d) E = 1.04. The solutions presented are electron-proton flow or ξ = 1

3.3 Relativistic MHD

Magnetically driven outflow was also studied with relativistic EoS. The electro-magnetic component of the energy momentum tensor is

$$\displaystyle \begin{aligned} T^{\mu \nu}_{\mathrm{EM}}=F^\mu_{\sigma}F^{\nu \sigma}-\frac{g^{\mu \nu}F^{\lambda \sigma}F_{\lambda \sigma}}{4}. \end{aligned} $$

(9)

Along with this, one has to also solve the electro-magnetic Maxwell’s equations which are,

$$\displaystyle \begin{aligned}\partial_\mu F_{\nu \lambda}+\partial_\nu F_{\lambda \mu}+\partial_\lambda F_{\mu \nu}=0; ~\&~~ F^{\mu \nu}_{;\nu}=-J^\mu , \end{aligned}$$

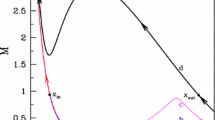
here, F _μν is the electro magnetic field tensor. We followed the methodologies of [33], but used CR EoS instead of fixed Γ EoS and obtained trans Alvenic and trans-fast MHD outflows in flat metric (see Fig. 4). The slow critical point is not obtained without gravity.

Fig. 4

(a) The Alven Mach number M with cylindrical radial distance in units of light cylinder radius. (b) Cylindrical radial coordinate x with the axial coordinate z is plotted. Junction between solid and dotted curve is the Alfven point, while between dotted and dashed curve is the fast sonic point. The solutions presented are electron proton flow or ξ = 1

4 Accretion Flows

4.1 Around Black Holes

Our investigation on accretion flows around black holes started mainly with fixed Γ EoS [10, 16, 17, 21, 25, 26]. Since the temperature distribution of an accretion flow varies by 3–4 order of magnitude, therefore from Fig. 1 it is clear that, the relativistic EoS has to be considered for correct physics. We used the CR EoS on accretion flow on to black holes in the inviscid as well as in the viscous regime [3, 9, 11, 12, 22,23,24]. Inviscid solutions are relatively easy to obtain, simply because, for a given specific energy and angular momentum, the sonic or critical points can be found out uniquely. However, for dissipative flow, the critical points cannot be known apriori. We integrated all the equations of motion in steady state to obtain the generalized Bernoulli parameter, and used it to generate the global solutions. The generalized Bernoulli parameter is expressed as,

$$\displaystyle \begin{aligned} E=h\gamma_v \mathrm{exp}X_f {} \end{aligned} $$

(10)

$$\displaystyle \begin{aligned}X_{f1}= \int\left[\frac{1-a^2_s/r^2}{r^2(1-2/r+a^2_s/r^2)}+\frac{l^2}{2r^3{\mathscr{D}}\gamma^2_v}- \frac{(0.5r^3{\mathscr{A}}+r^3-a^2_s)(l^2/{\mathscr{A}}+\omega\gamma \sqrt{\frac{\mathscr{A}}{\mathscr{D}}})}{r^2\gamma^2_v} \right]dr \end{aligned}$$

$$\displaystyle \begin{aligned}X_{f2}=\int\left[\frac{g^{\phi \phi}g_{rr}{\tilde \tau}\rho u^r (L-L_0)^2}{2\eta(f+2\varTheta)}- \frac{\varLambda}{(e+p)u^r g^{rr}\gamma^2_v}-\frac{S^r}{(e+p){\mathscr{D}}} \right]dr \end{aligned}$$

and

$$\displaystyle \begin{aligned}X_f=X_{f1}+X_{f2}, \end{aligned}$$

S ^r = u ^rt _ϕrσ ^rϕ, t _μν are the components of viscous stress tensor, and σ _μν are components of shear tensor, Λ is the combined radiative cooling term, ${\tilde \tau }$ is the composition function, L = hu _ϕ, γ _v is the Lorentz factor related to three velocity along the radial direction, γ is the total Lorentz factor, ${\mathscr {A}}= 1+a^2_s/r^2+2a^2_s/r^3$, and ${\mathscr {D}}=1-2/r+a^2_s/r^2$, where a _s is the Kerr parameter. E is constant of motion even in presence of viscosity and cooling. We use this constant of motion to obtain all possible accretion solutions.

We found that, accretion solutions may admit shock solutions, but in addition to energy or angular momentum of the flow, the fluid has to contain significant protons to make it hot enough. Accretion flows are convergent flows and become hotter as they accrete towards the central object. Due to the property of the space-time around a black hole, the inflow geometry is approximately a radial flow, independent of the nature of flow geometry further out. Lepton dominated flows are not hot, and even in convergent flow on to a black hole, it only becomes hot enough to produce a sonic point close to the horizon and not hot enough to form a shock. Therefore, lepton dominated accretion flow around a black hole cannot produce a shock or very high energy radiation, and this is true for inviscid as well as viscous accretion flow as well.

We also estimated formation of bipolar jets from accretion flows around black holes. We solved the equations of Von-Zeipel surfaces to obtain the jet streamlines. We showed that for Kerr parameter a _s > 0.6, shocks can even form in jets. Interestingly, the shock in jets imposed by the curved space-time of a highly spinning black hole, is stronger than shock in accretion flow. The related radiative properties is yet to be worked out.

4.2 Accretion Around Compact Objects with Hard Surface

Accretion flow onto a neutron star or a white dwarf is different from that around a black hole, essentially on two accounts—(1) neutron stars or white dwarfs have hard surfaces, while a black hole has none, and (2) space time around a neutron star or white dwarf has intrinsic magnetic field anchored to the star itself, but a black hole has no intrinsic magnetic field.

We solved the equations of motion in the strong field approximation and showed that in addition to the shock formed close to the star surface, there is a possibility of a second shock forming further away from the surface. Moreover, we also showed that the temperature profile considered is distinctively different if one considers a fixed Γ EoS or CR EoS [28, 29]. Another major difference is in the flow geometry around a neutron star, controlled by the magnetic field around it. The cross-section decreases at a steeper rate than a radial flow geometry, such that shocks may form even for lepton dominated accretion flow. The major advancement in this field is in consideration of cooling processes in order to obtain a solution which matches the inner boundary condition on the surface of the star.

5 Summary and Future Direction

In this paper we showed, how our understanding of relativistic fluid-mechanics as applied to astrophysics has affected our understanding of the physics related to compact objects. We showed that, the composition indeed affects the flow structure. The choice of Γ in fixed Γ EoS is critical to obtain a magnetically driven outflow which passes through both the Alfven and fast points. But using CR EoS relieves us from such constraints. In relativistic simulations we obtained flow structure which depend on composition of relativistic jets, which is not seen in simulations with fixed Γ EoS. Accretion of lepton dominated flows around a black hole is distinctly different from that around a neutron star. We also showed that if some protons are present in the accretion flow then high energy phenomena like shocks will occur for some choice of flow parameters. Some workers have used relativistic EoS and failed to detect accretion shock around black holes [20]. Their limitation was that they used electron-positron flow, which will not only not show shocks but also fail to produce multiple sonic points even in the inviscid limit.

Two major aspects remains to be investigated, (1) two temperature accretion solution with CR EoS, (2) treating ξ as a flow variable rather than a constant. The problem with two temperature solution is that, there is another increase in flow variable i.e., instead of one temperature Θ, we now have two temperatures Θ _e and Θ _p, without any increase of the number of governing equations. Therefore, one can construct multiple transonic solutions for the same generalized Bernoulli parameter. In Fig. 5 we show three transonic two temperature Bondi solution in general relativity, all corresponds to the same E and ${\dot M}$. One needs to find a principle to try and obtain the unique two temperature solution. In addition, one has also to consider how a variable ξ would affect the solutions.

Fig. 5

Transonic Bondi two-temperature solution in Schwarzschild metric for the same E = 1.0001, ${\dot M}=0.1$ and M _BH = 10 but multiple transonic solutions. Here ξ = 1, accretion rate ${\dot M}$ is in units of Eddington rate and black hole mass, in units of solar mass