1 Extending the Schwarzschild Solution Beyond the Singularity

As it is well known, the Schwarzschild solution of Einstein’s equation is

$$\begin{aligned} \text {d} s^2 = -\left( 1-\frac{2m}{r}\right) \text {d} t^2 + \left( 1-\frac{2m}{r}\right) ^{-1}\text {d} r^2 + r^2\text {d}\sigma ^2, \end{aligned}$$
(8.1)

where

$$\begin{aligned} \text {d}\sigma ^2 = \text {d}\theta ^2 + \sin ^2\theta \text {d} \phi ^2 \end{aligned}$$
(8.2)

is the metric of the unit sphere \(S^2\), m the mass of the body, and the units are chosen such that \(c=1\) and \(G=1\) (see for example [1], p. 149). It represents a spherically symmetric static and electrically neutral black hole. The metric (8.1) has singularities at \(r=0\) and \(r=2m\), which puzzled Schwarzschild, who decided to replace the coordinate r with \(R=r-2m\), so that the only singularity is in the new origin \(R=0\).

However, there are other coordinates for the Schwarzschild black hole, which remove the singularity \(r=2m\), for example the Eddington–Finkelstein coordinates [2, 3]. This shows that the event horizon singularity is due to the coordinates, which themselves are singular.

Unfortunately, changing the coordinates cannot be used to remove the singularity \(r=0\), as can be seen from the fact that the Kretschmann scalar \(R_{abcd}R^{abcd}\) is infinite at \(r=0\) in any coordinates.

Fortunately, coordinate transformations can remove “half” of the singularity, so that the metric \(g_{ab}\) is made finite and extends analytically beyond the singularity [4].

Theorem 8.1

The Schwarzschild metric can be extended analytically at \(r=0\).

Proof

To see this, let us apply the coordinate transformation

$$\begin{aligned} \begin{array}{l} \left\{ \begin{array}{ll} r &{}= \tau ^2 \\ t &{}= \xi \tau ^T \\ \end{array} \right. \\ \end{array} \end{aligned}$$
(8.3)

where \(T\ge 2\) is an integer. Then, the components of the Jacobian matrix are

$$\begin{aligned} \frac{\partial r}{\partial \tau } = 2\tau ,\, \frac{\partial r}{\partial \xi } = 0,\, \frac{\partial t}{\partial \tau } = T\xi \tau ^{T-1},\, \frac{\partial t}{\partial \xi } = \tau ^T. \end{aligned}$$
(8.4)

In the new coordinates, the components of the metric metric become

$$\begin{aligned} g_{\tau \tau } = -\frac{4\tau ^4}{2 m - \tau ^2} + T^2\xi ^2(2m - \tau ^2) \tau ^{2T-4} \end{aligned}$$
(8.5)
$$\begin{aligned} g_{\tau \xi } = T\xi (2m - \tau ^2) \tau ^{2T-3}\end{aligned}$$
(8.6)
$$\begin{aligned} g_{\xi \xi } = (2m - \tau ^2) \tau ^{2T-2} \end{aligned}$$
(8.7)

and its determinant

$$\begin{aligned} \det g = - 4 \tau ^{2T+2}. \end{aligned}$$
(8.8)

Then, the four-metric becomes

$$\begin{aligned} \text {d} s^2 = -\frac{4\tau ^4}{2m-\tau ^2}\text {d} \tau ^2 + (2m-\tau ^2)\tau ^{2T-4}(T\xi \text {d}\tau + \tau \text {d}\xi )^2 + \tau ^4\text {d}\sigma ^2, \end{aligned}$$
(8.9)

which remains finite and is in fact analytic at \(r=0\).    \(\square \)

Given that T can be any integer \(T\ge 2\), we have obtained an infinite number of solutions. However, a unique solution among them has special properties, as I will explain in the following.

2 The Most Regular Extension

From geometric point of view, the problem with singular metrics is the following. In semi-Riemannian geometry (where the metric is regular), one can define in a natural way a unique connection which preserves the metric and is torsionless. Then, we can define covariant derivatives for tensor fields, which enable us to write field equations. Also, the curvature tensor, needed for the Einstein equation, can be defined and is unique. But if the metric becomes singular, there is no way to define a covariant derivative and curvature tensor by usual means. The reason is that both the metric tensor \(g_{ab}\) and its reciprocal \(g^{ab}\) are used in the construction of these objects. When \(g_{ab}\) has infinite components–as it happens in the Schwarzschild metric (8.1), the connection and curvature can no longer be defined. Even if all of the components of \(g_{ab}\) are finite, but it is degenerate (its determinant vanishes), \(g^{ab}\) is not defined or is singular, and one cannot define the connection and curvature. If the metric is degenerate with constant signature, Kupeli showed one can define a sort of connection and curvature, but his construction is not invariant and not unique, relying on choosing at each point a subspace of the tangent space complementary to the isotropic subspace [5, 6]. But in [7, 8] it was shown that we can do this in an invariant way, and it also works for a large class of metrics with variable signature (which are the ones needed in GR). For this kind of metrics (named semi-regular in [7]) the covariant derivatives can be defined for a large class of differential forms. Also, a differential operator which plays the same role as the covariant derivative can be defined for vector fields. It turns out that for semi-regular metrics we can also define the Riemann curvature tensor \(R_{abcd}\) (although \(R^a{}_{bcd}\) usually is still singular). Moreover, the Einstein equation can be cast in a form which has the same content outside the singularities, but also works at semi-regular singularities [7, 9].

If the spacetime events where the metric is regular form a dense subset of the spacetime, the metric is semi-regular if the contractions \(g^{st}\Gamma _{abs}\Gamma _{cdt}\) are smooth [7], where \(\Gamma _{abc}=\frac{1}{2} (\partial _a g_{bc} + \partial _b g_{ca} - \partial _c g_{ab})\) are Christoffel’s symbols of the first kind. The reciprocal metric \(g^{st}\) becomes infinite at the singularity, but \(g^{st}\Gamma _{abs}\Gamma _{cdt}\) remains smooth. For a general and invariant definition of semi-regular metrics see [7].

Among the solutions (8.9), there is only one with semi-regular metric [4].

Theorem 8.2

The solution (8.9) can be extended analytically so that the singularity at \(r=0\) is semi-regular, if and only if \(T=4\).

Proof

In the coordinate system (8.3), Christoffel’s symbols of the first kind \(\Gamma _{abc}\) are also smooth. Since at \(r=0\) the determinant of the metric vanishes, \(g^{st}\) is singular. But we can find T so that \(\Gamma _{abs}\Gamma _{cdt}\) compensates this singularity and the contractions \(g^{st}\Gamma _{abs}\Gamma _{cdt}\) are smooth.

The reciprocal metric has the components

$$\begin{aligned} g^{\tau \tau } = -\frac{1}{4}(2m - \tau ^2)\tau ^{-4} \end{aligned}$$
(8.10)
$$\begin{aligned} g^{\tau \xi } = \frac{1}{4}T\xi (2m - \tau ^2)\tau ^{-5} \end{aligned}$$
(8.11)
$$\begin{aligned} g^{\xi \xi } = \frac{\tau ^{-2T+2}}{2 m - \tau ^2} - \frac{1}{4}T^2 \xi ^2 (2m - \tau ^2)\tau ^{-6} \end{aligned}$$
(8.12)

The partial derivatives of the coefficients of the metric are

$$\begin{aligned} \partial _{\tau }g_{\tau \tau } = 8\frac{\tau ^5 - 4m\tau ^3}{(2 m - \tau ^2)^2} + 2T^2(2T-4) m \xi ^2\tau ^{2T-5}- T^2 (2T-2)\xi ^2\tau ^{2T-3}, \end{aligned}$$
(8.13)
$$\begin{aligned} \partial _{\tau }g_{\tau \xi } = 2 T (2T-3) m\xi \tau ^{2T-4} - T (2T-1) \xi \tau ^{2T-2}, \end{aligned}$$
(8.14)
$$\begin{aligned} \partial _{\tau }g_{\xi \xi } = 2 m (2T-2)\tau ^{2T-3} - 2T\tau ^{2T-1}, \end{aligned}$$
(8.15)
$$\begin{aligned} \partial _{\xi }g_{\tau \tau } = 2 T^2 \xi (2m - \tau ^2)\tau ^{2T-4}, \end{aligned}$$
(8.16)
$$\begin{aligned} \partial _{\xi }g_{\tau \xi } = T(2m - \tau ^2)\tau ^{2T-3}, \end{aligned}$$
(8.17)
$$\begin{aligned} \partial _{\xi }g_{\xi \xi } = 0. \end{aligned}$$
(8.18)

From (8.13)–(8.18) we find that the least power of \(\tau \) in the partial derivatives of the metric is \(\min (3,2T-5)\). From the (8.10)–(8.12), the least power of \(\tau \) in the reciprocal metric is \(\min (-6,-2T+2)\). Hence, the least power of \(\tau \) in \(g^{st}\Gamma _{abs}\Gamma _{cdt}\) is non-negative only if

$$\begin{aligned} -1 - 2T + 3\min (3,2T-5) \ge 0. \end{aligned}$$
(8.19)

Therefore \(g^{st}\Gamma _{abs}\Gamma _{cdt}\) are smooth only for \(T=4\), and the metric in two dimensions \((\tau ,\xi )\) is semi-regular. The metric in all four dimensions is the warped product between the two-dimensional space \((\tau ,\xi )\) and the sphere \(S^2\), with warping function \(\tau ^2\), which according to [10], is semi-regular.    \(\square \)

The geodesics of the extended solution are given by

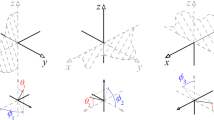
$$\begin{aligned} \frac{\text {d}\xi }{\text {d}\tau } = -\frac{4\xi }{\tau } \pm \frac{2}{(2 m - \tau ^2)\tau }, \end{aligned}$$
(8.20)

which become tangent to the hypersurface \(\tau =0\). The causal structure is represented in Fig. 8.1. We can see that, although the lightcones at events from the singularity are flattened, they have the same topology as those outside the singularity [11].

Fig. 8.1
figure 1

The causal structure of the extended Schwarzschild solution. The lightcones at the singularity are flattened, but they have the same topology as the lightcones outside the singularity

Full size image

3 Globally Hyperbolic Spacetimes with Black Holes

The analytic extension of the Schwarzschild metric from (8.9) is symmetric at the time reversal \(\tau \mapsto -\tau \), which means that it extends beyond the singularity as a white hole. If we modify the Schwarzschild solution to describe a black hole which forms by gravitational collapse, for example as in the Oppenheimer–Snyder model [12], then the solution extends beyond the singularity as an evaporating black hole (Fig.  8.2b). It is interesting that, while one would normally expect that spacetime ends at the singularity (Fig. 8.2a), solution (8.9) does not behave like this, and is compatible with globally hyperbolic spacetimes like that in Fig. 8.2b [13].

In order for information to be preserved, this is not enough. The field equations normally involve covariant derivatives, which are not defined in general when the metric is degenerate. But the solution (8.9) with \(T=4\) allows us to define covariant derivatives and even to rewrite the Einstein equation without infinities [7, 9]. What about other fields? In [14] it is shown how we can write the Maxwell and Yang–Mills equations when the metric is semi-regular. There are still some open problems related to this, in particular how to formulate the Dirac equation for semi-regular metrics.

Fig. 8.2
figure 2

a Standard evaporating black hole, whose singularity destroys the information. b Evaporating black hole extended through the singularity preserves information

Full size image

4 Implications of Singularities to Quantum Gravity

The dimension of Newton’s constant is \(2-D=-2\) in mass units, where D is the dimension of spacetime. This makes Quantum Gravity (QG) perturbatively non-renormalizable even without matter, at two loops [15, 16], by requiring an infinite number of higher derivative counterterms, with their coupling constants. Various approaches to make QG perturbatively renormalizable indicate that in the UV limit a dimensional reduction to two dimensions takes place (for a review, see [17]), either as a consequence of other hypotheses, or by being directly postulated to obtain the desired result.

At a semi-regular singularity, the metric becomes degenerate, behaving like a lower-dimension metric. Moreover, the Weyl curvature tensor also becomes lower-dimensional, and for this reason it vanishes [18]. Such effects happen at the singularities of the Schwarzschild, but also of the charged and rotating black holes [8]. In particular they accompany pointlike particles. Some of the dimensional reduction effects postulated in several approaches to QG follow naturally at singularities [19]. This suggests that when we use perturbative methods, by taking into consideration the corrections introduced by the singularities, the desired dimensional reduction occurs naturally.