Thermal Analysis of Glass

Abstract

This chapter explores the use of thermal analysis in the characterization of glassy materials. Common characterization methods are described as well as a basic overview of the techniques mentioned. Differential scanning calorimetry, thermomechanical analysis, and measurement of glass viscosity are among the primary topics covered. The inner workings of each of the instruments in question is touched upon, along with general calibration procedures and best practices for measurement. Where appropriate, basic material science principles are used to improve the readers' understanding of the reason for a measurement or particular method. While outlining the most important instruments in the thermal analysis of glasses, key glass properties such as glass transition temperature, crystallization temperature, melting temperature, and softening point are explained. Finally, a discussion of glass viscosity necessary for an understanding of the most common viscosity measurement instruments and methods is included.

Thermal analysis is a major part of scientific discovery. Scientists use the thermal radiation of distant objects to interpret the history of gas expansion in the far reaches of the known universe on a scale of 10's of Giga-light-years. On the other end of the spectrum, thermal analysis can be used in material science to probe the bonding of molecules on a scale of 10's of nanometers. The field of material science relies heavily on thermal analysis, while in the study of glass, it is absolutely essential. Thermal analysis in this case is testing that analyzes the properties of a material with thermal energy. In materials, the study of thermal properties is most often carried out with either the stimulus or the measurement of temperature. The measurement of temperature is the easiest and most common way to characterize the thermal properties of a material. Thermocouples and thermistors are well characterized, well understood, and relatively inexpensive technologies used to measure the temperature of a given target. Thermocouples in particular are in widespread use and capable of very accurate temperature measurement over a wide range of temperatures. Different types of thermocouples are used to characterize different temperatures, and the most common types are capable of measuring temperatures from well below freezing to nearly ${\mathrm{1500}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$. This ability to measure temperature over such a large range makes characterization of many glass properties possible.

Temperature in itself is often not sufficient to reveal details about a material's thermodynamic response to nonthermodynamic stimuli or its nonthermodynamic response to thermodynamic stimuli. When temperature measurement is combined with the measurement of heat flow, which is also dependent on temperature measurement over a physical distance, a large amount of material property information can be gained. Heat capacity, thermal conductivity, phase change temperatures, and other parameters can be measured and analyzed using thermal analysis.

The broader field of material science, into which glass science falls, often utilizes nonthermal testing methods to determine material properties. Mechanical characterization methods are useful for determining material properties like hardness, Young's Modulus, fracture toughness, and related values. However, mechanical testing of glasses can be difficult. This difficulty is because of the fracture mechanisms in glasses. Crystalline materials fracture along crystal planes; the fracture can be aided by defects in the material. Because of this, crystalline materials made by similar processes and having a similar concentration of defects exhibit consistent mechanical properties. Glasses are more difficult to analyze mechanically because flaws and imperfections in the material's surface are usually the dominant modes of fracture. This means that slight cracks, chips, or irregularities in the glass surface can cause the mechanical properties, measured by mechanical means, to vary greatly. Mechanical testing of glasses requires extensive sample preparation, aided by the testing of a large volume of samples in order to statistically determine the validity of measured results. This is one of the main reasons that glass scientists rely heavily on thermal analysis. Another reason that mechanical testing of glasses is not as common as thermal analysis, is that glasses are typically used in nonstructural applications. There are exceptions to this, of course, but a lack of load-bearing applications and the difficulty of mechanical property measurements makes thermal analysis a more attractive tool for characterizing glasses.

The thermal analysis methods discussed in this chapter generally fit into one of two main categories. The first is what we will call thermodynamic properties; this includes material properties such as phase transitions, glass transition temperatures, decomposition temperatures, etc. These are thermal properties that are uncovered by modulating the temperature of the sample and measuring the thermal response. Thermal properties are responses of the material to thermal changes that have thermodynamic form. When a material is heated past melting, the additional heat energy input is not the only occurrence. The material must go through a transition from one thermodynamic state to another in order to go from solid to liquid.

The second general type of measurement that falls under the umbrella of thermal analysis is the observable mechanical response of a material to an increase or decrease in temperature. Thermal expansion properties and viscosity fall under this type. The actual change in average bond lengths that lead to an apparent thermal expansion are a thermodynamic change. This change in bond lengths with temperature is observed as thermal expansion in both solids and liquids. Similarly, a change in viscosity is observable when a glassy material is heated. The fundamental change behind this is a thermodynamic one, however that change can be measured mechanically. It is possible to measure bond lengths in glasses and in doing so learn how a material's expansion and viscosity behavior scales with temperature, but oftentimes in thermal analysis of glasses a material's macroscopic properties are of more interest. Additionally, x-ray diffraction is used to measure bond lengths in solids and the scientific know-how to carry out this technique precludes its use in many cases [24.1]. Glass scientists in industry and academia often rely on macroscopic thermomechanical testing to obtain the data needed in relation to the expansion and viscosity versus temperature behavior of glasses.

Thermal analysis of glass is a highly empirical part of glass science. As more computing power enables advanced modeling, more experimentation is required to serve as the basis of assumptions and validation of theoretical calculations. Without concrete measurement techniques, models and calculations hover as educated deduction between theory and fact. From simple industrial qualification of the most basic properties, to the pursuit of a detailed understanding of the glass transition, thermal analysis is an indispensable tool for the manufacture and study of glass.

1 Differential Scanning Calorimetry (DSC)

Differential Scanning Calorimetry () is a technique used to detect phase transitions and other thermodynamic events occurring within a material. DSC can detect phase changes such as melting, crystallization, and solidification (or fusion). Additionally, DSC is a powerful tool for measuring percent crystallinity, heat of reaction, and heat capacity in glasses. Not only are DSCs capable of identifying temperatures of reactions as well as the magnitude of energies involved in those reactions, but they are also capable of identifying the kinetics of a given reaction. Reaction kinetics can help glass scientists identify the way in which reactions take place. This is particularly useful when studying the way in which reaction kinetics differ when heating through a reaction as opposed to cooling through a reaction. On the most basic level, a DSC allows a scientist or engineer to determine where in terms of temperature these transition events occur. However, a DSC involves not just the measurement of temperature with respect to transitions but also the magnitude of thermal energy absorbed or evolved by those transitions. If the mass of the sample is accurately known it is possible to determine properties like the heat of fusion, heat capacity of the material in different phases, and other critical material properties.

Before discussing the physical operating principles of DSC, a few basic points related to thermal analysis and reactions within materials should be discussed. The first basic principle to understand when measuring or interpreting the heat flow data output by a DSC is the difference between exothermic and endothermic reactions. An exothermic reaction is one in which heat is one of the byproducts of the reaction. This type of reaction is easily demonstrated when a strong base like potassium hydroxide (KOH) is added to liquid water ($\mathrm{H_{2}O}$). The chemical result of this mixture is a KOH solution that is produced through a very exothermic reaction. The vessel used for such a reaction becomes too hot to touch. This same principle is seen in reactions such as the solidification of liquids, i. e., when a liquid is cooled to its melting point, it must get rid of a significant amount of heat as its structure changes from a disordered liquid to a much lower energy solid. The difference in internal energy between the two states must be output as heat. That is the essence of an exothermic reaction. An endothermic reaction is a reaction that requires energy to be absorbed into the system. This is evident in an everyday task such as boiling water. In order to move from the liquid phase to a higher energy gaseous phase a large amount of energy must be absorbed into the system. Each DSC readout has a positive and negative heat flow direction. It is necessary to carefully observe whether the DSC readout uses the sign convention of exothermic up or exothermic down. This will affect the appearance of the graph and could lead to confusion if not clearly understood. All graphs in this chapter follow the sign convention exothermic up.

DSC measurements produce heat flow versus temperature diagrams as seen in Fig. 24.3; the features of interest in these heat flow diagrams are phase transitions. A phase transition is a thermodynamic transition from one material phase to another (i. e., liquid to gas, solid to liquid, gas to plasma, and the reverse). More specifically, those types of transitions are called 1st-order phase transitions. First-order transitions are defined as phase transitions that show a discontinuity in entropy and volume. Within a particular phase, materials exhibit a continuous entropy versus temperature and volume versus pressure behavior. However, when undergoing a 1st-order phase transition, a latent heat is involved. Latent heat is the energy increase or decrease needed to facilitate a transition, however, this absorption or release of heat does not apparently change the temperature of the material. This increase or decrease in energy without an increase or decrease in temperature or pressure causes an observable peak or valley in a DSC measurement. The practical effect of this can be seen when boiling water. The 1st-order phase transition from liquid to gas creates a mixture of the two phases which are both at ${\mathrm{100}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$; the liquid water which is boiling can never be at a temperature higher than ${\mathrm{100}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$ at standard atmospheric pressure and the latent heat (of vaporization) is being absorbed to complete the transition to steam.

Mathematically, the definition of a 1st-order transition is a transition over which the Gibbs free energy as a function of temperature and pressure is continuous, while the partial derivative of the Gibbs free energy with respect to temperature and with respect to pressure are discontinuous. The Gibbs free energy is essentially the amount of thermodynamic potential energy in a material at constant temperature and pressure. The expressions in (24.1) are discontinuous for a 1st-order transition.

$$S=-\left(\frac{\partial G}{\partial T}\right)_{p}\quad\text{and}\quad V=\left(\frac{\partial G}{\partial p}\right)_{T},$$

(24.1)

where $G$ is the Gibbs free energy, $T$ is temperature, $p$ is pressure, $V$ is volume, and $S$ is entropy.

Glassy materials exhibit what is known as a glass transition. This transition occurs at the glass transition temperature ($T_{\mathrm{g}}$). This transition falls into the category of what is known as a 2nd-order phase transition [24.2]. A 2nd-order phase transition has a continuous Gibbs free energy with respect to temperature and pressure. The first derivatives of Gibbs free energy (24.1) are continuous, but the second derivatives are discontinuous. This is true for all partial 2nd derivatives of Gibbs free energy as functions of temperature and pressure. Equation (24.2) shows the 2nd derivative which has greater relevance when making DSC measurements.

$$C_{p}=-T\left(\frac{\partial^{2}G}{\partial T^{2}}\right)_{p},$$

(24.2)

where $C_{p}$ is the heat capacity, and all other values are the same as those defined in (24.1). Heat capacity is a property that defines how much heat must be input into a specific mass of a material in order to increase its temperature. The SI unit for heat capacity is $\mathrm{J/K}$.

Fig. 24.1

Schematic representation of a Netzsch DSC cell

There are two ways of measuring the flow of heat into a material. The first is called power compensation DSC. Power compensation DSC operates by ensuring that the temperatures of both the sample and the reference are kept identical (as far as possible). In order to keep the temperature equal between two different materials, different magnitudes of power (heat flow) are necessary for each of the different samples. It is this difference in heat flow that provides the essential information on a DSC readout. If the sample is going through a phase transition such as melting which requires an instantaneous, large input of energy to the sample, the heat flow from the DSC will need to be increased to keep the sample and reference at the same temperature. This spike in heat flow will appear on the DSC readout and can be interpreted as the melting point of the sample material.

The other method is called the heat flux method. The heat flux method works by keeping the heat flux to the samples constant and measuring the resultant temperature change. The standard relation between heat flow, ramp rate, and heat capacity for DSC is shown in (24.3).

$$\frac{\mathrm{d}H}{\mathrm{d}t}=C_{p}\left(\frac{\mathrm{d}T}{\mathrm{d}t}\right)+f(T,t)\;,$$

(24.3)

where $H$ is enthalpy in Joules, $t$ is time in seconds, $C_{p}$ is heat capacity in $\mathrm{J/K}$, $T$ is temperature in Kelvin, and $f(T,t)$ is a temperature- and time-dependent function of the system.

The principles that guide how a DSC measures material properties are quite straightforward. The essential makeup of what is called the DSC cell can be seen in Fig. 24.1. DSC is a comparative technique, meaning one reference material is measured alongside the sample material of interest, and the difference between the two is the recorded information. Materials measured in a DSC are placed in pans; these pans can be made of different materials. Most commonly, the pans (Fig. 24.2a-c) are made of aluminum, platinum, or for high temperatures, alumina. The pans can be hermetically sealed or left open to the environment within the DSC cell which is typically flushed with a dry inert gas.

Fig. 24.2a-c

Aluminum DSC pans: top (a) and bottom (b) half and assembled pan (c)

Within the DSC cell, two smooth flat spots mark the placement locations for the sample and reference materials. The pans containing these materials are placed on each of these spots. The skin of the DSC cell is made of a very heat-conductive material, often Inconel.

When considering homogenous crystalline materials, the transitions that can be seen are often clearly defined. As the temperature is increased, transitions from one crystalline phase to another can be observed, and finally melting can be seen. If the temperature is then lowered, solidification and any reversible crystalline phase changes will be seen during cooling. The heights of these peaks or valleys (depending on the direction of the heat flow) combined with the mass of the sample undergoing transition, will allow the various energies associated with those transitions to be calculated.

Fig. 24.3

DSC curve of an example glass ceramic

In the case of glass, the major transitions are the same with some notable exceptions. Glass is amorphous, therefore it has no long range order even when it is in its solid state. Figure 24.3 shows the DSC trace of a glass ceramic material. A glass ceramic is a glass that has been crystallized to some extent; the amount of crystal versus glass in a glass ceramic is typically discussed as $\mathrm{vol.\%}$ crystallinity.

In Fig. 24.3, the key transitions have been noted. Low to high temperature, the first transition that can be seen is a 2nd-order transition known as the glass transition. $T_{\mathrm{g}}$ is the temperature at which a solid glass transitions to a viscous material with a liquid-like structure. The glass transition is a topic of much study in glass science [24.2, 24.3, 24.4, 24.5, 24.6, 24.7]. The next transition, labeled $T_{x1}$, is the first observable crystallization peak. This 1st-order transition from a disordered liquid-like structure occurs in different material phases at different temperatures. This exothermic event involves the release of an amount of energy specific to the mass of the sample and the percentage of the sample made up by the phase that is crystallizing. That energy value, known as the heat of reaction, is calculated in J or kJ as the area under the crystallization peak. The integral of the heat flow during that event produces the enthalpy of the reaction. In Fig. 24.3, the enthalpy of reaction of the 1st crystallization peak is graphically demonstrated.

It is important to note that in a glass or glass ceramic with more than one phase present, there will be a crystallization event for each phase. If those crystallization events are separated in temperature, then it is possible to discern them. In Fig. 24.3, there is more than one crystallization peak. The heat of reaction associated with the first crystalline peak appears higher than the energy associated with the second at $T_{x2}$. It is also possible that there is a third crystallization peak overlapping with the second, but that is not important for this example. The final feature is a melting valley, indicated by $T_{\mathrm{m}}$. This valley shows the melting of at least one phase and, similar to crystallization, the heat of reaction can be measured by calculating the area under the curve. In a multiphase system there could be multiple melting peaks.

Now that the principle behind how a DSC measures heat flow has been explained, as well as the key 1st- and 2nd-order transitions most important to DSC of glasses, we will go on to explain that there are a few variations in measurement technique which are best suited for different measurements within a material. Different techniques are driven by different fundamental questions that the experimenter wants to ask of the material. These techniques are explored below.

1.1 DSC Techniques

1.1.1 Standard DSC

The most common type of DSC measurement used in both industry and academia is a simple ramp rate method. This method involves a sample of known mass (typically a few mg) in a pan, opposite a reference pan that contains either a reference material or sometimes no material at all. DSC samples are most commonly powder, crushed to a fine particle size by mortar and pestle. If very detailed, mass-dependent properties are to be measured, monosized particles are desired. Conduction is the main method of heat transfer in a DSC cell, so good conductive contact between the pan and sample material is necessary for accurate results. The smaller the particle size, the faster each particle will absorb and expel heat energy and the faster the temperature change response will be. In the case of surface crystallization measurements, powder size can strongly affect the measured crystallization response.

Bulk samples are sometimes used in DSC measurements, but the samples must be flat and sometimes polished to make the interface between the bottom of the sample and the sample pan as seamless as possible. In glass science, low-temperature glasses can be synthesized in the DSC pan from raw elements; this creates a sample that has an exceptional interface with the bottom of the pan.

A typical DSC is capable of reaching temperatures of $\approx{\mathrm{800}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$ and heating rates from $\approx 0.1$ to ${\mathrm{100}}\,{\mathrm{{}^{\circ}\mathrm{C}/min}}$. Cooling rates vary based on the equipment and accessories purchased for a DSC. Ambient cooling could be used for cooling rates of $\approx{\mathrm{10}}\,{\mathrm{{}^{\circ}\mathrm{C}/min}}$, forced gas cooling (nitrogen, argon, etc.) could be used for higher cooling rates of $20{-}50\,{\mathrm{{}^{\circ}\mathrm{C}/min}}$. Very high cooling rates can be achieved with liquid nitrogen DSC accessories up to $\approx{\mathrm{100}}\,{\mathrm{{}^{\circ}\mathrm{C}/min}}$ [24.8]. This same liquid nitrogen option can be used to do DSC scans on materials well below room temperature. Most inorganic glasses do not require very low temperature DSC scans because $T_{\mathrm{g}}$ for these types of glasses is typically well above room temperature. However, many polymers, plastics, and rubbers have sub-room temperature $T_{\mathrm{g}}$ and may require liquid nitrogen cooling accessories.

Calibration is crucial when doing thermal analysis of glasses. There are three main types of calibration for a DSC: baseline, temperature, and heat capacity. Establishing the baseline of the DSC involves running the instrument through a temperature window using a ramp rate similar or identical to the intended experimental ramp rate that is planned. This run is usually done without any sample pans; this ensures no influence from differences in the two sample pans. The instrument measures what are typically subtle heat flow differences between the two nodes of the sample and reference nodes of the DSC cell. In theory an empty DSC cell should have a flat heat flow versus temperature signal. In reality that is never exactly the case. So the DSC software takes the slope of the empty cell heat flow signal and removes it by rotating the signal. The result is a software correction that should yield a flat DSC heat flow versus temperature signal. This calibration file is usually present in the background during DSC runs allowing the software to constantly remove the difference in heat flow rate and show data which is free of that bias.

Temperature calibration employs a metal with a well-defined melting temperature that is heated in the DSC until it melts. The melting temperature as determined by the DSC is compared to the known melting temperature of the pure material. The difference is used to calibrate the DSC temperature readings. Several metals (In, Sn, Zn) with various melting temperatures are used in separate runs to calibrate the DSC over the temperature range of interest. The calibration consists of a simple temperature shift to force the DSC temperature readout to match the known melting temperature.

The final type of calibration is the calibration of the DSC's heat capacity measurement. This test involves a bulk sample, usually made of a well-known crystalline material such as sapphire. The heat capacity of the sample is measured and compared to the known heat capacity, this allows a calibration adjustment to be applied. A value known as a DSC cell constant is used to correct for errors in heat capacity measurement [24.9]. The general form of the cell constant calculation can be seen below in (24.4), it is simply the ratio of the known and measured heat capacity of the sample.

$$K=\frac{\left(C_{p}\ \text{Heating Rate}\right)}{\text{Heat Flow}}\;,$$

(24.4)

where $K$ is the dimensionless DSC cell constant, $C_{p}$ is the known heat capacity of the standard samples in $\mathrm{J/(g{\,}{}^{\circ}\mathrm{C})}$, Heating Rate is the programmed heating rate of the DSC for the calibration run in $\mathrm{{}^{\circ}\mathrm{C}/min}$, and Heat Flow is the measured heat flow into the sample in $\mathrm{W/g}$. This calibration takes into account the heat capacity of the DSC cell, hence the same cell constant. When an old DSC cell has been exchanged for a new one a calibration must be done to determine the correct cell constant to use during measurement. It is also advisable to calibrate a DSC when beginning a suite of measurements or greatly changing the temperature range at which samples are being measured.

As with any form of analysis, asking the right question is critical to obtaining a useful answer. Programming a DSC run that ‘‘asks the right questions'' of the glass is dependent on understanding some basic properties of glasses. A typical DSC run involves, at a minimum, a commanded temperature ramp from room temperature up to the final desired temperature, at a constant ramp rate ($\mathrm{{}^{\circ}\mathrm{C}/min}$). The end temperature of the ramp depends on what knowledge is desired. For instance, if an operator only wants to measure the glass transition temperature ($T_{\mathrm{g}}$), then a ramp to $50^{\circ}$ above the anticipated $T_{\mathrm{g}}$ is all that is needed. An investigation of crystallization in glasses requires a higher final temperature. It is important not to forget the sample and reference pan material in this calculation. When studying the crystallization behavior of $\mathrm{As_{40}Se_{60}}$ glass, an aluminum pan is easily able to withstand the necessary temperatures as well as chemical interactions with the glass. However, a platinum pan used with the same glass, even though it has a much higher melting point than aluminum, would be quickly corroded even at relatively low temperatures. On a similar note, reaching the crystallization temperature of a common oxide glass like Schott's N-BK7 would turn an aluminum pan into a puddle and likely ruin an expensive DSC cell. The other thing to keep in mind is to stay below the temperature at which the material under test outgasses. In the best case it is an unnecessary result that can dirty or even corrode the DSC cell, and in the worst it can be a health hazard if the glass under test off-gases toxic constituents.

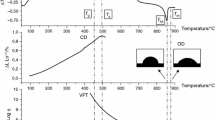
One of the unique things about glassy materials is that they have what is known as a glass transition. As discussed in Sect. 24.1 above, the glass transition is a 2nd-order transition. This is the region of temperature in which the kinetics of the material begin to allow rearrangement of the glass network, upon heating, to achieve thermodynamic equilibrium. Because of this interaction between thermodynamics and kinetics, glasses retain information based on their thermal history. Thermal history is a general term used to describe the unique network structure of a glass based on prior exposures to specific temperatures over specific times and based on heating and cooling rates that the glass was subjected to. In order to talk about thermal history in a more precise way, it is necessary to define something called the fictive temperature $T_{\mathrm{f}}$. Since glass is an amorphous material, its structure is nonperiodic and disorganized compared to the crystalline state for the same material. The structure of a solid glass resembles that of a liquid at a specific temperature, that temperature is known as the fictive temperature [24.10]. Figure 24.4 demonstrates the idea of thermal history and where it comes from. The $x$-axis is temperature and the $y$-axis is some intrinsic property $P(T)$ which is a function of temperature. The blue line represents a generic glass material. The dashed green line is known as the liquidus or liquid equilibrium line of the glass. At high temperatures such as $T_{1}$, where the glass is liquid, the network structure of the glass and therefore the intrinsic properties of the glass will remain on the liquid equilibrium (liquidus) line. As the glass is cooled towards $T_{2}$ however, the viscosity of the glass continually increases until the glass structure is unable to relax faster than the rate at which it is being cooled. The region in which the material behavior diverges from the liquidus line is the glass transition region. At lower temperatures, the glass behaves like an elastic solid and the property versus temperature relationship becomes essentially linear. The straight, dashed red line is extended backwards from the linear region of the blue curve until it intersects with the liquid equilibrium line. The point at which those lines intersect defines the fictive temperature. The rate at which the glass is cooled has an effect on the fictive temperature, and the fictive temperature defines what we call the thermal history. The blue curve in Fig. 24.4 represents a glass that was cooled at a slower rate than the glass represented by the brown curve. This demonstrates the effect of cooling rate on the properties and structure of the glass. Faster cooling results in a higher temperature departure from the liquid equilibrium line and therefore a higher fictive temperature. So, a glass with a higher fictive temperature was cooled at a higher rate than the same glass with a lower fictive temperature, thus yielding different thermal histories and different final results when measuring them side by side.

Fig. 24.4

Intrinsic material property $P$ (e. g., volume) versus temperature graph for a generic glass material (after [24.11])

The thermal history can affect the results of almost any thermal analysis of glass. Take for instance the example in Fig. 24.4. The expression ${\Updelta}P_{\mathrm{L}}$ which in this case is the change in property $P$ while the glass is in the liquid region, is greater for the blue curve than it is for the brown curve. Because the blue curve was cooled or quenched at a slower rate, there was more time for the property to relax than for the brown curve which was cooled at a higher rate. What that means for the glass structure, is that the more slowly cooled glass is closer to liquid equilibrium at room temperature than the glass represented by the brown curve which represents a faster cooling rate. The farther from equilibrium the property $P$ is, the higher the thermodynamic driving force is for the glass to reach the equilibrium line. If a scientist was to heat both glasses up from room temperature at the same rate, the glass farthest from equilibrium would move towards equilibrium at a lower temperature and more energetically than the glass that was cooled more slowly. That is the effect that differing thermal histories can have on, for instance, the measurement of $T_{\mathrm{g}}$ by DSC. For that reason, a common DSC method involves ramping the temperature above the $T_{\mathrm{g}}$ of the glass in order to reset the thermal history of the material. In this way, even glasses with differing fictive temperatures and thermal histories are heated to a temperature that is high enough to allow them to relax to the equilibrium line. Cycling all glasses within a set of experiments in this manner ensures that they have identical thermal histories and removes that potential difference from the experimental results. Then the DSC temperature is dropped to near room temperature and then ramped up through $T_{\mathrm{g}}$ once again. This same method is used on all measured samples ensuring that the measured properties of the glass are not affected by variations in the sample's thermal history. The results of the first run to above $T_{\mathrm{g}}$ and the second run are different. The magnitude of the difference is dependent on how different the glass structures were before and after the annealing step. Figure 24.5 demonstrates how the apparent glass transition is different from the initial ramp to the final ramp.

The first ramp in Fig. 24.5 has a significantly lower dip than the 2nd ramp. In this graph, exothermic is defined as positive on the $y$-axis. Therefore, the $T_{\mathrm{g}}$ feature seen on the 1st ramp absorbed a greater amount of energy to allow it to go through the glass transition from a super cooled liquid state to an equilibrium liquid state. Because the $T_{\mathrm{g}}$ feature on the 1st ramp is more energetic it shows that the glass was further from equilibrium prior to the 1st ramp above $T_{\mathrm{g}}$. The 2nd ramp, which contains a smaller $T_{\mathrm{g}}$ feature shows the difference in apparent thermal history between the two conditions.

Fig. 24.5

DSC example: 1st ramp for annealing and 2nd ramp for $T_{\mathrm{g}}$ measurement

One of the most important and commonly measured thermal properties of glasses is the glass transition temperature ($T_{\mathrm{g}}$). It often appears as a dip in the heat flow graph as the glass absorbs energy to transition from a solid-like state to a liquid-like state. However, not all $T_{\mathrm{g}}$ features appear the same when measured. Both $T_{\mathrm{g}}$ features shown in Fig. 24.5 are comprised of a dip followed by what looks like a recovery or peak directly afterwards; not all $T_{\mathrm{g}}$ features are like this. Some measurements of $T_{\mathrm{g}}$ reveal a dip in the curve that never recovers and simply remains at a lower heat flow baseline. This difference is due to the difference between the temperature at which $T_{\mathrm{g}}$ occurs and the fictive temperature of the glass. If $T_{\mathrm{f}}$ for a given glass is far above $T_{\mathrm{g}}$, that is to say far from equilibrium, the rapidity and energy involved in the glass transition can actually overshoot the equilibrium liquid structure represented by $T_{\mathrm{f}}$. As the glass network relaxes toward equilibrium during $T_{\mathrm{g}}$, the momentum gathered during that transition can sometimes carry the glass structure past equilibrium. At some point the glass has to adjust for that overshoot, this adjustment can be seen when the heat flow during $T_{\mathrm{g}}$ dips and then rises after the minimum is achieved. In cases where $T_{\mathrm{f}}$ is not too high above $T_{\mathrm{g}}$, the glass structure relaxes directly to the equilibrium structure with no overshoot, causing the $T_{\mathrm{g}}$ feature to dip to a minimum and remain at that baseline until the next phase transition.

The glass transition is a 2nd-order phase transition unlike melting or vaporization which are 1st-order transitions. It is generally described as a range of temperature/viscosity below which a glass behaves most like a solid and above which it behaves more like a liquid.

Fig. 24.6

Example of the three most common ways to calculate $T_{\mathrm{g}}$, $T_{\mathrm{g}}$ onset, $T_{\mathrm{g}}$ inflection, $T_{\mathrm{g}}$ peak

There are three accepted ways to indicate $T_{\mathrm{g}}$; Fig. 24.6 gives a graphic example. Each of these three methods are used by various academic and industry professionals, however very rarely is the method of $T_{\mathrm{g}}$ determination noted on datasheets and academic publications. Therefore, for the same glass, different entities often report different $T_{\mathrm{g}}$ values. This can lead to confusion because it causes people to use different temperatures for what they assume to be the same material property.

The first method is called the onset method, which involves drawing a line tangent to the curve just before the transition begins and another line tangent to the curve during the first down slope after $T_{\mathrm{g}}$ begins. This method effectively assigns a temperature to the knee of the glass transition and when used as the reported $T_{\mathrm{g}}$ of a glass, is the value that best describes the beginning or onset of the glass transition region.

The second common way of indicating $T_{\mathrm{g}}$ is the inflection point method. This method is the only one of the three that relies on a mathematical approach for the determination and designation of $T_{\mathrm{g}}$. Directly following the onset knee in the graph, the heat flow curve decreases faster and faster until it hits an inflection point. This is the point where the decrease begins to slow as the heat flow curve heads towards its local transition minimum. The most reliable way of determining this point is by taking the derivative of the heat flow curve and finding the minimum in that region. A local extreme in the derivative indicates an inflection or change in the direction of acceleration. The temperature at which this inflection occurs is called the inflection point $T_{\mathrm{g}}$. This representation of $T_{\mathrm{g}}$ is preferred by some because it is a well-defined mathematical point rather than the intersection of arbitrarily chosen tangents. However, as we discuss below the experimental parameters used during a DSC run have an even greater effect, so in some sense the method of $T_{\mathrm{g}}$ measurement is not the most important factor. The inflection point $T_{\mathrm{g}}$ is the best representation of the center of the glass transition region.

The third method for determining $T_{\mathrm{g}}$ is the peak method. Near the end of the glass transition bump or dip in the heat flow curve, there is another knee which is the opposite of the onset knee. Using the same method of drawing lines tangential to the rising curve before the knee and the approximately flat curve after the knee, the peak $T_{\mathrm{g}}$ is determined. This value gives a temperature for the end of the glass transition region. It is the least commonly used of the three methods. It is important to stress that the width of $T_{\mathrm{g}}$ and the values themselves are just as dependent on the experimental conditions of the DSC run as they are to the method of designating $T_{\mathrm{g}}$.

When measuring the $T_{\mathrm{g}}$ of a glass via DSC, it is important to understand the ramp rate dependence of the observed $T_{\mathrm{g}}$. The basic understanding for this concept is based on the difference between the rate of temperature change induced in the material and the rate of kinetic change in the glass from a solid-like to a liquid-like structure. Take for instance a heating rate of ${\mathrm{1}}\,{\mathrm{{}^{\circ}\mathrm{C}/min}}$ versus a heating rate of ${\mathrm{10}}\,{\mathrm{{}^{\circ}\mathrm{C}/min}}$ for two identical samples with the same thermal history. At the slow heating rate, the speed at which the glass structure can relax towards equilibrium upon passing through $T_{\mathrm{g}}$ is closer to the actual heating rate of the DSC. This means that structural relaxation is taking place along with the temperature increase. Given a higher DSC ramp rate, the structural relaxation will occur at a rate relatively slower compared to the heating rate. The result of this is to push the apparent $T_{\mathrm{g}}$ feature to higher temperatures. Because the heating rate is higher, the relaxation of the glass structure actually lags and does not become apparent in the heat flow until a higher temperature. This is one effect of heating rate. The second is in the energy of the transition or the depth of the $T_{\mathrm{g}}$ feature. A lower heating rate allows the glass to relax along with the heating rate so that the glass gradually comes to equilibrium and remains at equilibrium as the temperature of the DSC increases. A higher heating rate, in addition to pushing the apparent $T_{\mathrm{g}}$ to higher temperatures, has the effect of increasing the difference between the glass structure and the equilibrium liquid state. This causes the resulting 2nd-order transition to be more energetic and therefore results in a $T_{\mathrm{g}}$ feature with a deeper dip and typically a more severe recovery after the structural overshoot past equilibrium [24.12].

Glass is defined by its lack of a crystalline structure in the form of periodic order. There is a temperature or temperature range at which a glass will begin to crystallize ($T_{x}$). Upon reheating of the glass this typically occurs above $T_{\mathrm{g}}$ when the kinetics of the glass speed up enough to allow crystallization to take place on a laboratory time scale. This is accomplished by thermodynamically driving the material system to seek the lowest energy state, which is an ordered or crystalline state. When experimenting with glass in the lab, when making raw glass in industry, and when processing glass into products using heat, staying away from this crystallization temperature or region is imperative. DSC heat flow curves are setup in one of two ways, either heat flow into the sample (endothermic) is positive on the graph or heat flow out of the sample (exothermic) is positive. The examples in this chapter are referenced by exothermic up which means that heat flow out of the sample will be shown as a peak on the graph. Crystallization is an exothermic process, when the glass moves from a relatively high-energy thermodynamic state of disorder to a relatively low-energy thermodynamic state of crystalline order it releases the amount of energy difference between those two states.

The crystallization temperature ($T_{x}$) is defined as the onset of the crystallization peak, and the temperature is determined the same way as the onset of $T_{\mathrm{g}}$. A line tangent to the curve just before the crystallization peak is drawn and a line tangent to the curve just after the beginning of the event is drawn, and the intersection of those two lines define the crystallization onset temperature. Crystallization can also be defined as the peak maximum, however, that is not commonly done because in many applications, once crystallization begins the material becomes unusable as a glass. The other piece of information that can be gleaned from the crystallization peak is the area under the curve (Fig. 24.3 shows an example). This area under the curve combined with the mass of the sample being measured, allows the energy per unit mass of crystallization to be calculated. This value is useful when researching crystallization of glasses and the forces that govern that crystallization [24.13, 24.14].

When observing the generic DSC curve of a generic glass as shown in Fig. 24.3, the final feature that can be detected is the melting feature. In the case of exothermic heat flow being positive, melting is clearly an endothermic process. This means that in order for the now-crystalline material to melt, it must absorb energy. As defined in this section, the melting temperature ($T_{\mathrm{m}}$) can be defined by its onset or its minimum, however as before, once you have begun to melt you are already in trouble from a practical standpoint. Once again the area under the curve of the melting valley will allow you to define the amount of energy needed for melting. If you know the mass of the sample that is being measured, then you can calculate the heat of fusion for that material as in (24.5).

$$H_{x}=\frac{\int q\ \mathrm{d}T}{\text{Heating Rate}}\;,$$

(24.5)

where $H_{x}$ is the intrinsic heat of crystallization in $\mathrm{J/g}$, $q$ is the heat flow measured by DSC in $\mathrm{W/g}$, Heating Rate is the heating rate in $\mathrm{{}^{\circ}\mathrm{C}/s}$, and $T$ is the temperature in $\mathrm{{}^{\circ}\mathrm{C}}$. It is also possible to calculate the total heat of crystallization by multiplying $H_{x}$ by the mass of the measured sample.

These crystallization and melting features are of interest to glass scientists, but from an industrial standpoint it is wise to stay far below either $T_{x}$ or $T_{\mathrm{m}}$ when processing glass material. Aside from the signature temperature measurements of the DSC, the intrinsic heats for crystallization and melting can be determined along with the heat capacity of the material in various phases. Calculations of mass-dependent properties require precise measurement of sample mass.

There is a subset of glassy materials known as glass ceramics which, as the name implies, are a mixture of some volume fraction of crystallized material and some volume fraction of glassy or amorphous material. These materials are most commonly created by first forming and then heat treating a base glass to nucleate and grow crystals within the material. Precise control of the volume fraction of crystal versus glass requires an understanding of the nucleation and crystallization temperatures of the glass as well as the nucleation and crystallization rate at those temperatures. A standard DSC run is not the best way to obtain accurate nucleation and crystallization information, and is discussed in the next section.

When considering DSC measurements of glasses, it is crucial to remember that the phenomena being measured are thermodynamic in nature but are subject to the kinetics of the glass structure. This is why all of the important temperature and material properties above are dependent on the ramp rate of the DSC run. A graphic example of measured material property variation as a function of temperature ramp rate can be seen in Fig. 24.7. Take $T_{\mathrm{g}}$ as an example; for $\mathrm{As_{40}Se_{60}}$ chalcogenide, infrared glass the onset $T_{\mathrm{g}}$ for a ${\mathrm{10}}\,{\mathrm{{}^{\circ}\mathrm{C}/min}}$ ramp rate is approximately ${\mathrm{185}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$. If you were to adjust the ramp rate on such a DSC run to ${\mathrm{100}}\,{\mathrm{{}^{\circ}\mathrm{C}/min}}$ the $T_{\mathrm{g}}$ feature observed on the heat flow curve could easily exceed ${\mathrm{200}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$ [24.11]. The specific form of this temperature dependence was derived by Moynihan et al and can be seen below in (24.6).

$$\frac{\mathrm{d}\ln|q|}{\mathrm{d}\left(\frac{1}{T_{\mathrm{g}}}\right)}=-\frac{\Updelta h^{*}}{R}\;,$$

(24.6)

where $|q|$ is the heating or cooling rate, $\Updelta h$ is the activation enthalpy for the relaxation time controlling structural enthalpy or volume relaxation, and $R$ is the ideal gas constant.

This illustrates the difficulty in thermal analysis of glasses, the material properties reported in so many places are dependent on very specific measurement conditions. In many cases there are no real standard measurements aside from generally accepted industry practices. Researchers must use and report the experimental parameters used for precise DSC measurements. Industrial applications using glass, whether in plate form like windows, or in optics require detailed material properties. It is important that the engineers and scientists using these data understand the parameters and assumptions used to make those measurements and use the data accordingly.

1.1.2 Isothermal DSC

Isothermal DSC measurements are a variation of standard DSC. The main drawback of standard DSC measurements is that all of the measured material responses are heating rate dependent and therefore there exists an influence on the measured properties that is an artifact of the measurement [24.11]. In experimentation of all kinds it is important to remove as many of these measurement artifacts as possible, to minimize the effect until it is negligible, or characterize the effect well enough to adjust the measured data and essentially remove the effect in postprocessing. Measurements such as those that seek to characterize the crystallization thermodynamics of glasses are particularly sensitive to the effects of ramp rate [24.15].

Fig. 24.7

Heat flow versus temperature curves measured at different heating rates by (differential thermal analysis) for a $\mathrm{70TeO_{2}}$-$\mathrm{10Bi_{2}O_{3}}$-20ZnO glass. Reprinted from [24.15] with permission from Elsevier

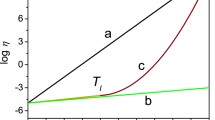
DSC crystallization measurements are a two-part question. Prior to crystal growth in a glass, seed crystals must be nucleated. Nucleation involves the probabilistic appearance and disappearance of very small crystals, and whether a nucleus survives to become a fully fledged crystal is dependent on whether it achieves some critical size as determined by the thermodynamic state of the material. Glasses have one thermodynamic range in which crystals are nucleated and once those nuclei exist there is another thermodynamic range in which those crystals grow. Determining the nucleation and growth behavior for a glass can be done by constructing nucleation-like and growth-like curves for a specific glass. This technique can also be used to compare varying glass compositions in the same family [24.15]. The nucleation-like curve is constructed using the following expression (24.7) defined by Marotta et al [24.16]

$$\ln\left(I_{0}\right)=\frac{E_{\text{c}}}{R}\left(\frac{1}{T_{\text{p}}}-\frac{1}{T_{\text{p}}^{0}}\right)+\text{ Const}\;,$$

(24.7)

where $I_{0}$ is the steady state nucleation rate, $E_{\text{c}}$ is the activation energy for crystallization, $T_{\text{p}}$ is the temperature at the maximum of the exothermic crystallization peak for a glass measured using a specific heating rate and an isothermal hold for a specific amount of time at a temperature $T$ which is a suspected nucleation temperature. $T_{\mathrm{p}}^{0}$ is the temperature at the maximum of the exothermic crystallization peak for a glass measured using the same heating rate as $T_{\mathrm{p}}$ but without the isothermal hold. The results of these measurements can then be plotted as ($1/T_{\mathrm{p}}-1/T_{\mathrm{p}}^{0}$) versus temperature to obtain nucleation-like curves resembling those seen in Fig. 24.8.

Likewise, the growth-like curves can be constructed using a technique pioneered by Ray et al [24.17]. The specific techniques for reaching the results shown in Fig. 24.8 are detailed by Massera et al [24.15]. The essence of the construction of growth-like curves is the heating of a glass sample to a potential growth temperature where an isothermal hold occurs. The sample is then cooled below $T_{\mathrm{g}}$ and ramped up through crystallization. The area of the crystallization peak for the glass subjected to the growth step ($A_{T}$) is subtracted from the area of the crystallization peak from a sample not subjected to a specific growth step ($A$). The resulting difference in area under the curve, called $\Updelta A$, is plotted versus temperature as shown in Fig. 24.8.

Fig. 24.8

Nucleation (open circles) and growth-like curves (full circles) for glasses investigated in the $\mathrm{(90-\mathit{x})TeO_{2}}$-$\mathrm{10Bi_{2}O_{3}}$-$\mathrm{\mathit{x}ZnO}$ system. Reprinted from [24.15] with permission from Elsevier

These curves create a picture of the nucleation and growth rates of a given glass. Since all nucleation and growth experiments were subjected to the same conditions (with the exception of temperature), the higher the nucleation-like and growth-like curves, the higher the rate of nucleation and growth at that temperature. This gives glass scientists a picture of the maximum nucleation and growth temperatures for a specific glass.

A typical crystallization experiment like the one discussed above is particularly sensitive to ramp rate. For instance, if you are heating a sample in a DSC or DTA to the peak crystal growth temperature at ${\mathrm{10}}\,{\mathrm{{}^{\circ}\mathrm{C}/min}}$, you likely have to pass through the nucleation region of the glass as well. If the nucleation region is ${\mathrm{40}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$ in width, it will take 4 minutes to pass through it. During that 4 minutes, significant nucleation could take place, additional nuclei significantly change the nucleation condition of the glass, and the actual glass material will then vary from the condition that was assumed when designing the measurement. This is an example of how a finite heating or cooling rate can make characterizing crystallization behavior in a glass difficult, ambiguous, or even impossible.

Isothermal DSC seeks to make the heating/cooling rate as high as possible, so high in fact that the movement from one temperature to another is practically instantaneous. One of the factors related to getting heat into a material, which cannot be as easily controlled, is the thermal conductivity of the sample material itself. Isothermal DSC allows the experimenter to eliminate the measurement instrument as the choke point for getting heat into a material but does not change the ability of the material to absorb heat. In order to reduce the time it takes for all of the material in the sample pan to reach the commanded temperature, two main options are available. First, the amount of sample mass tested can be reduced and this will generally allow faster heating, however, it has the drawback of reducing the strength of the crystallization signal that will be detected by the DSC therefore reducing the sensitivity of the measurement. The second and more effective way of forcing the actual temperature in the material to follow the commanded temperature more closely is to use a smaller particle size in the powder sample. Even materials with low thermal conductivities will heat up quickly with small-enough particle sizes. The downside to this is that the crystallization behavior will likely be dominated by surface crystallization and not volume crystallization. The purpose of the measurement must be taken into account when determining whether to use this approach or not.

Adjusting for all of these factors, the advantages of isothermal DSC become clear. In order to measure the energy associated with crystallization, the DSC would be brought to a temperature just below the nucleation range and held until isothermal equilibrium was reached. Then a high ramp rate such as ${\mathrm{100}}\,{\mathrm{{}^{\circ}\mathrm{C}/min}}$ would be used to go quickly through the nucleation region, and directly to the target temperature in the crystallization region. The resulting measurement would be much less affected by ramp rate and time spent in the nucleation region. This is one of the main advantages of using an isothermal DSC technique for glass property measurements. The study of the time-dependent properties at a given temperature rely on isothermal DSC [24.18].

The rapid temperature ramp of an isothermal DSC has applications in other areas of glass science. In the study of structural relaxation, which is the time- and temperature-dependent process of the glass network relaxing from its current network configuration towards equilibrium, it is preferable to move as quickly as possible to the relaxation temperature of interest. Structural relaxation measurements using isothermal DSC are carried out by ramping the temperature of a glass sample from a temperature at which relaxation is not occurring (typically ${\mathrm{40}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$ below $T_{\mathrm{g}}$ or more), to the test temperature [24.19]. The test temperature is typically somewhere above ${\mathrm{40}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$ below $T_{\mathrm{g}}$. If the relaxation temperature was above $T_{\mathrm{g}}$, for instance, then a slow ramp through $T_{\mathrm{g}}$ to reach that temperature would cause a certain amount of relaxation thus affecting the measured result. Using an isothermal DSC ensures the fastest ramp possible through temperature to the target. The effective heating rate is still limited by the sample's thermal conductivity, but isothermal DSC removes the measurement as the limiting factor. This is yet another example of the advantages of an isothermal DSC measurement.

1.1.3 Modulated DSC

Standard DSC heat flow measurements of materials, including glasses, are comprised of a summation of two different types of heat flow. These are reversing and nonreversing. The reversing portion of heat flow in and out of a material is comprised of heat flow related to thermodynamic events. For instance, a 2nd-order phase transition like the glass transition temperature which involves a change in heat capacity, demonstrates reversing heat flow. Heating through the glass transition and then cooling back down, the change in heat capacity, excluding any kinetics such as relaxation, will be the same in both directions. The nonreversing portion, which can be determined by taking the total heat flow (measured like a traditional DSC) and subtracting the reversing component, will reveal kinetic events in the glass. These events can include things like any relaxation or viscous flow that occur as the experiment passes through $T_{\mathrm{g}}$. It is important not to confuse reversing and nonreversing heat flow with the reversibility or irreversibility of transitions within the glass.

Modulated DSC (MDSC) is a technique involving a modulated temperature ramp, which produces an average ramp rate but applies a periodic modulation of the commanded temperature, keeping the system in a slight state of perturbation. The resultant heating curve appears often as a sinusoid or stochastic modulation whose average temperature is changing the same way a traditional DSC heats or cools [24.21]. An example of a sinusoid modulation can be seen in Fig. 24.9. This allows the dependent and independent components of the heat flow to be analyzed separately. The component of the temperature that is ramping linearly provides information similar to a standard DSC while the sinusoidal component is simultaneously measuring the heat capacity of the material. This allows kinetic events, such as crystallization, to be deconvolved from changes in heat capacity, such as $T_{\mathrm{g}}$.

Fig. 24.9

Example of the temperature change during a modulated DSC experiment (after [24.20]). The average temperature change (solid line, left axis) is programmed to ${\mathrm{4}}\,{\mathrm{{}^{\circ}\mathrm{C}/min}}$, while the modulated temperature change (dashed line, right axis) is programmed with a sinusoidal oscillation of $\pm{\mathrm{0.42}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$ every ${\mathrm{40}}\,{\mathrm{s}}$

This method of DSC has several advantages. First, it allows overlapping transitions to be discerned within a single material. Testing materials that are comprised of different chemical components is something that is more commonly done in pharmaceuticals than glass, however when studying the properties of a glass ceramic or glass composite, there may be instances where one or more of the components are going through different phase changes or transitions at the same time. If those instances overlap in temperature, a standard DSC would miss that information and depict the average heat flow response of the components. The average heat flow would likely not show a $T_{\mathrm{g}}$ event if a phase change was taking place at the same time and would report an erroneous value for the phase change energy. With MDSC, the standard heat flow information coupled with the change in heat capacity information can reveal the crystallization characteristics of the first material while indicating the $T_{\mathrm{g}}$ of the other simultaneously. A further advantage of MDSC is the capability of detecting events that are very faint or weak. Sampling both the kinetics and heat capacity based changes gives this technique increased sensitivity [24.22, 24.23].

Figure 24.10 shows an example of how MDSC can be used to separate the heat flow behavior of different materials that are mixed together; the same capability can be used when measuring a glass material. Figure 24.10 shows an MDSC scan of a composite polyethylene terephthalate (PET) and polycarbonate (PC). The blue line in the figure is the reversing heat flow, the red is the nonreversing, and the green is the total heat flow signal. The key thing to note is that the total heat flow (green curve) would be the result of a standard DSC measurement. In such a measurement, the PC $T_{\mathrm{g}}$ which can be seen in the reversing heat flow curve would be totally obscured by the PET crystallization seen in the nonreversing and total heat flow curves. That is information that is only discovered due to the ability of MDSC to separate the reversing and nonreversing heat flows through combination of a linear temperature ramp overlaid with a sinusoidal or stochastic modulated temperature profile.

Fig. 24.10

MDSC scan of total, reversing, and nonreversing heat flow in a PET and PC composite. After [24.20]

As MDSC is a relatively new technique there has not been extensive study done to reveal all that it is capable of and where its main limitations lie. It is certainly useful for thermal analysis of composite materials and materials with weak thermodynamic and kinetic events. Future applications of MDSC could include greater study of the nature of the glass transition as well as the complex relationship between multiple phases within a phase-separated glass.

2 Differential Thermal Analyzer (DTA)

Differential thermal analysis (DTA), is analogous to DSC. The end material information gained using this technique is essentially the same as DSC, however the method used to gain that information is different. DTA uses a comparative method, with a sample and reference material that are ramped through various temperature ranges to gain the information desired.

Whereas a DSC holds the temperature of the sample and reference equivalent and measures the heat flow difference, a DTA, maintains an equivalent heat flow while monitoring temperature difference. In this way, a DTA is capable of measuring the same signature temperatures ($T_{\mathrm{g}}$, $T_{x}$, $T_{\mathrm{m}}$) as a DSC. The area under a DTA curve is the enthalpy of the system, but because the heat flow is held constant, the heat capacity of the sample material cannot be determined.

Because DSC and DTA conduct very similar analysis and the DSC can be used to calculate heat capacities, the use of DTAs has dwindled compared to that of DSCs in more recent years. The physical structure of the DTA makes it suited to measuring at very high temperatures (as high as ${\mathrm{1400}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$). Since DSC cells are typically made of Inconel and can only reach a max temperature of $\approx{\mathrm{800}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$, a DTA may be more suitable for higher temperature experiments. There are high-temperature DSCs that can reach nearly the temperature of a DTA, but they are currently very expensive. As always, the instrument most suitable for each inquiry must be chosen.

3 Thermomechanical Analysis

Thermomechanical analysis involves the measurement of mechanical material properties in response to thermodynamic changes. Thermodynamic changes within a material are most commonly effected using changes in temperature. A thermomechanical analyzer () is the most common instrument used for this type of analysis for inorganic glasses.

As in most measurements, sample geometry can be optimized to provide the best measurement response and sensitivity. There are three major considerations when choosing or fabricating a sample for TMA measurement. First, it is best to have a sample that is taller than it is wide. The taller the sample, the greater the change in length of that sample per degree change in temperature, and as seen in (24.8), the more sensitive the length change is to temperature change, the more sensitive the system is in detecting temperature-related phenomena in the material.

$$\alpha=\Updelta T*\frac{\Updelta L}{L_{i}}\;,$$

(24.8)

where ${\alpha}$ is the linear thermal expansion coefficient, $\Updelta T$ is the difference between the final and initial temperature over the range considered, $\Updelta L$ is the change in sample length over that same range, and $L_{i}$ is the original length of the sample. A longer sample will effectively increase the sensitivity of the measurement. Second, the width of the sample effects the TMA measurement because it directly impacts the effective heat transfer rate into or out of the sample. A sample with a larger cross section will respond more slowly to commanded temperature changes when all other factors are equal. It is also best to have a TMA sample with a consistent cross section throughout its length; when a material expands or contract in one axis, it also contracts or expands in the two other dimensions. This relation is described by Poisson's ratio. Having an inconsistent sample cross section means that the internal resistance of the material to shape change in the two dimensions not being measured will have a different effect on the dimension being measured at different heights on the sample. This is alright if you are always measuring samples with the exact same cross-sectional distribution, but for fundamental material property measurements it is better to maintain a consistent cross section. The final and most important sample-geometry-related necessity is that of having a column of material unbroken by bubbles, cracks, or other macro flaws from the base of the sample to the measurement head. This is necessary because the thermal expansion calculations are done assuming a continuous column of material.

Inside a TMA, the sample sits on a fused silica stage, which is used for its very low thermal expansion properties. The height change of the sample is measured at its top by a shepherd's hook, this piece of fused silica rod rests on the top of the sample, and then curves 180${}^{\circ}$ from vertical facing upward to vertical facing downward and extends down into the instrument. The rod attached to the shepherd's hook probe is fused to a metal rod. This metal rod is used to measure the height change of the entire probe using a linear variable differential transformer (). The LVDT very accurately tracks the increase or decrease in height of the metal part of the rod and hence can measure the changing height of the sample.

An LVDT is an absolute position sensor. As seen in Fig. 24.11 it is comprised of two main parts. The first is the outer cylinder which serves as the sensor. This outer cylinder has three electrically conductive rings embedded in it, an upper, lower, and middle ring. These three rings work in concert with a ferromagnetic cylindrical core which is attached to the object whose position is being measured. The center ring of the outer cylinder works like the primary coil of a transformer, the inner core acts as the core of the transformer, and the power from the center conducting ring is transformed to the upper and lower secondary rings. The voltage differential between the upper and lower ring (the two secondary transformer coils) is measured. When the magnetic cylinder is perfectly positioned amongst all three coils, the voltage differential is zero. As the core is moved up or down that voltage differential changes either positively or negatively (which is determined by whether the voltage difference is in-phase or out-of-phase with the primary coil voltage). LVDTs are designed so that the voltage differential between the upper and lower secondary coils is linear over a long displacement. This linearity ensures that measurement over a given displacement can be accurate and repeatable without any nonlinear effects.

Fig. 24.11

(a) Construction and (b) circuit connection of LVDT. After [24.24]

A furnace is placed over the entire assembly and used to control the sample temperature as needed. The sketch in Fig. 24.12 depicts the inner workings of a TMA. Most TMAs can be flushed with air for cooling and inert gas for materials that are sensitive to oxidation. When it is necessary, the TMA has a place onto which small masses can be placed to increase the static force of the TMA probe on the top of the sample.

Fig. 24.12

TMA schematic. After [24.25]

Although the most common TMA samples are tall thin bulk pieces of glass, changing the probe type allows for the measurement of thermal expansion of powders using a wide probe head and the measurement of viscosity as described in a following section, using a ball penetration probe.

An alternative instrument to the TMA is a dilatometer. A dilatometer is very similar to a TMA, the main difference being that a dilatometer does not allow the operator to control the force exerted on the sample by the measurement probe, but instead uses a passive spring system to hold the measuring head in contact with the sample. Dilatometers often orient the sample in a horizontal, rather than vertical, position. The discussion of property measurement below pertains to both instruments but the TMA is more versatile.

The most important calibrations for a standard TMA are temperature and expansion calibrations. Temperature calibration can be done by testing a sample of a pure metal with a well-known melting point (aluminum for example). When the metal reaches its melting point, the sample rapidly begins to loose height. Choosing at least two different calibration materials over the anticipated test range will ensure accurate temperature measurements, although at least three calibration points are needed to ensure the temperature measurement behavior of the instrument is linear. It is also important to pay attention to the temperature distribution within the TMA furnace. A TMA furnace will often have a radial and vertical temperature gradient within the furnace even at ‘‘isothermal equilibrium.'' This can become a significant factor when testing rather tall samples, as the temperature at the top of the sample will be different from the bottom. This difference can be made even worse while ramping the system up to temperature. If the experiment being done is a high-precision experiment it may be necessary to use a shorter sample or track the temperature distribution within the furnace using additional thermocouples. The downside of using a shorter sample is decreased measurement sensitivity.

Calibration of the system's deflection can be done using any material with a linear and well-characterized expansion rate. Preferred sample geometries for an expansion calibration standard are either a cube or right cylinder with both ends polished parallel to one another. It is best to calibrate with a reference material that has an expansion within the same order of magnitude as the expected expansion behavior of the sample that will be tested on the instrument.

3.1 TMA Property Measurement

The coefficient of thermal expansion () is the property most often measured using a TMA. Standard TMA chambers can be heated, and some can be cooled to cryogenic temperatures for testing of materials whose glassy state is below ambient temperature. Standard CTE measurement for glasses involves a tall and thin sample with a constant cross section, and it is optimal if both the top and bottom of the sample are polished, flat, and parallel to one another. The measurement of CTE differs for different materials and even for different glass families. The heating rate must be tuned depending on the thermal conductivity and sample thickness of each glass. It is important to note that the exact same sample measured at two different heating or cooling rates will produce a different expansion result. This behavior is analogues to the heating and cooling rate dependence described in the previous DSC section. Great care must be taken to only compare data that has been measured using either (a) the same heating/cooling rate setting on the instrument, or (b) the same effective heating rate calculated using the thermal conductivities and thicknesses of each different material.

Fig. 24.13

Example of a TMA expansion curve of L-BAL35 glass

The heating rate for a CTE measurement depends on the glass type. There is no well-defined standard, the important thing is to choose a heating rate that will allow the desired behaviors to be investigated. Factors such as the sensitivity of your sample material to thermal shock, the thermal conductivity of your sample, and the ramp rate sensitivity of any features you intend to measure should be taken into account. The key is to keep the heating rate, or the effective heating rate consistent when comparing results. A typical CTE run begins with the sample at ambient temperature ramping to the final test temperature at the desired rate. Figure 24.13 shows the resultant curve for a typical TMA run. The initial part of the curve in Fig. 24.13 is the glassy behavior of the material, this is when the glass behaves more or less like a solid. The change in sample height versus temperature is relatively linear. The linear CTE of any region can be calculated using (24.8) above. The liner CTE is the expansion coefficient measured in only one axis. This number is different from the volumetric CTE. In materials that are considered isotropic (meaning there are no measurable differences in material properties based on the axis in which the measurement is taken) the volumetric CTE is assumed to be three times that of the linear CTE. This assumption holds true for most well-annealed glasses. Glasses are disordered systems with negligible long-range order, and by nature that disorder creates an average response to stimuli making glasses respond isotropically to measurements. The only exception to these assumptions would likely be cases where there is an extreme difference between the length and the cross section of the sample. Glass fibers, for instance, have different properties along their long axis than their transverse axis due to the stress involved in their fabrication.

At some point in temperature the linear behavior of the glass expansion begins to undergo a transition. This departure from linear behavior marks the beginning of the glass transition as measured by thermomechanical means. A TMA can also be used to identify the $T_{\mathrm{g}}$ of a glass, although as stated before, the value for $T_{\mathrm{g}}$ depends on how it is measured. Precise identification of $T_{\mathrm{g}}$ will be dealt with a little later on.

After the transition, a brief period of linear behavior can be seen in the sample deflection rate versus temperature. The glass has transitioned from a material exhibiting a solid-like behavior to a material exhibiting a more liquid-like behavior. This is evidenced by the dramatic increase of the deflection rate and therefore the effective CTE of the glass in that region. The CTE measured in the liquid-like region is many times higher than the CTE measured in the glassy region as Fig. 24.13 demonstrates. This is due to the changing of the glass structure to a liquid-like bonding state where attraction between structural units is weaker and therefore expansion and contraction are much more sensitive to temperature change.

Measurement of $T_{\mathrm{g}}$ by TMA can be done using the linear portions of the glassy and liquid regions. If the linear region of expansion in the glassy section of the measurement is extended beyond the transition region, and likewise the linear region of the liquid section is extended back towards room temperature, the point at which they cross can be used to define $T_{\mathrm{g}}$. This value is different to the $T_{\mathrm{g}}$ values determined by DSC. A TMA measures the kinetics of a glass while a DSC measures the thermodynamics, causing the $T_{\mathrm{g}}$ values to differ.

The final information that a standard TMA run reveals is a temperature known as the dilatometric softening point ($T_{\mathrm{d}}$). This temperature is defined as the temperature at which the glass begins to deform under its own weight. In Fig. 24.13 this is seen as the expansion in the liquid-like region slowing, and stopping, and if the test continues the curve will begin deflecting negatively. $T_{\mathrm{d}}$ is defined as the global maximum on a TMA curve. Once $T_{\mathrm{d}}$ has been reached, the sample will rapidly loose height, and if heating is continued past this point it could result in a puddle of glass stuck to the inside of the TMA cell. Depending on the test sample, this could ruin the cell, and cost significant money to repair or replace.

A TMA can also be used to measure the viscosity of a glass sample. Ball penetration viscometry using TMA is described below in Sect. 24.5.1.

3.2 Structural Relaxation

Thermal expansion measurements makeup the vast majority of TMA runs. However, there are more advanced measurements that can be made using thermomechanical analysis. One such measurement is the characterization of structural relaxation [24.26].

Structural relaxation is the rearrangement of the glass structural network in response to a thermodynamic change. In the temperature region just below, at, and above $T_{\mathrm{g}}$ the kinetics of the glass are sufficiently fast to allow the glass structure to rearrange on a timescale of seconds to days. If a glass is held at a specific temperature and pressure near $T_{\mathrm{g}}$, then the temperature of the glass is changed, the volume, specific heat and enthalpy relax toward equilibrium. This effect is called structural relaxation. Figure 24.14 shows a TMA representation of structural relaxation. In that plot, the temperature of the sample in the TMA is equilibrated at $T_{0}$ and then rapidly changes to $T_{1}$. The time-dependent response of the sample height change is represented by the brown curve after $t_{i}$.

Fig. 24.14

Graphical representation of structural relaxation, temperature and dimension change versus time

Structural relaxation can be measured by tracking how the intrinsic properties of the glass change with temperature or pressure. DSC measurements are often used to measure enthalpy relaxation, and in a similar way TMA measurements can be used to measure volume relaxation of a glass. These measurements are carried out by placing a glass sample in a TMA, ramping to a temperature near the transition region, and holding the glass at this temperature until the glass has reached structural equilibrium. When the glass has finished relaxing at the specific temperature, the temperature is either raised or lowered and held isothermally at the new temperature. The volume of the glass as measured by height change in the TMA is slower to change than the temperature. Since the structural rearrangement of atoms typically follows an Arrhenius-like trend, the change of volume appears exponential or nearly exponential. Figure 24.15 shows the normalized change in height for various structural relaxation steps between various temperatures for Schott N-BK7 optical glass.

Fig. 24.15

Normalized change in height versus time for structural relaxation data from Schott N-BK7 measured by TMA. Relaxation for temperature ranges between 552 and ${\mathrm{587}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$. After [24.25]

Structural relaxation is a topic of academic study, but is also important when manufacturing glass through thermoforming. The most common type of thermoforming of glasses is precision glass molding. When molding, a piece of glass is deformed at high temperature which corresponds to a specific viscosity. The molded optic is then cooled. While cooling, the glass structurally relaxes which can change the shape of the optic. Structural relaxation can also affect the shape of the optic during postprocess annealing. Significant work has been done to better understand the role of structural relaxation as it pertains to precision glass molding [24.27, 24.28].

Using the TMA for a purpose other than its common application allows glass scientists to measure the viscoelastic nature of glass and demonstrate the temperature dependence of that behavior. Figure 24.15 clearly displays the temperature sensitivity of viscoelastic glass behavior. The high-temperature experiment carried out between 587 and ${\mathrm{577}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$ shows that the structural change that occurs from one thermodynamic state to the other is fully completed in $\approx{\mathrm{10^{3}}}$ seconds and reaches its halfway point at approximately $\mathrm{10^{1.5}}$ seconds. In contrast, the lowest temperature step, which takes place ${\mathrm{35}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$ below the previous test and ${\mathrm{15}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$ below $T_{\mathrm{g}}$, takes nearly $\mathrm{10^{4.5}}$ seconds to complete. This is approximately $30{\times}$ longer than the highest temperature test. Additionally, the nature of the structural relaxation can be seen in the shapes of normalized change in height curves. All of the curves are more similar at the beginning of each test, suggesting that the short-time relaxations of each are similar. The largest difference in behavior is seen as the volume relaxation nears the end.

It is also possible to view the curves in Fig. 24.15 in relation to the $T_{\mathrm{g}}$ of the material. N-BK7 has a reported $T_{\mathrm{g}}$ at ${\mathrm{557}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$. The blue dashed curve in the center is a clear divider between the higher and lower temperature behaviors. At temperatures above the blue dashed curve, the high temperature curves have the same shape as one another with the only difference being an increasing decay time as the temperature of the test decreases. However, below the blue dashed curve, which was a test carried out at $T_{\mathrm{g}}$, the nature of the curves changes and they become shallower. The lower temperature curves seem to reach a limit in time after which further relaxation appears difficult. This suggests a lack of structural modes for rearrangement at decreasing temperatures.

Figure 24.16 shows a graphical representation of the reduction of possible structural relaxation modes with the decrease of temperature in a generic glassy system. In the left-most picture, individual atoms or groups of atoms are free to move along any of the available lines shown on the diagram. However, as the temperature decreases and begins to pass through $T_{\mathrm{g}}$, the center schematic shows some formerly free relaxation modes being closed off. Finally, after reaching a low-enough temperature, the right-most sketch describes a system in which relaxation is only possible when done within those specified regions. Structural relaxation which must take place cooperatively within regions is relatively much slower than relaxation which occurs at or above $T_{\mathrm{g}}$ [24.29].

Fig. 24.16

Graphical representation of decreasing relaxation modes with decreasing temperature. After [24.29]

These structural relaxation data can be fit with various exponential functions such as the Kohlrausch–Williams–Watts function, or a Prony series in order to characterize the specific parameters related to the materials' structural relaxation behavior [24.30, 24.31, 24.32]. This ongoing research seeks to study the structure and modes of kinetics within the glass to better understand the glass structure and how it changes with the thermodynamics of the material. Studies such as this demonstrate the power of thermal analysis to advance glass science.

4 Thermogravimetric Analysis (TGA)

Thermogravimetric analysis () is a technique whereby the mass of a sample is measured relative to a known mass as the system is increased in temperature at a specific rate. TGA is a technique used widely in the pharmaceutical and polymer fields, however it has several uses within glass science and industry.

The mass measurement capabilities of a TGA allow researchers to measure a sample's weight loss or gain. For instance, some glasses absorb constituents from their environment upon heating. This can often be seen in the mass change of a sample. Likewise, other glasses lose constituents and mass at the same time. In glasses that contain toxic elements, it is important to know the upper use temperature in order to avoid burning off dangerous elements during DSC or DTA experiments; a TGA can be used to determine this temperature. There are no clear universal standards for measuring the upper use temperature of glasses. However, it is convenient to define a percent loss that is characterized as the target of the test and end the test once that percentage of mass is lost. The value set for this cutoff will vary depending on the material that you are measuring and the expected chemical components that will burn off. If you are analyzing the decomposition temperature of an oxide glass, you may set the cutoff at ${\mathrm{5}}\%$ or ${\mathrm{3}}\%$ weight loss as long as none of the byproducts of decomposition are harmful or toxic. If you are measuring the upper use temperature of a chalcogenide glass that is comprised most often of chemicals like arsenic and selenium, then a ${\mathrm{1}}\%$ cutoff might be wisest, coupled with adequate safety precautions such as placing the instrument in a fume hood or providing suction at the TGA gas outlet port.

Often the data produced by a TGA measurement is more valuable when coupled with other thermal analysis data, so TGA/DSC or TGA/DTA combination instruments are more common than simple TGAs. A TGA/DSC combo can record the mass of the sample while also measuring heat flow during heating or cooling; this allows researchers to tie changes in the mass of a sample to transitions like vaporization or sublimation. One example is a study by Schiavon et al in which the decomposition of polycyclic silazane and then subsequent cross-linking to form silicon carbonitride glass is measured by a TGA/DTA [24.33]. TGA alone could only characterize the decomposition component of the transformation of polycyclic silazane, but running DTA in combination allows the second crucial part of the transformation to be characterized. Not only do the two tools give a more complete picture of the reaction, but they also help identify the relative position in temperature-space of the two events.

5 Viscometry

Glass formers in general exhibit unique properties at elevated temperatures. Whereas crystalline materials heat up until melting at a specific temperature, glasses undergo a second-order transition from a solid-like state to a liquid-like state prior to going through the melting phase change. Once the temperature of the glass increases past $T_{\mathrm{g}}$ it becomes quite evident that glasses behave in some ways like liquids, and the temperature of the glass determines how thick or thin this liquid-like material is. At temperatures just above $T_{\mathrm{g}}$ glass flow under pressure or the weight of gravity might resemble caramel that has just come out of the freezer, while glasses at temperatures double their $T_{\mathrm{g}}$ would likely resemble water. This property is called viscosity.

The measurement of viscosity in glasses is generally known as viscometry or rheology. The methods and instruments for measuring viscosity are various. Measuring the same property in a liquid that has a high viscosity (a liquid which is thick) and a liquid that has a low viscosity is not trivial. Real viscosity data is valuable to glass researchers and scientists alike. The effects of glass viscosity on macroscopic glass properties is present above, at, and even slightly below $T_{\mathrm{g}}$. Viscosity is an influential factor for many material properties. If a glass remains at sufficient temperature for a length of time similar to the magnitude of the timescale for viscous flow, then there will often be observable viscosity effects. Understanding how viscosity changes with temperature and effects other properties is one of the main goals of fundamental glass science research.

Figure 24.17 shows a typical glass viscosity curve as well as signature temperatures associated with glass study and manufacturing. The two most common viscosity measurement techniques for inorganic glasses are noted on the graph.

Fig. 24.17

Example glass viscosity graph with approximations for key temperatures and regions

5.1 Measuring Viscosity

Viscosity is most commonly described by two different but interchangeable units, poise and pascal-seconds ($\mathrm{Pa{\,}s}$). The units of viscosity are most often referred to in log scale, with a viscosity of 5 poise being really a viscosity of ${\mathrm{10^{5}}}\,{\mathrm{poise}}$. The following equation relates poise and $\mathrm{Pa{\,}s}$

$${\mathrm{10}}\,{\mathrm{poise}}={\mathrm{1}}\,{\mathrm{Pa{\,}s}}\therefore\log\ \left(\text{poise}\right)=\log({\mathrm{Pa{\,}s}})+1\;.$$

(24.9)

The range of viscosities that are of interest in glass science and manufacturing is quite wide. Academic experiments or industrial handling of glasses near $T_{\mathrm{g}}$ involve glasses with viscosities in the $E13{-}E9\,{\mathrm{Pa\mskip 3.0mus}}$ range, while fiber drawing is done in the $E3{-}E1\,{\mathrm{Pa\mskip 3.0mus}}$ range. Because of the wide range of temperatures at which glass is processed and used, it is necessary to measure glass viscosity at a wide range of temperatures. The following techniques are the most common for measurement of inorganic glass viscosity.

5.1.1 Parallel Plate Viscometer

Measurement of glass viscosities in the $E4{-}E8\,{\mathrm{Pa\mskip 3.0mus}}$ range is typically done using a parallel plate viscometer (). The theory behind the measurement is based on simple mechanics. The sample for a PPV measurements should be a flat disk, preferably with polished faces, with a height-to-diameter ratio of greater than 1 for maximum sensitivity. This sample is placed between two parallel plates inside of a furnace. The top plate is attached to a linear variable differential transformer () which accurately measures the change in vertical position of the parallel plate. The plates are commonly made of Inconel which is chosen for its rigidity even at high temperature, high melting point, and high heat transfer coefficient.

Once the sample has been placed between the two plates (Fig. 24.18a-ca), a mass is sometimes added to the top plate, the entire system is enclosed and the temperature is increased. Accurate and repeatable temperature control and vertical height measurement are essential to achieve a true measurement of the glass viscosity versus temperature behavior. As the sample heats and passes $T_{\mathrm{g}}$ and the dilatometric softening point ($T_{\mathrm{d}}$), the glass begins to deform under its own weight, the weight of the upper plate above it, and any mass added to the upper plate. During this deformation one of two boundary conditions is assumed for the plates and the glass disc. Either a no stick condition is assumed (Fig. 24.18a-cb), where the disc becomes thinner and wider while the edges stay parallel to one another, or a no slip condition is assumed (Fig. 24.18a-cc) where the glass disc retains its initial diameter where it contacts the upper and lower plates but barrels in the middle.

Fig. 24.18a-c

Different conditions in a PPV measurement: (a) Initial condition, (b) no stick and (c) no slip PPV condition

Depending on the boundary condition, the rate of height change can be used, along with the other experimental parameters to calculate viscosity as a function of temperature. The equation for doing this in the most common case, no slip, is seen in (24.10).

$$\eta=2\uppi\frac{Mgh^{5}}{30V\left(\frac{\mathrm{d}h}{\mathrm{d}t}\right)\left(2\uppi h^{3}+V\right)\left(1+\alpha\right)}\;,$$

(24.10)

where ${\eta}$ is the glass viscosity in $\mathrm{Pa{\,}s}$, $M$ is the applied load in g, $g$ is the acceleration due to gravity in $\mathrm{cm/s^{2}}$, $t$ is time, $V$ is specimen volume in $\mathrm{cm^{3}}$, $h$ is specimen thickness at time $t$ in cm, $\mathrm{d}h/\mathrm{d}t$ is compression rate in $\mathrm{cm/s}$, and ${\alpha}$ is the glass mean coefficient of thermal expansion from ${\mathrm{25}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$ to the measuring temperature $T$ in $\mathrm{m/(m/{}^{\circ}\mathrm{C})}$ [24.34]. The ‘‘no slip'' condition is most commonly assumed because it is the general nature of materials to have increased frictional forces at higher loads. This leads to the result that an experimental setup can come much closer to a perfect full sticking or no slip scenario than it could to a perfect no stick scenario. In real life experimentation there is no achievable no slip condition. This measurement relies on the accuracy of the $\mathrm{d}h/\mathrm{d}t$ measurement which is a function of the internal resistance of the glass to volume change. If the viscosity of the glass is calculated using a no slip assumption, then any amount of slipping which might occur will essentially increase the observed rate at which the height of the sample is changed leading to an error skewing the calculated viscosity downward. PPV measurements are done at viscosities at which it is assumed the glass material's internal resistance to volumetric change is much lower than the resistance of the material's surface to sliding along the top and bottom plates [24.35].

All of the material and sample parameters in the above equation can be measured or found in the literature; the experimental aspect of this test is the relationship between $\mathrm{d}h/\mathrm{d}t$ versus $T$ for each specific sample. Figure 24.19 is an example of a PPV measurement curve for Schott N-FK5 oxide glass.

Fig. 24.19

Viscosity versus temperature curve measured by PPV for Schott N-FK5 glass

Several tests should be done with identical samples of each glass to ensure the repeatability of the experimental setup and the consistency of glass behavior. A variety of sample sizes can be used for this test, provided they are adequately tall compared to their diameter. Another consideration is that at high temperature the Inconel plates and sample material will likely interact chemically. To prevent any sticking to or corroding of the PPV plates, a very thin foil of an appropriate material must be chosen. The chemical interaction of many oxide glasses at high temperature can be reduced using a platinum foil on both top and bottom between the parallel plate and glass. For other glasses such as chalcogenides which will corrode platinum, an aluminum foil can be used assuming the test temperature does not exceed the melting temperature of aluminum. It is important to use a foil or very thin piece of buffer material so that the thermal expansion behavior of that material does not affect the measurement of the glass viscosity.

The use of the PPV as a viscosity measurement tool is rarely complete by itself. To gain a thorough understanding of the entire viscosity region, viscosity must also be measured at lower temperatures, in the temperature region near $T_{\mathrm{g}}$. The beam-bending viscometer () is the instrument of choice to complete the measurement of glass viscosity versus temperature.

5.1.2 Beam-Bending Viscometer

A beam-bending viscometer (BBV), works on a principle similar to a PPV. Instead of deforming a thick and narrow disk into a thin and wide disk, a BBV works by bending a thin and long beam of glass at temperatures significantly lower than a PPV. Both methods rely on a change in height measurement which is a result of the volumetric deformation of a well-defined glass cross section.

In order to test glass at higher viscosities ($E13{-}E8\,{\mathrm{Pa\mskip 3.0mus}}$) without dedicating days or weeks to the test, a small cross section glass sample is used. The BBV setup consists of a fused silica tube approximately ${\mathrm{50}}\,{\mathrm{mm}}$ in diameter with two notches at the top located $180^{\circ}$ from one another. The notches are typically $\approx 5{\times}{\mathrm{5}}\,{\mathrm{mm}}$. The prepared BBV sample is typically $\approx 3{\times}{\mathrm{3}}\,{\mathrm{mm}}$, and slightly longer than the tube is wide. The beam is set into the notches. A fused silica shepherd's hook, hangs on the sample like a hangar. The shepherd's hook is attached to a long piece of fused silica that is connected to another length of metal rod. A furnace lowers down over the entire fixture and the metal rod, attached to the shepherd's hook hangs through a hole in the bottom of the furnace. This rod is passed through an LVDT to measure sample deflection. Attached to the bottom of the metal rod is a cage or basket that holds calibrated weights. The weights are added to the basket depending on the temperature of the test. For a viscosity test at or even slightly below $T_{\mathrm{g}}$, for instance, a larger mass is needed to affect a deformation on the sample. An example of a BBV sample setup can be seen in Fig. 24.20.

Fig. 24.20

BBV initial condition

The BBV test consists of first placing the sample on the slots in the tube, then lowering the furnace and ramping the temperature. The placement of the shepherd's hook on the sample is dependent on the temperature and viscosity condition being measured. During PPV testing, the temperature is ramped without pausing from room temperature until the sample has reached the max deformation target. However, in BBV testing, the temperature is ramped to the test temperature and held until the sample has reached the max deformation commanded by the program. Tests that target relatively low temperatures (around $T_{\mathrm{g}}$), allow the shepherd's hook to be placed on the sample before closing the furnace and beginning the temperature ramp at the beginning of the test. Tests at temperatures near the upper edge of feasibility for the BBV may require the technician to keep the weight of the hook and attached mass off of the sample until the test temperature is reached. Deformation of the beam adheres to common mechanical principles and is described by an equation similar to that of the PPV.

$$\eta=\frac{gL^{3}}{1440I_{\text{c}}\left(\frac{\mathrm{d}h}{\mathrm{d}t}\right)}\left(M+\frac{\rho AL}{1.6}\right)\left[\frac{\left(1+\alpha_{\text{s}}T\right)^{3}}{\left(1+\alpha_{\text{g}}T\right)^{4}}\right],$$

(24.11)

where ${\eta}$ is viscosity in $\mathrm{Pa{\,}s}$, $M$ is the mass of the shepherd's hook and fixturing plus any applied load in g, $\mathrm{d}h/\mathrm{d}t$ is the midpoint deflection rate of the test beam in $\mathrm{cm/s}$, $g$ is the acceleration due to gravity in $\mathrm{cm/s}$, $I_{\text{c}}$ is the cross-sectional moment of inertia of the test sample in $\mathrm{cm^{4}}$, ${\rho}$ is the density of the glass in $\mathrm{g/cm^{3}}$, $A$ is the cross-sectional area of the beam in $\mathrm{cm^{2}}$, $L$ is the support span, and $\alpha_{\text{s}}$ and $\alpha_{\text{g}}$ are the coefficients of expansion of the stand and sample glass respectively from ${\mathrm{25}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$ to the measurement temperature [24.36].

Common BBVs are intended to measure viscosity over a temperature ramp; this allows a range of viscosity to be sampled on a single run. However, measurement over a temperature ramp adds a heating rate element to the measurement. During a temperature ramp test the ramp rate of the system as well as the thickness and heat transfer coefficient of the sample material come in to play. In order to obtain more precise viscosity data without the uncertainty added due to an effective ramp rate, it is possible to carry out a BBV measurement at a single temperature. A result of the BBV measuring viscosity at a single temperature is that it becomes necessary to sample several different temperatures in the range of interest. A single BBV test produces only a single data point, while a single PPV test produces several hundred or more. Figure 24.21 shows BBV test results for a sample glass, it is made up of three separate measurement runs. As seen in the figure below, the viscosity versus temperature behavior of many glasses is more or less linear over the typical test range of a BBV. This is not representative of viscosity behavior over the entire temperature range above $T_{\mathrm{g}}$, however it does allow practical viscosities within that region of temperature to be assumed as linear, making the need for measurement at the exact use temperature within that range unnecessary in many cases. This is just a generalization and each glass must be evaluated to test whether or not such assumptions can be made.

Fig. 24.21

Viscosity versus temperature curve comprised of three separate runs, measured by BBV for Schott N-FK5 glass

5.1.3 Fiber Elongation Test(Littleton Softening Point)

The fiber elongation test is a unique way of measuring glass viscosity. In principle it is similar to the first two methods discussed. A glass sample of known dimensions is heated and deflected and the deflection rate is measured and used to calculate glass viscosity using simple mechanics.

A fiber of test glass is drawn to a diameter of $0.55{-}0.57\,{\mathrm{mm}}$, one end of the fiber is heated into a ball large enough to suspend the fiber, and the fiber is cut to a length of ${\mathrm{23.5}}\,{\mathrm{mm}}$. The ball end of the fiber is used to hang the sample vertically in a furnace. The furnace is heated to a starting temperature, the sample is inserted, then the furnace is ramped through a range of temperatures while the deflection rate of the end is measured using a laser. The laser tracks the end of the fiber sample and calculates the deflection rate. Testing at temperatures near $T_{\mathrm{g}}$ may require a load to be applied to the sample in order to force deflection of the sample at an experimentally observable rate.

The fiber elongation test is unique, in that it is used to define a standard glass viscosity and temperature known as the Littleton softening point. When the fiber elongation test is carried out, the temperature at which the fiber elongates at ${\mathrm{1}}\,{\mathrm{mm/min}}$ is designated the Littleton Softening point, and this corresponds to a viscosity of ${\mathrm{10^{6}}}\,{\mathrm{Pa{\,}s}}$ for most glasses. Certain glasses do not conform to criteria of the Littleton Softening Point, meaning that when the above condition is met, the viscosity of the glass is not precisely ${\mathrm{10^{6}}}\,{\mathrm{Pa{\,}s}}$. This does not mean that the fiber elongation test cannot be used to measure the viscosity of those glasses, only that the Littleton Softening point as a viscosity benchmark does not hold up for certain glass families.

The drawback to this fiber elongation test is that a fiber must be drawn to make the sample, which is a fairly laborious process, involves expensive equipment, and is not practical for many companies and researchers. Additionally, some glasses cannot be drawn into fibers due to crystallization or thermal shock problems [24.37, 24.38].

5.1.4 Ball Penetration Viscometry

Ball penetration viscosity testing operates on a different principle than the macroscopic sample deformation methods discussed above. In this test, a hemispherical probe is forced into the surface of a glass sample. This is usually done using a special probe on a TMA. An example of a penetration probe viscosity setup can be seen in Fig. 24.22. The deflection rate of the probe into the glass is used to calculate the viscosity using (24.12).

$$\eta=\frac{2\uppi Mgh^{5}}{3V\left(\frac{\mathrm{d}h}{\mathrm{d}t}\right)(2\uppi h^{3}+V)(1+\alpha\Updelta T)}\;,$$

(24.12)

where ${\eta}$ is the glass viscosity, $M$ is the applied load in grams, $g$ is the acceleration due to gravity, $h$ is the sample height in cm, $V$ is the sample volume, $\mathrm{d}h/\mathrm{d}t$ is the sample deformation rate, ${\alpha}$ is the linear coefficient of thermal expansion, and $\Updelta T$ is the temperature difference between the test temperature and ambient temperature [24.39, 24.40]. All length dimensions should match.

Fig. 24.22

Penetration probe for measuring viscosity behavior by TMA. After [24.41]. Copyright TA Instruments. Used with permission

5.2 Quantifying Viscosity

Beam bending and parallel plate viscometry are the primary ways of characterizing glass viscosity over a large range of temperature. However, they are only physically capable of measuring viscosity in certain temperature windows. Therefore, there must be a way to infer or predict viscosities at intermediate temperatures.

There are several fitting equations that have been developed to take PPV and BBV data, fit them, and then extract certain parameters which will allow anyone with those parameters to reconstruct the viscosity curve for a given material. The most common model is the Vogel, Fulcher, Tammann () model which was developed in the 1920s and uses a three-parameter equation to describe the viscosity of glass-forming melts [24.42, 24.43]. The VFT equation can be seen below in (24.13).

$$\eta(T)=A+\left(\frac{B}{T-T_{0}}\right),$$

(24.13)

where ${\eta}$ is the glass viscosity in $\log({\mathrm{Pa{\,}s}})$, $A$ and $B$ are fitting parameters, $T_{0}$ is the temperature at which the model supposes the configurational entropy of the system to be zero and must be in either $\mathrm{{}^{\circ}\mathrm{C}}$ or K, and $T$ is the temperature whose units must correspond to $T_{0}$. When the parameters of the glass are known, the viscosity versus temperature curve can be reconstructed using this equation. However, if the properties are not known, they must be determined through experimentation. In Fig. 24.23, the set of PPV data for Schott N-FK5 seen in Fig. 24.19 and the set of BBV data seen in Fig. 24.21 are shown combined and fitted with a VFT curve. Assuming the experiments were carefully conducted, this fit can reveal the VFT parameters thereby allowing an approximation of the viscosity at any temperature between the two testing temperatures to be calculated. The VFT parameters for this glass, based on these experiments are as follows: $A=-2.528$, $B=475.96$, and $T_{0}={\mathrm{139.45}}\,{\mathrm{{}^{\circ}\mathrm{C}}}$.

Fig. 24.23

Temperature versus viscosity measured data for Schott N-FK5, overlaid with a VFT fit of the viscosity data

Interpolation of viscosity for the majority of the range from $T_{\mathrm{g}}$ to $T_{\mathrm{m}}$ is fairly well described by the VFT equation; it is sufficient in a production environment and even in many research settings.

Viscosity is important for glass makers and fabricators, but the viscosity of glasses is a heavily researched topic because the way in which material properties change with temperature is very closely linked to the type of bonding and molecular interactions that occur as a material is heated or cooled. Another important viscosity linked parameter is what is known as the fragility of a glass. The fragility is the rate at which the viscosity changes with respect to temperature when measured at a viscosity of ${\mathrm{10^{12}}}\,{\mathrm{Pa{\,}s}}$. For instance, certain glasses (known as strong glasses) have a viscosity that is relatively insensitive to temperature, while other glasses (known as fragile glasses) have viscosities that change very quickly with respect to temperature [24.45]. Studying the fragility can give researchers a window into the structure and bonding within a glass. A paper by Musgraves et al explores the viscosity curves and fragility values for various compositions in the $\mathrm{As_{\mathit{x}}Se_{100-\mathit{x}}}$ glass system [24.44]. This study, demonstrated in Fig. 24.24, shows how viscosities of glasses with different concentrations of arsenic change with respect to temperature. Further analysis of the fragility parameter derived from each composition shows a definite difference in the type of bonding present in the various glasses of the $\mathrm{As_{\mathit{x}}Se_{100-\mathit{x}}}$ system. At high selenium compositions, Se–Se chains sliding and rotating are believed to be the primary method of rearrangement of the glass structure, while at higher As concentrations, chemical bonds must be completely broken and reformed to allow rearrangement.

Fig. 24.24

(a) Viscosity versus temperature curves for glasses in the $\mathrm{As_{\mathit{x}}Se_{100-\mathit{x}}}$ system. (b) Fragility versus arsenic content for the same glass system. Reprinted from [24.44] with the permission of AIP Publishing

Several other fitting methods have been developed to either improve on or extend the prediction capability of the VFT. Methods developed by Mauro et al, and Avramov and Milchev are designed to fit viscosity data using a single equation, while others, including those developed by Wang and Fecht use a two-branch method to fit high and low viscosity data assuming cooperative rearrangement at temperatures nearer to $T_{\mathrm{g}}$ and truly Arrhenius behavior at high temperatures approaching $T_{\mathrm{m}}$ [24.46, 24.47, 24.48].

While more recent efforts have attempted to link an expression of glass viscosity versus temperature data to physical phenomena within the material, for the majority of industrial uses and many academic uses the VFT equation represents glass behavior sufficiently.