Interleave Division Multiple Access (IDMA)

Abstract

In this chapter, we start with a comparison on non-orthogonal multiple access (NOMA) and orthogonal multiple access (OMA). We show that the performance difference between NOMA and OMA is marginal assuming perfect channel state information (CSI), capacity-achieving coding, and centralized control. The real challenges arise from channels without such idealistic assumptions. We will then discuss an interleave division multiple access (IDMA) scheme that provides an efficient NOMA solution in non-idealistic channel considerations. We will outline the following attractive features of IDMA:

• IDMA facilitates a low-cost iterative technique for multi-user detection (MUD) .

• IDMA with proper power control can achieve near-capacity multi-user sum-rate.

• IDMA with decentralized power control can offer significantly higher throughput than conventional ALOHA in random-access environments.

• IDMA together with data-aided channel estimation (DACE) can fully exploit the advantages of massive multiple-input multiple-output (MIMO) systems.

Finally, we will briefly compare several proposals for LTE fifth-generation (5G) cellular systems. We will show that they share with IDMA the principle of reducing short cycles in their graphic representations so as to facilitate iterative detection. Some of the software used in this chapter are available in the following site: http://www.ee.cityu.edu.hk/7Eliping/Research/Simulationpackage/.

1 Overview

The capacity of a multiple access channel was studied in [1, 2]. It can generally be achieved by random coding together with other techniques, e.g., power control, linear precoding, and dirty paper coding [3,4,5,6]. Random coding does not involve orthogonality among users so it is inherently non-orthogonal. The sub-optimality of orthogonal multiple access (OMA) was investigated in [7, 8]. The gain of non-orthogonal multiple access (NOMA) over OMA was assessed in [9, 10] for both single-input single-output (SISO) and multiple-input multiple-output (MIMO) systems. Recently, NOMA has been promoted for improving system fairness [11, 12].

However, many practical systems still belong to OMA category. This is mainly due to complexity concerns. OMA can work with low-cost single-user detection (SUD), while NOMA may require more complex multi-user detection (MUD). Thus, these two options entail different trade-off between cost and performance.

Historically, the third-generation (3G) direct-sequence code-division multiple access (DS-CDMA) system is non-orthogonal. Normally, only SUD is used in DS-CDMA to avoid high complexity, which is sub-optimal. The spreading operation in DS-CDMA reduces rate, so DS-CDMA is not convenient for high-rate applications. The fourth-generation (4G) orthogonal frequency division multiple access (OFDMA) system returns to OMA. OFDMA allows flexibility for resource allocation over time and frequency, which can bring about noticeable gain.

Recently, NOMA has been discussed widely for the fifth-generation (5G) [13,14,15,16]. A natural question is whether the possible gain of NOMA can justify its higher receiver cost. We examine this question using achievable sum-rate below.

Fig. 13.1

Achievable sum-rate of NOMA and OMA under equal energy constraint. Note that the two strategies have exactly the same performance. $SNR_\mathrm{sum}$ is the sum signal-to-noise ratio (SNR) of all users. Complex channels with both slow- and fast-fading factors are considered. Path loss is based on a hexagon cell with a normalized side length = 1. The minimum normalized distance between users and the base station is 35/289, corresponding to an unnormalized distance of 35 m for an LTE cell with radius 289 m. Path loss factor = 3.76 and lognormal fading deviation = 8 dB. The channel samples are normalized such that the average power gain = 1

In Fig. 13.1, we compare the achievable sum-rate of NOMA and OMA with equal energy constraint per frame per user in a multi-user SISO system. We can see NOMA improves sum-rate when the number of users K increases, but OMA can achieve the same gain through resource allocation. NOMA has no advantage here since OMA is capacity achieving in this case.

The situation is slightly different if the energy per frame per user can also be freely optimized under the sum energy constraint. For example, consider maximizing sum-log-rate under the proportional fairness criterion [3]. Figure 13.2 illustrates the related numerical results for $K = 2$. The sum-rate curves in Fig. 13.2 show that NOMA is only slightly better than OMA with resource allocation (about 8% gain at $SNR_\mathrm{sum} = 10\,\mathrm{dB}$).

Fig. 13.2

Achievable sum-rate of NOMA and OMA under sum energy constraint with proportional fairness, $K = 2$. Other system settings are the same as those in Fig. 13.1

The advantage of NOMA over OMA seen in Figs. 13.1 and  13.2 is disappointing compared with many results in the literature. This is mainly for two reasons. First, comparisons with OMA without resource allocation are not fair as resource allocation has already been widely used in LTE. Second, a practical signal-to-noise ratio (SNR) range should be used for comparison. A standard way for this purpose is using the following approximation of the signal-to-noise-plus-interference ratio (SINR) in a cellular system [3]:

$$\begin{aligned} SINR_\mathrm{sum}=\frac{P_\mathrm{sum}}{\beta P_\mathrm{sum}+\sigma ^2}, \end{aligned}$$

(13.1)

where $P_\mathrm{sum}$ is the sum received powers of all users in a cell, $\beta$ a cross-cell interference factor and $\sigma ^2$ the noise power. As a rule of thumb, a typical value is $\beta = 0.6$. Then, we have $SINR_\mathrm{sum} \le 2.2\,\mathrm{dB}$. Treating interference as noise and allowing a certain range of $\beta$, we may consider 0–10 dB as a typical range for $SNR_\mathrm{sum}$, as used in Figs. 13.1 and 13.2. Clearly, the gain of NOMA is marginal over such a practical SNR range.

Furthermore, NOMA performance may deteriorate seriously if a practical forward error control (FEC) code is used. To see this, consider a successive interference cancelation (SIC) process with K users in a descendant order of user index k. We employ an FEC code that can achieve (almost) error-free decoding at SNR = $\varGamma$. Assume that, when we decode for user k, the signals of all users with indexes $k' > k$ have been successfully decoded and subtracted from the received signal. Let $q_k$ be the received power of user k. Then, user k can achieve error-free decoding provided that

$$\begin{aligned} SNR_k = \frac{q_k}{\sum \nolimits _{k' < k}q_{k'}+\sigma ^2} \ge \varGamma . \end{aligned}$$

(13.2a)

For sum-power minimization, $q_k$ can be calculated using the following recursion (with $q_0=0$):

$$\begin{aligned} q_k = \varGamma \times \left( \sum \limits _{k' < k}q_{k'}+\sigma ^2\right) . \end{aligned}$$

(13.2b)

Ideally, the minimum value for $\varGamma$ can be found from Shannon capacity $R=\mathrm{log}_2(1+\varGamma )$. For a practical code, however, a larger $\varGamma$ is required to ensure (almost) error-free decoding. This overhead accumulates during SIC, which can amount to a considerable loss.

Specifically, we consider a practical rate-1/6 channel coding as an example. It achieves bit error rate (BER) $\approx 10^{-5}$ (approximately error-free) at about SNR = $-3.5$ dB with a relatively short block length. There is a 2.35 dB gap compared with SNR = $-5.85$ dB calculated from the Shannon formula for Gaussian signaling. Such loss accumulates in the SIC process as shown in Fig. 13.3. The accumulated loss is roughly 7.4 dB for 12 users.

Fig. 13.3

Accumulated loss in the SIC process

The problem is more serious for higher rate, as seen from Fig. 13.3 for rate-1/2 coding. Assume the same initial single-user gap of 2.35 dB. The accumulated gap for six users is 8 dB.

Nevertheless, NOMA is still useful. In many situations, it is difficult to establish orthogonality due to the lack of centralized control or accurate channel state information (CSI). Then, we may have to resort to NOMA. In particular, as we will show below, NOMA based on interleave-division multiple access (IDMA) [17,18,19,20,21,22] offers robust and flexible solutions in such environments. IDMA can also recover a considerable portion of the accumulated loss suffered by SIC as shown in Fig. 13.3. We will use numerical results to verify these claims. Some of the software used in this chapter are available at: http://www.ee.cityu.edu.hk/%7Eliping/Research/Simulationpackage/.

2 Basic Principles of IDMA

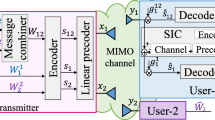
Following the advent of turbo and low-density parity-check (LDPC) codes [23,24,25], iterative detection techniques were developed in late 1990s for equalization in multipath channels [26] and MUD in DS-CDMA systems [27,28,29]. It was shown in [30] that two independently interleaved code sequences can be separated by iterative detection. This inspired the IDMA scheme in which users are solely separated by interleavers [17]. Intuitively, a randomly interleaved code results in a different code. Thus we may also say that different users in IDMA are separated by different codes. This follows the basic principle of CDMA, except now the set of codes are generated by a master code followed by different interleavers. We therefore can regard IDMA as a special case of CDMA. However, IDMA is fundamentally different from DS-CDMA. The former does not rely on spreading for user separation and so can avoid the rate loss suffered by the latter.

In the following, we will start with a graphic model originally presented in [31]. We will show that the primary motivation behind IDMA is to break short cycles, since the latter is detrimental for message-passing detection. The same principles have been successfully used in turbo and LDPC codes.

2.1 IDMA Transmitter Principles

Throughout this chapter, we will assume an underlying OFDMA layer that removes inter-symbol interference (ISI). We will focus on uplink multiple access techniques built on this OFDMA layer.

Let K be the user number and $\varvec{c}_k = \{ {c}_k(j), j = 1, 2, \ldots , J\}$ a length-J codeword generated by users k. The transmitted symbols $\{x_k(j), j = 1, 2, \ldots , J\}$ are generated from $\{c_k(j)\}$ after certain operations, such as spreading, scrambling, interleaving, and modulations. At the receiver, the received signals $\{y(j)\}$ are given by

$$\begin{aligned} y(j) = \sum \limits _{k = 1}^K h_k \sqrt{e_k}x_k(j) + \eta (j), j = 1, 2, \ldots , J, \end{aligned}$$

(13.3)

where $h_k$ is the channel coefficient for user k, $e_k$ the transmitted power of user k and $\eta (j)$ an additive white Gaussian noise (AWGN) sample with variance $\sigma ^2$ per dimension.

Figure 13.4 illustrates the factor graph representation [32] for (13.3) with $K = 2$, $J = 8$, and the same LDPC coding for all users. A circle in Fig. 13.4 represents a variable and a square a constraint. Three types of constraints are involved, namely a square marked with “+” for linear additions in (13.3), a white square for LDPC coding, and a square marked with “$\times$” for modulation.

Fig. 13.4

Factor graph of a NOMA LDPC-coded system where $K = 2$ and $J = 8$

Optimal detection for the system in (13.3) typically requires prohibitively high complexity. Low-cost message-passing detection, similar to that used for LDPC codes, can be applied instead, as Fig. 13.4 is sparse when $K \ll J$. However, short cylices constitute a problem. To see this, let us call a circle involving m coded bits as a size-m cycle. An example of a size-4 cycle is shown by the black circles $\{c_1(1), c_1(3), c_2(1), c_2(3)\}$ in Fig. 13.4. There are a large number of such size-4 cycles in Fig. 13.4. Correlation may build up along these short cycles during message-passing detection, which is detrimental to performance [33].

Fig. 13.5

a Factor graph of a two-user IDMA system. b An equivalence form of (a) with re-shuffled $\{c_k(j)\}$. Note that in (a) the interleavers for LDPC coding are the same for both users, while in (b) they are different

Figure 13.4 can also be used to represent a DS-CDMA system. For example, a spreading operation involving binary sequence of ${\pm } 1$ can be regarded as a repetition code plus a scrambling operation of sign changes. Repetition coding can be merged with FEC coding. Scrambling can be incorporated in function of the modulation nodes in Fig. 13.4. Note that scrambling does not change the topology of the graph. The problem of short cycles remains the same with or without scrambling. The same conclusion applies to other modulation techniques.

Inspired by the success of turbo and LDPC codes [23, 25], the IDMA scheme proposed in [31] employs user-specific interleaving to reduce short cycles in a statistical sense. This is illustrated by the shuffled edge connections between $\{c_k(j)\}$ and $\{x_k(j)\}$ in Fig. 13.5a. For example, compared with Fig. 13.4, $\{c_1(1), c_1(3), c_2(1), c_2(3)\}$ no longer form a size-4 cycle after interleaving in Fig. 13.5a. This is beneficial for message-passing detection. Similar principles can also be applied to systems involving convolutional or turbo coding.

Two interleavers are used by each user in Fig. 13.5a, one for LDPC encoding and one for multiple access. The former is the same for all users, and the latter is user-specific. We can combine these two interleavers by re-shuffling $\{c_k(j)\}$ for each user, resulting in Fig. 13.5b. The latter interpretation of IDMA is based on [34].

The advantage of Fig. 13.5b is its simpler implementation. If an interleaver is random, its shifted version can be approximately regarded as another independent random interleaver. Thus, Fig. 13.5b can actually be realized by using a shifted version of an LDPC encoder involving a common underlying interleaver. The users, in this case, are separated by the amount of shift after the common encoder structure. Such shifting can be realized with very little cost. We may name such a scheme as code-shift division multiple access (CsDMA).¹ This concept was first discussed in [35].

Note that the use of interleavers in Fig. 13.5 does not incur any rate loss. This is a noticeable advantage of IDMA for high-rate applications.

2.2 Operations on a Multiple Access Node

We now consider message-passing detection based on Fig. 13.5. For convenience, we refer to a square marked with “+” in Fig. 13.5 as a multiple access (MA) node. We will only discuss the operations for such an MA node shown in Fig. 13.6. The operations for other nodes follow the standard treatments for an LDPC code [25].

Fig. 13.6

An MA node. Here, an inbound message $LLR_\mathrm{DEC}(x_k(j))$ is from an LDPC decoder. An outbound message $LLR_\mathrm{ESE}(x_k(j))$ is generated from the MA node. ESE stands for “elementary signal estimation” and DEC for decoder

Denote by DEC k the decoder for user k. We define two messages: an inbound message $LLR_\mathrm{DEC}(x_k(j))$ and an outbound message $LLR_\mathrm{ESE}(x_k(j))$ that are, respectively log-likelihood ratios (LLRs), generated by DEC k and elementary signal estimation (ESE) operations at the jth MA node in Fig. 13.6. The discussions for $LLR_\mathrm{DEC}(x_k(j))$ follow the standard LDPC decoding principles [25] and so will be omitted. We will focus on $LLR_\mathrm{ESE}(x_k(j))$ below since its computation is not part of a standard LDPC decoder.

For simplicity, let us first assume binary phase-shift keying (BPSK) modulation $x_k(j) = {\pm }1$ for all k. We define $LLR_\mathrm{ESE}(x_k(j))$ by the following LLR for $x_k(j)$:

$$\begin{aligned} LLR_\mathrm{ESE}\left( x_k(j)\right) = \mathrm{log}\frac{\mathrm{Pr}\left( y(j)|x_k(j)=+1\right) }{\mathrm{Pr}\left( y(j)|x_k(j)=-1\right) }, \end{aligned}$$

(13.4)

where y(j) and $x_k(j)$ are defined in (13.3). Assume that $\eta (j)$ in (13.3) is Gaussian with mean $\mu (j) =$ E$(\eta (j))$ and variance $v =$ Var$(\eta (j))$. (For simplicity, we will assume that v is not a function of j. We will explain the rationale for this assumption later.) For a single-user system with $K=1$ in (13.3), the conditional probabilities in (13.4) are given by

$$\begin{aligned} \mathrm{Pr}\left( y(j)|x_1(j)= \pm 1\right) = \frac{\mathrm{exp}{\left( -\frac{\left( y(j)-(\mu (j)\pm h_{1}\sqrt{e_{1}})\right) ^2}{2{ v}}\right) }}{\sqrt{2\pi { v}}}, \end{aligned}$$

(13.5)

so

$$\begin{aligned} LLR_\mathrm{ESE}\left( x_{1}(j)\right) = 2h_{1}\sqrt{e_{1}}\frac{y(j)-\mu (j)}{{{v}}}. \end{aligned}$$

(13.6)

For $K>1$, the problem is much more complicated. We need to consider all possible combinations of $\{x_k(j)\}$. The exact result is the maximum likelihood (ML) estimator [36] below:

$$\begin{aligned} LLR_\mathrm{ESE}\left( x_k(j)\right) = \mathrm{log}\frac{\sum \nolimits _i\mathrm{Pr}\left( y(j)|x_k(j)=+1,X_{{\sim }k}^i(j)\right) \mathrm{Pr}\left( X_{{\sim }k}^i(j)\right) }{\sum \nolimits _i\mathrm{Pr}\left( y(j)|x_k(j)=-1,X_{{\sim }k}^i(j)\right) \mathrm{Pr}\left( X_{{\sim }k}^i(j)\right) }, \end{aligned}$$

(13.7)

where $X_{\sim k}^i(j)$ is one among all $2^{K-1}$ possibilities of the set $\{x_1(j), x_2(j), \ldots , x_{k-1}(j)$, $x_{k+1}(j), \ldots , x_K(j)\}$ (since $x_{k'}(j) \in \{-1, +1\}, \forall k'$). In (13.7), $\mathrm{Pr}\left( y(j)|x_k(j)= \pm 1,X_{{\sim }k}^i(j)\right)$ can be computed similarly to (13.5) and $\mathrm{Pr}\left( X_{\sim k}^i(j)\right)$ can be computed from messages $\{LLR_\mathrm{DEC}(x_k(j))\}$. Following [25], we define $LLR_\mathrm{DEC}(x_k(j))$ by an LLR:

$$\begin{aligned} LLR_\mathrm{DEC}\left( x_k(j)\right) = \mathrm{log}\frac{\mathrm{Pr}\left( x_k(j)=+1\right) }{\mathrm{Pr}\left( x_k(j)=-1\right) }. \end{aligned}$$

(13.8)

We can obtain $\mathrm{Pr}(x_k(j) = \pm 1)$ by solving (13.8) together with $\mathrm{Pr}(x_k(j) = +1) + \mathrm{Pr}(x_k(j) = -1)=1$. Then,

$$\begin{aligned} \mathrm{Pr}\left( X_{{\sim }k}^i(j)\right) = \prod \limits _{k'=1,k'\not = k}{\mathrm{Pr}\left( x_{k'}(j)\right) }. \end{aligned}$$

(13.9)

The complexity of ML is $O(2^K)$ for BPSK, which increases exponentially with K. For a higher order modulation with an M-point constellation, the complexity of ML is $O(M^K)$. This can be a serious problem in practice.

Gaussian approximation (GA) is a low-cost alternative. We rewrite (13.3) as

$$\begin{aligned} y(j) = h_k\sqrt{e_k}x_k(j) + \zeta _k(j), \end{aligned}$$

(13.10a)

where

$$\begin{aligned} \zeta _k(j) = y(j) - h_k\sqrt{e_k}x_k(j) = \sum \limits _{k' = 1, k' \not = k }^K h_{k'} \sqrt{e_{k'}}x_{k'}(j) + \eta (j) \end{aligned}$$

(13.10b)

is the distortion (including interference-plus-noise) with respect to user k. From the central limit theorem, we apply GA to $\zeta _k(j)$ in (13.10b) and assume $\zeta _k(j)\sim N(\mu _k(j), \mathrm{Var}(\zeta _k(j)))$. Now we can treat (13.10a) as a single-user system. For simplicity, we assume a real channel. (We will discuss a complex channel in Sect. 13.5.2.) Then, we have

$$\begin{aligned} \mathrm{Pr}\left( y(j)|x_k(j)= \pm 1\right) = \frac{\mathrm{exp}{\left( -\frac{\left( y(j)-(\mu _{k}(j)\pm h_{k}\sqrt{e_{k}})\right) ^2}{2\mathrm{Var}(\zeta _k(j))}\right) }}{\sqrt{2\pi \mathrm{Var}(\zeta _k(j))}}. \end{aligned}$$

(13.11)

Substituting (13.11) into (13.4) and evaluating $\mu _k(j)$ via (13.10b), we have the following ESE operations for the jth MA node in Fig. 13.6. (We will discuss the generation of $\mathrm{Var}(\zeta _k(j))$ in (13.12c) later in (13.13).)

ESE operations

$$\begin{aligned} \mathrm{(i)}~&\mathrm{E}(x_k(j)) = \mathrm{Pr}(x_k(j) = +1)- \mathrm{Pr}(x_k(j) = -1),\end{aligned}$$

(13.12a)

$$\begin{aligned} \mathrm{(ii)}~&\mu _k(j) = \sum \limits _{k' = 1}^K h_{k'} \sqrt{e_{k'}}\mathrm{E}(x_{k'}(j)) - h_{k} \sqrt{e_{k}}\mathrm{E}(x_k(j)),\end{aligned}$$

(13.12b)

$$\begin{aligned} \mathrm{(iii)}~&LLR_\mathrm{ESE}\left( x_{k}(j)\right) = 2h_{k}\sqrt{e_{k}}\frac{y(j)-\mu _{k}(j)}{\mathrm{Var}(\zeta _k(j))}. \end{aligned}$$

(13.12c)

The following are some details related to the ESE operations.

• Initially, there is no decoder feedback, and we can set $\mathrm{E}(x_k(j)) = 0$ in (13.12a) for $\forall k, j$.

• GA is approximate. However, we observed a very good performance based on GA.

• The summation in (13.12b) can be shared by all users. The cost per information bit per user is independent of the number of users K.

• The principles of GA for higher-order modulations (such as quadrature phase-shift keying (QPSK)) and complex channels can be derived similarly. Related discussions will be shown in Sect. 13.5.2.

We now discuss the evaluation of $\mathrm{Var}(\zeta _k(j))$ involved in (13.12c). From (13.10b),

$$\begin{aligned} \mathrm{Var}(\zeta _k(j)) = \sum \limits _{k' = 1}^K |h_{k'}|^2 {e_{k'}}\mathrm{Var}(x_{k'}(j)) - |h_{k}|^2 {e_{k}}\mathrm{Var}(x_k(j)) + \sigma ^2. \end{aligned}$$

(13.13a)

We observed that the system performance is not sensitive to $\mathrm{Var}(\zeta _k(j))$. Therefore, we take the following approximation

$$\begin{aligned} \mathrm{Var}(\zeta _k(j)) \approx \sum \limits _{k' = 1}^K |h_{k'}|^2 {e_{k'}}v_{k'} - |h_{k}|^2 {e_{k}}v_k + \sigma ^2 \end{aligned}$$

(13.13b)

based on the following assumption

$$\begin{aligned} \mathrm{Var}(x_k(j)) = 1-\left( \mathrm{E}(x_k(j))\right) ^2 \approx v_k, \forall j. \end{aligned}$$

(13.13c)

To evaluate $v_k$ in (13.13c), we can simply compute a few samples of $\mathrm{Var}(x_k(j))$ and take their average. In practice, computation for each $\mathrm{Var}(x_k(j))$ can be implemented using a look-up table. We observed that the required number of samples is small, so the related cost is negligible.

From the above discussions, the total cost for the ESE operations is (approximately) four additions and two multiplications per chip per iteration. (Some operations, such as $h_{k} \sqrt{e_{k}}$ and $2h_{k} \sqrt{e_{k}}/\mathrm{Var}(\zeta _k(j))$, can be precalculated and need not be repeated for every j. The related cost is negligible.)

2.3 Overall IDMA Receiver

Now return to an overall IDMA system in Fig. 13.5. We divide the receiver into an ESE module and K DEC modules. The operations in the ESE module is based on (13.12). Consider two types of schedules below.

• Serial schedule: In each iteration, operations are carried out as follows:

  $\quad \text {ESE for user 1, DEC for user 1, ESE for user 2, DEC for user 2,}\ldots$

  As an example, ESE for user 1 means running (13.12) for every j with k fixed to 1. The LLRs generated in (13.12) are then fed to DEC for user 1. Then, $\{\mu _1(j)\}$ and $v_1$ are updated based on the DEC outputs and the process continues to user 2.

• Parallel schedule: In each iteration, operations are carried out as follows:

  $\begin{array}{ll} &{} \quad \qquad \quad \qquad \text {ESE for all users in parallel, then}\\ &{} \quad \qquad \quad \qquad \text {DEC for all users.} \end{array}$

  In the above, in each iteration, (13.12) is run through every pair of j and k. After the ESE operations, the outputs are fed to the K local DECs. Then, the K DECs are run in parallel. Afterward, $\{\mu _k(j)\}$ and $v_k$ are updated simultaneously for all k.

Note that in the parallel schedule, the value of the summation in (13.12b), that is generated using the results of the previous iteration, remains the same for all users in one iteration. In the serial schedule, this summation is updated user-by-user. We noticed that serial scheduling converges slightly faster than the parallel one.

A question arises whether it is helpful if multiple inner DEC iterations are carried out between two consecutive ESE iterations. For example, with the serial schedule, we can run multiple LDPC decoding iterations for one user before going to the next user. We observed that such inner iterations are generally unnecessary. For fixed overall cost, better performance is achieved without inner iterations. However, slipping some inner or outer iterations may lead to reduced complexity.

Intuitively, we can treat an IDMA system in Fig. 13.5 as a generalized code system on a graph (where an MA node is just for a special type of constraint). The inner-iteration method means more iterations on some parts of the graph for LDPC coding constraints. Such uneven message-passing process does not help in general.

For comparison of overall cost, let us consider a K-user TDMA system in which LDPC decoding is individually carried out for each user. The only difference between SUD for such a TDMA system and MUD for IDMA is the ESE operations. As we have seen above, the cost of the extra ESE operations is quite moderate. Thus, an IDMA receiver involving (13.12) has only moderately higher complexity than SUD for corresponding TDMA systems with the same number of users.

Fig. 13.7

Performance of IDMA with GA in AWGN channels

Figure 13.7 shows an example of a four-user IDMA system in AWGN channels. A rate-1/2 LTE turbo code with 1200 information bits per user is used, followed by a rate-1/8 repetition code and QPSK modulation. We can see that iterative detection nearly converges with about ten outer iterations between ESE and DECs with one inner-iteration. Here, one inner-iteration means running each component decoder once in a turbo decoder. We can also run multiple iterations in each turbo decoder within each outer iteration. The result of five inner iterations is shown in Fig. 13.7. We can see that multiple inner iterations can only offer marginal improvement on performance, even though at considerably higher overall cost.

Figure 13.7 also shows the result with user-specific scrambling by spreading each coded bit with a random binary sequence of $+1$ and $-1$ before modulation. No user-specific interleaving is used in this case. It is seen that interleaving offers better performance than scrambling. This is due to the short cycle problem as explained earlier.

2.4 Performance Evaluation Through SNR Evolution

We now outline an SNR evolution technique [17] for tracking IDMA performance. Similar techniques have been successfully applied to turbo and LDPC codes [25] and more recently to AMP algorithms [37]. This analysis method also provides the basis of power allocation for IDMA performance optimization in the next section.

Figure 13.8a is a so-called protograph [38] representation of Fig. 13.5, in which each circle represents a vector and each edge represents a vector connection. Relatively thick lines are used in Fig. 13.8a to distinguish it from Fig. 13.5. The messages ${\varvec{LLR}}_{\mathrm{DEC},k}$ and ${\varvec{LLR}}_{\mathrm{ESE},k}$ in Fig. 13.8a are LLR sequences generated by the coding and MA constraints, respectively.

Fig. 13.8

a Protograph representation of Fig. 13.5. b Evolution characterization for (a)

We will use the following SNR-variance relationship to characterize the behavior of the system in Fig. 13.8a. Recall (13.10a): $y_k(j) = h_k\sqrt{e_k}x_k(j) + \zeta _k(j)$. We define the average SNR for user k as

$$\begin{aligned} SNR_k \equiv \frac{\mathrm{E}\left( |h_k\sqrt{e_k}x_k(j)|^2\right) }{\mathrm{E}(\mathrm{Var}(\zeta _k(j)))} = \frac{|h_k|^2e_k}{\mathrm{E}(\mathrm{Var}(\zeta _k(j)))}. \end{aligned}$$

(13.14)

From (13.13), we have

$$\begin{aligned} \mathrm{E}(\mathrm{Var}(\zeta _k(j))) = \sum \limits _{k' = 1, k' \not = k}^K |h_{k'}|^2 e_{k'}v_{k'} + \sigma ^2. \end{aligned}$$

(13.15)

Since ${\varvec{LLR}}_{\mathrm{DEC},k}$ is the output of DEC k with input ${\varvec{LLR}}_{\mathrm{ESE},k}$ characterized by $SNR_k$, we can write $v_k$ as a function $v_k = \psi (SNR_k)$. Here for simplicity, we assume that all users employ the same LDPC code and therefore have the same $\psi (\cdot )$. (Note that the re-shuffling operation in Fig. 13.5b has no effect on $\psi (\cdot )$.) Combining this with (13.14) and (13.15), we have the following recursion to characterize an iterative IDMA detector:

$$\begin{aligned}&SNR_k^{(t)} = \frac{|h_k|^2e_k}{\sum \nolimits _{k' = 1, k' \not = k}^K |h_{k'}|^2 e_{k'}v_{k'}^{(t)} + \sigma ^2} \equiv \phi _k\left( v_{1}^{(t)},\ldots v_{k-1}^{(t)},v_{k+1}^{(t)},\ldots v_{K}^{(t)}\right) ,\end{aligned}$$

(13.16a)

$$\begin{aligned}&v_{k}^{(t)}=\psi \left( SNR_{k}^{(t-1)}\right) , \end{aligned}$$

(13.16b)

where t is an iteration index. The initialization is $v_k^{(0)} = 1, \forall k$, implying no information from DECs. In general, there is no closed form expression for $\psi (\cdot )$, but it can be obtained by simulating a single-user APP decoder in an AWGN channel with specified SNRs. Using $\{SNR_k^{(T)}\}$ in the final iteration in (13.16), we can estimate the BER by a function

$$\begin{aligned} BER_k = g\left( SNR_k^{(T)}\right) , \end{aligned}$$

(13.17)

where $g(\cdot )$ can be obtained through simulation of DECs [17].

2.5 Superposition Coded Modulation (SCM)

The above IDMA scheme involves multiple signal streams from different users. We may simply allocate these signal streams to a single-user. Such scheme is referred to as superposition coded modulation (SCM) [39, 40].

We define a standard QPSK constellation as $S_\mathrm{QPSK} = \{00 \rightarrow (+1,+1),01 \rightarrow (+1,-1),10 \rightarrow (-1,+1),11 \rightarrow (-1,-1)\}$. Figure 13.9a is a 16-ary scheme formed by superimposing $S_\mathrm{QPSK}$ and a scaled version of $S_\mathrm{QPSK}$ with a scaling factor of 2 and a $45^{\circ }$ phase shift [39]. Figure 13.9b is a 64-ary scheme formed by superimposing $S_\mathrm{QPSK}$ and two scaled versions of $S_\mathrm{QPSK}$ with, respectively, scaling factors of 1.18 and 1.10 plus $60^{\circ }$ and $120^{\circ }$ phase shifts. From the central limit theorem, the SCM signaling is more Gaussian-like when the number of streams is large. This can offer the so-called shaping gain as analyzed in [41, 42]. It has been proved that, among all possible signaling methods, an SCM constellation achieves the minimum mean squared error (MMSE) bound; that is, it minimizes the function $\psi (\cdot )$ in (13.16b) for a fixed underlying binary decoder. The details are discussed in [39].

Fig. 13.9

a A 16-ary SCM signaling by superimposing two streams of QPSK constellations. b A 64-ary SCM signaling by superimposing three streams of QPSK constellations

3 Power Control for IDMA

At a relatively low sum-rate, such as less than 1 in a complex channel, IDMA with a GA receiver works well with equal received power. At a higher sum-rate, unequal power control is required. The situation is similar to power control for SIC in (13.2), except that iterative detection makes the problem more complicated.

3.1 Transmitted and Received Power Minimization

Denoting the received powers by

$$\begin{aligned} q_k = |h_{k}|^2 e_{k}. \end{aligned}$$

(13.18)

We combine (13.16a) and (13.16b) into a compact form as

$$\begin{aligned} SNR_k^{(t)} = \frac{q_k}{\sum \nolimits _{k' = 1, k' \not = k}^K q_{k'}\psi \left( SNR_{k'}^{(t-1)}\right) + \sigma ^2}, \forall k. \end{aligned}$$

(13.19)

Let $\sum e_k$ and $\sum q_k$ be, respectively, sum transmitted power and sum received power. We can minimize them, respectively. The latter is simpler since the channel gains $\{|h_k|^2\}$ are not involved. The following Remark establishes a connection between these two problems [7, 9, 43].

Remark 1

Assume that $\{q_k^*\}$ is a minimizer for $\sum q_k$. Then, $\{e_k^*= q_k^*/|h_k|^2\}$ is a minimizer for $\sum e_k$ provided that $\{q_k^*\}$ and $\{|h_k|^2\}$ have the same order, i.e., $q_k^* \le q_{k'}^*$ if $|h_k|^2 \le |h_{k'}|^2$.

Based on Remark 1, we can first find the minimizer $\{q_k^*\}$ for $\sum q_k$. We then re-label $\{q_k^*\}$ such that it has the same order as $\{|h_k|^2\}$. Then, the minimizer for $\sum e_k$ can be obtained as $\{e_k^*= q_k^*/|h_k|^2\}$.

Incidentally, Remark 1 implies that a user with a higher channel gain should be assigned a higher transmitted power and vice versa. Next, we focus on minimizing $\{q_k\}$.

3.2 Feasible Profile

We now impose an SNR requirement $\varGamma$ after T iterations. This SNR requirement can be equivalently translated into a BER requirement through (13.17). We write the received power optimization problem as follows.

$$\begin{aligned}&\mathrm{minimize} \quad \sum q_k,\end{aligned}$$

(13.20a)

$$\begin{aligned}&\mathrm{subject~to}\quad SNR_k^{(t)} = \frac{q_k}{\sum \nolimits _{k' = 1, k' \not = k}^K q_{k'}\psi \left( SNR_{k'}^{(t-1)}\right) + \sigma ^2}, \forall k,\end{aligned}$$

(13.20b)

$$\begin{aligned}&\quad \quad \quad \quad \quad SNR_k^{(T)} \ge \varGamma , \forall k. \end{aligned}$$

(13.20c)

The problem in (13.20) is non-convex. We will outline two searching techniques for this problem. For convenience, we will call $\{q_k\}$ a feasible profile if it ensures the constraints in (13.20b) and (13.20c).

Incidentally, it is interesting to compare (13.2a) and (13.20b). In (13.20b), $q_{k'}\psi \left( SNR_{k'}^{(t-1)}\right)$ represents the residual interference from user $k'$ after soft cancelation. Such terms disappear in (13.2a) for decoded users due to the error-free assumption and hard cancelation.

3.3 Greedy Search

We first set $T = 1$ , i.e., only one iteration. Assume that approximate error-free decoding can be achieved at a sufficiently large SNR in the single-user case. We can construct an initial feasible profile $\mathscr {Q}=\{q_k\}$ according to (13.2). The sum-power for such a $\mathscr {Q}$ is typically large.

We next consider a general T. Starting from the above initial $\mathscr {Q}$, we search for a minimum value for each $q_k$ individually to achieve (13.20c), while keeping other elements in $\mathscr {Q}$ unchanged. This involves a one-dimensional search, so its complexity is affordable. Let the search result be $q_k^*$. We then update $q_k \leftarrow q_k - \epsilon (q_k - q_k^*)$ in $\mathscr {Q}$, where $\epsilon$ is a damping factor (e.g., $\epsilon = 0.5$). We repeat the above process for all k iteratively. We observed reasonably good performance of this simple method for a relatively small K.

3.4 Approximate Linear Programming Method

Inspired by the linear program technique for LDPC code design [25], we can use the approximate technique below for a large K. The key idea is to transform the problem of finding the power for each user into finding the number of users on different given power levels, which makes the problem convex [44, 45].

Let us quantize the received power into $M +1$ discrete values: $\{q(m), m = 0, 1, \ldots , M\}$ with $q(m-1) < q(m)$. The received powers of all users are selected from $\{q(m)\}$. We partition K users into $M+1$ groups according to their power levels. Let $\lambda (m)$ be the number of users assigned with power level q(m) and z(m) be the total power of these $\lambda (m)$ users. As such,

$$\begin{aligned}&\sum \limits _m\lambda (m) = K,\end{aligned}$$

(13.21a)

$$\begin{aligned}&z(m) = \lambda (m)q(m) \end{aligned}$$

(13.21b)

and the sum received power

$$\begin{aligned} \sum \limits _k q_k = \sum \limits _m\lambda (m)q(m) = \sum \limits _m z(m). \end{aligned}$$

(13.21c)

Denote by SNR(m) the SNR for the users in the mth group with power q(m). Define

$$\begin{aligned} I = \sum \limits _m z(m)\psi (SNR(m))+ \sigma ^2, \end{aligned}$$

(13.22)

which is the total interference power (including noise) after soft cancelation. When K is large, (13.20b) can be approximated as

$$\begin{aligned} SNR(m)^{(t)} = \frac{q(m)}{I^{(t)}-q(m)\psi \left( SNR(m)^{(t-1)}\right) } \approx \frac{q(m)}{I^{(t)}}, \end{aligned}$$

(13.23)

where $I^{(t)}$ denotes the value of I at the tth iteration. Using (13.22) and (13.23), we have the update rule

$$\begin{aligned} I^{(t)} = \sum \limits _m z(m)\psi \left( \frac{q(m)}{I^{(t-1)}}\right) +\sigma ^2. \end{aligned}$$

(13.24)

Equation (13.24) characterizes the evolution of the total interference at each iteration. If iterative detection converges, $I^{(t)}$ should be lower than $I^{(t-1)}$. Equivalently, we can write the convergence condition as

$$\begin{aligned} \sum \limits _m z(m)\psi \left( \frac{q(m)}{I}\right) +\sigma ^2 \le (1-\delta )I,\quad I_\mathrm{min}\le I \le I_\mathrm{max} . \end{aligned}$$

(13.25)

where $0< \delta < 1$ is a decay factor that controls the convergence speed. $I_\mathrm{max}$ and $I_\mathrm{min}$ specify the total interference at the beginning and end of the iterative detection. In summary, we re-formulate the optimization problem as,

$$\begin{aligned}&\mathrm{minimize} \quad \sum z(m),\end{aligned}$$

(13.26a)

$$\begin{aligned}&\mathrm{subject~to}\quad \sum \limits _m z(m)\psi \left( \frac{q(m)}{I}\right) +\sigma ^2 \le (1-\delta )I,\quad I_\mathrm{min}\le I \le I_\mathrm{max},\end{aligned}$$

(13.26b)

$$\begin{aligned}&\quad \quad \quad \quad \quad z(m) \ge 0, \forall m. \end{aligned}$$

(13.26c)

The above optimization problem is linear with respect to $\{z(m)\}$. Hence, it can be resolved by linear programming. More details can be found in [44, 45].

Figure 13.10 is an example to illustrate the necessity of unequal power control (UPC). We can see that UPC improves the system performance for all the three cases of $K = 3$, 6, and 12 compared with equal power control (EPC). Particularly, when $K = 12$, the IDMA system does not work at all with EPC, but works well with UPC. The gap between IDMA with UPC and capacity is about 3.7 dB for $K = 12$.

Fig. 13.10

IDMA with EPC and UPC in AWGN channels. Rate-1/3 turbo coding followed by rate-1/2 repetition coding is used for each user. Information length of each user is 1200. QPSK modulation. Sum-rate = 1, 2, and 4 for K = 3, 6, and 12, respectively

Compared with the 12-user example in Fig. 13.3, we can see that IDMA recovers about 3.7 dB relative to the loss incurred by SIC. This is impressive, but there is definitely room for improvement. The gap towards capacity can potentially be further narrowed using more sophisticated techniques, such as curve-matching-based degree sequence optimization [46, 47], spatial coupling [48,49,50,51,52,53,54,55,56,57], or more sophisticated modulations [58].

A criterion called overloading, which represents the user capacity in a NOMA system, is used to assess the system performance in the recent literature. Figure 13.10 demonstrates that IDMA can offer very high overloading with centralized power control. In the next section, we will discuss IDMA techniques to achieve high throughput without centralized power control.

4 Random Access via IDMA

4.1 Limitations of Conventional Systems

A conventional uplink system with centralized control involves a connection setup procedure before data transmission. The overhead incurred by this procedure is not serious for services with long-lasting connections since it can be amortized across the connection duration. One of the main tasks envisaged for the next 5G cellular systems is to support machine-type communication (MTC) which is characterized by short and sporadic data communication. In this case, the cost of establishing centralized control can be substantial.

Random access is decentralized, in which each user makes an individual decision to transmit data packets. This avoids the overhead of connection setup, but the packets from different users may collide. In a conventional random-access scheme, such as ALOHA [59], colliding packets are discarded, which reduces throughput. For this reason, such techniques cannot satisfy the demand of high spectral efficiency in 5G cellular systems.

In a fading channel, the received powers of different users may form a feasible profile defined in Sect. 13.3.2, even without centralized control. This is captured in the multi-packet reception (MPR) model [60, 61]. Most existing MPR techniques rely on channel fading to form feasible profiles. Such a passive approach achieves limited throughput gain. In what follows, we will discuss an active approach based on the power control technique. The main idea is to optimize the probability of forming a feasible profile through decentralized power control at the transmitters.

4.2 Random IDMA with Decentralized Power Control

4.2.1 Problem Formulation

Recall from Sect. 13.3.2, a feasible received power profile $\{q_k\}$ can be formed by centralized control. Without centralized control, however, it is difficult to guarantee this. A randomized power control (RPC) technique [62,63,64,65,66,67] is discussed below to handle this difficulty.

The principles of RPC are as follows. Let $\{Q^{(l)}, l =1, 2, \ldots , L\}$ (L is the maximum level index) be a set of pre-defined power levels and $\{P^{(l)}, l =1, 2, \ldots , L\}$ a set of related probabilities. Upon a packet arrival, each user randomly draws a power level $Q^{(l)}$ with probability $P^{(l)}$ and uses it to transmit. Different users act individually and so their transmissions may collide. However, as long as their received powers $\{q_k\}$ form a feasible profile, their signals can still be recovered. Our aim is to optimize the probability that $\{q_k\}$ form a feasible profile.

Mathematically, $\{q_k\}$ defined above are the realizations of an underlying random variable. The random variable is characterized by a probability mass distribution $\{P^{(l)}\}$. Each $q_k$ is independently drawn by a user from the support $\{Q^{(l)}\}$. Once the distribution is given, there is no need for centralized control.

4.2.2 Type-2 Collisions

The problem formulated above turns out to be difficult when K is large. So far, we have no general solution. We will discuss a sub-optimal technique below.

We say that a collision is of type-M if it involves M active users. Let $Q^{(0)} = 0$ be an element in $\{Q^{(l)}\}$. In RPC, a user will not transmit if its selected power is $Q^{(0)}$. The related $P^{(0)}$ is equivalent to the back-off probability in 802.11 Wi-fi systems. Intuitively, collisions are dominated by type-2 ones when $P^{(0)}$ is sufficiently large. Therefore, we will focus on type-2 collisions.

We consider a type-2 collision involving user i and user j. We define the union of all possible feasible profiles of the received power pair $\{q_i, q_j\}$ as a feasible region. The collision is resolvable if $\{q_i, q_j\}$ falls in this region. Figure 13.11a shows an example of the feasible region for SIC with ideal coding and decoding. The area marked by “A” in Fig. 13.11a is formed by all possible $\{q_i, q_j\}$ that meets the following conditions (see (13.2)):

$$\begin{aligned}&SNR_j = \frac{q_j}{q_i+\sigma ^2} \ge \varGamma ,\end{aligned}$$

(13.27a)

$$\begin{aligned}&SNR_i = \frac{q_i}{\sigma ^2} \ge \varGamma . \end{aligned}$$

(13.27b)

The area marked by “B” in Fig. 13.11a is formed similarly by changing decoding order. The value of $\varGamma$ here is determined by the Shannon capacity R = log$_2(1 + \varGamma )$. Any power pair in the feasible region is resolvable by SIC.²

Figure 13.11b is an example of an IDMA system involving two LDPC-coded users with coding rate 0.5 per user. The receiver can achieve BER $\le 10^{-5}$ in the feasible region, which is regarded as approximately error-free. The border of this feasible region is obtained using simulation.

Fig. 13.11

Feasible regions for a a two-user ideally coded system with SIC, and b a two-user LDPC-coded IDMA system

Each of the two feasible regions in Fig. 13.11 is bounded by four curves $q_i = Q^{(1)}, q_j = \phi (q_i), q_j = Q^{(1)}$ and $q_i = \phi (q_j)$. Here, the function $\phi (\cdot )$ is determined by (13.27a) taking mark of equality (for Fig. 13.11a) or by simulation (for Fig. 13.11b). $Q^{(1)}$ is the minimum power for successful single-user transmission. We construct the set $\{Q^{(l)}\}$ as follows:

$$\begin{aligned} Q^{(l)}=\left\{ \begin{aligned}&0, \quad \quad \quad \quad ~~ l = 0,\\&Q^{(1)}, \quad \quad \quad ~ l = 1,\\&\phi (Q^{(l-1)}), \quad l > 1. \end{aligned} \right. \end{aligned}$$

(13.28)

For $\{q_k\}$ randomly selected from $\{Q^{(l)}\}$, we have the following situations:

Case 1: All $\{q_k\}$ are zeros. In this case, throughput is zero.

Case 2: Only one element in $\{q_k\}$ is nonzero. The transmission of the only active user will be successful.

Case 3: Exactly two elements in $\{q_k\}$, say $q_i$ and $q_j$, are nonzero. This is a type-2 collision. It can be shown that $\{q_i, q_j\}$ falls in the feasible region (so collision is resolvable) provided that $q_i \ne q_j$.

Case 4: More than two elements in $\{q_k\}$ are nonzero. For simplicity, such events are regarded as unresolvable, which is a pessimistic assumption.

Based on the above cases, we can find an optimized probability set $\{P^{(l)}\}$ for a K user system. For convenience, we assume that the packets of all users arrive independently, following the Bernoulli process with parameter $\lambda$. The system throughput is then given by

$$\begin{aligned} T = T_1 + T_2. \end{aligned}$$

(13.29)

In (13.29), $T_1$ is the throughput related to transmissions without collision:

$$\begin{aligned} \begin{aligned} T_1=&\sum \limits _{k=1}^KC_K^k\lambda ^k (1-\lambda )^{(K-k)}C_k^1(1-P^{(0)})(P^{(0)})^{k-1} \\ =&K\lambda (1-P^{(0)})(1-\lambda +\lambda P^{(0)})^{K-1}, \end{aligned} \end{aligned}$$

(13.30)

where $C_K^k\lambda ^k (1-\lambda )^{(K-k)}$ is the probability of k users among total K users having packets to transmit and $C_k^1(1-P^{(0)})(P^{(0)})^{k-1}$ the probability of only one user among these k users transmitting with nonzero power. Also in (13.29), $T_2$ is the throughout related to type-2 collisions. From case 3 above, a type-2 collision is unresolvable only if the two transmitting users are using the same received powers. Therefore, we have

$$\begin{aligned} \begin{aligned} T_2=&2\sum \limits _{k=2}^KC_K^k\lambda ^k (1-\lambda )^{(K-k)}C_k^2\left( (1-P^{(0)})^2-\sum \limits _{l>0}(P^{(l)})^2\right) (P^{(0)})^{k-2} \\ =&K(K-1)\lambda ^2(1-\lambda +\lambda P^{(0)})^{K-2}\left( (1-P^{(0)})^2-\sum \limits _{l>0}(P^{(l)})^2\right) , \end{aligned} \end{aligned}$$

(13.31)

where $(1-P^{(0)})^2-\sum \limits _{l>0}(P^{(l)})^2$ is the probability that two active users transmit with different received powers.

We further consider an average transmitted power constraint $\bar{q}$ for each user. In AWGN channels with unit channel power gain, the constraint is given by

$$\begin{aligned} \sum \limits _{l \ge 0} Q^{(l)}P^{(l)} \le \bar{q}. \end{aligned}$$

(13.32)

Under such power constraint, we can search for $\{P^{(l)}\}$ that maximize the throughput T in (13.29). It can be verified that the problem is convex if $P^{(0)}$ is fixed. The treatments for fading channels are somewhat more complicated. The details can be found in [63].

Figure 13.12 shows two examples, one for an ideally coded system and the other for an LDPC-coded IDMA system [63]. Conventional ALOHA is included as a reference. We can see that the RPC-based scheme can offer noticeably throughput gain compared with ALOHA.

Fig. 13.12

Performance comparison of RPC and ALOHA in a an ideally coded system and b an LDPC-coded IDMA system. Rayleigh fading channel with averaged power gain 1 for all users. Same power constraint for RPC and ALOHA

It is proved in [63] that the $\{Q^{(l)}\}$ in (13.28) forms an optimal support for the decentralized power control when $K = 2$. It is sub-optimal for $K > 2$, but it can still provide excellent performance gain, as seen in Fig. 13.12.

As a short summary, we can treat collisions as NOMA cases. A conventional scheme, such as ALOHA, treats such NOMA cases as failures. The discussions in this section aim at optimizing the probability of successful detection in such NOMA cases.

5 IDMA in MIMO Systems

5.1 Multi-User Gain in MIMO Systems

MIMO is a wireless technology employing multiple transmit and receive antennas [68,69,70,71,72,73,74]. Multi-user gain refers to the advantage of allowing a large number of users to transmit simultaneously over the same time and same frequency in MIMO [10, 75]. This is illustrated in Fig. 13.13 by the potential sum-rate capacity gain for a single-cell system. Perfect CSI is assumed in Fig. 13.13. The curves apply to both up- and downlinks following the duality principle [3, 76, 77]. We can see that multi-user gain is very attractive. The potential gain is in the order of tens of times. Diversifying power over more users, i.e., increasing K, is a very effective way to increase sum-rate.

Fig. 13.13

Achievable sum-rate of ZF under perfect CSI. The number of antennas at the base station is 64. Single antenna assumed is for each user. Other system parameters are the same as those in Fig. 13.1

Figure 13.13 also includes the performance of zero-forcing (ZF) with proper power allocation. ZF is an OMA technique [75]. Different users are divided into different orthogonal subspaces in ZF, which avoids interference among users. It is seen from Fig. 13.13 that, with accurate CSI, ZF can offer very good multi-user gain. Since the gap between ZF and capacity is small, any further gain by NOMA is limited. In this case, OMA via ZF can be preferred for its low-cost SUD receiver.

However, in practice, we usually do not have reliable CSI to establish spatial orthogonality initially. ZF performance deteriorates seriously when CSI is not accurate. In the following, we will see that NOMA via IDMA offers a solution to the problem.

5.2 Iterative Maximum Ratio Combining (I-MRC)

We first extend the GA-based detection technique in Sect. 13.2.2 to MIMO. Consider a multi-user uplink system model with $N_\mathrm{BS}$ antennas at the base station. For simplicity, we assume a single antenna at each user. The IDMA principle discussed in Sect. 13.2.1 can be directly used here. We assume perfect CSI first and will return to the CSI estimation problem later.

The received signal at time j is written as

$$\begin{aligned} {\varvec{y}}(j) = \sum \limits _{k = 1}^K {\varvec{h}}_k \sqrt{e_k}x_k(j) + {\varvec{\eta }}(j), \end{aligned}$$

(13.33)

where ${\varvec{y}}(j)$ is an $N_\mathrm{BS} \times 1$ signal vector received at base station antennas, $h_k$ an $N_\mathrm{BS} \times 1$ complex channel coefficient vector, $e_k$ the transmitted power of user k, $x_k(j)$ a symbol transmitted from user k, and ${\varvec{\eta }}(j)$ an $N_\mathrm{BS} \times 1$ vector of complex AWGN with mean 0 and variance $\sigma ^2 = N_0/2$ per dimension.

Maximum ratio combining (MRC) is a common strategy for MIMO systems. An MRC estimator is defined in a symbol-by-symbol form as

$$\begin{aligned} {\hat{x}_k}(j) = \varvec{h}_k^{{H}}\varvec{y}\mathrm{{(}}j\mathrm{{)}}. \end{aligned}$$

(13.34)

Substituting (13.33) into (13.34),

$$\begin{aligned} {\hat{x}_k}\mathrm{{(}}j\mathrm{{)}} = \lambda _k^{}{x_k}\mathrm{{(}}j\mathrm{{)}} + \xi _k^{}\mathrm{{(}}j\mathrm{{)}}, \end{aligned}$$

(13.35a)

where $\lambda _k^{} \equiv {\left\| {{\varvec{h}_k}} \right\| ^2}\sqrt{e_k} = \varvec{h}_k^{{H}}\varvec{h}_k^{}\sqrt{e_k}$ is a scalar and

$$\begin{aligned} \xi _k^{}\mathrm{{(}}j\mathrm{{)}} \equiv \sum \limits _{k' = 1,k' \ne k}^K {\varvec{h}_k^{{H}}\varvec{h}_{k'}^{}\sqrt{e_{k'}}{x_{k'}}} \mathrm{{(}}j\mathrm{{)}} + \varvec{h}_k^{{H}}\varvec{\eta }\mathrm{{(}}j\mathrm{{)}} \end{aligned}$$

(13.35b)

is an interference (from $\{x_{k'}(j), k' \ne k \}$ to $x_k(j)$) plus noise term. MRC does not involve matrix inversion and so has low cost. However, interference is a problem for MRC, especially when K is large. Iterative GA technique can alleviate this problem. Similar as that in Sect. 13.2.2, we approximate $\xi _k(j)$ in (13.35b) by a Gaussian random variable. We assume that the real and imaginary parts of $x_k(j)$ carry two bits of information in the QPSK modulation. Similar to (13.12), the real part of $x_k(j)$ can be estimated as

$$\begin{aligned} {LLR_{\mathrm{{ESE}}}}\left( \mathrm{Re}(x_k(j))\right) = \frac{{2{\lambda _k} }}{{\mathrm{{Var}}\left( {{\mathrm{Re}} \left( {\xi _k^{}\mathrm{{(}}j\mathrm{{)}}} \right) } \right) }}{\mathrm{Re}} \left( {{{\hat{x}}_k}\mathrm{{ - E}}\left( {\xi _k^{}\mathrm{{(}}j\mathrm{{)}}} \right) } \right) . \end{aligned}$$

(13.36)

The mean and variance in (13.36) are updated as

$$\begin{aligned}&{\mathrm {E}}\left( {\xi _k^{}{\mathrm {(}}j{\mathrm {)}}} \right) ={\varvec{h}_k}^H \left( \sum \limits _{k' = 1}^K {{\varvec{h}_{k'}}\sqrt{e_{k'}}{\mathrm E}(x_{k'}(j))}-{{\varvec{h}_{k}}\sqrt{e_{k}}{\mathrm E}(x_{k}(j))}\right) , \end{aligned}$$

(13.37a)

$$\begin{aligned}&{\mathrm {Var}}\left( {{{\mathrm Re}} \left( {\xi _k^{}{\mathrm {(}}j{\mathrm {)}}} \right) } \right) \nonumber \\ =&\sum \limits _{k' = 1}^K {{\mathrm {Var}}\left( {{{\mathrm {Re}}} \left( {\varvec{h}_k^{{H}}\varvec{h}_{k'}^{}\sqrt{e_{k'}}{x_{k'}}{\mathrm {(}}j\mathrm{{)}}} \right) } \right) }- {\mathrm Var}\left( {\mathrm {Re}}\left( {\left\| \varvec{h}_k\right\| ^2\sqrt{e_k}{x_{k}}{\mathrm {(}}j{\mathrm {)}}} \right) \right) {\mathrm { + }}\left\| \varvec{h}_k\right\| ^2{\sigma ^2}. \end{aligned}$$

(13.37b)

Some detailed computation techniques for (13.37) can be found in [75]. The imaginary part of $x_{k}(j)$ can be estimated similarly. We call the above process iterative MRC (I-MRC).

Fig. 13.14

Multi-user gain for $K = 8$ with I-MRC. Rayleigh fading. $N_\mathrm{BS} = 64$. Equal transmitted power is assumed for different users. Power control is used for the streams assigned to the same user. The power allocation levels are obtained through heuristic search. Rate-1/2 turbo coding and information length $= 1200$ for each stream. QPSK modulation. A codeword is transmitted over ten resource blocks. Each resource block contains 180 symbols experiencing the same fading conditions

Figure 13.14 illustrates the effectiveness of I-MRC [75]. We consider three different settings:

• (i) $K = 1$ and sum-rate $R_\mathrm{sum} = 5$ with five signal streams (each stream with rate 1) assigned to the sole user using the SCM principle discussed in Sect. 13.2.5,

• (ii) $K = 8$ and $R_\mathrm{sum} = 16$ with two streams per user, and

• (iii) $K = 8$ and $R_\mathrm{sum} = 24$ with three streams per user.

For $K = 1$, all the signal streams see the same channel so there is no spatial diversity among them, which results in poor performance. Increasing K from 1 to 8 results in drastically enhanced rate or reduced power or both in Fig. 13.14. Figure 13.14 is a compelling evidence for multi-user gain: allowing more concurrent transmitting users is more efficient than increasing single-user rate.

5.3 Data-Aided Channel Estimation (DACE)

We now consider the CSI acquisition problem. Many factors may affect CSI accuracy in MIMO. In particular, the correlation among the pilots used by different users can lead to the pilot contamination problem [78].

IDMA with data-aided channel estimation (DACE) [17, 79,80,81,82,83] technique can be used to improve CSI accuracy. The basic principle of DACE is as follows. Recall that a key difference between pilot and data is that the former is known at the receiver, while the latter is not. Therefore, if a data symbol is known, it can be used as a pilot. Furthermore, partial information of a data symbol, such as its mathematical mean, can also be used to refine the channel estimates. Such partial information is readily available in an IDMA receiver (as given in (13.8)).

DACE can be used jointly with I-MRC, which involves iterations of the following two operations [75]:

• (a) using both pilots and partially decoded data information to refine CSI, and

• (b) using improved channel estimates to refine data estimation by I-MRC.

The advantages of DACE are twofolds: (i) With DACE, the estimated data is gradually used for channel estimation. Pilot energy can be greatly reduced since only very coarse CSI is required initially. (ii) Data sequences are typically much longer than pilots and correlation is low among them. Therefore, DACE is robust against the pilot contamination problem. Such problem is typically caused by the correlation among the pilot sequences re-used in neighboring cells. Without DACE, longer pilot sequences will be required to reduce such correlation. Thus, DACE also reduces the time overhead related to pilots.

Fig. 13.15

Performance comparison of a ZF and b I-MRC-DACE with different $\beta$ values. Rayleigh fading. $N_\mathrm{BS} = 64$ and $K = 16$. Rate-1/3 turbo coding and information length $= 1312$ for each user. QPSK modulation. Each codeword is divided into 12 sections, and each section is transmitted over a resource block (including 16 pilot symbols). Different users in a cell are assigned different orthogonal pilots. These pilots are repeated for users in different cells. The pilot and data symbols have the same average power

I-MRC and DACE can be naturally combined in an overall iterative process. After MRC and decoding operations in each iteration, partially detected data are used to refine channel estimates that are in turn used for MRC and decoding in the next iteration. This is referred to as I-MRC-DACE. Figure 13.15 compares BER performance for ZF and I-MRC-DACE, in which $\beta$ is the cross-cell interference factor defined in (13.1). A larger $\beta$ indicates a more serious pilot contamination problem due to more severe interference among the pilots. From Fig. 13.15, we can see that I-MRC-DACE noticeably outperforms ZF. The difference becomes very significant when $\beta$ is large (e.g., $\beta \ge 0.6$).

IDMA is a natural choice for I-MRC-DACE since it is beneficial for iterative detection. Note that Fig. 13.5 can also be used to characterize IDMA in MIMO systems, if each scalar y(j) in Fig. 13.5 is replaced by its vector counterpart ${\varvec{y}}(j)$ in (13.33). The discussions on short cycles in Sect. 13.2.1 are still applicable after such replacement.

IDMA also allows a superimposed pilot scheme that can reduce the power overhead and rate loss. The related discussions can be found in [83,84,85,86].

6 Prospective Applications of IDMA in 5G Systems

Various approaches have been proposed recently for 5G radio link under LTE, including IDMA [87], RSMA [88], IGMA [89], PDMA [90] and SCMA [91, 92]. In the following, we will show that these schemes all share, explicitly or implicitly, the basic principle of IDMA.

We first represent these different schemes using a unified protograph framework. Assume that N resource blocks (RBs) defined in LTE are available for transmission. We label the observations from these RBs by $\{{\varvec{y}}^{(1)}, {\varvec{y}}^{(2)}, \ldots , {\varvec{y}}^{(N)}\}$.

Fig. 13.16

Protograph representations of DS-CDMA and IDMA with a three users over two RBs, and b six users over four RBs

Figure 13.16 shows a scheme in which each user transmits on all available RBs as illustrated for two system settings: (a) three users over two RBs, and (b) six users over four RBs. This can be realized by transmitting replicas of each $x_k$ over multiple RBs. Alternatively, we may use a low-rate code to generate each $x_k$. Each $x_k$ can be segmented into several blocks, with each block transmitted over an RB. The latter approach can potentially provide higher coding gain [93]. We may also use different modulations for the bits on different RBs, as for SCMA [92].

Incidentally, both DS-CDMA and IDMA can be represented using the protographs in Fig. 13.16. They are distinguished by the absence or presence of user-specific interleaving within each RB. RSMA [88] is a DS-CDMA scheme. However, user-specific interleaving is stated as an option for RSMA. If this option is used, it is equivalent to IDMA. The advantage of this option can be seen in Fig. 13.7.

Alternatively, each user can transmit over only some of the available RBs. This is referred to as sparse coding in [91]. Figure 13.17 shows an example for sparse coding. IGMA, PDMA, and SCMA all involve such treatment. Note that symbol-level interleaving as in Fig. 13.5a is not explicitly seen in Figs. 13.16 and  13.17. If such underlying interleaving is not used, size-4 cycles can be a problem in Fig. 13.16. Sparse coding in Fig. 13.17 avoids this problem. Clearly, sparse coding leads to user-specific edge connections between users and RBs. It has the same effect as symbol-level interleaving; they both reduce short cycles.

With sparse coding, each user does not fully occupy all RBs. This may cause problem for decentralized grant-free [13] or random-access applications, where each user determines its activity individually. In these cases, the number of active users, denoted by $K_\mathrm{active}$, is a random variable. When $K_\mathrm{active}$ is small, sparse coding may lead to inefficient use of the available RBs and so low power efficiency. This implies poor scalability of user numbers. On the other hand, an IDMA system in Fig. 13.16 based on symbol-level interleaving does not have this problem, since all available RBs are fully used for any value of $K_\mathrm{active}$.

Also, multi-user gain in MIMO is determined by the number of users concurrently transmitting in each RB. Therefore, sparse coding may not be an efficient option in MIMO (especially in massive MIMO).

Fig. 13.17

Protograph representation of sparse coding

Fig. 13.18

IDMA with GA versus SCMA with ML. Ten iterations for both schemes

Figure 13.18 compares IDMA and SCMA in quasi-static Rayleigh fading channels. The channels remain unchanged within each transmission. Both schemes are with six users, two receiver antennas, sum-rate = 3 and equal transmitted power per user. A rate-1/2 LTE turbo code is used followed the following transmitter structures:

• IDMA is with a length-2 spreading and QPSK modulation.

• SCMA is based on Fig. 13.17 with the 16-point modulation in [92].

We can see from Fig. 13.18 that the two schemes have similar performance. However, SCMA in Fig. 13.18 is based on ML, while IDMA based on GA. The latter has much lower complexity.

7 Summary

We have shown that the real attractiveness of NOMA is in systems without centralized control or without accurate CSI. It is difficult or too costly to establish orthogonality in such channels, so we have to resort to NOMA. Iterative processing holds the key; interference can be gradually resolved and CSI can be gradually refined through iterative processing. IDMA is a simple implementation technique for NOMA. The features of IMDA can be seen from its sparse graphic representation. The interleaved edge connections in IDMA facilitate iterative processing at the receiver. We have demonstrated that IDMA can offer significant performance gain in random access and MIMO systems. IDMA also offers lower detection complexity compare with other alternatives.