Keywords

1 Introduction

Much interest has been shown in fundamental problems of failure due to mesoscopic nature of this phenomenon related to the multiscale damage accumulation (microcracks, microshears). Solid with these defects reveals the properties of out-of-equilibrium systems and field description of deformed solids should be consistent with theory of defects and physics of damage-failure transition in terms of continuous variables characterizing the behavior of defect ensembles. Statistical approach for the description of out-of-equilibrium states of solid with defects was developed in [1] and allowed the formulation of the field description. Mechanisms of multiscale structural relaxation induced by mesoscopic defects is the consequence of characteristic form of out-of-equilibrium free energy, corresponding free energy release in terms of internal variables and realizes as specific type of critical phenomena in solids with defects – structural-scaling transition. Internal variables represent the defect induced strain (defect density tensor) and the susceptibility of material to the defects growth in terms of the ratio of two characteristic scales: mean size of defects and spacing between defects as parameters of defects interaction. Nonlinearity of free energy release provides the qualitative changes in the kinetics for defect density tensor (defect induced strain) leading to the nucleation of damage localization areas (with characteristic fractography images on the fracture surface). The sizes of damage localization areas and temporal dynamics of defects accumulation are given by the self-similar “blow-up” solution for damage evolution equation. These self-similar solutions are localized on characteristic lengths and represent the set of collective modes of defects. The subjection of solid behavior to the set of these collective modes leads to qualitative changes of crack dynamics (transition from steady to branching regime of crack propagation), scale universality of fragmentation statistics and self-similar scenario of failure under dynamic and shock wave loading [2].

2 Collective Modes of Defects

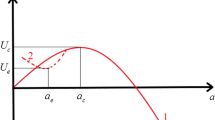
One of the key results of the statistical approach and statistically based phenomenology are the establishment of two “order parameters” responsible for the structure evolution – the defect density tensor \( p_{ik} \) and the structural scaling parameter \( \delta = \left( {{R \mathord{\left/ {\vphantom {R {r_{0} }}} \right. \kern-0pt} {r_{0} }}} \right)^{3} \), which represents the ratio of the spacing between defects and characteristic size of defects [6, 7]. The value of structural-scaling parameter characterizes the current susceptibility of material to the nucleation and growth of defects. Dependence of solid responses on structural-scaling parameter reflects important feature of damage kinetics, statistical self-similarity [1], that was established for microshear (microcrack) distribution function for different stages of damage accumulation represented in dimensionless (self-similar) coordinates. Statistically predicted non-equilibrium free energy \( F \) represents generalization of the Ginzburg-Landau expansion in terms of mentioned order parameters – the defect density tensor (defect induced deformation \( p\left( x \right) = p_{zz} \) in uni-axial loading in z-direction) and structural scaling parameter \( \delta \):

$$ F = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}A\,\left( {\delta ,\delta_{*} } \right)p_{{}}^{2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}Bp_{{}}^{4} - {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0pt} 6}C\,{\kern 1pt} \left( {\delta ,\delta_{c} } \right)p_{{}}^{6} - D\sigma \,p + \chi \,\left( {{{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial x}}} \right. \kern-0pt} {\partial x}}} \right)^{2} , $$
(1)

The damage evolution is determined by the kinetic equations for the defect density \( p \) and structural-scaling parameter \( \delta \)

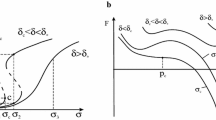
$$ \dot{p} = - \Upgamma_{p} \frac{\Delta F}{\Delta p},\quad \dot{\delta } = - \Upgamma_{\delta } \frac{\partial F}{\partial \delta } , $$
(2)

where \( \Upgamma_{p} ,\Upgamma_{\delta } \) are the kinetic coefficients, \( {{\Delta ( \ldots )} \mathord{\left/ {\vphantom {{\Delta ( \ldots )} {\Delta t}}} \right. \kern-0pt} {\Delta t}} \) is the variation derivative. Kinetic equations (Eq. 2) and the equation for the total deformation \( \varepsilon_{{}} = \hat{C}_{{}} \sigma_{{}} + p_{{}} \) (\( \hat{C} \) is the component of the elastic compliance tensor) represent the constitutive equations of materials with mesodefects. Material responses include the generation of characteristic collective modes – the autosolitary waves in the range of \( \delta_{c} < \delta < \delta_{*} \) and the “blow-up” dissipative structure in the range \( \delta < \delta_{c} \approx 1 \). The generation of these collective modes under the loading provides the change of the system symmetry according to the group properties of equations in corresponding ranges of structural-scaling parameter and initiates specific mechanisms of damage-failure transition on the scales of damage localization with the blow-up defect kinetics.

The damage localization kinetics follows to the “blow-up” self-similar solution [1]

$$ p = g\left( t \right)f\left( \xi \right),\xi = {x \mathord{\left/ {\vphantom {x L}} \right. \kern-0pt} L}_{H} ,g(t) = G(1 - {t \mathord{\left/ {\vphantom {t {\tau_{c} }}} \right. \kern-0pt} {\tau_{c} }})^{ - m} , $$
(3)

and can be considered as the precursor of crack nucleation.

The parameters in Eq. 3 are: \( \tau_{c} \) is the so-called “peak time” (\( p \to \infty \) at \( t \to \tau_{c} \) for the self-similar profile \( f\left( \xi \right) \) localized on the scale \( L_{H} \), \( G > 0,\;m > 0 \) are the parameters of non-linearity, which characterize the free energy release rate for \( \delta < \delta_{c} \). The self-similar solution Eq. 3 describes the blow-up damage kinetics for \( t \to \tau_{c} \) (on the set of spatial scales \( L_{H} = kL_{c} ,\;k = 1,2, \ldots K \), where \( L_{c} \) and \( L_{H} \) corresponds to the so-called “simple” and “complex” blow-up dissipative structures. Generation of the complex blow-up dissipative structures appears when the distance \( L_{S} \) between simple structures approaches to the scale \( L_{c} \). Similar scenario of the “scaling transition” proceeds for the blow-up structures of different complexity to involve in damage localization the larger scales of material.

The description of damage kinetics as the structural-scaling transition allowed the consideration of solid with defects as a dynamic system with spatial-temporal degrees of freedom (corresponding to the set of blow-up dissipative structures of different complexity). Stochastic behavior in this case can be linked with the dynamics of out-of-equilibrium system with the features of flicker noise, or \( {1 \mathord{\left/ {\vphantom {1 f}} \right. \kern-0pt} f} \)- statistics [3]. The self-similar nature of mentioned collective modes associated with damage localization zones has the importance in the case of dynamic loading, when the “excitation” of these modes can lead to the subjection of failure to the dynamics of these modes.

3 Fragmentation Statistics. Resonance Excitation of Failure (Failure Waves)

Fragmentation statistics was studied during in situ experiments for impact loaded fused quartz rods and fracture luminescence recording to analyze the temporal sequences of failure hotspots initiation and the following study of fragmentation statistics for recovered samples after the fragment weighing [3, 4]. Temporal fracture luminescence events and fragment size distribution demonstrated the power law statistics (the flicker or \( {1 \mathord{\left/ {\vphantom {1 f}} \right. \kern-0pt} f} \)- noise) that is characteristic for the out-of-equilibrium critical systems revealing the so-called self-organized criticality (SOC).

It is interesting the limit case of failure revealing the temporal-spatial independence of failure evolution on stress. Namely this situation is observed in experiment for failure wave initiation [4].

Experimental study of failure wave generation and propagation was realized for the symmetric Taylor test on fused-quartz rods. Figure 1 shows the processing of a high-speed photography (upper picture) for the flyer rod travelling at 534 m/s at impact.

Fig. 1.
figure 1

The Taylor test data

Full size image

Three dark zones correspond to the image of impact surface (green triangle), failure wave (red square) and (blue diamond) the shock wave. The initial slope for the failure wave gives the front velocity \( V{}_{fw} \approx 1.57\,{\text{km/s}} \) that is close to traditionally measured in the plate impact test [3, 4].

However, the experiment revealed the increase of failure front velocity up to the value \( V{}_{fw} \approx 4\,{\text{km/s}} \). Approaching of failure wave front velocity to the shock front velocity supports theoretically based result concerning the failure wave nature as “delayed failure” with the limit of “delay time” corresponding to the “peak time” \( t_{c} \) in the self-similar solution, Eq. 3. Theoretical analysis of this situation allowed the interpretation of damage kinetics as the “resonance excitation” of blow-up damage localization modes.

4 Summary

It is shown that the process of damage-failure transition can be considered as specific type of criticality in out-of-equilibrium system “solid with defects” and wide range constitutive model was proposed as the generalization of the Ginzburg-Landau approach in terms of independent field variables describing typical mesoscopic defects (microshears, microcracks). Specific types of the collective modes of defects were established as self-similar solution of the evolution equation for mentioned damage parameter. The set of blow-up self-similar collective modes of defects can be considered as the independent variables provided universality of nonlinear dynamics of damage-failure transition: transition from steady-state crack propagation to the branching regime with pronounced intermittency in crack propagation velocity, “resonance” excitation of damage localization in shocked materials (“dynamic branch” under spall failure, failure waves), spatial-temporal power law universality in dynamic fragmentation. Original experimental data supported the assumption concerning the role of multiscale blow-up collective modes of defects on self-similar responses of materials in wide range of load intensity.