Batyrev Mirror Symmetry

Abstract

We describe Batyrev’s construction of the mirror to a family of Calabi–Yau hypersurfaces in a Fano toric variety, based on polar duality for lattice polytopes. We revisit the example of the quintic threefold in this language, and briefly mention connections with later developments, such as the Batyrev–Borisov construction for complete intersections in Fano toric varieties, and the Gross–Siebert program.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

This short note is a survey about an explicit construction for mirror families of Calabi–Yau varieties, due to Batyrev and later generalized by Batyrev–Borisov, that uses toric geometry and polar duality for lattice polytopes. The construction is about Calabi–Yau hypersurfaces in a Fano toric variety.

Historically, after the first example of the quintic threefold [1], many other examples of Calabi–Yau threefolds and mirror pairs were constructed using hypersurfaces in weighted projective spaces. For some of these examples though, the mirror was missing. Batyrev’s construction [2] put these examples in a more systematic framework and provided the missing mirrors. Moreover it was later generalized to complete intersections in Fano toric varieties by Batyrev–Borisov [3], and brought combinatorics and toric geometry into the picture. It also partly inspired the Gross–Siebert program [4,5,6].

The material for this contribution is mostly taken from Cox’s expository paper “Mirror Symmetry and Polar Duality of Polytopes” [7], and parts of Cox–Katz, “Mirror Symmetry and Algebraic Geometry” [8] (in particular Sects. 4.1 and 4.2).

2 Polar Duality of Lattice Polytopes

Batyrev’s construction relates mirror pairs with a duality for lattice polytopes.

Definition 1

A polytope $\varDelta$ is the convex envelope $\mathrm {Conv}(x_1,\ldots x_m)$ of a finite number of points in $\mathbb {R}^n$.

A supporting hyperplane of a polytope $\varDelta$ is a hyperplane H in $\mathbb {R}^n$ such that $\varDelta \cap H\ne \emptyset$, and $\varDelta$ is completely contained in one of the two closed half-spaces that H determines in $\mathbb {R}^n$. A face of a polytope $\varDelta$ is the intersection $\varDelta \cap H$, where H is a supporting hyperplane. This is again a polytope. The dimension of a polytope is the dimension of the affine subspace of $\mathbb {R}^n$ spanned by $\varDelta$. Every polytope $\varDelta$ determines a unique minimal set of points $\{v_1,\ldots , v_k\}$, called its vertices, such that $\varDelta =\mathrm {Conv}(v_1,\ldots , v_k)$. These points also coincide with the faces of $\varDelta$ of dimension 0.

Recall also that a lattice M is a free abelian group of finite rank, i.e. an abelian group isomorphic to $\mathbb {Z}^n$ for some n. Sometimes it is better not to choose a basis (i.e. the subset corresponding to the standard basis of $\mathbb {Z}^n$ via some isomorphism $M\cong \mathbb {Z}^n$), but we will always assume to have chosen one.

Definition 2

A lattice polytope is a polytope in some affine space $\mathbb {R}^n$ whose vertices have coordinates in $\mathbb {Z}^n$.

From now on we will assume that our lattice polytopes are full dimensional (i.e. they are not contained in any proper affine hyperplane of the ambient space) and that $0\in \mathrm {Int}(\varDelta )$. Here $\mathrm {Int}(\varDelta )$ denotes the topological interior of $\varDelta$, which also coincides with the complement of all proper faces.

The dual or polar $\varDelta ^\circ$ of $\varDelta$ is another polytope, defined by

$$\begin{aligned} \varDelta ^\circ&= \{a \in \mathbb {R}^n \mid \langle a,b\rangle \ge -1 \text { for all } b\in \varDelta \} \\&= \{a\in \mathbb {R}^n \mid \langle a,v\rangle \ge -1 \text { for all vertices } v \text { of } \varDelta \} \;\;\; \text { (by convexity)} \end{aligned}$$

where we denote by $\langle \cdot , \cdot \rangle$ the standard scalar product of $\mathbb {R}^n$. Note that if one does not want to choose a basis of the lattice M, then the same formulas define the dual of a polytope $\varDelta \subseteq M_\mathbb {R}:=M\otimes \mathbb {R}$ as a polytope in the dual vector space $\varDelta ^\circ \subseteq M^\vee _\mathbb {R}=M^\vee \otimes \mathbb {R}$, and in this case $\langle \cdot , \cdot \rangle :M_\mathbb {R}\times M^\vee _\mathbb {R}\rightarrow \mathbb {R}$ denotes the natural pairing $(v,f)\mapsto f(v)$.

It is not hard to check that the set $\varDelta ^\circ$ is indeed a polytope (by the second description it follows that it is a finite intersection of half-spaces, so it is enough to show that it is bounded).

Example 1

If $\varDelta$ is the square $[-1,1]\times [-1,1]$ then $\varDelta ^\circ$ is the polygon with vertices $(\pm 1,0), (0, \pm 1)$, as in the following picture.

One can also check that $(\varDelta ^\circ )^\circ =\varDelta$, so that this operation is indeed a “duality.” Moreover, there is an inclusion-reversing combinatorial correspondence between i-dimensional faces of $\varDelta$ and $(n-1-i)$-dimensional faces of $\varDelta ^\circ$.

The polytope $\varDelta ^\circ$ is not always a lattice polytope. For example, it is easily verified that $(2\varDelta )^\circ =\frac{1}{2}\varDelta ^\circ$, and the latter might not be a lattice polytope. This applies to the previous example, as $\frac{1}{2}\varDelta ^\circ =\mathrm {Conv}((\pm \frac{1}{2},0), (0, \pm \frac{1}{2}))$ is not a lattice polytope in that case.

Definition 3

A lattice polytope $\varDelta$ is reflexive if ($0\in \mathrm {Int}(\varDelta )$ and) $\varDelta ^\circ$ is a lattice polytope.

There are a few equivalent characterizations of this property. We will mention a couple of these; for details, see for example [9, Chap. 2].

One can prove that every facet (i.e. codimension 1 face) F of a polytope $\varDelta$ has a unique inward-pointing normal vector $u_F$ such that

$$F=\{a\in \varDelta \mid \langle a, u_F \rangle =-1\}.$$

In Example 1, if F is the segment $[-1,1]\times \{1\}$, then $u_F=(0,-1)$, and for the other facets we get the other vertices of the dual $\varDelta ^\circ$.

In fact we always have $\varDelta ^\circ =\mathrm {Conv}(u_F\mid F \text { a facet of } \varDelta )$, so that

Proposition 1

A lattice polytope $\varDelta$ is reflexive if and only if every $u_F\in \mathbb {R}^n$ is a lattice point (i.e. is in $\mathbb {Z}^n\subseteq \mathbb {R}^n$).

Another characterization is the following (which is given as the definition of a reflexive polytope in [2]):

Proposition 2

A lattice polytope $\varDelta$ is reflexive if and only if for every facet F of $\varDelta$ there is no lattice point between the affine hyperplane spanned by F and its translate passing through the origin.

As a consequence, the origin is the only lattice point in the interior of a reflexive polytope $\varDelta$.

Remark 1

From the last observation, via the results of [10], it follows that in every dimension n there is only a finite number of reflexive lattice polytopes up to integral change of coordinates (i.e. transformation by an element of $\mathrm {GL}(n,\mathbb {Z})$). For $n=2$ there are 16 equivalence classes, for $n=3$ they are $4\,319$ and for $n=4$ (which is the important case for Mirror Symmetry, since it corresponds to 3-folds) there are $473\,800\,776$ (!) equivalence classes (this was proven in [11]).

The idea for Batyrev Mirror Symmetry is that this duality among lattice polytopes realizes Mirror Symmetry for Calabi–Yau hypersurfaces in Fano toric varieties, as we will explain in the next sections.

3 Varieties from Lattice Polytopes

A lattice polytope in $\mathbb {R}^n$ gives rise to a projective variety. This process is part of a long story, the theory of toric varieties (see [9, 12]).

Definition 4

A toric variety is a normal algebraic variety X with an open embedding $T\subseteq X$ of a torus $T=(\mathbb {C}^\times )^n$ and an action $T\times X\rightarrow X$ that extends the multiplication action of T on itself.

It turns out that this set of data is completely encoded by a combinatorial polyhedral object in a lattice (the co-character lattice of the torus $\mathrm {Hom}(\mathbb {C}^\times , T)$, usually denoted by N in the literature), called a fan: this is a collection of cones, intersecting nicely (i.e. along common faces). The geometry of the toric variety is completely controlled by the combinatorics of this object: geometric properties of the variety can be translated in combinatorial or convex-geometric properties of the fan, and some algebraic invariants (for example sheaf cohomology of divisors) are explicitly computable. Because of this, toric varieties are usually a useful testing ground for new conjectures and theories about varieties in general.

A lattice polytope is an alternative incarnation of the underlying combinatorics of a certain class of toric varieties. Strictly speaking, the polytope also records the information of a torus invariant ample divisor on X, that gives in particular embeddings in projective space.

Here is a quick way to define the toric variety $X_\varDelta$ associated to a lattice polytope $\varDelta$. First note that any lattice point $m=(a_1,\ldots , a_n) \in \mathbb {Z}^n$ gives a “Laurent monomial”

$$t^m=t_1^{a_1}\cdots t_n^{a_n}$$

which is a regular function on the torus $(\mathbb {C}^\times )^{n}$ (so that negative exponents make perfect sense).

Now we need to assume that $\varDelta$ has “enough lattice points”, or else modify it a bit. This is a technical condition, called normality of the polytope: a lattice polytope $\varDelta \subseteq \mathbb {R}^n$ is normal if for all $n,m \in \mathbb {N}$ we have

$$(n\varDelta )\cap \mathbb {Z}^n + (m\varDelta )\cap \mathbb {Z}^n=((n+m)\varDelta )\cap \mathbb {Z}^n.$$

Here $n\varDelta$ denotes the dilated polytope $\{a\in \mathbb {R}^n\mid a= n b \text { for some } b\in \varDelta \}$, and $+$ denotes the Minkowski sum of polytopes, defined as

$$ \varDelta +\varDelta '=\{a+b\in \mathbb {R}^n \mid a\in \varDelta , b\in \varDelta '\} $$

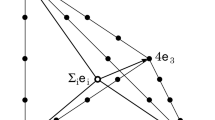
for polytopes $\varDelta , \varDelta '\subseteq \mathbb {R}^n$. For example, one can show that the standard simplex $\mathrm {Conv}(0,e_1,\ldots , e_n)\subseteq \mathbb {R}^n$ is a normal polytope, while the polytope $\mathrm {Conv}(0,e_1,e_2,e_1+e_2+3e_3)\subseteq \mathbb {R}^3$ is not normal. Here and in what follows, as customary, $e_i$ denote the elements of the standard basis of $\mathbb {R}^n$.

If $\varDelta$ is not normal, one uses instead the polytope $k\varDelta$ (which will be normal for $k\ge n-1$, see [9, Theorem 2.2.12]) in the construction that follows. This is related to ampleness versus very ampleness of the toric divisor encoded by the given polytope $\varDelta$. There is also a property of polytopes called very ampleness, implied by normality, and relevant for this construction. See [9, Sect. 2.2] for details.

Assuming that $\varDelta$ is normal, consider $\varDelta \cap \mathbb {Z}^n=\{m_0,\ldots , m_k\}$, which is a finite set, and the map

$$(\mathbb {C}^\times )^{n}\rightarrow \mathbb {P}^k \;\;\;\;\;\;\;\text {given by} \;\;\;\;\;\;\;\; (t_1,\ldots , t_n)\mapsto [t^{m_0}:\cdots : t^{m_k}]$$

where $t^{m_i}$ is the Laurent monomial described above. This map turns out to be injective, and one defines the toric variety $X_\varDelta$ as the closure of its image.

Reflexive lattice polytopes give rise, in this manner, to projective Fano toric varieties. Recall that “Fano” means that the anticanonical divisor $-K_{X_\varDelta }$ is ample, for a smooth variety. We will allow some singularities and say that a variety X is Fano if it is Gorenstein and the dual of the dualizing sheaf $\omega _X^\vee$ (which is a line bundle) is ample.

Proposition 3

[8, Proposition 3.5.5] The toric variety $X_\varDelta$ is Fano if and only if $\varDelta$ is a reflexive polytope.

Lattice points on $\varDelta$ also give interesting hypersurfaces in $X_\varDelta$: keeping the notation as before, the equation

$$\begin{aligned} a_0t^{m_0}+\cdots + a_kt^{m_k}=0 \end{aligned}$$

(1)

defines a hypersurface in $(\mathbb {C}^\times )^n$ (for any given coefficients $a_0,\ldots , a_k\in \mathbb {C}$), and the closure of this in $X_\varDelta$ is then a hypersurface $V\subseteq X_\varDelta$. Moreover, if $\varDelta$ is reflexive every such hypersurface is a divisor in the same divisor class, the anticanonical class $|-K_{X_\varDelta }|$.

Example 2

The quintic threefold in $\mathbb {P}^4$ can be recovered using this construction. Let $\varDelta _n$ denote the standard simplex $\mathrm {Conv}(0,e_1,\ldots , e_n)$ in $\mathbb {R}^n$.

Let us take $\varDelta \subseteq \mathbb {Z}^4$ to be

$$5\varDelta _4-(1,1,1,1)=\{a\in \mathbb {R}^4\mid a=5b-(1,1,1,1)\text { for some } b\in \varDelta _4\}.$$

In other words, $\varDelta$ is the convex envelope of the vectors

$$(-1,-1,-1,-1),(4,-1,-1,-1), (-1,4,-1,-1), (-1,-1,4,-1), (-1,-1,-1,4)$$

obtained from the vertices $0,5e_1, 5e_2, 5e_3, 5e_4$ of $5\varDelta _4$ by subtracting the vector (1, 1, 1, 1).

This is a reflexive polytope in $\mathbb {R}^4$, and by applying the construction described above, one can check that $X_\varDelta =\mathbb {P}^4$, and that (after homogenizing the corresponding Eq. (1)) the hypersurface V is an arbitrary quintic threefold in $\mathbb {P}^4$ (the exponent vectors that show up in the lattice points of $\varDelta$ give all homogeneous monomials of degree 5 after homogenizing).

4 Batyrev’s Construction

We can now talk about Batyrev’s construction. Given a reflexive n-dimensional polytope $\varDelta$, one can consider the projective toric variety $X_\varDelta$ (of dimension n), which will be a Fano toric variety, and a general divisor in the anticanonical linear system $V\in |-K_{X_\varDelta }|$. For example one can take V to be determined by a Laurent polynomial as in Eq. (1). For the moment let us pretend that everything is smooth (typically this is false).

A (nice) anticanonical hypersurface in a Fano variety is going to have trivial canonical bundle (by the adjunction formula $K_D=(K_X+D)|_D$), so, taking for granted that also the other conditions about vanishing of cohomologies will be satisfied, it is going to be a Calabi–Yau variety, of complex dimension $n-1$. The basic idea is that by considering the dual $\varDelta ^\circ$ and a general divisor in the anticanonical linear system of $X_{\varDelta ^\circ }$, we get a different Calabi–Yau variety $V^\circ$ which should be mirror to V (or rather, the family of hypersurfaces V should be mirror to the family of hypersurfaces $V^\circ$ - we will make this abuse of terminology from now on).

In reality things are more technical, because often $X_\varDelta$ is too singular, and needs to be resolved via blowups in order for the divisor V to be a “nice” Calabi–Yau variety (i.e. with nice singularities). One also wants the resolution to be crepant, i.e. to preserve the canonical bundle, and for $n\ge 3$ the projective toric variety given by an n-dimensional lattice polytope does not need to admit a full crepant resolution (i.e. producing a smooth variety as its outcome), so the best one can do is partially resolve it.

Blowing up along a torus-invariant subvariety is quite convenient using toric language, because it corresponds to combinatorial operations on the fan and polytope associated to the toric variety. We will not go into details here, we will only mention that Batyrev introduces the notion of a “maximal projective crepant partial (MPCP) desingularization” for $X_\varDelta$, corresponding to certain triangulations of the polytope $\varDelta$. This is a birational map $X'\rightarrow X_\varDelta$ which partially resolves the singularities of $X_\varDelta$ and preserves the canonical divisor. By taking a general anticanonical divisor on $X'$ we get a nice Calabi–Yau variety V (see [8, Proposition 4.1.3]). These MPCP desingularizations always exist in this context, and usually there is more than one choice.

By choosing a MPCP for $X_\varDelta$ and one for $X_{\varDelta ^\circ }$, we get Calabi–Yau varieties V and $V^\circ$ as general anticanonical sections of the partial resolutions, and these should form mirror pairs. In the case of threefolds (so when $\varDelta$ lives in $\mathbb {R}^4$), V and $V^\circ$ actually turn out to be smooth. Some of the expected consequences of Mirror Symmetry have indeed been proven for Batyrev mirrors V and $V^\circ$.

Recall that, for a smooth projective complex variety X, the Hodge number $h^{p,q}(X)$ is the dimension $\dim \, H^q(X,\varOmega _X^p)$ as a complex vector space, where $\varOmega _X^p=\varOmega _X\wedge \cdots \wedge \varOmega _X$ is the wedge product of p copies of the sheaf of Kähler differentials $\varOmega _X$ of X. The Hodge numbers are usually arranged in a diagram called the Hodge diamond, depicted below for $\dim \, X=3$.

These numbers have two important symmetries: Hodge theory implies that $h^{p,q}=h^{q,p}$, and Serre duality implies that $h^{n-p,n-q}=h^{p,q}$. If in addition X is a Calabi–Yau threefold, we also have $h^{0,0}=h^{3,0}=1$ and $h^{1,0}=h^{2,0}=0$, so that the above diagram can be simplified to the following one

whose only relevant numbers are $h^{1,1}$ and $h^{2,1}$. Recall also that these Hodge numbers $h^{1,1}=\dim \, H^1(X,\varOmega _X)$ and $h^{2,1}=\dim \, H^1(X,\varOmega _X^2)=\dim \, H^1(X,T_X)$ (where $T_X\cong \varOmega _X^\vee$ is the tangent bundle of X, and we used the fact that $\varOmega _X^3\cong \mathcal {O}_X$) give the number of parameters of deformations of a complexified Kähler class on X, and of the complex structure of X respectively. Mirror symmetry predicts that $h^{1,1}(X)=h^{2,1}(X^\vee )$ and $h^{2,1}(X)=h^{1,1}(X^\vee )$, where $X^\vee$ denotes the mirror of X; in other words, the Hodge diamonds of X and $X^\vee$ should be related by a reflection with respect to a diagonal line through the center.

More generally, if X is a Calabi–Yau manifold of dimension bigger than 3, Mirror symmetry predicts (among other facts) that $h^{p,q}(X)=h^{n-p,q}(X^\vee )$ and $h^{n-p,q}(X)=h^{p,q}(X^\vee )$. For Batyrev’s construction, indeed this is known to be the case for $p=q=1$ (see below for some discussion about the general statement).

Theorem 1

([8, Theorem 4.1.5], [2, Theorem 4.4.3]) The “Hodge numbers Mirror Symmetry” for $p=q=1$ holds for Batyrev mirrors, i.e. we have the equality of Hodge numbers $h^{1,1}(V)=h^{\dim \, V-1,1}(V^\circ )$ and $h^{\dim \, V-1,1}(V)=h^{1,1}(V^\circ )$.

If we perform the construction starting from a reflexive lattice polytope $\varDelta \subseteq \mathbb {R}^4$, so that $\dim \, V=\dim \, V^\circ =3$, then this is all that is needed to get the full symmetry relation between the Hodge diamonds of V and $V^\circ$. The proof of the theorem is a computation of the Hodge numbers by using the dictionary of toric geometry to reduce to combinatorics.

There are also other (partial) results about correspondence of complex/Kähler moduli spaces and correlation functions of the A-model and B-model, that we will not get into. See [8, Section 4.1.2] for a thorough discussion.

On the other hand, there are still also some open questions: it is not known

• 1. whether using this construction with a 4-dimensional reflexive polytope, V and $V^\circ$ give isomorphic SCFTs (this is known for some cases, like the quintic threefold);

• 2. whether for a reflexive n-dimensional polytope with $n\ge 5$, the relations $h^{p,q}(V)=h^{\dim \, V-p,q}(V^\circ )$ and $h^{\dim \, V-p, q}(V)=h^{p,q}(V^\circ )$ hold or not.

Question (2) has been partially answered in later work of Batyrev and Borisov [13]. Namely, they prove that for the string-theoretic Hodge numbers $h^{p,q}_{st}$ (defined in [14]), one has the equalities $h^{p,q}_{st}(V)=h^{\dim \, V-p,q}_{st}(V^\circ )$ and $h^{\dim \, V-p,q}_{st}(V)=h^{p,q}_{st}(V^\circ )$ where V and $V^\circ$ are Batyrev mirrors. Their result [13, Theorem 4.15] actually also covers the more general case of complete intersections in Fano toric varieties of [3]. Moreover, if V is smooth or $q=1$, then $h^{p,q}_{st}(V)=h^{p,q}(V)$, so with these assumptions the answer to question (2) is known to be positive.

5 The Quintic Threefold

The original example of Mirror Symmetry for the quintic threefold falls into this general framework. We already saw how to obtain the quintic as a Calabi–Yau hypersurface in the Fano toric variety $\mathbb {P}^4$, using a polytope $\varDelta$ in Example 2.

The dual of that polytope $\varDelta$ is

$$\varDelta ^\circ =\mathrm {Conv}(e_1,e_2,e_3,e_4, (-1,-1,-1,-1)).$$

In fact, $\varDelta$ has 5 facets $F_1,F_2,F_3, F_4, F_5$, with supporting hyperplanes with equations $x_i = -1$ for $0\le i\le 4$ and $x_1+x_2+x_3+x_4 = 1$. The corresponding inner normal vectors (i.e. the vector $u_F$ such that the facet F is described as the intersection of $\varDelta$ with the hyperplane $\langle a, u_F\rangle =-1$) are then given by $e_1, e_2, e_3, e_4$ and $(-1,-1,-1,-1)$ respectively. The claim now follows by the description of $\varDelta ^\circ$ as $\varDelta ^\circ =\mathrm {Conv}(u_F\mid F \text { a facet of } \varDelta ).$ Note that both $\varDelta$ and $\varDelta ^\circ$ are combinatorially standard simplices (in the sense that there is a bijection between their faces and the faces of a standard simplex, compatible with inclusion and intersections), but the way they are positioned in the lattice is important. For example $\varDelta$ has 125 lattice points, whereas $\varDelta ^\circ$ has only 6.

Using $\varDelta ^\circ$ as lattice polytope, one can check that $X_{\varDelta ^\circ }$ can be identified with the quotient $\mathbb {P}^4/G$, where G is the group

$$ G=\{(a_1,a_2,a_3,a_4,a_5)\in (\mathbb {Z}/5)^5\mid a_1+a_2+a_3+a_4+a_5=0 \}/(\mathbb {Z}/5). $$

Here the quotient is by the diagonal subgroup, and G acts on $\mathbb {P}^4$ by multiplication by roots of unity in the obvious way.

Indeed, the primitive lattice generators of the rays of the normal fan of $\varDelta ^\circ$ (which is the fan corresponding to the toric variety $X_{\varDelta ^\circ }$) are precisely the vertices

$$\begin{aligned} (-1,-1,-1,-1),(4,-1,-1,-1), (-1,4,-1,-1), (-1,-1,4,-1), (-1,-1,-1,4) \end{aligned}$$

of $\varDelta$. if we denote by $M\subseteq \mathbb {Z}^4$ the sublattice generated by these vectors, then by [9, Proposition 3.3.7] there is an isomorphism $X_{\varDelta ^\circ }\cong X_{\varDelta ^\circ , \, M}/(\mathbb {Z}^4/M)$, where $X_{\varDelta ^\circ ,\, M}$ denotes the toric variety corresponding to the polytope $\varDelta ^\circ$ with respect to the lattice M, and the quotient is for the natural action of the finite group $(\mathbb {Z}^4/M)$ on $X_{\varDelta ^\circ , \,M}$. The quotient $(\mathbb {Z}^4/M)$ is isomorphic to the group G described above, and $X_{\varDelta ^\circ , \,M}$ is isomorphic to $\mathbb {P}^4$, as can be verified by checking that the normal fan of $\varDelta ^\circ$ in M is isomorphic to the fan for $\mathbb {P}^4$. See [9, Example 5.4.10] for more details.

As mentioned above the polytope $\varDelta ^\circ$ has 6 lattice points (the five vertices and the origin), so Eq. (1) in this case becomes

$$ c_0+c_1t_1+c_2t_2+c_3t_3+c_4t_4+c_5t_1^{-1}t_2^{-1}t_3^{-1}t_4^{-1}=0 $$

which by using the coordinates of $\mathbb {P}^4$ and homogenizing (in a “toric” sense - see [9, Sect. 5.4]) becomes

$$ c_0x_0^5+c_1x_1^5+c_2x_2^5+c_3x_3^5+c_4x_4^5+c_5x_0x_1x_2x_3x_4=0. $$

By rescaling the coordinates one can assume $c_0=c_1=c_2=c_3=c_4=1$. This recovers the equation

$$ x_0^5+x_1^5+x_2^5+x_3^5+x_4^5+\psi x_0x_1x_2x_3x_4=0 $$

that gives the mirror pencil of hypersurfaces (after resolving the singularities).

6 Further Developments

Batyrev–Borisov [3, 15] generalize the above to Calabi–Yau complete intersections in Fano toric varieties. The combinatorics becomes more complicated, but the basic idea is similar.

This time, the starting data is an $(r+d)$-dimensional reflexive polytope $\varDelta$, together with a decomposition as a Minkowski sum

$$ \varDelta =\varDelta _1+\cdots +\varDelta _r $$

where $\varDelta _i$ are lattice polytopes containing the origin (possibly on their boundary). This is called a nef-partition. The lattice points of each $\varDelta _i$ determine a family of hypersurfaces of the Fano toric variety $X_\varDelta$, and choosing for each i a generic hypersurface $V_i$ among these, the intersection $V_1\cap \cdots \cap V_r$ is a a d-dimensional complete intersection Calabi–Yau variety, that needs to be partially resolved, as in the case of hypersurfaces.

To produce the mirror family the idea is to use polar duality again, but with a variation with respect to the hypersurface case, because the origin might not be an interior lattice point of $\varDelta _i$. Instead, one defines polytopes $\nabla _i$ by the formula

$$ \nabla _i=\{a\in \mathbb {R}^d\mid \langle a, b\rangle \ge -1 \text { for all } b\in \varDelta _i \text { and } \langle a, b\rangle \ge 0 \text { for all } b\in \varDelta _j, j\ne i\}. $$

One can prove that $\nabla _i$ are lattice polytopes containing the origin, and the Minkowski sum $\nabla =\nabla _1+\cdots \nabla _r$ is a reflexive polytope of dimension $r+d$. This gives the dual nef-partition, and by applying the same procedure outlined above, one obtains the mirror of the subvariety corresponding to the original nef-partition. See [7, Sect. 6] or the original papers for more details.

The Gross–Siebert program [4,5,6] mixes SYZ Mirror Symmetry with the Batyrev–Borisov construction. The idea of that is the following: given a Calabi–Yau manifold X, in order to find a mirror $X^\vee$, degenerate it (in a nice way) to a union of toric varieties glued along toric strata (i.e. orbits for the action of the torus on the respective toric variety). Note that this “degenerate” variety will not be smooth.

From the degeneration one can extract combinatorial gadget (which actually has more structure...), called the dual intersection complex, that one can dualize via a discrete Legendre transform, in a way that is similar to the polar polyhedron construction. From the dual of the dual intersection complex we can construct a central fiber, again union of toric varieties glued along toric strata, and (with a lot of work!) construct a smoothing. The idea is that the smoothing should be mirror to the X that we started with.

In [16] Gross compares this construction to the one of Batyrev–Borisov. He shows that indeed nef-partitions give rise to toric degenerations, and that the algorithm that we crudely outlined above produces the same result as the Batyrev–Borisov construction.