A Privacy-Preserving Framework for Subgraph Pattern Matching in Cloud

Abstract

The growing popularity of storing large data graphs in cloud has inspired the emergence of subgraph pattern matching on a remote cloud, which is usually defined in terms of subgraph isomorphism. However, it is an NP-complete problem and too strict to find useful matches in certain applications. In addition, there exists another important concern, i.e., how to protect the privacy of data graphs in subgraph pattern matching without undermining matching results. To tackle these problems, we propose a novel framework to achieve the privacy-preserving subgraph pattern matching via strong simulation in cloud. Firstly, we develop a k-automorphism model based method to protect structural privacy in data graphs. Additionally, we use a cost-model based label generalization method to protect label privacy in both data graphs and pattern graphs. Owing to the symmetry in a k-automorphic graph, the subgraph pattern matching can be answered using the outsourced graph, which is only a subset of a k-automorphic graph. The efficiency of subgraph pattern matching can be greatly improved by this way. Extensive experiments on real-world datasets demonstrate the high efficiency and effectiveness of our framework.

1 Introduction

A graph can be a powerful model tool to represent objects and their relationships. The increasing number of applications that take use of graph data in recent years, such as disease transmission [1, 2], communication patterns [3], and social networks [4,5,6,7], has promoted the development of graph data management, especially subgraph pattern matching. Typically, subgraph pattern matching is defined in terms of subgraph isomorphism [8, 9], which is an NP-complete problem [10]. It is often too strict to catch sensitive matches, as it requires matches to have same topology with data graphs. The problem will hinder its applicability in some certain applications like social networks and crime detection. Our work focus on subgraph pattern matching via strong simulation [11]. Strong simulation is a revision of graph simulation, which imposes more flexible constraints on topology in data graphs, and it retains cubic-time complexity.

Example 1

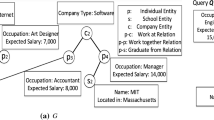
Consider a real-life social network shown in Fig. 1. Each vertex in graph G represents an entity, such as a human resources $(HR_i)$ person, a development manager $(DM_i)$, and a project manager $(PM_i)$. Each directed edge in G indicates one recommendation relationship, e.g., edge $HR_1\rightarrow PM_1$ represents $HR_1$ recommends $PM_1$. Each entity has some attributes like “name”, “gender”, “state”, and “school”.

A headhunter wants to employ a DM to help a PM. A qualified candidate must live in Illinois and at the same time, he must recommend the PM and be recommended by the HR and PM. The headhunter issues a subgraph pattern matching of Q over G, as shown in Fig. 1. When subgraph isomorphism is taken, there is no match can be found, since there is no subgraph that has the same topology with the pattern Q in graph G. However, when it comes to strong simulation, we can find the subgraph $G_1$ is an appropriate match to pattern Q, since there exists a path $(DM_1, PM_2, PM_1)$ from $DM_1$ to $PM_1$. Obviously, compared with the subgraph isomorphism that imposes a very strict constraint on the topology of the matched graphs, strong simulation provides a more flexible constraint.

Fig. 1.

An original data graph G and pattern graph Q.

Meanwhile, the popularity of storing the large number of data graphs in cloud to save storage brings another inevitable challenge, i.e., how to process users’ queries without compromising sensitive information in cloud [12]. In many real scenarios, we can not make sure that the cloud platform is completely credible, as many adversaries may attack the cloud and cause serious privacy leakage. The main privacy leakage problem is the “identity disclosure” problem [13, 14]. A naive anonymous approach is to remove all identifiable personal information before uploading the data graph to cloud. However, even though the data graph is uploaded without any sensitive information, it is still possible for an adversary to locate the target through structural attacks [13, 15, 16]. To protect privacy of data graphs from multiple structural attacks, many methods have been proposed [17,18,19]. One typical approach is k-automorphism, which uses the symmetry of the published data graph [19]. For each vertex v in a k-automorphic graph, there are at least $k-1$ structurally equivalent counterparts. An adversary can not distinguish v from the other $k-1$ symmetric vertices, because there is no structural difference between them.

Consider the Example 1 in Fig. 1, uploading the original graph G to cloud directly will cause privacy leakage. To address the problem, we propose the following solution. On one hand, we propose a k-automorphism model based method to protect structural privacy of data graphs. Firstly, we transform the original graph G to an “undirected” graph $G^*$. During the process, if an edge $u\rightarrow v$ is unidirectional, we will add an edge $v\rightarrow u$. For example, we add an edge $PM_2\rightarrow DM_1$ for the edge $DM_1\rightarrow PM_2$ in Fig. 1. Then, we can use the k-automorphism model to generate graph $G^k$, where k = 2 in Fig. 2. On the other hand, to protect the label privacy in both data graphs and pattern graphs, we apply a cost-model based label generalization technique [12], where each vertex label in $G^k$ and Q is replaced by a label group. The mapping between label groups and vertex labels are given in the Label Correspondence Table (LCT), presented in Fig. 2(a).

Fig. 2.

The k-automorphic graph $G^k$ and anonymous pattern $Q^0$.

However, the solution suffers from the following limitation. During the generation of $G^*$ and $G^k$, it may generate a large number of noise edges, which will result in more expensive storage cost and much larger communication overhead. Thus, we upload the outsourced graph $G^0$ (The definition of $G^0$ is given in Subsect. 4.3), which is only a subset of $G^k$, to cloud. Next, the cloud executes subgraph pattern matching via strong simulation of $Q^0$ over $G^0$ to obtain $r(Q^0,G^0)$, i.e., subgraph matches of $Q^0$ over $G^0$, and transmits it to the client side. On the basis of k-automorphic functions $F_{k_i}\ (i=1,2,\dots ,k-1)$, client can firstly compute $r(Q^0,G^k)$ according to $r(Q^0,G^0)$. Then, it filters out false positives based on the original data graph G and pattern Q to derive r(Q, G). Note that we assume the client is the data owner who has access to the original graph G for the filtering step.

Contributions. The main contributions of our work are summarized as follows:

• To the best of our knowledge, we are the first to support privacy-preserving subgraph pattern matching via strong simulation in cloud.

• We re-design a cost-model based label generalization method to select effective vertex label combinations for anonymizing labels in both data graphs and pattern graphs.

• We conduct extensive experiments on several real-world datasets to study the efficiency and effectiveness of our framework.

The rest of the paper is organized as follows. Section 2 narrates the related work. Section 3 gives the problem formulation. Section 4 describes the main solution. Section 5 reports the experimental analysis. Section 6 concludes the paper.

2 Related Work

Strong Simulation. Subgraph pattern matching is typically defined in terms of subgraph isomorphism [8, 9], an NP-complete problem [20]. It is often too restrictive to catch sensible matches. Subgraph simulation and its various extensions have been considered to lower the complexity [10, 21, 22]. Fan et al. [21] proposed bounded simulation which extended simulation by allowing bounds on the number of hops in pattern graphs and further, they extended it by incorporating regular expressions as edge constraints on pattern graphs [22]. Both the two extensions of simulation are in cubic-time. Nevertheless, the lower complexity comes with the price that they do not preserve the topology of data graphs and yield false matches. Thus, Ma et al. [11] proposed the notation of strong simulation by enforcing two additional conditions: the duality to preserve the parent relationships and the locality to eliminate excessive matches. Strong simulation is capable of capturing the topological structures of pattern and data graphs, and it retains the same cubic-time complexity of former extensions of graph simulation [10].

k -Automorphism. The question of how to publish information on graphs in a privacy-preserving way has been of interest for a number of years [13, 23,24,25]. Most previous work focus on protecting data privacy from structural attacks [13, 23, 24]. Some of them assume that the adversary launches one type of structural attack only [13, 23, 24]. Liu and Terzi [13] studied how to protect privacy in published data from degree attack only. However, an attacker can launch multiple types of structural attacks to identify the target in practice. Thus, Zou et al. [19] proposed the k-automorphism framework. Each vertex in a k-automorphic graph has at least $k-1$ counterparts so that it is hard for an adversary to identify the vertex from others. The framework can protect privacy of data graph from multiple structural attacks and furthermore, the k-automorphism model does not need to delete any vertices or edges from data graph, which can significantly preserve the integrity of the data.

3 Problem Formulation

In this section, we first present the basic notations and definitions frequently used in this paper. Then we give a definition of our problem.

We model a social network as an attributed graph [12], $G=\{V(G), E(G), L_G(V(G))\}$, where V(G) is the set of vertices, E(G) is the set of edges, and $L_G(V(G))$ is the set of vertex labels. The notational convention of this paper are summarized in Table 1.

Table 1. Table of notations

Definition 1

$\mathbf{Path }$. A directed path p is a sequence of nodes $(v_1, v_2, \dots , v_n)$, where $i \in [1,n-1]$ and $(v_i, v_{i+1})$ is an edge in graph G. The number of edges in a path p is the length of p, denoted by len(p).

Definition 2

$\mathbf{Distance~and~diameter }$. Consider two nodes u, v in graph G, the distance from u to v is the length of the shortest undirected path from u to v, denoted by dis(u, v). The diameter of the connected graph G is defined as the longest distance of all pairs of nodes in G, denoted by $d_G$. More specifically, $d_G = max\{dis(u,v)\}$ for all nodes u, v in graph G.

Definition 3

$\mathbf{Ball }$ [11]. For a node v in graph G, a ball is a subgraph of G, where v is the center node and r is the radius, denoted by $\overset{\frown }{G}[v, r]$. For all nodes u in $\overset{\frown }{G}[v, r]$, the shortest distance between u and v should satisfy $dis(u, v)\le r$ and edges must exactly appear in graph G over the same node set.

Consider the pattern graph Q and data graph G in Fig. 1, we can figure out that $d_Q=1$ according to the Definition 2. If we take the vertex $DM_1$ as the center node and $d_Q$ as the radius, then we can obtain the ball $\overset{\frown }{G}[DM_1, d_Q]$ (i.e., $G_1$), which is a subgraph of G based on Definition 3.

Definition 4

$\mathbf{Subgraph~ Pattern~ Match }$. Given a data graph $G=\{V(G), E(G), L_G(V(G))\}$ and a pattern graph $Q=\{V(Q), E(Q), L_Q(V(Q))\}$, Q is a subgraph match to G via strong simulation, if there exists a node u in Q and a connected subgraph $G_s$ of G such that:

• (1) There exists a match relation R, and for each pair (u, v) in R:

  • (a) $L_Q(u)\subseteq L_{G_s}(v)$;

  • (b) $\forall (u', u) \in E(Q)$, there exists a path $(v',\dots , v)$ in $E(G_s)$;

  • (c) $\forall (u, u') \in E(Q)$, there exists a path $(v,\dots , v')$ in $E(G_s)$;

• (2) $G_s$ is contained in the ball $\overset{\frown }{G}[v, d_Q]$, where $d_Q$ is the diameter of pattern Q. The set of subgraph pattern matches of Q over G via strong simulation is denoted as r(Q, G).

Problem Definition. Given a data graph G and a pattern graph Q, our work is to find all subgraph pattern matches of Q over G via strong simulation in cloud, without compromising the privacy of both data graph G and pattern graph Q.

4 Privacy Preserving in Cloud

4.1 Structural Privacy

To protect the structural privacy in data graphs, we develop a novel approach based on k-automorphism model. When a directed data graph G is given, we firstly transform it to an “undirected” graph $G^*$ by introducing noise edges. Then we convert $G^*$ into graph $G^k$, where $G^k$ satisfies the k-automorphic graph model.

Definition 5

k -automorphic Graph [12]. A k-automorphic graph $G^k$ is defined as $G^k = \left\{ V(G^k), E(G^k)\right\}$, where $V(G^k)$ can be divided into k blocks and each block has $\left\lceil \frac{V(G^k)}{k}\right\rceil$ vertices.

Intuitively, for any vertex v in a k-automorphic graph $G^k$, there are $k-1$ symmetric vertices. An adversary can hardly distinguish v from its structurally equivalent counterparts. Thus, the structural privacy in data graphs can be well preserved. According to Definition 5, we can transform $G^*$ to a k-automorphic graph $G^k$ as follows.

Fig. 3.

The Alignment Vertex Table (AVT) and automorphic function.

Firstly, we adopt the METIS algorithm [12, 26] to partition the graph $G^*$ into k blocks. In order to guarantee that each block has exactly $\left\lceil \frac{V(G^k)}{k}\right\rceil$ vertices, some noise vertices will be introduced if $V(G^*)$ can not be divided into k blocks. There is an efficient method to build Alignment Vertex Table (AVT) after the partition [19]. For example, we divide the graph $G^k$ in Fig. 2(b) into two blocks and build the corresponding AVT, which is presented in Fig. 3(a). Each row in AVT denotes they are symmetric vertices, such as $p_1$ and $p_7$ in Fig. 2(b). Each column in AVT contains the vertices in one block, such as ($p_1, p_2, p_3, p_4, p_5, p_6$) in the first block of $G^k$. According to the AVT, we define the k-automorphic function $F_{k_1}$, as shown in Fig. 3(b).

Secondly, we perform block alignment and edge copy [19] to obtain the k-automorphic graph $G^k$. For example, we can obtain 2 isomorphic blocks: $B_0(p_1, p_2, p_3, p_4, p_5, p_6)$ and $B_1(p_7, p_8, p_9, p_{10}, p_{11}, p_{12})$ by adding noise edges $(p_8, p_{10})$ and $(p_{11}, p_{12})$ via block alignment in Fig. 2. According to the crossing edge $(p_6, p_7)$ between 2 blocks, we add an edge $(p_1, p_{10})$ based on the edge copy techniques.

4.2 Label Privacy

Since the k-automorphism model based method can only protect structural privacy of the original graph G, we define a cost-model based label generalization method to protect label privacy of both data graph G and pattern graph Q. The method considers two factors: label matching and searching space, while estimating the number of candidates of a vertex u in $Q^0$, denoted as sim(u).

According to the definition of strong simulation [11], when a vertex v in graph $G^k$ matches the vertex u in pattern $Q^0$, it must firstly contain u’s label groups. We let $\left| V_g(G^k, i)\right|$ and $\left| V_g(Q^0, i)\right|$ denote the set of vertices with the label group i in $G^k$ and $Q^0$ that are obtained after the label generalization respectively. Then, we can define:

$$\begin{aligned} P_{G^k}^g(i)=\frac{|V_g(G^k,i)|}{|V(G^k)|}, P_{Q^0}^g(i)=\frac{|V_g(Q^0,i)|}{|V(Q^0)|} \end{aligned}$$

(1)

$P_{G^k}^g(i)$ and $P_{Q^0}^g(i)$ estimate the probability of a vertex in $G^k$ and $Q^0$ having an i-th label group after the label generalization, respectively. Then, the estimating number of vertices that can match vertex u in $Q^0$ while considering label matching can be defined as follows:

$$\begin{aligned} |V(G^k)| \sum _{i=1}^\alpha P_{G^k}^g(i) \varvec{\cdot }P_{Q^0}^g(i) \end{aligned}$$

(2)

Next we need to consider the search space of checking whether each of u’s parent vertices and child vertices can find matching vertices. We define the average in-degree $D_i(G^k)$ and average out-degree $D_o(G^k)$ to represent the in-degree and out-degree of vertex v (u’s matching vertex) respectively. Similarly, $D_i(Q)$ and $D_o(Q)$ represent the in-degree and out-degree of vertex u in $Q^0$ separately. Note that $D_o(Q^0)=D_o(Q)$, and $D_i(Q^0)=D_i(Q)$. Therefore, the maximum potential searching space of u’s first child vertex is ${D_o(G^k)}^{2d_Q}$, and that of the second child vertex is $(D_o(G^k)\!-\!1)D_o(G^k)^{2d_Q-1}$. Thus, the total searching space of u’s child vertices can be estimated as ${D_o(G^k)}^{2d_Q}\cdot (D_o(G^k)\!-\!1)D_o(G^k)^{2d_Q-1} \cdot \cdot \cdot (D_o(G^k)-D_o(Q)+1)D_o(G^k)^{2d_Q-1}$. We estimate it as $D_o(G^k)^{D_o(Q)}\cdot D_o(G^k)^{(2d_Q-1)^{D_o(Q)}}$ for simplicity, i.e., $D_o(G^k)^{D_o(Q)+(2d_Q-1)^{D_o(Q)}}$. Similarly, we can define the searching space of u’s parent vertices as $D_i(G^k)^{D_i(Q)+(2d_Q-1)^{D_i(Q)}}$. Thus, the estimation of searching space can be defined as follows:

$$\begin{aligned} \begin{aligned}&\left\{ D_o(G^k)\left[ \sum _{i=1}^\alpha P_{G^k}^g(i)P_{Q^0}^g(i) \right] \right\} ^{D_o(Q)\!+(2d_Q\!-\!1)^{D_o(Q)}} \\&\varvec{\cdot }\left\{ D_i(G^k)\left[ \sum _{i=1}^\alpha P_{G^k}^g(i)P_{Q^0}^g(i) \right] \right\} ^{D_i(Q)\!+(2d_Q\!-\!1)^{D_i(Q)}} \end{aligned} \end{aligned}$$

(3)

We assume the total labels in original graph G can be divided into $\alpha$ groups, each group contains $\theta$ different labels without loss of generality. We define $\langle p_1, p_2, p_3, \dots , p_{\alpha \theta } \rangle$ to form a permutation of $\langle 1, 2, 3, \dots , \alpha \theta \rangle$. According to [12], we can obtain that $P_{G^k}^g(i) \le \sum _{j=1}^\theta P_G(p_{\theta (i-1)+j})$. Thus, we can define the cost model:

$$\begin{aligned} \begin{aligned}&|sim(u)| = |V(G^k)|\left[ \sum _{i=1}^\alpha P_{G^k}^g(i)P_{Q^0}^g(i) \right] \! \varvec{\cdot }\! \left\{ D_o(G^k)\left[ \sum _{i=1}^\alpha P_{G^k}^g(i)P_{Q^0}^g(i) \right] \right\} ^{D_o(Q)\!+(2d_Q\!-\!1)^{D_o(Q)}}\varvec{\cdot }\\&\left\{ D_i(G^k)\left[ \sum _{i=1}^\alpha P_{G^k}^g(i)P_{Q^0}^g(i) \right] \right\} ^{D_i(Q)\!+(\!2d_Q\!-\!1)^{D_i(Q)}}\\ \!&=\!|V(G^k)|{D_o(G^k)}^{D_o(Q)\!+(2d_Q\!-\!1)^{D_o(Q)}} \varvec{\cdot }{D_i(G^k)}^{D_i(Q)\!+(2d_Q\!-\!1)^{D_i(Q)}}\varvec{\cdot }\\&{\left[ \sum _{i=1}^\alpha P_{G^k}^g(i)P_{Q^0}^g(i) \right] }^{D_o(Q)\!+\! D_i(Q) \!+\! (2d_Q \!-\! 1)^{D_o(Q)} \!+\!(2d_Q \!-\! 1)^{D_i(Q)} \!+\! 1} \\ \!&\le \!|V(G^k)|{D_o(G^k)}^{D_o(Q)\!+(2d_Q\!-\!1)^{D_o(Q)}}\varvec{\cdot }{D_i(G^k)}^{D_i(Q)\!+(2d_Q\!-\!1)^{D_i(Q)}} \varvec{\cdot }\\&\left\{ \sum _{i=1}^\alpha \left[ \sum _{j=1}^\theta P_G(p_{\theta (i-1)+j})\right] \left[ \sum _{j=1}^\theta P_Q(p_{\theta (i - 1) + j})\right] \right\} ^{D_o(Q)\!+\! D_i(Q) \!+\! (2d_Q \!-\! 1)^{D_o(Q)} \!+\!(2d_Q \!-\! 1)^{D_i(Q)} \!+\! 1} \end{aligned} \end{aligned}$$

(4)

According to the cost model in Eq. (4), an effective permutation of $\langle 1, 2, 3, \dots , \alpha \theta \rangle$, i.e., $\langle p_1, p_2, p_3, \dots , p_{\alpha \theta } \rangle$, can decrease the cost of the searching space of pattern graph Q over G. We choose the component that concerns the label combination to define Label Combination Cost.

$$\begin{aligned} cost(L)= \sum _{i=1}^\alpha \left[ \sum _{j=1}^\theta P_G(p_{\theta (i-1)+j})\right] \varvec{\cdot }\left[ \sum _{j=1}^\theta P_Q(p_{\theta (i-1)+j})\right] \end{aligned}$$

(5)

There is an iterative solution that can explore the optimal permutation to decrease cost(L) according to Eq. (5). Firstly, a random label combination is generated; then, we try to swap two labels in two different label groups for each iteration. If the swap leads to smaller cost, we will keep the swap; otherwise, we will ignore that. When there is no swap that can lead to smaller cost, the iteration stops and we can obtain an effective permutation.

4.3 Outsourced Graph

After obtaining an anonymous k-automorphic graph $G^k$, a basic solution is to upload $G^k$ to cloud directly. However, $G^k$ is more larger than the original graph G since $G^k$ contains large number of noise edges. Therefore, we only upload the outsourced graph, which is only a subset of $G^k$, denoted as $G^0$, to the cloud platform. The definition of $G^0$ is given below.

Definition 6

Outsourced Graph. An outsourced graph is defined as $G^0 = \{V(G^0), E(G^0), L_{G^0}(V(G^0))\}$ where $(1)\, V(G^0)$ is the set of vertices in the first block of $G^k$ (i.e. block $B_0$), denoted as $V(B_0)$, together with their neighbors within $2d_Q$-hops, denoted as $V(N_{2d_Q}); (2)\, E(G^0)$ is the set of edges that connected vertices within $V(B_0)$ and vertices between $V(B_0)$ and $V(N_{2d_Q}); (3)\, L_{G^0}(V(G^0))$ is the set of vertex labels in graph $G^0$.

Fig. 4.

The outsourced graph $G^0$ for $G^k$

According to Definition 6, we can generate an outsourced graph $G^0$ based on the graph $G^k$ and upload it to cloud. For example, an outsourced graph $G^0$ (as shown in Fig. 4) can be generated based on graph $G^k$ in Fig. 2. Although $G^0$ is a part of $G^k$, we can easily recover $G^k$ based on $G^0$ together with k-automorphic functions $F_{k_i} (i=1,2,\dots ,k-1)$.

4.4 Result Processing

When $G^0$ and $Q^0$ are uploaded, the cloud executes subgraph pattern matching via strong simulation to obtain the matching result $r(Q^0, G^0)$ and transmits it to client. There are two steps for the client side to process the result.

Firstly, the client computes $r(Q^0,G^k)$ based on $r(Q^0,G^0)$ together with k-automorphic functions $F_{k_i} (i=1,2,\dots ,k-1)$ (Lines 1–3 in Algorithm 1). For each subgraph $G_s$ in $r(Q^0,G^0)$, we can compute $F_{k_i}(G_s)\ (i=1,2,\dots , k-1$) and add them to $r(Q^0,G^k)$. Then, we obtain the final $r(Q^0,G^k)$ by adding $r(Q^0,G^0)$ (Line 4 in Algorithm 1).

Secondly, the client needs to filter out the false matches in $r(Q^0,G^k)$ according to the original data graph G and pattern Q. For each matching subgraph $G_s$ in $r(Q^0,G^k)$, if there exist vertices that are not contained in graph G or whose labels cannot match those of the corresponding vertices in the original pattern Q (We have anonymized the vertex labels in pattern Q via label generalization method), remove them from $G_s$ (Lines 7–11 in Algorithm 1). Note that we have introduced noise edges when generating “undirected” graph $G^*$ and k-automorphic graph $G^k$, if $G_s$ contains edges that do not exist in the original graph G, remove them from $G_s$ (Lines 12–14 in Algorithm 1). When all the noise vertices or edges and unmatch vertices are filtered out from $G_s$, we need to consider whether $G_s$ is a candidate. We define that if there exists a subgraph which is a match (meets the requirements of strong simulation) to pattern Q in $G_s$, it is a right positive and we need to add it to r(Q, G) (Lines 15–16 in Algorithm 1).

5 Experimental Study

5.1 Datasets and Setup

We evaluate our method in three real-world datasets in our experiments. The statistics on these datasets are given in Table 2.

Table 2. Real-world data graphs

p2p-Gnutella08. p2p-Gnutella08 is a sequence of snapshots of the Gnutella peer-to-peer file sharing network collected in August 8, 2002. Nodes represent hosts in the Gnutella network topology and edges represent connections between the Gnutella hosts.

Brightkite-edges. Brightkite-edges is the friendship network collected using Brightkite’s public API. Nodes correspond to users having checked-in Brightkite and directed edges correspond to relationships among them.

Web-NotreDame. Web-NotreDame is a web graph collected in 1999. Nodes represent pages from University of Notre Dame and directed edges represent hyperlinks between them.

SETUP. In our experiments, we compare four methods All_Ran, All_Eff, Part_Ran, and Part_Eff, where All_Ran applies the random label generalization method and upload $G^k$ to cloud; All_Eff applies the cost-model based label generalization method introduced in Sect. 4.2 and upload $G^k$ to cloud; Part_Ran applies the same label generalization approach with All_Ran but only upload $G^0$ to cloud; Part_Eff applies same label generalization method with All_Eff but upload $G^0$ to cloud.

All methods are implemented in C++. We use a Windows 10 PC with 2.30 GHz Intel Core i5 CPU and 8 GB of memory as the client side. The cloud server is on a virtualized Linux machine within Microsoft Azure Cloud with 4 CPU cores and 200 GB main memory.

5.2 Experiments Analysis

We evaluate the cost of our experiments from three aspects: time cost of generating $G^k$, time cost of pattern matching, and time cost of result processing in client.

Time Cost of Generating $G^k\mathbf .$ We first evaluate the performance of the proposed methods while generating graph $G^k$. In these experiments, we define that each label group contains two labels, i.e. the default value of $\theta$ is 2.

Fig. 5.

Time cost in generating $G^k$

According to Fig. 5, the cost-model based label generalization method and the random label generalization method have similar performance while generating graph $G^k$, i.e., the four proposed methods have similar time cost. The reason is that all of them need to generate graph $G^k$ firstly despite the ultimately uploaded graph is either $G^k$ or $G^0$. We note that the time cost on the three datasets increases when k goes from 2 to 5. The reason is that when k increases, more and more noise edges are added to $G^k$, as shown in Table 3. Note that each “undirected” edge in $G^k$ represents two directed edges. We can intuitively see that the number of noise edges has slightly difference when using different label generalization methods and increases with k.

Table 3. Number of noise edges in generating $G^k$

Time Cost of Pattern Matching. Then we pay attention to the time cost of subgraph pattern matching via strong simulation in cloud. Firstly, we evaluate the time cost of the proposed methods while varying the number of edges in pattern Q, i.e., |E(Q)|. Pattern graphs are generated by randomly extracting subgraphs from the original data graph G. We use |E(Q)| to control the size of pattern graphs. In these experiments, the value of k is set to 3. According to Fig. 6, we can clearly find out that Part_Eff performs better than the other three approaches on the three datasets. The one reason is that Part_Eff only uploads $G^0$ to cloud. Note that Part_Ran and Part_Eff are only different in label generalization. Thus, the results demonstrate the effectiveness of our cost-based label generalization method. The matching time increases with $\left| E(Q)\right|$ varying from 4 to 10, since the searching space will become larger for subgraph pattern matching when $\left| E(Q)\right|$ increases.

Fig. 6.

Matching time vs. $\left| E(Q) \right|$. ($k=3$)

Fig. 7.

Matching time vs. k. ($\left| E(Q) \right| =6$)

Next, we evaluate the running time of subgraph pattern matching while varying the parameter k. The time cost increases with k varying from 2 to 5, as shown in Fig. 7. This is because $\left| E(G^0)\right|$ increases with k varying from 2 to 5, since more noise edges will be inserted when k becomes larger. The method Part_Eff, which uses the cost-model based label generalization method and uploads $G^0$ to cloud, has better performance than other methods in all three datasets. It demonstrates the superiority of our cost-model based generalization method as well.

Time Cost of Result Processing in Client. At last, we evaluate the performance of four methods involving result processing in the client side while varying parameters k and $\left| E(Q) \right|$ respectively. According to Fig. 8, the result processing time increases with k varying from 2 to 5 for all four methods, since client need to filter out more noise edges when k becomes larger. Note that both All_Ran and All_Eff upload $G^k$ to cloud, the step to obtain $r(Q^0,G^k)$ on the basis of $r(Q^0,G^0)$ together with $F_{k_i} (i=1,2,\dots ,k-1)$ can be omitted. Thus, the time cost of result processing with All_Ran and All_Eff are smaller than the other two methods. However, the method Part_Eff that uses our cost-model based label generalization method still performs better than the Part_Ran.

Fig. 8.

Result processing time vs. k. ($\left| E(Q) \right| =6$)

Fig. 9.

Result processing time vs. $\left| E(Q) \right|$. ($k=3$)

Table 4. Overall running time (s) ($\left| E(Q) \right| =6$ and $k=3$)

The result processing time increases with |E(Q)| varying from 4 to 10, as shown in Fig. 9. The reason lies in that the search space will become larger for the filtering process when |E(Q)| increases. Similarly, the time cost of All_Ran and All_Eff are smaller than other two methods. However, the gap is small compared to the time cost of pattern matching. As shown in Table 4, Part_Eff runs faster than other three methods in terms of the overall running time. Note that the overall running time consists of the subgraph pattern matching time in cloud and the result processing time in the client side.

6 Conclusion

In this paper, we propose an effective framework to protect privacy of subgraph pattern matching via strong simulation in the cloud. Without losing utility, the framework protects structural and label privacy of both data graphs and pattern graphs. We introduce noise edges to transform a directed graph to an “undirected” graph so that the k-automorphism model based method can be applied to protect structural privacy of the data graph. We apply a cost-model based label generalization method to protect label privacy in both data graphs and pattern graphs additionally. In our framework, we only upload the outsourced graph to cloud so that the time cost of subgraph pattern matching can be decreased. Experiments on three real-world datasets illustrate the superior performance of our method.