On the Problem of Shock Wave Structure

Abstract

We consider the problem of internal structure of the triple point appearing in Mach reflection, which is considered to be important for the cause study of the von Neumann paradox as well as the shock reflection itself in rarefied gas. We investigate it in an adequately made finite region near the triple point and use analytical approach rather than numerical to have a solution of 2D Navier-Stokes equations system, by which we can avoid the difficulties such as the need for ever finer mesh size for the region not known in the beginning. We consider first one-dimensional flow in a finite region, which gives a flow with a hump unlike conventional one of monotonous change for the infinite region. Then we seek a solution of the 2D Navier-Stokes equations system in polar coordinates to the flow field between two curved boundaries. Results show the incoming parallel flow bents to the direction of the slip flow and the density distribution along the streamline increases similar to that for one-dimensional shock structure but a small hump as the solution over to the flow for a finite range.

1 Introduction

We consider the problem of internal structure of shock wave especially its non-Rankine-Hugoniot zone [1] at the triple point in Mach reflection. It is important for the cause study of the von Neumann paradox [2] of weak Mach reflection. Also it is needed to see the change in feature of reflecting shock wave in rarefied gas as the zone is widened enough to influence the main flow field [3].

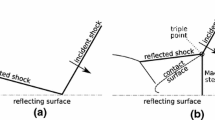
The aim of the problem of shock wave structure is to find the distributions of pressure, density, and velocity within shock wave to satisfy boundary values at its up- and downstream conditions. We investigate the problem in the same way as the one for ordinary plane shock wave surface, which usually considers the problem in studying the solution of the Navier-Stokes equation system of one-dimensional viscous gas flow to satisfy the Rankine-Hugoniot shock condition for up- and downstream in respective regions in infinities. Here we have to consider the problem in finite region. So we divide the flow region into three zones (I), (II), and (III) bounded by two curved boundaries r _a, r _b, as seen in Fig. 1b, which correspond to the two straight lines ${r}_a^{\prime }$, ${r}_b^{\prime }$, in Fig. 1a for the plane shock wave flow case. So we consider first the problem of shock wave structure in a finite region in Sect. 2 and utilize the process to construct a solution in region (II) in Fig. 1b.

Fig. 1

(a) Plane shock wave; (b) triple wave configuration; (I), incoming uniform flow; (II), non-R-H flow; (III), flow of triple-point singularity

2 Internal Structure of Plane Shock Wave

Here we are concerned with the solution of one-dimensional Navier-Stokes equation system of viscous gas in a finite region as being illustrated in Fig. 1a. We have equations of continuity, momentum, and energy as

$$ {\displaystyle \begin{array}{l}\frac{d}{dx}\left(\rho u\right)=0,\\ {}\frac{d}{dx}\left(\rho {u}^2+p\right)=\frac{d}{dx}\left(\frac{4}{3}\mu \frac{du}{dx}\right)\\ {}\frac{d}{dx}\left[\rho u\left(\frac{u^2}{2}+h\right)\right]=\frac{d}{dx}\left(\frac{4}{3}\mu u\frac{du}{dx}\right)+\frac{d}{dx}\left(\kappa \frac{dT}{dx}\right),\end{array}} $$

(1)

which are supplemented by the gas relations

$$ h={c}_pT\kern0.5em \mathrm{and}\kern0.5em p= \rho RT, $$

where ρ, p, u, T, and h are the density, the pressure, the velocity, the temperature, and the enthalpy of the flow field, with c _p, R the specific heat and the gas constant. The flow is supposed to be bounded by x = x ₁, x ₂, x ₁ < x ₂, and

$$ \rho ={\rho}_1,{\rho}_2;p={p}_1,{p}_2;u={u}_1,{u}_2;h={h}_1,{h}_2 $$

Here we follow Becker [4] to assume that the Prandtl number σ = μc _p/κ = 3/4, where the σ value of 3/4 = 0.75 is nearly equal to the corresponding value of 0.73 for air. This assumption can simplify the system of Eq. (1) greatly to have

$$ -\frac{u}{\alpha}\frac{du}{dx}=u\left(B-u\right)-\frac{\gamma -1}{\gamma}\left(A+{A}^{\prime }{e}^{\alpha x}-\frac{u^2}{2}\right)\equiv F(u), $$

(2)

where α ≡ (4μ/3m)⁻¹ and integration constants A, A ^′ are determined by the boundary values as

$$ {\displaystyle \begin{array}{l}{A}^{\prime }={\left({e}^{\alpha {x}_2}-{e}^{\alpha {x}_1}\right)}^{-1}\left({u}_1^2/2+{h}_1-{u}_2^2/2-{h}_2\right),\\ {}A={\left({e}^{\alpha {x}_2}-{e}^{\alpha {x}_1}\right)}^{-1}\left[\left({u}_1^2/2+{h}_1\right){e}^{\alpha {x}_2}-\left({u}_2^2/2+{h}_2\right){e}^{\alpha {x}_1}\right]\end{array}} $$

Furthermore, it is conventional to have the solution as considered in Becker [4] and Taylor [5] to the shock region being infinite and ∂u/∂x, ∂p/∂x,… →0 as x approaches infinities. In that case, we have A ^′ = 0 to result

$$ F(u)=\frac{\gamma +1}{2\gamma}\left({u}_1-u\right)\left(u-{u}_2\right),{u}_1>{u}_2\kern0.5em \mathrm{and}\kern0.5em mB={\rho}_1{u}_1^2+{p}_1={\rho}_2{u}_2^2+{p}_2, $$

from which we can integrate Eq. (2) to have

$$ {u}_1\;\log \left({u}_1-u\right)-{u}_2\;\log \left(u-{u}_2\right)= Dx+c,D\equiv \alpha \left({u}_1-{u}_2\right),\nonumber\\ c:\mathrm{integration}\kern0.5em \mathrm{constant}. $$

(3)

Notice that these are true also for ∂u/∂x, ∂p/∂x,… →0 at x = x ₁, x ₂, of finite x = x ₁, x ₂. This solution shows monotonous feature as seen in Fig. 1a for its pressure distribution.

Now for the present finite region case, the solution of Eq. (2) satisfying the shock boundary condition approximately at its both ends is sought numerically in determining B-value as a proper value, and the result shows that it provides a hump in pressure distribution profile as shown in Fig. 1b. The actual numerical example is presented in Sakurai et al. [6].

It is noted that this problem itself is simple as such and its solution is basically known, so that it is used for the test problem for a new numerical scheme or various models other than fluid dynamics such as molecular kinetic equation as the Boltzmann equation. It is often reported in this trial that the obtained distribution is not monotonous but takes a form with hump as sketched in Fig. 1b.

3 Solution in Zone (II)

3.1 Non-Rankine-Hugoniot Zone

In practice, we use polar coordinate system (r, θ) and postulate bounding two curves r _a, r _b between zones (I), (II), and (III) as shown in Fig. 2b in two hyperbolas given by

$$ {\displaystyle \begin{array}{l}{r}_a:\left[y-\tan \left(\pi -\omega \right)x\right]\left[y-\tan \left(2\pi -\lambda \right)x\right]=\tan \left(\pi -\omega \right)\tan \left(2\pi - {\lambda} \right){a}^2\\[1pc] {}{r}_b:\left[y-\tan\;{\omega}^{\prime }x\right]\left[y-\tan \left(2\pi -\lambda \right)x\right]=\tan\;{\omega}^{\prime}\;\tan \left(2\pi -\lambda \right){b}^2\end{array}} $$

where a, b are, respectively, the distance of r _a, r _b from the origin along x-axis. These can be expressed more conveniently in polar coordinates (r, θ) as

$$ {r}_a:r=a{\left[\frac{\sin\;\omega\;\sin\;\lambda }{\sin \left(\theta +\omega \right)\sin \left(\theta +\lambda \right)}\right]}^{1/2},\kern1em {r}_b:r=b{\left[\frac{-\sin\;{\omega}^{\prime}\;\cos\;\lambda }{\sin \left(\theta -{\omega}^{\prime}\right)\sin \left(\theta +\lambda \right)}\right]}^{1/2} $$

(4)

Fig. 2

Pressure distributions, (a) in infinite region and (b) in finite region

We assume that the flow in (I) is the incoming uniform flow of velocity U in x-direction with its density and pressure ρ ₀, p ₀. For the flow on the boundary r _b, we utilize the flow of the triple-point singularity in (III) given in references [7, 8], to which we give some in Appendix below. So we have

$$ {\displaystyle \begin{array}{l}{V}_r=U\;\cos \left(\pi -\theta \right),{V}_{\theta }=U\;\sin \left(\pi -\theta \right),p={p}_0,\rho ={\rho}_0\kern0.5em \mathrm{on}\kern0.5em r={r}_a\\ {}{V}_r={\tilde{V}}_r,{V}_{\theta }={\tilde{V}}_{\theta },p=\tilde{p},\rho =\tilde{\rho}\kern4.5em \mathrm{on}\kern0.5em r={r}_b\end{array}} $$

(5)

3.2 2D Navier-Stokes Equation System in Polar Coordinates

The Navier-Stokes equation systems for 2D viscous gas flow in cylindrical coordinates are the following equations of continuity, motion, and energy supplemented by equations of perfect gas:

$$ {\displaystyle \begin{array}{l}\frac{\partial }{\partial r}\left(\rho {V}_rr\right)+\frac{\partial }{\partial \theta}\left(\rho V\theta \right)=0\\[0.7pc] {}\rho \left({V}_r\frac{\partial {V}_r}{\partial r}+\frac{V_{\theta }}{r}\frac{\partial {V}_r}{\partial \theta }-\frac{V_{\theta}^2}{r}\right)+\frac{\partial p}{\partial r}=\mu \left[\Delta {V}_r-\frac{V_r}{r^2}-\frac{2}{r^2}\frac{\partial {V}_{\theta }}{\partial \theta }+\frac{1}{3}\frac{\partial }{\partial r}\frac{1}{r}\left(\frac{\partial {\mathrm{rV}}_r}{\partial r}\frac{\partial {V}_{\theta }}{\partial \theta}\right)\right],\\[0.7pc] {}\rho \left({V}_r\frac{\partial {V}_{\theta }}{\partial r}+\frac{V_{\theta }}{r}\frac{\partial {V}_{\theta }}{\partial \theta }-\frac{V_r{V}_{\theta }}{r}\right)+\frac{\partial p}{r\partial \theta }=\mu \left[\Delta {V}_{\theta }-\frac{V_{\theta }}{r^2}+\frac{2}{r^2}\frac{\partial {V}_r}{\partial \theta }+\frac{1}{3}\frac{\partial }{\partial \theta}\frac{1}{r}\left(\frac{\partial {\mathrm{rV}}_r}{\partial r}\frac{\partial {V}_{\theta }}{\partial \theta}\right)\right]\\[0.7pc] {}\rho \left[\left({V}_r\frac{\partial }{\partial r}+\frac{V_{\theta }}{r}\frac{\partial }{\partial \theta}\right)E+p\left({V}_r\frac{\partial }{\partial r}+\frac{V_{\theta }}{r}\frac{\partial }{\partial \theta}\right)\frac{1}{\rho}\right]=\kappa \Delta T+\\[0.7pc] {}\mu \left[2{\left(\frac{\partial {V}_r}{\partial r}\right)}^2+{\left(\frac{1}{r}\frac{\partial {V}_{\theta }}{\partial \theta }+\frac{V_r}{r}\right)}^2+{\left(\frac{1}{r}\frac{\partial {V}_r}{\partial \theta }+\frac{\partial {V}_{\theta }}{\partial r}-\frac{V_{\theta }}{r}\right)}^2-\frac{2}{3}{\left(\frac{\partial {V}_r}{\partial r}+\frac{\partial {V}_{\theta }}{r\partial \theta }+\frac{V_r}{r}\right)}^2\right]\end{array}} $$

(6)

$$ {{where}\kern0.5em \Delta \equiv \frac{\partial^2}{\partial {r}^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{\partial^2}{\partial {\theta}^2},\kern0.5em E={c}_vT,\kern0.5em p=\rho RT,} $$

and (V _r, V _θ) stands for (r, θ) components of the velocity; ρ, p, T for the density, the pressure, and the temperature; μ for the coefficient of the viscosity; and κ for the heat conductivity. These μ and κ are assumed constants.

3.3 r-Expansion Solution

We consider a solution of Eq. (6) near the origin r = 0. In the present circumstances, we express the solution in the form of the power series in r and use the approximation of the expansion to its second-order term. To this after some algebra under the condition that the solution must be single valued at r = 0, we have the following for the velocity V, the density ρ, the pressure p, and the temperature T:

$$\begin{array}{*{20}{c}} {{\mathbf{V}} = }&{{V_r} + i\,{V_\theta }:} \\ {{\mathbf{V}} = }&{ - {\mathbf{\tilde C}}{e^{ - i\theta }} + r\left[ {{\mathbf{A}}{e^{ - 2i\theta }} + {\mathbf{B}}} \right],\;\;\;{\mkern 1mu} {\mathbf{A}} = {A_1} + {\text{i}}{{\text{A}}_2},{\mathbf{B}} = {B_1} + {\text{i}}{{\text{B}}_2}\;\:{\mathbf{\tilde C}} = \tilde C{e^{i{\theta ^\prime }_0}},} \end{array}$$

(7)

$$ {\displaystyle \begin{array}{c}\rho ={C}_5^{(0)}\left\{1+\mathrm{r}{\mathrm{C}}^{\prime}\left[\cos \left(\theta +{\theta}_0^{\prime}\right)-{C}^{(1)}\;\sin \left(\theta +{\theta}_0^{\prime}\right)\right],\kern0.6em {C}^{\prime}\equiv 2{B}_1/\overset{\frown }{C}\right.\\ {}p=\rho RT,\kern0.48em T={D}_0+r\left({D}_1+{D}_2\theta \right),\end{array}} $$

(8)

where A, B, $\tilde{\mathbf{C}}$, ${C}_5^{(0)},{\theta}_0^{\prime }$, D ₀, D ₁, and D ₂ are to be determined by the conditions at r = r _a and r = r _b in Eq. (5). In this connection, we express the uniform velocity to the zone (I) in a complex form as

$${\mathbf{V}} = {V_r} + {\text{i}}{{\text{V}}_\theta } = {\text{U}}{{\text{e}}^{ - i\theta }}.$$

Now, firstly in observing Eq. (8) with $\tilde{\rho}$ in Appendix A, we can see ${\theta}_0={\theta}_0^{\prime }$. Next for A, B, and $\tilde{\mathbf{C}}$ to the velocity, we have from Eq. (5)

$$r = {r_a}: - {\mathbf{\tilde C}}{e^{ - i\theta }} + {r_a}\left[ {{\mathbf{A}}{e^{ - 2i\theta }} + {\mathbf{B}}} \right] = {\text{U}}{{\text{e}}^{ - i\theta }},$$

(9)

$$r = {r_b}: - {\mathbf{\tilde C}}{e^{ - i\theta }} + {r_b}\left[ {{\mathbf{A}}{e^{ - 2i\theta }} + {\mathbf{B}}} \right] = {\left[ {{\mathbf{\tilde V}}} \right]_{r = b}}$$

(10)

Obviously we cannot have solution to satisfy this completely, but we seek a solution from its approximation to a small region near the origin of non-R-H zone. So we put θ = π + φ, in Eq. (9), and $\theta =-{\theta}_0+\tilde{\phi},$ in Eq. (10), and expand these equations, respectively, in φ and $\tilde{\phi},$ to have from the expansion coefficients

$${ - {\mathbf{\tilde C}} + a\left( {{\mathbf{A}} + {\mathbf{B}}} \right) = - U} \\ {i{\mathbf{\tilde C}} + s\left( {{\mathbf{A}} + {\mathbf{B}}} \right) - 2i{\mathbf{A}} = {\text{iU}}} \\ {{\mathbf{\tilde C}}{e^{i{\theta _0}}} + {{\widehat r}_b}\left( {{\mathbf{A}}{e^{2i{\theta _0}}} + {\mathbf{B}}} \right) = {{\left( {{\mathbf{\tilde V}}} \right)}_{r = {r_b},\theta = - {\theta _0}}} = - \tilde A\left( {1 - k{\theta _0}} \right)} $$

where we put ${r_a}^{\prime}\left(-{\theta}_0\right)=s,\kern0.48em {r}_b\left(-{\theta}_0\right)={\widehat{r}}_b$. From these above we can determine $\tilde{\mathbf{C}}$, A, and B. In the same manner, we can determine the constants ${C}_5^{(0)},{C}^{(1)}$ for ρ and D ₀, D ₁, and D ₂ for p, T.

4 Streamline

Let r = r(θ, θ _a) be a streamline from a point r(θ _a) on r _a, which is given by the equation

$$ \frac{1}{r}\frac{d r}{d\theta}=\frac{V_r}{V_{\theta }}\kern0.5em \mathrm{with}\kern0.5em r=r\left({\theta}_a,{\theta}_a\right)={r}_a\left({\theta}_a\right). $$

Here we use ${V}_r={V}_r^{(0)}+{rV}_r,\kern0.84em {V}_{\theta }={V}_{\theta}^{(0)}+r\kern0.36em {V}_{\theta}^{(1)},$ and expand the right-hand side term in the power of r to have an approximation, which can be integrated, and we use the initial condition above to have

$$ \frac{1}{r\;\sin \left(\theta +{\theta}_0\right)}={\frac{1}{r_a\;\sin \left({\theta}_a+{\theta}_0\right)}}_1+\underset{\theta {}_a}{\overset{\theta }{\int }}\frac{K\left({\theta}^{\prime}\right)}{\sin \left({\theta}^{\prime }+{\theta}_0\right)}d{\theta}^{\prime },\\ K\left(\theta \right)\equiv -\frac{{V_r}^{(0)}}{{V_{\theta}}^{(0)}}\left(\frac{{V_r}^{(1)}}{{V_r}^{(0)}}-\frac{{V_{\theta}}^{(1)}}{{V_{\theta}}^{(0)}}\right) $$

(11)

We can see in Eq. (11) that this without the term of integral represents simply straight line and the term contributes to make a distortion from it. This feature of streamlines is illustrated in Fig. 3. We use this for r in the density distribution solution Eq. (8) to have

$$ \rho ={C}_5^{(0)}\left\{1+r\left(\theta, {\theta}_a\right){C}^{\prime}\left[\cos \left(\theta +{\theta}_0\right)-{C}^{(1)}\sin \left(\theta +{\theta}_0\right)\right]\right., $$

which provide the changing feature of the density along the streamline s in showing that its main change is sinusoidal with a distortion by the factor r(θ, θ _a) as shown schematically in Fig. 4. Starting from the same density, it becomes different after passing through shock wave(s) on different streamlines. It looks similar to the one for one-dimensional flow in a finite region shown in Fig. 1b.

Fig. 3

Streamlines

Fig. 4

Density distribution along streamline

5 Conclusion

The importance of structure study of the triple point has been recognized for the cause study of von Neumann paradox in Mach reflection as well as its effect to shock reflection itself in rarefied gas flow. We proceed the study in a parallel way as for plane shock surface in a finite region. We used analytical approach rather than numerical to have a solution of 2D Navier-Stokes equation system, which can avoid the difficulties such as the need for ever finer mesh size for the region not known in the beginning. Using this solution we can see streamlines bent from the original parallel flow line to the direction of the one for the slip flow line and the density distribution along the streamline behaves as the one for plane shock surface with a hump in between as seen in Fig. 1b. These suggest the understanding of the relation representing the feature of non-Rankine-Hugoniot zone. Also these can serve as the guide for numerical work for more details.

Appendix: Solution of Triple-Point Singularity [7, 8]

This is a r-power expansion solution of Eq. (6) in angler region between the reflected and Mach stems satisfying the shock boundary condition at the two shock lines so that it is singular at the triple point r = 0, which in fact represents the flow in the non-R-H zone caused by shock lines with different shock values meeting there. Some of the results relevant to this study are

$$ {\displaystyle \begin{array}{l}{\tilde{V}}_{\theta }={\tilde{V}}_{\theta}^{(0)}+r{\tilde{V}}_{\theta}^{(1)},{\tilde{V}}_r={\tilde{V}}_r^{(0)}+r{\tilde{V}}_r^{(1)},\tilde{\rho}={\tilde{\rho}}^{(0)}+r{\tilde{\rho}}^{(1)},\tilde{p}={\tilde{p}}^{(0)}+\mathrm{r}{\tilde{\mathrm{p}}}^{(1)}\\ {}{\tilde{V}}_{\theta}^{(0)}{=}\tilde{A}\left(1{+} k\theta \right)\sin \left(\theta {+}{\theta}_0\right),{\tilde{V}}_r^{(0)}=-\tilde{A}\left[\left(1{+} k\theta \right)\cos \left(\theta {+}{\theta}_0\right){+}k/7\sin \left(\theta {+}{\theta}_0\right)\right]\\ {}{\tilde{\rho}}^{(0)}=E{\left(1+ k\theta \right)}^{-6/7},{\tilde{p}}^{(0)}={\tilde{\rho}}^{(0)}\left( F\theta +G\right),\\ {}{\tilde{V}}_{\theta}^{(1)}=-\left(1/2\right)\tilde{A}{}_1\;\sin \left(\theta +{\theta}_0-2\alpha \right)\sin \left(\theta +{\theta}_0\right)+{S}_1\left(\theta \right)\\ {}{\tilde{V}}_r^{(1)}=-\left(1/2\right)\tilde{A}{}_1\;\cos \left(\theta -{\theta}_0-2\alpha \right)\sin \left(\theta +{\theta}_0\right)+{S}_2\left(\theta \right),\\ {}{S}_1\left(-{\theta}_0\right)={S}_1\left(-{\theta}_0\right)={\tilde{\rho}}^{(1)}\left(-{\theta}_0\right)={\tilde{p}}^{(1)}\left(-{\theta}_0\right)=0\end{array}} $$