Abstract
Fragments of Tarski’s relation algebra form the basis of many versatile graph and tree query languages including the regular path queries, XPath, and SPARQL. Surprisingly, however, a systematic study of the relative expressive power of relation algebra fragments on trees has not yet been undertaken. Our approach is to start from a basic fragment which only allows composition and union. We then study how the expressive power of the query language changes if we add diversity, converse, projections, coprojections, intersections, and/or difference, both for path queries and Boolean queries. For path queries, we found that adding intersection and difference yields more expressive power for some fragments, while adding one of the other operators always yields more expressive power. For Boolean queries, we obtain a similar picture for the relative expressive power, except for a few fragments where adding converse or projection yields no more expressive power. One challenging problem remains open, however, for both path and Boolean queries: does adding difference yields more expressive power to fragments containing at least diversity, coprojections, and intersection?
This material is based on work supported by the National Science Foundation under Grant No. NSF 1438990.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Trees can be used to model data that has a hierarchical or nested structure including taxonomies, organizational charts, documents, genealogies, and file and directory structures. It is therefore not surprising that tree data models have been continuously studied since the 1960s [5, 9, 25]. Modern query languages for querying tree data have a heavy reliance on navigating the tree structure. Prime examples of this are XPath [4, 6, 7, 22] and the various JSON query languages [19]. At its core, this navigation can be captured by fragments of Tarski’s relation algebra [24]. Consequently, tree querying based on fragments of the relation algebra has already been studied in great detail (e.g. [3, 16, 17, 26]). Unfortunately, these studies only covered some very basic fragments of the relation algebra, and a comprehensive study of all relation algebra fragments has not yet been undertaken.
In this work, we undertake such a comprehensive study by investigating the relative expressive power of fragments of the relation algebra with respect to both path queries and Boolean queries. Concretely, the basic relation algebra fragment \(\mathcal {N}()\) we start from only allows the constants empty-set and identity (\(\emptyset \) and \(\mathrm {id}\)), edge labels, and the operators composition and union (\(\circ \) and \(\cup \)). This fragment allows for basic querying based on navigating alongside the parent-child axis and corresponds with the first-order fragment of the regular path queries (RPQs) [8]. We study how the expressive power changes if we add the remaining relation algebra constants and operators. This includes adding converse (\({}^{\mathord {-1}}\)) which enables navigation alongside the child-parent axis, yielding the first-order fragment of the 2RPQs [1]. We also add projections (\(\pi _1\) and \(\pi _2)\) which enable simultaneous navigation alongside several branches in the tree, yielding the first-order fragment of the nested RPQs [2]. As it turns out, the first-order fragments of the RPQs, 2RPQs, and nested RPQs are rather weak on trees. To increase their expressive power, we consider adding diversity (\(\mathrm {di}\)) and intersection (\(\cap \)). The diversity constant evaluates to all pairs of distinct nodes and combined with intersection this constant can be used to, e.g., construct all pairs of distinct siblings. This enables branching and counting queries, even on unlabeled structures. Finally, we study adding negation in the form of coprojections (\(\overline{\pi }_1\) and \(\overline{\pi }_2)\) and difference (\(-\)). All the above notations that are at the basis of this study can be found in Sect. 2.
Unfortunately, the relative simplicity of the tree data model turns out to be a curse rather than a blessing: compared to the graph data model [10,11,12, 24], this simplicity makes it much more difficult to establish separation results using strong brute-force methods. Consequently, the study on trees forces us to search for deeper methods to reach our goals. Therefore, we believe that our study not only gives insight in the expressive power of the relation algebra and its fragments, but also contributes to a better understanding of the fundamental differences between graph data models and tree data models. The main contribution presented in this paper is the introduction of several properties that can be used to categorize relation algebra fragments according to their expressive power. This in turn yields several separation results on trees:
-
1.
Recognizing branches and siblings. The language \(\mathcal {N}()\) can only query trees by navigating alongside a single path from ancestor to descendant. Consequently, no query in \(\mathcal {N}()\) can distinguish between chains and trees. Other query languages support recognizing branching up to a certain degree, and we can classify these languages accordingly. To do so, we introduce a notion called k-subtree reductions in Sect. 3. Languages that are closed under k-subtree-reduction steps allow the removal of a child of a node that is structurally equivalent to at least k other children of that node without changing the outcome of Boolean queries. First, the query language \(\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap )\) is 1-subtree-reducible and, consequently, can only recognize siblings if they are not structurally equivalent. Next, query languages \(\mathcal {N}(\mathcal {F})\) with \(\mathrm {di}\in \mathcal {F}\) and \(\cap \notin \overline{\mathcal {F}}\) are 2-subtree-reducible and can, in very limited circumstances, distinguish up to two structurally equivalent children of a node. Finally the full relation algebra is 3-subtree-reducible, and query languages \(\mathcal {N}(\mathcal {F})\) with \(\{ {}^{\mathord {-1}},-\} \subseteq \mathcal {F}\) or \(\{\mathrm {di},\cap \} \subseteq \mathcal {F}\) can always distinguish between nodes that have one, two, or at least three structurally equivalent children.
-
2.
Local queries versus non-local queries. Queries in \(\mathcal {N}(\mathcal {F})\) with \(\mathcal {F}\subseteq \{ {}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -\}\) yield node pairs (m, n) such that one can navigate between m and n by traversing a number of edges, with the number depending only on the length of the query. Hence, we call these query languages local. Diversity is intrinsically non-local. From this observation, it follows that languages with diversity are not path-equivalent to local query languages. This can be strengthened towards Boolean inequivalence, as diversity can, in many cases, be used to express non-local properties on which trees and chains can be distinguished. We do so in Sect. 4 by exploiting the fact that many properties on which trees and chains can be distinguished are non-local and rely on a limited form of counting. A simple example of this are chain queries of the form “are there k edges in the chain labeled with edge-label \(\ell \)”.
-
3.
Downward queries versus non-downward queries. Queries in \(\mathcal {N}(\mathcal {F})\) with \(\mathcal {F}\subseteq \{ \pi , \overline{\pi }, \cap , -\}\) yield node pairs (m, n) such that one can navigate from m to n by traversing along a sequence of parent-child axes. Hence, we call these query languages downward [16, 17]. We observe that these downward query languages are all 1-subtree-reducible, which puts an upper bound on their expressive power. Diversity and the converse operator are non-downward in nature. Based on this observation, it follows that languages with diversity or converse are not path-equivalent to downward query languages.
-
4.
Monotonicity. A query language is monotone if, for every query \(q\), every graph \(\mathcal {G}\), and every graph \(\mathcal {G}'\) obtained by adding nodes and edges to \(\mathcal {G}\), we have
 . One the one hand, one can show that the query language \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi , \cap )\) is monotone [16, 17]. On the other hand, the query languages \(\mathcal {N}(\mathcal {F})\) with \(\overline{\pi }\in \overline{\mathcal {F}}\) are non-monotone. For example, we only need coprojections to construct a Boolean query that puts an upper bound on the length of a chain. Such queries are not monotone and consequently not expressible in \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi , \cap )\).
. One the one hand, one can show that the query language \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi , \cap )\) is monotone [16, 17]. On the other hand, the query languages \(\mathcal {N}(\mathcal {F})\) with \(\overline{\pi }\in \overline{\mathcal {F}}\) are non-monotone. For example, we only need coprojections to construct a Boolean query that puts an upper bound on the length of a chain. Such queries are not monotone and consequently not expressible in \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi , \cap )\).
In Fig. 1, we visualize the above categorization, which yields an initial classification of the expressive power of the query languages we study on trees. It does not provide all details, however, which we will start to unravel in this paper, mainly in Sects. 3 and 4. For an index on how specific results are proven, we refer the reader to Fig. 12.
Some separation results are obtained through brute-force methods, which we will show in Sect. 5. Besides separation results, we also establish collapse results in this paper. In Sect. 6, we obtain these by introducing a notion called condition tree queries for the local relation algebra fragments. They prove to be a powerful tool to show that intersection never adds expressive power beyond the ability to express projections. We also use this tool to establish limitations on the expressive power of projections in Boolean queries.
What remains open is whether adding difference to the fragments containing diversity, coprojections (and hence also projections), and intersection yields a collapse or separation, even in the presence of converse. We claim this a very challenging open case, and we consider identifying it as the third major contribution of this paper. We discuss this open case in Sect. 8, in which we also discuss other directions for future research.
Initial classification of the relative expressive power of fragments of the relation algebra with respect to path queries on labeled trees. In each box, the largest fragment(s) that satisfy the classification of that particular box are included. The more to the right and to the top a certain box is situated, the stronger the expressiveness of the corresponding fragment(s) become.
2 Preliminaries
Our formalization of graphs, the relation algebra, and equivalence notions is adapted from concepts used by Fletcher et al. [10, 11].
A graph is a triple \(\mathcal {G}= (\mathcal {V}, \varSigma , \mathbf {E})\), with \(\mathcal {V}\) a finite set of nodes, \(\varSigma \) a finite set of labels, and \(\mathbf {E}: \varSigma \rightarrow 2^{\mathcal {V}\times \mathcal {V}}\) a function mapping labels to edge relations. We denote by \(\mathcal {E}\) the union of all edge relations. If \(|\varSigma |=1\), \(\mathcal {G}\) is unlabeled. A tree \(\mathcal {T}= (\mathcal {V}, \varSigma , \mathbf {E})\) is a connected acyclic graph in which one node, the root, has no incoming edges, and all other nodes have one incoming edge. In an edge \((m, n) \in \mathcal {E}\), m is the parent of n, and n a child of m. A chain is a tree in which all nodes have at most one child.
In this paper, we limit our study to queries on trees and chains. A query \(q\) maps a tree to a set of node pairs. We write  to denote the evaluation of \(q\) on tree \(\mathcal {T}\). We can interpret a query \(q\) literally as a path query, or, alternatively, as a Boolean query, in which case \(\texttt {True}\) stands for
to denote the evaluation of \(q\) on tree \(\mathcal {T}\). We can interpret a query \(q\) literally as a path query, or, alternatively, as a Boolean query, in which case \(\texttt {True}\) stands for  .
.
The syntax of a relation algebra expression is given by
where \(\ell \in \varSigma \) and \(j \in \{ 1, 2 \}\). Its evaluation on a tree \(\mathcal {T}= (\mathcal {V}, \varSigma , \mathbf {E})\) is defined by

Notice that it suffices to consider converse (\({}^{\mathord {-1}}\)) at the level of labels only. If an expression always evaluates to a subset of \(\mathrm {id}\), as is the case for projections and coprojections, then it is called a node expression.
Example 1
Consider the labeled tree in Fig. 2. The expression \(e= \pi _{1}[\ell ] \circ \ell \circ \pi _{1}[\ell ] \circ \ell \) matches this tree structure, and will return the node pair (m, n). The expressions \((\smash {\ell ^{\mathord {-1}}} \circ \ell ) \cap \mathrm {di}\) and \((\smash {\ell ^{\mathord {-1}}} \circ \ell ) -\mathrm {id}\) both return pairs of siblings in the tree.
For \(k>0\), we write \(\mathcal {E}^{k}\) to represent k-fold composition of \(\mathcal {E}\) and \(\mathcal {E}^{-k}\) for its converse, we use \(\mathcal {E}^0\) to denote \(\mathrm {id}\), \([\mathcal {E}]^{\mathord {+}}\) to denote the descendant-axis defined by \([\mathcal {E}]^{\mathord {+}} = \smash {\bigcup _{k>0}\ \mathcal {E}^k}\), and \([\smash {\mathcal {E}^{\mathord {-1}}}]^{\mathord {+}}\) to denote the ancestor-axis defined by \([\smash {\mathcal {E}^{\mathord {-1}}}]^{\mathord {+}} = \smash {\bigcup _{k>0}\ \mathcal {E}^{-k}}\). Given \(\mathcal {F}\subseteq \{ \mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -\}\), \(\mathcal {N}(\mathcal {F})\) denotes the relation algebra fragment in which only the atoms \(\emptyset \), \(\ell \in \varSigma \), and \(\mathrm {id}\), the operators \(\circ \) and \(\cup \), and all operators in \(\mathcal {F}\) are allowed. In the above, we used \(\pi \) as shorthand for \(\pi _1\) and \(\pi _2\), and \(\overline{\pi }\) as shorthand for \(\overline{\pi }_1\) and \(\overline{\pi }_2\).
Let \(q_1\) and \(q_2\) be expressions. We say that \(q_1\) and \(q_2\) are path-equivalent, denoted by \(q_1 \equiv _{\mathrm {path}}q_2\), if, for every tree \(\mathcal {T}\),  and are Boolean-equivalent, denoted by \(q_1 \equiv _{\mathrm {bool}}q_2\), if, for every tree \(\mathcal {T}\),
and are Boolean-equivalent, denoted by \(q_1 \equiv _{\mathrm {bool}}q_2\), if, for every tree \(\mathcal {T}\),  . Let \(z \in \{{\mathrm {path}}, {\mathrm {bool}}\}\). We say that the class of expressions \(\mathcal {L}_1\) is z-subsumed by the class of expressions \(\mathcal {L}_2\), denoted by \(\mathcal {L}_1 \preceq _z \mathcal {L}_2\), if every expression in \(\mathcal {L}_1\) is z-equivalent to an expression in \(\mathcal {L}_2\). In this connection, the following rewrite rules can be used to express operators using other operators:
. Let \(z \in \{{\mathrm {path}}, {\mathrm {bool}}\}\). We say that the class of expressions \(\mathcal {L}_1\) is z-subsumed by the class of expressions \(\mathcal {L}_2\), denoted by \(\mathcal {L}_1 \preceq _z \mathcal {L}_2\), if every expression in \(\mathcal {L}_1\) is z-equivalent to an expression in \(\mathcal {L}_2\). In this connection, the following rewrite rules can be used to express operators using other operators:
For \(\mathcal {F}\subseteq \{ \mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -\}\), \(\overline{\mathcal {F}}\) denotes the closure of \(\mathcal {F}\) under the rules above.Footnote 1
Example 2
The equivalence \(e_1 \cap e_2 \equiv _{\mathrm {path}}e_1 -(e_1 -e_2)\) is well-known. Hence, also \(e_1 \cap e_2 \equiv _{\mathrm {bool}}e_1 -(e_1 -e_2)\). We also have \(\pi _{1}[\ell ] \equiv _{\mathrm {bool}}\ell \equiv _{\mathrm {bool}}\pi _{2}[\ell ]\), but \(\pi _{1}[\ell ] \not \equiv _{\mathrm {path}}\ell \) and \(\ell \not \equiv _{\mathrm {path}}\pi _{2}[\ell ]\). Finally, let \(e\) be the expression as in Example 1. We have \(e\equiv _{\mathrm {path}}\ell _1 \circ \smash {\ell _1^{\mathord {-1}}} \circ \ell _2 \circ \ell _3 \circ \smash {\ell _3^{\mathord {-1}}} \circ \ell _4\).
3 Subtree Reductions
Most relation algebra fragments are able to detect obvious labeled branching in trees.
Example 3
Consider the expressions \(e_1 = \smash {(\ell _1)^{\mathord {-1}}} \circ \ell _2\) and \(e_2 = \pi _{1}[\ell _1] \circ \pi _{1}[\ell _2]\), which are Boolean-equivalent. Clearly, for any tree \(\mathcal {T}\) we have  , \(i \in \{1,2\}\) only if \(\mathcal {T}\) has a node with at least two children, one reachable via an edge labeled \(\ell _1\) and another via an edge labeled \(\ell _2\).
, \(i \in \{1,2\}\) only if \(\mathcal {T}\) has a node with at least two children, one reachable via an edge labeled \(\ell _1\) and another via an edge labeled \(\ell _2\).
Detecting branches in the situation above, where a single node has several structurally distinct branches, is relatively simple. Next, we look at which language fragments are able to detect branching if all branches are structurally identical. As a first step towards this goal, we derive limitations on the expressive power of relation algebra fragments, taking advantage of the simple structure of trees. Thereto, we introduce subtree-reduction steps.
Let \(k>0\). A k-subtree-reduction step on tree \(\mathcal {T}= (\mathcal {V}, \varSigma , \mathbf {E})\) consists of first finding different nodes \(m,n_1,\ldots ,n_{k+1}\in \mathcal {V}\) and an edge label \(\ell \in \varSigma \) such that \((m, n_1), \dots , (m, n_{k+1}) \in \mathbf {E}\left( \ell \right) \) and the subtrees rooted at \(n_1,\ldots ,n_{k+1}\) are isomorphic, and then picking a node \(n_i\), \(1 \le i \le k+1\), and removing the subtree rooted at \(n_i\).
Definition 4
We say that a tree is k-subtree-reducible if we can apply a k-subtree-reduction step.Footnote 2
Example 5
Consider the unlabeled trees \(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\) in Fig. 3. The tree \(\mathcal {T}_1\) can be obtained by a 1-subtree-reduction step on \(\mathcal {T}_2\) and \(\mathcal {T}_2\) can be obtained by a 2-subtree-reduction step on \(\mathcal {T}_3\). Consequently, \(\mathcal {T}_1\) can also be obtained by two 1-subtree-reduction steps on \(\mathcal {T}_3\). Hence, \(\mathcal {T}_2\) is 1-subtree-reducible and \(\mathcal {T}_3\) is 1-subtree-reducible and 2-subtree-reducible.
We now exhibit conditions under which the result of a relation algebra expression is invariant under subtree reduction at the Boolean level.
Proposition 6
Let \(\mathcal {F}\subseteq \{ \mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -\}\), \(e\) an expression in \(\mathcal {N}(\mathcal {F})\), \(\mathcal {T}\) a tree, and \(\mathcal {T}'\) obtained from \(\mathcal {T}\) by a k-subtree-reduction step. Each of the following conditions separately implies  :
:
-
(i)
\(k\ge 3\);
-
(ii)
\(k=2\) and \(\cap \notin \overline{\mathcal {F}}\); and
-
(iii)
\(k=1\) and \(\{\mathrm {di}, -\} \cap \mathcal {F}= \emptyset \).
Proof
(sketch). Using k-pebble games [13, 14, 21], we can see that  if \(q\) is a query in \(\mathrm {FO}\)[k], which is first-order logic restricted to k variables. Since the relation algebra and \(\mathrm {FO[3]}\) path-subsume each other [12, 24], (i) follows. In Statement (ii), \(\mathcal {F}\subseteq \{ \mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi }\}\). Hence, by a result of Hellings et al. [18, Theorem 6.1], (ii) also follows.Footnote 3 To prove (iii), let \(\mathcal {T}= (\mathcal {V}, \varSigma , \mathbf {E})\) and \(\mathcal {T}' = (\mathcal {V}', \varSigma ', \mathbf {E}')\). Let \(n_1,n_2 \in \mathcal {V}\) be the siblings in \(\mathcal {T}\) such that \(\mathcal {T}'\) is obtained from \(\mathcal {T}\) by eliminating the subtree rooted at \(n_2\). Let \(\mathcal {V}_1\) and \(\mathcal {V}_2\) be the nodes in the subtrees of \(\mathcal {T}\) rooted at \(n_1\) and \(n_2\), respectively, and let \(b : \mathcal {V}_1 \rightarrow \mathcal {V}_2\) be a bijection establishing that these subtrees are isomorphic. Let g be the identity on \(\mathcal {V}-(\mathcal {V}_1 \cup \mathcal {V}_2)\), and let \(f = b \cup b^{-1}\cup g\). Since f is an automorphism of \(\mathcal {T}\), we have, for \(m,n\in \mathcal {V}\),
if \(q\) is a query in \(\mathrm {FO}\)[k], which is first-order logic restricted to k variables. Since the relation algebra and \(\mathrm {FO[3]}\) path-subsume each other [12, 24], (i) follows. In Statement (ii), \(\mathcal {F}\subseteq \{ \mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi }\}\). Hence, by a result of Hellings et al. [18, Theorem 6.1], (ii) also follows.Footnote 3 To prove (iii), let \(\mathcal {T}= (\mathcal {V}, \varSigma , \mathbf {E})\) and \(\mathcal {T}' = (\mathcal {V}', \varSigma ', \mathbf {E}')\). Let \(n_1,n_2 \in \mathcal {V}\) be the siblings in \(\mathcal {T}\) such that \(\mathcal {T}'\) is obtained from \(\mathcal {T}\) by eliminating the subtree rooted at \(n_2\). Let \(\mathcal {V}_1\) and \(\mathcal {V}_2\) be the nodes in the subtrees of \(\mathcal {T}\) rooted at \(n_1\) and \(n_2\), respectively, and let \(b : \mathcal {V}_1 \rightarrow \mathcal {V}_2\) be a bijection establishing that these subtrees are isomorphic. Let g be the identity on \(\mathcal {V}-(\mathcal {V}_1 \cup \mathcal {V}_2)\), and let \(f = b \cup b^{-1}\cup g\). Since f is an automorphism of \(\mathcal {T}\), we have, for \(m,n\in \mathcal {V}\),  . By induction on the length of \(e\), one can prove that, if \((m, n) \in \mathcal {V}_1 \times \mathcal {V}_2\) or \((m, n) \in \mathcal {V}_2 \times \mathcal {V}_1\), then
. By induction on the length of \(e\), one can prove that, if \((m, n) \in \mathcal {V}_1 \times \mathcal {V}_2\) or \((m, n) \in \mathcal {V}_2 \times \mathcal {V}_1\), then  . Since \(f=f^{-1}\), it then also follows that, if \((m, n) \in \mathcal {V}_1 \times \mathcal {V}_2\) or \((m, n) \in \mathcal {V}_2 \times \mathcal {V}_1\), then
. Since \(f=f^{-1}\), it then also follows that, if \((m, n) \in \mathcal {V}_1 \times \mathcal {V}_2\) or \((m, n) \in \mathcal {V}_2 \times \mathcal {V}_1\), then  . A final induction on the length of \(e\) then yields that, for \(m', n' \in \mathcal {V}'\),
. A final induction on the length of \(e\) then yields that, for \(m', n' \in \mathcal {V}'\),  . Hence,
. Hence,  , \(\square \)
, \(\square \)
From the limitations imposed by Proposition 6 on the Boolean expressive power of the fragments considered, we deduce the following separation results:
Proposition 7
Already on unlabeled trees, we have \(\mathcal {N}(\mathrm {di}) \npreceq _{\mathrm {bool}}\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap )\), \(\mathcal {N}({}^{\mathord {-1}}, -)\) \(\npreceq _{\mathrm {bool}}\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap )\), and \(\mathcal {N}(\mathrm {di}, \cap ) \npreceq _{\mathrm {bool}}\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi })\).
Proof
Consider the unlabeled trees \(\mathcal {T}_1\), \(\mathcal {T}_2\), and \(\mathcal {T}_3\) in Example 5. Since \(\mathcal {T}_1\) can be obtained by a 1-subtree-reduction on \(\mathcal {T}_2\), we have, by Proposition 6(iii), that, for every \(e\) in \(\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap )\),  . Now consider \(e_1 = \mathcal {E}\circ \mathrm {di}\circ \mathrm {di}\circ \mathcal {E}\) in \(\mathcal {N}(\mathrm {di})\) and \(e_2 = (\smash {\mathcal {E}^{\mathord {-1}}} \circ \mathcal {E}) -\mathrm {id}\) in \(\mathcal {N}({}^{\mathord {-1}}, -)\). We have
. Now consider \(e_1 = \mathcal {E}\circ \mathrm {di}\circ \mathrm {di}\circ \mathcal {E}\) in \(\mathcal {N}(\mathrm {di})\) and \(e_2 = (\smash {\mathcal {E}^{\mathord {-1}}} \circ \mathcal {E}) -\mathrm {id}\) in \(\mathcal {N}({}^{\mathord {-1}}, -)\). We have  and
and  , while
, while  , establishing the first and second separations. Since \(\mathcal {T}_2\) can be obtained by a 2-subtree-reduction on \(\mathcal {T}_3\), we have, by Proposition 6(ii), that, for every \(e\) in \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi })\),
, establishing the first and second separations. Since \(\mathcal {T}_2\) can be obtained by a 2-subtree-reduction on \(\mathcal {T}_3\), we have, by Proposition 6(ii), that, for every \(e\) in \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi })\),  . Now consider \(e_3 = (((\mathrm {di}\circ \mathcal {E}) \cap \mathrm {di}) \circ ((\mathrm {di}\circ \mathcal {E}) \cap \mathrm {di})) \cap \mathrm {di}\) in \(\mathcal {N}(\mathrm {di}, \cap )\). We have
. Now consider \(e_3 = (((\mathrm {di}\circ \mathcal {E}) \cap \mathrm {di}) \circ ((\mathrm {di}\circ \mathcal {E}) \cap \mathrm {di})) \cap \mathrm {di}\) in \(\mathcal {N}(\mathrm {di}, \cap )\). We have  , while
, while  , establishing the third separation. \(\square \)
, establishing the third separation. \(\square \)
The proof of Proposition 7 relies on languages being able to distinguish at least one, two, or three structurally equivalent children of a node. To do so, the proof uses minimal languages that satisfy the conditions of Proposition 6. Hence, the classification provided by k-subtree-reductions is strict.
4 The Power of Diversity
Relation algebra expressions without diversity can only inspect a local neighborhood around a given node. With respect to path queries, this puts obvious limitations on the expressive power of language fragments that do not contain diversity. With respect to Boolean queries, the situation is more subtle. To study this in more detail, we first define the notion of locality:
Definition 8
Given a tree, and disregarding the direction of its edges, the distance between two nodes is the number of edges on the unique shortest path between them. A query \(q\) is local if there exists \(k\ge 0\) such that, for every tree \(\mathcal {T}\), and for all nodes m and n,  , with \(\mathcal {T}'\) the smallest subtree of \(\mathcal {T}\) containing all nodes at distance at most k from the nearest common ancestor of m and n.
, with \(\mathcal {T}'\) the smallest subtree of \(\mathcal {T}\) containing all nodes at distance at most k from the nearest common ancestor of m and n.
By an induction on their length, it can be shown that all expressions in \(\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -)\) are local.
4.1 Adding Diversity to Local Fragments
As already noticed, diversity always adds power to a local relation algebra fragment at the path level, as it can construct non-local relation algebra expressions. We can also use this property to our advantage to prove that diversity often adds expressive power at the Boolean level, too.
Proposition 9
Already on unlabeled trees, \(\mathcal {N}(\mathrm {di}, \cap ) \npreceq _{\mathrm {bool}}\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -)\).
Proof
By the rewrite rules at the end of Sect. 2, \(\mathcal {N}(\mathrm {di}, \pi , \cap ) \preceq _{\mathrm {path}}\mathcal {N}(\mathrm {di}, \cap )\). Consider the expression \(e= P_{2,\lnot r} \circ \mathrm {di}\circ P_{2,\lnot r}\) in which \(P_{2,\lnot r} = \pi _{2}[\mathcal {E}] \circ P_2\), \(P_2 = \pi _{1}[S_2]\), and \(S_2 = \left( \mathcal {E}\circ \mathrm {di}\right) \cap \mathcal {E}\). The expression \(e\) selects node pairs among distinct non-root nodes such that each node in the pair has at least two distinct children. Now, assume there exists an expression \(e'\) in \(\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -)\) such that \(e\equiv _{\mathrm {bool}}e'\). Since \(e'\) is local, we know there exists \(k\ge 0\) such that \(e'\) satisfies Definition 8. Now consider the trees \(\mathcal {T}\) and \(\mathcal {T}'\) shown in Fig. 4. Clearly,  and
and  . By \(e\equiv _{\mathrm {bool}}e'\), we must have
. By \(e\equiv _{\mathrm {bool}}e'\), we must have  . Let
. Let  . Since every subtree of \(\mathcal {T}\) containing all nodes at distance at most k from some given node is contained in a subtree of \(\mathcal {T}\) that is isomorphic to \(\mathcal {T}'\), we may conclude that
. Since every subtree of \(\mathcal {T}\) containing all nodes at distance at most k from some given node is contained in a subtree of \(\mathcal {T}\) that is isomorphic to \(\mathcal {T}'\), we may conclude that  . However,
. However,  , contradicting \(e\equiv _{\mathrm {bool}}e'\). Hence, no expression in \(\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -)\) is Boolean-equivalent to \(e\). \(\square \)
, contradicting \(e\equiv _{\mathrm {bool}}e'\). Hence, no expression in \(\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -)\) is Boolean-equivalent to \(e\). \(\square \)
Trees \(\mathcal {T}\) and \(\mathcal {T}'\) in the proof of Proposition 9. The symbol  represents a chain of k edges, with k as in that proof.
represents a chain of k edges, with k as in that proof.
We can use a similar locality argument for two more separations:
Proposition 10
Already on chains, we have \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}) \npreceq _{\mathrm {bool}}\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -)\) and \(\mathcal {N}(\mathrm {di}, \pi ) \npreceq _{\mathrm {bool}}\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -)\).
Proof
Consider the path-equivalent expressions \(e_1 = (\ell \circ \smash {\ell ^{\mathord {-1}}}) \circ \mathrm {di}\circ (\ell \circ \smash {\ell ^{\mathord {-1}}})\) in \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}})\) and \(e_2 = \pi _{1}[\ell ]\circ \mathrm {di}\circ \pi _{1}[\ell ]\) in \(\mathcal {N}(\mathrm {di}, \pi )\), and let \(e\) be either \(e_1\) or \(e_2\). Now, assume there exists an expression \(e'\) in \(\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -)\) such that \(e\equiv _{\mathrm {bool}}e'\). Since \(e'\) is local, we know there exists \(k\ge 0\) such that \(e'\) satisfies Definition 8. Now consider the chains \(\mathcal {C}\) and \(\mathcal {C}'\) shown in Fig. 5. Clearly,  . Hence,
. Hence,  . By \(e\equiv _{\mathrm {bool}}e'\), we must have
. By \(e\equiv _{\mathrm {bool}}e'\), we must have  . Let
. Let  . Notice that every subchain of \(\mathcal {C}\) containing all nodes at distance at most k from some given node is a subchain of \(\mathcal {C}\) of length at most 2k. Since each such subchain of \(\mathcal {C}\) is isomorphic to some subchain of \(\mathcal {C}'\), we may conclude that
. Notice that every subchain of \(\mathcal {C}\) containing all nodes at distance at most k from some given node is a subchain of \(\mathcal {C}\) of length at most 2k. Since each such subchain of \(\mathcal {C}\) is isomorphic to some subchain of \(\mathcal {C}'\), we may conclude that  . However,
. However,  , contradicting \(e\equiv _{\mathrm {bool}}e'\). Hence, no expression in \(\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -)\) is Boolean-equivalent to \(e\). \(\square \)
, contradicting \(e\equiv _{\mathrm {bool}}e'\). Hence, no expression in \(\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -)\) is Boolean-equivalent to \(e\). \(\square \)
Chains \(\mathcal {C}\) and \(\mathcal {C}'\) in the proof of Proposition 10. The symbol  represents a chain of 2k edges all labeled \(\ell '\), with k as in that proof.
represents a chain of 2k edges all labeled \(\ell '\), with k as in that proof.
Observe that the separation \(\mathcal {N}(\mathrm {di}, \cap ) \npreceq _{\mathrm {bool}}\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap ,-)\) also holds on chains, because the expression \(e_3 = (\ell \circ \mathrm {di}\cap \mathrm {id}) \circ \mathrm {di}\circ (\ell \circ \mathrm {di}\cap \mathrm {id})\) is path-equivalent to \(e_1\) and \(e_2\) in the proof of Proposition 10.
4.2 Adding Other Operators to Non-local Fragments
The erratic behavior of diversity in the non-local relation algebra fragments on trees (allowing one to jump from any node to any other node in a tree) makes studying the expressive power of these fragments inherently difficult. Luckily, we can obtain several separation results by studying these fragments on chains.
For local expressions on chains, we have the following:
Lemma 11
Let \(\mathcal {F}\subseteq \{ {}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -\}\), and \(e\) be a union-free expression in \(\mathcal {N}(\mathcal {F})\).Footnote 4 There exists \(k\ge 0\) such that, for every chain \(\mathcal {C}\),  or
or  .
.
Lemma 11 simplifies the reasoning about local expressions on chains. In addition, diversity on chains can be expressed using the ancestor axis and the descendant axis, as \(\mathrm {di}= [\mathcal {E}]^{\mathord {+}} \cup [\smash {\mathcal {E}^{\mathord {-1}}}]^{\mathord {+}}\). While the descendant and ancestor axes are not operators of the fragments considered in this paper, we can still use them in intermediate steps to rewrite expressions that contain \(\mathrm {di}\). This in turn allows us to simplify projection terms that contain \(\mathrm {di}\), as we show next.
Lemma 12
Let \(\mathcal {F}\subseteq \{ \mathrm {di}, {}^{\mathord {-1}}, \pi \}\) and \(\pi _{j}[e]\), \(j \in \{ 1, 2\}\), be an expression in \(\mathcal {N}(\mathcal {F})\). There exists a finite set S of expressions of the form \(\pi _{1}[\mathcal {E}^{v}]\circ \pi _{2}[\mathcal {E}^{w}]\), \(v, w\ge 0\), such that, on unlabeled chains, \(\pi _{j}[e] \equiv _{\mathrm {path}}\bigcup S\).
Proof
We have \(\mathrm {di}\equiv _{\mathrm {path}}[\mathcal {E}]^{\mathord {+}} \cup [\smash {\mathcal {E}^{\mathord {-1}}}]^{\mathord {+}}\). We also have \(\pi _{2}[e] \equiv _{\mathrm {path}}\pi _{1}[\smash {e^{\mathord {-1}}}]\). Hence, every projection expression \(\pi _{j}[e]\), \(j \in \{1,2\}\), can be written as a union of expressions of the form \(\pi _{1}[e']\) in which \(e'\) is built over the atoms \(\mathrm {id}\), \(\mathcal {E}\), \(\smash {\mathcal {E}^{\mathord {-1}}}\), \([\mathcal {E}]^{\mathord {+}}\), and \([\smash {\mathcal {E}^{\mathord {-1}}}]^{\mathord {+}}\), using the operators \(\circ \) and \(\pi _1\).Footnote 5 We shall call such expressions \(e'\) normal in the remainder of this proof. So, it remains to show that Lemma 12 holds for expressions \(\pi _{1}[e']\), with \(e'\) normal. We do this by structural induction on \(e'\). We have the following base cases:

Now, assume that Lemma 12 holds for expressions \(\pi _{1}[e'']\), with \(e''\) a normal expression containing at most i operators, \(i\ge 0\), and let \(e=\pi _{1}[e']\) with \(e'\) a normal expression containing \(i+1\) operators. Then either \(e'=\pi _{1}[e'_1]\) or \(e'=e'_1\circ e'_2\), with \(e'_1\) and \(e'_2\) normal expressions containing at most i operators. In the first case, \(e\equiv _{\mathrm {path}}\pi _{1}[e'_1]\), and Lemma 12 holds for \(e\) by the induction hypothesis. In the second case, we have that \(e=\pi _{1}[e'_1\circ e'_2]\equiv _{\mathrm {path}}\pi _{1}[e'_1\circ \pi _{1}[e'_2]]\). By the induction hypothesis, \(e'_2\) is path-equivalent to a finite union of expressions of the form \(\pi _{1}[\mathcal {E}^{v_2}]\circ \pi _{2}[\mathcal {E}^{w_2}]\), \(v_2,w_2\ge 0\). For \(e'_1\), we distinguish again two cases:
-
1.
Expression \(e'_1 = \pi _{1}[e''_1]\), with \(e''_1\) again a normal expression containing at most i operators. Hence, by the induction hypothesis, \(e'_1\) is path-equivalent to a finite union of expressions of the form \(\pi _{1}[\mathcal {E}^{v_1}]\circ \pi _{2}[\mathcal {E}^{w_1}]\), \(v_1,w_1\ge 0\). It now suffices to observe that
$$\begin{aligned} \pi _{1}[\mathcal {E}^{v_1}]\circ \pi _{2}[\mathcal {E}^{w_1}]\circ \pi _{1}[\mathcal {E}^{v_1}]\circ \pi _{2}[\mathcal {E}^{w_1}]\equiv _{\mathrm {path}}\pi _{1}[\mathcal {E}^{\max (v_1,v_2)}]\circ \pi _{2}[\mathcal {E}^{\max (w_1,w_2)}] \end{aligned}$$to conclude that Lemma 12 holds for \(e\).
-
2.
In the other case, we can assume without loss of generality that \(e'_1\) is an atom. Hence, it suffices to observe that, for \(v,w\ge 0\),

to conclude that Lemma 12 holds for \(e\) in this case, too. \(\square \)
Example 13
Consider the expression \(e= \pi _{1}[\mathrm {di}\circ \mathcal {E}\circ \mathcal {E}]\). We have
As Example 13 shows, we can use Lemma 12 to partially eliminate diversity from non-local expressions on unlabeled chains, and then use locality-based arguments on subexpressions to establish the following separations:
Proposition 14
Already on unlabeled chains, \(\mathcal {N}(\mathrm {di}, \cap ) \npreceq _{\mathrm {path}}\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi ), \mathcal {N}({}^{\mathord {-1}}) \npreceq _{\mathrm {path}}\mathcal {N}(\mathrm {di}, \pi )\), and \(\mathcal {N}(\pi ) \npreceq _{\mathrm {path}}\mathcal {N}(\mathrm {di})\).
Proof
Consider the expression \(e= (\mathrm {di}\circ \mathcal {E}) \cap \mathrm {di}\) in \(\mathcal {N}(\mathrm {di}, \cap )\). On a chain, this expression yields all pairs of distinct non-root nodes that are not edges. Now, assume there exists an expression \(e'\) in \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi )\) such that, on unlabeled chains, \(e\equiv _{\mathrm {path}}e'\). Since \(e\) is non-local, \(e'\) must be non-local, too, hence, it must contain diversity. Using Lemma 12, we can rewrite \(e'\) into a union of terms each of which is a composition of units of the form \(\mathrm {id}\), \(\mathrm {di}\), \(\mathcal {E}\), \(\smash {\mathcal {E}^{\mathord {-1}}}\), \(\pi _{1}[\mathcal {E}^v]\), or \(\pi _{2}[\mathcal {E}^w]\), \(v,w\ge 0\). Let \(t=t_1 \circ \cdots \circ t_n\) be such a term in which at least one unit is diversity (\(\mathrm {di}\)). Since on chains \(\mathrm {di}\equiv _{\mathrm {path}}[\mathcal {E}]^{\mathord {+}} \cup [\smash {\mathcal {E}^{\mathord {-1}}}]^{\mathord {+}}\), t is path-equivalent to the infinite union \(\bigcup _{k_1,\dots ,k_n\ne 0}\,t_{1k_1}\circ \cdots \circ t_{nk_n}\) in which \(t_{ik_i} = t_i\) if \(t_i\ne \mathrm {di}\) and \(t_{ik_i}=\mathcal {E}^{k_i}\) if \(t_i=\mathrm {di}\), \(1\le i\le n\). For a term \(t_{1k_1}\circ \cdots \circ t_{nk_n}\) in this infinite union, we define \(\exp (t_{1k_1}\circ \cdots \circ t_{nk_n})=\sum _{1\le i\le n}\exp (t_{ik_i})\), where \(\exp (t_{ik_i})=1\) if \(t_{ik_i}=\mathcal {E}\); \(\exp (t_{ik_i})=-1\) if \(t_{ik_i}=\smash {\mathcal {E}^{\mathord {-1}}}\); \(\exp (t_{ik_i})=k_i\) if \(t_{ik_i}=\mathcal {E}^{k_i}\); and \(\exp (t_{ik_i})=0\) otherwise. Since t contains at least one diversity unit, the set \(\{\exp (t_{1k_1}\circ \cdots \circ t_{nk_n})\mid k_1,\ldots ,k_n\ne 0\}\) covers all integer numbers with at most one exception (there is exactly one exception if t contains exactly one diversity unit). We can therefore choose a term \(t'=t_{1k_1}\circ \cdots \circ t_{nk_n}\) for which \(\exp (t')=0\) or \(\exp (t')=1\). Now, choose an unlabeled chain \(\mathcal {C}\) which is sufficiently long to ensure that for the local expression \(t'\) in \(\mathcal {N}({}^{\mathord {-1}}, \pi )\),  . Then,
. Then,  contains either an identical node pair (if \(\exp (t')=0\)) or an edge (if \(\exp (t')=1\)). Hence, by construction,
contains either an identical node pair (if \(\exp (t')=0\)) or an edge (if \(\exp (t')=1\)). Hence, by construction,  contains either an identical node pair or an edge, contradicting \(e\equiv _{\mathrm {path}}e'\). Hence, no expression in \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi )\) is path-equivalent to \(e\).
contains either an identical node pair or an edge, contradicting \(e\equiv _{\mathrm {path}}e'\). Hence, no expression in \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi )\) is path-equivalent to \(e\).
Using similar arguments, we can prove that \(\smash {\mathcal {E}^{\mathord {-1}}}\) cannot be expressed in \(\mathcal {N}(\mathrm {di}, \pi )\) and that \(\pi _{1}[\mathcal {E}]\) and \(\pi _{2}[\mathcal {E}]\) cannot be expressed in \(\mathcal {N}(\mathrm {di})\) to establish the other two statements of Proposition 14. \(\square \)
5 Brute-Force Results
Using a brute-force approach in the style of Fletcher et al. [10], we establish several separations, both at the path and Boolean levels. At the core of these brute-force results is the observation than one can effectively compute the set of query results obtainable by queries in some relation algebra fragment \(\mathcal {N}(\mathcal {F})\), \(\mathcal {F}\subseteq \{ \mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -\}\), on a given graph. We refer to Fletcher et al. [10] and Hellings [15] for further details.
For path separations between languages \(\mathcal {L}_1\) and \(\mathcal {L}_2\), we may conclude that \(\mathcal {L}_1\npreceq _{\mathrm {path}}\mathcal {L}_2\) if there exists a query \(q\) in \(\mathcal {L}_1\) and a tree \(\mathcal {T}\) such that no query in \(\mathcal {L}_2\) evaluates to  . Using this approach, we prove the following.
. Using this approach, we prove the following.
Proposition 15
Already on unlabeled trees, we have \(\mathcal {N}({}^{\mathord {-1}}) \npreceq _{\mathrm {path}}\mathcal {N}(\mathrm {di}, \pi , \overline{\pi })\) and \(\mathcal {N}(\pi ) \npreceq _{\mathrm {path}}\mathcal {N}({}^{\mathord {-1}})\).
Proof
Consider the expressions \(e_1 = \smash {\mathcal {E}^{\mathord {-1}}}\) and \(e_2 = \pi _{1}[\mathcal {E}] \circ \pi _{2}[\mathcal {E}]\), and let \(\mathcal {T}\) be the tree in Fig. 6. An exhaustive search reveals that no expression in \(\mathcal {N}(\mathrm {di}, \pi , \overline{\pi })\) evaluates to  and no expression in \(\mathcal {N}({}^{\mathord {-1}})\) evaluates to
and no expression in \(\mathcal {N}({}^{\mathord {-1}})\) evaluates to  . \(\square \)
. \(\square \)
The unlabeled tree \(\mathcal {T}\) in the proof of Proposition 15.
At the Boolean level, the key notion in the brute-force approach is the ability to distinguish a pair of trees. We say that a query \(q\) distinguishes a pair of trees \(\mathcal {T}_1\) and \(\mathcal {T}_2\) if  and
and  , or vice versa. Given two languages \(\mathcal {L}_1\) and \(\mathcal {L}_2\), we may conclude that \(\mathcal {L}_1\npreceq _{\mathrm {bool}}\mathcal {L}_2\) if we can find a query \(q\) in \(\mathcal {L}_1\) and a pair of trees \(\mathcal {T}_1\) and \(\mathcal {T}_2\), indistinguishable by any query in \(\mathcal {L}_2\), but distinguishable by \(q\). Using this approach, we prove the following.
, or vice versa. Given two languages \(\mathcal {L}_1\) and \(\mathcal {L}_2\), we may conclude that \(\mathcal {L}_1\npreceq _{\mathrm {bool}}\mathcal {L}_2\) if we can find a query \(q\) in \(\mathcal {L}_1\) and a pair of trees \(\mathcal {T}_1\) and \(\mathcal {T}_2\), indistinguishable by any query in \(\mathcal {L}_2\), but distinguishable by \(q\). Using this approach, we prove the following.
Proposition 16
Already on unlabeled trees, we have \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}) \npreceq _{\mathrm {bool}}\mathcal {N}(\mathrm {di})\), \(\mathcal {N}(\mathrm {di}, \pi ) \npreceq _{\mathrm {bool}}\mathcal {N}(\mathrm {di})\), \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \cap ) \npreceq _{\mathrm {bool}}\mathcal {N}(\mathrm {di}, \pi , \overline{\pi }, \cap , -)\), and \(\mathcal {N}(\mathrm {di}, \pi ) \npreceq _{\mathrm {bool}}\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}})\).
Proof
Consider the following four expressions:

and let \((\mathcal {T}_i,\mathcal {T}'_i)\), \(1\le i\le 4\), be the trees in Fig. 7. We have  and
and  , and
, and  and
and  . Observe that \(e_4\) is in \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi )\), but, by Proposition 34, \(e_4\) is Boolean-equivalent to an expression in \(\mathcal {N}(\mathrm {di}, \pi )\). An exhaustive search reveals that no expression in \(\mathcal {N}(\mathrm {di})\) can distinguish \(\mathcal {T}_1=\mathcal {T}_2\) from \(\mathcal {T}_1'=\mathcal {T}'_2\); no expression in \(\mathcal {N}(\mathrm {di}, \pi , \overline{\pi }, \cap , -)\) can distinguish \(\mathcal {T}_3\) from \(\mathcal {T}_3'\); and no expression in \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}})\) can distinguish \(\mathcal {T}_4\) from \(\mathcal {T}_4'\). \(\square \)
. Observe that \(e_4\) is in \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi )\), but, by Proposition 34, \(e_4\) is Boolean-equivalent to an expression in \(\mathcal {N}(\mathrm {di}, \pi )\). An exhaustive search reveals that no expression in \(\mathcal {N}(\mathrm {di})\) can distinguish \(\mathcal {T}_1=\mathcal {T}_2\) from \(\mathcal {T}_1'=\mathcal {T}'_2\); no expression in \(\mathcal {N}(\mathrm {di}, \pi , \overline{\pi }, \cap , -)\) can distinguish \(\mathcal {T}_3\) from \(\mathcal {T}_3'\); and no expression in \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}})\) can distinguish \(\mathcal {T}_4\) from \(\mathcal {T}_4'\). \(\square \)
Pairs of unlabeled trees \((\mathcal {T}_i, \mathcal {T}_i')\), \(1\le i\le 4\), in the proof of Proposition 16.
6 Collapse Results
In Sects. 3, 4, and 5, we focused on separation results. Here, we focus on collapse results. The key tool to prove these are what we call condition tree queries, a generalization of the tree queries of Wu et al. [26], which were used to prove Proposition 30 (see Sect. 7 on related work).
6.1 Condition Tree Queries
We first define condition tree queries syntactically and semantically:
Definition 17
A condition tree query is a tuple \(\mathcal {Q}= (\mathcal {T}, C, \mathsf {s}, \mathsf {t}, \gamma )\), where \(\mathcal {T}= (\mathcal {V}, \varSigma , \mathbf {E})\) is a tree, \(C\) is a set of node expressions that represent node conditions, \(\mathsf {s}\in \mathcal {V}\) is the source node, \(\mathsf {t}\in \mathcal {V}\) is the target node, and \(\gamma \subseteq \mathcal {V}\times C\) is the node-condition relation. We write \(\gamma (n)\) to denote the set \(\{c \mid (n, c) \in \gamma \}\).
Let \(\mathcal {T}' = (\mathcal {V}', \varSigma , \mathbf {E}')\) be a tree. Then,  consists of all the node pairs \((m,n)\in \mathcal {V}'\times \mathcal {V}'\) for which there exists a mapping \(f : \mathcal {V}\rightarrow \mathcal {V}'\) satisfying the following conditions:
consists of all the node pairs \((m,n)\in \mathcal {V}'\times \mathcal {V}'\) for which there exists a mapping \(f : \mathcal {V}\rightarrow \mathcal {V}'\) satisfying the following conditions:
-
(i)
\(f(\mathsf {s}) = m\) and \(f(\mathsf {t}) = n\);
-
(ii)
for all \(v \in \mathcal {V}\) and \(c \in \gamma (v)\),
 ; and
; and -
(iii)
for all \(\ell \in \varSigma \) and \((v, w) \in \mathbf {E}\left( \ell \right) \), \((f(v), f(w)) \in \mathbf {E}'\left( \ell \right) \).
We slightly extend Definition 17 to allow the empty condition tree where \(\mathcal {V}=\emptyset \) and \(\mathsf {s}\) and \(\mathsf {t}\) have some null value. On every tree, the empty condition tree evaluates to the empty set.
Example 18
The condition tree query \(\mathcal {Q}\) in Fig. 8 selects a node pair \((\mathsf {s},\mathsf {t})\) if the following tree traversal steps are all successful: (1) from \(\mathsf {s}\), go up via two edges labeled \(\ell _1\) and \(\ell _2\); (2) check if the node where we have arrived satisfies the condition \(\overline{\pi }_{2}[\ell _3]\); (3) from there, go down via two edges labeled \(\ell _3\), after which we arrive at \(\mathsf {t}\); and (4) check if \(\mathsf {t}\) has outgoing edges labeled \(\ell _1\) and \(\ell _2\). The condition tree query \(\mathcal {Q}\) is path-equivalent to the expression \(\smash {\ell _1^{\mathord {-1}}}\circ \smash {\ell _2^{\mathord {-1}}} \circ \overline{\pi }_{2}[\ell _3]\circ \ell _3\circ \ell _3\circ \pi _{1}[\ell _1]\circ \pi _{1}[\ell _2]\), in \(\mathcal {N}({}^{\mathord {-1}}, \overline{\pi })\).
The condition tree query of Example 18.
In the remainder of this subsection, we formalize the relationship between condition tree queries and relation algebra expressions exhibited in Example 18. Thereto, let \(\mathcal {F}\subseteq \{ {}^{\mathord {-1}}, \pi , \overline{\pi }\}\), and let \(\mathbf {Q}_{\mathrm {tree}}(\mathcal {F})\) be the class of all condition tree queries in which node conditions are restricted to union-free expressions in \(\mathcal {N}(\mathcal {F})\). We claim that, for \(\overline{\mathcal {F}} = \{{}^{\mathord {-1}},\pi \}\) or \(\overline{\mathcal {F}} = \{{}^{\mathord {-1}},\pi ,\overline{\pi }\}\), \(\mathbf {Q}_{\mathrm {tree}}(\mathcal {F})\) and the class of all union-free expressions in \(\mathcal {N}(\mathcal {F})\) path-subsume each other.
Using a straightforward rewriting argument, we can show the following:
Proposition 19
Let \(\mathcal {F}\subseteq \{ {}^{\mathord {-1}}, \pi , \overline{\pi }\}\), and \(e\) be a union-free expression in \(\mathcal {N}(\mathcal {F})\). There exists a condition tree query \(\mathcal {Q}\) in \(\mathbf {Q}_{\mathrm {tree}}(\mathcal {F})\) such that \(e\equiv _{\mathrm {path}}\mathcal {Q}\).
For the translation in the other direction, we introduce up-down queries:
Definition 20
An up-down query is a condition tree query \(\mathcal {Q}= (\mathcal {T}, C, \mathsf {s}, \mathsf {t}, \gamma )\) in which all edges of \(\mathcal {T}\) are on the unique path from \(\mathsf {s}\) to \(\mathsf {t}\) not taking into account the direction of the edges.
Example 21
An up-down query can look like a chain if the target node is an ancestor of the source node, or vice versa, as illustrated by Fig. 9, left. This up-down query is path-equivalent to \(\overline{\pi }_{2}[\ell _3] \circ \smash {\ell _2^{\mathord {-1}}} \circ \smash {\ell _1^{\mathord {-1}}}\). The condition tree query in the middle is not up-down, but is path-equivalent to the up-down tree query on the right. Observe that the right query is obtained by pushing the parts of the tree traversal described by the middle query that are not on the path from source to target into node conditions. The middle and right queries are path-equivalent to \(\pi _{1}[\ell _2 \circ \overline{\pi }_{2}[\ell _3]]\circ \smash {\ell _1^{\mathord {-1}}}\circ \pi _{2}[\ell _3]\circ \ell _2\circ \pi _{1}[\ell _2]\circ \ell _1\).
As illustrated in Example 21, we can rewrite a condition tree query to an up-down query by pushing into node conditions those parts of the condition tree query not on the path from source to target:
Lemma 22
Let \(\{\pi \} \subseteq \overline{\mathcal {F}} \subseteq \{ {}^{\mathord {-1}}, \overline{\pi }, \pi \}\), and \(\mathcal {Q}\) be a condition tree query in \(\mathbf {Q}_{\mathrm {tree}}(\mathcal {F})\). There exists an up-down query \(\mathcal {Q}'\) in \(\mathbf {Q}_{\mathrm {tree}}(\mathcal {F})\) such that \(\mathcal {Q}\equiv _{\mathrm {path}}\mathcal {Q}'\).
As also illustrated in Example 21, an up-down query can be translated straightforwardly into a path-equivalent relation algebra expression, provided we have the converse operator (\({}^{\mathord {-1}}\)) at our disposal:
Lemma 23
Let \(\{{}^{\mathord {-1}}\} \subseteq \mathcal {F}\subseteq \{ {}^{\mathord {-1}}, \overline{\pi }, \pi \}\), and \(\mathcal {Q}\) be an up-down query in \(\mathbf {Q}_{\mathrm {tree}}(\mathcal {F})\). There exists a union-free expression e in \(\mathcal {N}(\mathcal {F})\) such that \(\mathcal {Q}\equiv _{\mathrm {path}}e\).
Finally, combining Lemmas 22 and 23 yields the following:
Proposition 24
Let \(\{{}^{\mathord {-1}},\pi \}\subseteq \overline{\mathcal {F}}\subseteq \{{}^{\mathord {-1}},\pi ,\overline{\pi }\}\), and \(\mathcal {Q}\) be a condition tree query in \(\mathbf {Q}_{\mathrm {tree}}(\mathcal {F})\). There exists a union-free expression in \(\mathcal {N}(\mathcal {F})\) such that \(\mathcal {Q}\equiv _{\mathrm {path}}e\).
6.2 Adding Intersection to Local Fragments
Hellings et al. [16, 17] already proved that adding intersection to local relation algebra fragments not containing the converse operator (the downward relation algebra fragments) never increases their expressive power (Proposition 31). Here, we show that this result actually holds for all local relation algebra fragments. As a first step, consider the following example:
Example 25
Suppose we want to compute the intersection of the two up-down queries in Fig. 10, left. Since the two up-down queries have different heights, a pair of nodes of a tree can only be in the result of the intersection of the two queries on that tree if the children of the root of the second query are mapped to the same node. Hence, we can replace the second up-down query by the one shown in the middle. Since both queries now have the same shape and corresponding edges have the same label, the intersection is easily obtained by merging the node conditions, resulting in the up-down query on the right.
We now generalize Example 25:
Proposition 26
Let \(\{ \pi \} \subseteq \overline{\mathcal {F}} \subseteq \{ {}^{\mathord {-1}}, \pi , \overline{\pi }\}\), and \(\mathcal {Q}_1\) and \(\mathcal {Q}_2\) be condition tree queries in \(\mathbf {Q}_{\mathrm {tree}}(\mathcal {F})\). There exists a condition tree query \(\mathcal {Q}\) in \(\mathbf {Q}_{\mathrm {tree}}(\mathcal {F})\) such that, for every tree \(\mathcal {T}\),  .
.
Up-down queries \(\mathcal {Q}_1\), \(\mathcal {Q}_2\), \(\mathcal {Q}'_2\) and \(\mathcal {Q}\) in the proof of Proposition 26.
Proof
(sketch). By Lemma 22, we may assume that \(\mathcal {Q}_1 = (\mathcal {T}_1, C_1, \mathsf {s}_1, \mathsf {t}_1, \gamma _1)\) and \(\mathcal {Q}_2 = (\mathcal {T}_2, C_2, \mathsf {s}_2, \mathsf {t}_2, \gamma _2)\) are up-down queries as in Fig. 11. Let \(\mathcal {T}'\) be an arbitrary tree. If \(u_2-d_2\ne u_1-d_1\), then, obviously  . Thus, assume \(u_2-d_2= u_1-d_1\), or, equivalently, \(u_2-u_1=d_2-d_1\). We distinguish two cases:
. Thus, assume \(u_2-d_2= u_1-d_1\), or, equivalently, \(u_2-u_1=d_2-d_1\). We distinguish two cases:
-
1.
\(u_1\ne u_2\). By symmetry, assume \(u_2>u_1\). We write \(\varDelta =u_2-u_1=d_2-d_1\). To find a pair of nodes of \(\mathcal {T}'\) common to
 and
and  , it is imperative that for all i, \(1\le i\le \varDelta \), \(m_{2,i}\) and \(n_{2,i}\) are mapped to the same node of \(\mathcal {T}\). Hence, if for some i, \(1\le i\le \varDelta \), \(\ell _{\mathsf {s}_{2,i}}\ne \ell _{\mathsf {t}_{2,i}}\),
, it is imperative that for all i, \(1\le i\le \varDelta \), \(m_{2,i}\) and \(n_{2,i}\) are mapped to the same node of \(\mathcal {T}\). Hence, if for some i, \(1\le i\le \varDelta \), \(\ell _{\mathsf {s}_{2,i}}\ne \ell _{\mathsf {t}_{2,i}}\), 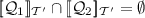 . Thus, assume for all i, \(1\le i\le \varDelta \), that \(\ell _{\mathsf {s}_{2,i}}=\ell _{\mathsf {t}_{2,i}}\). Then,
. Thus, assume for all i, \(1\le i\le \varDelta \), that \(\ell _{\mathsf {s}_{2,i}}=\ell _{\mathsf {t}_{2,i}}\). Then, 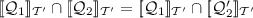 , where \(\mathcal {Q}'_2 =(\mathcal {T}'_2, C'_2, \mathsf {s}'_2, \mathsf {t}'_2, \gamma '_2)\) is as in Fig. 11, with $$\begin{aligned} \gamma '_2(r'_2)&= \pi _{2}[\gamma _2(r_2)\circ \ell _{\mathsf {s}_{2,1}}\circ \gamma _2(m_{2,1})\circ \gamma _2(n_{2,1})\circ \cdots \circ \ell _{\mathsf {s}_{2,\varDelta }}\circ \gamma _2(m_{2,\varDelta })\circ \gamma _2(n_{2,\varDelta })], \end{aligned}$$
, where \(\mathcal {Q}'_2 =(\mathcal {T}'_2, C'_2, \mathsf {s}'_2, \mathsf {t}'_2, \gamma '_2)\) is as in Fig. 11, with $$\begin{aligned} \gamma '_2(r'_2)&= \pi _{2}[\gamma _2(r_2)\circ \ell _{\mathsf {s}_{2,1}}\circ \gamma _2(m_{2,1})\circ \gamma _2(n_{2,1})\circ \cdots \circ \ell _{\mathsf {s}_{2,\varDelta }}\circ \gamma _2(m_{2,\varDelta })\circ \gamma _2(n_{2,\varDelta })], \end{aligned}$$in which \(\gamma _2(v)\) is a shorthand for the composition of the node expressions in \(\gamma (v)\).Footnote 6 For all other nodes \(v'\) of \(\mathcal {T}'_2\), \(\gamma '_2(v')=\gamma _2(v)\), v being the node of \(\mathcal {T}_2\) corresponding to \(v'\). Notice that the left (an hence also the right) branches of \(\mathcal {Q}_1\) and \(\mathcal {Q}'_2\) have equal length, which allows us to apply the next case on \(\mathcal {Q}_1\) and \(\mathcal {Q}'_2\).
-
2.
\(u_1=u_2=u\), and hence \(d_1=d_2=d\). To find a pair of nodes of \(\mathcal {T}'\) common to
 and
and  , it is imperative that corresponding nodes of \(\mathcal {T}_1\) and \(\mathcal {T}_2\) are mapped to the same node of \(\mathcal {T}'\). Hence, if for some i, \(1\le i\le u\), \(\ell _{\mathsf {s}_{1,i}}\ne \ell _{\mathsf {s}_{2,i}}\), or for some j, \(1\le j\le d\), \(\ell _{\mathsf {t}_{1,i}}\ne \ell _{\mathsf {t}_{2,i}}\),
, it is imperative that corresponding nodes of \(\mathcal {T}_1\) and \(\mathcal {T}_2\) are mapped to the same node of \(\mathcal {T}'\). Hence, if for some i, \(1\le i\le u\), \(\ell _{\mathsf {s}_{1,i}}\ne \ell _{\mathsf {s}_{2,i}}\), or for some j, \(1\le j\le d\), \(\ell _{\mathsf {t}_{1,i}}\ne \ell _{\mathsf {t}_{2,i}}\),  . Thus, assume for all i, \(1\le i\le u\), that \(\ell _{\mathsf {s}_{1,i}}=\ell _{\mathsf {s}_{2,i}}=\ell _{\mathsf {s}_i}\), and, for all j, \(1\le j\le d\), that \(\ell _{\mathsf {t}_{1,i}}=\ell _{\mathsf {t}_{2,i}}=\ell _{\mathsf {t}_i}\). Then,
. Thus, assume for all i, \(1\le i\le u\), that \(\ell _{\mathsf {s}_{1,i}}=\ell _{\mathsf {s}_{2,i}}=\ell _{\mathsf {s}_i}\), and, for all j, \(1\le j\le d\), that \(\ell _{\mathsf {t}_{1,i}}=\ell _{\mathsf {t}_{2,i}}=\ell _{\mathsf {t}_i}\). Then,  , where \(\mathcal {Q}=(\mathcal {T}, C_1\cup C_2, \mathsf {s}, \mathsf {t}, \gamma )\) is as in Fig. 11, where, for all nodes v of \(\mathcal {T}\), \(\gamma (v)=\gamma _1(v_1)\circ \gamma _2(v_2)\), \(v_1\) and \(v_2\) being the nodes of \(\mathcal {T}_1\) and \(\mathcal {T}_2\) corresponding to v. \(\square \)
, where \(\mathcal {Q}=(\mathcal {T}, C_1\cup C_2, \mathsf {s}, \mathsf {t}, \gamma )\) is as in Fig. 11, where, for all nodes v of \(\mathcal {T}\), \(\gamma (v)=\gamma _1(v_1)\circ \gamma _2(v_2)\), \(v_1\) and \(v_2\) being the nodes of \(\mathcal {T}_1\) and \(\mathcal {T}_2\) corresponding to v. \(\square \)
Propositions 19, 24, and 26 now yield the following:
Proposition 27
For \(\{{}^{\mathord {-1}},\pi \}\subseteq \overline{\mathcal {F}} \subseteq \{ {}^{\mathord {-1}}, \pi , \overline{\pi },\cap \}\), \(\mathcal {N}(\mathcal {F}) \preceq _{\mathrm {path}}\mathcal {N}(\mathcal {F}-\{\cap \})\).
6.3 The Boolean Equivalence of Projection and Converse
From a result by Fletcher et al. [10, 11] (Proposition 34 in Sect. 7 on related work), it follows that \(\mathcal {N}({}^{\mathord {-1}}) \preceq _{\mathrm {bool}}\mathcal {N}(\pi )\). Here, we also prove the other direction:
Proposition 28
\(\mathcal {N}(\pi ) \preceq _{\mathrm {bool}}\mathcal {N}({}^{\mathord {-1}})\).
Proof
Let e be an expression in \(\mathcal {N}(\pi )\). By a result of Wu et al. [26, Theorem 4.1], there exists a condition-free condition tree query \(\mathcal {Q}=(\mathcal {T},C,\mathsf {s},\mathsf {t},\gamma )\) in \(\mathbf {Q}_{\mathrm {tree}}()\) such that \(e\equiv _{\mathrm {path}}\mathcal {Q}\).Footnote 7 Let r be the root of \(\mathcal {T}\), and \(\mathcal {Q}_r=(\mathcal {T},C,r,r,\gamma )\). Obviously, \(\mathcal {Q}\equiv _{\mathrm {bool}}\mathcal {Q}_r\). Because the target node is now the root of \(\mathcal {T}\), the translation from \(\mathcal {Q}_r\) to a path-equivalent up-down query (Lemma 22) only requires the first projection. Hence, there exists an up-down query \(\mathcal {Q}'_r=(\mathcal {T}',C',r',r',\gamma ')\) in \(\mathbf {Q}_{\mathrm {tree}}(\pi _1)\) such that \(\mathcal {Q}_r\equiv _{\mathrm {path}}\mathcal {Q}'_r\). Since source and target coincide in \(\mathcal {T}'\), \(r'\) is necessarily the only node of \(\mathcal {T}'\). Hence, \(\mathcal {Q}'_r\) is path equivalent to the composition of the node expressions in \(\gamma (r')\), which is in \(\mathcal {N}(\pi _1)\). Now, a projection expression in \(\mathcal {N}(\pi _1)\) can always be rewritten in the form \(\pi _{1}[e]=\pi _{1}[\ell _1\circ \pi _{1}[e_1]\circ \cdots \ell _n\circ \pi _{1}[e_n]]\), with \(e_1,\ldots ,e_n\) in \(\mathcal {N}(\pi _1)\), which is equivalent to \(e\circ \smash {\ell _n^{\mathord {-1}}} \circ \cdots \circ \smash {\ell _1^{\mathord {-1}}}\). By applying this rewriting top-down, we conclude that \(\mathcal {N}(\pi _1)\preceq _{\mathrm {path}}\mathcal {N}({}^{\mathord {-1}})\). \(\square \)
Hence, \(\mathcal {N}(\pi )\) and \(\mathcal {N}({}^{\mathord {-1}})\) are Boolean-equivalent in expressive power.
7 Related Work
Results on node-labeled trees are usually straightforward to translate to the edge-labeled trees we use. Benedikt et al. [3] studied path-equivalence of \(\mathcal {N}({}^{\mathord {-1}}, \pi )\) and its fragments on labeled trees:
Proposition 29
([3, Proposition 2.1]). For \(\mathcal {F}_1,\mathcal {F}_2\!\subseteq \!\{{}^{\mathord {-1}},\pi \}\), \(\mathcal {N}(\mathcal {F}_1)\preceq _{\mathrm {path}}\mathcal {N}(\mathcal {F}_2)\!\!\iff \!\!\mathcal {F}_1\!\subseteq \!\mathcal {F}_2\).
Where applicable, we generalize Proposition 29 to Boolean separation, in Sect. 5. Wu et al. [26] proved a collapse result for relation algebra fragments with intersection:Footnote 8
Proposition 30
([26, Theorem 4.1]). Both \(\mathcal {N}({}^{\mathord {-1}}, \pi , \cap ) \preceq _{\mathrm {path}}\mathcal {N}({}^{\mathord {-1}}, \pi )\) and \(\mathcal {N}({}^{\mathord {-1}}, \pi , \cap ) \preceq _{\mathrm {path}}\mathcal {N}({}^{\mathord {-1}}, \cap )\).
In Sect. 6, we generalize Proposition 30 to also include coprojections.
Finally, Hellings et al. [16, 17] studied the relative expressiveness of the fragments of \(\mathcal {N}(\pi , \overline{\pi }, \cap , -)\),Footnote 9 and obtained the following results which are used in this study:
Proposition 31
([16, Theorem 3]). For \(\mathcal {F}\subseteq \{\pi ,\overline{\pi },\cap ,-\}\), \(\mathcal {N}(\mathcal {F})\preceq _{\mathrm {path}}\mathcal {N}(\overline{\mathcal {F}}-\{\cap , -\})\).
Proposition 32
([17, Proposition 10]). On unlabeled chains, \(\mathcal {N}(\mathrm {di}) \npreceq _{\mathrm {path}}\mathcal {N}(\pi , \overline{\pi }, \cap , -)\) and \(\mathcal {N}({}^{\mathord {-1}}) \npreceq _{\mathrm {path}}\mathcal {N}(\pi , \overline{\pi }, \cap , -)\).
Proposition 33
([17, Propositions 19 and 21]). We have \(\mathcal {N}(\pi ) \npreceq _{\mathrm {bool}}\mathcal {N}()\), \(\mathcal {N}({}^{\mathord {-1}}) \npreceq _{\mathrm {bool}}\mathcal {N}()\), and \(\mathcal {N}(\overline{\pi }) \npreceq _{\mathrm {bool}}\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi , \cap )\).
The graph query results of Fletcher et al. [10, 11] include many separation results of which the proofs do not specialize to trees. They also proved a collapse result, that automatically does hold on trees:
Proposition 34
([11, Proposition 4.2]). Let \(\mathcal {F}\subseteq \{ \mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi }\}\). On labeled and unlabeled graphs, we have \(\mathcal {N}(\mathcal {F}\cup \{ {}^{\mathord {-1}}\}) \preceq _{\mathrm {bool}}\mathcal {N}(\mathcal {F}\cup \{ \pi \})\).
Several other well-known expressiveness results are known in the context of Conditional XPath and Navigational XPath [6, 22, 23], which are strongly related to the relation algebra. Unfortunately, these results are proved with respect to the sibling-ordered tree data model, and do not apply to our unordered tree data model. We observe that on chains, no sibling relation exists. Hence, the separation results we have proved on chains translate to separation results in the sibling-ordered tree data model.
Index to the separation and collapse results discussed in this paper. Let \((\mathcal {N}(\mathcal {F}), \textit{op})\) be a field in the “z semantics” part of the table, \(z \in \{ {\mathrm {bool}}, {\mathrm {path}}\}\). A check mark ✓ in the field \((\mathcal {N}(\mathcal {F}), \textit{op})\) means that \(\mathcal {N}(\mathcal {F}\cup \{ \textit{op} \}) \preceq _z \mathcal {N}(\mathcal {F})\). A cross ✗ in the field \((\mathcal {N}(\mathcal {F}), \textit{op})\) means that \(\mathcal {N}(\mathcal {F}\cup \{ \textit{op} \}) \npreceq _z \mathcal {N}(\mathcal {F})\). Finally, a question mark \(\mathbf ? \) indicates an open problem.
8 Conclusion and Future Work
In this paper, we settled the relative expressive power of queries in fragments of the relation algebra when used to query trees. A summary of our results can be found in Fig. 12. To compensate for the limited flexibility of the tree data model, compared to the graph data model, we needed to develop several new techniques to make this study feasible. For the local fragments, i.e., fragments of \(\mathcal {N}({}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -)\), we provided a complete characterization of their relative expressive power, and with respect to the non-local fragments, only one challenging problem remains open:
Problem 35
Let \(\{ \mathrm {di}, \overline{\pi }, \cap \} \subseteq \mathcal {F}\subseteq \{ \mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi }, \cap \}\) and let \(z \in \{ {\mathrm {bool}}, {\mathrm {path}}\}\). Do we have \(\mathcal {N}(\mathcal {F}\cup \{ -\}) \preceq _z \mathcal {N}(\mathcal {F})\) or not?
The difficulties in solving this open problem are manifold. For example, consider the language \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi }, \cap )\). In this fairly rich query language, there are several instances of expressions for which one can express the complement. For \(k>0\), we have, e.g., \(\overline{\mathcal {E}^{-k}} \equiv _{\mathrm {path}}(\mathcal {E}^{-k} \circ \mathrm {di}) \cup (\overline{\pi }_{1}[\mathcal {E}^{-k}] \circ \mathrm {all})\). Unfortunately, we have not been able yet to express complement in every instance or been able to prove that expressing the complement is impossible in some instances. Additional difficulties arise from the fact that we can prove that a possible separation between \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi }, \cap )\) and \(\mathcal {N}(\mathrm {di}, {}^{\mathord {-1}}, \pi , \overline{\pi }, \cap , -)\) cannot be established on a single pair of trees, ruling out the applicability of brute-force techniques and many techniques developed in our work. Hence, we definitely face a challenging open problem, which we hope to solve in the future.
Another interesting direction for future work is augmenting the relation algebra with operators beyond the expressive power of \(\mathrm {FO[3]}\). Possible candidates would be an iteration construct such as an ancestor-descendant axis, or the more general and powerful Kleene-star transitive closure operator.
Notes
- 1.
The basic atoms and operators, \(\emptyset \), \(\ell \in \varSigma \), \(\mathrm {id}\), \(\circ \), and \(\cup \) are left implicit because they are assumed to be present in every fragment.
- 2.
The 1-subtree reductions bear a close relationship to the F+B-index and the F&B-index used for indexing the structure of tree data [20].
- 3.
Notice that in the formalism of Hellings et al. [18], projection is considered to be a standard operator.
- 4.
Observe that, in relation algebra expressions, unions can always be pushed out to the outermost level.
- 5.
Recall from Sect. 2 that we need to consider converse only at the level of edges.
- 6.
Observe that the composition of node expressions is associative and that this composition is path-equivalent to the intersection of node expressions.
- 7.
Recall that the tree queries in Wu et al. [26] are essentially the same as the condition-free condition tree queries in this paper.
- 8.
Strictly speaking, they deal with union-free expressions, but since unions can always be pushed out to the outermost level, this is not a real restriction.
- 9.
These are generally referred to as the downward fragments of the relation algebra.
References
Barceló, P.: Querying graph databases. In: Proceedings 32nd Symposium on Principles of Database Systems, pp. 175–188. ACM (2013)
Barceló, P., Pérez, J., Reutter, J.L.: Relative expressiveness of nested regular expressions. In: Proceedings of 6th Alberto Mendelzon International Workshop on Foundations of Data Management, pp. 180–195. CEUR Workshop Proceedings (2012)
Benedikt, M., Fan, W., Kuper, G.: Structural properties of XPath fragments. Theor. Comput. Sci. 336(1), 3–31 (2005)
Benedikt, M., Koch, C.: XPath leashed. ACM Comput. Surv. 41(1), 3:1–3:54 (2009)
Bray, T., Paoli, J., Sperberg-McQueen, C.M., Maler, E., Yergeau, F., Cowan, J.: Extensible Markup Language (XML) 1.1 (Second Edition). W3C Recommendation, W3C (2006). http://www.w3.org/TR/2006/REC-xml11-20060816
ten Cate, B.: The expressivity of XPath with transitive closure. In: Proceedings of 25th Symposium on Principles of Database Systems, pp. 328–337. ACM (2006)
Clark, J., DeRose, S.: XML Path Language (XPath) Version 1.0. W3C Recommendation, W3C (1999). http://www.w3.org/TR/1999/REC-xpath-19991116
Cruz, I.F., Mendelzon, A.O., Wood, P.T.: A graphical query language supporting recursion. In: Proceedings of 1987 ACM SIGMOD International Conference on Management of Data, pp. 323–330. ACM, New York (1987)
Ecma International: The JSON data interchange format, 1st Edition (2013). http://www.ecma-international.org/publications/standards/Ecma-404.htm
Fletcher, G.H.L., Gyssens, M., Leinders, D., Van den Bussche, J., Van Gucht, D., Vansummeren, S., Wu, Y.: Relative expressive power of navigational querying on graphs. In: Proceedings of 14th International Conference on Database Theory, pp. 197–207. ACM (2011)
Fletcher, G.H.L., Gyssens, M., Leinders, D., Surinx, D., Van den Bussche, J., Van Gucht, D., Vansummeren, S., Wu, Y.: Relative expressive power of navigational querying on graphs. Inform. Sci. 298, 390–406 (2015)
Givant, S.: The calculus of relations as a foundation for mathematics. J. Autom. Reason. 37(4), 277–322 (2006)
Grädel, E., Otto, M.: On logics with two variables. Theor. Comput. Sci. 224(1–2), 73–113 (1999)
Grohe, M.: Finite variable logics in descriptive complexity theory. Bull. Symb. Logic 4, 345–398 (1998)
Hellings, J.: On Tarski’s Relation Algebra: querying trees and chains and the semi-join algebra. Ph.D. thesis, Hasselt University and Transnational University of Limburg (2018)
Hellings, J., Gyssens, M., Wu, Y., Van Gucht, D., Van den Bussche, J., Vansummeren, S., Fletcher, G.H.L.: Relative expressive power of downward fragments of navigational query languages on trees and chains. In: Proceedings of 15th Symposium on Database Programming Languages, pp. 59–68 (2015)
Hellings, J., Gyssens, M., Wu, Y., Van Gucht, D., Van den Bussche, J., Vansummeren, S., Fletcher, G.H.L.: Comparing downward fragments of the relational calculus with transitive closure on trees. Technical report. Hasselt University (2018). https://arxiv.org/abs/1803.01390
Hellings, J., Pilachowski, C.L., Van Gucht, D., Gyssens, M., Wu, Y.: From relation algebra to semi-join algebra: an approach for graph query optimization. In: Proceedings of 16th International Symposium on Database Programming Languages, pp. 5:1–5:10 (2017)
Hidders, J., Paredaens, J., Van den Bussche, J.: J-logic: logical foundations for JSON querying. In: Proceedings of 36th Symposium on Principles of Database Systems, pp. 137–149 (2017)
Kaushik, R., Bohannon, P., Naughton, J.F., Korth, H.F.: Covering indexes for branching path queries. In: Proceedings of 2002 ACM SIGMOD International Conference on Management of Data, pp. 133–144. ACM (2002)
Libkin, L.: Elements of Finite Model Theory. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-662-07003-1
Marx, M.: Conditional XPath. ACM Trans. Database Syst. 30(4), 929–959 (2005)
Marx, M., de Rijke, M.: Semantic characterizations of navigational XPath. SIGMOD Rec. 34(2), 41–46 (2005)
Tarski, A.: On the calculus of relations. J. Symb. Log. 6(3), 73–89 (1941)
Tsichritzis, D.C., Lochovsky, F.H.: Hierarchical data-base management: a survey. ACM Comput. Surv. 8(1), 105–123 (1976)
Wu, Y., Van Gucht, D., Gyssens, M., Paredaens, J.: A study of a positive fragment of path queries: expressiveness, normal form and minimization. Comput. J. 54(7), 1091–1118 (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Hellings, J., Wu, Y., Gyssens, M., Van Gucht, D. (2018). The Power of Tarski’s Relation Algebra on Trees. In: Ferrarotti, F., Woltran, S. (eds) Foundations of Information and Knowledge Systems. FoIKS 2018. Lecture Notes in Computer Science(), vol 10833. Springer, Cham. https://doi.org/10.1007/978-3-319-90050-6_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-90050-6_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-90049-0
Online ISBN: 978-3-319-90050-6
eBook Packages: Computer ScienceComputer Science (R0)





 . One the one hand, one can show that the query language
. One the one hand, one can show that the query language 







 ; and
; and



 and
and  , it is imperative that for all i,
, it is imperative that for all i, 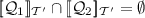 . Thus, assume for all i,
. Thus, assume for all i, 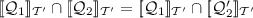 , where
, where  and
and  , it is imperative that corresponding nodes of
, it is imperative that corresponding nodes of  . Thus, assume for all i,
. Thus, assume for all i,  , where
, where 