Keywords

1 Introduction

In a couple of recent papers of Bodnar and Bodnar on the estimation of the efficient frontier of a portfolio of risky assets [1, 2], the Authors prove that the sample estimator of such a frontier is biased and provide, under proper but questionable hypotheses, an analytical expression for its unbiased estimator. Furthermore, they highlight that the sample estimator of the efficient frontier is overoptimistic, in the sense that the latter systematically underestimates the variance of each efficient portfolio.

In this contribution: first, we study the behavior of the unbiased estimator of the efficient frontier when the length of the return time series tends to infinity; then, we investigate a “strange” behavior of the same unbiased estimator in correspondence of particular combinations of the means of the returns of the assets and of their variances and covariances with respect to the number of the assets and the length of the associated time series of returns; finally, we analyze the operational effectiveness of the proposed unbiased estimator by a bootstrap-based approach.

The remainder of this note is organized as follows. In the next section, we synthetically present the model of O. Bodnar and T. Bodnar. In Sect. 3, we provide our main results.

2 Unbiased Estimator of the Efficient Frontier

The unbiased estimator of the efficient frontier proposed by Bodnar and Bodnar [2] is based on the following hypotheses:

  1. 1.

    All the considered K > 2 assets are risky;

  2. 2.

    The returns of these assets are serial independent;

  3. 3.

    The returns of these assets are normally distributed;

  4. 4.

    Indicated by N the length of the return time series, N > K.

Note that, without entering into detailed discussion, there exists an extensive literature following which the hypotheses (2) and (3) do not appear particularly realistic.

Given these hypotheses, the Authors prove that the following sample estimator of the efficient frontier is biased:

$$\displaystyle \begin{aligned} BEF \mathrel{\mathop:}= \left( R - \hat{R}_{GMV} \right)^2 - \hat{s}\left( V - \hat{V}_{GMV} \right)^2 = 0 \end{aligned}$$

where

  • R is the expected return of the portfolio,

  • \(\hat {R}_{GMV}\) is the sample estimate of the expected return of the global minimum variance portfolio,

  • \(\hat {s} = \hat {\boldsymbol {\mu }}' \hat {\boldsymbol {R}} \hat {\boldsymbol {\mu }}\), in which: \(\hat {\boldsymbol {\mu }}\) is the vector of the sample estimates of the expected rates of return of the assets; \(\hat {\boldsymbol {R}} = \hat {\boldsymbol {\varSigma }}^{-1} - \Big (\hat {\boldsymbol {\varSigma }}^{-1} {\boldsymbol 1}' {\boldsymbol 1} \hat {\boldsymbol {\varSigma }}^{-1}\Big ) \left / \Big ({\boldsymbol 1}' \hat {\boldsymbol {\varSigma }}^{-1} {\boldsymbol 1}\Big ) \right .\), where \(\hat {\boldsymbol {\varSigma }}\) is the matrix of the sample estimates of the variances and of the covariances of the rates of return, and 1 is a vector of ones,

  • V  is the variance of the return of the portfolio,

  • \(\hat {V}_{GMV}\) is the sample estimate of the variance of the return of the global minimum variance portfolio.

Then, under the same conditions, the Authors provide the following expression for the unbiased estimator of the efficient frontier:

$$\displaystyle \begin{aligned}UEF \mathrel{\mathop:}= \left( R - \hat{R}_{GMV} \right)^2 - A \cdot \hat{V}_{GMV} - \left( B \cdot \hat{s} - C \right) \left( V - D \cdot \hat{V}_{GMV} \right)^2 = 0 \end{aligned}$$

where

  • \(A = [(n-2)(n-1)] \left / [(n-k)(n-k+1)n] \right .\),

  • \(B = (n-k-1) \left / [(n-k)(n-1)] \right .\),

  • \(C = (k-1) \left / n \right .\),

  • \(D = [(n-k-2)(n-1)] \left / [(n-k)(n-k+1)] \right .\).

Finally, the Authors present an empirical application in which they consider time series of monthly returns from the equity markets of ten developed countries. Note that for these monthly returns, the above hypotheses (2) and (3) seem acceptable.

3 Our Main Results

With respect to the framework described above, in this section we present our main results.

3.1 The Asymptotic Behavior of the Biased Estimator

First, we study the behavior of the unbiased estimator of the efficient frontier when the length of the return time series tends to infinity. In this regard, we present the statement of our following theoretical result.

Theorem 1

lim N→+∞ BEF = UEF.

From practical purpose, this result ensures the convergence of the biased efficient frontier to the unbiased one when the length of the return time series is large enough.

3.2 The “Strange” Behavior of the Unbiased Estimator

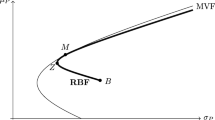
The unbiased estimator of the efficient frontier is characterized by a “strange” behavior in correspondence of particular combinations of the means of the returns of the assets and of their variances and covariances with respect to the number of the assets and the length of the associated time series of returns. In fact, in these cases, the estimator of the efficient frontier develops toward North-West instead of towards North-East, as usual (and theoretically correct). In particular, this “strange” behavior appears when N ≫ 0 and the returns are daily. In Fig. 1 we give a graphical exemplification of such an occurrence: the North-East efficient frontier and the North-West one are both generated by the same stocks but using different subsets of the original return time series.

Fig. 1
figure 1

Example of the “strange” behavior of the unbiased estimator of the efficient frontier. As usual, the x-axis stands for the variance of the return of the portfolio and the y-axis stands for the expected return of the portfolio

Full size image

Also in this regard, we present the statement of our following theoretical result.

Theorem 2

The unbiased estimator of the efficient frontier develops towards North-West when

$$\displaystyle \begin{aligned} \hat{s} < \frac{(n-1)(k-1)}{n(n-k-1)} \end{aligned} $$
(∗)

3.3 The Operational Effectiveness of the Unbiased Estimator

In conclusion, an important question rises: is the proposed unbiased estimator of efficient frontier operationally effective?

In order to give an answer to this question, given a set of real assets which are components of the Italian stock index FTSE MIB, we perform two empirical analysis.

  • The first one concerns the determination of the confidence interval of the sample estimate of the efficient frontier through a bootstrap approach (see [3]) by using 100 resampling. In particular, for preserving the autocorrelation structure of the return time series we adopt the block bootstrap (see [4]). We obtain that the unbiased estimate of the efficient frontier is not statistically different with respect to the sample estimate of the same efficient.

  • The second empirical analysis, similar to the previous one, is based on 100 simulated portfolio with different distributional properties and different combination of means, variances and covariances of the returns of the assets. By doing so, we obtain interesting results. In fact, different distributional properties produce different results. In case of the normal probability distribution, in the 69% of the simulations the unbiased estimate of the efficient frontier and the sample estimate of the same frontier are statistically equal, while in case of the Student’s t probability distribution only the 28% are. Furthermore, repeating this analysis by removing the serial independence in the return time series, the percentage in case of normal probability distribution and of Student’s t one are similar (54% and 58%, respectively).