Abstract
This book is devoted to the study of Euclidean Geometry , so named after the famous book Elements , of Euclid of Alexandria .
Access provided by CONRICYT-eBooks. Download chapter PDF
Similar content being viewed by others
This book is devoted to the study of Euclidean Geometry , so named after the famous book Elements [11], of Euclid of Alexandria .Footnote 1
We will guide our discussions, as much as possible, by the use of logical reasoning. However, we shall not be too seriously concerned with the problem of listing an exhaustive set of postulates from which one could construct Euclidean Geometry axiomatically.Footnote 2 To such a program, we refer the reader to [12] or [19]. For more than we shall present here, we suggest [1, 7, 14, 16, 24–26] or [27].
In this chapter, we present the most basic concepts and results involved in the construction of Euclidean Geometry in a plane.
1.1 Introduction
The reader certainly has a good idea, from both daily experience and previous studies, of what is a point , a line and a plane . Therefore, we shall assume these notions as primitive concepts , so that we shall not present formal definitions of them. We shall further assume that every line is a set of (at least two) points.Footnote 3
Figure 1.1 shows points A and B and lines r and s (we shall denote points and lines by upper case and lower case Latin letters, respectively). Roughly speaking, we could say that Plane Euclidean Geometry studies the properties of points and lines situated in a plane.
The following discussion will serve as a basis for all further developments of the theory. Throughout, all statements made without proofs should be taken as axioms.
Given a point P and a line r, there are only two possibilities: either the point P belongs to the line r or it doesn’t; in the first case, we write P ∈ r (P belongs to r) whereas, in the second, we write P∉r (P does not belong to r) . In Fig. 1.2, we have A ∈ r and B∉r.
At this point, it is natural to ask how many lines join two different given points. We assume (as an axiom!) that there is exactly one such line. In short, there is exactly one line passing through two distinct given points (cf. Fig. 1.3). In this case, letting r be such a line, we denote \(r=\,{\stackrel {\longleftrightarrow }{AB}}\), whenever convenient.
A point A on a line r divides it into two pieces, namely, the half-lines of origin A. By choosing points B and C on r, each one situated in one of these two pieces, we can denote the half-lines of origin A by \(\,{\stackrel {\longrightarrow }{AB}}\) and \(\,{\stackrel {\longrightarrow }{AC}}\). In Fig. 1.4, we show the portion of line r corresponding to the half-line \(\,{\stackrel {\longrightarrow }{AB}}\) (the portion corresponding to the half-line \(\,{\stackrel {\longrightarrow }{AC}}\) has been erased).
Given two distinct points A and B on a line r, the line segment AB is the portion of r situated from A to B. We write \(\,{\overline {AB}}\) to denote the length of the line segment AB (and, unless we explicitly state otherwise, such a length will be measured in centimeters). In order to decide whether two given line segments are equal (i.e., have equal lengths) or, on the contrary, each of which has greatest length, we can use a compass, transporting one of these line segments to the line determined by the other. This is done in the coming.
Example 1.1
Transport line segment AB to line \(\,{\stackrel {\longleftrightarrow }{CD}}\) and decide whether \(\,{\overline {AB}}>\,{\overline {CD}}\) or vice-versa.Footnote 4
Solution

Construction steps
-
1.
Place the nail end of the compass at A and open it until the other end is exactly over B.
-
2.
By maintaining the opening of the compass, place its nail end at C and draw an arc that intersects half-line \(\,{\stackrel {\longrightarrow }{CD}}\) at a point E, so that \(\,{\overline {CE}}=\,{\overline {AB}}\).
-
3.
Compare the lengths of line segments \(\,{\overline {AB}}=\,{\overline {CE}}\) and \(\,{\overline {CD}}\).
□
We can also use straightedge and compass to add line segments and to multiply a line segment by a natural number, as the next example shows.
Example 1.2
Let line segments AB and CD be given, as shown below. Draw line segments EF and GH, such that \(\,{\overline {EF}}=\,{\overline {AB}}+\,{\overline {CD}}\) and \(\,{\overline {GH}}=3\,{\overline {AB}}\).
Solution

Construction steps
-
1.
With the aid of a straightedge, trace a line r.
-
2.
Mark on the line r a point X and, then, transport line segment AB to r, obtaining a line segment EX, such that \(\,{\overline {EX}}=\,{\overline {AB}}\).
-
3.
Transport line segment CD to r, starting at the point X, to get the point F, such that \(\,{\overline {XF}}=\,{\overline {CD}}\) and X ∈ EF. Line segment EF has length equal to \(\,{\overline {AB}}+\,{\overline {CD}}\).
-
4.
Compose an analogous chain of steps to construct a line segment GH as in the statement of the example. To this end, note that \(3\,{\overline {AB}}=\,{\overline {AB}}+\,{\overline {AB}}+\,{\overline {AB}}\).
□
We shall make a last (though important) remark on line segments: given points A and B, we define the distance d(A, B) between them as the length \(\,{\overline {AB}}\) of the line segment AB:
Besides points, lines, half-lines and segments, circles will be of great importance in our study of Plane Euclidean Geometry. In order to define them in a precise way, let a point O and a real number r > 0 (that should be thought of as the length of a line segment) be given (Fig. 1.5). The circle of center O and radius r is the set of points P in the plane that are at a distance r from O, i.e., such that \(\,{\overline {OP}}=r\).
In a more concrete way, the circle of center O and radius r is the plane curve we get when we fix the nail end of a compass at the point O, fix its opening as equal to the length r and let its pencil end complete a whole turn around O. The complement of a circle in the plane consists of two regions, a limited one, called its interior , and an unlimited one, called its exterior . More precisely, the interior of the circle of center O and radius r is the set of points P in the plane, whose distance from the center O is less than r, i.e., such that \(\,{\overline {OP}}<r\) (cf. Fig. 1.6); analogously, the exterior of such a circle is the set of points P in the plane whose distance from the center O is greater than r, i.e., such that \(\,{\overline {OP}}>r\). Sometimes, we shall refer to the set of points P in the plane for which \(\,{\overline {OP}}\leq r\) as the (closed) disk of center O and radius r.
As a general rule, we shall denote circles by upper case greek letters. For instance, the circle of Fig. 1.7 is denoted by Γ (one reads gamma), and we usually write Γ(O;r) to stress that O is the center and r is the radius of Γ.
Given a circle Γ of center O and radius r, we also say that every line segment joining O to a point of Γ is a radius of it; for example, in Fig. 1.7, line segments OA, OB and OP are all radii of Γ. A chord of Γ is a line segment joining two of its points; a diameter of Γ is a chord that passes through O. In the notations of Fig. 1.7, AB and CD are chords of Γ, and AB is also a diameter. Every diameter of a circle divides it into two equalFootnote 5 parts, called two semicircles of the circle; conversely, if a chord of a circle divides it into two equal parts, then such a chord must necessarily be a diameter of it.
Concerning Fig. 1.7, the reader has surely noticed that a bold line traces out one of the portions of Γ limited by points C and D. Such a portion corresponds to one of the arcs of Γ whose endpoints are C and D, and will be denoted by \(\,{\stackrel {\frown }{CD}}\). Since two points on a circle determine two different arcs, in order to distinguish between the two possible arcs \(\,{\stackrel {\frown }{CD}}\), we shall generally refer to the minor arc \(\,{\stackrel {\frown }{CD}}\), or else to the major arc \(\,{\stackrel {\frown }{CD}}\). Hence, we should more properly say that the bold portion of Γ in Fig. 1.7 is the minor arc \(\,{\stackrel {\frown }{CD}}\). Another possibility (quite useful when the ends of the arc form a diameter of the circle) would be to choose another point on the arc we wish to refer to, and then denote it with the aid of this extra point; in Fig. 1.7, for instance, we could have written \(\,{\stackrel {\frown }{CPD}}\) to denote the major arc \(\,{\stackrel {\frown }{CD}}\).
Example 1.3
Draw the circle of center O and passing through the point A. Then, mark all possible points B on this circle, such that the chord AB has length equal to l.
Solution

Construction steps
-
1.
Put the nail end of the compass at O, with opening equal to \(\,{\overline {OA}}\). Then, draw the circle of center O and radius \(\,{\overline {OA}}\).
-
2.
As in item 1., draw the circle of center A and radius l.
-
3.
The possible positions of point B are the intersection points of the circles drawn in items 1. and 2.
□
Problems: Sect. 1.1
-
1.
Let A, B, C and D be distinct points on a line r. How many half-lines are contained in r and have one of these points as origin?
-
2.
Points A, B and C are all situated on a line r, with C ∈ AB. If \(\,{\overline {AB}}=10\)cm and \(\,{\overline {AC}}=4\,{\overline {BC}}\), compute \(\,{\overline {AC}}\).
-
3.
Let A, B, C and D be distinct points on a line r, such that \(D\in \,{\stackrel {\longrightarrow }{AC}}\), \(B\in \,{\stackrel {\longrightarrow }{DC}}\) and \(\,{\overline {AC}}=\,{\overline {BD}}\). Prove that \(\,{\overline {AB}}=\,{\overline {CD}}\).
-
4.
On a line r points A, B and C are given, so that B ∈ AC, \(\,{\overline {AB}}=3\)cm and \(\,{\overline {AC}}=5.5\)cm. Use a compass to find, on the segment AB, a point D such that \(\,{\overline {AD}}=\,{\overline {BC}}\).
-
5.
With the aid of straightedge and compass, mark points A, B and C on the plane, such that \(\,{\overline {AB}}=5\)cm, \(\,{\overline {AC}}=6\)cm and \(\,{\overline {BC}}=4\)cm.
1.2 Angles
The concepts of angle and angle measurement are absolutely fundamental to almost everything we will do in the rest of these notes. Prior to discussing them, we shall need to introduce another important notion, which is the object of our first formal
Definition 1.4
A region \(\mathbb R\) in the plane is said to be convex if, for all points \(A,B\in \mathbb {R}\), we have \(AB\subset \mathbb R\). Otherwise, \(\mathbb R\) is said to be a non-convex region.
According to the previous definition, for a region \(\mathbb R\) in the plane to be non-convex, it suffices to find points \(A,B\in \mathbb R\) such that at least one point of the line segment AB does not belong to \(\mathbb R\) (Fig. 1.8).
A line r in the plane divides it into two convex regions, called the (closed) half-planes bounded by r. By definition, the line r is considered to be a part of each one of them. On the other hand, given points A and B, one in each of these two half-planes, we always have AB ∩ r ≠ ∅ (cf. Fig. 1.9).
Definition 1.5
Let \(\,{\stackrel {\longrightarrow }{OA}}\) and \(\,{\stackrel {\longrightarrow }{OB}}\) be two distinct half-lines in the plane. An angle or angular region ) of vertex O and sides \(\,{\stackrel {\longrightarrow }{OA}}\) and \(\,{\stackrel {\longrightarrow }{OB}}\) is one of the regions in which the plane is divided by the half-lines \(\,{\stackrel {\longrightarrow }{OA}}\) and \(\,{\stackrel {\longrightarrow }{OB}}\).
An angle can be convex or non-convex; in Fig. 1.10, the angle at the left side is convex, whereas that at the right side is nonconvex. We shall denote an angle with sides \(\,{\stackrel {\longrightarrow }{OA}}\) and \(\,{\stackrel {\longrightarrow }{OB}}\) by writing \(\angle AOB\); the context will make it clear whether we are referring to the convex angle or to the non-convex one.
Now, it is our purpose to associate to each angle a measure of the region of the plane it occupies. To this end (cf. Fig. 1.11), let us consider a circle Γ centered at O, and divide it into 360 equal arcs; then, take two of the 360 partitioning points, say X and Y , which are the ends of one of these 360 equal arcs. We then say that the measure of the angle \(\angle XOY\) is one degree , and denote this by writing

Actually, there is a problem with our definition of degree, as given above. How can we know that it doesn’t depend on the chosen circle Γ? In other words, how can we know that, if we choose another circle Γ′, also centered at O, and divide it into 360 equal parts, then we will obtain an angle \(\angle X'OY'\) which could be said to have the same measure as \(\angle XOY\)?
In order to answer this question, let us consider Fig. 1.12, in which we have two circles Γ and Γ′, both centered at the point O, and two points A, B ∈ Γ. Letting A′ and B′ be the points of intersection of the half-lines \(\,{\stackrel {\longrightarrow }{OA}}\) and \(\,{\stackrel {\longrightarrow }{OB}}\) with Γ′, we shall assume as an axiom that the fraction of Γ represented by the bold arc \(\,{\stackrel {\frown }{AB}}\) equals the fraction of Γ′ represented by the bold arc \(\,{\stackrel {\frown }{A'B'}}\). Therefore, if in the definition of degree we had taken a circle Γ′, also centered at O but of radius different from that of Γ, then we would have got the same angle representing  .
.
From the definition of degree, it is clear that a complete circle corresponds to  . On the other hand, given an angle \(\angle AOB\), there remains the question of how one can actually measure it. In order to answer such a question,Footnote 6 we start by making the following construction: we draw any circle Γ, centered at O, and mark the points A′ and B′ in which Γ intersects the sides \(\,{\stackrel {\longrightarrow }{OA}}\) and \(\,{\stackrel {\longrightarrow }{OB}}\) of \(\angle AOB\) (cf. Fig. 1.13). Then, we compute the fraction of the total length of Γ the arc \(\,{\stackrel {\frown }{A'B'}}\) represents. The measure \(A\widehat OB\) of the angle \(\angle AOB\) will be equal to that fraction of
. On the other hand, given an angle \(\angle AOB\), there remains the question of how one can actually measure it. In order to answer such a question,Footnote 6 we start by making the following construction: we draw any circle Γ, centered at O, and mark the points A′ and B′ in which Γ intersects the sides \(\,{\stackrel {\longrightarrow }{OA}}\) and \(\,{\stackrel {\longrightarrow }{OB}}\) of \(\angle AOB\) (cf. Fig. 1.13). Then, we compute the fraction of the total length of Γ the arc \(\,{\stackrel {\frown }{A'B'}}\) represents. The measure \(A\widehat OB\) of the angle \(\angle AOB\) will be equal to that fraction of  . For instance, if the length of the arc \(\,{\stackrel {\frown }{A'B'}}\) equals \(\frac {1}{6}\) of the total length of Γ, then the measure of \(\angle AOB\) will be
. For instance, if the length of the arc \(\,{\stackrel {\frown }{A'B'}}\) equals \(\frac {1}{6}\) of the total length of Γ, then the measure of \(\angle AOB\) will be

Remarks 1.6
-
i.
We shall say that two angles are equal if their measures are equal.
-
ii.
In order to avoid any danger of confusion, we shall always use different notations for an angle and its measure. More precisely, \(\angle AOB\) will always refer to the angle with vertex O and sides \(\,{\stackrel {\longrightarrow }{OA}}\) and \(\,{\stackrel {\longrightarrow }{OB}}\) (which is a region in the plane), whereas \(A\widehat OB\) will always refer to the measure, in degrees, of the angle \(\angle AOB\).
-
iii.
In context, we will also frequently use lower case greek letters to denote measures of angles.Footnote 7 For example, we shall write \(A\widehat OB=\theta \) (one reads teta) to mean that the measure of the angle \(\angle AOB\) is θ degrees.
The next example teaches us how to use straightedge and compass to construct an angle with a prescribed vertex, side and measure. The construction steps to be listed will be justified when we study the SSS postulate of congruence of triangles, in Sect. 2.1.
Example 1.7
Construct an angle with vertex O′, such that one of its sides is contained in the line r and its measure equals α.
Solution

Construction steps
-
1.
Draw a circle of some radius R, centered at the vertex O of the given angle, thus marking points X and Y along the sides of it.
-
2.
Draw another circle of radius R, this time centered at O′, and mark one of the points, say Y ′, in which it intersects line r.
-
3.
Mark X′ as one of the points of intersection of the circles Γ(O′;R) and \(\Sigma (Y';\,{\overline {XY}})\).
-
4.
The angle \(\angle X'O'Y'\) has measure equal to α.
As we have pointed out before, each diameter of a circle divides it into two equal parts. Therefore, if \(\angle AOB\) is such that \(\,{\stackrel {\longrightarrow }{OA}}\) and \(\,{\stackrel {\longrightarrow }{OB}}\) are opposite half-lines (i.e., such that A, O and B lie on the same line, with O ∈ AB—see Fig. 1.14), then  .
.
We shall rarely encounter angles whose measures are greater than  . Thus, in all that follows and unless stated otherwise, whenever we write \(\angle AOB\) we will be referring to the convex angle \(\angle AOB\) (i.e., to the angle \(\angle AOB\) such that
. Thus, in all that follows and unless stated otherwise, whenever we write \(\angle AOB\) we will be referring to the convex angle \(\angle AOB\) (i.e., to the angle \(\angle AOB\) such that  . Accordingly (cf. Fig. 1.15) we shall say that an angle \(\angle AOB\) is acute
if
. Accordingly (cf. Fig. 1.15) we shall say that an angle \(\angle AOB\) is acute
if  , right
if
, right
if  and obtuse
if
and obtuse
if  . We call the reader’s attention (cf. Fig. 1.15), to the particular way of denoting a right angle.
. We call the reader’s attention (cf. Fig. 1.15), to the particular way of denoting a right angle.
It will be sometimes useful to have a special name attached to two angles whose sum of measures equals  ; from now on, we shall say that two such angles are complementary
. This way, if α and β are the measures of two complementary angles, then
; from now on, we shall say that two such angles are complementary
. This way, if α and β are the measures of two complementary angles, then  . Also, in such a case we shall say that the angle of measure α (or that α itself) is the complement
of the angle of measure β (or of β itself), and vice-versa. For example, two angles whose measures are
. Also, in such a case we shall say that the angle of measure α (or that α itself) is the complement
of the angle of measure β (or of β itself), and vice-versa. For example, two angles whose measures are  and
and  are complementary, since
are complementary, since  ; we can then say that one angle is the complement of the other, or that
; we can then say that one angle is the complement of the other, or that  is the complement of
is the complement of  (and vice-versa).
(and vice-versa).
The first proposition of Euclidean Geometry we shall prove provides a sufficient condition for the equality of two given angles. Before we can state and prove it, we need yet another piece of terminology.
Definition 1.8
Angles \(\angle AOB\) and \(\angle COD\) (with a common vertex O) are said to be opposite (we abbreviate OPP) if their sides, in pairs, are opposite half-lines.
As indicated, angles \(\angle AOB\) and \(\angle COD\) in Fig. 1.16 are opposite, for \(\,{\stackrel {\longrightarrow }{OA}}\) and \(\,{\stackrel {\longrightarrow }{OC}}\), as well as \(\,{\stackrel {\longrightarrow }{OB}}\) and \(\,{\stackrel {\longrightarrow }{OD}}\), are opposite half-lines. Note that the same is true of angles \(\angle AOD\) and \(\angle BOC\).
Proposition 1.9
Two opposite angles have equal measures.
Proof
In the notations of Fig. 1.16, since \(\,{\stackrel {\longrightarrow }{OB}}\) and \(\,{\stackrel {\longrightarrow }{OD}}\) are opposite to each other, we have  . Similarly,
. Similarly,  , so that
, so that

□
Problems: Sect. 1.2
-
1.
Assume that the intersection of two convex regions of a plane is a nonempty set. Prove that it is also a convex region.
-
2.
If we add the measure of an angle to the triple of the measure of its complement, we get
 . What is the measure of the angle?
. What is the measure of the angle? -
3.
Compute the measures of two complementary angles, knowing that the complement of the double of one of them equals one third of the measure of the other.
-
4.
The measures α and β of two opposite angles are expressed, in degrees, by 9x − 2 and 4x + 8. Compute the measure, in degrees, of α + β.
-
5.
Compute the measure of an acute angle, knowing that it exceeds the measure of its complement in
 .
. -
6.
* If two lines intersect, prove that one of the angles formed by them equals
 if and only if all four angles formed by them equal
if and only if all four angles formed by them equal  .
. -
7.
In the figure below, the angle α equals one sixth of the angle γ, plus half of the angle β. Compute α.

-
8.
Five half-lines, of same origin O, form five angles that cover all of the plane and have measures, in degrees, respectively proportional to the numbers 2, 3, 4, 5 and 6. Compute the measure of the greatest of these five angles.
-
9.
Construct, with straightedge and compass, an angle whose measure equals the sum of the measures of the angles \(\angle AOB\) and \(\angle A'O'B'\) of the figure below:

-
10.
Points A, B and C are chosen on a circle of center O, such that the measures of the minor arcs \(\,{\stackrel {\frown }{AB}}\), \(\,{\stackrel {\frown }{BC}}\) and \(\,{\stackrel {\frown }{AC}}\) are all equal. Compute the measures of the angles \(\angle AOB\), \(\angle BOC\) and \(\angle AOC\).
-
11.
Three half-lines of the same origin O form three angles that cover all of the plane. Show that at least one of these angles is greater than or equal to
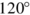 , and at least one of them is less than or equal to
, and at least one of them is less than or equal to  .
.
1.3 Convex Polygons
Let A, B and C be three given points in the plane. If C is on the line \(\,{\stackrel {\longleftrightarrow }{AB}}\), we say that A, B and C are collinear ; otherwise, we say that A, B and C are non collinear (cf. Fig. 1.17).
Three non collinear points A, B and C form a triangle ABC. In this case, we say that A, B and C are the vertices of the triangle ABC, and that the line segments AB, AC and BC are the sides or edges of ABC. The triangular region corresponding to the triangle ABC (also denoted by ABC, whenever there is no danger of confusion) is the bounded portion of the plane whose boundary is the union of the sides of ABC (the dashed portion of the plane in Fig. 1.17).
Given a triangle ABC, whenever there is no danger of confusion we shall also refer to the lengths of the line segments AB, BC and AC as the sides of the triangle. In this case, we usually write (cf. Fig. 1.18) \(\,{\overline {AB}}=c\), \(\,{\overline {AC}}=b\) and \(\,{\overline {BC}}=a\). The sum of the lengths of the sides of a triangle is its perimeter , which will be denoted, from now on, by 2p. Hence, p is the semiperimeter of the triangle and, in the notations of Fig. 1.18, we have
Angles \(\angle A=\angle BAC\), \(\angle B=\angle ABC\) and \(\angle C=\angle ACB\) (or their measures \(\widehat A=B\widehat AC\), \(\widehat B=A\widehat BC\) and \(\widehat C=A\widehat CB\)) are the interior angles of the triangle.
Triangles are usually classified in two different ways: with respect to the lengths of their sides or with respect to the measures of their interior angles. For the time being, let us see how to classify a triangle with respect to the lengths of its sides. Since each triangle has exactly three sides, the only possibilities for their lengths are that at least two of them are equal or that they are pairwise distinct. Thus, we have the following definition.
Definition 1.10
A triangle ABC is said to be:
-
(a)
Equilateral , if \(\,{\overline {AB}}=\,{\overline {AC}}=\,{\overline {BC}}\).
-
(b)
Isosceles , if at least two of \(\,{\overline {AB}}\), \(\,{\overline {AC}}\) and \(\,{\overline {BC}}\) are equal.
-
(c)
Scalene , if \(\,{\overline {AB}}\neq \,{\overline {AC}}\neq \,{\overline {BC}}\neq \,{\overline {AB}}\).
Note that, by the previous definition, every equilateral triangle is also isosceles. However, the converse statement is not true; for instance, for the triangle ABC at the center of Fig. 1.19, we clearly have \(\,{\overline {AB}}=\,{\overline {AC}}\neq \,{\overline {BC}}\), so that it is isosceles but not equilateral.
If ABC is an isosceles triangle with \(\,{\overline {AB}}=\,{\overline {AC}}\), we say that the third side BC is a basis for the triangle. Thus, each side of an equilateral triangle is a basis of it, but we rarely use this term in the context of equilateral triangles. In other words, we usually reserve the word basis for the unequal side of an isosceles triangle which is not equilateral.
A triangle is a particular type of convex polygon, according to the definition that follows.
Definition 1.11
Let n ≥ 3 be a natural number, and A 1, A 2, …, A n be n distinct points in the plane. We say that A 1 A 2…A n is a convex polygon if, for 1 ≤ i ≤ n, the two following conditions are satisfied (in both items below, we take A n+1 = A 1):
-
(a)
\(\,{\stackrel {\longleftrightarrow }{A_iA}}_{i+1}\) does not contain any of the other points A j .
-
(b)
\(\,{\stackrel {\longleftrightarrow }{A_iA}}_{i+1}\) leaves all of the other points A j in a single half-plane, of the two it determines.
The points A 1, A 2, …, A n are the vertices of the convex polygon A 1 A 2…A n ; the line segments A 1 A 2, A 2 A 3, …, A n−1 A n , A n A 1 (ou, whenever there is no danger of confusion and is convenient, their lengths) are the sides or edges of it. As with triangles, the sum of the lengths of the sides of a convex polygon is its perimeter . Also, the polygonal region corresponding to the convex polygon A 1 A 2…A n is the bounded region of the plane whose boundary is the union of the sides of the polygon. Figure 1.21 shows the polygonal region corresponding to the convex polygon of Fig. 1.20.
The polygonal region corresponding to the polygon of Fig. 1.20
As in Figs. 1.18 and 1.21, it can be shown that the polygonal region corresponding to a convex polygon is a convex region. From now on, we shall assume this to be true, without further comments.
A diagonal of a convex polygon is any of the line segments A i A j that is not a side of the polygon; for example, the convex polygon A 1 A 2…A 5 of Fig. 1.20 has exactly five diagonals: A 1 A 3, A 1 A 4, A 2 A 4, A 2 A 5 and A 3 A 5. In Proposition 1.12, we shall prove that every convex polygon of n sides has exactly \(\frac {n(n-3)}{2}\) diagonals (see, also, Problem 1).
The interior angles of the convex polygon A 1 A 2…A n are the convex angles \(\angle A_{i-1}A_iA_{i+1}\) (with the convention that A −1 = A n and A n+1 = A 1), or simply \(\angle A_i\), if there is no danger of confusion. In particular, A 1 A 2…A n has exactly n interior angles. The exterior angles of A 1 A 2…A n at the vertex A i are the opposite angles that are the supplements of the interior angle of the polygon at A i . Figure 1.20 shows the interior angles of the convex polygon A 1 A 2…A 5, and Fig. 1.22 shows the exterior angles of A 1 A 2…A 5 at vertex A 1.
In general, we say that a convex polygon A 1 A 2…A n is a convex n-gon, in reference to the fact that it has n sides (and n vertices). However, we use to say that the polygon is a quadrilateral if n = 4, a pentagon if n = 5, an hexagon if n = 6, heptagon if n = 7, octagon if n = 8 and a decagon if n = 10. Also concerning specific numbers of sides, we shall sometimes label the vertices of a polygon with upper case distinct Latin letters. For instance, we shall generally let ABCD denote a quadrilateral and, in this case, we will always assume, unless stated otherwise, that their sides are AB, BC, CD and DA. Analogous remarks are valid for pentagons, hexagons and so on.
The following proposition counts the number of diagonals of a convex n-gon.
Proposition 1.12
Every convex n-gon has exactly \(\frac {n(n-3)}{2}\) diagonals.
Proof
If n = 3 there is nothing to prove, for triangles have no diagonals and \(\frac {n(n-3)}{2}=0\) for n = 3. Suppose, then, that n ≥ 4. Joining vertex A 1 to the other n − 1 vertices A 2, …, A n we obtain n − 1 line segments, two of which are sides of the polygon (A 1 A 2 and A 1 A n ) and the remaining n − 3 (A 1 A 3, …, A 1 A n−1) are diagonals (cf. Fig. 1.23). Since an analogous reasoning is valid for every other vertex of the polygon, we conclude that exactly n − 3 diagonals depart from each vertex.
Adding all of these diagonals would give us a total of n(n − 3) diagonals (i.e., n − 3 diagonals for each of the n vertices). Nevertheless, this reasoning has counted each diagonal A i A j exactly twice: one when we counted the diagonals departing from A i and the other when we counted those departing from A j . Hence, in order to obtain the correct number of diagonals, we have to divide n(n − 3) by 2, thus obtaining \(\frac {n(n-3)}{2}\) diagonals. □
Problems: Sect. 1.3
-
1.
Use the principle of mathematical induction (cf. [5], for instance) to prove the formula for the number of diagonals of a convex polygon.
-
2.
A convex polygon is such that, from one of its vertices, we can draw as many diagonals as those of a convex hexagon. How many sides does the polygon have?
-
3.
Three convex polygons have numbers of sides equal to three consecutive natural numbers. Knowing that the sum of their numbers of diagonals is equal to 133, compute the number of sides of the polygon with the largest number of diagonals.
Notes
- 1.
Euclid of Alexandria , Greek mathematician of the fourth and third centuries bc, and one of the most important mathematicians of classical antiquity. The greatest contribution of Euclid to Mathematics, and to science in general, was the treatise Elements, in which he systematically exposed all knowledge of his time in Geometry and Arithmetic. The importance of the Elements lies in the fact that it was the first book ever written in which a body of mathematical knowledge was presented in an axiomatic way, with all arguments relying solely on Logic.
- 2.
An axiom or postulate is a property imposed as true, without the need of a proof. The use of the axiomatic method is one of the most fundamental characteristics of Mathematics as a whole.
- 3.
For the time being, we also implicitly assume that all points under consideration are contained in a single plane, and that there exists at least three points not situated in the same line.
- 4.
This is the first one of a series of examples whose purpose is to develop, in the reader, a relative ability on the use of straightedge and compass. In all of them, we list a sequence of steps which, once followed, execute a specific geometric construction. After attentively reading each of these examples, we strongly urge the reader to reproduce the listed steps by him/herself to actually execute the geometric constructions under consideration. Finally, and for the sake of rigor, we observe that a geometric construction does not constitute a proof of a geometric property, for it necessarily involves precision errors and particular choices of positions. Its main purpose is to help developing geometric intuition.
- 5.
Of course, at this point we rely on the reader’s intuition, or previous knowledge, for the meaning of equal.
- 6.
Strictly speaking, the following argument is fallacious, for, among other things, it invokes the notion of length of an arc of a circle, something which has not yet been defined. Nevertheless, it develops quite a useful intuition for the measurement of angles that is enough for our purposes along these notes. For a thorough discussion of the measurement of angles, we refer the reader to [19].
- 7.
The exception will be the lower case greek letter π (one reads pi). As we shall see in Chap. 5, we will reserve π to denote the area of a disk or radius 1.
References
A.V. Akopyan, A.A. Zaslavsky, Geometry of Conics (Providence, AMS, 2007)
A. Caminha, An Excursion Through Elementary Mathematics I - Real Numbers and Functions (Springer, New York, 2017)
H.S.M. Coxeter, S.L. Greitzer, Geometry Revisited (MAA, Washington, 1967)
T.L. Heath, The Thirteen Books of Euclid’s Elements (Dover, Mineola, 1956)
D. Hilbert, Foundations of Geometry (Open Court Publ. Co., Peru, 1999)
R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry (MAA, Washington, 1995)
R. Johnson, Advanced Euclidean Geometry (Dover, Mineola, 2007)
E.E. Moise, Elementary Geometry from an Advanced Standpoint (Addison-Wesley, Boston, 1963)
I.M. Yaglom, Geometric Transformations I (MAA, Washington, 1962)
I.M. Yaglom, Geometric Transformations III (MAA, Washington, 1973)
I.M. Yaglom, A. Shenitzer, Geometric Transformations IV (MAA, Washington, 2009)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Caminha Muniz Neto, A. (2018). Basic Geometric Concepts. In: An Excursion through Elementary Mathematics, Volume II. Problem Books in Mathematics. Springer, Cham. https://doi.org/10.1007/978-3-319-77974-4_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-77974-4_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-77973-7
Online ISBN: 978-3-319-77974-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





















 . What is the measure of the angle?
. What is the measure of the angle? .
. if and only if all four angles formed by them equal
if and only if all four angles formed by them equal  .
.

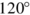 , and at least one of them is less than or equal to
, and at least one of them is less than or equal to  .
.





