On Fitting a Continuous-Time Stochastic Process Model in the Bayesian Framework

Abstract

Process models can be viewed as mathematical tools that allow researchers to formulate and test theories on the data-generating mechanism underlying observed data. In this chapter we highlight the advantages of this approach by proposing a multilevel, continuous-time stochastic process model to capture the dynamical homeostatic process that underlies observed intensive longitudinal data. Within the multilevel framework, we also link the dynamical processes parameters to time-varying and time-invariant covariates. However, estimating all model parameters (e.g., process model parameters and regression coefficients) simultaneously requires custom-made implementation of the parameter estimation; therefore we advocate the use of a Bayesian statistical framework for fitting these complex process models. We illustrate application to data on self-reported affective states collected in an ecological momentary assessment setting.

3.1 Introduction

Process modeling offers a robust framework for developing, testing, and refining substantive theories through mathematical specification of the mechanisms and/or latent processes that produce observed data. Across many fields of application (e.g., chemistry, biology, engineering), process modeling uses detailed mathematical models to obtain accurate description and explanation of equipment and phenomena, and to support prediction and optimization of both intermediate and final outcomes. In the social and behavioral sciences, the process modeling approach is being used to obtain insight into the complex processes underlying human functioning. In particular, the approach offers a way to describe substantively meaningful components of behavior using mathematical functions that map directly to theoretical concepts. In cognitive science, for example, drift diffusion models (see, e.g., Ratcliff and Rouder 1998) have been used to derive rate of information accumulation, non-decision time, bias, and decision boundaries from observed data on reaction time and correctness of response. Applied to data about individuals’ decisions in gambling tasks, process models are used to describe people’s tendency to take risks, their response consistency, and their memory for payoffs (Wetzels et al. 2010). In sociology, multinomial tree-based process models have been used to infer cultural consensus, latent ability, willingness to guess, and guessing bias from individuals’ judgments on a shared knowledge domain (Oravecz et al. 2014). In psychology, process models are proving especially useful for study of regulatory and interpersonal processes. Process models based on principles governing thermostats and reservoirs are being used to describe regulation of negative affect and stress (Chow et al. 2005; Deboeck and Bergeman 2013), and process models based on physical principles of pendulums are being used to describe interaction and coordination between partners of a dyad (e.g., wife-husband, mother-child; see in Chow et al. 2010; Ram et al. 2014; Thomas and Martin 1976). In this paper we present and illustrate how a specific process model, a multilevel Ornstein-Uhlenbeck model, can be used to describe and study moment-to-moment continuous-time dynamics of affect captured in ecological momentary assessment studies.

Process modeling is, of course, sometimes challenging. Mathematically precise descriptions of humans’ behavior are often complex, with many parameters, non-linear relations, and multiple layers of between-person differences that require consideration within a multilevel framework (e.g., repeated measures nested within persons nested within dyads or groups). The complexity of the models often means that implementation within classical statistical frameworks is impractical. Thankfully, the Bayesian statistical inference framework (see, e.g., Gelman et al. 2013) has the necessary tools. The algorithms underlying the Bayesian estimation framework are designed for highly dimensional problems with non-linear dependencies.

Consider, for example, the multilevel extension of continuous-time models where all dynamic parameters are allowed to vary across people, thus describing individual differences in intraindividual variation or velocity of changes. Driver et al. (2017) offer an efficient and user-friendly R package for estimation of multilevel continuous-time models, cast in the structural equation modeling framework. However, at the time of writing, person differences are only allowed in the intercepts and not in the variance or velocity parameters. A flexible Bayesian extension of the package that allows for all dynamics parameters to be person-specific is, though, in progress (Driver and Voelkle 2018). Importantly, flexible Markov chain Monte Carlo methods (Robert and Casella 2004) at the core of Bayesian estimation also provide for simultaneous estimation of model parameters and regression coefficients within a multilevel framework that supports identification and examination of interindividual differences in intraindividual dynamics (i.e., both time-invariant and time-varying covariates).

In the sections that follow, we review how process models are used to analyze longitudinal data obtained from multiple persons (e.g., ecological momentary assessment data), describe the mathematical details of the multilevel Ornstein-Uhlenbeck model, and illustrate through empirical example how a Bayesian implementation of this model provides for detailed and new knowledge about individuals’ affect regulation.

3.1.1 The Need for Continuous-Time Process Models to Analyze Intensive Longitudinal Data

Psychological processes continuously organize behavior in and responses to an always-changing environment. In attempting to capture these processes as they occur in situ, many researchers make use of a variety of experience sampling, daily diary, ecological momentary assessment (EMA), and ambulatory assessment study designs. In EMA studies, for example, self-reports and/or physiological measurements are collected multiple times per day over an extended period of time (i.e., weeks) from many participants as they go about their daily lives—thus providing ecological validity and reducing potential for reporting bias in the observations (Shiffman et al. 2008; Stone and Shiffman 1994). The data obtained are considered intensive longitudinal data (ILD, Bolger and Laurenceau 2013; Walls and Schafer 2006), in that they contain many replicates across both persons and time, and support modeling of interindividual differences in intraindividual dynamics. ILD, however, also present unique analytical challenges. First, the data are often unbalanced. The number of measurements is almost never equal across participants because the intensive nature of the reporting means that study participants are likely to miss at least some of the prompts and/or (particularly in event contingent designs) provide a different number of reports because of natural variation in exposure to the phenomena of interest. Second, the data are often time-unstructured. Many EMA studies purposively use semi-random time sampling to reduce expectation biases in reporting and obtain what might be considered a representative sampling of individuals’ context. Although the in situ and intensive nature of the data obtained in these studies provides for detailed description of the processes governing the moment-to-moment continuous-time dynamics of multiple constructs (e.g., affect valence, affect arousal), the between-participant differences in data collection schedule (length and timing) make it difficult to use traditional statistical modeling tools that assume equally spaced measurements or equal number of measurements. Modeling moment-to-moment dynamics in the unbalanced and time-unstructured data being obtained in EMA studies requires continuous-time process models (see more discussion in Oud and Voelkle 2014b).

3.1.2 The Need for Continuous-Time Process Models to Capture Temporal Changes in Core Affective States

To illustrate the benefits of a process modeling approach and the utility of continuous-time process models, we will analyze data from an EMA study in which participants reported on their core affect (Russell 2003) in the course of living their everyday lives. In brief, core affect is a neurophysiological state defined by an integral blend of valence (level of pleasantness of feeling) and arousal (level of physiological activation) levels. Core affect, according to the theory of constructed emotion (see, e.g., Barrett 2017), underlies all emotional experience and changes continuously over time. People can consciously access their core affect by indicating the level of valence and arousal of their current experience. Our empirical example makes use of data collected as part of an EMA study where N = 52 individuals reported on their core affect (valence and arousal) for 4 weeks, six times a day at semi-random time intervals. Specifically, participants’ awake time was divided into six equal-length time intervals within which a randomly timed text prompt arrived asking participants about their current levels of core affect (along with other questions related to general well-being). The intensive longitudinal data, obtained from four individuals, are shown in Fig. 3.1. Interval-to-interval changes in arousal and valence are shown in gray and blue, respectively. Some individual differences are immediately apparent: the four people differ in terms of the center of the region in which their core affect fluctuates, the extent of fluctuation, and the degree of overlap in arousal and valence. The process modeling goal is to develop a mathematical specification of latent processes that underlie the moment-to-moment dynamics of core affect and how those dynamics differ across people.

Fig. 3.1

Changes in core affect over time from four participants

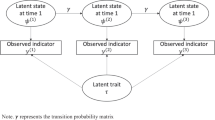
Based on reviews of empirical studies of temporal changes in emotions and affect, Kuppens et al. (2010) proposed the DynAffect framework, wherein intraindividual affective dynamics are described in terms of three key elements: affective baseline, homeostatic regulatory force, and variation around the baseline. Using a process modeling approach, these features are translated into a mathematical description of core affect dynamics—a continuous-time process model. Important general features of the mathematical parameterization include the following: (1) the latent person-level temporal dynamics of core affect are explicitly mapped to the substantive theory, (2) measurement noise in observed data is accommodated through addition of a measurement model, and (3) simultaneous modeling of person and population-level characteristics (e.g., organization of interindividual differences) is accommodated within a multilevel framework. Previous studies using similar process models have confirmed the utility of the approach for studying interindividual differences in intraindividual dynamics. In particular, it has been shown that people who score high on the neuroticism scale of Big Five personality model show lower baseline pleasantness and increased fluctuation (Oravecz et al. 2011), people who tend to apply reappraisal as emotion regulation strategy show higher levels of moment-to-moment arousal regulation (Oravecz et al. 2016), and older people tend to have higher arousal baseline with less fluctuation (Wood et al. 2017). In this chapter we add new information about how interindividual differences in the temporal dynamics of core affect are related to interindividual differences in trait-level emotional well-being (i.e., relatively stable characteristics of individuals’ emotional patterns).

3.2 The Ornstein-Uhlenbeck Process to Describe Within-Person Latent Temporal Dynamics

3.2.1 The Stochastic Differential Equation Definition of the Ornstein-Uhlenbeck Process

As noted earlier, process modeling requires specification of a mathematical model that describes the mechanisms and/or latent processes that produce observed data. Here, three key features of the temporal dynamics of core affect are described by using an Ornstein-Uhlenbeck process model (OU; Uhlenbeck and Ornstein 1930), the parameters of which will be estimated using EMA data that are considered noisy measurements of this latent process. Let us denote the position of the latent process at time t with θ(t). The OU process can be defined as a solution of the following first-order stochastic differential equation (Langevin equation):

$$\displaystyle \begin{aligned} \begin{array}{rcl} d \theta(t) &\displaystyle = &\displaystyle \beta(\mu-\theta(t))dt + \sigma d W(t). {} \end{array} \end{aligned} $$

(3.1)

Parameter θ(t) represents the latent variable evolving in time, and Eq. (3.1) describes the change in this latent variable, dθ(t), with respect to time t. As can be seen, changes in the latent state are a function of μ, which represents the baseline level of the process, β, which represents attractor or regulatory strength, W(t), which is the position of a standard Wiener process (also known as Brownian motion; Wiener 1923) at time t, and σ, which scales the added increments (dW(t)) from the Wiener process (together, also called the innovation process). The Wiener process evolves in continuous time, following a random trajectory, uninfluenced by its previous positions. If you consider Eq. (3.1) as a model for temporal changes in a person’s latent core affect dynamics, μ corresponds to the baseline or homeostatic “goal,” and β quantifies the strength of the regulation toward this goal.

The first part of the right-hand side of Eq. (3.1), β(μ − θ(t))dt, describes the deterministic part of the process dynamics. In this part of the model, the degree and direction of change in θ(t) is determined by the difference between the state of the process at time t, θ(t), and the baseline, μ, which is scaled by an attractor strength coefficient β (also called drift). We only consider stable processes here, meaning that the adjustment created by the deterministic part of the dynamics is always toward the baseline and never away from it. This is achieved in the current parameterization by restricting the range of β to be positive.¹ More specifically, when the process is above baseline (θ(t) > μ), the time differential dt is scaled by a negative number (μ − θ(t) < 0); therefore the value of θ(t) will decrease toward baseline as a function of the magnitude of the difference, scaled by β. Similarly, when the process is below baseline (μ > θ(t)), time differential dt part is positive, and the value of θ(t) will increase toward baseline. As such, the OU process is a mean-reverting process: the current value of θ(t) is always adjusted toward the baseline, μ, which is therefore characterized as the attractor point of the system. The magnitude of the increase or decrease in θ(t) is scaled proportional to distance from the baseline by β, which defines the attractor strength. When β goes to zero, the OU process approaches a Wiener process, that is, a continuous-time random walk process. When β becomes very large (goes to infinity), the OU process fluctuates around the baseline μ with a certain variance (stationary variance, see next paragraph).

The second part of the right-hand side of Eq. (3.1), σdW(t), describes the stochastic part of the process dynamics. This part adds random input to the system, the magnitude of which is scaled by β and σ. Parameter σ can be transformed into a substantively more interesting parameter γ, by scaling it with the regulation strength β, that is $\gamma = \frac {\sigma ^2}{2 \beta }$. The γ parameter expresses the within-person fluctuation around baseline due to inputs to the system-defined as all affect-provoking biopsychosocial (BPS) influences internal and external to the individual. As such, γ can be viewed substantively as the degree of BPS-related reactivity in the core affect system or the extent of input that constantly alters the system. Parameter γ is the stationary variance of the OU process: if we let the process evolve over a long time (t →∞), the OU process converges to a stationary distribution, a normal distribution with mean μ and variance γ, given that we have a stable process (i.e., β > 0; see above).

Together, the deterministic and stochastic parts of the model describe how the latent process of interest (e.g., core affect) changes over time: it is continuously drawn toward the baseline while also being disrupted by the stochastic inputs. Psychological processes for which this type of perturbation and mean reversion can be an appropriate model include emotion dynamics and affect regulation (Gross 2002), semantic foraging (i.e., search in semantic memory, see Hills et al. 2012), and so on. In our current example on core affect, the deterministic part of the OU process is used to describe person-specific characteristics of a self-regulatory system, and the stochastic part of the process is used to describe characteristics of the biopsychosocial inputs that perturb that system—and invoke the need for regulation.

To illustrate the three main parameters of the Ornstein-Uhlenbeck process, we simulated data with different μ, γ, and β values, shown in Fig. 3.2. Baseline (μ) levels are indicated with dotted gray lines. In the first row of the plot matrix, only the baseline, μ, differs between the two plots (set to 50 on the left and 75 on the right), and γ and β are kept the same (100 and 1, respectively). In the second row, only the level of the within-person variance, γ, differs between the two plots (set to 100 on the right and 200 on the left), while μ and β are kept the same (50 and 1, respectively). Finally, in the last row, we manipulate only the level of mean-reverting regulatory force, with a low level of regulation set on the left plot (β = 0.1) and high regulation on the right (β = 5). The baseline and the BPS-reactivity kept the same (μ = 50 and γ = 100). As can be seen, the process on the left wanders away from the baseline and tends to stay longer in one latent position. Descriptively, low β (i.e., weak regulation) on the left produces θ with high autocorrelation (e.g., high “emotion inertia”), while high β (i.e., strong regulation) on the right produces θ with low autocorrelation (e.g., low “emotion inertia”).

Fig. 3.2

Six Ornstein-Uhlenbeck process trajectories. Each trajectory in the plot matrix consists of 150 irregularly spaced data points. In the first row, the μ was set to 50 for the left plot and 75 for the right plot, with γ kept at 100 and β at 1 for both plots. In the second row, μ and β were kept the same (50 and 1), and γ was set to 100 for the right and 200 for the left. For the last row, μ and γ were kept the same (50 and 100), and β-s were set to 0.1 for the left plot and 5 for the right plot

3.2.2 The Position Equation of the Ornstein-Uhlenbeck Process

Once the temporal dynamics have been articulated in mathematical form, parameters of the model can estimated from empirical data. With the OU model, however, the estimation algorithm for obtaining parameters in Eq. (3.1) would require approximation of the derivatives from the data shown in Fig. 3.1, potentially introducing some approximation errors. Instead, we take a different approach, solving the stochastic integral in Eq. (3.1) and then estimating the parameters in the integrated model directly from the actual observed data.

We can integrate over Eq. (3.1), to get the value of the latent state θ (i.e., the position of the process) at time t, after some time difference Δ:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \theta(t)= \mu + e^{-\beta \varDelta} (\theta(t-\varDelta)-\mu)+ \sigma e^{-\beta \varDelta} \int_{t-\varDelta}^{t} e^{\beta u}d W(u). {} \end{array} \end{aligned} $$

(3.2)

The integral in Eq. (3.2) is a stochastic integral, taken over the Wiener process. For the OU process, the above stochastic integral was solved based on Itô calculus (see, e.g., Dunn and Gipson 1977), resulting in the conditional distribution of OU process positions, more specifically:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \theta(t) \mid \theta(t - \varDelta) \sim N(\mu+e^{-\beta \varDelta}(\theta(t - \varDelta)-\mu),\hspace{0.1cm} \gamma-\gamma e^{-2\beta \varDelta}). {} \end{array} \end{aligned} $$

(3.3)

Equation (3.3) is the conditional distribution of the position of the OU process, θ(t), based on the previous position of the process at θ(t − Δ) after elapsed time Δ and based on its three process parameters, μ, γ, and β, described earlier. Equation (3.3) is a particularly useful representation of the OU process as it can be used to formulate the likelihood function for the OU model without the need of approximating derivatives in Eq. (3.1).

The mean of the distribution presented in Eq. (3.3) is a compromise between the baseline μ and the distance of the process from its baseline (θ(t) − μ), scaled by e ^−βΔ. The larger β and/or Δ is, the closer this exponential expression gets to 0, and the mean of Eq. (3.3) will get closer to μ. When β and/or Δ are small, the exponential part approaches 1, and the mean will be closer to θ(t). In fact, β controls the continuous-time exponential autocorrelation function of the process; larger β-s correspond to lower autocorrelation and more centralizing behavior. Naturally, autocorrelation also decreases with the passage of time (higher values of Δ). Figure 3.3 shows a graphical illustration of the continuous-time autocorrelation function of the OU process. Larger values of β correspond to faster regulation to baseline μ, therefore less autocorrelation in the positions of θ over time. Smaller β values correspond to more autocorrelation over time.

Fig. 3.3

Continuous-time autocorrelation function of the OU process

The variance of the process presented in Eq. (3.3) is γ − γe ^−2βΔ. We can re-arrange this expression to the form of γ(1 − e ^−2βΔ). Now if we consider a large Δ value (long elapsed time), the exponential part of this expression goes to 0. Therefore γ represents all the variation in the process—it is the stationary (long run) variance, as described above. The moment-to-moment variation is governed by γ but scaled by the elapsed time and the attractor strength.

3.2.3 Extending the Ornstein-Uhlenbeck Process to Two Dimensions

Thus far, we have presented the model with respect to a univariate θ(t). Many psychological processes, however, involve multiple variables. Core affect, for example, is defined by levels of both valence and arousal. Process models of core affect, thus, might also consider how the two component variables covary. We can straightforwardly extend into multivariate space by extending θ(t) into a multivariate vector, Θ, and the corresponding multivariate (n-dimensional) extension of Eq. (3.1) is:

$$\displaystyle \begin{aligned} \begin{array}{rcl} d{\boldsymbol{\varTheta}}(t) &\displaystyle = &\displaystyle B(\boldsymbol{{\mu}}-{\boldsymbol{\varTheta}}(t))dt + \boldsymbol{\varSigma} d\mathbf{W}(t) {}, \end{array} \end{aligned} $$

(3.4)

where μ is an n × 1 vector, B and Σ are n × n matrices. The conditional distribution of a bivariate OU process model based on this equation is (see, e.g, Oravecz et al. 2011):

$$\displaystyle \begin{aligned} \begin{array}{rcl} \boldsymbol{\varTheta} (t)| \boldsymbol{\varTheta}(t-\varDelta) \sim N_2\left(\boldsymbol{{\mu}}+e^{-B\varDelta }(\boldsymbol{\varTheta}(t-\varDelta) -\boldsymbol{{\mu}}), \boldsymbol{\varGamma}-e^{-B \varDelta}\boldsymbol{\varGamma} e^{-B ^{\mbox{{T}}} \varDelta} \right). {}\qquad \quad \end{array} \end{aligned} $$

(3.5)

The latent state at time t is now represented in a 2 × 1 vector Θ. Parameter μ is 2 × 1 vector representing the baselines for the two variables (μ ₁ and μ ₂); Γ is a 2 × 2 stationary covariance matrix, with within-person variances (γ ₁ and γ ₂) in the diagonal and covariance in the positions of the process in the off-diagonal, with $\gamma _{12} = \gamma _{21} = \rho _{\gamma } \sqrt {\gamma _1 \gamma _2} = \frac {\sigma _{12}}{\beta _1 \beta _2}$. Drift matrix B is defined as a 2 × 2 diagonal matrix with attractor strength parameters (β ₁ and β ₂) on its diagonals (^T stands for transpose).

It is straightforward to use Eq. (3.5) to describe positions for the latent process dynamics for a single person p (p = 1, …, P). Let us assume that we want to model n _p positions for person p, at times $t_{p,1},t_{p,2},\ldots ,t_{p,s},\ldots ,t_{p,n_{p}}$. The index s denotes the sth measurement occasion of person p. Now elapsed time Δ can be written specifically as elapsed time between two of these time points: t _p,s − t _p,s−1. We let all OU parameters be person-specific, and then Eq. (3.5) becomes:

$$\displaystyle \begin{aligned} \boldsymbol{\varTheta}(t_{p,s})| \boldsymbol{\varTheta}(t_{p,s-1}) \sim N_2 \big(\boldsymbol{{\mu}}_{p,s} & + e^{-B_{p}(t_{p,s}-t_{p,s-1})}(\boldsymbol{\varTheta}(t_{p,s-1})-\boldsymbol{{\mu}}_{p,s}), \\ & \boldsymbol{\varGamma}_{p}-e^{-B_{p} (t_{p,s}-t_{p,s-1})}\boldsymbol{\varGamma}_{p} e^{-B_{p}^{\mbox{{T}}}(t_{p,s}-t_{p,s-1})} \big), \end{aligned} $$

(3.6)

where Θ(t _p,s) = (Θ ₁(t _p,s), Θ ₂(t _p,s))^T and the rest of the parameters are defined as before in Eq. (3.5).

We note here that our choice of notation of the OU parameters was inspired by literature on modeling animal movements with OU processes (see, e.g., Blackwell 1997; Dunn and Gipson 1977). However, in time-series literature in many of the works referenced so far, the following formulation of the multivariate stochastic differential equation is common:

$$\displaystyle \begin{aligned} \begin{array}{rcl} d{\boldsymbol{\eta}}(t) &\displaystyle = &\displaystyle (A \boldsymbol{\eta}(t) + \mathbf{b})dt + G d\mathbf{W}(t), {} \end{array} \end{aligned} $$

A simple algebraic rearrangement of our Eq. (3.4) gives:

$$\displaystyle \begin{aligned} \begin{array}{rcl} d{\boldsymbol{\varTheta}}(t) &\displaystyle = &\displaystyle (-B{\boldsymbol{\varTheta}(t) + B\boldsymbol{{\mu}}})dt + \boldsymbol{\varSigma} d\mathbf{W}(t). {} \end{array} \end{aligned} $$

If we work out the correspondence between the terms, we find that differences for the latent states (Θ(t) = η(t)) and the scaler for the effect of the stochastic fluctuations (Σ = G) are only on the level of the notation. With respect to the drift matrix across the two formulations, A = −B, the correspondence is straightforward (the sign only matters when stationarity constraints are to be implemented). The only real difference between the two formulations concerns the b and μ parameters: in the formulation introduced in this chapter, μ has a substantively interesting interpretation, since it represents a homeostatic baseline to which the process most often returns. In contrast, the b parameter, in the more typical SDE formulation, only denotes the intercept of the stochastic differential equation. Our process baseline parameter derives from the typical SDE formulation as μ = −A ⁻¹ b.

3.2.4 Accounting for Measurement Error

In many social and behavioral science applications, it is reasonable to assume that observed data are actually noisy measurements of the latent underlying process. Therefore, we add a state-space model extension to link the latent OU process variables to the observed data. Equation (3.6) is considered a transition equation, describing changes on the latent level. The observed data is denoted as Y(t _p,s) = (Y ₁(t _p,s), Y ₂(t _p,s))^T at time point t _p,s for person p at observation s. The measurement equation is then specified as:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathbf{Y}}(t_{p,s})= \boldsymbol{\varTheta}(t_{p,s}) + \boldsymbol{e}_{p,s} {} \end{array} \end{aligned} $$

(3.7)

with the error in measurement distributed as e _p,s ∼ N ₂(0, E _p), with the off-diagonals of E _p fixed to 0, and person-specific measurement error variances, 𝜖 _1,p and 𝜖 _2,p, on the diagonals.

3.3 A Multilevel/Hierarchical Extension to the Ornstein-Uhlenbeck Process

The above sections have outlined how the OU model can be used to describe intraindividual dynamics for a given person, p. Also of interest is how individuals differ from one another—interindividual differences in the intraindividual dynamics, and how those differences are related to other between-person differences. The multilevel framework allows for inferences on the hierarchical (or population, or group) level while accommodating individual differences in a statistically coherent manner (Gelman and Hill 2007; Raudenbush and Bryk 2002). The multilevel structure of the model parameters assumes that parameters of the same type share a certain commonality expressed by their superordinate population distributions. In brief, when estimating OU parameters for multiple persons p = 1, …, P in the multilevel framework, we pool information across participants by placing the parameters into a distribution with specific shape (e.g., Gaussian). Treating the person-specific parameters as random variables drawn from a particular interindividual difference distribution thus improves the recovery of the person-level parameters. Further, the multilevel modeling framework allows for a straightforward way to include covariates in the model, without needing to resort to a two-stage analysis (i.e., first estimating person-level model parameters, then exploring their association with the covariates through correlation or regression analysis). We will include both time-varying covariates (TVCs) and time-invariant covariates (TICs) in the model. The modeling of process model parameters such as the regulatory (attractor) force as a function of covariates has not yet been a focus in continuous-time models, although in many cases it can be done in a straightforward manner. In the next paragraphs, we outline how reasonable population distributions are chosen for each person-specific process model parameter.

3.3.1 Specifying the Population Distribution for the Baseline

The two-dimensional baseline, μ _p,s, shown in Eq. (3.6), can be made a function of both time-varying and time-invariant covariates. For the TICs, let us assume that K covariates are measured and x _jp denotes the score of person p on covariate j (j = 1, …, k). All person-specific covariate scores are collected into a vector of length K + 1, denoted as x _p = (x _p,0, x _p,1, x _p,2, …, x _p,K)^T, with x _p,0 = 1, to allow for an intercept term. Regarding the TVCs, suppose that we repeatedly measure person p on D time-varying covariates which are collected in a vector z _p,s = (z _p,s,1, …, z _p,s,D)^T, where index s stands for sth measurement occasion for person p. In order to avoid collinearity problems, no intercept is introduced in the vector z _p,s.

For the applied example, we use time of the self-report (e.g., time of day) as an indicator of timing within a regular diurnal cycle as TVC (z _p,s). We expected that some people will show low levels of valence and arousal in the morning, with the baseline increasing and decreasing in a quadratic manner over the course of the day. We also consider interindividual differences in gender and self-reported emotional health as TICs (x _p). We expected that person-specific baselines, regulatory force, and extent of BPS input would all differ systematically across gender and linearly with general indicators of individuals’ emotional health.

The level 2 (population-level) distribution of μ _p,s with regression on the time-invariant and time-varying covariates person-specific random variation can be written as follows:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \boldsymbol{{\mu}}_{p,s} \sim N_2 \left(\boldsymbol{\varDelta}_{p \mu} \boldsymbol{{z}}_{p,s} + \boldsymbol{\mathbf{A}}_{\mu} \boldsymbol{{x}}_{p}, \boldsymbol{\varSigma}_{\boldsymbol{\mu}}\right). {} \end{array} \end{aligned} $$

(3.8)

The covariance matrix Σ _μ is defined as:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \boldsymbol{\varSigma}_{\boldsymbol{\mu}}=\Bigg[\begin{array}{ccc} \sigma^{2}_{\mu_{1}} & \sigma_{\mu_{1}\mu_{2}}\\ \sigma_{\mu_{1}\mu_{2}} & \sigma^{2}_{\mu_{2}} \end{array} \Bigg], {} \end{array} \end{aligned} $$

(3.9)

where $\sigma ^{2}_{\mu _{1}}$ and $\sigma ^{2}_{\mu _{2}}$ quantify the unexplained (by covariates) individual differences in baseline values in the two dimensions (in our case valence and arousal), and the covariance parameter $\sigma _{\mu _{1}\mu _{2}}$ describes how person-specific levels of valence and arousal covary on the population level, that is, it provides a between-person measure of covariation in the core affect dimensions. The TVC regression coefficient matrix Δ _pμ has dimensions 2D × P, allowing between-person differences in the time-varying associations. The TIC regression coefficient matrix A _μ is of dimensions 2 × (K + 1), containing the regression weights for the time-invariant covariates x _p.

3.3.2 Specifying the Population Distribution for the Regulatory Force

The regulatory or attractor force is parameterized as a diagonal matrix B _p, with diagonal elements β _1p and β _2p representing the levels of regulation for the two dimensions. By definition this matrix needs to be positive definite to ensure that there is always an adjustment toward the baseline and never away from it, implying that the process is stable and stationary. This constraint will be implemented by constraining both β _1p and β _2p to be positive. The population distributions for these two will be set up with a lognormal population distribution. For β _1p this is,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \beta_{1p} \sim LN\left(\boldsymbol{{x}}^{\mbox{{T}}}_{p}\boldsymbol{{\alpha}}_{\beta_{1}}, \sigma^{2}_{\beta_{1}}\right). \end{array} \end{aligned} $$

The mean of this distribution is written as the product of time-invariant covariates and their corresponding regression weights, with the vector $\boldsymbol {{\alpha }}_{\beta _{1}}$ containing the (fixed) regression coefficients and parameter $\sigma ^2_{\beta _{1}}$ representing the unexplained interindividual variation in the regulatory force, in the first dimensions. The specification and interpretation of the parameters for the second dimension follow the same logic.

3.3.3 Specifying the Population Distribution for the BPS Input

The 2 × 2 stationary covariance matrix Γ _p models the BPS-related reactivity of the OU-specified process and is formulated as:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \boldsymbol{\varGamma}_{p} = \left[\begin{array}{ccc} \gamma_{1p} & \gamma_{12p} \\ \gamma_{21p} & \gamma_{2p} \end{array} \right]. \end{array} \end{aligned} $$

(3.10)

Its diagonal elements (i.e., γ _1p and γ _2p) quantify the levels of fluctuation due to BPS input in the two dimensions, in our case valence and arousal. The off-diagonal γ _12p = γ _21p quantifies how valence and arousal covary within-person. The covariance can be decomposed into $\gamma _{12p} = \rho _{\gamma _p}\sqrt {\gamma _{1p}\gamma _{2p}}$, where $\rho _{\gamma _p}$ is the contemporaneous (i.e., at the same time) correlation of the gamma parameters on the level of the latent process. The diagonal elements of the covariance matrix (γ _1p and γ _2p), that is, the variances, are constrained to be positive. We will model the square root of the variance, that is, the intraindividual standard deviation, and assign a lognormal (LN) population distribution to it to constrain it to the positive real line:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \sqrt{\gamma_{1p}} \sim LN\left(\boldsymbol{{x}}^{\mbox{{T}}}_{p}\boldsymbol{{\alpha}}_{\gamma_{1}}, \sigma^{2}_{\gamma_{1}}\right). \end{array} \end{aligned} $$

The mean of this population-level distribution is modeled via the product of time-invariant covariates and their corresponding regression weights, in the same manner that was described for the regulatory force above. The vector $\boldsymbol {{\alpha }}_{\gamma _{1}}$ contains the (fixed) regression coefficients, belonging to the set of person-level covariates. The first element of $\boldsymbol {{\alpha }}_{\gamma _{1}}$ relates to the intercept and expresses the overall mean level of BPS-related reactivity. The parameter $\sigma ^2_{\gamma _{1}}$ represents the unexplained interindividual variation in BPS-related reactivity in the first dimension. The specification and interpretation of the parameters for the second dimension follow the same logic.

The cross-correlation $\rho _{\gamma _{p}}$ is bounded between − 1 and 1. By taking advantage of the Fisher z-transformation $F(\rho _{\gamma _{p}})=\frac {1}{2} \log \frac {1+\rho _{\gamma _{p}}}{1-\rho _{\gamma _{p}}}$, we can transform its distribution to the real line:

$$\displaystyle \begin{aligned} \begin{array}{rcl} F(\rho_{\gamma_{p}})\sim N\left(\boldsymbol{{x}}^{\mbox{{T}}}_{p}\boldsymbol{{\alpha}}_{\rho_{\gamma}},\sigma^{2}_{\rho_{\gamma}}\right). \end{array} \end{aligned} $$

Again, ${\alpha }_{\rho _{\gamma }}$ contains K + 1 regression weights and $\boldsymbol {{x}}^{\mbox{ {T}}}_{p}$ the K covariate values for person p with 1 for the intercept, and $\sigma ^{2}_{\rho _{\gamma }}$ quantifies the unexplained interindividual variation. The first coefficient of $\boldsymbol {\alpha }_{\rho _{\gamma }}$ belongs to the intercept and represents the overall population-level within-person (standardized) correlation between the two dimensions. We note that while the model can capture covariation across the two dimensions, the current implementation is limited in the sense that it does not capture how the processes may influence each other over time (i.e., the off-diagonal elements of B _p are not estimated).

3.4 Casting the Multilevel OU Process Model in the Bayesian Framework

Estimation of the full model and inference to both individuals and the population are facilitated by the Bayesian statistical framework. In brief, the Bayesian statistical inference framework entails using a full probability model that describes not only our uncertainty in the value of an outcome variable (y) conditional on some unknown parameter(s) (θ) but also the uncertainty about the parameter(s) themselves. The goal of Bayesian inference is to update our beliefs about the likely values of model parameters using the model and data. The relationship between our prior beliefs about the parameters (before observing the data) and our posterior beliefs about the parameters (after observing the data) is described by Bayes’ theorem: p(θ∣y) = p(y∣θ)p(θ)∕p(y), which states that the posterior probability distribution, p(θ∣y), of parameter(s) θ given data y is equal to the product of a likelihood function p(y∣θ) and prior distribution p(θ), scaled by the marginal likelihood of the data p(y). With the posterior distribution, we can easily make nuanced and intuitive probabilistic inference. Since in Bayesian inference we obtain a posterior probability distribution over all possible parameter values, instead of merely point estimates, we can use the posterior distribution to make probabilistic statements about parameters (and functions of parameters) of interest. For example, we can easily derive the probability that the parameter value lies in any given interval.

To cast the described multilevel process model in Bayesian framework, we used Eqs. (3.6) and (3.7) as our likelihood function, and we specified non-informative prior distributions on all parameters. The posterior can be thought of as a compromise between the likelihood and the prior distributions and describes the relative plausibility of all parameter values conditional on the model being estimated. In the Bayesian framework, parameter estimation and inference focuses on the posterior distribution. For some simple models, posterior distributions can be calculated analytically, but for almost all nontrivial models, the posterior has to be approximated numerically. Most commonly, Bayesian software packages employ simulation techniques such as Markov chain Monte Carlo algorithms to obtain many draws from the posterior distribution. After a sufficiently large number of iterations, one obtains a Markov chain with the posterior distribution as its equilibrium distribution, and the generated samples can be considered as draws from the posterior distribution. Checks that the algorithm is behaving properly are facilitated by use of multiple chains of draws that are started from different initial values and should converge to the same range of values.

3.5 Investigating Core Affect Dynamics with the Bayesian Multilevel Ornstein-Uhlenbeck Process Model

3.5.1 A Process Model of Core Affect Dynamics Measured in an Ecological Momentary Assessment Study

Data used in the current illustration of the process modeling approach were collected at Pennsylvania State University in the United States from N = 52 individuals (35 female, mean age = 30 years, SD = 10) who participated in an EMA study of core affect and well-being. Participants were informed that the study protocol consisted of (1) filling out short web-based survey via their own smartphones, six times a day for 4 weeks, while going on with the course of their everyday life and (2) completing a battery of personality tests and demographics items during the introductory and exit sessions. After consent, the participants provided their phone number and were registered with a text messaging service. Over the course of the next month, participants received and responded to up to 168 text-message-prompted surveys. Compliance was high, with participants completing an average of 157 (SD = 15) of the surveys. Participants were paid proportional to their response rate, with maximum payment of $200. In addition to the core affect ratings of valence and arousal from the repeated surveys, we make use of two sets of covariates. Linear and quadratic representations of the time of day of each assessment, which ranged between 7 and 24 o’clock (centered at 12 noon), were used as TVCs. Select information from the introductory and exit batteries were used as TICs, namely, gender (n = 35 female) and two measures of emotional functioning: the emotional well-being (M = 74, SD = 18) and role limitations due to emotional problems (M = 77, SD = 36) scales from the 36-Item Short Form Health Survey (SF-36; Ware et al. 1993) (centered and standardized for analysis).

The parameter estimation for the multilevel, bivariate OU model described by Eqs. (3.6) and (3.7), was implemented in JAGS (Plummer 2003) and fitted to the above data.² Six chains of 65,000 iterations each were initiated from different starting values, from which the initial 15,000 were discarded (adaptation and burn-in). Convergence was checked using the Gelman-Rubin $\hat {R}$ statistic (for more information, see Gelman et al. 2013). All $\hat {R}$’s were under 1.1 which indicated no problems with convergence.

3.5.2 Population-Level Summaries and Individual Differences of Core Affect Dynamics

Table 3.1 summarizes the results on the population level by showing posterior summary statistics for the population mean values and interindividual standard deviation for each process model parameter. The posterior summary statistics are the posterior mean (column 2) and the lower and upper ends of the 90% highest probability density interval (HDI; columns 3 and 4), designating the 90% range of values with the highest probability density. We walk through each set of parameters in turn.

Table 3.1 Population-level results

The valence and arousal baselines were allowed to vary as function of time of day (linear and quadratic). The displayed estimates for the population mean baselines therefore represent estimated baselines at 12 noon. As seen in the first line of Table 3.1, average core affect at noon is somewhat pleasant (59.60 on the 0–100 response scale) and activated (57.63). Posterior means for the linear and quadratic effects of time of day indicate practically no diurnal trend for valence (1.30 for linear time, −0.04 for quadratic time), but an inverted U-shaped pattern for arousal (6.32 for linear, −0.22 for quadratic). The interindividual SDs for baselines and the linear and quadratic time effects quantify the extent of between-person differences in baseline throughout the day. These differences are illustrated in Fig. 3.4. As can be seen, most of the interindividual differences are in the baseline intercepts (differences in level at 12 noon) and not in the shape of the trajectories. For example, the left panel shows that while there is remarkable inverted U-shaped trend in the daily arousal baselines, this pattern is quite similar across people. Similarly, the right panel shows the extent of between-person differences in level, and similarities in shape of the daily trends, for valence.

Fig. 3.4

Individual differences in changes in core affect over the day

The population-level estimates of the biopsychosocial input-related reactivity are also summarized Table 3.1. The prototypical participant (male) had BPS input to valence of γ ₁ 7.53 and to arousal of γ ₂ = 13.58, with the amount of perturbation differing substantially between-persons for both valence (SD = 4.94) and arousal (SD = 5.17).³

The population-level estimates of regulatory force (β ₁ and β ₂) are also shown in Table 3.1. These values quantify how quickly individuals’ core affect is regulated back to baseline after perturbation. The prototypical participant had regulatory force of β ₁ = 0.17 for valence and β ₂ = 0.44 for arousal, with substantial between-person difference in how quickly the regulatory force acted (SD = 0.19 for valence, SD = 0.39 for arousal). As noted above, these parameters control the slope of the exponential continuous-time autocorrelation function of the process. Illustrations of the differences across persons for both valence and arousal are shown in Fig. 3.5.

Fig. 3.5

Individual differences in the continuous-time autocorrelation functions for valence and arousal

Finally, the population-level estimates of the cross-effects, within-person and between-person covariation of valence and arousal, are shown in the bottom of Table 3.1. For the prototypical participant (male), valence and arousal are very strongly coupled within-person, r = 0.99, suggesting that valence and arousal change in similar ways when BPS-related perturbations come in (but see also covariate results regarding gender differences for this parameter in the next section). Across persons, individuals with higher baselines in valence also tend to have higher baselines in arousal, r = 0.68.

3.5.3 Results on the Time-Invariant Covariates

Selected results on the time-invariant covariates are shown in Table 3.2. Only the TICs for which most of the posterior mass was positive or negative (90% highest density interval did not contain 0) were selected, as these are the coefficients that we consider remarkably different from 0. As mentioned before, γ (BPS-related reactivity) and β (regulation) were constrained to be positive; therefore their log-transformed values were regressed on the covariates; for these parameters relative effect sizes are reported in Table 3.2 (instead of the original regression coefficients that relate to the log scale). With regard to the covariates, gender was coded as 0 for male and 1 for female, and higher values on the emotional well-being scale indicate better well-being, while lower values on the role limitations due to emotional problems scale indicate more difficulties.

Table 3.2 Results on the covariates

As expected, results show that higher levels of emotional well-being were associated with higher baseline levels of valence ($\alpha _{3,\mu _{1}}$ = 8.00) and higher baseline levels of arousal ($\alpha _{3,\mu _{2}}$ = 6.54). Higher levels of emotional well-being were also associated with greater BPS input into arousal: $\alpha _{3,\sqrt {\gamma _2}}$ = 1.14. Again, the 1.14 value here is a relative effect size that relates to the original scale of the BPS-related reactivity and is interpreted the following way: consider a comparison point to be at 1, then the relative effect size expresses how many percent of change in the outcome (i.e., BPS-related reactivity) is associated with one standard deviation (or one point in case of gender) change in the covariate. For example, if we consider the association between emotional well-being and BPS-related reactivity, one standard deviation increase in emotional well-being is associated with 14% (1.14 − 1 = 0.14) increase in BPS-related reactivity. Relative effect sizes related to regulation are interpreted the same way.

Greater role limitation due to emotional problems was associated with higher levels of BPS-related valence reactivity ($\alpha _{4,\sqrt {\gamma _{1}}}$ = 0.79; 21%) and stronger regulatory force on arousal (i.e., quicker return to baseline; $\alpha _{4,\beta _{2}}$ = 0.73; 27%). There were also some notable gender differences: female participants tended to have higher levels of BPS-related valence reactivity ($\alpha _{2,\sqrt {\gamma _{1}}}$ = 1.46; 46%) and stronger regulatory force for valence ($\alpha _{2,\beta _{1}}$ = 2.21; 121%). This suggests that women participants experienced both greater fluctuations in pleasantness over time and regulated more quickly toward baseline. In line with the idea that females must contend with a more varied and less predictable set of perturbations, they also have less synchronicity between changes in valence and arousal ($\alpha _{2,\rho _{\gamma }}$ = −0.89).

Note that this is an exploratory approach of looking at associations between-person traits and dynamical parameters. As can be seen, some coefficients in Table 3.2 represent very small effect sizes with 90% highest density interval (HDI) being close to 1 (the cutoff for the relative effect sizes). For more robust inference in a follow-up study, we would recommend using a stricter criterion (e.g., 99% HDI) or, more ideally, calculating a Bayes factor for these coefficients.

3.6 Discussion

In this paper we presented process modeling as a framework that can contribute to theory building and testing through mathematical specification of the processes that may produce observed data. We illustrated how the framework can be used to examine interindividual differences in the intraindividual dynamics of core affect. In conceptualization, core affect is a continuously changing neurophysiological blend of valence and arousal that underlies all emotional experiences (Barrett 2017)—a video. Measurement of core affect, however, requires that individuals consciously access their core affect and indicate their current level of pleasantness (valence) and activation (arousal)—a selfie. The inherent discrepancy between the continuous-time conceptualization of core affect and the moment-to-moment measurement of core affect requires a framework wherein the parameters of process models governing action in an individual’s movie biopic can be estimated from a series of selfies that were likely snapped at random intervals (e.g., in an EMA study design).

Our illustration developed a mathematical description for the continuous-time conceptualization of core affect based on a mean-reverting stochastic differential equation, the OU model. From a theoretical perspective, this mathematical model is particularly useful because it explicitly maps key aspects of the hypothesized intraindividual regulatory dynamics (e.g., DynAffect model) of core affect, to three specific parameters, μ, β, and γ, that may differ across persons. Expansion into a bivariate model provides opportunity to additionally examine interrelations between affect valence and affect arousal. A key task in tethering the mathematical model to the psychological theory is “naming the betas” (Ram and Grimm 2015). Explicitly naming the parameters facilitates interpretation, formulation and testing of hypotheses, and potentially, theory building/revision. Here, we explicitly tethered μ to a baseline level of core affect—the “goal” or attractor point of the system; β to the strength of the “pull” of the baseline point—an internal regulatory force; and γ to the variability that is induced by affect-provoking biopsychosocial inputs. This content area-specific naming facilitated identification and inclusion into the model of a variety of time-varying and time-invariant covariates—putative “causal factors” that influence the intraindividual dynamics and interindividual differences in those dynamics. In particular, inclusion of time-of-day variables (linear and quadratic) provided for testing of hypotheses about how baseline valence and arousal change across the day in accordance with diurnal cycles, and inclusion of gender and indicators of emotional well-being provide for testing of hypotheses about how social roles and psychological context may influence affective reactivity and regulation. Generally, parameter names are purposively selected to be substantively informative in order that theoretical considerations may be easily engaged.

Statistical considerations come to the fore when attempting to match the model to empirical data, and particularly in situations like the one illustrated here, where a model with measurement and dynamic equations is placed within a multilevel framework that accommodates estimation of interindividual differences in intraindividual dynamics from noisy ILD that are unbalanced and time-unstructured. Our empirical illustration was constructed to highlight the utility of a multilevel Bayesian statistical estimation and inference framework (Gelman et al. 2013). The flexible Markov chain Monte Carlo methods provide for estimation of increasingly complex models that include multiple levels of nesting and both time-varying and time-invariant covariates. Specification of the full probability model, for both the observed outcomes and the model parameters, provides for robust and defensible probabilistic statements about the phenomena of interest. In short, the Bayesian estimation framework offers a flexible alternative to frequentist estimation techniques and may be particularly useful when working with complex multilevel models.

We highlight specifically the benefits of estimation for EMA data. Generally, these data are purposively collected to be time-unstructured. Intervals between assessments are kept inconsistent in order to reduce validity threats related to expectation bias in self-reports. This is problematic when a discrete-time mathematical model is used to describe the processes that may produce observed data, because the data cannot be mapped (in a straightforward way) to relations formulated in terms of θ(t) and θ(t − 1). As such, when working with EMA data, the model is better formulated with respect to continuous time, θ(t) and dθ(t). Theoretically, continuous-time models may also be more accurate to describe any measured phenomena that do not cease to exist between observations: most processes in behavioral sciences unfold in continuous time and should be modeled as such, see more discussion in, for example, Oud (2002) and Oud and Voelkle (2014a). In our case, core affect is by definition continuously changing and thus requires a mathematical description based in a continuous-time model. The process modeling framework stands taller and with more confidence when the data, mathematical model, and theory are all continuously aligned.