Non-Hermitian Coherent States for Finite-Dimensional Systems

Abstract

We introduce Gilmore-Perelomov coherent states for non-unitary representations of non-compact groups, and we discuss the main similarities and differences with respect to ordinary unitary Gilmore-Perelomov coherent states. The example of coherent states for the non-unitary finite dimensional representations of SU(1, 1) is considered and they are used to describe the propagation of light in coupled PT-symmetric optical devices.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

10.1 Introduction and Physical Motivation

Non-hermitian Hamiltonians have been used for a long time as effective Hamiltonians (think, for instance, of the optical potential in nuclear physics [1]). With the introduction of PT-symmetric Hamiltonians [2] in Quantum Mechanics they became very popular, however only a few papers have been devoted to coherent states (CS) for non-Hermitian systems (see [3], where Gazeau-Klauder CS are constructed using the definition of scalar product in terms of the CPT norm, [4,5,6,7,8,9] where the notion of pseudo-bosons and bi-coherent states are introduced, or [10, 11]) as compared with the huge amount of papers devoted to usual coherent states.

Non-hermitian systems, in particular PT-symmetric ones, have found the goose that laid the golden eggs in optics, in particular in discrete photonic systems (DPS), where the first experimental¹ realization of PT-symmetry was realized [13].

Let us describe briefly DPS and later we shall study the implications on non-hermiticity on these systems.

Fig. 10.1

Planar array of coupled waveguides

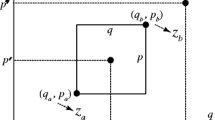
Consider an (infinite) planar array of optical waveguides, like the one of Fig. 10.1. Using Maxwell theory of electromagnetism, and performing some approximations (valid in a wide range of applications in DPS), we arrive to a set of coupled first-order differential equations describing the scalar magnitude of the (either electric or magnetic) field inside the waveguides (see for instance, [14]):

$$\begin{aligned} -i\frac{d\mathcal{E}_n}{dz} = f(n,z)\mathcal{E}_n+ g(n,z)\mathcal{E}_{n-1}+g(n+1,z)\mathcal{E}_{n+1}\,, \qquad \mathcal{E}_n(z_0)=\mathcal{E}_n^{(0)} \end{aligned}$$

(10.1)

where we have supposed that the couplings between adjacent waveguides g(n, z) (with units inverse of length) and the propagation constant (proportional to the refractive index and also with units inverse of length) f(n, z) depend both on the waveguide number n and the distance z along the waveguide [15].

Note that if the coupling g(n, z) vanishes for one value of n (for all z) the array can be semiinfinite. If it vanishes for two or more values of n the array can be finite.

Writing (10.1) in matrix form and using Dirac’s bra-ket notation we see that this set of equations can be written in Schrödinger-like form (equivalence is established by simply changing $z\rightarrow -t$):

$$\begin{aligned} -i\frac{d\,}{dz} |\mathcal{E}(z)\rangle =\hat{H}(z) |\mathcal{E}(z)\rangle \,, \qquad |\mathcal{E}(z_0)\rangle = |\mathcal{E}^{(0)}\rangle \end{aligned}$$

(10.2)

where

$$\begin{aligned} |\mathcal{E}(z)\rangle =\sum _{j\in \mathcal{I}}\mathcal{E}_j(z) |j\rangle \,\qquad \mathcal{I}\subset \mathbb {Z}\,, \end{aligned}$$

(10.3)

and

$$\begin{aligned} |j\rangle =\left( \begin{array}{c} \vdots \\ 0\\ 1 \\ 0 \\ \vdots \end{array}\right) \leftarrow j\text {-th}\,. \end{aligned}$$

The Hamiltonian $\hat{H}(z)$ reads:

$$\begin{aligned} \hat{H}(z)=f(\hat{n},z)+ g(\hat{n},z)\hat{V}^\dag + \hat{V}g(\hat{n},z) \,, \end{aligned}$$

(10.4)

where $\hat{n} |j\rangle =j |j\rangle$ is the number operator, and $\hat{V} |j\rangle = |j-1\rangle$ and $\hat{V}^\dag |j\rangle = |j+1\rangle$ are the step-down and step-up operators, respectively.

10.1.1 Symmetric DPS

The differential equation

$$\begin{aligned} -i\frac{d\,}{dz} |\mathcal{E}(z)\rangle =\hat{H}(z) |\mathcal{E}(z)\rangle \,,\qquad |\mathcal{E}(z_0)\rangle = |\mathcal{E}^{(0)}\rangle \end{aligned}$$

(10.5)

can be solved by group-theoretical methods (like Wei-Norman factorization [16]) if

$$\begin{aligned} \hat{H}(z)=\sum _{k=1}^N \alpha _k(z) \hat{A}_k\,, \end{aligned}$$

(10.6)

with $\hat{A}_k$ constant matrices realizing a representation of a Lie algebra $\mathcal{G}$ (associated with the Lie group G) with $[ \hat{A}_i,\hat{A}_j]=\sum _{k=1}^N c_{ij}^{\,\,k}\hat{A}_k$. In this case the propagator (evolution operator in the case of Schrödinger equation) can be explicitly computed:

$$\begin{aligned} |\mathcal{E}(z)\rangle =U(z,z_0) |\mathcal{E}(z_0)\rangle =\Pi _{k=1}^N e^{i u_k(z,z_0)\hat{A}_k} |\mathcal{E}(z_0)\rangle \equiv \hat{\rho }(g(z,z_0)) |\mathcal{E}(z_0)\rangle \,, \end{aligned}$$

(10.7)

where $z_0$ is the initial value of z and the functions $u_k(z,z_0)$ satisfy non-linear first-order coupled differential equations (in z) involving the structure constants $c_{ij}^{\,\,k}$ and the coefficients $\alpha _k(z)$. Here $g(z,z_0)$ represents an element of the group G that, for fixed $z_0$, describes a curve in G, and $\hat{\rho }$ is a representation of G (the one obtained by exponentiation of the representation of $\mathcal{G}$ defined by the matrices $\hat{A}_k$).

Note that the propagator satisfies the composition property

$$\begin{aligned} \hat{U}(z_2,z_1)\hat{U}(z_1,z_0)=\hat{U}(z_2,z_0) \end{aligned}$$

(10.8)

(i.e. defining a groupoid), and if the Hamiltonian $\hat{H}(z)\equiv \hat{H}$ does not depend on z, then $\hat{U}(z,z_0)=\hat{U}(z-z_0)$ and the composition property becomes the usual homomorphysm property

$$\begin{aligned} \hat{U}(z_2)\hat{U}(z_1)=\hat{U}(z_2+z_1)\,. \end{aligned}$$

(10.9)

In this case the curve $g(z,z_0)=g(z-z_0)$ constitutes a one-parameter subgroup of G generated by the Lie algebra element $\hat{H}$. Let’s denote this subgroup by H.

Define as $|\mathcal{E}(g)\rangle =\hat{\rho }(g) |\mathcal{E}^{(0)}\rangle \,,\forall g\in G$ the family of Gilmore-Perelomov coherent states [17] associated with the group G, the representation $\hat{\rho }$, and the fiducial vector $|\mathcal{E}^{(0)}\rangle$. Then $|\mathcal{E}(z)\rangle = |\mathcal{E}(g(z,z_0))\rangle \,,\forall z\in \mathbb {R}$ is a one-parameter subfamily of coherent states. If $\hat{H}$ does not depend on z, then the subfamily $|\mathcal{E}(z)\rangle$ is by itself a family of coherent states associated with the subgroup H, the representation $\hat{\rho }$ restricted to H, and the fiducial vector $|\mathcal{E}^{(0)}\rangle$.

An interesting fact is that, since the Hamiltonian $\hat{H}(z)$ is always an element of the Lie algebra $\mathcal{G}$, we have temporal (or rather, spatial) stability [18], since the propagation along z always remains in the family $|\mathcal{E}(g)\rangle$ (i.e. $|\mathcal{E}(z)\rangle = |\mathcal{E}(g)\rangle$ for some $g\in G$). If further $\hat{H}$ does not depend on z and it is a compact operator, there will be periodic revivals, i.e. the system returns to the original state $|\mathcal{E}^{(0)}\rangle$ after multiples of some length L, and in general $|\mathcal{E}(z+L)\rangle = |\mathcal{E}(z)\rangle \,,\forall z\in \mathbb {R}$.

Strictly speaking, for $|\mathcal{E}(g)\rangle$ to be a coherent state it is required that the representation $\hat{\rho }$ be unitary and square-integrable (modulo a subgroup, perhaps [19]), and the fiducial vector $|\mathcal{E}^{(0)}\rangle$ be admissible. However, in the examples we are considering (and in the general discussion we provide later in Sect. 10.2), we shall drop the requirement of unitarity, but keeping square-integrability, and see how this still provides a well defined notion of coherent states.

We shall focus on finite DPS, i.e. the index set $\mathcal{I}$ will be finite. If G is a compact group (like SU(2)), U(z) is unitary and the total light power $P(z)=\sum _{j\in \mathcal{I}}|\mathcal{E}_j(z)|^2$ is conserved along propagation. If G is a non-compact group (like SO(2, 1) or SO(3, 1)), U(z) is not unitary and the total power P(z) is not conserved. Non-unitarity is caused by non-Hermiticity of the Hamiltonian. Non-Hermitian Hamiltonians describe DPS with losses and/or gain, or non-symmetrical couplings (due, for instance, to torsion of non-identical waveguides or in effective Hamiltonians for some non-linear DPS [20]).

10.1.2 Non-Hermitian Dimer

Let us focus on a finite DPS with two waveguides, usually known as dimer. Consider the most general non-Hermitian coupling matrix

$$\begin{aligned} \hat{H}_{nH}(z) = \left( \begin{matrix} \alpha _{1}(z) &{} \beta _{1}(z) \\ \beta _{2}(z) &{} \alpha _{2} (z) \end{matrix} \right) ,\qquad \alpha _i(z)\,,\beta _j(z)\in \mathbb {C}\,. \end{aligned}$$

(10.10)

Setting the propagation constants relative to their average,

$$\begin{aligned} \vert \mathcal {E}(z) \rangle = e^{i \int _{z_{0}}^{z} \alpha _{0}(t) dt } \vert E(z) \rangle , \qquad \alpha _{0}(z) = \frac{1}{2} \left[ \alpha _{1}(z) + \alpha _{2}(z) \right] \,, \end{aligned}$$

(10.11)

gives the traceless effective non-Hermitian coupling matrix,

$$\begin{aligned} \hat{H}(z) = \left( \begin{matrix} \alpha (z) &{} \beta _{1}(z) \\ \beta _{2}(z) &{} -\alpha (z) \end{matrix} \right) , \qquad \alpha (z) = \frac{1}{2} \left[ \alpha _{1}(z) - \alpha _{2}(z) \right] \,, \end{aligned}$$

(10.12)

and the differential system,

$$\begin{aligned} -i \partial _{z} \vert E(z) \rangle = \hat{H}(z) \vert E(z) \rangle \,. \end{aligned}$$

(10.13)

Note that the Hamiltonian $\hat{H}(z)$ is an element of the $sl(2,\mathbb {C})\approx so(3,1)$ Lie algebra, where $sl(2,\mathbb {C})=so(3)\oplus i\, so(3)$, with basis $\{\hat{J}_x,\hat{J}_y,\hat{J}_z,i\hat{J}_x,i \hat{J}_y,i \hat{J}_z\}$, $\hat{J}_k$ being the standard angular momentum operators (Pauli matrices in the case of the dimer). More precisely, it can be written as:

$$\begin{aligned} \hat{H}(z)= & {} \mathfrak {Re}(\beta _1(z)+\beta _2(z))\hat{J}_x +\mathfrak {Im}(\beta _1(z)+\beta _2(z)(i \hat{J}_x)\nonumber \\&+ \mathfrak {Im}(\beta _2(z)-\beta _1(z))\hat{J}_y+\mathfrak {Re}(\beta _1(z)-\beta _2(z))(i \hat{J}_y)\\&+ 2\mathfrak {Re}(\alpha (z)) \hat{J}_z + 2\mathfrak {Im}(\alpha (z)) (i \hat{J}_z) \nonumber \end{aligned}$$

(10.14)

Designing appropriately the parameters in the Hamiltonian, some of the coefficients in the right hand side of the previous equation can vanish and thus $\hat{H}(z)$ will be an element of the Lie subalgebra $su(1,1)\approx so(2,1)\subset so(3,1)$, whose generators are denoted by $\{\hat{K}_{x},\hat{K}_{y},\hat{K}_{z}\}$. For this purpose, there are various possibilities:

$$\begin{aligned} \{\hat{K}_{x}, \hat{K}_{y},\hat{K}_{z} \} \equiv \{i\hat{J}_{x}, i\hat{J}_{y},\hat{J}_{z}\}, ~ \{ i\hat{J}_{y}, i\hat{J}_{z},\hat{J}_{x}\}, ~\{i\hat{J}_{z}, i\hat{J}_{x},\hat{J}_{y}\} \ldots \,. \end{aligned}$$

(10.15)

Experimentally, it is easier to realize a Hamiltonian that can be written as a combination of $\{\hat{K}_{x},\hat{K}_{y},\hat{K}_{z}\} \equiv \{i \hat{J}_{y}, i \hat{J}_{z},\hat{J}_{x}\}$, imposing $\mathfrak {Re}(\alpha (z))=0$, $\mathfrak {Im}(\beta _1(z)+\beta _2(z))=0$ and $\mathfrak {Im}(\beta _2(z)-\beta _1(z))=0$. If we further impose i.e. $\beta _1(z)=\beta _2(z)$ and real (i.e. real and symmetrical couplings), this system corresponds to a PT-symmetric DPS with balanced gain/loss [21, 22]. In the next subsection a realization of this case is discussed in detail.

10.1.3 Finite DPS with SO(2, 1) Symmetry: PT-Symmetric DPS

The Hamiltonian for a finite DPS with underlying $SO(2,1)\approx SU(1,1)$ symmetry can be taken as

$$\begin{aligned} \hat{H}(z) = i \gamma (z) \hat{J}_{z} + \lambda (z) \hat{J}_x \equiv \gamma (z) \hat{K}_{y} + \lambda (z) \hat{K}_z\,. \end{aligned}$$

(10.16)

If we take a unitary representation of $so(3)\approx su(2)$ with spin $j\in \frac{\mathbb {Z}}{2}$, we obtain a non-unitary representation of $SO(2,1)\approx SU(1,1)$ with “spin” $j\in \frac{\mathbb {Z}}{2}$. Since this representation is finite dimensional with dimension $2j+1$, our system will have $2j+1$ waveguides.

Under the P transformation ($n\rightarrow 2j -n$) and “T” transformation ($i\rightarrow -i$, $z\rightarrow -z$) the Hamiltonian changes to:

$$\begin{aligned} \hat{H}(z) \rightarrow \hat{H}(z)^{PT}=- i \gamma (-z) \left( -\hat{J}_{z}\right) + \lambda (-z) \hat{J}_x = \hat{H}(z)\,, \end{aligned}$$

(10.17)

provided $\gamma (z)$ and $\lambda (z)$ are even. Therefore the system is PT-symmetric.

However, for some values of the parameters, the PT-symmetry can be spontaneously broken, in the sense that wavefunctions are not PT-symmetric.

For the case $\gamma (z)=\gamma$ and $\lambda (z)=\lambda$, simple analytical expressions can be obtained. Three cases have to be considered, depending on whether $\varOmega =\sqrt{\lambda ^2-\gamma ^2}$ is positive, zero or pure imaginary, corresponding to three qualitatively different propagations: periodic (but with total power not conserved along propagation, unbroken PT-symmetry), growing with a power law, or growing with an exponential law, respectively (broken PT-symmetry). See Fig. 10.2 showing the light intensities for a PT-symmetric DPS with three waveguides.

Fig. 10.2

Plots of light intensity for the PT-symmetric DPS with 3 waveguides for the cases $\gamma <\lambda$ (left), $\gamma =\lambda$ (center) and $\gamma >\lambda$ (right). Light is impinged in the central waveguide (in black), while the waveguide with gain is shown in red and the one with loss in blue. In the last two cases light intensity has been renormalized to show the asymptotic behavior

Guided by the physical motivation of non-Hermitian DPS, we shall try to provide in the rest of the paper a mathematical framework that describes the propagation of light in these devices as non-Hermitian (or non-unitary) Gilmore-Perelomov coherent states.

10.2 Non-Hermitian Coherent States

As we have seen in the physical example, in some situations one has to handle systems possessing a symmetry group that it is realized through a non-unitary representation. To mathematically describe this situation, one has to resort (in the infinite-dimensional case) to a more general setting than Hilbert spaces, and this is the notion of Banach space. However, to simulate some of the properties of unitary representations on Hilbert spaces, a “dual” representation is needed. Let us introduce the notion of contragredient representation $\hat{\rho }^*$ associated to a non-unitary representation $\hat{\rho }$, following [23].

Let $\hat{\rho }$ be a representation of a locally compact Lie group G with Lie algebra $\mathcal{G}$ in a reflexive² Banach space $\mathcal{V}$:

$$\begin{aligned} \hat{\rho }:\,G\rightarrow GL(\mathcal{V})\,. \end{aligned}$$

(10.18)

Define the contragredient representation $\hat{\rho }^*$ on the dual space $\mathcal{V^*}$, $\hat{\rho }^*:\,G\rightarrow GL(\mathcal{V^*})$ as $\hat{\rho }^*(g)=\hat{\rho }(g^{-1})^\dag$.

Note that, since $\mathcal{V}$ is assumed to be reflexive, we have that if $\hat{\rho }$ is bounded and continuous, then $\hat{\rho }^*$ is continuous, and that $\hat{\rho }$ is irreducible if and only if $\hat{\rho }^*$ is irreducible.

By definition, the pair $(\hat{\rho },\hat{\rho }^*)$ verifies

$$\begin{aligned} \langle \hat{\rho }^*(g)\tilde{\varPsi },\hat{\rho }(g)\varPhi \rangle = \langle \tilde{\varPsi },\varPhi \rangle \,\qquad \forall \tilde{\varPsi }\in \mathcal{V^*},\,\forall \varPhi \in \mathcal{V}\,, \end{aligned}$$

(10.19)

where $\langle \tilde{\varPsi },\varPhi \rangle =\tilde{\varPsi }(\varPhi )$ denotes the usual pairing between $\mathcal{V}$ and $\mathcal{V^*}$.

Note that if $\hat{\rho }$ is unitary (and $\mathcal{V}$ is a Hilbert space, where $\langle \cdot ,\cdot \rangle$ is the scalar product, related to the pairing by Riesz representation theorem) then $\hat{\rho }^*=\hat{\rho }$. In this sense, the pair $(\hat{\rho },\hat{\rho }^*)$ generalizes the unitary case to the non-unitary case, in the more general setting of Banach spaces.

The notion of square integrability of a representation should be adapted to this more general setting as follows:

Definition 10.1

([23]) A representation $\hat{\rho }$ on a reflexive Banach space $\mathcal{V}$ is square integrable if there exist a non-zero vector $\varPhi \in V$ (called admissible) such that

$$\begin{aligned} \int _G |\langle \tilde{\varPsi },\hat{\rho }(g)\varPhi \rangle |^2 d\mu (g) <\infty \,,\qquad \forall \tilde{\varPsi }\in \mathcal{V}^* \,, \end{aligned}$$

(10.20)

where $d\mu (g)$ is the (left) Haar measure on G.

An analogous definition can be given for the contragredient representation:

Definition 10.2

([23]) The contragredient representation $\hat{\rho }^*$ on $\mathcal{V}^*$ is ${}^*$-square integrable if there exist a non-zero vector $\tilde{\varPsi }\in V^*$ (called ${}^*$-admissible) such that

$$\begin{aligned} \int _G |\langle \hat{\rho }^*(g)\tilde{\varPsi },\varPhi \rangle |^2 d\mu (g) <\infty \,,\qquad \forall \varPhi \in \mathcal{V}\,, \end{aligned}$$

(10.21)

where $d\mu (g)$ is the (left) Haar measure on G.

The set of admissible (resp. ${}^*$-admissible) vectors is invariant under $\hat{\rho }$ (resp. $\hat{\rho }^*$).

From now on we shall say, to simplify the notation, that the representation $\hat{\rho }^*$ is square integrable if it is ${}^*$-square integrable and that the non-zero vector $\tilde{\varPsi }\in \mathcal{V}^*$ is admissible if it is ${}^*$-admissible.

10.2.1 Non-hermitian Gilmore-Perelomov Coherent States

Let us generalize the notion of Gilmore-Perelomov coherent states [17, 19] to this wider setting.

Definition 10.3

Given a square integrable representation $\hat{\rho }$ on a reflexive Banach space $\mathcal{V}$ and an admissible vector $\varPhi \in \mathcal{V}$, a family of non-Hermitian Gilmore-Perelomov Coherent States is given by:

$$\begin{aligned} \varPhi _g =\hat{\rho }(g)\varPhi \,,\quad \forall g\in G\,. \end{aligned}$$

(10.22)

The analogous “dual” definition is:

Definition 10.4

Given the square integrable representation $\hat{\rho }^*$ on $\mathcal{V}^*$ and an admissible vector $\tilde{\varPsi }\in \mathcal{V}^*$, the dual family of non-Hermitian Gilmore-Perelomov Coherent States is given by:

$$\begin{aligned} \tilde{\varPsi }_g =\hat{\rho }^*(g)\tilde{\varPsi }\,,\quad \forall g\in G\,. \end{aligned}$$

(10.23)

The idea of defining two families of coherent states can be seen as a generalization (in the sense of Gilmore-Perelomov coherent states) of bi-coherent states for the standard bosonic operators [4,5,6,7,8,9].

The notion of square integrability (and its dual) is required to make sense of the following concepts (to avoid cluttering of notation we shall omit the dependence on the representation and the admissible vector on $\hat{T}$ and $\hat{\widetilde{T}}$).

Definition 10.5

([23]) Let $\hat{\rho }$ be a square integrable representation of the locally compact group G on the reflexive Banach space $\mathcal{V}$, and $\varPhi \in \mathcal{V}$ an admissible vector for $\hat{\rho }$. Then the sampling (or analysis) operator is given by

$$\begin{aligned} \hat{T}:\, \mathcal{V}^*\rightarrow & {} L^2(G) \nonumber \\ \tilde{\varPsi }\mapsto & {} \hat{T}(\tilde{\varPsi })(g)=\overline{\langle \tilde{\varPsi },\varPhi _g\rangle }\,. \end{aligned}$$

(10.24)

The adjoint defines the synthesis operator:

$$\begin{aligned} \hat{T}^\dag :\,L^2(G)\rightarrow & {} \mathcal{V} \nonumber \\ \gamma\mapsto & {} \hat{T}^\dag (\gamma )=\int _G \gamma (g)\varPhi _g d\mu (g)\,. \end{aligned}$$

(10.25)

There is an analogous definition for the dual case:

Definition 10.6

([23]) Let $\hat{\rho }^*$ be a square integrable representation of the locally compact group G on $\mathcal{V}^*$, and $\tilde{\varPsi }\in \mathcal{V}^*$ an admissible vector for $\hat{\rho }^*$. Then the dual sampling (or analysis) operator is given by

$$\begin{aligned} \hat{\widetilde{T}}:\, \mathcal{V}\rightarrow & {} L^2(G) \nonumber \\ \varPhi\mapsto & {} \hat{\widetilde{T}}(\varPhi )(g)=\langle \tilde{\varPsi }_g,\varPhi \rangle \,. \end{aligned}$$

(10.26)

The adjoint defines the synthesis operator:

$$\begin{aligned} \hat{\widetilde{T}}^\dag :\,L^2(G)\rightarrow & {} \mathcal{V}^* \nonumber \\ \gamma\mapsto & {} \hat{\widetilde{T}}^\dag (\gamma )=\int _G \gamma (g)\tilde{\varPsi }_g d\mu (g)\,. \end{aligned}$$

(10.27)

Let us introduce the Resolution operator $\hat{A}=\hat{T}^\dag \hat{\tilde{T}}$:

$$\begin{aligned} \hat{A}:\,\mathcal{V}\rightarrow & {} \mathcal{V} \nonumber \\ \phi\mapsto & {} \hat{T}^\dag \hat{\tilde{T}}\phi = \int _G \langle \tilde{\varPsi }_g,\phi \rangle \varPhi _g d\mu (g)\,, \end{aligned}$$

(10.28)

and its dual $\hat{\tilde{A}}=\hat{A}^\dag = \hat{\tilde{T}}^\dag \hat{T}$.

A non-unitary version of Schur’s lemma can be stated. For this purpose, denote by $L(\mathcal{V})$ the Banach algebra of bounded linear operators on the Banach space $\mathcal{V}$. We need the following results, that can be obtained by a slight modification of those in [24] (Corollary 3.2.9 and Theorem 4.2.2).

Lemma 10.1

Let $\hat{\rho }$ be a bounded and irreducible representation of the Lie group G on the Banach space $\mathcal{V}$. If we define $C=\{\hat{B}\in L(\mathcal{V}):\,\hat{\rho }(g)\hat{B}=\hat{B}\hat{\rho }(g)\,,\,\forall g\in G\}$, then C is isomorphic to $\mathbb {C}$.

With this Lemma we can prove:

Proposition 10.1

Let $\mathcal{V}$ be a reflexive Banach space. If $\hat{\rho }$ is continuous and irreducible, the resolution operators $\hat{A}$ and $\hat{\tilde{A}}$, if non-zero and bounded, are proportional to the identity operator on $\mathcal{V}$ and $\mathcal{V}^*$, respectively.

Proof

Using the definitions of $\hat{A}$ and $\hat{\tilde{A}}$ and the invariance of the left Haar measure on G, it is easy to check that

$$\begin{aligned} \hat{\rho }(g)\hat{A}=\hat{A}\hat{\rho }(g)\,,\quad \hat{\rho }^* (g)\hat{\tilde{A}}=\hat{\tilde{A}}\hat{\rho }^*(g)\,,\quad \forall g\in G\,. \end{aligned}$$

(10.29)

Thus $\hat{A}\in C$ and $\hat{\tilde{A}}\in C^*$ (defined analogously for $\hat{\rho }^*$). Since $\hat{\rho }$ is irreducible also $\hat{\rho }^*$ is and by the previous Lemma both C and $C^*$ are isomorphic to $\mathbb {C}$, and therefore $\hat{A}$ and $\hat{\tilde{A}}$ are proportional to the identity operators. $\blacksquare$

It should be stressed that the requirement that $\hat{A}$ (and thus $\hat{\tilde{A}}$) be bounded is crucial for the validity of the previous results (otherwise $\hat{A}\notin C$ and it cannot be granted that $\hat{A}^{-1}$ is bounded). Also, the requirement of irreducibility is necessary to have that $\hat{A}$ is bijective (and not just that $\hat{A}$ is injective with $\hat{A}^{-1}$ having dense domain in $\mathcal{V})$.

If $(\hat{\rho },\hat{\rho }^*)$ are square-integrable (with their respective admissible vectors), then we have that $\hat{A}$ and $\hat{\tilde{A}}$ are bounded (see [23]), and therefore Proposition 10.1 applies.

Similarly to the unitary case, a reproducing (or overlapping) kernel can be defined.

Definition 10.7

Let $\mathcal{V}$ be a reflexive Banach space and $\hat{\rho }$ a continuous representation of a Lie group G on $\mathcal{V}$, with $\hat{\rho }^*$ its contragredient representation. Define the Overlapping Kernel as:

$$\begin{aligned} \kappa (g',g)=\langle \tilde{\varPsi }_{g'},\varPhi _g\rangle =\langle \hat{\rho }^*(g')\varPsi ,\hat{\rho }(g)\varPhi \rangle \,. \end{aligned}$$

(10.30)

Proposition 10.2

The overlapping kernel $\kappa (g',g)$ depends only on $g'^{-1}g$.

Proof

$$\begin{aligned} \kappa (g',g) =\langle \hat{\rho }^*(g')\varPsi ,\hat{\rho }(g)\varPhi \rangle = \langle \varPsi ,\hat{\rho }(g')^{-1}\hat{\rho }(g)\varPhi \rangle = \kappa (e, g'^{-1}g)\equiv \kappa (g'^{-1}g)\,, \end{aligned}$$

(10.31)

where e is the identity element in G. $\blacksquare$

Proposition 10.2 means that $\kappa (g',g)$ is the kernel of a convolution operator on $L^2(G)$ when $\kappa (g',g)$ is square integrable.

The overlapping kernel, in the unitary and square-integrable case, endorses the Hilbert subspace $Im(\hat{T})\subset L^2(G)$ with a reproducing kernel Hilbert space structure, with kernel $\kappa (g',g)$, which is square-integrable, hermitian ($\kappa (g,g')=\overline{\kappa (g',g)}$) and positive definite. In the non-unitary case, if $(\hat{\rho },\hat{\rho }^*)$ are square-integrable, we still have that the overlapping kernel is square-integrable, but since $\mathcal{V}^*\ne \mathcal{V}$, we need two admissible functions $(\varPhi ,\tilde{\varPsi })$ and therefore $\kappa (g',g)$ and $\kappa (g,g')$ in general are not related to each other and does not make sense to speak about hermiticity and positive definiteness. Therefore, $\kappa (g',g)$ does not endorses $Im(\hat{T})$ with a reproducing kernel Hilbert space structure.

10.2.2 The Non-square Integrable Case

If the representations $(\hat{\rho },\hat{\rho }^*)$ are not square integrable, previous expressions are purely formal in the sense that the norm of $\varPhi _g$ and $\widetilde{\varPsi }_g$ can be unbounded on G (implying $\hat{A}$ unbounded and $\kappa (g',g)$ non-integrable) due to the non-unitarity of $\hat{\rho }$ and non-compactness of G.

This means that, although it is possible to define a family of coherent states, it is useless in the sense that we cannot use it as a “basis”, and in particular it is not possible to reconstruct a function $\phi$ from its coefficients $\langle \tilde{\varPsi }_g,\phi \rangle$ in this “basis”. This process requires the inverse of the resolution operator $\hat{A}$ and this operator is not bounded (and even can be “infinite” in the sense that the integral on G defining it is divergent).

Despite of these problems related to the lack of square-integrability, non-Hermitian Coherent States can be physically meaningful in some situations, as shown in previous sections.

The reason can be understood as follows. Suppose G is a non-compact Lie group and $\hat{\rho }$ a non-unitary representation, with $\hat{\rho }^*$ its contragredient representation. Suppose they are not square integrable and consider the maximal compact subgroup K of G. Since K is compact, the restriction of the representations $(\hat{\rho }|_K,\hat{\rho }^*|_K)$ are both equivalent to a unitary representation $\hat{\sigma }$ of K. Redefine $(\hat{\rho },\hat{\rho }^*)$ such that restricted to K coincide with $\hat{\sigma }$. Since K is compact $\hat{\sigma }$ is square-integrable, thus consider $(\varPhi ^K,\tilde{\varPsi }^K)$ admissible vectors in $\mathcal{V}$ and $\mathcal{V}^*$, respectively. The resolution operator $\hat{A}_K$ is

$$\begin{aligned} \hat{A}_{K}\phi =\int _{K} \langle \tilde{\varPsi }^K_k,\phi \rangle \varPhi ^K_k d\mu _K(k)\,, \end{aligned}$$

(10.32)

where $d\mu _K(k)$ is a left-invariant Haar measure on K and $(\varPhi ^K_k,\tilde{\varPsi }^K_k)=(\hat{\sigma }(k)\varPhi ^K,\hat{\sigma }(k)\tilde{\varPsi }^K)$. $A_K$ is bounded and satisfy the interwinning property, (10.29), with respect to $\hat{\sigma }$. In general $\hat{\sigma }$ is not irreducible (even if $\hat{\rho }$ is) and therefore we cannot apply Proposition 10.1 to conclude that $\hat{A}_{K}$ is proportional to the identity operator on $\mathcal{V}$ (the same applies to $\hat{\tilde{A}}_K$ on $\mathcal{V}^*$).

Consider now $X=G/K$ and define the elliptic subgroups $K_{[v]}=\{k_v=v k v^{-1}\,,k\in K\}$, where $v\in G$ is a representative for a class $[v]\in X$. Define $(\hat{\rho }_{[v]},\hat{\rho }^*_{[v]})$ as the restriction to $K_{[v]}$ of $(\hat{\rho },\hat{\rho }^*)$. Then we have that the representations $(\hat{\rho }_{[v]},\hat{\rho }^*_{[v]})$ are square integrable and the resolution operator $\hat{A}_{K_{[v]}}$ is given by: $\hat{A}_{K_{[v]}}\phi = \hat{\rho }(v) \hat{A}_K \hat{\rho }(v^{-1})$ .

As before, in general $(\hat{\rho }_{[v]},\hat{\rho }^*_{[v]})$ are not irreducible (even if $\hat{\rho }$ is) and therefore we cannot apply Proposition 10.1 to conclude that $\hat{A}_{[v]}$ is proportional to the identity operator on $\mathcal{V}$.

These considerations can even be extended to the general case. Let $\hat{\rho }$ be a non-unitary representation of the non-compact group G on the Banach space $\mathcal{V}$. If $\hat{\rho }$ is square integrable, then $\mathcal{V}$ is topologically isomorphic to a Hilbert space $\mathcal{H}$ and $(\hat{\rho },\hat{\rho }^*)$ are equivalent to a unitary representation on $\mathcal{H}$ (see [23], Theorem 3.13). This result can be seen as a group-theoretical version of the concept of pseudo-hermiticity (see [25]).

In the next section, motivated by the PT-symmetric dimer, we consider the example of the non-unitary finite-dimensional representations of SU(1, 1), and discuss various ways of tackling the lack of square-integrability of the representations.

10.3 Example: SU(1, 1) Non-hermitian Coherent States

Consider the realization (see [17]) of $su(1,1)\approx so(2,1)$ $\{\hat{K}_x\equiv i \hat{J}_x,\hat{K}_y\equiv i \hat{J}_y, \hat{K}_z=\hat{J}_z\}$. Note that this is a different realization to that of the PT-symmetric dimer, we shall use this one in this example since the compact generator of SU(1, 1) is $\hat{K}_z=\hat{J}_z$, the usual convention in mathematics. All results discussed here apply to the case of the PT-symmetric dimer by changing

$$\begin{aligned} \hat{J}_z\rightarrow \hat{J}_x\,\,\qquad \hat{J}_y\rightarrow \hat{J}_z\,, \qquad \hat{J}_x\rightarrow \hat{J}_y\,. \end{aligned}$$

(10.33)

Thus, if we take the $2j+1$-dimensional unitary irreducible representation of SU(2), we get a $2j+1$-dimensional non-unitary irreducible representation of SU(1, 1).

We shall use the following parametrization of the group elements (for the case $j=1/2$, leading to the fundamental o defining representation, for other values of j provides the different non-unitary representations of the group):

$$\begin{aligned} \hat{\rho }(\zeta ,\zeta ^*,\beta )=e^{\xi \hat{K}_+-\xi ^*\hat{K}_-}e^{i\beta \hat{K}_z}\,, \quad \xi \in \mathbb {C}\,, \quad \zeta =\frac{\xi }{|\xi |} \tanh |\xi |\,, \end{aligned}$$

(10.34)

where $\zeta \in \mathbb {D}$ (the unit disk in the complex plane), $\beta \in [0,4\pi )$ and $\hat{K}_\pm =-\hat{K}_y\pm i \hat{K_x}$. Note that $\hat{K}_\pm$ are not the adjoint of each other, but instead $\hat{K}_+^\dag =-\hat{K}_-$. For this reason $e^{\xi \hat{K}_+-\xi ^*\hat{K}_-}$ is not a unitary operator, in fact it is hermitian positive-definite. Thus (10.34) provides explicitly the polar decomposition of the representation, and shows that it is non-unitary.

For instance, the $j=1/2$ case is:

$$\begin{aligned} \hat{\rho }_{1/2}(\zeta ,\zeta ^*,\beta )=\frac{1}{\sqrt{1-|\zeta |^2}} \left( \begin{array}{cc} e^{i \beta /2 } &{} e^{i \beta /2} \zeta \\ e^{-i \beta /2 }\zeta ^*&{} e^{-i \beta /2 } \end{array} \right) \,. \end{aligned}$$

(10.35)

The contragredient representation for this case is:

$$\begin{aligned} \hat{\rho }_{1/2}^*(\zeta ,\zeta ^*,\beta )=\frac{1}{\sqrt{1-|\zeta |^2}} \left( \begin{array}{cc} e^{i \beta /2 } &{} -e^{i \beta /2} \zeta \\ -e^{-i \beta /2 }\zeta ^*&{} e^{-i \beta /2 } \end{array} \right) \,. \end{aligned}$$

(10.36)

It is important to mention that, for general j, matrix elements of both representations diverge as $(1-|\zeta |)^{-j}$ when $|\zeta |\rightarrow 1$. This is also the behavior of the largest eigenvalue.

Let us choose as fiducial vectors (other choices lead to similar results in this case) $\varPhi =\tilde{\varPsi }=\left( \begin{array}{c} 1 \\ 0 \end{array} \right)$.

Then the coherent states are:

$$\begin{aligned} \varPhi (\zeta ,\beta )_{1/2}= & {} \frac{1}{\sqrt{1-|\zeta |^2}}\left( \begin{array}{c}e^{i\beta /2} \\ e^{-i\beta /2}\zeta ^*\end{array} \right) \\ \widetilde{\varPsi }(\zeta ,\beta )_{1/2}= & {} \frac{1}{\sqrt{1-|\zeta |^2}}\left( \begin{array}{c}e^{i\beta /2} \\ -e^{-i\beta /2}\zeta ^*\end{array} \right) \,. \end{aligned}$$

The resolution operator is:

$$\begin{aligned} \hat{A}_{1/2}=\int _{\mathbb {D}\times [0,4\pi )} \frac{d\zeta d\zeta ^*}{(1-|\zeta |^2)^2}\frac{d\beta }{4\pi } \frac{1}{1-|\zeta |^2} \left( \begin{array}{cc} 1 &{} e^{i \beta } \zeta \\ e^{-i \beta }\zeta ^*&{} -|\zeta |^2 \end{array} \right) \,. \end{aligned}$$

(10.37)

where $\frac{d\zeta d\zeta ^*}{(1-|\zeta |^2)^2}\frac{d\beta }{4\pi }$ is the left-invariant Haar measure on the group. The dual version is simply the adjoint. $\hat{A}_{1/2}$ is divergent since the representation is not square integrable. The reason is that the behavior for $|\zeta |\rightarrow 1$ of the matrix elements of $\hat{A}_j$, for arbitrary j, is $(1-|\zeta |)^{-2j}$, and together with the integration measure gives $(1-|\zeta |)^{-2j-2}$ which is divergent when integrated on $\mathbb {D}$.

This should be compared with the unitary representations of the discrete series of SU(1, 1), which are infinite-dimensional, and the behavior for $|\zeta |\rightarrow 1$ of the matrix elements of the corresponding resolution operator $\hat{A}_k$ is $(1-|\zeta |)^{2k}$, where k is the Bargmann index characterizing the representation. Together with the integration measure gives $(1-|\zeta |)^{2k-2}$ and this is convergent when integrated on $\mathbb {D}$ if $k>1/2$. Therefore, the representations of the discrete series are unitary and square-integrable for $k>1/2$.

Note that all expressions can be derived from those of the discrete series simply performing the change $k\rightarrow -j$, with $j>0$ and half-integer.

The overlapping kernel is given by:

$$\begin{aligned} \kappa _{1/2}((\zeta ',\beta '),(\zeta ,\beta ))=\frac{1}{\sqrt{(1-|\zeta |^2)(1-|\zeta '|^2)}} (e^{i \frac{\beta -\beta '}{2}}-e^{-i \frac{\beta -\beta '}{2}}\zeta ^*\zeta ')\,. \end{aligned}$$

(10.38)

In this case the overlapping kernel is hermitian and positive definite (since $\mathcal{V}^*$ is isomorphic to $\mathcal{V}$ and $\varPhi =\tilde{\varPsi }$), but it is not bounded on $\mathbb {D}$ and therefore it is not square-integrable. In fact, as commented previously, it coincides with the overlapping kernel for the coherent states associated with the representation of the discrete series with Bargmann index $k=-1/2$.

To overcome these problems there are many alternatives, as suggested in Sect. 10.2. We shall discuss some of them in the following subsections.

10.3.1 Restriction to the Maximal Compact Subgroup

If we restrict the representation to the maximal compact subgroup $K=\{(0,0,\beta )\,,\beta \in [0,4\pi )\}= U^{(2)}(1)$, a double cover of U(1), we obtain a unitary, although reducible, representation of $U^{(2)}(1)$. It decomposes into $2j+1$ (for general j) irreducible unitary characters, labeled by $m=-j,\ldots ,j$. This case coincides with that of a representation of SU(2) restricted to $U^{(2)}(1)$. In a sense this case is trivial since it reduces to a well-known, unitary case.

Denote by $\hat{A}_K$ the restriction of the resolution operator to the compact subgroup K (as defined in (10.32)). Since the representation restricted to K is reducible, $\hat{A}_K$ is not proportional to the identity, and even non-invertible, in general. In this case $\hat{A}_K$ is invertible only if the component-wise product of the vectors $\varPhi$ and $\tilde{\varPsi }$ is a vector with all its components different from zero. If all the components of this vector are identical, then $\hat{A}_K$ is proportional to the identity.

The overlapping kernel restricted to K, $\kappa _K(k',k)$, is square-integrable on $U^{(2)}(1)$. Since in this finite-dimensional case $\mathcal{V}$ and $\mathcal{V}^*$ are isomorphic, we can choose $\tilde{\varPsi }=\varPhi$ as before and therefore $\kappa _K(k',k)$ is positive definite and hermitian. Thus, $\kappa _K(k',k)$ is a reproducing kernel for the Hilbert subspace $Im(\hat{T})\subset L^2(U^{(2)}(1))$.

This case corresponds to taking $\gamma (z)=0$ in (10.16) (with the changes given in (10.33)), leading to a unitary propagator identical to the one used for SU(2) (known as $J_x$ array when $\lambda$ is constant [27, 28]). The propagator produces usual SU(2) coherent states (restricted to $U^{(2)}(1)$) starting from an arbitrary initial state.

10.3.2 Restriction to a Subgroup of Elliptic Elements

Consider now the non-trivial case of a subgroup of elliptic elements in SU(1, 1) of the form $K_{[v]}=v K v^{-1}$, with v a representative element of the class $[v]\in SU(1,1)/U^{(2)}(1)\approx \mathbb {D}$ [26]. Restricting the representation to $K_{[v]}$ leads to a non-unitary finite-dimensional representation of $U^{(2)}(1)$, and this corresponds (with the changes (10.33)) to taking the propagator associated with a Hamiltonian in (10.16) that is a compact operator. For the case of constant parameters $\gamma$ and $\lambda$, this corresponds to the case $\gamma <\lambda$, see Fig. 10.2(left). This propagator generates non-Hermitian coherent states with bounded (but non constant) norm on $K_{[v]}$.

The resolution operator is bounded and invertible for arbitrary nonzero vectors $\varPhi$ and $\tilde{\varPsi }$ (there are only a few values of $\nu$, depending on the components of $\varPhi$ and $\tilde{\varPsi }$ for which it is non-invertible). For a given non-zero $\varPhi$ and a given v, there is a unique non-zero $\tilde{\varPsi }$ (up to normalization) that makes the resolution operator proportional to the identity. The overlapping kernel is square-integrable on $K_{[v]}$.

10.3.3 Restriction to Subgroups of Hyperbolic and Parabolic Elements

The restriction to subgroups of parabolic or hyperbolic elements [26] always leads to non-square integrable representations for any choices of nonzero $\varPhi$ and $\tilde{\varPsi }$. The subgroup of parabolic elements correspond (with the changes (10.33)) to the case $\gamma =\lambda$, see Fig. 10.2(center), and subgroups of hyperbolic elements correspond to the case $\gamma >\lambda$, see Fig. 10.2(right).

In these last cases other strategies should be adopted to overcome non-square integrability, and this will be considered in the next subsection.

10.3.4 Restriction to Compact Subsets

The non square-integrability of the representation is caused by the integration on the non-compact subset $\mathbb {D}$. We can consider compact subsets of $\mathbb {D}$ (times $U^{(2)}(1)$) that avoid the non square-integrability. For instance, we can take the following subsets:

• (a) $\{\zeta ,\zeta ^*,\beta \}$, with $0<|\zeta |=r_0<1$ fixed. The integration in this case is over the compact subset $S^1\times U^{(2)}(1)$.

• (b) $\{\zeta ,\zeta ^*,\beta \}$, with $0\le r_m\le |\zeta |\le r_M<1$. The integration in this case is over the compact subset $[r_m,r_M]\times S^1\times U^{(2)}(1)$.

• (c) $\{\zeta ,\zeta ^*,\beta \}$ with $\zeta =r_0e^{i \frac{2\pi k}{N}}$, $k=0,1,\ldots ,N-1$, $0<r_0<1$. The integration in this case is over $U^{(2)}(1)$ times a sum in $k=0,\ldots ,N-1$.

In all these cases the resolution operator for the corresponding subfamily of coherent states is bounded and proper choices of $\varPhi$ and $\tilde{\varPsi }$ can be made to render it invertible and even proportional to the identity. Case (c) is similar to the construction made in [29,30,31] where discrete (pseudo-) frames of coherent states were constructed for unitary representations of SU(2), SU(1, 1) and the Heisenberg-Weyl group, respectively.

In none of these cases the subset constitutes a subgroup of SU(1, 1), not even an homogeneous space, i.e. of the form SU(1, 1) / H for some subgroup H. Therefore some of the properties of Gilmore-Perelomov [17] coherent states or coherent states modulo a subgroup [19] are lost. In particular, the subfamily of coherent states associated with them does not contain all the states generated by the propagator for Hamiltonians with $\gamma \ge \lambda$, although they contain them for finite propagation distances (chosing appropriately $r_m$ and $r_M$ in case (b), for instance).

In any case, if the subfamily of coherent states associated with a compact subset leads to an invertible resolution operator, they form an overcomplete family and any state of the system can be expressed in terms of them.

10.4 Conclusions and Outlook

In this work coherent states associated with non-unitary representations of non-compact Lie groups have been introduced motivated by the behavior of certain DPS with non-Hermitian Hamiltonians (in particular PT-symmetric DPS), and following the general theory outlined in [23]. We have called these families of coherent states “non-Hermitian” rather than “non-unitary” since we focus in the physical motivation (non-Hermitian systems with a symmetry Lie group) rather than the mathematical setting (non-unitary representation of the symmetry Lie group).

Although we discuss for completeness the general, infinite-dimensional case, which requires the use of Banach spaces (versus Hilbert spaces for the unitary case) to account for the maximum generality (infinite-dimensional examples will be discussed elsewhere), we shall focus in the examples in finite-dimensional, non-unitary representations, where all the subtleties of Banach spaces do not appear. See [23] for infinite-dimensional examples with non-trivial Banach spaces ($\mathcal{V}=L^p(\mathbb {R})$ and $\mathcal{V}^*=L^q(\mathbb {R})$ with $\frac{1}{p}+\frac{1}{q}=1$).

The main obstruction for constructing coherent states for non-unitary representations comes from the lack of square-integrability of the representation. Different approaches have been used to circumvent this problem in the example of SU(1, 1) considered in Sect. 10.3, the most interesting one being the restriction to certain subgroups (in particular elliptic subgroups), where the representation restricted to the subgroup is still non-unitary but it is square-integrable. This is related to the physically interesting case of a PT-symmetric waveguide array in the regime of unbroken PT-symmetry. Other possibilities have been discussed, like the restriction to certain compact subsets of SU(1, 1).

Other approaches could be used to study this kind of systems. For instance, we could use Riesz basis like in [5,6,7,8,9], or the property of pseudo-hermiticity [25].