Power and Sample Size Considerations in Psychometrics

Abstract

An overview and discussion of the latest developments regarding power and sample size determination for statistical tests of assumptions of psychometric models are given. Theoretical as well as computational issues and simulation techniques, respectively, are considered. The treatment of the topic includes maximum likelihood and least squares procedures applied in the framework of generalized linear (mixed) models. Numerical examples and comparisons of the procedures to be introduced are quoted.

1 Introduction

The development and the application of psychometric models including techniques of estimation of model parameters and statistical tests of model assumptions have experienced a rapid growth in recent decades. Classical frequentist as well as Bayesian approaches to statistical inference have been treated and applied extensively in psychometric literature. An overview is given by, for example, Rao and Sinharay [21]. Strangely, power and sample size considerations in the classical (frequentist) sense have been neglected for a long time. Reasons may be the influence of nuisance parameters on the precision of inferential statements about the parameters of interest and the difficulty of predetermining a reasonable level of precision (e.g., the deviation from the hypothesis to be tested or the length of a confidence interval) which depends on the practical context.

This summary chapter refers to these issues and their related problems. It reviews and discusses the latest advancements concerning power and sample size planning in psychometrics developed by [5,6,7] on the one hand and by [11, 12, 30] on the other hand. The treatment refers to generalized linear models [1, 14, 15] and the exponential family of probability distributions (e.g., [4]). It is concerned with both maximum likelihood and least squares approaches. Statistical tests derived from asymptotic theory are considered as well as so-called exact tests based on discrete probability distributions. Results quoted are either derived analytically or from numerical procedures. The focus lies on the Rasch model [8, 23].

2 Power and Sample Size in a Conditional Maximum Likelihood Framework

Draxler and Alexandrowicz [6] treat questions of sample size computations within the scope of the conditional maximum likelihood (CML) approach [3] and refer to the trinity of Wald [27], score [20, 24], and likelihood ratio tests [16, 28]. Let f($\varvec{y},\mathbf {\theta },\mathbf {\tau }$) denote a probability distribution (density or mass function) of the random vector Y of the natural exponential family indexed by the parameter vectors $\mathbf {\theta }$ and $\mathbf {\tau }$ taking values in natural parameter spaces ${\Theta }$ and $\mathrm {T}$. The vector $\mathbf {\theta }$ is treated as the parameter of interest and $\mathbf {\tau }$ as a nuisance parameter vector. Denote by T(Y) a vector-valued sufficient statistic for $\mathbf {\tau }$ with probability distribution g($\varvec{t},\mathbf {\theta },\mathbf {\tau }$). Consider the sequence of independent random vectors Y$_{1},\ldots ,$ Y$_{n}$, a sample of n independent observations, and their sufficient statistics T(Y$_{1}$), $\ldots ,$ T(Y$_{n}$) with respective distributions $f(\varvec{y}_{i},\mathbf {\theta },\mathbf {\tau }_{i})$ and $g(\varvec{t}_{i},\mathbf {\theta },\mathbf {\tau }_{i})$, for $i=1,\ldots ,n$. Given T(Y$_{i}$) $=$ t(y$_{i}$), the conditional probability distribution $h(\varvec{y}_{i},\mathbf {\theta }\mid \varvec{T}_{i}=\varvec{t}_{i})=f(\cdot )/g(\cdot ), g (\cdot ) > 0$, does not depend on $\mathbf {\tau }_{i}$ $\forall$ i so that one obtains by

$$\begin{aligned} L(\mathbf {\theta })=\sum \limits _{i=1}^n \log [h(\varvec{y}_{i},\mathbf {\theta } \mid \varvec{T}_{i}=\varvec{t}_{i})]\; \end{aligned}$$

(3.1)

the logarithm of the conditional likelihood as a function of the parameter of interest $\mathbf {\theta }$ only and by

$$\begin{aligned} \hat{\mathbf {\theta }} = \underset{{\mathbf {\theta }}\,\in \,\Theta }{\text {arg max}}\, L(\mathbf {\theta })\; \end{aligned}$$

(3.2)

the CML estimate. The properties of the CML estimator are established by [3, 18] by proving a number of convergence theorems. Its asymptotic distribution is multivariate normal with mean vector $\mathbf {\theta }$ and covariance matrix $\mathbf {\Sigma }(\mathbf {\theta })=\varvec{I}(\mathbf {\theta })^{-1}$, where the Fisher information matrix is obtained by

$$\begin{aligned} \varvec{I}(\mathbf {\theta })=-E\left[ \frac{\partial ^2 L(\mathbf {\theta })}{\partial \mathbf {\theta }\partial \mathbf {\theta }^\prime }\right] .\; \end{aligned}$$

(3.3)

The latter is assumed to be positive definite. The presupposed regularity conditions generally hold for the exponential family except the following very mild condition. Roughly speaking, too many too large absolute values in the sequence of the nuisance parameters have to be excluded for the CML estimator to be (weakly) consistent. In a practical context, one will mostly be safe to assume this condition to be satisfied. Further considerations regarding power and sample size computations depend on the asymptotic properties of the CML estimator.

The precision of inferential statements about $\mathbf {\theta }$ and thus also power and sample size of tests of hypotheses regarding $\mathbf {\theta }$ obviously depend on the covariance of the estimator $\hat{\mathbf {\theta }}$. To attain a desired level of precision, the rate of decrease of Cov($\hat{\mathbf {\theta }}$) or equivalently the rate of increase of the Fisher information with increasing sample size n must be known. Unfortunately, this is not the case since the information depends on the unknown distributions of the sequence of sufficient statistics T$_{1},\ldots ,$ T$_{n}$ which themselves depend on the sequence of the unknown nuisance parameters $\mathbf {\tau }_{1}$,...,$\mathbf {\tau }_{n}$. It is an obvious consequence of the assumption that the Ys need not be identically distributed. By rewriting the information matrix as

$$\begin{aligned} \varvec{I}(\mathbf {\theta })=-E\left[ \frac{\partial ^2 L(\mathbf {\theta })}{\partial \mathbf {\theta }\partial \mathbf {\theta }^\prime }\right] = -\sum \limits _{i=1}^n E\left\{ \frac{\partial ^2 \log [h(\varvec{y}_{i},\mathbf {\theta }\mid \varvec{T}_{i}=\varvec{t}_{i})]}{\partial \mathbf {\theta }\partial \mathbf {\theta }^\prime }\right\} \; \end{aligned}$$

(3.4)

it can be seen that the information depends on the observed sequence of the sufficient statistics T$_{1}=$ t$_{1},\ldots ,$ T$_{n}=$ t$_{n}$. Since the summands on the right-hand side of (3.4), the separate pieces of information, need not be equal given different observed values of the sufficient statistics, the total information in the sample does not only depend on the total number of observations n but on the particular sequence T$_{1}=$ t$_{1},\ldots ,$ T$_{n}=$ t$_{n}$ observed. This is a problem for planning the power and sample size in experiments (before the data have been collected) since the Ts are random and it cannot be planned (deterministically) which values to be observed. As a consequence [6], introduce an additional assumption on the nuisance parameters so that a common distribution for the Ts is obtained which, besides, has another advantage. By choosing an appropriate distribution, it may be avoided to observe too many too large absolute values of the nuisance parameters meeting the requirements for the CML estimator $\hat{\mathbf {\theta }}$ to be consistent. Let the sequence of nuisance parameters be independent and identically distributed with probability density function $\varphi$($\mathbf {\tau }$) $=\varphi$($\mathbf {\tau }_1$) $=\cdots =\varphi$($\mathbf {\tau }_n$) so that

$$\begin{aligned} g(\varvec{t},\mathbf {\theta })=\int g(\varvec{t}_1,\mathbf {\theta },\mathbf {\tau }_1) \varphi (\mathbf {\tau }_1) \mathrm {d}\mathbf {\tau }_1=\cdots =\int g(\varvec{t}_n,\mathbf {\theta },\mathbf {\tau }_n) \varphi (\mathbf {\tau }_n) \mathrm {d}\mathbf {\tau }_n. \; \end{aligned}$$

(3.5)

It follows for the information matrix

$$\begin{aligned} \varvec{I}(\mathbf {\theta })=-n\int E\left\{ \frac{\partial ^2 \log [h(\varvec{y}_{i},\mathbf {\theta }\mid \varvec{T}_{i}=\varvec{t}_{i})]}{\partial \mathbf {\theta }\partial \mathbf {\theta }^\prime }\right\} g(\varvec{t},\mathbf {\theta }) \mathrm {d} \varvec{t}=n\varvec{H}(\mathbf {\theta }),\; \end{aligned}$$

(3.6)

where the matrix H($\mathbf {\theta }$) denotes the integral in (3.6) times $-1$. Hence, given the assumption (3.5) and given $\mathbf {\theta }$, the information matrix (3.6) and Cov($\hat{\mathbf {\theta }}$) are simple (one to one) functions of the sample size n.

Consider testing a class of linear hypotheses given by J$\mathbf {\theta }=$ c, with c as a vector of constants and J as the Jacobian matrix of the transformation $\mathbf {\phi }$($\mathbf {\theta }$). The latter is assumed to be a vector-valued continuously differentiable function with lower dimensionality than $\mathbf {\theta }$. As is well known, the three test statistics of the trinity of testing procedures under consideration will be asymptotically equivalent if J$\mathbf {\theta }=$ c is true, with common asymptotic distribution given by the central $\chi ^2$ with df $=$ rank(J). If J$\mathbf {\theta }=$ c does not hold asymptotic equivalence and a common distribution will only be obtained under an additional technical assumption of a sequence of alternative hypotheses (or contiguous alternative). This is a rather general result quoted by many authors. For details, the reader is referred to [6] and the references quoted therein. For computational purposes of planning the sample size, a deviation from the hypothesis to be tested must be chosen depending on practical considerations concerning the consequences of the error of the second kind of the statistical test. Provided the predetermined deviation is not too far from J$\mathbf {\theta }=$ c, the distributions of the test statistics are well approximated by the non-central $\chi ^2$ density with df $=$ rank(J) and non-centrality parameter $\lambda$ as a (quadratic) function of the chosen deviation and the sample size n (e.g., [1, 9, 10]. For the CML case and the Rasch model, results of a Monte Carlo analysis quoted by [6] hint at quite satisfying approximations of the distributions of the test statistics by the non-central $\chi ^2$ family for different levels of deviations chosen from a range of particular interest in practice. Poor approximations have only been observed in cases where the chosen deviation is tremendously large and thus unrealistic in practice. Regarding the likelihood ratio test statistic, a more extensive Monte Carlo analysis with very detailed results is provided by [2].

Let $\mathbf {\theta }=\mathbf {\theta }_1$ be a vector defining a deviation from the hypothesis to be tested so that J$\mathbf {\theta }_1$ $\ne$ c and denote by $\lambda _0$ the particular value of the non-centrality parameter of the $\chi ^2$ distribution with df $=$ rank(J) for which the $\beta$ quantile equals the value of the $1-\alpha$ quantile of the central $\chi ^2$ (with the same degrees of freedom), where $\alpha$ and $\beta$ are the probabilities for the errors of the first and second kind of the statistical test. The sample size of the tests can be determined by replacing all random quantities (functions of the observations) in the expressions of the test statistics by their expectations evaluated at $\mathbf {\theta }=\mathbf {\theta }_1$. Then, the expectations of the test statistics are set equal to the expectation of the non-central $\chi ^2$ distribution with df $=$ rank(J) and non-centrality parameter $\lambda _0$. Given $\mathbf {\theta }=\mathbf {\theta }_1$ and the assumption on the distributions of the sufficient statistics given by (3.5), the expectations of all three test statistics are one-dimensional functions of the sample size n so that the (three) equality restrictions simply have to be solved according to n. In all three cases, explicit solutions exist. Exemplarily, for the Wald test statistic W, one obtains

$$\begin{aligned} E\left\{ \chi ^2 \left[ \mathrm {df=rank}(\varvec{J}),\lambda _0 \right] \right\} =E\left[ W(\mathbf {\theta }_1) \right] \; \end{aligned}$$

(3.7)

$$\begin{aligned} \lambda _0+ \mathrm {rank}(\varvec{J}) = (\varvec{J}\mathbf {\theta }_1 - \varvec{c})^\prime \left[ \varvec{J}^\prime n^{-1} \varvec{H}(\mathbf {\theta }_1)^{-1} \varvec{J} \right] ^{-1} (\varvec{J}\mathbf {\theta }_1 - \varvec{c}) + \mathrm {rank}(\varvec{J})\; \end{aligned}$$

(3.8)

$$\begin{aligned} n=\mathrm {ceil} \left\{ \frac{\lambda _0}{(\varvec{J}\mathbf {\theta }_1 - \varvec{c})^\prime \left[ \varvec{J}^\prime \varvec{H}(\mathbf {\theta }_1)^{-1} \varvec{J} \right] ^{-1} (\varvec{J}\mathbf {\theta }_1 - \varvec{c})} \right\} .\; \end{aligned}$$

(3.9)

Regarding score and likelihood ratio tests, the sample size is determined on the same lines but the derivation of their expectations is slightly more complicated. For details, one is referred to [6].

3 Power of Pseudo-Exact or Conditional Tests of Assumptions of the Rasch Model

The following considerations are restricted to the Rasch model and are based on a Markov Chain Monte Carlo (MCMC) approach developed by [25]. Draxler and Zessin [7] discuss the power function of conditional or pseudo-exact tests which may be viewed as generalizations (multivariate and more general covariances) of Fisher’s well-known exact test. The exact discrete probability distributions under the hypothesis to be tested and under a given deviation and the power function of the tests, respectively, are well approximated using the cited MCMC technique.

The Rasch model determines the discrete probability distributions of a number of persons indexed by $i=1,\ldots ,n$ to a number of items indexed by $j=1,\ldots ,k$. Let $Y_{ij} \in \left\{ 0,1 \right\}$ be the binary response of person i to item j and consider a $n \times k$ matrix with entries given by the binary responses of every person to every item. Given the observed values of all row sums $R_1=r_1,\ldots ,R_n=r_n$ and all column sums $C_1=c_1,\ldots ,C_k=c_k$, the conditional probability distribution of all free Bernoulli variables (binary responses) is discrete uniform and simply obtained by the reciprocal number of (possible) matrices not violating the given row and column sums of the observed matrix. The exact distribution of any suitable test statistic under the hypothesis to be tested can easily be derived from this conditional distribution. A number of practically interesting examples are quoted by [19]. The conditional distribution of a test statistic under a given deviation from the hypothesis to be tested and the power of the respective conditional test may also be derived from the uniform distribution as shown by [7]. Counting the total exact number of matrices with fixed row and column sums is a complicated problem in realistic cases with the usual numbers of persons and items. Thus, for computational purposes, the exact distributions and exact power may be sufficiently approximated by random sampling from the uniform distribution of matrices with given row and column sums which is well accomplished by the application of a MCMC approach suggested by [25].

A general expression of the power function of conditional tests may be derived as follows. Consider a generalization of the Rasch model determining the discrete probability distribution of the binary response $Y_{ij}$. Denote it by $P(Y_{ij}=y_{ij} \mid \varvec{X}=\varvec{x})$, with $\varvec{X}$ as a (random) vector of covariates or a vector of any responses (of any persons to any items) other than $Y_{ij}$ on which $Y_{ij}$ may depend. The distribution $P(\cdot )$ is indexed by a parameter vector $\mathbf {\eta }$, and it is assumed that the logit of P($\cdot$) is linear in $\mathbf {\eta }$. Restricting the parameter space of $\mathbf {\eta }$ so that the Rasch model is obtained as a special case yields the hypothesis to be tested. Given X $=$ x and $\mathbf {\eta }$, all binary responses are assumed to be independent so that their joint probability distribution is obtained by the product over all persons and items. Let ${\Omega }$ denote the sample space which consists of all $n \times k$ matrices with given row and column sums. Then, it follows for the joint conditional distribution

$$\begin{aligned} P({\varvec{Y}} = {\varvec{y}} \mid {\varvec{X}} = \varvec{x}, R_1=r_1,\ldots ,R_n=r_n,C_1=c_1,\ldots ,C_k=c_k) = \nonumber \\ \frac{\prod \limits _{i=1}^n \prod \limits _{j=1}^k P(Y_{ij}=y_{ij} \mid \varvec{X} = \varvec{x})}{\sum \limits _{{\Omega }} \prod \limits _{i=1}^n \prod \limits _{j=1}^k P(Y_{ij}=y_{ij} \mid \varvec{X} = \varvec{x})},\nonumber \\ \end{aligned}$$

(3.10)

where Y consists of all free Bernoulli variables (binary responses). Let $\textit{C} \subseteq {\Omega }$ be the critical region with size $\alpha$ of the conditional test of the hypothesis of any restriction of the parameter space of $\mathbf {\eta }$ yielding the Rasch model. The power function $\beta$($\mathbf {\eta }$) of this test is then easily obtained by summation of (3.10) over all elements in $\textit{C}$.

The denominator on the right-hand side of (3.10) is a normalizing constant. The summation has to be taken over the complete set ${\Omega }$. In practice, for computational purposes, a random sample of matrices from ${\Omega }$ is drawn so that the summation has only to be taken over all matrices drawn. For this purpose, for instance, the R package Rasch Sampler [26] may be used. The conditional distribution of Y, the size $\alpha$ of the critical region $\textit{C}$, and the power function of the test can be approximated in this way. The critical region $\textit{C}$ will be most powerful at level $\alpha$ if it is chosen according to the fundamental lemma of [17]. Thus, it has to be composed of those 100${\alpha }$% of matrices from ${\Omega }$ yielding the largest values of (3.10).

An example of the parameterization of the general model which is of particular interest in practice assumes the Rasch model to hold conditionally on an additional covariate. For simplicity, consider a fixed (not random) binary covariate $x_i \in \left\{ 0,1 \right\}$, for instance sex. Then,

$$\begin{aligned} P(Y_{ij}=y_{ij} \mid x_i) = \frac{\mathrm {exp} \left[ y_{ij} (\theta _i + \beta _j + \delta _j x_i) \right] }{1+\mathrm {exp} (\theta _i + \beta _j + \delta _j x_i)}. \end{aligned}$$

(3.11)

Factorization of the product of (3.11) over all persons and items immediately shows that the statistics $R_i = \sum _j Y_{ij}$, $C_j = \sum _i Y_{ij}$ and $T_j = \sum _i Y_{ij}x_i$ are sufficient for the parameters $\theta _i$, $\beta _j$, and $\delta _j$ so that for the joint conditional distribution of the Ts one obtains

$$\begin{aligned} P(\varvec{T} = \varvec{t} \mid x_1,\ldots ,x_n, R_1=r_1,\ldots ,R_n=r_n,C_1=c_1,\ldots ,C_k=c_k) = \nonumber \\ \frac{\sum \limits _{\mathrm {T}} \mathrm {exp} \left( \sum \limits _{j=1}^k t_j \delta _j \right) }{\sum \limits _{\mathrm {\Omega }} \mathrm {exp} \left( \sum \limits _{j=1}^k t_j \delta _j \right) }, \end{aligned}$$

(3.12)

with $\varvec{T}^\prime$ = (T $_{1},\ldots ,$ T$_{k-1}$). Note that one of the Ts is not free. The summation in the numerator of the right side of (3.12) has to be taken over the subset $\mathrm {T} \subseteq \mathrm {\Omega }$ consisting of those matrices contained in $\mathrm {\Omega }$ which satisfy $\varvec{T} =$ t. The parameters $\theta _i \in \mathbb {R}$ and $\beta _j \in \mathbb {R}$ are person and item parameters which are treated as nuisance by conditioning on the observed values of their sufficient statistics, and $\delta _j \in \mathbb {R}$ is characterizing a violation of the assumption of the Rasch model of independence of the items of the covariate. Thus, $\delta _j$ is the conditional effect of item j given the covariate. For identifiability reasons, let $\delta _k = 0$ or $\sum \delta _j = 0$. Note that in this example, the $\theta$ parameters (person parameters) are nuisance parameters. This is inconsistent with the notation introduced. This is only for a notational convenience in psychometric literature (e.g., [8]).

A second example concerns a conditional test of the assumption of local independence of the responses of a person to the items. Consider the following model

$$\begin{aligned} P(Y_{i2} = y_{i2} \mid Y_{i1} = y_{i1}) \propto \mathrm {exp} \left[ y_{i2} (\theta _i + \beta _2 + \vartheta y_{i1}) \right] \end{aligned}$$

(3.13)

which introduces local dependence of item 2 on item 1. The probability distributions of the binary responses of all persons to all other items (except item 2) are assumed to be given by the Rasch model. Unlike the previous example, in this case, the joint conditional distribution of all free binary responses and the power function of the conditional test of $\vartheta = 0$ is not only a function of the parameter of interest $\vartheta$ characterizing a violation of the assumption of local independence (of item 2 on item 1) but of all parameters (since the row and column sums of the matrix of responses are not sufficient for the person and item parameters). In practice, it seems to be rather difficult to choose reasonable values for all parameters of the model, in particular for the person parameters, so that the power can be computed.

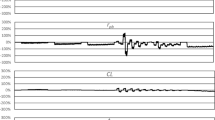
Finally, a numerical example from [7] shall be presented but using different seeds for the pseudo-random number generator (so that the results will not be identical). It refers to the model given by (3.11) and (3.12), respectively, and is concerned with power computations of the conditional test of the hypothesis that all $\delta$s are equal to 0 with size $\alpha = 0.05$. Consider $n = 100$ persons and $k = 15$ items. The column sums of the observed matrix of binary responses are between 4 and 97. The row sums have large frequencies for values in the middle of the possible range and low frequencies for values near 0 and 15. For one half of the total number of respondents, the covariate takes the value 1, and for the other half, it is 0. Item 9 is chosen as the only deviating item, where item 9 is an item with a given column sum of 53 which is roughly in the middle of the possible range of values. The power is computed for different values of $\delta _9$ deviating from 0. The R Package Rasch Sampler is used to sample from $\mathrm {\Omega }$. For every chosen $\delta _9$ value, 8000 matrices are drawn, and for each matrix, its conditional probability is computed using (3.12). The critical region C is chosen to consist of the 5% of matrices (400 matrices) with the largest values of (3.12). The power is computed by summation of the conditional probabilities over all matrices in $\textit{C}$. This procedure is replicated 100 times to observe the precision of the approximation of the exact power. Figure 3.1 shows summaries of the results.

Fig. 3.1

Summaries of power computations of conditional tests of the hypothesis that all $\delta$s in (3.11) and (3.12), respectively, equal 0 considered as a function of $\delta _9$ (deviation of item 9)

4 Linear Models and Least Squares Approach

Starting traditionally, one has to realize that most statistical tests of assumptions of the Rasch model apply test statistics which are (asymptotically) $\chi ^2$ distributed. These test statistics’ degrees of freedom do not depend on the sample size but only on the number of parameters estimated. In the following, an approach is discussed where the number of degrees of freedom does depend on the sample size so that it can be used for power and sample size considerations. Kubinger, Rasch, and Yanagida [11, 12, 30] aimed for some F-distributed test statistic within the framework of analysis of variance. In general, such an approach provides a variety of procedures for power and sample size planning, whether there are one- or multi-way designs, whether there is the case of models with fixed or random effects or a mixed model, and whether the factors are crossed, nested, or mixed classified.

Since the Rasch model is a generalized linear model with logit link function, the idea of testing assumptions of the model within the framework of analysis of variance (linear models with identity link) may sound strange at first sight, but surprisingly, it works pretty well. Consider a three-way analysis of variance of the kind $(A~ \succ ~\varvec{B})~\times ~C$, with A as a fixed factor characterizing a covariate associated with the persons, for instance the persons$^\prime$ sex, C as another fixed factor with levels given by the different items and B as a random factor with levels given by the persons (which are assumed to be drawn randomly from the population). The latter is nested within the levels of A. Hence, linear effects of the factors on the expectations of Bernoulli variables (the binary responses of persons to items) are assumed. Of interest is the hypothesis that there is no interaction effect $A \times C$. It is tested using a F test statistic obtained by dividing the mean of squares of the interaction $A \times C$ by the mean of squares of the interaction $\varvec{B} \times C$ within A. Roughly speaking, providing the number of levels of A is restricted to two, this approach may be viewed as equivalent to considering the logit model given by (3.11) and testing the hypothesis that all $\delta$s (conditional effect parameters or the interaction of the covariate and the items) equal 0.

It is obvious that the probability distribution of the test statistic introduced cannot be assumed to belong to a known family of distributions, like F, since the distributions of the binary responses of persons to items cannot be of the class of normal distributions. Rasch, Rusch, Simeckova, Kubinger, Moder, and Simecek [22] provide results of a simulation study obtaining actual type I risks sometimes far exceeding the nominal level (up to five times as high). Thus, power and sample size computations have been based on numerical procedures approximating the probability distributions of the test statistic under the hypothesis to be tested as well as under a given deviation. In doing so, Kubinger, Rasch, and Yanagida [11] showed that their approach will only work if no main effect of A exists. Strictly speaking, the nominal type I risk of the statistical test of the hypothesis of no interaction $A \times C$ holds as long as no main effect of A is assumed; otherwise, the type I risk will be far too high.

5 Numerical Examples and Comparisons

In the following, a few numerical examples are quoted comparing the power of the $\chi ^2$ tests with the F test introduced. The size of the tests is predetermined as $\alpha = 0.05$ (nominal type I risk). The hypothesis to be tested assumes equality of the item parameters of the Rasch model between two groups of persons. The number of persons is chosen to be 300 in each of both groups, and the person parameters are drawn from the standard normal distribution. The number of items is chosen as $k = 15$. Under the hypothesis to be tested, it is assumed that the item parameters are given by $-3.5$, $-3$, $-2.5$, $-2$, $-1.5$, $-1$, $-0.5$, 0, 0.5, 1, 1.5, 2, 2.5, 3, and 3.5 in both groups (equality of item parameters between the groups).

The following scenarios of deviations from this hypothesis are considered. In each case, two items are considered as deviating items. The respective columns in Tables 3.1 and 3.2 quote the absolute deviations of the two deviating items from the respective values assumed under the hypothesis to be tested within both groups of persons. For example, referring to the first row and first column of Table 3.1, the parameter of item 7 is 0.1 smaller than the value under the hypothesis to be tested (so that it equals ${-}0.6$), whereas the parameter of item 9 is 0.1 larger (so that it equals 0.6) in the first group of persons. In the second group, the deviations are exactly the other way round (deviations of reversed sign). Thus, the absolute differences of the item parameters of the two items between the two groups are both 0.2 (symmetrically around the value assumed under the hypothesis to be tested).

The power for the Wald test is computed using the relations given by (3.7)–(3.9), where the distribution of each $\mathbf {\tau }$ (which corresponds to the person parameter in the Rasch model) is assumed to be the standard normal. The common distribution $g(\varvec{t}, \mathbf {\theta })$ of the sufficient statistics for the $\mathbf {\tau }$ s is obtained using numerical integration (Gauss–Hermite). The power of the F tests is computed using simulation procedures provided by the R package pwrRasch [29]. The number of simulation runs (number of replications) is chosen to be 3600. Tables 3.1 and 3.2 show the results for all considered scenarios of deviations.

Table 3.1 Power computations for Wald and F tests referring to scenarios with deviating items 7 and 9 as well as 5 and 11

Table 3.2 Power computations for Wald and F tests referring to scenarios with deviating items 3 and 13 as well as 1 and 15

The main implication of the results is to be expected from theory and may be stated as follows. In terms of power, the F test performs better than the Wald test in the cases shown in Table 3.1, whereas its performance is worse in the cases shown in Table 3.2. Table 3.1 refers to examples in which the parameter values of the two deviating items are approximately in the middle of the assumed range of values matching the (assumed) mean of the distribution of person parameters. Consequently, the majority of expectations of the binary responses of persons to the respective deviating items are around 0.5, and for an expectation in a close interval around 0.5, the dependence on the assumed factors is close to linearity as is assumed in the linear modeling framework of analysis of variance. On the contrary, Table 3.2 refers to scenarios assuming the expectations of the binary responses to both deviating items to be farther from 0.5 and thus closer to the natural boundaries 0 and 1 so that the assumed linear dependence (of the expectation on the factors) is more inappropriate.

It must also be remarked that the F test seems to be biased, but the bias seems to be small. At least, this is what can be observed in the examples considered. In all scenarios, the observed type I risk is slightly larger than the nominal one as is seen by the values in parenthesis in both tables.

6 Discussion

In the analysis of psychometric data, one is usually confronted with nuisance parameters influencing the precision of inferential statements about parameters of interest. One way of eliminating the effect of nuisance parameters is conditioning on the observed values of their sufficient statistics and pursuing the well-known CML approach, respectively, which is, for instance, applicable for the class of Rasch models. When the data and in particular the sufficient statistics (as functions of the data) have already been observed, such an approach allows for estimating the parameters of interest and testing hypotheses about them. It is even possible to compute the power of statistical tests post hoc. Before observing the data, like in cases the sample size of an experiment is to be planned in advance, the CML approach is obviously not applicable without additional assumptions on the nuisance parameters and their sufficient statistics as discussed by [6]. Thus, one may argue that in this case CML as well as the consideration of conditional tests described in Sect. 3.3 is not suitable solutions of the problem of the influence of nuisance parameters.

Developing this thought further, one may arrive at another common approach of dealing with nuisance parameters termed as marginal maximum likelihood which is widely used for psychometric models. This approach assumes a probability distribution for the nuisance parameters since in most applications the nuisance parameters are treated as random variables anyway (since they are assumed to be drawn randomly from the population). Maydeu-Olivares and Montano [13] used the marginal maximum likelihood framework to develop procedures for power and sample size computations for a few particular statistical tests of assumptions of psychometric models.

Another point worth discussing is the problem of predetermining a deviation from the hypothesis to be tested in practice (for the computation of power and sample size, respectively). In most applications, not only one but multiple parameters are of interest and the practical meaning of a deviation from the parameter value to be tested usually differs from one parameter to the other and depends on the practical context as well. A suitable contribution on this topic is provided by [5] describing a three-step procedure facilitating the evaluation of the practical meaning of deviations from the hypothesis to be tested.

An essential difference between the conditional tests based on discrete probability distributions and all other approaches described in this summary chapter is that the conditional tests are one-sided. Hence, the power of these tests is expected to be considerably larger so that comparisons with the $\chi ^2$ and F tests (in terms of power) do not make much sense. From the practical point of view, one-sided tests may be less suitable in the context of psychometric modeling since one is usually interested in the question whether model assumptions hold or not. The directions or signs of deviations from the parameter values to be tested do not play an important role.

Finally, some comments on the utility of the F test shall be discussed. Power computations depend on Monte Carlo procedures. On the one hand, it is nice to have an R package providing the necessary numerical procedures for the approximation of the power of the tests. On the other hand, the computation of the power with the R package pwrRasch is restricted to tests of hypotheses of the following type. Regarding every single parameter of interest, exactly one value has to be chosen. That is, the item parameters have to be chosen for both groups of persons and under the hypothesis to be tested they are chosen so that they are equal between both groups (like it is described in the first two paragraphs of Sect. 3.5). Such a hypothesis is usually not the hypothesis one is interested in. Of interest is the hypothesis that the differences between the item parameters equal 0. The problem is that the power of the test does not only depend on the difference of an item parameter between the groups but also on the level on which this difference is assumed (whether it is an easy or difficult item that possibly differs between two groups) and, again, the latter is usually not of interest in an application and it will hardly ever be possible to reasonably predetermine it. Furthermore, the procedure is restricted to the Rasch model and to the question of group differences. Tests of other important assumptions of the model like local independence and equal item discriminations are excluded.