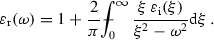Universal Dispersion Model for Characterization of Thin Films Over Wide Spectral Range

Abstract

The universal dispersion model is a collection of dispersion models (contributions to the dielectric response) describing individual elementary excitation in solids. All contributions presented in this chapter satisfy the basic conditions that follow from the theory of dispersion (time reversal symmetry, Kramers–Kronig consistency and finite sum rule integral). The individual contributions are presented in an unified formalism. In this formalism the spectral distributions of the contributions are parameterized using dispersion functions normalized with respect to the sum rule. These normalized dispersion functions must be multiplied by the transition strengths parameters which can be related to the density of charged particles. The separation of contributions into the transitions strengths and normalized spectral distributions is beneficial since it allows us to elegantly introduce the temperature dependencies into these models.

1 Introduction

The dispersion models are used to describe dielectric response of materials. From the theory of dispersion it follows that the dielectric response must fulfill three fundamental conditions [1,2,3,4,5,6,7] and one supplementary condition. For isotropic materials without spatial dispersion in thermodynamic equilibrium these conditions can be written for the dielectric function as follows:

• 1. Time-reversal symmetry

  $$\begin{aligned} \hat{\varepsilon }(\omega ) = \hat{\varepsilon }^*(-\omega ) \,, \end{aligned}$$

  (3.1)

  where the star denotes the complex conjugation. This condition ensures that the response function is a real function in time domain.

• 2. Kramers–Kronig (KK) relations

  

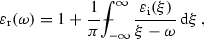  (3.2)

  where the subscripts ‘r’ and ‘i’ denote the real and imaginary parts and the integral must be understood as the Cauchy principal value. The condition (3.1) allows us to write the KK relation (3.2) as

  

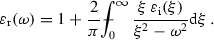  (3.3)

  The KK relations follow from the causality of the response function.

• 3. Sum rule

  $$\begin{aligned} \int _0^\infty \omega \, \varepsilon _\mathrm {i}(\omega ) \mathrm {d}\omega = \frac{\pi }{2} \omega _\mathrm{p}^{2} \,, \end{aligned}$$

  (3.4)

  where the constant $\omega _\mathrm{p}$ is called the plasma frequency and it is related to the electron density $\mathcal {N}_\mathrm {e}$ as follows [7]

  $$\begin{aligned} \omega _\mathrm{p}^2 = \frac{e^2 \mathcal {N}_\mathrm {e}\mathcal {U}}{\epsilon _0 m_\mathrm {e}} \,. \end{aligned}$$

  (3.5)

  The dimensionless correction factor $\mathcal {U}$ compensates the influence of the positive nuclei. If the ratio of nucleon number to proton number is assumed be 2:1 then the theoretical value of this factor is $\mathcal {U}=1.000274$ [7,8,9,10,11]. The sum rule can be derived with the help of the superconvergence theorem , assuming that at high frequencies, the dielectric function is the same for all materials as

  $$\begin{aligned} \hat{\varepsilon }(\omega ) \approx 1 - \frac{\omega _\mathrm{p}^2}{\omega ^2} \,. \end{aligned}$$

  (3.6)

  The term plasma frequency is motivated by the equation above since it corresponds to the model of sparse noninteracting plasma . The sum rule can be also derived on the basis of either classical or quantum laws of motion.

• 4. Dissipative system condition

  $$\begin{aligned} \varepsilon _\mathrm {i}(\omega ) \ge 0 \qquad \text{ for } \qquad \omega > 0 \,. \end{aligned}$$

  (3.7)

  This condition corresponds to systems in thermodynamic equilibrium.

This chapter will discuss only models of linear dielectric response of nonmagnetic media without spatial dispersion, which satisfy the three fundamental conditions. In principle the tensor of dielectric functions should be used instead of the scalar dielectric function . For simplicity, only results for the scalar dielectric function will be presented, i. e. for isotropic materials. It is, however, not difficult to generalize these models to anisotropic media .

In this chapter, the collection of models suitable for describing various elementary excitations will be presented. A combination of these models can be used for the description of complete dielectric response of a wide range of materials in the spectral range form far IR to X-ray. Therefore, the collection of these models will be further called the universal dispersion model (UDM). The emphasis will be placed on models for which the dielectric function can be calculated analytically. Although this chapter aims to present the dispersion models from the practical point of view, basic knowledge of condensed matter physics will be necessary in order to understand the principles behind the presented models. Thus, in this chapter, the isotropic version of the UDM will be presented.

The Kramers–Kronig relations (3.2) and (3.3) allow us to calculate the real part of the dielectric function if the imaginary part is known. It is even possible to understand these relations in the sense of generalized dielectric functions, i. e. the imaginary part of the dielectric function can contain delta functions or discontinuities. The situation is more complicated for the inverse Kramers–Kronig relation expressing the imaginary part of the dielectric function. The general form of this Kramers–Kronig relation is as follows

(3.8)

or

(3.9)

The second term in (3.2) and the first term in (3.8) represent the Hilbert transform and the inverse Hilbert transform of the imaginary and real parts of the susceptibility $\hat{\chi }(\omega )=\hat{\varepsilon }(\omega )-1$. The second term in (3.8) is zero for dielectrics, but it is nonzero for conducting materials. Therefore, for conducting materials it is not possible to calculate the imaginary part of the susceptibility function simply as the inverse Hilbert transform of its real part [6]. This problem can be avoided if the Kramers–Kronig relations are written for the quantity proportional to $\omega \hat{\chi }(\omega )$ (e. g. complex optical conductivity $\hat{\sigma }(\omega )=-\mathrm{i}\omega \epsilon _0 \hat{\chi }(\omega )$). For such quantity the Kramers–Kronig relations are given only by the Hilbert transforms.

2 Theoretical Background

2.1 Classical Model

In the beginning, there was the classical model, and the classical model was used for modeling of everything. Within the frame of the classical model, the medium is described as a system of massive charged particles forming quasi-neutral environment. Two types of forces are considered, the restoring forces which act to return the particles to the equilibrium positions and damping forces slowing down the particles. It is not necessary to consider all the particles forming the system. Since identical particles in equivalent configurations exhibit identical behavior, it is possible to consider an equivalently behaving system consisting of m nonequivalent coupled particles. Taking into account the above considerations (in the isotropic case) the problem leads to m linear ordinary differential equations which can be easily solved [12]. The dielectric function of such a system can be written in a closed matrix form

$$\begin{aligned} \hat{\varepsilon }(\omega ) = 1 + \mathbf {\omega }_\mathrm{p}^\mathrm{T} [\mathbf S - \omega ^2 \mathbf I - \mathrm{i}\omega \mathbf G]^{-1} \mathbf {\omega }_\mathrm{p} \,, \end{aligned}$$

(3.10)

where the column vector $\mathbf {\omega }_\mathrm{p}$ contains plasma frequencies. These are proportional to square roots of the effective densities of individual modes:

$$\begin{aligned} \mathbf {\omega }_\mathrm{p}^\mathrm{T} = ( \omega _{\mathrm{p},1} , \omega _{\mathrm{p},2} , \cdots , \omega _{\mathrm{p},m}) \,, \end{aligned}$$

(3.11)

where the symbol $^\mathrm{T}$ denotes transposition. The matrix $\mathbf S$ is diagonal with squares of central frequencies on the diagonal (zero frequencies for the description of free carriers are possible):

$$\begin{aligned} \mathbf S = \left( \begin{array}{cccc} \omega _{\mathrm{c},1}^2 &{} 0 &{} \cdots &{} 0 \\ 0 &{} \omega _{\mathrm{c},2}^2 &{} \cdots &{} 0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{}\cdots &{} \omega _{\mathrm{c},m}^2 \end{array} \right) \,, \end{aligned}$$

(3.12)

$\mathbf I$ denotes the unit matrix and $\mathbf G$ is real symmetric positive definite matrix

$$\begin{aligned} \mathbf G = \left( \begin{array}{cccc} \gamma _{11} &{} \gamma _{12} &{} \cdots &{} \gamma _{1m} \\ \gamma _{12} &{} \gamma _{22} &{} \cdots &{} \gamma _{2m} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \gamma _{1m} &{} \gamma _{2m} &{} \cdots &{} \gamma _{mm} \end{array} \right) \,, \end{aligned}$$

(3.13)

where $\gamma _{lk}$ are the damping parameters . The positive definiteness of the matrix $\mathbf G$ ensures that system is dissipative . The matrix $\mathbf G$ can be conveniently parameterized using Cholesky decomposition as

$$\begin{aligned} \mathbf G = \mathbf B \mathbf B^\mathrm{T} \,, \end{aligned}$$

(3.14)

where $\mathbf B$ is a lower triangular matrix with positive entries on the diagonal. The classical model contains 3 parameters for each mode determining the frequency, strength and damping plus additional $m(m-1)/2$ parameters determining the coupling between modes, therefore, the total number of dispersion parameters is $3 m + m(m-1)/2$.

The dielectric response (3.10) is a general result for the system of damped harmonic oscillators (DHO) with coupled modes . In practice, it is often possible to assume that the oscillators are independent. If this is the case, the matrix $\mathbf G$ is diagonal and the resulting model is known as the Drude–Lorentz model . The dielectric function of the Drude–Lorentz model is then given as [13]

$$\begin{aligned} \hat{\varepsilon }(\omega ) = 1 + \sum _k \frac{\omega _{\mathrm{p},k}^2}{ \omega _{\mathrm{c},k}^2 - \omega ^2 - \mathrm{i}\gamma _k \omega } \,, \end{aligned}$$

(3.15)

where $\gamma _k \equiv \gamma _{kk}$. The terms for which $\omega _{\mathrm{c},k}=0$ corresponds to the Drude model describing the dielectric response of free charges. The terms with nonzero $\omega _{\mathrm{c},k}$ correspond to the Lorentz model describing dielectric response of bound charges.

The classical model is derived from equations of motion which ensures that it fulfills the time reversal symmetry and it is KK consistent. From the asymptotic behavior it is possible to prove that the sum rule integral depends only on the plasma frequency parameters as

$$\begin{aligned} \int _0^\infty \omega \, \varepsilon _\mathrm {i}(\omega ) \ \mathrm {d}\omega = \frac{\pi }{2} \sum _k \omega _{\mathrm{p},k}^2 \,. \end{aligned}$$

(3.16)

The classical model presented above is expressed in the basis of eigenmode vibrations, i. e. $\omega _{\mathrm{p},k}^2$ describes the strength of the vibration mode, but the sum rule takes the same form also in the basis of individual particles. Thus, the sum of the plasma frequencies over all the vibration modes is

$$\begin{aligned} \sum _k \omega _{\mathrm{p},k}^2 = \omega _\mathrm{p}^2 \,, \end{aligned}$$

(3.17)

where $\omega _\mathrm{p}$ is the plasma frequency related to the density of the particles in the system by (3.5).

The classical model is universal in the sense that it can be used to model a wide range of absorption phenomena in solids. For some phenomena the accuracy of the classical model is sufficient but for many others, it is not possible to achieve the desired accuracy with a reasonable number of terms. This is not surprising since a number of quantum mechanical effects cannot be described by models based purely on classical mechanics (e. g. bandgap). Therefore, one should look for other models which would be more appropriate for the description of such phenomena.

2.2 Models Based on Quantum Mechanics

In principle it is possible to describe solids as many body systems and use the laws of quantum mechanics to derive the dielectric response. This approach, known as ab initio calculations, is very important for the study of the properties of solids since they does not need any experimental input. It is, however, numerically intensive and moreover, the current approximate approaches are not accurate or fast enough to be utilized as dispersion models in practice (see Chap. 4 for details). The practical dispersion models are based on the results known from the quantum mechanical theory but apart from that they also require some empirical knowledge.

A good starting point for expressing the dielectric function is using the Fermi golden rule (or alternatively Kubo formula) [10, 13,14,15,16] for an open quantum mechanical system at temperature T. The real and imaginary parts of the dielectric function in the frame of the dipole approximation are then expressed as

$$\begin{aligned} \varepsilon _\mathrm {r}(E)&= 1 + \frac{2}{\epsilon _0 V} \sum _{i,f}^{f \ne i} P_i(T) |\langle f | \hat{d}_x | i \rangle |^2 \frac{E_f-E_i}{(E_f-E_i)^2-E^2} \,, \end{aligned}$$

(3.18)

$$\begin{aligned} \varepsilon _\mathrm {i}(E)&= \frac{\pi }{\epsilon _0 V} \sum _{i,f}^{f \ne i} P_i(T) |\langle f | \hat{d}_x | i \rangle |^2 \left[ \delta (E_f-E_i-E) - \delta (E_i-E_f-E) \right] \,, \end{aligned}$$

(3.19)

where the summation runs over all possible initial states $| i \rangle$ and final states $| f \rangle$. The symbol V denotes the volume of the system and the symbol E denotes the photon energy, which is related to frequency as $E=\hbar \omega$. The symbols $E_i$ and $E_f$ are the initial and final state energies of the system. The interaction of light with the quantum system is represented by stimulated absorption or emission of the photons with simultaneous transitions of the system from the initial to the final state. In (3.19) the absorption and emission processes are represented by delta functions in the imaginary part. The use of the delta functions is correct in the approximation of infinite lifetime of the states. The finite lifetime of the states leads to fluctuation of the energies of the states and the delta functions must be replaced by functions with finite width. This will be discussed in detail in Sect. 3.2.3. The real part (3.18) is calculated using the KK relation (3.2) which leads to the poles. The signs of these functions depend on whether an absorption process is taking place $E_i<E_f$ or an emission process is taking place $E_i>E_f$. The probability of the transition is given by the square of the size of dipole matrix element $\langle f | \hat{d}_x | i \rangle$, where $\hat{d}_x$ is the dipole operator along the coordinate x parallel to the external electric field

$$\begin{aligned} \hat{d}_x = \sum _j q_j \hat{x}_j \,. \end{aligned}$$

(3.20)

In the expression above, the summation over j runs over all particles with the charges $q_j$ and position operator $\hat{x}_j$. Therefore, for each term in (3.19) representing absorption process, there is a term representing a reverse emission process with the same transition probability. These terms have opposite signs but the probability $P_i(T)$ of finding the system in the initial state $| i \rangle$ is different for the absorption processes $E_i<E_f$ and for the emission processes $E_i>E_f$. For this reason, the net contribution is nonzero. In equilibrium, the system is described by the canonical distribution with the probability of finding the system in state $| i \rangle$ given by:

$$\begin{aligned} P_i(T) = \exp \left( \frac{\Omega -E_i}{k_\mathrm {B}T}\right) \,, \end{aligned}$$

(3.21)

with the canonical potential $\Omega$ determined from the normalization condition

$$\begin{aligned} \sum _i P_i(T) = \sum _i \exp \left( \frac{\Omega -E_i}{k_\mathrm {B}T}\right) = 1 \,. \end{aligned}$$

(3.22)

Note that for systems in equilibrium, the probability for the absorption process is higher than for the reverse emission process. Therefore, the contribution to the imaginary part of the dielectric function in (3.19) is positive for all positive photon energies E. The condition that the imaginary part of the dielectric function is positive is the fourth supplementary condition for dissipative systems that must be fulfilled by dispersion models. In the classical model the fulfillment of this condition is ensured by the positive definiteness of the matrix $\mathbf G$ composed of damping coefficients (3.13).

The dipole matrix elements in (3.18) and (3.19) can be rewritten using the current matrix elements as

$$\begin{aligned} |\langle f | \hat{d}_x | i \rangle |^2 = \frac{\hbar ^2 |\langle f | \hat{j}_x | i \rangle |^2}{(E_f-E_i)^2} \,, \end{aligned}$$

(3.23)

where $\hat{j}_x$ is the volume integrated current density operator (or simply current operator [16]) related to the momentum operators of individual particles $\hat{p}_{x,j}$ as

$$\begin{aligned} \hat{j}_x = \sum _j \frac{q_j}{m_j} \hat{p}_{x,j} \,. \end{aligned}$$

(3.24)

The imaginary part of the dielectric function is then expressed as

$$\begin{aligned} \varepsilon _\mathrm {i}(E) = \frac{\pi \hbar ^{2}}{\epsilon _0 V} \sum _{i,f}^{f \ne i} P_i(T) \frac{|\langle f | \hat{j}_x | i \rangle |^2}{(E_f-E_i)^2} \left[ \delta (E_f-E_i-E) - \delta (E_i-E_f-E) \right] \,, \end{aligned}$$

(3.25)

Since the delta functions ensure that $\vert E_f-E_i\vert =E$, the factor $(E_f-E_i)^2$ in the denominator can be written as $E^2$ and placed outside of the sum. Therefore, if we define the joint density of states (JDOS) function as

$$\begin{aligned} J(E) = \frac{\pi \hbar ^2}{\epsilon _0 V} \sum _{i,f}^{f \ne i} P_i(T) |\langle f | \hat{j}_x | i \rangle |^2 \left[ \delta (E_f-E_i-E) - \delta (E_i-E_f-E) \right] \,, \end{aligned}$$

(3.26)

then the imaginary part of the dielectric function reduces to

$$\begin{aligned} \varepsilon _\mathrm {i}(E) = \frac{J(E)}{E^2}\,. \end{aligned}$$

(3.27)

In some cases, the JDOS function is defined without the matrix elements inside the sum

$$\begin{aligned} \mathcal {J}(E) = \frac{1}{V} \sum _{i,f}^{f \ne i} P_i(T) \left[ \delta (E_f-E_i-E) - \delta (E_i-E_f-E) \right] \,. \end{aligned}$$

(3.28)

This function coincides, up to a constant factor, with the JDOS function (3.26) only if the matrix elements are independent on i and f. The approximation of constant matrix elements is commonly used in the case of transitions of the same type occurring in the narrow energy range. In general, however, the matrix elements cannot be assumed to be constant.

Apart from the functions $\varepsilon _\mathrm {i}(E)$ and J(E) it is convenient to also introduce the function F(E) given as

$$\begin{aligned} F(E) = \frac{\pi \hbar ^2}{\epsilon _0 V} \sum _{i,f}^{f \ne i} P_i(T) \frac{|\langle f | \hat{j}_x | i \rangle |^2}{E_f-E_i} \left[ \delta (E_f-E_i-E) + \delta (E_i-E_f-E) \right] \,. \end{aligned}$$

(3.29)

This function will be called the transition strength function and it is related to the imaginary part of the dielectric function as

$$\begin{aligned} \varepsilon _\mathrm {i}(E) = \frac{F(E)}{E}\,. \end{aligned}$$

(3.30)

Note that, the transition strength function in the frame of the dipole approximation is, up to the constant factor, equivalent to the real part of the complex optical conductivity $\sigma _\mathrm{r}(E) = F(E) \, \epsilon _0/\hbar$. The function F(E) is important because it provides a bridge between the classical sum rule and the quantum mechanical Thomas–Reiche–Kuhn (TRK) sum rule [13, 17]. The TRK sum rule can be applied separately to each type of the charged particles (electrons, different nuclei) existing in the system. The TRK sum rule further says that the sum of dimensionless oscillator strengths $f_{if}^k$ over the final states f is independent on the initial states i and is equal to the number of particles of type k in the system:

$$\begin{aligned} \frac{1}{V} \sum _{f}^{f \ne i} f_{if}^k = \mathcal {N}_k \,. \end{aligned}$$

(3.31)

In the formula above, V is the volume of the system and $\mathcal {N}_k$ is the density of the particles of type k. The oscillator strength can be defined with the help of the matrix elements of the dipole $\hat{d}_{xk}$ or current $\hat{j}_{xk}$ operators for particles of type k as

$$\begin{aligned} f_{if}^k = \frac{2m_k}{\hbar ^2 q_k^2} (E_f-E_i) | \langle f | \hat{d}_{xk} | i \rangle |^2 = \frac{2 m_k}{q_k^2} \dfrac{| \langle f | \hat{j}_{xk} | i \rangle |^2}{E_f-E_i}\,, \end{aligned}$$

(3.32)

where $q_k$ and $m_k$ are the charge and mass of the particles of type k, respectively. Note that the TRK sum rule (3.31) is derived from the general principles of quantum mechanics and the assumption that the Hamiltonian is a sum of kinetic energy, which depends only on momentum operators, and the potential energy, which depends only on position operators. In the frame of the dipole approximation, the TRK sum rule can be written using of the transition strength function as [7]

$$\begin{aligned} \int _0^\infty F(E) \ \mathrm {d}E = \sum _k \frac{\pi }{2} \frac{(q_k \hbar )^2}{\epsilon _0 m_k} \mathcal {N}_k = \frac{\pi }{2} \frac{(e \hbar )^2}{\epsilon _0 m_\mathrm {e}} \mathcal {N}_\mathrm {e}\mathcal {U}= N \,, \end{aligned}$$

(3.33)

which is equivalent to the classical sum rule (3.16). The quantity N introduced in the above equation will be called the total transition strength. In theory, the quantity N can be determined from the known density of charged particles.

Although the right side of (3.19) is expressed as a sum of delta functions, the number of energy levels in the system is sufficiently high so that it is possible to use the continuous JDOS functions. In practice, it is convenient to express the JDOS function as a sum of contributions corresponding to individual elementary absorption processes. The JDOS function corresponding to the individual elementary absorption processes are modeled on the basis of both the theoretical and empirical knowledge. Although these contributions can be expressed using the transition strength function or the imaginary part of the dielectric function, this method is always referred to as parameterization of the JDOS function (PJDOS). It is beneficial to express the individual contributions using the terms normalized with respect to the sum rule and the transition strength parameters corresponding to the individual absorption processes. The total transition strength function is then given as

$$\begin{aligned} F(E) = \sum _t N_t F^0_t(E) \,, \end{aligned}$$

(3.34)

where the index t distinguishes individual contributions (terms), $N_t$ are the transitions strengths parameters and $F^0_t(E)$ are normalized transition strength functions. The dispersion parameters of the whole model consist of the transition strength parameters $N_t$ and parameters of the functions $F^0_t(E)$ which determine spectral distributions of individual contributions (e. g. bandgap energy). The dielectric function is calculated as

(3.35)

$$\begin{aligned} \varepsilon _\mathrm {i}(E)&= \sum _t N_t \frac{F^0_t(E)}{E} = \sum _t N_t \varepsilon _{\mathrm{i},t}^0(E) \,. \end{aligned}$$

(3.36)

The expression for the imaginary part follows from (3.30) and the real part is calculated from the KK relation (3.3). In the adopted formalism, the quantities $\hat{\varepsilon }_t^0(E)$ are normalized susceptibilities of individual contributions but they will be called normalized contributions to the dielectric function or just normalized dielectric functions.

Note that in the derivation of the above expressions it was assumed that the eigenstates of the Hamiltonian are known. For the description of specific elementary excitations of the dielectric response we often utilize the second quantization, i. e. describing the system using one-particle states and quasiparticles. It should be further emphasized that the total transition strength N can be expressed on the basis of the real number of particles in the system but the transition strengths of individual elementary excitations cannot be used to calculate the densities of particles involved in these processes. These transition strengths must be understood as strengths corresponding to the effective number of particles or, alternatively, particles with effective masses or effective charges must be considered. For example, the transition strength of valence electron excitations is usually described using the effective number of valence electrons per atom $n_\mathrm{ve}$ [4]

$$\begin{aligned} N_\mathrm{ve} = \frac{2}{\pi } \frac{(e \hbar )^2}{\epsilon _0 m_\mathrm {e}} \mathcal {N}_\mathrm {a}n_\mathrm{ve} \,, \end{aligned}$$

(3.37)

where $\mathcal {N}_\mathrm {a}$ is the density of atoms . The transition strength of free carriers is usually described using the effective mass $m^*m_\mathrm {e}$

$$\begin{aligned} N_\mathrm{fc} = \frac{2}{\pi } \frac{(e \hbar )^2}{\epsilon _0 m^*m_\mathrm {e}} \mathcal {N}_\mathrm{d} \,, \end{aligned}$$

(3.38)

where $\mathcal {N}_\mathrm{d}$ is the density of dopants . Finally the transition strength of phonon excitations is usually expressed using the effective charge $q^*e$

$$\begin{aligned} N_\mathrm{ph} = \frac{2}{\pi } \frac{(q^* e \hbar )^2}{\epsilon _0 m_\mathrm{n}} \mathcal {N}_\mathrm{n} \,, \end{aligned}$$

(3.39)

where $\mathcal {N}_\mathrm{n}$ and $m_\mathrm{n}$ are density and mass of the nuclei.

2.3 Broadening

As mentioned above, it is not possible to obtain an exact quantum mechanical solution for the complex systems encountered in the solid state physics. In practice, different approximate models are employed for individual elementary excitations. For example, the approximation of non-interacting particles applied to crystalline materials often leads to discrete spectrum or discontinuities in the JDOS (or its first derivative) known as Van Hove singularities [18] , which are, however, usually not observed in the real absorption spectra. In reality, the sharp structures are blurred as a consequence of different effects neglected in the approximate models. The effects that contribute to the blurring (broadening) of the sharp structures in the absorption spectra are the finite lifetime of the states (temperature dependent, intrinsic for open systems) or various irregularities in the lattice (usually temperature independent). An empirical broadening procedure is then used to model the blurring of the sharp structures [19,20,21,22,23,24,25,26,27,28,29,30].

In practice, the unbroadened JDOS is determined based on an approximate model and the broadened dielectric response is then calculated as a convolution of the function representing this dielectric response with appropriately chosen normalized broadening function $\beta (x)$. Since the broadening procedure is an empirical approach, it is not evident on which function, representing the dielectric response, should the broadening procedure be applied. For example, the broadening procedure can be applied to functions $\varepsilon _\mathrm {i}(E)$, F(E) or J(E) [31]:

$$\begin{aligned} \tilde{\varepsilon }_\mathrm {i}(E)&= \int _{-\infty }^\infty \beta (E-t) \, \varepsilon _\mathrm {i}(t) \, \mathrm {d}t&\varepsilon -\text{ broadening, } \end{aligned}$$

(3.40)

$$\begin{aligned} \tilde{\varepsilon }_\mathrm {i}(E)&= \frac{\tilde{F}(E)}{E} = \frac{1}{E} \int _{-\infty }^\infty \beta (E-t) \, F(t) \, \mathrm {d}t&F-\text{ broadening, } \end{aligned}$$

(3.41)

$$\begin{aligned} \tilde{\varepsilon }_\mathrm {i}(E)&= \frac{\tilde{J}(E)}{E^2} = \frac{1}{E^2} \int _{-\infty }^\infty \beta (E-t) \, J(t) \, \mathrm {d}t&J-\text{ broadening, } \end{aligned}$$

(3.42)

where the tilde denotes the broadened functions. Two one-parametric normalized distribution functions are used for the broadening, the first being the Gaussian function

$$\begin{aligned} \beta _\mathrm{G}(x) = \frac{1}{\sqrt{2\pi } B} \exp \left( -\frac{x^2}{2 B^2}\right) \,, \end{aligned}$$

(3.43)

where B is the broadening parameter representing the root mean square (RMS) value. The second distribution function is the Lorentzian function

$$\begin{aligned} \beta _\mathrm{L}(x) = \frac{1}{\pi } \frac{B/2}{x^2+B^2/4} \,, \end{aligned}$$

(3.44)

where the broadening parameter B represents the full width half maximum (FWHM) value. The Gaussian distribution function is more universal (thanks to central limit theorem) than the Lorentzian distribution function but the Lorentzian distribution function often leads to expressions that can be calculated analytically.

It was previously shown that the J-broadening or F-broadening procedure can give nonzero static conductivity [21, 31] even if the unbroadened dielectric response had zero static conductivity ($F(0)=0$). On the other hand the $\varepsilon$-broadening always gives a dielectric response with zero static conductivity [31]. Therefore, the $\varepsilon$-broadening is appropriate for dispersion models of contributions representing bounded charges (interband electronic transitions, phonon absorption, etc.) and J-broadening or F-broadening is appropriate for dispersion models of contributions having nonzero static conductivity (e. g. contributions of free charges or direct electronic transitions in 2D graphene sheet). Furthermore, it was shown that only the $\varepsilon$-broadening and F-broadening preserve the sum rule integral [31] and, therefore, they preserve the normalization if applied to the normalization contributions.

The $\varepsilon$-broadening and the F-broadening can be written in a concise form with the help of the symbol $*$ denoting the operation of convolution as

$$\begin{aligned} \tilde{\varepsilon }_\mathrm {i}^0 = \beta * \varepsilon _\mathrm {i}^0 \qquad \text{ and } \qquad \tilde{\varepsilon }_\mathrm {i}^0 = \frac{1}{E} ( \beta * F^0 ) \,. \end{aligned}$$

(3.45)

The KK relation for the real part of the normalized dielectric function can be written with the help of the Hilbert transform H as [32]

(3.46)

Since the order of the Hilbert transform and the convolution can be exchanged [31], the real part of the $\varepsilon$-broadened normalized dielectric function can be written as

$$\begin{aligned} \tilde{\varepsilon }_\mathrm {r}^0 = H[\tilde{\varepsilon }_\mathrm {i}^0] = H[ \beta * \varepsilon _\mathrm {i}^0 ] = H[\beta ] * \varepsilon _\mathrm {i}^0 \,. \end{aligned}$$

(3.47)

A similar expression can be derived for the real part of the F-broadened normalized dielectric function

$$\begin{aligned} \tilde{\varepsilon }_\mathrm {r}^0 = H\left[ \frac{\tilde{F}^0}{E}\right] = \frac{1}{E} H[ \beta * F^0 ] = \frac{1}{E} \bigg (H[\beta ] * F^0 \bigg ) \,. \end{aligned}$$

(3.48)

Both the $\varepsilon$-broadened and F-broadened normalized dielectric functions can be written very compactly as

$$\begin{aligned} \tilde{\hat{\varepsilon }}^0 = \hat{\beta }* \varepsilon _\mathrm {i}^0 \qquad \text{ and } \qquad \tilde{\hat{\varepsilon }}^0 = \frac{1}{E} ( \hat{\beta }* F^0 ) \,. \end{aligned}$$

(3.49)

where the complex function $\hat{\beta }$ is defined as

$$\begin{aligned} \hat{\beta }= H[\beta ] + \mathrm{i}\beta \,. \end{aligned}$$

(3.50)

The fact that the real part of the broadened dielectric function can be calculated with the help of only a single integral instead of double integral (convolution followed by the Hilbert transform) is important if this function is calculated numerically.

The Hilbert transform of the Gaussian distribution function (3.43) is given by

$$\begin{aligned} H[\beta _\mathrm{G}](x) = -\frac{\sqrt{2}}{\pi B} \mathrm {D}\left( \frac{x}{\sqrt{2}B}\right) \,, \end{aligned}$$

(3.51)

where D(x) denotes the Dawson function (integral) [33,34,35] defined as

$$\begin{aligned} \mathrm {D}(x) = \exp (-x^2) \int _0^x \exp (t^2) \, \mathrm {d}t \,. \end{aligned}$$

(3.52)

The Dawson function can be efficiently evaluated in numerical calculations. The Hilbert transform of the Lorentzian distribution function (3.44) is given by

$$\begin{aligned} H[\beta _\mathrm{L}](x) = -\frac{1}{\pi } \frac{x}{x^2+B^2/4} \,. \end{aligned}$$

(3.53)

The complex Lorentzian broadening function can be elegantly written as

$$\begin{aligned} \hat{\beta }_\mathrm{L}(x) = -\frac{1}{\pi } \frac{1}{x+ \mathrm{i}B/2} \,. \end{aligned}$$

(3.54)

The Lorentzian $\varepsilon$-broadened dielectric function $\hat{\beta }_\mathrm{L} * \varepsilon _\mathrm {i}^0$ can be calculated as [30]

(3.55)

The Lorentzian $\varepsilon$-broadening provides a bridge between the quantum and classical dispersion models. The imaginary part of the normalized dielectric function of a discrete transition with the energy difference $E_\mathrm {r}$ in the two-level system is given by

$$\begin{aligned} \varepsilon _\mathrm {i}^0(E) = \frac{1}{E_\mathrm {r}} \bigg ( \delta (E-E_\mathrm {r}) - \delta (E+E_\mathrm {r}) \bigg ) \,. \end{aligned}$$

(3.56)

The Lorentzian $\varepsilon$-broadening of this response function gives

$$\begin{aligned} \tilde{\varepsilon }_\mathrm {r}^0(E)&= H[\beta _\mathrm{L}] * \varepsilon _\mathrm {i}^0 = - \frac{1}{\pi E_\mathrm {r}} \left( \frac{E-E_\mathrm {r}}{(E-E_\mathrm {r})^2 + B^2/4} - \frac{E+E_\mathrm {r}}{(E+E_\mathrm {r})^2 + B^2/4} \right) \,, \end{aligned}$$

(3.57)

$$\begin{aligned} \tilde{\varepsilon }_\mathrm {i}^0(E)&= \beta _\mathrm{L} * \varepsilon _\mathrm {i}^0 = \frac{B}{2 \pi E_\mathrm {r}} \left( \frac{1}{(E-E_\mathrm {r})^2 + B^2/4} - \frac{1}{(E+E_\mathrm {r})^2 + B^2/4} \right) \,, \end{aligned}$$

(3.58)

which is equivalent to the Lorentz term in the classical model because the real and imaginary part of the normalized dielectric function (3.15) are expressed as

$$\begin{aligned} \varepsilon _\mathrm {r}^0(E) = \frac{2}{\pi } \frac{E_\mathrm {c}^2 - E^2}{ (E_\mathrm {c}^2 - E^2)^2 + B^2 E^2 } \,, \quad \varepsilon _\mathrm {i}^0(E) = \frac{2}{\pi } \frac{B E}{ (E_\mathrm {c}^2 - E^2)^2 + B^2 E^2 } \,. \end{aligned}$$

(3.59)

The broadened functions (3.57) and (3.58) can be written as (3.59) with the central energy equal to

$$\begin{aligned} E_\mathrm {c}=\sqrt{E_\mathrm {r}^2+B^2/4} \,. \end{aligned}$$

(3.60)

Note that that the Lorentz terms corresponding to critically damped ($E_\mathrm {c}=B/2$) or overdamped ($E_\mathrm {c}<B/2$) harmonic oscillator cannot be expressed as Lorentzian $\varepsilon$-broadened discrete transitions.

Fig. 3.1

Schematic diagram of the electronic density of states (DOS) distribution function and possible interband an intraband transitions in dielectrics and metals

3 Dispersion Models of Elementary Excitations

Linear dielectric response corresponds to the transitions of the system between two states, which are accompanied by absorption or emission of photons. The absorption (emission) processes involving electron excitation (recombination) are called electronic transition (absorption) processes. If the phonon occupation numbers are not changed in the electronic transition processes, they are referred to as direct electronic transition processes while if the phonon occupation numbers are changed, they are referred to as indirect electronic transition processes. Phonon absorption (emission) processes, on the other hand, are those without electron excitation (recombination). The electronic transitions cover the whole spectral range from zero frequency (photon energy) up to X-ray. If the Fermi energy lies inside the band of valence electrons or close to it, the states in this band are partially filled and indirect intraband transitions are possible. Indirect intraband transitions are referred to as free carrier contributions. The schematic diagram of the band structure and classification of electronic transitions is depicted in Fig. 3.1. In the materials with the filled valence band which is separated from the empty conduction band, both the direct and indirect interband transitions can exist. The origin of the valence and conduction band is in the splitting of the partially occupied atomic valence orbital states. The band above the conduction band which originates from the orbital states above the valence shell is called higher energy excitation band. The excitations of the valence electrons into these states are called higher energy excitations (see Fig. 3.1). These higher energy excitations can also be understood as the scattering processes. The orbitals below the valence shell result in discrete core level states and excitations from these states are called core electron excitations.

3.1 Phonon Absorption

The phonon absorption exhibits different behavior in different types of materials (crystals vs. disordered, homopolar vs. ionic, etc.). In the following subsections, several dispersion models describing phonon absorption will be discussed.

3.1.1 One-Phonon Absorption in Disordered Materials

From the point of view of vibrational modes, disordered solids can be viewed as a collection of a very large number of atoms having independent vibrational modes with the total number of vibrational modes given by the number of degrees of freedom minus three. In disordered solids the vibrational modes are localized, i. e. the eigenvectors describing the amplitudes of to the vibrational modes have non-negligible values concentrated in blocks corresponding to small volumes in the solid. Each of these blocks can be viewed as a molecule with a relatively small number of vibrational modes. The transition strength function of such a molecule is given as a sum of delta functions

$$\begin{aligned} F_\mathrm{1ph}(E) = \sum _p N_p \left[ \delta (E-E_p) + \delta (E+E_p) \right] \,, \end{aligned}$$

(3.61)

where the index p distinguishes individual vibrational modes (peaks in the spectra). The symbols $E_p$ and $N_p$ denote the energy and transition strength of individual modes, respectively. The imaginary part of the dielectric function is then calculated as (3.30)

$$\begin{aligned} \varepsilon _\mathrm{i,1ph}(E) = \sum _p \frac{N_p}{E_p} \left[ \delta (E-E_p) - \delta (E+E_p) \right] \,. \end{aligned}$$

(3.62)

This is the same result that one would obtain for non-interacting molecular gases. For this reason the terminology used in the absorption spectroscopy of gases is often adopted also in the study of phonon absorption in disordered solids.

The atoms, which are lying outside of the blocks forming the above mentioned molecules lead to the broadening of the delta functions, forming the absorption spectra. If the molecules are weakly interacting (which is true for gases) then the Lorentzian $\varepsilon$-broadening is appropriate. This is because the interactions (collisions) of molecules can be described by the relaxation time and, therefore, the Lorentz model provides a suitable description.

In disordered solids, the assumption of weak interactions is not valid. The interactions are so strong that they cannot be described by the relaxation time and it is more correct to imagine the interactions as something that distorts (deforms) the molecules. The random deformations of the molecules cause changes in the frequencies of the localized vibrational modes. According to the central limit theorem, the Gaussian distribution provides accurate distribution of the changes in these frequencies [34,35,36,37]. Therefore, the Gaussian $\varepsilon$-broadening is more appropriate in this case.

Fig. 3.2

Spectral dependencies of the normalized dielectric functions of $\varepsilon$-broadened discrete spectrum calculated using three different broadening functions: $E_p=0.1$ eV (peak energy), $B_p=0.05$ eV (FWHM), $L_p=0.5$ (Lorentzian fraction in Voigt profile)

The $\varepsilon$-broadened contribution to the dielectric function (susceptibility) describing one-phonon absorption in disordered solids is then

$$\begin{aligned} \hat{\varepsilon }_\mathrm{1ph}(E) = \sum _p \frac{N_p}{E_p} \, \hat{\beta }_{\mathrm{G},p} * \left[ \delta (E-E_p) - \delta (E+E_p) \right] \,, \end{aligned}$$

(3.63)

where the complex Gaussian broadening functions $\hat{\beta }_{\mathrm{G},p}$ are given by (3.50), (3.43) and (3.51). The spectral dependency of the normalized Gaussian $\varepsilon$-broadened dielectric function is compared with different $\varepsilon$-broadened dielectric functions in Fig. 3.2. The explicit expression for the normalized dielectric function corresponding to one mode is given by

$$\begin{aligned} \varepsilon ^0_{\mathrm{r},p}(E)&= \frac{- \sqrt{2}}{\pi B_p E_p} \left[ \mathrm {D}\!\left( \frac{E-E_p}{\sqrt{2} B_p} \right) - \mathrm {D}\!\left( \frac{E+E_p}{\sqrt{2} B_p} \right) \right] \,, \end{aligned}$$

(3.64)

$$\begin{aligned} \varepsilon ^0_{\mathrm{i},p}(E)&= \frac{1}{\sqrt{2\pi } B_p E_p} \left[ \exp \!\left( -\frac{(E-E_p)^2}{2 B_p^2}\right) - \exp \!\left( -\frac{(E+E_p)^2}{2 B_p^2}\right) \right] \,, \end{aligned}$$

(3.65)

where $B_p$ is the broadening parameter which may be different for individual vibrational modes. The real part is calculated using the the Dawson integral $\mathrm {D}(x)$ defined in (3.52). The broadening factor $B_p$ in (3.64) and (3.65) gives the RMS value. Since we usually work with FWHM values in the IR spectroscopy (the RMS value is not defined for the Lorentzian distribution), it is useful to point out that in the case of the Gaussian distribution, the RMS and FWHM values are related as

$$\begin{aligned} \sqrt{2}B^\mathrm{RMS} = \frac{B^\mathrm{FWHM}}{2\sqrt{\ln 2}} \,. \end{aligned}$$

(3.66)

3.1.2 One-Phonon Absorption in Crystalline Materials

The one-phonon absorption in ideal crystalline materials is represented by a discrete spectrum of vibrational modes. These modes correspond to the transverse optical (TO) phonons with zero momentum (i. e. in the $\Gamma$ point). The number of TO modes depends on the number of atoms in the primitive cell. Only the optically active modes, i. e. those with a non-vanishing dipole matrix element, appear in the absorption spectra. The appropriate model in this case is the classical model of independent underdamped harmonic oscillator, which is equivalent to the model of the Lorentzian $\varepsilon$-broadened discrete transitions. The normalized dielectric function corresponding to the TO mode p is then given by

$$\begin{aligned} \hat{\varepsilon }_p^0(E) = \frac{1}{E_p} \hat{\beta }_{\mathrm{L},p} * \left[ \delta (E-E_p) - \delta (E+E_p) \right] = \frac{2/\pi }{E_p^2+B_p^2/4-E^2-\mathrm{i}B_p E}\,, \end{aligned}$$

(3.67)

where the complex Lorentzian broadening function $\hat{\beta }_{\mathrm{L},p}$ is given by (3.54). The broadening parameter $B_p$ is the FWHM of the absorption peak and $E_p$ is the resonant energy. The expression $E_p^2+B_p^2/4$ in the denominator is often written with the help of the central energy defined as $E_{\mathrm{c},p}^2=E_p^2+B_p^2/4$. The form with $E_p^2+B_p^2/4$ is, however, more convenient since the condition that the DHO is underdamped can then be written as $E_p>0$.

In some cases the phonon absorption cannot be described by independent DHO (Lorentz) model and the model of DHO with coupled modes must be used. The model of DHO with coupled modes was already discussed in Sect. 3.2.1. In this model the contribution to the dielectric function (susceptibility) can be expressed using matrices as

$$\begin{aligned} \hat{\varepsilon }_\mathrm{1ph}(E) = \frac{2}{\pi } \mathbf {N}^\mathrm{T} [\mathbf S - E^2 \mathbf I - \mathrm{i}E \mathbf B \mathbf B^\mathrm{T} ]^{-1} \mathbf {N} \,, \end{aligned}$$

(3.68)

where $\mathbf {N}$ is a real vector formed by the square roots of transition strengths of individual TO modes $N_p$, $p=1,\ldots ,m$:

$$\begin{aligned} \mathbf {N}^\mathrm{T} = (\sqrt{N_1},\sqrt{N_2},\ldots ,\sqrt{N_m}) \,. \end{aligned}$$

(3.69)

The matrix $\mathbf S$ is a real diagonal matrix with squares of central frequencies $E_{\mathrm{c},p}$ on the diagonal

$$\begin{aligned} \mathbf S = \left( \begin{array}{cccc} E_\mathrm{c,1}^2 &{} 0 &{} \cdots &{} 0 \\ 0 &{} E_\mathrm{c,2}^2 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{}\cdots &{} E_{\mathrm{c,}m}^2 \end{array} \right) \,, \end{aligned}$$

(3.70)

the symbol $\mathbf I$ denotes the unit matrix and the matrix $\mathbf B$ is a real lower triangular matrix with positive values on the diagonal

$$\begin{aligned} \mathbf B = \left( \begin{array}{cccc} \sqrt{B_1} &{} 0 &{} \cdots &{} 0 \\ \nu _{12}\,B_{12}/\sqrt{|B_{12}|} &{} \sqrt{B_2} &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \nu _{1m}\,B_{1m}/\sqrt{|B_{1m}|} &{}\, \nu _{2m}B_{2m}/\sqrt{|B_{2m}|} &{}\cdots &{} \sqrt{B_m} \end{array} \right) \,, \end{aligned}$$

(3.71)

where the constants $B_p$ and $B_{kl}$ determine the broadening and coupling of modes. The constants $\nu _{kl}$ are defined as follows

$$\begin{aligned} \nu _{kl} = \frac{\sqrt{N_k N_l}}{\mathbf {N}^\mathrm{T} \mathbf {N}} \,. \end{aligned}$$

(3.72)

The constants $\nu _{kl}$ are introduced in order to ensure that the corresponding elements in the matrix $\mathbf B$ vanish if $N_k$ or $N_l$ is zero.

Fig. 3.3

Contributions to the dielectric function of DHO model with three independent (Drude-Lorentz model) and three coupled modes: $N_1=0.02\,\mathrm{eV}^2$, $E_\mathrm{c,1}=0.1\,\mathrm{eV}$, $B_1=0.005\,\mathrm{eV}$, $N_2=0.1\,\mathrm{eV}^2$, $E_\mathrm{c,2}=0.2\,\mathrm{eV}$, $B_2=0.01\,\mathrm{eV}$, $N_3=0.1\,\mathrm{eV}^2$, $E_\mathrm{c,3}=0\,\mathrm{eV}$, $B_3=0.05\,\mathrm{eV}$. The third mode with zero central frequency describes contribution from free charges. The values of the parameters $B_{12}$, $B_{13}$ and $B_{23}$ are different for each curves

This model of DHO with coupled modes produces asymmetrically shaped absorption peaks (see Fig. 3.3). In contrast to the simpler model of independent DHO, the parameters $B_p$ cannot be interpreted as FWHMs of the peaks in the model. The relation between the FWHM of the peaks and parameters $B_p$ and $B_{kl}$ is, in this case, very complicated. Furthermore, the relation between the central energies $E_{\mathrm{c},p}$, which are used to parameterize the model, and resonant energies $E_p$, which correspond to the photon energies of the peaks, is also very complicated. If the broadening and coupling factors are small then the resonant energies differ only slightly from the central energies.

3.1.3 One-Phonon Absorption in Partially Disordered Materials

In some cases the phonon absorption peaks are properly described neither by the Lorentzian nor the Gaussian $\varepsilon$-broadened discrete spectrum and both the broadening procedures must be combined. The resulting broadening procedure is described by a two parameter broadening function known as the Voigt profile corresponding to the convolution of the Lorentzian and Gaussian distribution

$$\begin{aligned} \hat{\beta }_{\mathrm{V},p} = \hat{\beta }_{\mathrm{G},p} * \beta _{\mathrm{L},p} = \hat{\beta }_{\mathrm{L},p} * \beta _{\mathrm{G},p} \,, \end{aligned}$$

(3.73)

or with the help of the complex Faddeeva function $\mathrm {W}(\hat{z})$ as [38,39,40,41,42]

$$\begin{aligned} \hat{\beta }_{\mathrm{V},p}(x) = \frac{\mathrm{i}}{\sqrt{2\pi } B_{\mathrm{G},p}} \mathrm {W}\!\left( \frac{x + \mathrm{i}B_{\mathrm{L},p}/2 }{\sqrt{2} B_{\mathrm{G},p}}\right) \,, \end{aligned}$$

(3.74)

where the Faddeeva function is given by the following integral

$$\begin{aligned} \mathrm {W}(\hat{z}) = \frac{\mathrm{i}}{\pi } \int _{-\infty }^\infty \frac{\exp \!\left( -t^2\right) }{\hat{z} - t} \mathrm {d}t \,. \end{aligned}$$

(3.75)

The normalized dielectric function corresponding to one mode could, in this case, be expressed as

$$\begin{aligned} \hat{\varepsilon }^0_p(E) = \frac{\mathrm{i}}{\sqrt{2\pi } B_{\mathrm{G},p} E_p} \left[ \mathrm {W}\!\left( \frac{E - E_p + \mathrm{i}B_{\mathrm{L},p}/2 }{\sqrt{2} B_{\mathrm{G},p}}\right) - \mathrm {W}\!\left( \frac{E + E_p + \mathrm{i}B_{\mathrm{L},p}/2 }{\sqrt{2} B_{\mathrm{G},p}}\right) \right] \,. \end{aligned}$$

(3.76)

The exact dependence of the FWHM of the Voigt profile on parameters $B_{\mathrm{L},p}$ (FWHM of the Lorentzian part) and $B_{\mathrm{G},p}$ (RMS of the Gaussian part) is quite complicated. However, the dependencies of these broadening parameters on the FWHM of the Voigt profile $B_p$ can be approximated with sufficient accuracy using the following formulas [43]

$$\begin{aligned} B_{\mathrm{L},p} \approx B_p L_p \,, \qquad B_{\mathrm{G},p} \approx \frac{B_p}{2\sqrt{2 \ln 2}} \sqrt{(1-a L_p)^2-(1-a)^2 L_p^2} \,, \end{aligned}$$

(3.77)

where $a=0.5346$ and $L_p$ is the parameter mixing the Gaussian and Lorentzian part. The comparison of the $\varepsilon$-broadened normalized dielectric functions calculated using the Voigt, Gaussian and Lorentzian broadening functions is in Fig. 3.2.

Since the evaluation of the complex Faddeeva function is more complicated than the evaluation of the real Dawson function, it is convenient to use an approximation in which the Voigt profile is replaced by the linear combination of the Gaussian and Lorentzian distributions. There are several approaches to define this linear combination and they differ in the choice of broadening factors for the Gaussian and Lorentz distributions. The simplest approach is to combine the Gaussian and Lorentzian functions with the same FWHM [44]:

$$\begin{aligned} \hat{\beta }_{\mathrm{V},p} \approx (1-L_p) \hat{\beta }_{\mathrm{G},p} + L_p \hat{\beta }_{\mathrm{L},p} \,, \end{aligned}$$

(3.78)

where $L_p$ is the parameter mixing the Gaussian and Lorentzian parts. Note that this mixing parameter has different meaning than the mixing parameter introduced in (3.77). The deviation from the exact values of the Voigt profile in this approximation is smaller than the usual experimental errors (absolute error lower than $10^{-4}$ peak value).

3.1.4 One-Phonon Absorption with Asymmetric Absorption Peaks

The classical model of DHO with coupled modes , which gives asymmetric peaks, can be approximated by the Lorentz model with complex transition strengths [45]. As mentioned above, the underdamped Lorentz model can be written as the Lorentzian $\varepsilon$-broadened discrete spectrum. The contribution to the dielectric function (susceptibility) can be then expressed as

$$\begin{aligned} \hat{\varepsilon }_\mathrm{1ph}(E) = \frac{1}{\mathcal {C}_\mathrm {N}} \sum _p \left( N_p + \mathrm{i}M_p \frac{E}{E_p} \right) \frac{1}{E_p} \, \hat{\beta }_p * \left[ \delta (E-E_p) - \delta (E+E_p) \right] \,, \end{aligned}$$

(3.79)

where $M_p$ determines the asymmetric part of the transition strength of the absorption peak and $\mathcal {C}_\mathrm {N}$ is a normalization constant. In the case of underdamped Lorentz model, the complex broadening function $\hat{\beta }_p$ is given by (3.54) but the model can be easily generalized using different types of broadening functions. While the real parts of transition strengths $N_p$ are always positive, the imaginary parts of transition strengths $M_p$ can be chosen arbitrarily. Such a model fulfills the first two fundamental conditions for the dielectric response (i. e. the time reversal symmetry (3.1) and KK consistency (3.2) and (3.8)). The dimensionless factor $E/E_p$ in (3.79) ensures the time reversal symmetry of the model. Using the superconvergence theorem it is easy to prove that the sum rule integral (3.4) is infinite for all individual asymmetric terms in the sum (3.79). In order to ensure the third fundamental condition (i. e. the convergence of the sum rule integral), the following sum must be equal to zero [45]:

$$\begin{aligned} \sum _p \frac{M_p}{E_p} = 0 \,. \end{aligned}$$

(3.80)

The asymmetric part contributes to the sum rule for a Lorentzian broadening function but not for Gaussian broadening. The normalization constant is then given from the superconvergence theorem as

$$\begin{aligned} \mathcal {C}_\mathrm {N}= \frac{1}{\sum _p N_p} \sum _p \left( N_p + \frac{M_p B_{\mathrm{L},p}}{E_p} \right) \,, \end{aligned}$$

(3.81)

where $B_{\mathrm{L},p}$ is the Lorentzian part of the broadening of the p-peak ($B_{\mathrm{L},p}=L_p B_p$ for both the Voigt and linear combination profile).

The advantage of this model is that for three and more modes the asymmetric part is determined by a smaller number of independent dispersion parameters ($m-1$) than in the DHO model with coupled modes ($m(m-1)/2$), where m denotes the number of modes. On the other hand, the disadvantage of this model is that the fourth auxiliary condition (i. e. $\varepsilon _\mathrm {i}\ge 0$ in the whole spectral range) is difficult to satisfy.

Fig. 3.4

Contributions to the dielectric function of two asymmetric Voigt $\varepsilon$-broadened peaks. Asymmetry represents the redistribution of transition strength due to coupling between phonon modes. The dielectric function without coupling is added for comparison. The parameters were chosen as follows: $N_1=0.02\,\mathrm{eV}^2$, $E_1=0.1\,\mathrm{eV}$, $B_1=0.01\,\mathrm{eV}$, $L_1=0.3$, $N_2=0.05\,\mathrm{eV}^2$, $E_2=0.2\,\mathrm{eV}$, $B_1=0.02\,\mathrm{eV}$, $L_2=0.7$. The values of the parameters $M_1$ and $M_2$ are different for each curves with $M_1=-(E_1/E_2)M_2$

For sufficiently small values of the parameters $M_p$, the model satisfies the fourth condition, though it is difficult to formulate the general limits under which this condition is satisfied. The asymmetric peaks in Fig. 3.4 do not fulfill this condition. For the selected parameters the fourth condition is fulfilled for $|M_2|<0.002767$. Thus, this model could be used only for modeling peaks which are only slightly asymmetric. For strongly asymmetric peaks, the model of the DHO with coupled modes must be used or the model presented in (3.79) has to be considered together with some other contribution to the dielectric function that ensures that the imaginary part of the resulting dielectric function is positive in the whole spectral range.

It is necessary to note that it is possible to prove [45] that the model (3.79) with Lorentzian broadening is equivalent to the the model known as ‘factorized Lorentz oscillators’ introduced in [46].

Fig. 3.5

Contributions to the dielectric function of asymmetric Voigt Fano $\varepsilon$-broadened peaks representing redistribution of transition strength due to Fano resonance effect between phonon peak and free carrier contribution. The dielectric functions with symmetrical peak (without Fano resonance effect) and without phonon peak (Drude contribution) are added for comparison. The parameters corresponding to Drude model and phonon peak were chosen as follows: $N_\mathrm{D}=2\,\mathrm{eV}^2$, $B_\mathrm{D}=0.1\,\mathrm{eV}$, $N_\mathrm{ph}=0.1\,\mathrm{eV}^2$, $E_\mathrm{ph}=0.1\,\mathrm{eV}$, $B_\mathrm{ph}=0.01\,\mathrm{eV}$ (FWHM), $L_\mathrm{ph}=0.2$. The value of the parameter $M_\mathrm{ph}$ is different for each curves

In the conducting materials (e. g. graphite [47,48,49]) there are one or more phonon absorption peaks in the IR region which have asymmetric profile. The asymmetry of the profile of these phonon absorption peaks is caused by quantum mechanical interference between the phonons and free charges, called the Fano resonance [50]. In this case, the asymmetric peaks cannot be described by the model based on the $\varepsilon$-broadened discrete transitions with the imaginary parts of transition strengths satisfying the condition (3.80). The problem can be solved if the factor $E_p/E$ is used instead of the factor $E/E_p$ used in (3.79)

$$\begin{aligned} \hat{\varepsilon }_\mathrm{1ph}(E) = \sum _p \left( N_p + \mathrm{i}M_p\frac{E_p}{E} \right) \frac{1}{E_p} \, \hat{\beta }_p * \left[ \delta (E-E_p) - \delta (E+E_p) \right] \,. \end{aligned}$$

(3.82)

In this case, the sum rule integral is always zero for the individual asymmetric parts. Therefore, this model satisfies all three fundamental conditions even if only one phonon vibrational mode is considered. The fourth auxiliary condition can be satisfied if the above dielectric function is used as a part of the UDM because it also contains the contribution from free carriers (see Fig. 3.5). The asymmetric part of the absorption peak should be understood as a redistribution of the transition strength function of free carriers. The asymmetric part of the model changes value of the imaginary part of the dielectric function in zero energy, i. e. static conductivity. Therefore, using this model as a part of a model without free carrier contribution leads to an artificial positive or negative Drude-like singularity in the dielectric function.

3.1.5 Temperature Dependence of One-Phonon Absorption

In the equilibrium the mean values of the phonon occupation numbers are determined by the Bose–Einstein statistics

$$\begin{aligned} f^\mathrm{BE}(E_p,T) = \frac{1}{\exp (E_p/(k_\mathrm {B}T)) - 1} \,. \end{aligned}$$

(3.83)

This statistical factor can be derived in the quasiparticle approximation from the probability factor of open systems (3.21). In the quasiparticle approximation the probability of the one-phonon absorption process is proportional to the occupation number plus one while the probability of the one-phonon emission process is proportional to the occupation number. The resulting transition strength of the one-phonon absorption peak at energy $E_p$ is a sum of the transition strength of the absorption process $N_{+p}(T)$, which is positive, and the transition strength of the emission process $N_{-p}(T)$, which is negative,

$$\begin{aligned} N_p(T) = N_{+p}(T) + N_{-p}(T) \sim f^\mathrm{BE}(E_p,T) + 1 - f^\mathrm{BE}(E_p,T) = 1 \,. \end{aligned}$$

(3.84)

This equation says that the strength of the one-phonon absorption is not temperature-dependent through the statistical factor. However, the resonant frequency of phonons $E_p$ and broadening $B_p$ are temperature dependent. Moreover, the phonon matrix elements are slightly temperature-dependent, meaning that the transition strength $N_p$ could also be slightly temperature-dependent. The temperature dependencies of the phonon frequencies are mostly a consequence of the thermal expansion and could be modeled by the average Bose–Einstein statistical factor with dependency given by the average phonon energy [51,52,53]. In this case, the temperature dependence can be parameterized using the following three parametric formula

$$\begin{aligned} E_p(T) = E_p^{0K}+ \left( E_p^{300K}-E_p^{0K} \right) \frac{\exp (\Theta /300K)-1}{\exp (\Theta /T)-1} \,, \end{aligned}$$

(3.85)

where $E_p^{0K}$ and $E_p^{300K}$ are the phonon energies for zero and room temperature. Note that the $E_p(T)$ decreases with temperature ($E_p^{300{{K}}}<E_p^{0K}$). The parameter $\Theta$ is the average phonon energy in Kelvins. This parameter is common to all phonon modes. It represents the contribution from all the phonons which participate in the thermal expansion (i. e. also the optically inactive phonons). Therefore, $k_\mathrm {B}\Theta$ is a completely different quantity than the discrete energies $E_p$ of the optically active phonons.

The same type of temperature dependency could be also used for the parts of the broadening factors $B_p$ representing the finite lifetime of phonons [54]. In this case, the broadening factors increase with temperature ($B_p^{300K}>B_p^{0K}$).

3.1.6 Multi-phonon Absorption

Multi-phonon absorption is very weak effect compared to the one-phonon absorption, with the exception of homopolar crystalline materials, such as diamond, silicon or germanium. In homopolar materials the multi-phonon absorption is the dominant effect in the IR region because it is not masked by the one-phonon absorption processes which are mostly prohibited due to the selection rules (vanishing dipole matrix elements).

In materials with non-negligible charge transfer (e. g. polar crystals, disordered solids) where the one-phonon absorption is dominant, it is difficult to separate the absorption spectra into parts corresponding to one-phonon and multi-phonon absorption. The magnitude of multi-phonon absorption effects often lies close to the limit of experimental accuracy. Therefore, the choice of the model used for the multi-phonon absorption is not usually very important and the same model as for one-phonon absorption but with broader peaks and smaller transition strength can be utilized. We will not discuss this model in this section and rather, we will focus on the models needed to describe the multi-phonon absorption in the homopolar crystalline materials.

In one-phonon absorption processes, only the phonons with zero momentum (i. e. at the $\Gamma$ point) contribute to the absorption processes. This is a consequence of the fact that the total momentum in the absorption process must be conserved and the momentum of photons is negligible. In multi-phonon processes the situation is more complicated since we must take into account all the absorption and emission processes for which the sum of momenta of all phonons participating in these processes is zero. In the case of two-phonon processes, the JDOS can be calculated using an integral over the Brillouin zone. In addition to the integration over the Brillouin zone, the summation over all the optical and acoustical phonon branches must be performed. For three and more phonon processes, the situation is even more complicated since multiple integrals over the Brillouin zone are needed and the summation over phonon branches is more complicated. In this section, we will concentrate on models describing the two-phonon absorption.

It is known from the theory of crystalline solids that the integration over the Brillouin zone mentioned above leads to singularities in the derivative of the JDOS function called Van Hove singularities  [15, 18]. The Van Hove singularities correspond to critical points in the Brillouin zone which are located at the points of high symmetry or near the points of lower symmetry. In the three-dimensional space (3D) there are four types of the Van Hove singularities. The $M_0$ type singularity corresponds to critical points representing the minima of energy of absorption processes, the $M_1$ and $M_2$ types correspond to saddle points and the $M_3$ type corresponds to maxima. From the theory, it follows that each type of critical point must occur at least once for each combination of phonon branches but some of them cannot be distinguished in the spectra due to the degeneracy of phonon branches in the points of symmetry. Note that even in the situation with many critical points the JDOS function can be expressed as a sum of contributions corresponding to basic sequences $M_0$–$M_1$–$M_2$–$M_3$ of critical points. Moreover, some Van Hove singularities may not be visible in the absorption spectra due to vanishing dipole matrix element. Therefore, the multi-phonon absorption for a single combination of phonon branches can be modeled using the $\varepsilon$-broadened piecewise continuous JDOS functions within the energy interval between $E_0$–$E_3$ and discontinuities in the energies $E_1$ and $E_2$. The number of absorption bands corresponding to combination of phonon branches is specific for each material. Although we will not discuss the individual materials here, the general aspects of the model of two-phonon absorption will be presented.

Table 3.1 Shape functions $L_i$ modeling 3D Van Hove singularities

The JDOS function for the 3D isotropic Van Hove singularities can be modeled by the shape functions $L_i$ introduced in Table 3.1. The functions $X_\mathrm{I}$, $X_\mathrm{II}$, $X_\mathrm{III}$ and $Y_\mathrm{I}$, $Y_\mathrm{II}$, $Y_\mathrm{III}$ are defined as follows

$$\begin{aligned} X_l(E) = \frac{E-E_{l-1}}{E_l-E_{l-1}} \,, \quad Y_l(E) = \frac{E_l-E}{E_l-E_{l-1}} \quad \text{ for } \quad E_{l-1} \le E \le E_l \,, \end{aligned}$$

(3.86)

where index $l=1(\mathrm I),2(II),3(III)$. The schematic diagram of the JDOS function corresponding to the basic sequence of the critical points is depicted in the upper panel of Fig. 3.6. The behavior around the isotropic critical points is described by the quadratic form with eigenvalues having the same size with the number of negative eigenvalues determining the type of the critical point. In reality, most of the critical points, especially at the boundary of the Brillouin zone, are anisotropic, i. e. with differently sized eigenvalues of the quadratic form. In the extreme cases, the anisotropic 3D critical points may appear as points in lower dimensions, i. e. as 2D (one eigenvalue is zero) or 1D (two eigenvalues are zero) critical points. The JDOS function for the anisotropic critical points can be approximated by the linear combination of contributions corresponding to 3D, 2D and in very rare cases also 1D Van Hove singularities. The functions corresponding to 2D and 1D singularities are introduced in Tables 3.2 and 3.3. The columns in these tables correspond to different alignment of 2D and 1D critical points with respect to 3D critical points. The schematic diagrams of the contributions to the JDOS function corresponding to the 2D and 1D singularities are shown in the middle and bottom panels of Fig. 3.6.

Fig. 3.6

Schematic diagram of joint density of states (JDOS) of two-phonon absorption processes corresponding to 3D, 2D and 1D Van Hove singularities. The individual contributions are calculated as $J_i(E)=E^2L_i(E)$ with assumptions $E_0=0.8 E_3$, $E_1=0.88 E_3$ and $E_2=0.93 E_3$

Table 3.2 Shape functions $L_i$ modeling 2D Van Hove singularities

Table 3.3 Shape functions $L_i$ modeling 1D Van Hove singularities

The resulting normalized imaginary part of the dielectric function describing the absorption band of two-phonon absorption combining the phonon branches A and B can be calculated as follows

$$\begin{aligned} \varepsilon _\mathrm{i,2ph}^0(E) = \frac{f_\mathrm{A\pm B}(E,T)}{\mathcal {C}_\mathrm {N}} H(E) \sum _{i=0}^{15} A_i L_i(E) \,, \end{aligned}$$

(3.87)

where $\mathcal {C}_\mathrm {N}$ is the normalization constant, $A_i$ are weights describing the strength of the individual $L_i$ contributions and $f_\mathrm{A\pm B}(E,T)$ is the temperature dependent factor. The index $\mathrm{A\pm B}$ distinguishes absorption bands corresponding to different combinations of A and B branches.

The function H(E) is introduced in order to change the shape of the dielectric function in the intervals between the critical points. This function is important because the linear combination of the $L_i$ functions provides correct description only in the vicinity of the Van Hove singularities, meaning that additional parameters influencing the shape of the dielectric function between these singularities are needed. The function H(E) can be, for example, defined as follows

$$\begin{aligned} H(E) = \frac{\kappa _l\lambda _l Y_l(E)}{(\kappa _l\lambda _l-1)Y_l(E)+1}+\frac{\kappa _l/\lambda _l X_l(E)}{(\kappa _l/\lambda _l-1)X_l(E)+1} \quad \text{ for } \quad E_{l-1} \le E \le E_l \,, \end{aligned}$$

(3.88)

where $\kappa _l$ and $\lambda _l$ are non-zero positive parameters regulating the shape in the corresponding intervals. This definition ensures that H(E) is continuous in the interval between $E_0$ and $E_3$ and it is equal to unity at the critical point energies. This function is smooth on the intervals between the critical point energies but its derivatives may exhibit jumps at $E_1$ and $E_2$. Note that if the shape modifying parameters $\kappa _l$ is equal to unity then the function H(E) is constant in the corresponding interval (see Fig. 3.7).

Fig. 3.7

Examples of the shape modifying function H(E) for different values of parameters

If the structure of the critical points is known for the studied material, it is convenient to express the critical point energies $E_0$–$E_3$, which are used to model the Van Hove singularities, using energies of individual phonons participating in the two-phonon absorption process. These energies are then given as a sum (A$+$B) or difference (A−B) of phonon energies at critical points

$$\begin{aligned} E_0=E_\mathrm{A}^{M_0}\pm E_\mathrm{B}^{M_0}, \quad \dots \quad E_3=E_\mathrm{A}^{M_3}\pm E_\mathrm{B}^{M_3}\,. \end{aligned}$$

(3.89)

This procedure reduces the number of independent parameters in the model. For example, the two-phonon absorption in crystalline silicon was modeled in [55] by 15 absorption bands with critical energies determined by the set of only 17 independent phonon frequencies.

The temperature dependencies of the critical point energies are modeled by the same average Bose–Einstein statistical factor as in the case of one-phonon absorption, i. e. the temperature dependency is described by the formula (3.85). The same average phonon energy parameter $\Theta$ is used for temperature dependencies of all phonon frequencies.

While in the case of one-phonon absorption the temperature dependencies of the probabilities of absorption and emission did not result in temperature dependent factor (see (3.84)) the situation is different for two-phonon absorption processes. The temperature dependent factor $f_\mathrm{A\pm B}(E,T)$ can be derived by the same procedure as for the one-phonon absorption in Sect. 3.3.1.5 but the creation/annihilation of two phonons must be taken into account. In the case of simultaneous creation of two phonons or simultaneous annihilation of two phonons temperature dependent factor is given by

$$\begin{aligned} f_\mathrm{A+B}(E,T) = 1+ f^\mathrm {BE}(E_\mathrm{A}(E),T) + f^\mathrm {BE}(E_\mathrm{B}(E),T)\,, \end{aligned}$$

(3.90)

where $E_\mathrm{A}(E)$ and $E_\mathrm{B}(E)$ describe the phonon energies in A and B branches participating in the absorption or emission processes of photon with energy E. A similar calculation gives the temperature dependent factor for processes, in which one phonon is created and one phonon is annihilated

$$\begin{aligned} f_\mathrm{A-B}(E,T) = f^\mathrm {BE}(E_\mathrm{B}(E),T) - f^\mathrm {BE}(E_\mathrm{A}(E),T)\,. \end{aligned}$$

(3.91)

The values of the functions $E_\mathrm{A}(E)$ and $E_\mathrm{B}(E)$ at the critical point energies are known from the known structure of phonon branches. In the regions between these energies they can be approximated with the help of linear interpolation:

$$\begin{aligned} E_\mathrm{A}(E) = E_\mathrm{A}^{M_{l-1}} Y_l(E) + E_\mathrm{A}^{M_l} X_l(E) \quad \text{ for } \quad E_{l-1} \le E \le E_l \,. \end{aligned}$$

(3.92)

The same linear interpolation is used to approximate $E_\mathrm{B}(E)$. We should emphasize that the temperature-dependent factors (3.90) and (3.91) do not require the introduction of any new parameters.

The complex dielectric function for two-phonon absorption is calculated from the unbroadened imaginary part of the dielectric function calculated with (3.87) by the $\varepsilon$-broadening procedure described in Sect. 3.2.3. This step can be performed only numerically, i. e. the convolution integrals in (3.49) must be performed numerically. Alternatively, we can split the intervals between the critical point energies into sufficiently small subintervals ($E_{j-1},E_j$), use the polynomial approximation of the function (3.87) on these subintervals (e.g. cubic splines) and then use the analytical results for broadened polynomials. On the j-th interval we can write

$$\begin{aligned} \varepsilon _{\mathrm{i},j}^0(E) = \sum _{n=0}^m a_{j,n} E^n \qquad \text{ for } \qquad E_{j-1} \le E \le E_j \,, \end{aligned}$$

(3.93)

where m is the degree of the approximating polynomial and $a_{j,n}$ are its coefficients. Thus, the contribution of this subinterval to the broadened dielectric function is expressed as follows:

$$\begin{aligned} \tilde{\hat{\varepsilon }}_{j+}^{0}(E) = \int _{E_{j-1}}^{E_j} \hat{\beta }(E-t) \sum _{n=0}^m a_{j,n} \, t^n \, \mathrm {d}t = \int _{E-E_{j-1}}^{E-E_j} \hat{\beta }(x) \sum _{n=0}^m A_{j,n}(E) \, x^n \, \mathrm {d}x \,, \end{aligned}$$

(3.94)

where

$$\begin{aligned} A_{j,n}(E) = (-1)^n \sum _{k=n}^m a_{j,k} \left( {\begin{array}{c}k\\ n\end{array}}\right) E^{k-n} \,. \end{aligned}$$

(3.95)

The contribution $\tilde{\hat{\varepsilon }}_{j+}^{0}(E)$ is calculated for the interval ($E_{j-1},E_j$) lying in positive values of energy. Because of the time reversal symmetry relating the dielectric function for positive and negative energies we can write the result that includes the contributions from both intervals ($E_{j-1},E_j$) and ($-E_j,-E_{j-1}$) as

$$\begin{aligned} \tilde{\hat{\varepsilon }}_{j}^0(E)&= \sum _{n=0}^m \sum _{k=n}^m a_{j,k} \left( {\begin{array}{c}k\\ n\end{array}}\right) (-E)^{k-n} \left[ (-1)^k \left( \hat{B}_n(E-E_{j-1}) - \hat{B}_n(E-E_j) \right) \right. \nonumber \\&\left. \qquad \qquad \qquad \qquad + \hat{B}_n(E+E_{j-1}) - \hat{B}_n(E+E_j) \right] \,, \end{aligned}$$

(3.96)

where $\hat{B}_n(x)$ are the functions defined by the following integrals

$$\begin{aligned} \hat{B}_n(x) = \int x^n \, \hat{\beta }(x) \, \mathrm {d}x \,. \end{aligned}$$

(3.97)

For the Lorentzian broadening, the results of the integrals can be expressed analytically

$$\begin{aligned} \hat{B}_{\mathrm{L},n}(x) = - \frac{1}{\pi } \left( \frac{-\mathrm{i}B}{2}\right) ^n \left[ \ln \!\left( 1-\frac{\mathrm{i}2x}{B}\right) + \sum _{k=0}^{n-1} \left( {\begin{array}{c}n\\ k\end{array}}\right) \frac{1}{n-k} \left( \frac{\mathrm{i}2x}{B}-1\right) ^{n-k} \right] \,. \end{aligned}$$

(3.98)

In the case of the Gaussian broadening the integrals can be expressed with the help of the following recurrent formulas

$$\begin{aligned} \hat{B}_{\mathrm{G},n}(x) = D_n(x) + \mathrm{i}G_n(x) \,, \end{aligned}$$

(3.99)

where

$$\begin{aligned} D_0(x) = - \frac{2}{\pi } \mathrm {D_i}\!\left( \frac{x}{\sqrt{2} B} \right) \,, \qquad G_0(x) = \frac{1}{2} \mathrm {erf}\!\left( \frac{x}{\sqrt{2} B} \right) \,, \end{aligned}$$

(3.100)

$$\begin{aligned} D_1(x) = \frac{\sqrt{2} B}{\pi } \mathrm {D}\!\left( \frac{x}{\sqrt{2} B}\right) - \frac{x}{\pi } \,, \qquad G_1(x) = \frac{B}{\sqrt{2\pi }} \left( 1 - \exp \!\left( - \frac{x^2}{2 B^2} \right) \right) \,, \end{aligned}$$

(3.101)

$$\begin{aligned} D_n(x)&= (n-1) B^2 D_{n-2}(x) + \frac{\sqrt{2} B}{\pi } x^{n-1} \mathrm {D}\!\left( \frac{x}{\sqrt{2} B}\right) - \frac{1}{n \pi } x^n \,, \end{aligned}$$

(3.102)

$$\begin{aligned} G_n(x)&= (n-1) B^2 G_{n-2}(x) - \frac{B}{\sqrt{2\pi }} x^{n-1} \exp \!\left( - \frac{x^2}{2 B^2} \right) \,. \end{aligned}$$

(3.103)

The recurrent formulas use three special functions, the Dawson function $\mathrm {D}(x)$ (3.52), its integral $\mathrm {D_i}(x)$ and the error function $\mathrm {erf}(x)$ defined as

$$\begin{aligned} \mathrm {D_i}(x) = \int _0^x \mathrm {D}(t) \, \mathrm {d}t \,, \qquad \mathrm {erf}(x) = \frac{2}{\sqrt{\pi }} \int _0^x \exp (-t^2) \, \mathrm {d}t \,. \end{aligned}$$

(3.104)

All three functions can be efficiently calculated in computer.

In the case of the Voigt broadening (3.74), it should be possible to write the result using complex special functions but in practice the approximation of the Voigt broadening by the linear combination of the Lorentzian and Gaussian broadening is sufficient (see Sect. 3.3.1.4).

In the presented model of the two-phonon absorption, the functions describing the Van Hove singularities $L_0$–$L_{15}$ are used to model the imaginary part of the dielectric function. Similar model of the two-phonon absorption in crystalline silicon was presented in [55]. The functions describing the Van Hove singularities were used to model the transition strength function instead of the imaginary part of the dielectric function. This required a different definition of the shape function H(E) because if the critical point energy $E_0$ is zero then the imaginary part of the dielectric function must behave as $\varepsilon _\mathrm {i}(E)\propto E$ for small energies.

3.2 Valence Electron Excitations

The valence electron excitations correspond to transition of electrons from the occupied valence band to the empty conduction band or to empty higher energy excitation band. In the crystalline solids in the quasiparticle approximation the one-particle states have well-defined momentum. Due to the momentum conservation it is possible to distinguish between direct and indirect valence-to-conduction interband electron transitions. This classification cannot, however, be used in the case of amorphous materials. Therefore, the valence electron excitations must be studied separately for crystalline and amorphous materials.

3.2.1 Direct Valence Electron Excitations in Crystalline Solids

In the frame of one-electron approximation the dielectric function can be modeled with the help of the 3D and 2D Van Hove singularities  [13, 15, 18, 21, 56, 57] described in detail in Sect. 3.3.1.6. The imaginary part of the normalized dielectric function is then given by the formula :

$$\begin{aligned} \varepsilon _\mathrm{i,dt}^0(E) = \frac{f_\mathrm{VC}(E,T)}{\mathcal {C}_\mathrm {N}E^2} H(E) \sum _{i=0}^{9} A_i J_i(E) \,, \end{aligned}$$

(3.105)

where $f_\mathrm{VC}(E,T)$ is a temperature dependent factor, $\mathcal {C}_\mathrm {N}$ is the normalization constant, the shape modifying function H(E) is defined by (3.88) and the weights $A_i$ describe the strength of individual contributions $J_i(E)$. In the absence of many-body effects, the contributions $J_i(E)$ are given as $J_i(E)=L_i(E)$ with functions $L_i(E)$ given in Tables 3.1 and 3.2. While in the case of two-phonon absorption described in Sect. 3.3.1.6 the functions $L_i(E)$ modeled the imaginary part of the dielectric function, the situation is different in the case of direct transitions (DT). More specifically, these functions are used to model the JDOS function (notice the factor $E^2$ in the denominator in (3.105)).

In contrast to phonons which could be, for most purposes, considered independent quasiparticles, the interactions between electrons cannot be neglected. The electron–hole interactions are manifested via two phenomena in the absorption spectra. The first phenomenon is the appearance of the discrete transitions, called excitons, in the region below the minimal energy of interband electronic transitions $E_0$. These discrete transitions correspond to bonded states between the electron–hole pairs. The second phenomenon is the redistribution of the transition strength (probability of transition) from higher energies to lower energies. This redistribution represents the effect of the continuum part of the spectra in the electron–hole system. In the frame of the Elliott theory [15, 24, 57,58,59], the contribution describing the discrete part $A_0 J_\mathrm{0ex}^\mathrm{3D}(E)$ must be added as an extra term in the sum in (3.105) and the square root parts of the contributions $J_0(E)$ and $J_3(E)$ must be modified. The schematic diagram of the JDOS function with and without the many-body effects is in the upper panel in Fig. 3.8. The function $J_\mathrm{0ex}^\mathrm{3D}(E)$ is defined as

$$\begin{aligned} J_\mathrm{0ex}^\mathrm{3D}(E) = S_0^\mathrm{3D}(E_1) \sum _{n=1}^{\infty } \frac{2 R}{n^3} \, \delta \!\left( E-E_0+\frac{R}{n^2} \right) \,, \end{aligned}$$

(3.106)

where the parameter R is the Rydberg energy describing the strength of the electron–hole interaction. Since the discrete part lies below the critical point energy $E_0$ we must extend the definition of the function H(E) in such a way that it is equal to unity for $E<E_0$. The functions $J_0(E)$ and $J_3(E)$ are changed to

$$\begin{aligned} J_0(E)&= \frac{S_0^\mathrm{3D}(E_1)}{S_0^\mathrm{3D}(E)}&\text{ for } \quad E_0 \le E \le E_1 \,, \end{aligned}$$

(3.107)

$$\begin{aligned} J_3(E)&= \frac{S_3^\mathrm{3D}(E_2)}{S_3^\mathrm{3D}(E)}&\text{ for } \quad E_2 \le E \le E_3 \,, \end{aligned}$$

(3.108)

The functions $S_0^\mathrm{3D}(E)$ and $S_3^\mathrm{3D}(E)$, which are called the Sommerfield factors, are defined as

$$\begin{aligned} S_0^\mathrm{3D}(E) = 1 - \exp \left( - 2\pi \sqrt{\frac{R}{E-E_0}}\right) \,, \quad S_3^\mathrm{3D}(E) = \exp \left( 2\pi \sqrt{\frac{R}{E_3-E}}\right) - 1 \,. \end{aligned}$$

(3.109)

In the limit of small R, the functions $J_0(E)$ and $J_3(E)$ are identical with $L_0(E)$ and $L_3(E)$.

Fig. 3.8

Schematic diagram of joint density of states (JDOS) of direct valence electron excitations corresponding to 3D and 2D Van Hove singularities, assuming $R=0.004 E_3$, $E_0=0.5 E_3$, $E_1=0.7 E_3$ and $E_2=0.8 E_3$. The dotted lines correspond to individual contributions without many-body effects while the solid lines correspond to contributions that include excitonic effects , i.e. corrected by the Sommerfield factors . The arrows indicate the positions of the first excitons ($n=1$) in the series of discrete transitions

In the case of the 2D Van Hove singularities the Elliott theory gives two series of discrete transitions, one below the critical point energy $E_0$ and the other below the $E_1$:

$$\begin{aligned} J^\mathrm{2D}_\mathrm{0ex}(E)&= S_0^\mathrm{2D}(E_1) \sum _{n=1}^{\infty } \frac{32 R}{(2n-1)^3} \, \delta \!\left( E - E_0 + \frac{4 R}{(2n-1)^2}\right) \,, \end{aligned}$$

(3.110)

$$\begin{aligned} J^\mathrm{2D}_\mathrm{1ex}(E)&= S_1^\mathrm{2D}(E_2) \sum _{n=1}^{\infty } \frac{32 R}{(2n-1)^3} \, \delta \!\left( E - E_1 + \frac{4 R}{(2n-1)^2}\right) \,. \end{aligned}$$

(3.111)

These functions must be added to the sum in (3.105) as two extra terms $A_4 J^\mathrm{2D}_\mathrm{0ex}(E) + A_7 J^\mathrm{2D}_\mathrm{1ex}(E)$. Moreover, the contributions 4, 6, 7 and 9 must be changed to:

$$\begin{aligned} J_4(E)&= Y_\mathrm{I}(E) \frac{S_0^\mathrm{2D}(E_1)}{S_0^\mathrm{2D}(E)}&\text{ for } \quad E_0 \le E \le E_1 \,, \end{aligned}$$

(3.112)

$$\begin{aligned} J_6(E)&= X_\mathrm{II}(E) \frac{S_2^\mathrm{2D}(E_1)}{S_2^\mathrm{2D}(E)}&\text{ for } \quad E_1 \le E \le E_2 \,, \end{aligned}$$

(3.113)

$$\begin{aligned} J_7(E)&= Y_\mathrm{II}(E)\frac{S_1^\mathrm{2D}(E_2)}{S_1^\mathrm{2D}(E)}&\text{ for } \quad E_1 \le E \le E_2 \,, \end{aligned}$$

(3.114)

$$\begin{aligned} J_9(E)&= X_\mathrm{III}(E) \frac{S_3^\mathrm{2D}(E_2)}{S_3^\mathrm{2D}(E)}&\text{ for } \quad E_2 \le E \le E_3 \,, \end{aligned}$$

(3.115)

where the 2D Sommerfield factors are defined as

$$\begin{aligned} S_0^\mathrm{2D}(E)&= 1 + \exp \left( - 2\pi \sqrt{\frac{R}{E-E_0}}\right) \,,&S_2^\mathrm{2D}(E)&= 1 + \exp \left( 2\pi \sqrt{\frac{R}{E_2-E}}\right) \,, \end{aligned}$$

(3.116)

$$\begin{aligned} S_1^\mathrm{2D}(E)&= 1 + \exp \left( - 2\pi \sqrt{\frac{R}{E-E_1}}\right) \,,&S_3^\mathrm{2D}(E)&= 1 + \exp \left( 2\pi \sqrt{\frac{R}{E_3-E}}\right) \,. \end{aligned}$$

(3.117)

The models of the discrete transitions below $E_0$, which were introduced above are correct as long as the critical point $M_0$ is purely 3D, purely 2D, or if the Rydberg energy R is smaller than the broadening parameter and the discrete transitions appear as a single structure (peak) in the absorption spectra. In the case of anisotropic critical point $M_0$ and Rydberg energy larger than the broadening parameter, it must be ensured that the series of discrete transitions is not doubled. A useful usable approximation is the formula with weighted averages for the amplitudes and positions of discrete transitions. The imaginary part of the normalized dielectric function is in this case given as

$$\begin{aligned} \varepsilon _\mathrm{i,dt}^0(E) =&\frac{f_\mathrm{VC}(E,T)}{\mathcal {C}_\mathrm {N}E^2} H(E) \left[ \sum _{n=1}^\infty A_{\mathrm{0ex},n} \, \delta (E-E_{\mathrm{0ex},n}) \right. \nonumber \\&+ \left. \sum _{n=1}^\infty A_{\mathrm{1ex},n} \, \delta (E-E_{\mathrm{1ex},n}) + \sum _{i=0}^{9} A_i J_i(E) \right] \,, \end{aligned}$$

(3.118)

where the amplitudes and energies of excitons are expressed as

$$\begin{aligned} A_{\mathrm{0ex},n} = \frac{R}{A_0+A_4} \left( \frac{2 A_0 S_0^\mathrm{3D}(E_1)}{n^3} + \frac{32 A_4 S_0^\mathrm{2D}(E_1)}{(2n-1)^3} \right) \,, \end{aligned}$$

(3.119)

$$\begin{aligned} E_{\mathrm{0ex},n} = E_0 - \frac{R}{A_0+A_4} \left( \frac{A_0}{n^2} + \frac{4 A_4}{(2n-1)^2} \right) \,, \end{aligned}$$

(3.120)

$$\begin{aligned} A_{\mathrm{1ex},n} = \frac{32 R A_7 S_1^\mathrm{2D}(E_2) }{(2n-1)^3} \,, \qquad E_{\mathrm{1ex},n} = E_1 - \frac{4 R}{(2n-1)^2} \,. \end{aligned}$$

(3.121)

The temperature-dependent factor $f_\mathrm{VC}(E,T)$ can be derived using the Fermi–Dirac statistics. If the Fermi energy lies in the band gap and both the valence and conduction bands are sufficiently far from the Fermi energy, then the value of this factor can be set to unity. Therefore, temperature dependency in dielectrics and semiconductors introduced by this factor is negligible. The temperature dependencies of the critical point energies could be described by the same formula as in the case of phonons, i. e. with the help of the average Bose–Einstein statistical factor (3.85). In contrast to phonons, separate average phonon energy parameters $\Theta _0$–$\Theta _3$ must be used for individual critical point energies $E_0$–$E_3$ [52, 53].

The presented model uses the functions $J_0$–$J_9$ describing the Van Hove singularities to model the JDOS function. In materials where all the critical point energies $E_0$ are greater than zero, i. e. dielectrics and semiconductors, it is not specifically important that the functions describing the Van Hove singularities are used to model the JDOS function, the transition strength function or the imaginary part of the dielectric function. Therefore, the factor $E^2$ in the denominator in (3.118) could be replaced by E or 1, it is even possible to use a generic factor $E^\kappa$ with $\kappa$ being the parameter of the model. The $\varepsilon$-broadening should be used if DT in dielectrics or semiconductors are modeled. In contrast to phonons, where only a single broadening parameter is typically used, in the case of the DT it is necessary to use several broadening parameters. It is often necessary to use different broadening parameters for structures belonging to individual critical points. For example, the structure around $M_0$ (contributions $J_\mathrm{0ex}$, $J_0$, $J_4$) are broadened using $B_0$, the structure around $M_1$ (contributions $J_\mathrm{1ex}$, $J_1$, $J_5$) by $B_1$ etc.

Only the 3D and 2D Van Hove singularities were considered in this section. In principle the model can be extended to include also 1D singularities with corresponding 1D excitonic effects.

The slightly modified variety of the model of DT discussed in this section was used in the temperature-dependent dispersion model of crystalline silicon [60]. It was shown that the presented model could be understood as the extension of the models of Adachi [19, 61], Kim et al. [21, 22], Tanguy [23, 24] and Herzinger and Johs [25, 26].

In metals, the parabolic band approximation cannot be used to describe the behavior around the minimal energy of DT if the initial or final band is not fully filled. Therefore, the JDOS around this minimal energy cannot be described as a Van Hove $M_0$ singularity and a special model must be devised. Moreover, the initial or final energy is given by the Fermi energy and, therefore, the thermal dependent factor cannot be approximated by unity. We will not discuss the models of DT in metals in this chapter.

Another special case is graphene. The graphene forms a two-dimensional structure in which the valence and conduction bands touch at the K points of the hexagonal Brillouin zone. Moreover, the bands around the points of contact form the cones with the Fermi energy lying exactly at the level where the vertexes of the cones touch. This band structure together with the assumption of the constant momentum (current) matrix element results in constant conductivity (constant transition strength function), known as the universal conductivity . In this case the unbroadened transition strength function of the ordinary part of the dielectric response can be modeled with the help of the functions $F_4(E)\equiv L_4(E)$, $F_5(E)\equiv L_5(E)$ and $F_6(E)\equiv J_6(E)$ describing the 2D Van Hove singularities with critical point energy $E_0=0$. In this special case the F-broadening must be used instead of $\varepsilon$-broadening and, furthermore, it must be performed prior to the multiplication by the the temperature dependent factor

$$\begin{aligned} \hat{\varepsilon }_\mathrm{dt}^0(E) = \frac{f_\mathrm{VC}(E,T)}{\mathcal {C}_\mathrm {N}E} \left[ \hat{\beta }* \left( \sum _{i=4,5,6} A_i F_i(E) \right) \right] \,, \end{aligned}$$

(3.122)

where the temperature dependent factor $f_\mathrm{VC}(E,T)$ is given as

$$\begin{aligned} f_\mathrm{VC}(E,T) = f^\mathrm {FD}(-E/2,T) - f^\mathrm {FD}(E/2,T) \,, \end{aligned}$$

(3.123)

where $f^\mathrm {FD}(E,T)$ is the Fermi–Dirac statistical factor with the Fermi energy equal to zero

$$\begin{aligned} f^\mathrm {FD}(E,T) = \frac{1}{\exp (E/(k_\mathrm {B}T)) + 1} \,. \end{aligned}$$

(3.124)

The similar absorption structure appears also in graphite [48] which is a 3D structure with strongly anisotropic critical points.

3.2.2 Indirect Valence Electron Excitations in Crystalline Solids

Apart from the direct electronic transitions there are also indirect electronic transitions in which the transitions of electrons between the valence and conduction bands are accompanied by a simultaneous change in phonon occupation numbers. The dominant absorption processes in this case are the processes involving creation or annihilation of one phonon. The processes in which multiple phonon occupation numbers are changed are much weaker and they can be neglected. Thus, the temperature-dependent imaginary part of the dielectric function can be separated into two parts

$$\begin{aligned} \varepsilon _\mathrm{i,idt}(E) = \sum _p \frac{N_p}{E} \frac{\left( f^\mathrm{BE}(E_p,T)+1\right) F_\mathrm{ab}^0(E-E_p) + f^\mathrm{BE}(E_p,T) F_\mathrm{ab}^0(E+E_p)}{2 f^\mathrm{BE}(E_p,300K)+1} \,, \end{aligned}$$

(3.125)

where the summation over p is performed for phonon branches corresponding to possible energies of phonons $E_p$ ensuring momentum conservation in indirect absorption processes. The part with $E-E_p$ corresponds to processes in which a phonon is created and the part with $E+E_p$ corresponds to processes in which a phonon is annihilated. The term in the denominator ensures proper normalization of the terms at 300 K. The parameters $N_p$ are the transition strengths for the corresponding phonon branches at 300 K. The Bose–Einstein statistical factors $f^\mathrm{BE}$ (3.83) determine the phonon occupation numbers, i. e. probabilities of the processes [7, 15, 62]. In principle we should also include the temperature dependent factor $f_\mathrm{VC}(E,T)$ but its effect can be usually neglected. The normalized transition strength function of indirect transitions (IDT) corresponding to one branch when the phonon is created or annihilated is calculated as

$$\begin{aligned} F_\mathrm{ab}^0(E) = \frac{(|E|-E_\mathrm {g})^2 (E_\mathrm {h}-|E|)^2}{\mathcal {C}_\mathrm {N}\, |E|^\kappa \left( (|E|-E_\mathrm {r})^2 + B^2/4 \right) ^\nu } \, \Pi _{E_\mathrm {g},E_\mathrm {h}}(|E|) \,, \end{aligned}$$

(3.126)

where the symbols $E_\mathrm {g}$ and $E_\mathrm {h}$ denote the minimal and maximal energy needed for excitation of electrons from the valence band to the conduction band. The parameter $\nu$ could be 0 or 1. If $\nu =0$, the formula represents the broad absorption band between $E_\mathrm {g}$ and $E_\mathrm {h}$ with quadratic behavior in neighborhoods above $E_\mathrm {g}$ and below $E_\mathrm {h}$. In the band gap region this behavior is known as the Tauc’s law discussed in Sect. 3.3.2.4. The parameter $\kappa$ regulates the asymmetry of this absorption band. If $\nu =1$, the shape of the absorption band is modified by the Lorentzian term and the symbols $E_\mathrm {r}$ and B denote the resonant energy and broadening, respectively. The function $\Pi _{E_\mathrm {g},E_\mathrm {h}}(E)$ ensures that the transition strength function is zero below $E_\mathrm {g}$ and above $E_\mathrm {h}$

$$\begin{aligned} \Pi _{E_\mathrm {g},E_\mathrm {h}}(E) = \Theta (E-E_\mathrm {g}) \, \Theta (E_\mathrm {h}-E) \,. \end{aligned}$$

(3.127)

In many cases  it is not possible to model the shape of the absorption band by using only one function (3.126) and several terms must be used. Note that separate parameters $E_\mathrm {r}$ and B should be used for each absorption band but it impossible in practice to distinguish individual absorption branches with the exception of the region around the band gap energy $E_\mathrm {g}$. Therefore, only one set of parameters $E_\mathrm {r}$ and B could be used for all phonon branches.

The real part of the dielectric function and normalization constant $\mathcal {C}_\mathrm {N}$ must be calculated using the KK relations and normalization integral. The result can be expressed in an analytic form for integer values of the parameter $\kappa$ (for $\kappa =1$ and $\nu =0,1$ see  [63, 64]). For $\kappa =0,1,2$ and $\nu =0$, the dielectric function is plotted in Fig. 3.9. In order to avoid the numerical integration when the parameter $\kappa$ has non-integer values, we can use the approximation in which the linear interpolation between integer values of $\kappa$ is used

$$\begin{aligned} F_\mathrm{ab}^0(E,\kappa ) \approx \left( \kappa -\lfloor \kappa \rfloor \right) F_\mathrm{ab}^0(E,1+\lfloor \kappa \rfloor ) + (1-\kappa +\lfloor \kappa \rfloor ) F_\mathrm{ab}^0(E,\lfloor \kappa \rfloor ) \end{aligned}$$

(3.128)

where $\lfloor \kappa \rfloor$ is the floor function.

Fig. 3.9

Contributions to the dielectric function of the IDT and IBT model (3.126) or (3.133) for $\nu =0$ and selected values of $\kappa$: $E_\mathrm {g}=1$ eV, $E_\mathrm {h}=15$ eV and $N=400\,\mathrm{eV}^2$

It is apparent that the total transition strength of IDT is strongly temperature-dependent because the probabilities of IDT depend on the occupation numbers of phonons which are determined by the Bose–Einstein statistics. The transitions strength of the whole system, which includes both the DT and IDT, is only weakly temperature-dependent due to the thermal expansion of the system. Therefore, the increase of the transition strength of IDT with temperature is at the expense of the transition strength of DT.

3.2.3 High Energy Valence Electron Excitations

Above a certain energy level the absorption spectra of crystalline solids are smooth without visible structures in the region of interband transitions. This can be explained by the fact that at higher energies, the electrons behave more like free electrons than bonded electrons. Although there is no clearly defined energy above which the transitions from the valence band lead to these structureless absorption spectra it is convenient to separate the excitations of valence electrons into those to conduction band (direct and indirect) and those to the band located above the conduction band (see Fig. 3.1). The transitions of the valence electrons to the states above the conduction band are called high energy valence electron excitations. The transition strength of these electron excitations is only weakly temperature dependent due to the thermal expansion of the system.

The simplest model of high energy transitions (HET) is a one-parametric model with the normalized dielectric function given by

$$\begin{aligned} \varepsilon _\mathrm{r,het}^0(E)&= \frac{3 E_\mathrm {x}}{\pi E^2} \left( -\frac{(E_\mathrm {x}-E)^2}{E^3} \ln \left| 1-\frac{E}{E_\mathrm {x}}\right| + \frac{(E_\mathrm {x}+E)^2}{E^3} \ln \left| 1+\frac{E}{E_\mathrm {x}}\right| - \frac{2}{3E_\mathrm {x}} - \frac{2E_\mathrm {x}}{E^2} \right) \,, \nonumber \\ \varepsilon _\mathrm{i,het}^0(E)&= \frac{3 E_\mathrm {x}(|E|-E_\mathrm {x})^2}{E^5} \Theta (|E|-E_\mathrm {x}) \,, \end{aligned}$$

(3.129)

where the parameter $E_\mathrm {x}$ is the energy threshold of the higher energy valence electron excitations. The value of this parameter must lie above the band gap energy $E_\mathrm {g}$ and is usually closer to $E_\mathrm {g}$ than to the maximal energy of valence-to-conduction interband transitions $E_\mathrm {h}$. The imaginary part of the dielectric function has quadratic behavior near the threshold energy $E_\mathrm {x}$ thus there is no pronounced structure associated with this energy in the absorption spectra.

The imaginary part of the dielectric function of the above models falls as $1/E^3$ at high energies. The classical models (see Sect. 3.2.1) exhibit the same behavior and for this reason it is called the classical asymptotic behavior of the dispersion model. From the experiment it is known that for energies in the X-ray region the imaginary part of the dielectric function given mainly by the elastic scattering losses falls faster than $1/E^3$. If we want to model the dielectric response in this region then we can include the term $(|E|+E_\mathrm {a})$ ensuring faster decay above the energy $E_\mathrm {a}$ in the denominator of (3.129)

$$\begin{aligned} \varepsilon _\mathrm{i,het}^0(E) = \frac{(|E|-E_\mathrm {x})^2}{\mathcal {C}_\mathrm {N}E^5 (|E|+E_\mathrm {a})} \Theta (|E|-E_\mathrm {x}) \,. \end{aligned}$$

(3.130)

For both the presented models of high energy valence electron excitations, it is possible to express the real parts $\varepsilon _\mathrm{r,het}^0(E)$ and normalization constants $\mathcal {C}_\mathrm {N}$ analytically. The imaginary parts of the dielectric functions corresponding to HET models are compared in Fig. 3.10.

Fig. 3.10

Contributions to the dielectric function corresponding to HET models (3.129) and (3.130): $E_\mathrm {x}=10$ eV, $E_\mathrm {a}=500$ eV, $N_\mathrm{het}=500\,\mathrm{eV}^2$

3.2.4 Valence Electron Excitations in Amorphous Materials

In disordered materials, it is not possible to distinguish between valence-to-conduction interband transitions that involve changes in phonon occupation numbers and those in which phonons do not participate. Therefore, the interband transitions can be described by a single broad absorption band between $E_\mathrm {g}$ (band gap energy) and $E_\mathrm {h}$ (maximal energy of interband transitions). The situation is similar to the case of IDT in the crystalline solids, but without the temperature dependency introduced by the average Bose–Einstein statistical factor for phonons (3.126). This is because the phonon assisted absorption processes have practically the same spectral distribution as the processes in which phonons do not participate and the sum of transitions strengths of both of these processes is only weakly temperature dependent (it is given mostly by the thermal expansion).

The behavior of the JDOS function in the vicinity of the bandgap can be derived using the one-particle approximation and quadratic band approximation. The JDOS function is then given as the correlation between the initial states in the valence band and final states in the conduction band

$$\begin{aligned} J(E) = \int _{-\infty }^\infty f_\mathrm{VC}(E,T) \, D_\mathrm{V}(S) \, D_\mathrm{C}(S+E) \, \mathrm {d}S \,, \end{aligned}$$

(3.131)

where the integration is performed over the energies of initial states S. The symbols $D_\mathrm{V}$ and $D_\mathrm{C}$ denote the densities of states (DOS) of initial and final states, respectively. If the momentum (current) matrix element is assumed to be constant, the probability of transition is given only by the temperature dependent factor $f_\mathrm{VC}(E,T)$ which is determined by the Fermi–Dirac distribution as

$$\begin{aligned} f_\mathrm{VC}(E,T) = f^\mathrm {FD}(S,T) \left( 1 - f^\mathrm {FD}(S+E,T) \right) \,. \end{aligned}$$

(3.132)

This factor is usually set to unity because the Fermi energy lies in the bandgap far from the valence and conduction bands (see Fig. 3.1). The result, known as the Tauc’s law , states that the JDOS function should be quadratic in the neighborhood above the band gap energy $E_\mathrm {g}$ and zero below $E_\mathrm {g}$. The similar result can be obtained for the behavior of the JDOS in the vicinity of the maximal energy of transitions $E_\mathrm {h}$.

The model of the interband transitions (IBT) which fulfills the quadratic dependencies above $E_\mathrm {g}$ and below $E_\mathrm {h}$ can be constructed as a linear combination of terms

$$\begin{aligned} \varepsilon _\mathrm{i,ibt}^0(E) = \frac{(|E|-E_\mathrm {g})^2 (E_\mathrm {h}-|E|)^2}{\mathcal {C}_\mathrm {N}\, E \, |E|^\kappa \left( (|E|-E_\mathrm {r})^2 + B^2/4 \right) ^\nu } \, \Pi _{E_\mathrm {g},E_\mathrm {h}}(|E|) \,. \end{aligned}$$

(3.133)

with the same values of $E_\mathrm {g}$, $E_\mathrm {h}$ and $\kappa$ but with different values of parameters $\nu$, $E_\mathrm {r}$ and B for each term. The real part of the dielectric function and normalization constant $\mathcal {C}_\mathrm {N}$ can be expressed in an analytic form for integer values of the parameter $\kappa$ (for $\kappa =1$ and $\nu =0,1$ see  [63, 64]). For $\kappa =0,1,2$ and $\nu =0$, the dielectric function is plotted in Fig. 3.9.

The high energy excitations in amorphous materials are modeled in the same way as in crystalline solids. Therefore, the dielectric response of the total valence electron excitations can be expressed as a sum of IBT and HET contributions

$$\begin{aligned} \hat{\varepsilon }_\mathrm{vee}(E) = N_\mathrm{ibt}\hat{\varepsilon }_\mathrm{ibt}^0(E) + N_\mathrm{het}\hat{\varepsilon }_\mathrm{het}^0(E) \,. \end{aligned}$$

(3.134)

The threshold energies $E_\mathrm {x}$ and $E_\mathrm {h}$ appearing in equations for the HET and IBT cannot be identified by any visible structures in the absorption spectra. Therefore, the HET and IBT are often described by the model which does not contain the parameters $E_\mathrm {x}$ and $E_\mathrm {h}$. The Tauc–Lorentz (TL) models combining the Tauc’s law valid in the vicinity of the bandgap with the Lorentz model (or Lorentz function) are utilized for this purpose.

The first physically correct model combining the Lorentz model with the Tauc’s law was suggested by Campi and Coriasso [65, 66]. The Campi–Coriasso (CC) model is based on the fact that the transition strength function of the Lorentz model (3.59) has quadratic form in the vicinity of zero energy

$$\begin{aligned} F_\mathrm{LM}^0(E) = \frac{2}{\pi } \frac{B E^2}{ (E_\mathrm {c}^2 - E^2)^2 + B^2 E^2 } \,. \end{aligned}$$

(3.135)

The Campi and Coriasso shifted the Lorentz model by the bandgap energy $E_\mathrm {g}$, i. e. they performed the substitution $E \rightarrow E-E_\mathrm {g}$, and for energies below the $E_\mathrm {g}$ they set the transition strength to zero. The normalized transition strength function is then given by

$$\begin{aligned} F_\mathrm{CC}^0(E)&= F_\mathrm{LM}^0(E-E_\mathrm {g}) \ \Theta (E-E_\mathrm {g}) \nonumber \\&= \frac{2}{\pi } \frac{B \ (E-E_\mathrm {g})^2 \ \Theta (E-E_\mathrm {g})}{ \Big ((E_\mathrm {c}-E_\mathrm {g})^2 - (E-E_\mathrm {g})^2\Big )^2 + B^2 \, (E-E_\mathrm {g})^2}\,, \end{aligned}$$

(3.136)

where the parameter $E_\mathrm {c}$ must fulfill the inequality $E_\mathrm {c}>E_\mathrm {g}$. The dielectric function is calculated using (3.30) and the KK relations, the analytic expressions can be found in [67].

Another approach to constructing the models combining the Tauc’s law with the Lorentz model includes multiplying the transition strength function of the Lorentz model by a truncate function that is zero below the bandgap, quadratic in the neighborhood above the bandgap and tends to unity at high energies. Two such models are widely used, the Jellison–Modine (JM) model [68] which uses the one-parametric truncate function

$$\begin{aligned} T_1(E) = \frac{(E-E_\mathrm {g})^2}{E^2} \, \Theta (E-E_\mathrm {g}) \,, \end{aligned}$$

(3.137)

and the A. S. Ferlauto et al.(ASF) model [69] which uses the two-parametric truncate function

$$\begin{aligned} T_2(E) = \frac{(E-E_\mathrm {g})^2}{(E-E_\mathrm {g})^2+E_\mathrm {q}^2} \, \Theta (E-E_\mathrm {g}) \,. \end{aligned}$$

(3.138)

In the literature the JM model is usually referred as the Tauc–Lorentz model whereas ASF model is known as the Cody–Lorentz model. Two models that use the same truncate functions as the JM and ASF models but with the transition strength of the Lorentz model (LM) replaced by the Lorentz function (LF) were suggested in [67]. We will refer to these models as to truncated Lorentz function models TLF1 and TLF2.

The imaginary part of the dielectric function of the JM, ASF, TLF1 and TLF2 models can be expressed with the help of the generic formula

$$\begin{aligned} \varepsilon _{\mathrm{i},m}^0 = \frac{T_a(E) F_b(E)}{\mathcal {C}_\mathrm {N}E} \,, \end{aligned}$$

(3.139)

where $\mathcal {C}_\mathrm {N}$ is the normalization constant, the truncate function $T_a(E)$ is either (3.137) or (3.138) and $F_b(E)$ is one of

$$\begin{aligned} F_\mathrm{LM}(E)&= \frac{E^2}{(E_\mathrm {c}^2 - E^2)^2 + B^2 E^2} \,,&F_\mathrm{LF}(E)&= \frac{1}{(E-E_\mathrm{r})^2+B^2/4} \,, \end{aligned}$$

(3.140)

where the energies $E_\mathrm {c}$ and $E_\mathrm {r}$ are related as (3.60). The summary of these models is in Table 3.4.

Table 3.4 The summary of the truncate functions and transition strength functions used in formula (3.139). The dispersion parameters and the rms value of differences $\delta \varepsilon$ corresponding to the fit to the CC model calculated with $N=100\,\mathrm{eV}^2$, $E_\mathrm {c}=3\,\mathrm{eV}$, $B=3\,\mathrm{eV}$ and $E_\mathrm {g}=1\,\mathrm{eV}$ are also introduced. Transition strength N for the IBT$+$HET model (3.134) is $N_\mathrm{ibt}+N_\mathrm{het}$

Each version of the TL model introduced above has a slightly different shape. In order to compare these models the dielectric function of the CC model calculated in the spectral range 0–10 eV for the selected dispersion parameters was fitted by the other versions of the TL model. The dispersion parameters corresponding to the best fits and the parameters $\delta \varepsilon$ representing the rms values of the differences between the models are in Table 3.4. The results for the IBT$+$HET model (3.134) with one IBT term (3.133) and one HET term (3.129) are introduced for comparison. In Fig. 3.11 the dielectric function of the CC model is compared with the four-parametric JM and TLF1 models. The curves corresponding to the five-parametric ASF and TLF2 models are not displayed since the differences from the CC model are too small to be visible in the figure. A more detailed comparison of these models can be found in [67].

Fig. 3.11

Contributions to the dielectric function of three versions of Tauc–Lorentz models. The dispersion parameters are in Table 3.4

From the physical point of view, there is no reason to prefer one of the TL models over another. The choice of the model giving the best results is specific for individual materials. If we are unsure which model to use, it is possible to model the valence electron excitations with a linear combination of several of the presented models.

3.3 Electronic Transitions Involving Localized States

Apart from the extended states forming the valence and conduction bands there are localized occupied and unoccupied states (see Fig. 3.1). In both disordered and crystalline solids there are localized states originating from the broken transition symmetry. In crystalline solids, the broken transition symmetry (disorder) is a consequence of the thermal motion of nuclei forming the crystal while in the disordered solids the disorder is both inherent and caused by the thermal motion. The localized states could originate also from the defects in the materials, such as vacancies, impurities, etc. If the initial and final states are localized states, we talk about localized excitations and if the initial or final state is the extended state, i. e. valence or conduction state, then the excitation is modeled by the subgap absorption tails.

3.3.1 Localized Excitations

The localized states are typically observable below the band gap energy as discrete transitions with the photon energies given as the differences between the energy of corresponding occupied and unoccupied localized states . This means that the JDOS cannot be calculated as the correlation between the initial and final states as in the case of IBT (3.131). In most cases, the Gaussian $\varepsilon$-broadened discrete transitions are an adequate model [63, 64], i. e. the same model as for phonons (see Sect. 3.3.1.1). In the case of excitations of $\pi$-electrons in diamond-like carbon (DLC) [70,71,72,73] or excitations of non-bonding electrons in chalcogenides [74,75,76] the corresponding absorption structures can be described by the IBT model (3.133). In these cases the degree of localization of the $\pi$-electron and non-bonding electron states is relatively low and, therefore, it is possible to represent the density of states as two valence bands and two conduction bands with different bandgap energies.

3.3.2 Exponential (Urbach) Tail

The exponential (Urbach) tail is employed to describe the weak absorption below the band gap caused by the transitions of electrons from the localized valence states to the unoccupied extended states and the transitions from the extended valence states to the unoccupied localized states [77] (see Fig. 3.1). The JDOS associated with these transitions are given as the correlation between the density of localized states with the density of states in valence or conduction bands. The density of localized states is given by the narrow peak with typical width in tens of meV which decays exponentially. Since the typical width of extended bands is around 10 eV the correlation gives the JDOS which looks like copies of the extended bands with exponential tails on both of its ends. The exponential tails have limited extent because the DOS of the localized states is bounded by the Fermi energy. The imaginary part of the normalized dielectric function corresponding to localized-to-extended or extended-to-localized transitions can be modeled by [63, 64]

$$\begin{aligned} \varepsilon _\mathrm{i, ut}^0(E)&= \dfrac{1}{\mathcal {C}_\mathrm {N}E |E|^\kappa } \left\{ \exp \!\left( \dfrac{|E|-E_\mathrm {g}}{E_\mathrm {u}}\right) \Pi _{E_\mathrm {g}/2,E_\mathrm {g}}(|E|) \right. \nonumber \\&+ \left[ 1 + \frac{E_\mathrm {m}-E_\mathrm {g}}{4E_\mathrm {u}} - \frac{(2 |E|-E_\mathrm {m}-E_\mathrm {g})^2}{4E_\mathrm {u}(E_\mathrm {m}-E_\mathrm {g})} \right] \Pi _{E_\mathrm {g},E_\mathrm {m}}(|E|) \\&\left. + \exp \!\left( \dfrac{E_\mathrm {m}-|E|}{E_\mathrm {u}}\right) \Pi _{E_\mathrm {m},E_\mathrm {m}+E_\mathrm {g}/2}(|E|) - \exp \!\left( -\dfrac{E_\mathrm {g}}{2E_\mathrm {u}}\right) \Pi _{E_\mathrm {g}/2,E_\mathrm {m}+E_\mathrm {g}/2}(|E|) \right\} \,, \nonumber \end{aligned}$$

(3.141)

where $E_\mathrm {u}$ is the parameter called the Urbach energy. It express the slope of the decrease of the exponential tail and the parameter $\kappa$ modifies the shape of the absorption band. The energy $E_\mathrm {m}$ is the difference between the energies of tops of the valence and conduction bands if the model describes the localized-to-extended transitions and the difference between the energies of the bottoms of the valence and conduction bands if the model describes extended-to-localized transitions. In principle two models (3.141) with different $E_\mathrm {m}$ should be used but because the absorption structures corresponding to these transitions are weak they are masked by other absorption structures above the $E_\mathrm {g}$. For this reason, it is possible to use one model with the mean value

$$\begin{aligned} E_\mathrm {m}=E_\mathrm {g}/2+E_\mathrm {h}/2 . \end{aligned}$$

(3.142)

Fig. 3.12

Schematic diagram of JDOS function of exponential (Urbach) tail model ($\kappa =1$)

A schematic diagram of this model constructed from three parts is plotted in Fig. 3.12. In (3.141) the first three terms correspond to the three parts of the model and the fourth constant term ensures the continuous course of the JDOS in energies $E_\mathrm {g}/2$ and $E_\mathrm {m}+E_\mathrm {g}/2$. As was mentioned above the exponential tail has extent limited by the Fermi energy. For this reason the model is constructed such that it is zero below $E_\mathrm {g}/2$ and above $E_\mathrm {m}+E_\mathrm {g}/2$, i. e. it is assumed that the Fermi energy lies in the middle of the bandgap. The analytic expressions for the real part of the normalized dielectric function and the normalization constant $\mathcal {C}_\mathrm {N}$ for $\kappa =1$ can be found in [64].

When the valence electron excitations are described by the Tauc–Lorentz models, it is possible to use the model of exponential (Urbach) tail, which is not limited by the energy $E_\mathrm {m}$ but extends to infinity

$$\begin{aligned} \varepsilon _\mathrm{i, ut}^0(E)&= \dfrac{1}{\mathcal {C}_\mathrm {N}E |E|^\kappa } \left\{ \left[ \exp \!\left( \dfrac{|E|-E_\mathrm {g}}{E_\mathrm {u}}\right) - \exp \!\left( -\dfrac{E_\mathrm {g}}{2E_\mathrm {u}}\right) \right] \Pi _{E_\mathrm {g}/2,E_\mathrm {g}}(|E|) \right. \nonumber \\&\left. + \frac{A (|E|-E_0)^2}{|E|^{4-\kappa }}\Theta (|E|-E_\mathrm {g}) \right\} \,. \end{aligned}$$

(3.143)

The model is parameterized by the energies $E_\mathrm {u}$, $E_\mathrm {g}$ and the integer $\kappa$. The values of $E_0$ and A must be determined so that the imaginary part of the dielectric function and its derivative are continuous at $E_\mathrm {g}$.

3.4 Free Carrier Contributions

If the valence or conduction band is partially occupied, i. e. the Fermi energy lies inside or sufficiently close to these bands, the indirect intraband transitions contribute to the dielectric response of the material. These transitions are called free carrier contributions (FCC) because they can be interpreted as movement of carriers of charge, i. e. electrons and holes, in the frame of quasiparticle approximation. Although the maximum energy of the FCC is given by the width of the partially filled band, it is possible to use the classical model, which is not bounded by any maximum energy. The absence of the upper energy limit is not a serious problem because it lies in the region of the interband electronic transitions which are, in this region, much stronger than the FCC. Since the dielectric function corresponding to the FCC has a singularity at the zero energy, it is more convenient to describe the free carrier dielectric response using the complex optical conductivity $\hat{\sigma }(\omega )=-\mathrm{i}\omega \epsilon _0 [\hat{\varepsilon }(\omega )-1]$ or equivalently using the transition strength function which is proportional to its real part $\sigma _\mathrm{r}$. The normalized transition strength function of the Drude model (3.15) is given as follows

$$\begin{aligned} F_{\!\mathrm fcc}^0(E) = \frac{2}{\pi } \frac{B}{E^2+B^2} \,. \end{aligned}$$

(3.144)

Instead of being bounded by a high energy limit, the Drude model exhibits classical asymptotic behavior. This could be problematic if we intent to model the dielectric response in the high energy X-ray region. In that case, it is better to use the modified version of the Drude model that introduces the high energy limit $E_\mathrm {w}$ as follows

$$\begin{aligned} F_{\!\mathrm fcc}^0(E) = \frac{(E_\mathrm {w}^2-E^2)^2 \Theta (E_\mathrm {w}-E)}{\mathcal {C}_\mathrm {N}(E^2+B^2)} \,, \quad \mathcal {C}_\mathrm {N}= \frac{(E_\mathrm {w}^2+B^2)^2}{B} \arctan \!\left( \frac{E_\mathrm {w}}{B}\right) - E_\mathrm {w}B^2 - \frac{5}{3} E_\mathrm {w}^3 \,. \end{aligned}$$

(3.145)

The dielectric function of this model can be expressed analytically by (3.35) and (3.36). The comparison of this model with the Drude model is in Fig. 3.13.

Fig. 3.13

Normalized transition strength functions $F^0(E)=E \varepsilon _\mathrm {i}^0(E)$ for models of free carrier contribution: $B=0.2$ eV, $E_\mathrm {w}=1$ eV

The temperature dependence of the intraband transitions is a complex phenomenon and it is impossible to describe it by a formula which is universally valid. Roughly speaking, it depends on the position of the Fermi energy within the band structure. For example, if the Fermi energy lies inside the valence band (like in metals), the electron occupation numbers are redistributed inside the partially filled band and the total transition strength is practically constant. The broadening parameter B increases with the temperature due to the blurring of the Fermi–Dirac statistics which results in the decrease of the static conductivity. If the Fermi energy lies inside the band gap (like in semiconductors) then the conductivity of the material increases with temperature because the density of holes in the valence band and electrons in the conduction band increases. In intrinsic semiconductors the the Fermi energy lies exactly in the middle of the bandgap and the temperature dependence of the transition strength of intraband indirect transitions is given as [78, 79]

$$\begin{aligned} F^0_{\!\mathrm fcc}(E,T) = \left( \frac{T}{300\,\mathrm{K}}\right) ^{3/2} \exp \left[ -\frac{E_\mathrm {g}}{2 k_\mathrm {B}} \left( \frac{1}{T} - \frac{1}{300\,\mathrm{K}} \right) \right] \ F^0_{\!\mathrm fcc}(E)\,, \end{aligned}$$

(3.146)

where the normalization of $F^0_{\!\mathrm fcc}(E)$ is performed for 300 K.

Although the description of materials in the superconducting state poses considerable theoretical problem, it is quite easy to write the part corresponding to superconductivity (SC) in the dielectric model. The normalized contribution to the transition strength is given as

$$\begin{aligned} F^0_{\!\mathrm sc}(E) = 2 \delta (E) \end{aligned}$$

(3.147)

and the contribution to the real part of the dielectric function is

$$\begin{aligned} \varepsilon ^0_\mathrm{r,sc}(E) = - \frac{2}{\pi E^2}\,. \end{aligned}$$

(3.148)

3.5 Core Electron Excitations

Apart from the valence electrons the core electrons can also be excited to the unoccupied electronic states (see Fig. 3.1). These excitations are manifested by sharp absorption edges in the spectra. The positions of these absorption edges are determined by the energies of the core electron states in the individual atoms forming the material. This means that each element contained in the material is manifested by absorption edges at energies characteristic for this element. The exact configuration of atoms in the material has only a small influence on the positions of these absorption edges.

The excitations of core electrons into conduction band influence the shape of the absorption structures near the absorption edges. These structures are called fine absorption structures and their shape is determined not only by the types and quantities of atoms forming the material but also by their configuration within this material. The excitation of core electrons into higher states contributes to the dielectric response by smooth functions. The strength of these smooth contributions is determined only by the types and quantities of the atoms and it is independent on the exact configuration of these atoms within the material.

The influence of the core electron excitations (CEE) on the dielectric response in the region of valence electron excitations is very small. Therefore, if the experimental data do not extend to very high energies, it is possible to neglect the contribution coming from the CEE or a simple analytical model that is sufficiently accurate at low energies could be used [7, 60, 64, 78]:

$$\begin{aligned} \hat{\varepsilon }_\mathrm{cee}^0(E) = \frac{E_\mathrm {s}}{\pi E^3} \left( \ln \left| \frac{E+E_\mathrm {s}}{E-E_\mathrm {s}} \right| - \frac{2 E}{E_\mathrm {s}} \right) + \mathrm{i}\frac{E_\mathrm {s}}{E^3} \Theta (|E|-E_\mathrm {s}) \,. \end{aligned}$$

(3.149)

At low energies this model gives a practically constant contribution to the real part of the dielectric function, which can be expressed as

$$\begin{aligned} \lim _{E\rightarrow 0} \hat{\varepsilon }_\mathrm{cee}^0(E) = \frac{2}{3\pi E_\mathrm {s}^2} \,. \end{aligned}$$

(3.150)

For example, in the case of hydrogenated amorphous silicon these contributions are $1.2 \times 10^{-5}$ for K and 0.0204 for L core electrons [64].

The model of the CEE (3.149) has classical asymptotic behavior and singularity at energy $E=E_\mathrm {s}$. Similarly as for the HET the correct model of the CEE should fall faster than the classical asymptotic behavior at high energies. The faster decay at high energies could be achieved by placing the term $(|E| + E_\mathrm {a})$ into the denominator of the imaginary part of (3.149). The singularity at $E=E_\mathrm {s}$ is caused by the Heaviside step function and it can be removed by the broadening procedure. Thus the normalized dielectric function of the corrected CEE dispersion model can be written as

$$\begin{aligned} \hat{\varepsilon }_\mathrm{cee}^0(E) = \hat{\beta }* \frac{1}{\mathcal {C}_\mathrm {N}E^3 (|E| + E_\mathrm {a})} \Theta (|E|-E_\mathrm {s}) \,, \end{aligned}$$

(3.151)

where $\mathcal {C}_\mathrm {N}$ is the normalization constant given by

$$\begin{aligned} \mathcal {C}_\mathrm {N}= \frac{E_\mathrm {s}[\ln (E_\mathrm {s}) - \ln (E_\mathrm {s}+E_\mathrm {a})] + E_\mathrm {a}}{E_\mathrm {s}E_\mathrm {a}^2} \,. \end{aligned}$$

(3.152)

If the Lorentzian broadening function (3.55) is used, the result can be expressed analytically as

$$\begin{aligned} \hat{\varepsilon }_\mathrm{cee}^0(E)&= \frac{1}{\pi \mathcal {C}_\mathrm {N}} \left\{ \frac{2}{E_\mathrm {a}^2 (\hat{E}^2-E_\mathrm {a}^2)} \ln (E_\mathrm {a}+E_\mathrm {s}) - \frac{2}{E_\mathrm {a}^2 \hat{E}^2} \ln (E_\mathrm {s}) - \frac{2}{E_\mathrm {s}E_\mathrm {a}\hat{E}^2} \right. \\&+ \frac{1}{\hat{E}^3 (E_\mathrm {a}- \hat{E})} \left[ \frac{1}{2} \ln \!\left( (E+E_\mathrm {s})^2+B^2/4\right) - \mathrm{i}\arctan \!\left( \frac{E+E_\mathrm {s}}{B/2} \right) + \mathrm{i}\frac{\pi }{2} \right] \nonumber \\&- \left. \frac{1}{\hat{E}^3 (E_\mathrm {a}+ \hat{E})} \left[ \frac{1}{2} \ln \!\left( (E-E_\mathrm {s})^2+B^2/4\right) - \mathrm{i}\arctan \!\left( \frac{E-E_\mathrm {s}}{B/2} \right) - \mathrm{i}\frac{\pi }{2} \right] \right\} \,. \nonumber \end{aligned}$$

(3.153)

Fig. 3.14

Contributions to the dielectric function corresponding to CEE models (3.149) and (3.153): $N_\mathrm{cee}=500\,\mathrm{eV}^2$, $E_\mathrm {s}=100$ eV, $B=1$ eV, $E_\mathrm {a}=500$ eV

In Fig. 3.14, the contributions to the dielectric function calculated by the CEE models are shown in a log-log plot. In this figure, it is observed that the Lorentzian broadening results in nonzero contribution to the imaginary part in the low energy region. This slowly decaying weak absorption tail is unphysical in the region below the bandgap where the exponential (Urbach) tail should be observed. For this reason it is better to use the Gaussian broadening in (3.151) but in this case the broadened dielectric function requires the use of numerical integration.

4 Conclusion

The UDM is a collection of models describing various elementary excitations presented in a unified form. The contributions corresponding to these elementary excitations must be combined in order to describe the dielectric response of a specific material. In order to decide which contributions should be included in the model some prior knowledge of the structure of the studied material is needed. Moreover, the exact number and types of the contributions depend on the spectral range in which the model should be valid and the desired precision of the model. The models presented in this chapter are only a basic set of models of elementary excitations and some modifications or extensions of these models are possible. An example of a software that uses the UDM is newAD project [80]. So far the UDM was used to describe the optical response of the following materials: a-Si:H [64, 81], HfO$_\mathrm{2}$ [63, 82], SiO$_\mathrm{2}$ [82, 83], Al$_\mathrm{2}$O$_\mathrm{3}$ [82], Ta$_\mathrm{2}$O$_\mathrm{5}$ [82], TiO$_\mathrm{2}$ [82], MgF$_\mathrm{2}$ [82, 84] and ZnSe [85].