Meet in the Middle Attack on Type-1 Feistel Construction

Abstract

We provide a key recovery attack on type-1 Feistel construction based on the meet-in-the-middle technique. This construction is described by Zheng, Matsumoto, and Imai in CRYPTO 1989. Type-1 Feistel structure is a well-known construction used to construct ciphers and hash functions, such as CAST-256 and Lesamnta. For Type-1 Feistel construction with n-bit blocks and d sub-blocks, we launch a $3d-1$ rounds distinguisher by using a special truncated differential. We present an attack on $5d-3$ rounds with the data complexity ${{2}^{\frac{3}{d}n}}$ chosen plaintexts, the memory complexity ${{2}^{\frac{d-1}{d}n}}$ blocks, each block is n bits, and the time complexity ${{2}^{\frac{d-1}{d}n}}$ encryptions, which is the best known generic key recovery attack on Type-1 Feistel construction. The attack is valid if the key length $k\ge n$.

1 Introduction

Feistel construction is proposed by Feistel and Coppersmith [1] from IBM when designing Lucifer in 1973. On the one hand, the procedure of encryption and decryption are similar for this construction, on the other hand, it has few limitations to round function. So this construction is widely used in cipher designs. Many famous ciphers are based on Feistel construction, such as DES, Twofish and Camellia.

Based on Feistel construction, some extend constructions called generic Feistel scheme (GFS) are proposed, such as Type-1, Type-2 and Type-3 Feistel constructions [10], contracting and expanding Feistel constructions [14]. These constructions provide many new methods for designers and a plenty of ciphers are given out, for instance, CAST-256 (type-1), RC-6 (type-2), MARS (type-3). Type-1 and Type-2 Feistel are also respectively used in the construction of the hash functions Lesamnta and SHAvite-3$_{512}$. Since the widely use of the Feistel construction and GFS, the security of these constructions raised many researchers’ interests. In SAC 2012, Sasaki et al. [3] proposed a kind of meet-in-the-middle distinguisher of Feistel construction. In SAC 2015, based on Fouque et al. [12] and Matsui et al. [13]’s work, Lin et al. [4] describe an algorithm for searching the improved meet-in-the-middle distinguisher on Feistel construction and GFS by using recursion and greedy algorithm. In CRYPTO 2015, Dinur et al. [5] proposed a new meet-in-the-middle distinguisher for Feistel construction, which improved the former best attack results for Feistel construction. In CRYPTO 2016, Derbez et al. [6] describe an automatic meet-in-the-middle attack tool of Feistel construction.

The best attacking result of Feistel and Feistel-SP constructions, contracting and expanding Feistel constructions are proposed by Guo et al. In AisaCrypt 2014, Guo et al. [7] constructed 5-round meet-in-the-middle distinguisher and recover 6-round key for Feistel construction. As for Feistel-SP construction, they constructed 7-round meet-in-the-middle distinguisher and recover 14-round key. They extend their work for the circumstance that the key length over the block length in 2016 [8]. In FSE 2017 [9], they studied contracting and expanding Feistel constructions. By using the meet-in-the-middle technique and the similar skills from their former work, they give out the best known generic key-recovery attack for contracting and expanding Feistel constructions.

Compared with so many researches on Feistel construction, contracting and expanding Feistel constructions, there are few papers on generic attacks on Type-1, Type-2 and Type-3 Feistel constructions. In CANS 2013, Nachef et al. [16] present the best distinguish attack on Type-1, Type-2 and Type-3 Feistel constructions. However, this attack only distinguishes the scheme from a random permutation. It didn’t recovery the key. In CSS 2014, Pudovkina et al. [17] provide upper and lower bounds for the maximum number of the rounds of impossible differential distinguisher on Type-1, Type-2 and Type-3 Feistel constructions. In FSE 2015, Blondeau et al. [15] analyze the relationship between impossible, integral and zero-correlation attacks on Type-2 Feistel construction. As for Type-1 Feistel construction, there is no generic key-recovery attack up till now and it is the aim of this paper.

Our Contribution. In this paper, we present a key-recovery attack on Type-1 Feistel. Our attack is derived from Guo et al. [7,8,9]’s work. We construct $3d-1$ rounds distinguisher by using a special truncated differential. We present an attack on $5d-3$ rounds Type-1 Feistel with the data complexity ${{2}^{\frac{3}{d}n}}$ chosen plaintexts, the memory complexity ${{2}^{\frac{d-1}{d}n}}$ blocks, each block is n bits, and the time complexity ${{2}^{\frac{d-1}{d}n}}$ encryptions, which is the best known generic attack on Type-1 Feistel construction. What’s more, our attack is generic and we generalize the block number as d. In former work, the researchers always just considered the case that $d=4$.

2 Preliminaries

2.1 Notation and Definition

Throughout the paper, we will use the following notation. We use d denote the number of sub-blocks for the Type-1 Feistel structure, n denote the block size, which is equal to the key length k. In the following, we define the Type-1 Feistel Construction:

Definition 1

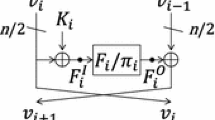
Type-1 Feistel Construction with d sub-blocks is the iteration of Fig. 1 for r times. Assume the input of the ith$\left( 1\le i\le r \right)$ round is $\big ( {{X}_{i,1}},{{X}_{i,2}},\cdots ,{{X}_{i,d}} \big ),{{X}_{i,j}}\in {{\left\{ 0,1 \right\} }^{{n}/{d}\;}}$, we call ${{X}_{i,j}}$ is the jth sub-block of the input of ith round. The round function is ${{F}_{i}}:{{\left\{ 0,1 \right\} }^{{n}/{d}\;}}\rightarrow {{\left\{ 0,1 \right\} }^{{n}/{d}\;}}$, and round sub-key is ${{K}_{i}}\in {{\left\{ 0,1 \right\} }^{{n}/{d}\;}}$. The transformation of the ith round ${{g}_{i}}$ is defined as follow:

$$\begin{aligned} {{g}_{i}}\left( {{X}_{i,1}},{{X}_{i,2}},\cdots ,{{X}_{i,d}} \right) =\left( {{F}_{i}}\left( {{X}_{i,1}}\oplus {{K}_{i}} \right) \oplus {{X}_{i,2}},{{X}_{i,3}},\cdots ,{{X}_{i,d}},{{X}_{i,1}} \right) \end{aligned}$$

Fig. 1.

Definition of 1-round Type-1 Feistel

Moreover, we make some assumptions about the round function ${{F}_{i}}$: assume that the round function of each round is nonlinear and invertible.

In the following context, for the jth sub-block of the ith round, we use ${{X}_{i,j}}$ and ${{Y}_{i,j}}$ to denote the input and output, $\varDelta {{X}_{i,j}}$ and $\varDelta {{Y}_{i,j}}$ denote the input difference and output difference, the input and output of the round function ${{F}_{i}}$ is $F_{i}^{I}$ and $F_{i}^{O}$, the input difference and output difference is $\varDelta F_{i}^{I}$ and $\varDelta F_{i}^{O}$.

Definition 2

Let F be a $3d-1$ rounds Type-1 Feistel Construction, defined: ${{F}^{\varDelta }}\left( m,\delta \right) =Trunc\left( F\left( m \right) \oplus F\left[ m\oplus \left( 0,0,\cdots ,0,\delta \right) \right] \right)$, where $m\in {{\left\{ 0,1 \right\} }^{n}},\delta \in {{\left\{ 0,1 \right\} }^{\frac{n}{d}}}$, Trunc(x) is the truncation of the second sub-blocks of x.

2.2 Properties

Property 1

Assume the sub-block numbers of the Feistel construction is d and the input of the round i is $\left( {{x}_{i,1}},{{x}_{i,2}},\cdots ,{{x}_{i,d}} \right)$, then

• (1) ${{x}_{i+1,1}}={{F}_{i}}({{x}_{i,1}}\oplus {{K}_{i}})\oplus {{x}_{i,2}}$, and we have ${{x}_{i+1,j}}={{x}_{i,(j+1)\bmod \,\, d}}$ for each $2\le j\le d$;

• (2) We have ${{x}_{i+t,j}}={{x}_{i,(j+t)\bmod \,\, d}}$ for $1\le t<d$ and $2\le j\le d+1-t$.

Proof

(1) We can obtain this property from Definition 1.

(2) From (1) we can see that (2) holds when $t=1$. Assume that (2) holds for $1\le t<m\le d$, we will prove that (2) holds when $t=m$. Assume $2\le j\le d+1-m$. we see that $m\ge 2$, $d+1-m\le d$ and $2\le j\le d$ since $1\le t<m$. So we obtain that ${{x}_{i+m,j}}={{x}_{i+m-1,(j+1)\bmod \,\, d}}$ from (1). Because $j\le d+1-m$, we know that $2\le j+1\le d+2-m=d+1-(m-1)$. then $d+1-(m-1)\le d+1-(2-1)=d$ Due to $m\ge 2$, thus $(j+1)\bmod \,\, m=j+1\le d+1-(m-1)$. Moreover, we find that ${{x}_{i+m-1,(j+1)\bmod \,\, d}}={{x}_{i,(j+m)\bmod \,\, d}}$ by the assumption that (2) holds for $t=m-1$, which means (2) holds for $t=m$. So we conclude that (2) holds by the means of mathematical induction.    $\square$

Property 2

Assume that the input difference and the output difference of the round i is $\left( \varDelta {{X}_{i,1}},\varDelta {{X}_{i,2}},\cdots ,\varDelta {{X}_{i,d}} \right)$ and $\left( \varDelta {{Y}_{i,1}},\varDelta {{Y}_{i,2}},\cdots ,\varDelta {{Y}_{i,d}} \right)$ respectively. Thus, we have $\varDelta F_{i}^{O} = \varDelta F_{i-d+1}^{I}\oplus \varDelta F_{i+1}^{I}$ for $i\ge d$.

Proof

By Property 1, we can deduce that $\varDelta {{X}_{i+1,1}}=\varDelta {{F}_{i}}^{O}\oplus \varDelta {{X}_{i,2}}$, hence $\varDelta F_{i}^{O}=\varDelta {{X}_{i,2}}\oplus \varDelta {{X}_{i+1,1}}$. Hence, $\varDelta {{X}_{i+t,j}}=\varDelta {{X}_{i,(j+t)\bmod \,\, d}}$ for $1\le t<d$ and $2\le j\le d+1-t$ by (2) of Property 1. Since $i\ge d$, then $i-\left( d-1 \right) \ge 1$. Therefore, we have: $\varDelta {{X}_{i,2}}=\varDelta {{X}_{i-\left( d-1 \right) ,\left[ 2-\left( d-1 \right) \right] \bmod \,\, d}}=\varDelta {{X}_{i-d+1,1}}$. Moreover, $\varDelta {{X}_{i,2}}\oplus \varDelta {{X}_{i+1,1}}=\varDelta {{X}_{i-d+1,1}}\oplus \varDelta {{X}_{i+1,1}}$, Because $\varDelta {{X}_{i-d+1,1}}=\varDelta F_{i-d+1}^{I},\varDelta {{X}_{i+1,1}} = \varDelta F_{i+1}^{I}$, then we have $\varDelta F_{i}^{O} = \varDelta F_{i-d+1}^{I}\oplus \varDelta F_{i+1}^{I}$.    $\square$

Property 3

For arbitrary nonlinear invertible function $F:{{\left\{ 0\ ,1 \right\} }^{m}}\rightarrow {{\left\{ 0\ ,1 \right\} }^{m}}$, given a set of input and output difference $\left\{ \left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right) \right\}$. Denote ${{\varOmega }_{F}}\left( \varDelta {{I}_{i}}\rightarrow \varDelta {{O}_{j}} \right) =\left\{ X:F\left( X\oplus \varDelta {{I}_{i}} \right) \oplus F\left( X \right) =\varDelta {{O}_{j}} \right\}$. Then, on average the number of solutions of equations $F\left( X\oplus \varDelta {{I}_{i}} \right) \oplus F\left( X \right) =\varDelta {{O}_{j}}$ for each $\left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right)$ is $\frac{\left| {{\varOmega }_{F}}\left( \varDelta {{I}_{i}}\rightarrow \varDelta {{O}_{j}} \right) \right| }{\left| \left\{ \left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right) \right\} \right| }$, and $\frac{\left| {{\varOmega }_{F}}\left( \varDelta {{I}_{i}}\rightarrow \varDelta {{O}_{j}} \right) \right| }{\left| \left\{ \left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right) \right\} \right| }\ =1$, if the set $\left\{ \left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right) \right\}$ satisfy one of the following conditions: (1) The input difference $\varDelta {{I}_{i}}$ fixed and the output difference $\varDelta {{O}_{j}}$ takes each values of ${{\left\{ 0,\,1 \right\} }^{m}}$ once. (2) The output difference $\varDelta {{O}_{j}}$ fixed and the input difference $\varDelta {{I}_{i}}$ takes each values of ${{\left\{ 0,\,1 \right\} }^{m}}$ once. (3) Both the input difference $\varDelta {{I}_{i}}$ and the output difference $\varDelta {{O}_{j}}$ takes each values of ${{\left\{ 0\ ,1 \right\} }^{m}}$ once.

Proof

For each $\left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right)$, we have an equation. So, the number of equations $F\left( X\oplus \varDelta {{I}_{i}} \right) \oplus F\left( X \right) =\varDelta {{O}_{j}}$ is $\left| \left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right) \right|$. ${{\varOmega }_{F}}\left( \varDelta {{I}_{i}}\rightarrow \varDelta {{O}_{j}} \right) =\left\{ X:F\left( X\oplus \varDelta {{I}_{i}} \right) \oplus F\left( X \right) =\varDelta {{O}_{j}} \right\}$ denotes the solutions of $F\left( X\oplus \varDelta {{I}_{i}} \right) \oplus F\left( X \right) =\varDelta {{O}_{j}}$, so we can find that on average the number of solutions of equations $F\left( X\oplus \varDelta {{I}_{i}} \right) \oplus F\left( X \right) =\varDelta {{O}_{j}}$ for each $\left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right)$ is $\frac{\left| {{\varOmega }_{F}}\left( \varDelta {{I}_{i}}\rightarrow \varDelta {{O}_{j}} \right) \right| }{\left| \left\{ \left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right) \right\} \right| }$.

• (1) If the input difference $\varDelta {{I}_{i}}$ fixed and the output difference $\varDelta {{O}_{j}}$ takes each values of ${{\left\{ 0,1 \right\} }^{m}}$ once. Then $\left| \left\{ \left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right) \right\} \right| \ ={{2}^{m}}$, Hence

  $$\begin{aligned}&\frac{\left| {{\varOmega }_{F}}\left( \varDelta {{I}_{i}}\rightarrow \varDelta {{O}_{j}} \right) \right| }{\left| \left\{ \left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right) \right\} \right| }\ =\frac{1}{{{2}^{m}}}\sum \limits _{\varDelta {{O}_{j}}\in {{\left\{ 0,1 \right\} }^{m}}}{\left| {{\varOmega }_{F}}\left( \varDelta {{I}_{i}}\rightarrow \varDelta {{O}_{j}} \right) \right| } \\&=\frac{1}{{{2}^{m}}}\sum \limits _{\varDelta {{O}_{j}}\in {{\left\{ 0,1 \right\} }^{m}}}{\left| \left\{ X:F\left( X\oplus \varDelta {{I}_{i}} \right) \oplus F\left( X \right) =\varDelta {{O}_{j}} \right\} \right| } \\&=\frac{1}{{{2}^{m}}}\left| \bigcup \limits _{\varDelta {{O}_{j}}\in {{\left\{ 0,1 \right\} }^{m}}}{\left\{ X:F\left( X\oplus \varDelta {{I}_{i}} \right) \oplus F\left( X \right) =\varDelta {{O}_{j}} \right\} } \right| \\&=\frac{{{2}^{m}}}{{{2}^{m}}}=1 \end{aligned}$$

• (2) If the output difference $\varDelta {{O}_{j}}$ fixed and the input difference $\varDelta {{I}_{i}}$ takes each values of ${{\left\{ 0,1 \right\} }^{m}}$ once. Since the function F is invertible, then we can analysis the number of average solutions by detect the reverse-function ${{F}^{-1}}$. For each X satisfy the equation $F\left( X\oplus \varDelta {{I}_{i}} \right) \oplus F\left( X \right) =\varDelta {{O}_{j}}$, if and only if there exists a $Y\in {{\left\{ 0,1 \right\} }^{m}}$ satisfy the equation ${{F}^{-1}}\left( Y\oplus \varDelta {{O}_{j}} \right) \oplus F\left( Y \right) =\varDelta {{I}_{i}}$. From (1) we can see that on average there is one solution for the equations ${{F}^{-1}}\left( Y\oplus \varDelta {{O}_{j}} \right) \oplus F\left( Y \right) =\varDelta {{I}_{i}}$, which means on average there is one solution for the equations $F\left( X\oplus \varDelta {{I}_{i}} \right) \oplus F\left( X \right) =\varDelta {{O}_{j}}$ too.

• (3) If both the input difference $\varDelta {{I}_{i}}$ and the output difference $\varDelta {{O}_{j}}$ takes each values of ${{\left\{ 0,1 \right\} }^{m}}$ once, then $\left| \left\{ \left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right) \right\} \right| \ ={{2}^{m}}\times {{2}^{m}}$, hence

  $$\begin{aligned}&\frac{\left| {{\varOmega }_{F}}\left( \varDelta {{I}_{i}}\rightarrow \varDelta {{O}_{j}} \right) \right| }{\left| \left\{ \left( \varDelta {{I}_{i}},\varDelta {{O}_{j}} \right) \right\} \right| }\ =\frac{1}{{{2}^{m}}}\times \frac{1}{{{2}^{m}}}\sum \limits _{\varDelta {{O}_{j}}\in {{\left\{ 0,1 \right\} }^{m}}}{\sum \limits _{\varDelta {{I}_{i}}\in {{\left\{ 0,1 \right\} }^{m}}}{\left| {{\varOmega }_{F}}\left( \varDelta {{I}_{i}}\rightarrow \varDelta {{O}_{j}} \right) \right| }} \\&=\frac{1}{{{2}^{2m}}}\sum \limits _{\varDelta {{O}_{j}}\in {{\left\{ 0,1 \right\} }^{m}}}{\sum \limits _{\varDelta {{I}_{i}}\in {{\left\{ 0,1 \right\} }^{m}}}{\left| \left\{ X:F\left( X\oplus \varDelta {{I}_{i}} \right) \oplus F\left( X \right) =\varDelta {{O}_{j}} \right\} \right| }}\\&=\frac{1}{{{2}^{2m}}}\left| \bigcup \limits _{\varDelta {{O}_{j}}\in {{\left\{ 0,1 \right\} }^{m}}}{\bigcup \limits _{\varDelta {{I}_{i}}\in {{\left\{ 0,1 \right\} }^{m}}}{\left\{ X:F\left( X\oplus \varDelta {{I}_{i}} \right) \oplus F\left( X \right) =\varDelta {{O}_{j}} \right\} }} \right| \\&=\frac{{{2}^{2m}}}{{{2}^{2m}}}=1 \end{aligned}$$

     $\square$

Property 4

Let the input of the first round is $\left( {{X}_{1,1}},{{X}_{1,2}},\cdots ,{{X}_{1,d}} \right)$. The input of round function ${{F}_{1}}$ is $F_{1}^{I}$. Then we have the sub-key of the first round ${{K}_{1}}=F_{1}^{I}\oplus {{X}_{1,1}}$.

Proof

Since $F_{1}^{I}={{X}_{1,1}}\oplus {{K}_{1}}$, we can obtain that ${{K}_{1}}=F_{1}^{I}\oplus {{X}_{1,1}}$.    $\square$

Property 5

Let the input of the 4dth round is $\left( {{X}_{4d,1}},{{X}_{4d,2}},\cdots ,{{X}_{4d,d}} \right)$ and the output of $5d-3$th round is $\left( {{Y}_{5d-3,1}},{{Y}_{5d-3,2}},\cdots ,{{Y}_{5d-3,d}} \right)$. The input of round function ${{F}_{4d}}$ is $F_{4d}^{I}$. Then we have the sub-key of the 4dth round ${{K}_{4d}}=F_{4d}^{I}\oplus {{Y}_{5d-3,3}}$.

Proof

Since $F_{4d}^{I}={{X}_{4d,1}}\oplus {{K}_{4d}}$, we have ${{K}_{4d}}=F_{4d}^{I}\oplus {{X}_{4d,1}}$. Hence, the output of $5d-3$th round equals to the input of $5d-2$th round, we can obtain that ${{Y}_{5d-3,3}}\text {=}{{X}_{5d-2,3}}$. From Property 1 (2), let $i=4d$, $j=3$ and $t=d-2$, then we have ${{X}_{5d-2,3}}={{X}_{(i+t),j\bmod \,\, d}}={{X}_{i,(j+t)\bmod \,\, d}}={{X}_{4d,(3+d-2) \bmod \,\, d}}={{X}_{4d,1}}$. So ${{K}_{4d}}=F_{4d}^{I}\oplus {{X}_{4d,1}}=F_{d}^{I}\oplus {{X}_{5d-2,3}}\text {=}F_{d}^{I}\oplus {{Y}_{5d-3,3}}$.    $\square$

3 Meet in the Middle Attacks on Type-1 Feistel Construction

3.1 $3d-1$ Rounds Distinguisher of Type-1 Feistel Construction

To make the following analysis more general, we study $3d-1$ rounds of the Tyep-1 Feistel construction which begin with the $t+1$th round and end to the $t+3d-1$th round $\left( t\ge 0 \right)$.

Proposition 1

Assume that $A,B,C\in {{\left\{ 0,1 \right\} }^{\frac{n}{d}}}\backslash \left\{ 0 \right\}$ and $A\ne B$. For any plaintext pair $\left( m,{m}' \right)$ with the input difference of the tth round is $\left( \text {0,0,}\cdots \text {,0,}A \right)$ and the output difference of the $t\,+\,3d\,-\,1$th round is $\left( B,C,?,\cdots \text {,0} \right)$. Let b be an arbitrary integer and $b\ge d$, then the sequence $\left( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) ,\cdots ,{{F}^{\varDelta }}\left( m,b \right) \right)$ can assume at most ${{\text {2}}^{\frac{\left( d-1 \right) }{d}n}}$ possible values, and the values of the sequence is irrelevant to the plaintext m and ${m}'$. It is determined by the values of A, B, C.

Fig. 2.

The $3d-1$ rounds Type-1 Feistel distinguisher

Proof

Firstly, we show that, for any pair of plaintexts $\left( m,{m}' \right)$ which input difference of the tth round is $\left( \ 0,0, \cdots \,0, A \right)$ and the output difference of the $t\,+\,3d\,-\,1$th round is $\left( B,C,?,\cdots ,0 \right)$, the possible value of $\left( F_{t+d}^{I},F_{t+d+1}^{I},\cdots ,F_{t+2d}^{I} \right)$ correspond to m is limited to ${{2}^{\frac{d-1}{d}n}}$ on average. As shown in Fig. 2, the input difference $\left( \ 0,0, \cdots \,0, A \right)$ leads to output difference $\left( A,0,\cdots \,0,0 \right)$ after $d-1$ round encryption. Namely, the input difference of the $t+d$th round is $\left( A,0,\cdots ,0,0 \right)$, $\varDelta F_{t+d}^{I}\ =A$. Note that ${{A}_{i}}\ =\varDelta F_{i+t+d-1}^{O}\left( i=1,2,\cdots ,d-1 \right)$, it follows that $\varDelta F_{i}^{O}={{A}_{i-t-d+1}}\left( i=t+d,\cdots ,t+2d-2 \right)$ and thus $\varDelta F_{i}^{I}=\varDelta {{X}_{i,1}}=\varDelta F_{i-1}^{O}\oplus \varDelta {{X}_{i-1,2}}={{A}_{i-t-d}}\oplus 0={{A}_{i-t-d}}$ $\left( i=t+d+1,\cdots ,t+2d-1 \right)$ . Similarly, because the output difference of the $t+3d-1$th round is $\left( B,C,?,\cdots ,0 \right)$, we can conclude that the input difference of the $t\,+\,3d\,-\,1$th round and the output difference of the $t+3d-2$th round is $\left( \ 0, B,C,\cdots \right)$. Since the input difference of the $t+3d-1$th round is $\left( \ 0, B,C,\cdots \, \right)$, from Property 1, we have $\varDelta F_{t+2d}^{I}=\varDelta {{X}_{t+2d,1}}=\cdots =\varDelta {{X}_{t+3d-1,2}}=B$ and $\varDelta F_{t+2d+1}^{I}=\varDelta {{X}_{t+2d+1,1}}=\cdots =\varDelta {{X}_{t+3d-1,3}}=C$. According to Property 2 , we have $\varDelta F_{i}^{O}=\varDelta F_{i-d+1}^{I}\oplus \varDelta F_{i+1}^{I}$, let $i=t+2d-1,t+2d$ , we can see that $\varDelta F_{t+2d-1}^{O}=\varDelta F_{t+d}^{I}\oplus \varDelta F_{t+2d}^{I}=A\oplus B$ and $\varDelta F_{t+2d}^{O}=\varDelta F_{t+d+1}^{I}\oplus \varDelta F_{t+2d+1}^{I}={{A}_{1}}\oplus C$.

Now we have derived the input and output difference of the $t+d,\cdots ,t+2d$th round function. It follows that $\left( \varDelta F_{t+d}^{I}, \varDelta F_{t+d}^{O} \right) =\left( A,{{A}_{1}} \right)$, $\big ( \varDelta F_{t+d+i}^{I},\varDelta F_{t+d+i}^{O} \big )\ =\left( {{A}_{i}},{{A}_{i+1}} \right) \left( i=1,2,\cdots ,d-2 \right)$, $\left( \varDelta F_{t+2d-1}^{I},\varDelta F_{t+2d-1}^{O} \right) \ =\big ( {{A}_{d-1}},A\oplus B \big )$, $\left( \varDelta F_{t+2d}^{I},\varDelta F_{t+2d}^{O} \right) \ =\left( B,{{A}_{1}}\oplus C \right)$. Therefore, we can build an equation set which has $d+1$ differential equations:

$$ \varDelta {{F}_{t+d}}\left( A \right) ={{A}_{1}} $$

$$ \varDelta {{F}_{t+d+i}}\left( {{A}_{i}} \right) ={{A}_{i+1}} \left( i=1,2,\cdots ,d-2 \right) $$

$$ \varDelta {{F}_{t+2d-1}}\left( {{A}_{d-1}} \right) =A\oplus B $$

$$ \varDelta {{F}_{t+2d}}\left( B \right) ={{A}_{1}}\oplus C $$

Since A, B, C are given non-zero values, upon the values of ${{A}_{i}}\big ( i=1,2,\cdots ,d-1 \big )$ are fixed, the input difference and output difference of the whole $d+1$ differential equations are fixed. As ${{A}_{i}}\left( i=1,2,\cdots ,d-1 \right)$ can take at most ${{\ 2}^{\frac{d-1}{d}n}}$ different values, we can assume only ${{\ 2}^{\frac{d-1}{d}n}}$ different equation set. According to Property 3, each differential equation has one solution on average, which means the value of $\left( F_{t+d}^{I},F_{t+d+1}^{I},\cdots , F_{t+2d}^{I} \right)$ correspond to m can get only ${{\ 2}^{\frac{d-1}{d}n}}$ different values on average. Since the solving process is irrelevant with the value of m and ${m}'$, We should also point out that the possible value of $\left( F_{t+d}^{I},F_{t+d+1}^{I},\cdots , F_{t+2d}^{I} \right)$ is only decided by the value of A, B, C.

Now we know that each value of $\left( {{A}_{1}},{{A}_{2}},\cdots ,{{A}_{d-1}} \right)$ correspond to a value of $\left( F_{t+d}^{I},F_{t+d+1}^{I},\cdots ,F_{t+2d}^{I} \right)$. We are going to proof that if we change the input difference from ${m}'$ to $m\oplus \left( 0,0,\cdots ,j \right)$, we are able to compute the truncation of the second sub-blocks of the output difference, as long as the value of $\left( {{A}_{1}},{{A}_{2}},\cdots ,{{A}_{d-1}} \right)$ is given. Moreover, the value of truncate difference is irrelevant to m. To distinguish the internal state while the plaintexts pair is $\left( m,m\oplus \left( 0,0,\cdots ,j \right) \right)$ from those for $\left( m,{m}' \right)$, we denote $\varDelta F_{i}^{\ *O}$ as the output difference of the round function ${{F}_{i}}$ correspond to $\left( m,m\oplus \left( 0,0,\cdots ,j \right) \right)$.

As shown in Fig. 2(b), the input difference of $\left( m,m\oplus \left( 0,0,\cdots ,j \right) \right)$ is j, we can conclude that the input value of round function ${{F}_{t+d}}$ correspond to $m\oplus \left( 0,0,\cdots ,j \right)$ is $F_{t+d}^{I}\oplus j$ and the output difference of the $t+d$th round is $\varDelta F_{t+d}^{\ *O}={{F}_{t+d}}\left( F_{t+d}^{I} \right) \oplus {{F}_{t+d}}\left( F_{t+d}^{I}\oplus j \right)$. Similarly, the output difference of the $t+d+1$th round is $\varDelta F_{t+d+1}^{\ *O}={{F}_{t+d+1}}\left( F_{t+d+1}^{I} \right) \oplus {{F}_{t+d+1}}\left( F_{t+d+1}^{I}\oplus \varDelta F_{t+d}^{\ *O} \right)$. Hence, we are able to compute the output difference of the $t+d+2,\cdots ,t+2d$th round: $\varDelta F_{i}^{\ *O}={{F}_{i}}\left( F_{i}^{I} \right) \oplus {{F}_{i}}\left( F_{i}^{I}\oplus \varDelta F_{i-1}^{\ *O} \right)$ $(i=t+d+2,\cdots ,t+2d)$. Since $\varDelta {{Y}_{t+3d-1,2}}=\varDelta {{X}_{t+2d+1,1}}=\varDelta F_{t+2d+1}^{I}$, according to Property 2, we can deduce that $\varDelta F_{t+2d+1}^{I}=\varDelta F_{t+d+1}^{I}\oplus \varDelta F_{t+2d}^{*O}=\varDelta F_{t+1}^{I}\oplus \varDelta F_{t+d}^{*O}\oplus \varDelta F_{t+2d}^{*O}$. Because $\varDelta F_{t+1}^{I}=0$, we can conclude that $\varDelta {{Y}_{t+3d-1,2}}\ =\varDelta F_{t+2d}^{\ *O}\oplus \varDelta F_{t+d}^{\ *O}$, which means we can compute the truncation of the second sub-blocks of the output difference by computing the value of $\varDelta F_{t+2d}^{\ *O},\varDelta F_{t+d}^{\ *O}$.

When the value of $\left( F_{t+d}^{I},F_{t+d+1}^{I},\cdots , F_{t+2d}^{I} \right)$ are fixed, we can compute the values of $\varDelta F_{t+d}^{\ *O},\varDelta F_{t+d+1}^{\ *O},\cdots ,\varDelta F_{t+2d}^{\ *O}$. Meanwhile, $j\rightarrow {{F}^{\varDelta }}\left( mj \right)$ is a fixed map and the value of ${{F}^{\varDelta }}\left( mj \right)$ can be computed in polynomial-level time. Besides, the solving process is suitable for any $j=1,2,\cdots ,b$, so we can get the $\left( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) ,\cdots , {{F}^{\varDelta }}\left( m,b \right) \right)$ sequence by repeat the solving process for b times. Since each $\left( F_{t+d}^{I},F_{t+d+1}^{I},\cdots , F_{t+2d}^{I} \right)$ correspond to a sequence and $\left( F_{t+d}^{I},F_{t+d+1}^{I},\cdots , F_{t+2d}^{I} \right)$ takes at most ${{\ 2}^{\frac{\left( d-1 \right) }{d}n}}$ values, therefore, the number of the sequence $\left( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) ,\cdots , {{F}^{\varDelta }}\left( m,b \right) \right)$ is limited to ${{\ 2}^{\frac{\left( d-1 \right) }{d}n}}$.    $\square$

Notes. (1) Due to ${{F}^{\varDelta }}\left( m,{{\delta }_{j}} \right) \in {{\left\{ 0,1 \right\} }^{{n}/{d}\;}}$, the sequence $\big ( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) \cdots {{F}^{\varDelta }}\left( m,b \right) \big )$ can assume ${{\ 2}^{\frac{b}{d}n}}$ different values. However, according to the analysis of Proposition 1, we found that the value can be tightened to ${{2}^{\frac{\left( d-1 \right) }{d}n}}$. In order to distinguish the possible value from the theoretical value, we need $b>d-1$.

(2) To compute the sequence $\left( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) ,\cdots , {{F}^{\varDelta }}\left( m,b \right) \right)$, we have to get the ${{2}^{\frac{d-1}{d}n}}$ different values of $\left( F_{t+d}^{I},F_{t+d+1}^{I},\cdots , F_{t+2d}^{I} \right)$. We find that we don’t need solve all $d+1$ differential equations. We give Algorithm 1 to compute the ${{2}^{\frac{d-1}{d}n}}$ different values of $\left( F_{t+d}^{I},F_{t+d+1}^{I},\cdots , F_{t+2d}^{I} \right)$. If we get the ${{2}^{\frac{d-1}{d}n}}$ different values of $\left( F_{t+d}^{I},F_{t+d+1}^{I},\cdots , F_{t+2d}^{I} \right)$, we can compute the ${{2}^{\frac{\left( d-1 \right) }{d}n}}$ possible sequences of $\left( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) \cdots {{F}^{\varDelta }}\left( m,b \right) \right)$. We use Algorithm 2 to compute these sequences.

From Proposition 1, we can find that if there is a pair of plaintext that follow the differential characteristic, then the sequence $\left( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) \cdots {{F}^{\varDelta }}\left( m,b \right) \right)$ can assume ${{2}^{\frac{\left( d-1 \right) }{d}n}}$ instead of ${{2}^{\frac{b}{d}n}}$ different values. In that way, we obtain a $3d-1$ rounds distinguisher of type-1 Feistel construction.

3.2 $5d-3$ Rounds Key Recovery Attack of Type-1 Feistel Construction

The aim of this section is to recover the 1st and 4dth round-key of the $5d-3$ rounds Type-1 Feistel construction. As shown in Fig. 3, to make the $5d-3$ rounds key recovery attack, we prepend d rounds at the top of the $3d-1$ rounds distinguisher and append $d-2$ rounds at the bottom of the distinguisher. If we can figure out the values of $F_{1}^{I}$ and $F_{4d}^{I}$, we are able to recover ${{K}_{1}}$ and ${{K}_{4d}}$ from Properties 4 and 5 with knowing the corresponding plaintext and cipher. In order to get the values of $F_{1}^{I}$ and $F_{4d}^{I}$, we choose many pairs satisfy the differential $\left( *,*,0,\cdots ,0,A \right) \rightarrow \left( *,0,B,*,\cdots ,* \right)$. But only the pairs satisfy the differential characteristic can be used to calculate the values of $F_{1}^{I}$ and $F_{4d}^{I}$. So we use Proposition 1 as a distinguisher to distinguish the pairs whether it satisfy the differential characteristic or not. Our attack consists of precomputation phase and online phase.

Fig. 3.

$5d-3$ rounds Type-1 Feistel attack model

To clarify the attack, we propose following 3 propositions before the introduction of details of attack.

First of all, we proposed Proposition 2 to clarify the necessary and sufficient condition that the differential characteristic of the first d rounds is $\left( *,*,0,\cdots ,0,A \right) \xrightarrow {d-round}\left( 0,\cdots ,0,A \right)$.

Proposition 2

Assume there is a pair of plaintexts of the d rounds type-1 Feistel $\left( m,{m}' \right)$, where $m=\left( {{m}_{1}},{{m}_{2}},\cdots ,{{m}_{d}} \right)$, ${m}'=\left( {{m}_{1}}^{\prime },{{m}_{2}}^{\prime },\cdots ,{{m}_{d}}^{\prime } \right)$. Moreover, the input difference is $\left( \varDelta {{m}_{1}},\varDelta {{m}_{2}},\cdots ,\varDelta {{m}_{d}} \right)$ and $\varDelta {{m}_{i}}\ne 0\left( i=1,2 \right) ,\varDelta {{m}_{j}}=0\left( j=3,\cdots ,d-1 \right) ,\varDelta {{m}_{d}}=A\ne 0$. Then the output difference is $\left( 0,0,\cdots ,0,A \right)$, if and only if ${{F}_{1}}\left( F_{1}^{I} \right) \oplus {{F}_{1}}\left( F{{_{1}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{2}}=0$ and ${{F}_{d}}\left( F_{d}^{I} \right) \oplus {{F}_{d}}\left( F{{_{d}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{1}}=0$, $F_{i}^{I}$ and $F{{_{i}^{I}}^{\prime }}$ denotes the input of round function ${{F}_{i}}$ correspond to m and ${m}'$, respectively (Fig. 4).

Fig. 4.

d rounds prepended before the distinguisher (Fig. of Proposition 2)

Proof

According to Property 1, we can see that $\varDelta {{X}_{d+1,j}}=\varDelta {{X}_{j,1}}\left( j=2,\cdots ,d \right)$. Meanwhile, $\varDelta {{X}_{d+1,1}}=\varDelta F_{d}^{O}\oplus \varDelta {{X}_{d,2}}=\varDelta F_{d}^{O}\oplus \varDelta {{X}_{1,1}}={{F}_{d}}\left( F_{d}^{I} \right) \oplus {{F}_{d}}\left( F{{_{d}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{1}}$. Which means the output difference equals to $\left( 0,0,\cdots ,0,A \right)$, if and only if ${{F}_{d}}\left( F_{d}^{I} \right) \oplus {{F}_{d}}\left( F{{_{d}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{1}}=0$ and $\varDelta {{X}_{j,1}}=0\left( j=2,3,\cdots ,d \right)$. Because $\varDelta {{X}_{2,1}}=\left[ {{F}_{1}}\left( F_{1}^{I} \right) \oplus {{F}_{1}}\left( F{{_{1}^{I}}^{\prime }} \right) \right] \oplus \varDelta {{m}_{2}}$, $\varDelta {{X}_{2,1}}=0$ if and only if ${{F}_{1}}\left( F_{1}^{I} \right) \oplus {{F}_{1}}\left( F{{_{1}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{2}}=0$. Assume that $\varDelta {{X}_{2,1}}=0$, we can obtain that $\varDelta F_{2}^{I}=0$, hence, we have $\varDelta F_{2}^{O}=0$. Since the input difference is $\left( 0,0,\cdots ,0,A \right)$, from Property 1, we have $\varDelta {{X}_{2,2}}=\varDelta {{X}_{1,3}}=\varDelta {{m}_{3}}=0$, moreover, we can see that $\varDelta {{X}_{3,1}}=\varDelta F_{2}^{O}\oplus \varDelta {{X}_{2,2}}=0$. Similarly, we can prove that $\varDelta {{X}_{j,1}}=0\left( j=2,3,\cdots ,d \right)$ if and only if $\varDelta {{X}_{2,1}}=0$. To conclude, the output difference is $\left( 0,0,\cdots ,0,A \right)$, iff ${{F}_{1}}\left( F_{1}^{I} \right) \oplus {{F}_{1}}\left( F{{_{1}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{2}}=0$ and ${{F}_{d}}\left( F_{d}^{I} \right) \oplus {{F}_{d}}\left( F{{_{d}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{1}}=0$.    $\square$

Next, we proposed Proposition 3 to clarify the necessary and sufficient condition that the differential characteristic of the last $d-2$ rounds is $\left( B,C,*,\cdots ,*,0 \right) \xrightarrow {d-2-round}\left( *,0,B,*,\cdots ,* \right)$.

Proposition 3

Assume there is a pair of cipher $\left( c,{c}' \right)$ of the $5d-3$ rounds type-1 Feistel, where $c=\left( {{c}_{1}},{{c}_{2}},\cdots ,{{c}_{d}} \right)$ and the output difference is $\left( \varDelta {{c}_{1}},\varDelta {{c}_{2}},\cdots ,\varDelta {{c}_{d}} \right)$, Moreover, $\varDelta {{c}_{2}}=0,\varDelta {{c}_{3}}=B$. Then $\varDelta {{X}_{4d,1}}=B$, $\varDelta {{X}_{4d,2}}=C$ and $\varDelta {{X}_{4d,d}}=0$ if and only if ${{F}_{4d}}\left( F_{4d}^{I} \right) \oplus {{F}_{4d}}\left( F_{4d}^{I}\oplus B \right) \oplus \varDelta {{c}_{4}}=C$, $F_{4d}^{I}$ denotes the input of round function ${{F}_{4d}}$ correspond to m (Fig. 5).

Fig. 5.

$d-2$ rounds appended to the distinguisher (Fig. of Proposition 3)

Proof

According to Property 1, we can see that $\varDelta {{X}_{4d,1}}=\varDelta {{X}_{5d-2,3}}=\varDelta {{c}_{3}}=B$, $\varDelta {{X}_{4d,d}}=\varDelta {{X}_{5d-2,2}}=\varDelta {{c}_{2}}=0$. Which means $\varDelta {{X}_{4d,1}}=B$, $\varDelta {{X}_{4d,2}}=C$ and $\varDelta {{X}_{4d,d}}=0$ if and only if $\varDelta {{X}_{4d,2}}=C$. From Property 1, we have $\varDelta {{X}_{4d+1,1}}=\varDelta {{X}_{5d-2,4}}=\varDelta {{c}_{4}}$. Since $\varDelta {{X}_{4d,2}}=\left[ {{F}_{4d}}\left( F_{4d}^{I} \right) \oplus {{F}_{4d}}\left( F{{_{4d}^{I}}^{\prime }}\oplus B \right) \right] \oplus \varDelta {{X}_{4d+1,1}}={{F}_{1}}\left( F_{1}^{I} \right) \oplus {{F}_{1}}\left( F{{_{1}^{I}}^{\prime }}\oplus B \right) \oplus \varDelta {{c}_{4}}$, we can obtain that $\varDelta {{X}_{4d,2}}=C$ if and only if ${{F}_{1}}\left( F_{1}^{I} \right) \oplus {{F}_{1}}\left( F{{_{1}^{I}}^{\prime }}\oplus B \right) \oplus \varDelta {{c}_{4}}=C$. To conclude, the input difference satisfy that $\varDelta {{X}_{4d,1}}=B$, $\varDelta {{X}_{4d,2}}=C$ and $\varDelta {{X}_{4d,d}}=0$ if and only if ${{F}_{4d}}\left( F_{4d}^{I} \right) \oplus {{F}_{4d}}\left( F_{4d}^{I}\oplus B \right) \oplus \varDelta {{c}_{4}}=C$.    $\square$

In Proposition 4, we show for any m, if we get a candidate of $\left( F_{1}^{I},F_{d}^{I} \right)$, how to construct a plaintext sequence $\left( {{M}_{1}},{{M}_{2}},\cdots ,{{M}_{b}} \right)$ such that the differential characteristic in the input of $d+1$th round satisfy the conditions of Proposition 1, which can be used to justify the candidate of $\left( F_{1}^{I},F_{d}^{I} \right)$ is right or not.

Proposition 4

Assume $m=\left( {{m}_{1}},{{m}_{2}},\cdots ,{{m}_{d}} \right)$ is a plaintext of the d rounds type-1 Feistel construction and the cipher is $c=\left( {{c}_{1}},{{c}_{2}},\cdots ,{{c}_{d}} \right)$. Then we can construct plaintext sequence $\left( {{M}_{1}},{{M}_{2}},\cdots ,{{M}_{b}} \right)$, ${{M}_{i}}=\left( {{m}_{i,1}},{{m}_{i,2}},\cdots ,{{m}_{i,d}} \right)$, which satisfy following equations: ${{m}_{i,1}}={{m}_{1}}\oplus {{F}_{d}}\left( F_{d}^{I} \right) \oplus {{F}_{d}}\left( F_{d}^{I}\oplus i \right)$, ${{m}_{i,2}}={{m}_{2}}\oplus {{F}_{1}}\left( F_{1}^{I} \right) \oplus {{F}_{1}}\left( F_{1}^{I}\oplus {{m}_{1}}\oplus {{m}_{i,1}} \right)$, ${{m}_{i,j}}={{m}_{j}}\left( j=3,\cdots ,d-1 \right)$, ${{m}_{i,d}}={{m}_{d}}\oplus i$. Such that the output difference of $\left( m,{{M}_{i}} \right)$ after d round encryption is $\left( 0,0,\cdots ,i \right)$ (Fig. 6).

Fig. 6.

Construct plaintext sequences $\left( {{M}_{1}},{{M}_{2}},\cdots ,{{M}_{b}} \right)$ (Fig. of Proposition 4)

Proof

For each $1\le i\le b$, since $\varDelta {{m}_{j}}={{m}_{j}}\oplus {{m}_{i,j}}=0\left( j=3,\cdots ,d-1 \right)$, $\varDelta {{m}_{d}}=i\ne 0$, from Proposition 2, we can see that the output difference of $\left( m,{{M}_{i}} \right)$ after d round encryption is $\left( 0,0,\cdots ,i \right)$ if and only if ${{F}_{1}}\left( F_{1}^{I} \right) \oplus {{F}_{1}}\left( F{{_{1}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{2}}=0$ and ${{F}_{d}}\left( F_{d}^{I} \right) \oplus {{F}_{d}}\left( F{{_{d}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{1}}=0$. Because ${{m}_{i,1}}={{m}_{1}}\oplus {{F}_{d}}\left( F_{d}^{I} \right) \oplus {{F}_{d}}\left( F_{d}^{I}\oplus i \right)$, ${{m}_{i,2}}={{m}_{2}}\oplus {{F}_{1}}\left( F_{1}^{I} \right) \oplus {{F}_{1}}\left( F_{1}^{I}\oplus {{m}_{1}}\oplus {{m}_{i,1}} \right)$, hence, $\varDelta {{m}_{1}}={{m}_{1}}\oplus {{m}_{i,1}}$ and $\varDelta {{m}_{2}}={{m}_{2}}\oplus {{m}_{i,2}}$, we can obtain that the output difference is $\left( 0,0,\cdots ,i \right)$.    $\square$

We will present the specific attack process in the following part. Our attack composed of two phases: precomputation and online phase.

Precomputation phase. In this phase, we need to build 4 tables. Firstly, we build a table ${{T}_{\delta }}$ that includes ${{2}^{\frac{\left( d-1 \right) }{d}n}}$ sequences of $\left( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) \cdots {{F}^{\varDelta }}\left( m,b \right) \right)$ describe in Proposition 1. We divided the computation of the sequences into three steps. (1) Find the ${{2}^{\frac{\left( d-1 \right) }{d}n}}$ different values of $\left( F_{t+d}^{I},F_{t+d+1}^{I},\cdots , F_{t+2d}^{I} \right)$. (2) Compute the ${{2}^{\frac{\left( d-1 \right) }{d}n}}$ possible sequences of $\left( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) ,\cdots , {{F}^{\varDelta }}\left( m,b \right) \right)$and store it in ${{T}_{\delta }}$. (3) Sort the sequences $\left( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) ,\cdots , {{F}^{\varDelta }}\left( m,b \right) \right)$ in table ${{T}_{\delta }}$ so that lookup the table by binary search takes less time. The procedure to build table ${{T}_{\delta }}$ is described as follows:

• 1. Compute all ${{2}^{\frac{\left( d-1 \right) }{d}n}}$ different values of $\left( F_{2d}^{I},F_{2d+1}^{I},\cdots ,F_{3d}^{I} \right)$ and store it in T by using Algorithm 1 for parameter $t=d$.

• 2. For all ${{2}^{\frac{d-1}{d}n}}$ distinct $\left( F_{2d}^{I},F_{2d+1}^{I},\cdots ,F_{3d}^{I} \right)$, compute all the ${{2}^{\frac{d-1}{d}n}}$ possible values of the sequences $\left( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) ,\cdots , {{F}^{\varDelta }}\left( m,b \right) \right)$ and store it in table ${{T}_{\delta }}$ by using Algorithm 2 for parameter $t=d$.

• 3. Sort the sequences in table ${{T}_{\delta }}$ according to the value of $\big ( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) ,\cdots , {{F}^{\varDelta }}\left( m,b \right) \! \big )$ by using quick sort algorithm. Secondly, to complete the attack, we have to get access to the values of $F_{1}^{I}$, $F_{d}^{I}$ and $F_{4d}^{I}$ according to Propositions 2 and 3. To solve the following equations: $\varDelta {{F}_{1}}\left( \varDelta {{m}_{1}} \right) =\varDelta {{m}_{2}}$, $\varDelta {{F}_{d}}\left( A \right) =\varDelta {{m}_{1}}$, $\varDelta {{F}_{4d}}\left( B \right) =C\oplus \varDelta {{c}_{4}}$ more efficient, we construct table ${{T}_{1}}$, ${{T}_{d}}$ and ${{T}_{4d}}$. The procedure to build table ${{T}_{1}}$, ${{T}_{d}}$ and ${{T}_{4d}}$ is describe as follows:

• 1. For each $i=0,1,\cdots ,{{2}^{{n}/{d}\;}}-1$, compute $\varDelta F_{d}^{O}={{F}_{d}}\left( i \right) \oplus {{F}_{d}}\left( i\oplus A \right)$ and $\varDelta F_{4d}^{O}={{F}_{4d}}\left( i \right) \oplus {{F}_{4d}}\left( i\oplus B \right)$. Store the values of $\left( i,\varDelta F_{d}^{O} \right) ,\left( i,\varDelta F_{4d}^{O} \right)$ in table ${{T}_{d}},{{T}_{4d}}$, respectively.

• 2. Sorted the values in ${{T}_{d}},{{T}_{4d}}$ by the values of $\varDelta F_{d}^{O},\varDelta F_{4d}^{O}$, respectively.

• 3. For $i=0,1,\cdots ,{{2}^{{n}/{d}\;}}-1$, store the values of $\left( i,{{F}_{1}}\left( i \right) \right)$ in a temple table $tm{{p}_{1}}$.

• 4. For all plaintext pairs $m=0,1,\cdots ,{{2}^{{n}/{d}\;}}-1$, ${m}'=0,1,\cdots ,{{2}^{{n}/{d}\;}}-1$, compute $\varDelta F_{1}^{O}=tm{{p}_{1}}\left( m \right) \oplus tm{{p}_{1}}\left( {{m}'} \right)$ and store $\left( m\oplus {m},'\varDelta F_{1}^{O},m \right)$ in ${{T}_{1}}$.

Online Phase. This phase is divided into two parts: the pairs sieve phase and the keys recovery phase. We shall define a structure, and then sieve and store all plaintext pairs in table T that satisfy the plaintext difference and ciphertext difference of our truncated differential in the pairs sieve phase for a structure. Then it comes into the key recovery phase. We assume that each plaintext pair $(m,m')$ satisfies our truncated differential, and construct $({{F}^{\varDelta }}(m,1),{{F}^{\varDelta }}(m,2)\cdots ,{{F}^{\varDelta }}(m,b),F_{1}^{I},F_{d}^{I},F_{4d}^{I})$. If the sequence $({{F}^{\varDelta }}(m,1),{{F}^{\varDelta }}(m,2)\cdots ,{{F}^{\varDelta }}(m,b))$ is a precomputed one, then we get a candidate of $({{k}_{1}},{{k}_{4d}})$ from $(F_{1}^{I},F_{4d}^{I})$. Otherwise, we conclude that $(m,m')$ don’t satisfy our truncated differential, and go ahead for next $(m,m')$ in T. After all plaintext pairs in T are checked, we release the space occupied by T and do the same for the next structure.

The pairs sieve phase. At first, we define a structure $S(a)={{S}_{0}}(a)\bigcup {{S}_{1}}(a)$ where $a=({{a}_{3}},{{a}_{4}},\cdots ,{{a}_{d}})$ with ${{a}_{3}},{{a}_{4}},\cdots ,{{a}_{d}}\in {{\{0,1\}}^{n/d}}$ and

$$\begin{aligned} {{S}_{0}}(a)=\{({{m}_{1}},\cdots ,{{m}_{d}}):{{m}_{1}},{{m}_{2}}\in {{\{0,1\}}^{n/d}},{{m}_{i}}={{a}_{i}}\ for\ i\ge 3\} \end{aligned}$$

$$\begin{aligned} {{S}_{1}}(a)=\{({{m}_{1}},\cdots ,{{m}_{d}})\oplus (0,\cdots ,0,A):({{m}_{1}},\cdots ,{{m}_{d}})\in {{S}_{0}}(a)\} \end{aligned}$$

Thus, for each a, there needs ${{2}^{\frac{2n}{d}+1}}$ chosen plaintexts to construct a structure, and we can get ${{2}^{4n/d}}$ plaintext pairs ${{2}^{4n/d}}$ from S(a) by $m\in {{S}_{0}}(a)$ and $m'\in {{S}_{1}}(a)$. For each $m\in {{S}_{0}}(a)$ and each $m'\in {{S}_{1}}(a)$, we have $m\oplus m'=(*,*,0,\cdots ,0,A)$. So the plaintext pair $(m,m')$ satisfies the condition on the plaintext difference of our truncated differential once the first and the second sub-blocks of $m\oplus m'$ are nonzero simultaneously. Next we may get all the plaintext pairs that satisfy the conditions on the plaintext difference and the ciphertext difference of our truncated differential for given a by the quick sort algorithm, and get about ${{2}^{2n/d}}$ pairs for a structure.

Theorem 1

Let $S(a)={{S}_{0}}(a)\bigcup {{S}_{1}}(a)$ is a structure. For each plaintext $m\in {{S}_{b}}(a)$ with $e\in \{0,1\}$, we define $h(m)=({{c}_{2}},{{c}_{3}},e)={{2}^{\frac{2n}{d}+1}}{{c}_{2}}+{{2}^{\frac{n}{d}+1}}({{c}_{3}}\oplus e\times B)+e$ where $c=({{c}_{1}},{{c}_{2}},\cdots ,{{c}_{d}})$ is the ciphertext of m. Let ${{\varOmega }_{e}}(x)=\{m:m\in {{S}_{e}}(a)\ and\ h(m)=(x,e)\}$ for each $e\in \{0,1\}$. Let $m,{m}'\in S(a)$, c and ${c}'$ are the ciphertexts of m and ${m}'$ respectively, $c'\oplus c=({{\varDelta }_{1}},{{\varDelta }_{2}},\cdots ,{{\varDelta }_{d}})$. Then ${{m}_{d}}\oplus {{{m}'}_{d}}=A$, ${{\varDelta }_{2}}=0$ and ${{\varDelta }_{3}}=B$ iff there exists x and $e\in \{0,1\}$, such that $m\in {{\varOmega }_{e}}(x)$ and ${m}'\in {{\varOmega }_{e\oplus 1}}(x)$ respectively.

Proof

Obviously, there exist $x,{x}'$ and $e,{e}'\in \{0,1\}$, such that $m\in {{\varOmega }_{e}}(x)$ and $m'\in {{\varOmega }_{{{e}'}}}({x}')$. Then we have ${{m}_{d}}\oplus {{{m}'}_{d}}=(e\oplus {e}')A$, and hence ${{m}_{d}}\oplus {{{m}'}_{d}}=A$ iff ${e}'=e\oplus 1$. Let ${e}'=e\oplus 1$, then $x\oplus {x}'={{2}^{\frac{2n}{d}}}({{c}_{2}}\oplus {{{c}'}_{2}})+{{2}^{\frac{n}{d}}}({{c}_{3}}\oplus {{{c}'}_{3}}\oplus B)$, and hence ${{c}_{2}}={{{c}'}_{2}}$ and ${{c}_{3}}\oplus {{{c}'}_{3}}=B$ hold simultaneously iff $x={x}'$, which concludes the proof.    $\square$

By Theorem 1, we may construct all plaintext pairs produced by S(a) that satisfy the conditions on the plaintext difference and the ciphertext difference of our truncated differential by the quick sort algorithm. We may rearrange the elements in S(a) by the magnitude of h(m) with $m\in S(a)$, and record the start points and the end points of any two successive runs that $h(m)=(x,0)$ for each element m in the first run, and $h(m)=(x,1)$ for each element m in the second run for some x. Then we pick out each plaintext pair $(m,m')$ that m located in the first run, $m'$ located in the second run and the first and the second sub-blocks of $m\oplus m'$ are nonzero simultaneously. At last, we save $(m,m')$ in table T.

Hence, we should also compute how many plaintext structures we need to choose such that there are one pair satisfy the differential characteristic on average. For an arbitrary plaintexts pair whose input difference is $\left( *,*,0,\cdots ,0,\,A \right)$, the output difference becomes $\left( *,0,B,*,\cdots ,* \right)$ with probability ${{2}^{{-2n}/{d}\;}}$. According to Proposition 2, the output difference is $\left( 0,0,\cdots ,0,\,A \right)$ after d round encryption, iff ${{F}_{1}}\left( F_{1}^{I} \right) \oplus {{F}_{1}}\left( F{{_{1}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{2}}=0$ and ${{F}_{d}}\left( F_{d}^{I} \right) \oplus {{F}_{d}}\left( F{{_{d}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{1}}=0$. These equations holds with probability ${{2}^{-{n}/{d}\;}}\times {{2}^{-{n}/{d}\;}}={{2}^{-{2n}/{d}\;}}$. Similarly, from Proposition 3, if $\varDelta {{c}_{2}}=0$, $\varDelta {{c}_{3}}=B$, then $\varDelta {{X}_{4d,1}}=B$, $\varDelta {{X}_{4d,2}}=C$ and $\varDelta {{X}_{4d,d}}=0$ if and only if ${{F}_{4d}}\left( F_{4d}^{I} \right) \oplus {{F}_{4d}}\left( F_{4d}^{I}\oplus B \right) \oplus \varDelta {{c}_{4}}=C$. This equation holds with probability ${{2}^{-{n}/{d}\;}}$. Which means for an arbitrary plaintexts pair whose input difference is $\left( *,*,0,\cdots \text {,0,}\,A \right)$, then this pair satisfy the whole differential characteristic $\left( *,*,0,\cdots ,0, A \right) \xrightarrow {d-round}\left( 0,\cdots ,0,A \right) \xrightarrow {3d-1-round}\left( B,C,*,\cdots ,*,0 \right) \xrightarrow {d-2-round}\left( *,0,B,*,\cdots ,* \right)$ with probability ${{2}^{-{2n}/{d}\;}}\times {{2}^{-{2n}/{d}\;}}\times {{2}^{-{n}/{d}\;}}={{2}^{-{5n}/{d}\;}}$. So we should construct ${{2}^{{n}/{d}\;}}\left( ={{2}^{{4n}/{d}\;}}\div {{2}^{{-5n}/{d}\;}} \right)$ distinct plaintext structures by choosing ${{2}^{{n}/{d}\;}}$ different $a=({{a}_{3}},{{a}_{4}},\cdots ,{{a}_{d}})$.

The keys recovery phase. As we choose ${{2}^{\frac{n}{d}}}$ plaintext structures, the previous phase result in ${{2}^{{n}/{d}\;}}\times {{2}^{{4n}/{d}\;}}\times {{2}^{-{2n}/{d}\;}}={{2}^{{3n}/{d}\;}}$ candidate pairs with a plaintexts difference $\left( *,*,0, \cdots ,0, A \right)$ and a ciphertext difference $\left( *,0,B,*,\cdots ,* \right)$. In this phase, for each plaintext structure, we execute these operations:

• 1. For each candidate $(m,m')$ in table T: (1) assume that the output difference is $\left( 0,\cdots ,0,A \right)$ at round d and $\left( 0,B,*,\cdots ,* \right)$ at round 4d. From Propositions 2 and 3, we have following three equations for each pair: ${{F}_{1}}\left( F_{1}^{I} \right) \oplus {{F}_{1}}\left( F{{_{1}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{2}}=0$, ${{F}_{d}}\left( F_{d}^{I} \right) \oplus {{F}_{d}}\left( F{{_{d}^{I}}^{\prime }} \right) \oplus \varDelta {{m}_{1}}=0$ and ${{F}_{4d}}\left( F_{4d}^{I} \right) \oplus {{F}_{4d}}\left( F_{4d}^{I}\oplus B \right) \oplus \varDelta {{c}_{4}}=C$.

  (2) Solve the equations by look up the tables ${{T}_{1}},{{T}_{d}},{{T}_{4d}}$ by using binary search algorithm. According to Property 3, each equation has one solution and we can get a pair of inputs of the round function. So we can obtain about ${{2}^{{3n}/{d}\;}}$ candidates of $\left( F_{1}^{I},F_{d}^{I},F_{4d}^{I} \right)$.

  (3) Construct plaintext sequence $\left( {{M}_{1}},{{M}_{2}},\cdots ,{{M}_{b}} \right)$ by knowing the values of $F_{1}^{I}$ and $F_{d}^{I}$ according to Proposition 4. Such that the output difference of $\left( m,{{M}_{j}} \right)$ after d round encryption is $\left( 0,0,\cdots ,j \right)$.

  (4) For each obtained $\left( {{M}_{1}},{{M}_{2}},\cdots ,{{M}_{b}} \right)$, store it with corresponding $\left( F_{1}^{I},F_{d}^{I} \right)$ as a sequence $({{M}_{1}},{{M}_{2}},\cdots ,{{M}_{b}},F_{1}^{I},F_{d}^{I},F_{4d}^{I})$.

• 2. For each sequence $({{M}_{1}},{{M}_{2}},\cdots ,{{M}_{b}},F_{1}^{I},F_{d}^{I},F_{4d}^{I})$, assume that cipher sequence $\left( {{C}_{1}},{{C}_{2}},\cdots ,{{C}_{b}} \right)$ is encrypted by the plaintext sequence $\left( {{M}_{1}},{{M}_{2}},\cdots ,{{M}_{b}} \right)$. ${{C}_{i}}=\left( {{c}_{i,1}},{{c}_{i,2}},\cdots ,{{c}_{i,d}} \right)$, denote that $\varDelta {{C}_{i}}=\left( \varDelta {{c}_{i,1}},\varDelta {{c}_{i,2}},\cdots ,\varDelta {{c}_{i,d}} \right) =\left( {{c}_{1}}\oplus {{c}_{i,1}},{{c}_{2}}\oplus {{c}_{i,2}},\cdots ,{{c}_{d}}\oplus {{c}_{i,d}} \right)$. Then execute following operations:

  (1) For $i=1,2,\cdots ,b$, compute ${{F}^{\varDelta }}\left( m,i \right) =\varDelta {{c}_{i,4}}\oplus {{F}_{4d}}\left( F_{4d}^{I} \right) \oplus {{F}_{4d}}\left[ F_{4d}^{I}\oplus \varDelta {{c}_{i,3}} \right]$. Thus, we can get $\left( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) ,\cdots , {{F}^{\varDelta }}\left( m,b \right) \right)$.

  (2) Check whether we can find a match of the sequence $\big ( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) ,\cdots , {{F}^{\varDelta }}\left( m,b \right) \! \big )$ in table ${{T}_{\delta }}$ or not by using binary search method.

  (3) If we find a match, it means the assumption that the output difference of round d is $\left( 0,0,\cdots ,0,A \right)$ and the output difference of round $4d-1$ is $\left( B,C,*,\cdots ,0 \right)$ with high probability. So we can deduce the corresponding values of $F_{1}^{I}$, $F_{d}^{I}$ while constructing sequence and $F_{4d}^{I}$ while partial decryption the ciphertext are right. Thus, from Properties 4 and 5, by compute ${{K}_{1}}=F_{1}^{I}\oplus {{m}_{1}}$, ${{K}_{4d}}=F_{4d}^{I}\oplus {{c}_{3}}$, we can get a correct guess of key $\left( {{K}_{1}},{{K}_{4d}} \right)$ with high probability. After that, return to step 2 and check the next sequence.

  (4) If we can’t find a match, return to step 2 and check the next sequence.

3.3 Complexity Analysis

In the online phases, we choose ${{2}^{\frac{n}{d}}}$ different plaintext structure, each plaintext structure contains ${{2}^{\frac{2}{d}n+1}}$ plaintexts. So the data complexity of this attack is ${{2}^{\frac{3}{d}n}}$ chosen plaintext. The time complexity and memory complexity mainly concentrate on the precomputation phase when building precomputation table ${{T}_{\delta }}$. To build the precomputation table ${{T}_{\delta }}$, we have to compute and storage all ${{2}^{\frac{d-1}{d}n}}$ possible sequence of $\left( {{F}^{\varDelta }}\left( m,1 \right) ,{{F}^{\varDelta }}\left( m,2 \right) \cdots {{F}^{\varDelta }}\left( m,b \right) \right)$. According to the Algorithm 1, for each ${{x}_{j}}\in {{\left( 0,1 \right) }^{\frac{n}{d}}}\left( j=i+d,\cdots ,i+2d-2 \right)$, we execute round function evaluation twice. So the time expenditure of Algorithm 1 is about $2\left( d-1 \right) \times {{2}^{\frac{\left( d-1 \right) }{d}n}}$ times round function evaluation. As for Algorithm 2, for each $F_{i}^{I}\left( i=t+d,t+d+1,\cdots ,t+2d \right)$, we have to execute round function evaluation twice, meanwhile, this operation should repeat b times. So the time expenditure of Algorithm 2 is about $2b\left( d+1 \right) \times {{2}^{\frac{\left( d-1 \right) }{d}n}}$ times round function evaluation. So the overall time expenditure of building the precomputation table ${{T}_{\delta }}$ is about $2bd\times {{2}^{\frac{\left( d-1 \right) }{d}n}}\left( \approx 2\left( d-1 \right) \times {{2}^{\frac{\left( d-1 \right) }{d}n}}+2b\left( d+1 \right) \times {{2}^{\frac{\left( d-1 \right) }{d}n}} \right)$ times round function evaluations. Hence, we should store table ${{T}_{\delta }}$, which includes $b\times {{2}^{\frac{d-1}{d}n}}$ sub-blocks, each sub-block is ${n}/{d}\;$ bits. The memory complexity of this phase is $b\times {{2}^{\frac{d-1}{d}n}}$ sub-blocks, each sub-block is ${n}/{d}\;$ bits.

Hence, we should to choose an optimal values of b. On the one hand , we need $b>d-1$ according to the note of Proposition 1. On the other hand, the larger b is, the higher time and memory complexity this attack need. So we choose $b=d$ to make a balance. Then the time complexity becomes $2{{d}^{2}}\times {{2}^{\frac{\left( d-1 \right) }{d}n}}$ times round function evaluations. Since the construction has $5d-3$ rounds, an encryption takes about 5d times round function evaluations. We can convert the time complexity into $\frac{2}{5}d\times {{2}^{\frac{\left( d-1 \right) }{d}n}}$ times encryptions. Since $\frac{2}{5}d$ is a very small factor compared with ${{2}^{\frac{d-1}{d}n}}$, to make the formula briefer, we omit the factor $\frac{2}{5}d$ when talking about the time complexity. In this case, we get the time complexity with ${{2}^{\frac{d-1}{d}n}}$ encryptions. The memory complexity is $d\times {{2}^{\frac{d-1}{d}n}}\left( {\text {since}} b=d \right)$ blocks, each block is ${n}/{d}\;$ bits, which can convert into ${{2}^{\frac{d-1}{d}n}}$ blocks, each block is n bits. Finally, we can conclude that the data complexity is ${{2}^{\frac{3}{d}n}}$ chosen plaintext, the memory complexity is ${{2}^{\frac{d-1}{d}n}}$ blocks, each block is n bits. And the time complexity is ${{2}^{\frac{d-1}{d}n}}$ times encryptions.

4 Conclusion

In this paper, we present a key recovery attack on Type-1 Feistel with d sub blocks for $d\ge 4$. We construct a $3d-1$ round distinguisher by using a special truncated differential. We present an attack on $5d-3$ rounds when key length is no less than block length n. The data complexity is ${{2}^{\frac{3}{d}n}}$ chosen plaintexts, the memory complexity is ${{2}^{\frac{d-1}{d}n}}$ blocks, each block is n bits, and the time complexity is ${{2}^{\frac{d-1}{d}n}}$ encryptions, which is the best known generic attack on Type-1 Feistel construction.