Keywords

1 Introduction

Recent developments in hydrodynamic research of ship manoeuvrability have greatly been done by the experimental means on captive models. However, the method of these tests and the expression of the results of analyses are so wide in variety that there are almost no unity to compare, except for the comparison made in the form of integral expressions for the predicted motions. If we use different polynomial expressions for fitting the hydrodynamic forces and moments obtained from captive model tests, the common derivatives will carry different meaning in accordance with the difference in the selected slope of the representative terms of the forces and moments, together with the differences in experimental condition. Moreover, the derivative terms may not have a definite physical meaning and the comparison with the theoretical values is difficult. This tendency, as a matter of fact causes problems among the captive model test and a major task is to select better models and derivatives for a better prediction of ship manoeuvring motions.

Incidentally, we are now familiar with another type of mathematical model, known as the ‘rudder to yaw response model’ which describes macroscopically the ship’s rate-of-turn response to the rudder actions by way of manoeuvring indices such as the ones defined by Nomoto. Such a model is good for treating weak motion with negligible variation in the advance speed; however for hard turning with speed loss, stopping or reversing, the model will be significantly diminished. Therefore, it is important to think about possible rationalizations of the mathematical model to use in a wider range with physical meaning in each term. In consideration of the above mentioned objective, a work group named MMG was specially organised in the Manoeuvrability Subcommittee of JTTC (Japan Towing Tank Conference). This paper will explain the model proposed as MMG in view of the betterment of the said frustrating situations as a result of discussions of the MMG group together with brief comments on the theoretical and experimental backgrounds [1]. More details of it can be found in [2,2,3,4].

2 Fundamental Requirement for the Mathematical Model

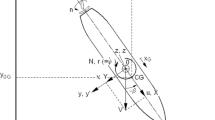
The concept is described by Fig. 1. This paper describes the model for a single screw ship and in deep water condition. However, the model for twin screw and shallow water can be developed with some modifications. The mathematical model needs to fulfil the following fundamental requirements:

Fig. 1
figure 1

Schematic diagram for MMG model

Full size image
  1. 1.

    The mathematical model should be based on the individual open water characteristics of the hull, the propeller, and the rudder.

  2. 2.

    A simplified expressions of the interactions among the hull, the propeller, and the rudder should be needed.

  3. 3.

    The representation of the hydrodynamic force acting on the hull should be as reasonable as possible.

3 Construction of Mathematical Model

The main objective to construct this model is to make it handy for practical usage. The coordinate system used to construct this model is given in Fig. 2.

Fig. 2
figure 2

Coordinate system

Full size image

3.1 Subject Ship

In order to construct the MMG model, ‘Esso Osaka’ 3-m tanker model is chosen as the subject ship. The model is scaled as 1:108.33. Its details are given in Table 1.

Table 1 Principal particulars and parameters of model ship
Full size table

3.2 Equations of Model

The equations of motion are described on the hull fixed coordinate system. Considering the origin at the centre of gravity of the ship as shown in Fig. 1, the equations of motion for surge sway and yaw are given as following:

$$ \begin{aligned} (m + m_{x} )\dot{u} - (m + m_{y} )vr & = X \\ (m + m_{y} )\dot{v} + (m + m_{x} )ur & = Y \\ (I_{{ZZ}} + J_{{ZZ}} )\dot{r} & = N \\ \end{aligned} $$
(1)

where, m is the mass of the ship, m x and m y are the added mass in x and y direction, I zz is the moment of inertia, J zz is the polar moment of inertia, u is the surge velocity, v is the sway velocity, r is the yaw rate and the right-hand side includes the total hydrodynamic forces and moment term due to hull, propeller, rudder. The force terms in Eq. (1) are expressed as follows:

$$ \begin{aligned} X & = X_{H} + X_{P} + X_{R} + X_{dis} \\ Y & = Y_{H} + Y_{P} + Y_{R} + Y_{dis} \\ N & = N_{H} + N_{P} + N_{R} + N_{dis} \\ \end{aligned} $$
(2)

where, X H , Y H , N H are the hydrodynamic forces and moments acting on a hull, X R , Y R , N R are the hydrodynamic forces and moments due to rudder, X P , Y P , N P are the hydrodynamic forces and moments due to propeller and X dis , Y dis , N dis are the disturbing forces and moments due to environmental disturbances like wind or current.

The hydrodynamic forces and moments acting on the hull during manoeuvring are usually expressed as a combination of linear and non-linear terms. The hydrodynamic forces and moments, considering advance motion can be described by the following equations.

$$ \begin{aligned} X_{H} & = \frac{1}{2}\rho LdU^{2} (X_{uu}^{\prime} (0) + X_{bb}^{\prime} b^{\prime2} + X_{br}^{\prime} b^{\prime} r^{\prime} + X_{rr}^{\prime} r^{\prime2} + X_{bbbb}^{\prime} b^{\prime4} ) \\ Y_{H} & = \frac{1}{2}\rho LdU^{2} \{ Y_{b}^{\prime} b^{\prime} + Y_{r}^{\prime} r^{\prime} + Y_{bb}^{\prime} b^{\prime} \left| {b^{\prime} } \right| + Y_{rr}^{\prime} r^{\prime} \left| {r^{\prime} } \right| + (Y_{bbr}^{\prime} b^{\prime} + Y_{brr}^{\prime} r^{\prime} )b^{\prime} r^{\prime} \} \\ N_{H} & = \frac{1}{2}\rho LdU^{2} \{ N_{b}^{\prime} b^{\prime} + N_{r}^{\prime} r^{\prime} + N_{bb}^{\prime} b^{\prime} \left| {b^{\prime} } \right| + N_{rr}^{\prime} r^{\prime} \left| {r^{\prime} } \right| + (N_{bbr}^{\prime} b^{\prime} + N_{brr}^{\prime} r^{\prime} )b^{\prime} r^{\prime} \} \\ \end{aligned} $$
(3)

where, the prime in each term denotes non-dimensional values, Xuu(0) is the hull resistance in straight motion, Yb ~ Yr, and Nb ~ Nr are the linear hydrodynamic derivatives, Xbb ~ Xbbbb, Ybb ~ Ybrr and Nbb ~ Nbrr are the non-linear hydrodynamic derivate terms. Here, ‘b’ denotes the drift angle and is considered instead of sway velocity ‘v’ term.

The hydrodynamic coefficients used in the expressions for the calculations of forces and moment acting on the hull during manoeuvring are determined by curve fitting through the experiment values for forces and moment for different drift angle and yaw rate which are collected from Hirano’s [5] paper. Surge force: The curve fitted for non-dimensional values is available in the case of the surge force, for 2.5 m model ship. So, the data are modified for a 3 m model by considering the relevant skin friction. The resulting representation after correction is given in Fig. 3. The derivatives for the surge force are calculated for these curve fitted experimental data. Sway force: Experimental data are collected for the sway force as well but for 4 m model ship. The hydrodynamic coefficients regarding the sway force and yaw moment are considered with no scale effect because the author believes that using experiment data for a 4 m model ship is still accurate enough to predict the hydrodynamic behaviour of 3 m. Figure 4 shows the data points from experiments together with curves fitted though such points that are used to get the derivatives for the sway force. Yaw moment: Same as for the sway force, experimental data for the yaw moment are available for the 4 m model ship. But due to the same reason as explained in the case of the sway force, the author uses these data for curve fitting and to predict the hydrodynamic behaviour of 3 m model ship. Figure 5 shows the data points from experiments together with curves fitted though such points.

Fig. 3
figure 3

Corrected curve fitted data for non-dimensional surge force

Full size image
Fig. 4
figure 4

Curve fitted data for non-dimensional sway force

Full size image
Fig. 5
figure 5

Curve fitted data for non-dimensional yaw moment

Full size image

The propeller thrust can be described by the longitudinal force of a propeller. The following expression is used to calculate the propeller thrust.

$$ \begin{aligned} X_{P} & = \rho D_{p}^{4} n^{2} (1 - t)K_{T} \\ Y_{P} & = 0 \\ N_{P} & = 0 \\ \end{aligned} $$
(4)

where, KT is the thrust coefficient and calculated as follows:

$$ \begin{aligned} K_{T} & = C_{1} + C_{2} J + C_{3} J^{2} \\ J & = {{u_{p} } \mathord{\left/ {\vphantom {{u_{p} } {nD_{p} }}} \right. \kern-0pt} {nD_{p} }} \\ u_{p} & = u(1 - w_{p} ) \\ (1 - w_{p} ) & = (1 - w_{p0} ) + \tau \left| {v^{\prime} + x_{p}^{\prime} r^{\prime} } \right| + C_{p}^{\prime} (v^{\prime} + x_{p}^{\prime} r^{\prime} )^{2} \\ \end{aligned} $$
(5)

Considering the above equations, J is the advance coefficient, C1 ~ C3 are the constant values from the KT-J relationship, Dp is the propeller diameter, n is the speed of propeller revolution, up is the effective relative inflow velocity in axial direction to propeller, (1 − wp0) represents the effect of wake at straight ahead motion, \( X_{\text{p}}^{\prime} \) denotes the x-coordinate of the propeller position, τ and Cp are determined experimentally, t is the thrust deduction factor (approximated by the value for straight ahead motion). Experimental data are available for (1 − wp0) versus advance speed, Js. A polynomial curve is fitted by the author for the experimental values and the corresponding value for (1 − wp0) is calculated for respective Js. Figure 6 shows the experimental data with curve fitting.

Fig. 6
figure 6

Curve fitting for experiment data to calculate wp0

Full size image

XR, YR, NR are expressed as the following formulas taking into account the interactions between the hull and rudder as shown in Fig. 7.

Fig. 7
figure 7

Schematic diagram of rudder force and hull-rudder interaction

Full size image
$$ \begin{aligned} X_{R} & = - (1 - t_{R} )F_{N} \,\sin \delta \\ Y_{R} & = - (1 + a_{H} )F_{N} \,\cos \delta \\ N_{R} & = - (x_{R} + a_{H} x_{H} )F_{N} \,\cos \delta \\ \end{aligned} $$
(6)

where, δ is the rudder angle, xR represents the location of the rudder (=−L/2), and tR, aH and xH are the interactive force coefficients between the hull and rudder. FN is the rudder normal force and can be described as follows:

$$ F_{N} = \frac{\rho }{2}A_{R} f_{\alpha } U_{R}^{2} \,\sin \alpha_{R} $$
(7)

where, AR is the rudder area, fα is the gradient of the lift coefficient of rudder, and can be approximated as the function of rudder aspect ratio Λ. The following is the well known Fujii’s prediction formula (Fig. 8).

Fig. 8
figure 8

Gradient of the lift coefficient of rudder, observed and estimated [6]

Full size image
$$ f_{\alpha } = 6.13\Lambda /(2.25 +\Lambda ) $$
(8)

As the rudder normal force is highly affected by the propeller stream especially when the rudder is located just behind the propeller. An example of measured rudder normal force for three different propellers thrust is shown in Fig. 9, where it can be seen that the stronger propeller thrust makes the larger rudder normal force. In the MMG model, the effect of propeller stream is included by the longitudinal inflow velocity of the rudder uR. It can be described as follows.

Fig. 9
figure 9

Rudder normal force for various propeller thrust [7]

Full size image
$$ \begin{aligned} u_{R}^{2} & = (1 - w_{R} )^{2} \{ 1 + Cg(s)\} \\ g(s) & = \frac{\eta K(2 - (2 - K)s)s}{{(1 - s)^{2} }} \\ \eta & = {{D_{P} } \mathord{\left/ {\vphantom {{D_{P} } {h_{R} }}} \right. \kern-0pt} {h_{R} }} \\ K & = {{0.6(1 - w_{p} )} \mathord{\left/ {\vphantom {{0.6(1 - w_{p} )} {(1 - w_{R} )}}} \right. \kern-0pt} {(1 - w_{R} )}} \\ S & = {{1.0 - (1 - w_{R} )U\cos \beta } \mathord{\left/ {\vphantom {{1.0 - (1 - w_{R} )U\cos \beta } {nP}}} \right. \kern-0pt} {nP}} \\ w_{R} & = {{w_{R0} w_{p} } \mathord{\left/ {\vphantom {{w_{R0} w_{p} } {w_{p0} }}} \right. \kern-0pt} {w_{p0} }} \\ \alpha_{R} & = \delta - \gamma \beta_{R}^{\prime} \\ \beta_{R}^{\prime} & = \beta - 2x_{R}^{\prime} r^{\prime} \\ \end{aligned} $$
(9)

where, γ represents the flow straightening factor of the ship hull. Since the lateral inflow angle is reduced by the ship motion v and r, the rudder normal force also depends on v and r. This effect is known as the course-stabilising factor of the rudder. The definition of γ is illustrated in Fig. 10. Figure 11 shows the schematic diagram of the longitudinal inflow velocity of the rudder, which also defines several parameters used in Eq. (9). The hydrodynamic derivatives and coefficients regarding hull, propeller and rudder are given in Table 2.

Fig. 10
figure 10

Definition of flow straightening factor

Full size image
Fig. 11
figure 11

Schematic diagram of longitudinal inflow velocity of rudder [6]

Full size image
Table 2 Hydrodynamic derivatives and coefficients
Full size table

4 Simulation Results and Comparison with that of Experiments

Using the above mentioned MMG model and the hydrodynamic derivatives mentioned in Table 2, simulations are done to predict the ship manoeuvring characteristics. Then the characteristics are validated using the free running experiment data. The details of the experiment model used is mentioned in Table 1.

4.1 Steady Surge Velocity During Turning

The steady surge velocity during turning is non-dimensionalised with respect to the ship’s initial velocity to compare with the non-dimensional experiment value. Such comparison is carried out for different rudder angle turnings for both port and starboard. Figure 12 illustrates such a comparison.

Fig. 12
figure 12

Comparison of non-dimensional steady surge velocity for different delta

Full size image

4.2 Speed Test

The speed test is carried out using the mentioned MMG for different propeller revolutions and compared with the experimental values, which are collected from Ueda and Ueno’s [7] paper. Figure 13 shows such a comparison for the ‘Esso Osaka’ 3-m tanker.

Fig. 13
figure 13

Comparison of surge velocity for different propeller revolution

Full size image

4.3 Turning Test

Figures 14, 15, 16 and 17 show the turning test results as compared with the simulation one. These tests are carried out for half-ahead speed. Here, each comparison contains not only the turning trajectory, but also the non-dimensional surge velocity and yaw rate for comparing the initial transition to a steady state value. Considering Figs. 14 and 15, each of the turning circles show a quite promising result as compared with experimental one. However, due to the existence of wind during the experiments shown in Figs. 16 and 17, the ship started to drift and the resulting circular trajectories shifted towards the direct of wind. In such cases, comparison of the tactical diameters proves the predictability of manoeuvring motion while using the mentioned MMG model. Although slight discrepancies exist, they are well within the acceptable limit.

Fig. 14
figure 14

Turning circle comparison for ±10°

Full size image
Fig. 15
figure 15

Turning circle comparison for ±15°

Full size image
Fig. 16
figure 16

Turning circle comparison for ±20°

Full size image
Fig. 17
figure 17

Turning circle comparison for ±25°

Full size image

5 MMG Including Disturbance Model

The above mentioned MMG is simulated for calm and deep water conditions. However, by considering the terms Xdis, Ydis and Ndis i.e. forces and moment due to any environmental disturbances like wind or current, the model can be used to predict the realistic ship trajectories. Different types of disturbance models are available, like the Fujiwara wind model [9]. Gust wind can also be taken into account using the Davenport spectrum [10]. Both uniform and non-uniform currents can be considered to simulate the ship manoeuvring characteristics.

6 Conclusions

The largest inconvenience in the field of manoeuvring research is the lack of a standard mathematical model. Hydrodynamic data are available from captive tests at various testing facilities and most of these have a lack of reasonable physical meaning. Therefore, comparison of the experimental results with corresponding theoretical calculations is difficult. This paper explains a well-developed concept proposed by the MMG group to develop a mathematical model, which not only takes hull, propeller and rudder effect separately but also their interactions. Most of the terms used in the model have a physical meaning, therefore for any design modification, one can clearly explain which coefficient needs to be modified instead of doing captive tests right from the beginning. Currently, the MMG model is already developed for twin screw MPVs, special types of ships like fishing trawlers etc. The model is also available considering shallow water effect and low speed manoeuvre.