On the Performance of Network Science Metrics as Long-Term Investment Strategies in Stock Markets

Abstract

Firms and individuals have always searched for investment strategies that perform well and are robust to market variations. Over the years, many strategies have claimed to be effective but few resist the effect of time, that is, most of them become outdated. It turns out that markets have a “self-correcting ability”; the secretive/novel nature of strategies firms employ cannot win forever; other firms eventually implement competing strategies causing the market to adjust. Nowadays, most investment firms “sell” to their clients two approaches: high reward and low reward. Unfortunately the possibility of high reward is generally coupled with low robustness (volatility) and if one wants high robustness the yields are low (low reward). In this paper, we use an approach based on network characteristics extracted from historical market data. Network Science has argued that all complex systems have an underlying network structure that explains the behavior of the system. With this in mind, we propose a long-term investment strategy that builds a network from historical investment data, and considers the current state of this network to decide how to create portfolios. We argue that our approach performs better than standard long-term approaches.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Stock markets consists of a collection of sellers and buyers of shares (stocks) of companies. Companies put shares (pieces of ownership papers) in the market as a way to build cash to invest in other areas and make the company grow. The idea of an exchange started in the $17^{\text {th}}$ century in Amsterdam with the Dutch East India Company. Today, markets, are completely inseparable from the world economy; nearly 100 trillion dollars are traded in stock exchanges around the world.¹ In these markets, prices of shares fluctuate as a function of the health of the company. This means that markets allow for people to buy shares of companies at a price and sell later at a different price. If the price one sells is higher than when he bought it, the investor makes money. In general, the world economy improves as a whole, which consequently means that investors should be able to make money if they are able to choose the right shares to buy and sell; this is called an investment strategy. Depending on how long a person wants to invest in the market, the strategy is called long term or short term. Because the aggregated value of stocks increases with time (generally), a long-term investor should be able to capitalize from this growth.

The field of finance and investment strategies is not new and can be traced as far back as the first stock markets started to appear in the $17^{\text {th}}$ century [10]. Investments play a large role in people’s lives and therefore it is crucial to know how to invest with maximum profits, while generating consistent returns. Although diversification of investments is a well-established practice, it was not until 1952 that a formal theory of investment, known as Modern Portfolio Theory (MPT), was introduced in Markowitz’s seminal paper Portfolio Selection [9]. Markowitz is now credited for being “the father of modern portfolio theory”. In his paper, Markowitz proposes a strategy to build a portfolio that maximizes the expected return within a class of risk, where risk is modeled as portfolio variance. He concludes that diversification (investing in several unrelated assets instead of one single asset) limits the variance within the return of the overall portfolio as long as the returns of the assets in the portfolio are not too intercorrelated [9].

In recent years, network science concepts has been applied to study economic networks which includes but are not limited to: mentions mergers and acquisitions [12], board members of multiple companies [6], the cascading failures of financial institutions [17], and stock markets [2]. There is evidence that these networks exhibit a complex behavior and scale-free properties [1]. The representation of the stock market as a network actually seems logical, considering that financial markets are complex and companies have complicated relationships. One way to represent this relationship is to have companies as the nodes of the network, while the links represent the historic correlation between the companies [4].

In this paper, we build a set of networks of USA stocks and introduce a portfolio strategy based on degree centrality and connected components that takes in account Markowitz’s ideas in the sense that it provides diversity of stocks. We show that stocks with low-degree centrality and low connectedness in a network build from historical stock performance significantly outperform those with high-degree centrality, and the standard indices like the Dow Jones Industrial Average, the NASDAQ and the S&P 500.

2 Related Works

There is a large body of research on stock market statistical analysis. Xu et al. [18] studied the microstructure of the Chinese stock market and the trading methods being used. The results suggested that there is no statistically significant correlation on stock market returns with respect to day of the week. Also, they advocated that the autoregressive model does well characterizing stock returns and instability of the market. Poklepović et al. [14] made a comparison between Altman’s Z-score and BEX index of stock market price centered on a data-set of companies of the Zagreb Stock Exchange (ZSE) for the 2006–2011 period. They proposed that it is better for stakeholders to use companies Z-scores and BEX as a provision of their choices in long-term investing.

The recent advances in network science encouraged researchers to utilize this framework to replace traditional statistical methods with network-based measures. For instance, Huang et al. [7] constructed a network of 1,080 stocks traded on both the Shanghai and Shenzhen exchanges (the Chinese stock market) for the 2003–2007 period, where a link is added whenever the correlation coefficient between individual stocks is greater than or equal to a certain threshold value. The results of their work showed that the network exhibits a power-law node degree distribution. Furthermore, they found that high degree stocks have the highest correlation to stock market price variation. Namaki et al. [11] utilized the Random Matrix Theory (RMT) to discard shared factors among stocks. Then they constructed the correlation and threshold network of stocks from the Dow Jones Industrial Average (DJIA) and stocks from the Tehran Stock Exchange (TSE). Their network showed scale-free behavior when the threshold was chosen between 0.02 and 0.31, which indicates that some stocks are very important in the market and they have substantial effect on price variation. Chi et al. [4] recognized that several other researchers have studied stock markets from a complex networks perspective but they have used a very small subset of stocks in their networks. Therefore, they built and studied a cross-correlation large-scale stock network using a winner-take-all method. The network consisted of 19,807 nodes from U.S. stock market covering two periods: from 2005 to 2007, and from 2007 to 2009. They proposed that the fluctuation of stock prices is closely related to only a few stocks. Also, Ma et al. [8] built a correlation threshold network based on 2,396 stocks in the Chinese stock market for the 2005–2012 period. The authors investigated the relationship between degree centrality and portfolio return. They concluded that it is better to invest in central nodes (i.e., nodes with high degree centrality) in the Chinese stock market. They found that the central nodes are more likely to rally after a market crash when positive policy is implemented by government organizations in order to bring the market out of its bearish state. Pozzi et al. [15] studied an average of 300 stocks at a time, for periods of one year, in the American Stock Exchange from 1981 to 2010. They used several methods to limit the number of stocks in the network, such as capitalization. They found that peripheral portfolios systematically outperformed central ones, in contrast to Ma et al. [8], they suggested that investing in peripheral stocks is better than in central stocks. Pozzi et al. [15] uses several characteristics to determine which nodes are considered as peripheral including degree, betweenness, eccentricity, closeness, and eigenvector centralities. Node centrality has been confirmed as a key factor in portfolio selection also by the work of Peralta et al. [13]. The authors built a network where the securities are the nodes and the links represent returns’ correlations between the securities. In such a network, they proved that peripheral assets and optimal weight in the Markowitz framework are positively linked and therefore portfolios should pick preferentially the peripheral securities.

Most of the work that has studied the stock market from a complex network perspective have shown that stock networks exhibit scale-free properties. What varies throughout is the subset of companies used to study the network and the correlation threshold used to determine when a link exists between two companies. However, these works do not do a proper correlation threshold analysis, which appears to be an arbitrary choice. In this work, we introduce an analysis to help determine what correlation threshold should be used in relation to a dataset before proceeding with any further network analysis. We also removed any sample bias that afflicted some of the work introduced above by including at least 1,800 nodes (companies) in each network we considered and also ensuring that survivorship bias (see Sect. 3) is not playing a role in skewing the results of the analysis.

3 Methods and Data

We collected the list of U.S. stock symbols from the NASDAQ FTP server.² The historical data of stock prices was collected using Yahoo Finance API.³ The historical data includes the open, close, adjusted close, and the daily volume information from Jan 1, 2000 to June 30, 2016 of 7,620 securities. The NASDAQ listing is maintained on a daily basis, therefore the list of securities currently on the market only resembles a small portion of all of the securities that were actually available to trade in the past. This is because several companies became delisted.⁴ There are several factors that can cause a company to become delisted but some examples are trading at a price per share less than one dollar for more than 30 days or falling below a certain market capital value for more than 30 days.⁵ This leads to a phenomena known as survivorship bias [3], which skews the data so that it appears to have higher returns overall than there would be in the actual market at that point in history. This happens because the sample set of securities that is selected contains only securities that have survived or existed until present day and ignores the securities that have been delisted from the exchange that they were listed on. Survivorship bias is often an issue in several datasets on historical stock price information. Therefore, we removed its effects by collecting data from Mergent online⁶ and taking in account the historical data for the delisted stocks, which added the historical information of 5,481 securities that would be ignored otherwise.

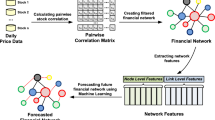
3.1 Network Representation

We built a set of undirected weighted networks of stocks; one for each of the 6-month time windows [15], where time windows overlap for 3 month at a time over the time frame considered, resulting in a total of 64 networks. In each network, the vertices are represented by the companies that are available on the market in that time window. A link exists between two companies if the time series of the returns of the two companies has a correlation greater than a threshold $\theta$. Let $x_i(t)$ be the time series data of a stock i at time t and $\bar{x}_i$ the average value of a stock i over the 6-month period, then we can calculate the correlation coefficient between stock i and stock j as [4]:

$$\begin{aligned} C_{ij} = \frac{\sum _{t}[(x_i(t)-\bar{x}_i)(x_j(t)-\bar{x}_j)]}{\sqrt{\sum _{t}(x_i(t)-\bar{x}_i)^{2}}\sqrt{\sum _{t}(x_j(t) - \bar{x}_j)^{2}}}\;. \end{aligned}$$

(1)

Fig. 1.

(a) Network density drops sharply as we increase the correlation threshold, $\theta$. (b) The scaling exponent, $\alpha$, follows the same scaling as the number of links when the threshold is increased and stabilizes in the range of $1< \alpha < 3$, which is a characteristic of scale-free networks, for $\theta > 0.4$.

Several studies that build networks of the stock market use a threshold $\theta$ to determine whether or not there will be a link between two nodes in the network. For example: Huang et al. [7] selected $\theta \in [0.55,0.69]$; Ma et al. [8] used a threshold $\theta = 0.7$; Chi et al. [4] used threshold values of 0.85, 0.90, and 0.95. However, these studies hardly justify their choice. Therefore, we introduce a qualitative threshold analysis to select an appropriate value of $\theta$ by comparing the density of the network (Fig. 1(a)) and the corresponding scaling exponent (Fig. 1(b)) as a function of the threshold $\theta$. The idea is that if we choose a low correlation threshold the network will be very dense, because any company is correlated (linked) to any other company, and behave like a random network. However, the correlation between stocks is not uniformly distributed. Many companies will exhibit low correlation, but only few have actually appreciable correlation. Therefore, when we increase the correlation threshold we observe a sharp drop in the number of links (and therefore density) with a stabilization after a certain threshold, once we are in the fat tail of the correlation distribution (Fig. 1(a)). This transition corresponds to a transition of the scaling exponent of the network, that starts following a power-law node degree distribution (Fig. 1(b)). We can observe that the scaling exponent stabilizes when $\theta \ge 0.4$, in agreement with the aforementioned works, therefore we chose it as a threshold. Using a threshold that is as low as possible helps to retain as much connectivity information as possible while capturing the actual topological properties of the stock network.

3.2 Portfolio Return

The portfolio return is computed from simple stock returns from the time series data to allow for a standardized comparison between the companies price per share. Also, adjusted closing prices are used within those calculations. The adjusted closing price takes into account things that would otherwise cause the regular closing price to be inaccurate such as when there is a stock split and the price per share is dropped significantly—in reality, a stock split does not affect the value of an individual’s portfolio because the decrease in share price is proportional to the increase in the number of shares for that individual. For each network, we compute the return that every stock in the network would have yielded three months after the network’s ending date. Let p be the adjusted closing price of a stock i, then the return of a stock i on day t is calculated as:

$$\begin{aligned} r_{i}(t) = \frac{p_{i}(t)-p_{i}(t-1)}{p_{i}(t-1)}\;. \end{aligned}$$

(2)

Let us assume an initial investment amount of capital C that is equally partitioned over s stocks in a 6-month time window, that is $C_1 = C_2 = \cdots = C_s$. The returns of the s stocks are then calculated for the three month time period starting on the ending date of the time window for that network. Then, the return $r_p$ of the portfolio is computed as

$$\begin{aligned} r_p = \frac{1}{C}\sum _{i=1}^{s} (1 + r_i)C_i\;. \end{aligned}$$

(3)

The investment growth IG, which is the ratio between the capital $C_F$ at the end of the investment life and the initially invested capital $C_I$ is then

$$\begin{aligned} IG = \frac{C_F}{C_I} = \prod _i r_{p}^{(i)}\;. \end{aligned}$$

(4)

3.3 Portfolio Strategy

Here it is proposed that stocks chosen to be part of an investment portfolio should have two properties:

• (i) They should have mostly above-average returns.

• (ii) They should correlate with very few other nodes in the network.

In order to achieve objective (i), we need to be able to compare stock returns that are in different networks and that could possibly be traded for years in between. In order to compare a companies return in one network to another company’s return in a different network, we need to normalize the stock returns. All of the individual returns yielded by each node are then converted to Z scores. We compute the average return of a network $\bar{r} = \frac{1}{n}\sum _{i=1}^{n}{r_{i}}$ and the standard deviation $\sigma _r$ of the returns in the network. The corresponding normalized return $Z_i$ of a stock i is then $Z_i = (r_i - \bar{r}) / \sigma _r$. This process also takes in account the current market conditions (growth or bearish), because the average return of two networks may not be equal. By analyzing the relationship between node degree and Z-score (Fig. 2(a)) and the amount of positive outliers over time (Fig. 2(b)), it is evident that simply choosing symbols with a low degree, that is nodes with a low degree centrality, increases the chances of selecting a high performing stock.

Fig. 2.

(a) Symbols with a low degree are more likely to have higher performance. In red are represented those symbols that are considered positive outliers because they have a Z-score greater than 3. The asymmetry between positive and negative outliers is caused by the fact that a company can loose only so much before going default, while the growth is potentially unlimited. (b) The positive outliers are spread over all the time frame considered; in the heatmap, the larger the number of positive outliers and darker is the tone of red.

To achieve objective (ii), we need to select stocks that are not correlated. By definition of degree centrality, the nodes with low degree centrality have low degree, and therefore are less connected to other nodes. This means that each node is less affected by the rest of the network and allows for a much easier way to diversify a portfolio based on Markowitz’s idea of portfolio theory. However, due to the power-law nature of the network, low-degree nodes are very likely to be connected to a hub, that is, likely to be affected by highly-connected high-degree nodes. Therefore, degree centrality is not enough to select low intercorrelated stocks. Hence, we introduce a second criteria for stock selection that exploits connectedness. The network is partitioned in disconnected components by progressively removing the links with the lower weight (correlation). Then, only one stock from each component is selected, until the portfolio is fulfilled. We also impose an additional constraint on the stocks to be selected: a minimum average volume of traded shares in a given period, where the volume is computed as the average shares traded per day. The volume restriction helps prevent unrealistic situations where the volume is so low that it would not be possible to actually fill an order at that price, or to fill the order at all. That is, we make sure that stock price and the single stock order are virtually independent. Furthermore, the minimum volume ensures that we also rule out the effect of small-cap stocks which tend to consistently outperform large-cap stocks [5]. In our experiments, we used 800,000 shares as the threshold which we consider as a good trade-off between the number of companies that can be selected and the ability to actually fulfill an order. Some people may argue that the threshold is actually rather high but as an extreme example, consider what would happen with penny stocks.

The portfolio selection algorithm is the following. Given a portfolio of size s, and an initial capital $C_I$, we select s stocks according to the aforementioned criteria. For each time window:

• 1. All of the nodes in the network associated with a time window are sorted based on their degree.

• 2. The first s nodes containing the lowest degree centrality, with a minimum value of one, are selected to possibly be included in the portfolio.

• 3. The network is partitioned in components and only one stock per component is chosen.

• 4. The average daily volume is then calculated for each selected node for the past six-month period. If the average daily volume is greater than or equal to the specified threshold, then the symbol is added to the portfolio.

• 5. The total return of the portfolio is computed as described in Sect. 3.2.

The steps 1–5 are repeated every three months to create the next portfolio based on the next 6-month network until the end of the portfolio life.

4 Experiments

We studied two classes of portfolios. One with only 5 stocks, representing people with limited capital, and one with 20 stocks, representing medium or large investors. In order to validate the performance of the proposed portfolio strategy—that the strategy ensured above average returns—we considered three metrics:

• (i) A student’s t-test to verify the statistical significance that the mean return of the stocks selected by the strategy during the portfolio life was in fact greater than a randomly chosen portfolio.

• (ii) The portfolio return and Sharpe ratio versus several well-known indices, a random-pick strategy, and a strategy that picks stocks with high degree centrality.

• (iii) The portfolio return over several time spans for the portfolio life.

For (i), we run 30 t-tests for both portfolio sizes where we compared the mean return of the stocks selected by the proposed strategy versus the mean return of picking those stocks randomly. Furthermore, we compared the mean of all the stocks chosen in the 30 portfolios and compared the average return versus the average return of the whole population. For the portfolio of size 5, 63% of the tests were positively significant ($p < 0.05$) and the t-test against the whole population having a value of 2.88 ($p < 0.01$). The portfolio of size 20 had 80% of the tests positively significant ($p < 0.05$) and the t-test versus the population had a value of 3.34 ($p < 0.01$). The portfolio of size 5 seems to perform worse than a portfolio of size 20 in this test, but it could be induced by the small sample size, which results in a much larger critical value of the t distribution (2.776 vs. 2.093).

In (ii) we compared the portfolios versus the indices considering the full time frame of our data. We observed that both the portfolio of size 5 and the portfolio of size 20 resulted in returns that were significantly greater than: the randomly chosen portfolios (Fig. 3(a)), confirming the results observed for (i); the high degree portfolios (Fig. 3(b)); the Dow Jones Industrial Average, NASDAQ, and S&P 500 (Fig. 3(c)). These results are in agreement with the annualized Sharpe ratios [16] of the portfolios of size 5 and 20 respectively, which are: 0.5845 and 0.3921 for the low degree portfolios, −0.0048 and 0.0794 for the high degree portfolios, 0.3224 and 0.3330 for the random portfolios.

Fig. 3.

The proposed strategy outperforms (a) a null model where stocks are picked randomly, (b) common stock indices (e.g., S&P), and (c) portfolios built by selecting stocks with a high degree centrality. (d) Sensitivity analysis to initial conditions of the market, as it is the case for most investments. In 2008 the market crashed. When market crashes the topology of the network changes and companies tend to become more connected, which prevent the strategy from being able to outperform the indices

While the strategy seems to always outperform market, it is important to reason on the sensitivity to initial conditions. In fact, in Fig. 3(d) we could argue that the portfolio followed the market rather closely, and it was only due to a divergence at the beginning (especially for the NASDAQ) that the proposed strategy ended up performing significantly better. For example, if we started the portfolio in 2007, the strategy did not completely outshine the indices (Fig. 3(c)), and the portfolio of size 20 ended up performing no better than the NASDAQ. This should not be surprising, the time to enter the market is often crucial with respect to the final performance of a portfolio. For example, investing during a growing phase of the market will most likely lead to positive returns, however the impossibility to predict a change in the market might also means that the market might have peaked and it will go into a decline phase. Hence, to better assess the overall performance when there is sensitivity to the initial conditions and to address (iii), we considered several time spans for the portfolio life, where each time frame has multiple starting years (as long as the end of life of the portfolio is within our data range, that is no later than 2016). For example, there are 6 possible starting years, from 2000 to 2006, for a portfolio with a life span of 10 years. Then, we computed the fraction of times the proposed strategy outperformed the other metrics for each time span (Fig. 4). In every case we had a winning ratio greater than 50%, therefore we can conclude that we outperform the common indices and alternative strategies. Furthermore, the longer the portfolio time span we considered, the better the strategy performed; if we considered a long term investment (e.g., greater than 8 years), we were almost guaranteed to outperform the market in every case (that is, independently of the initial conditions).

Fig. 4.

A portfolio of size 5 selected according to the proposed strategy. For each portfolio longevity considered, the winning percentage represents the fraction of times the proposed strategy outperform the other metrics. The proposed strategy outperforms any other benchmark considered, because the winning percentage is always greater than $50\%$

5 Conclusion

Throughout this study, we investigated a long-term stock market investment strategy that attempts to minimize portfolio variance while simultaneously maintaining returns. At the same time, we attempted to address some of the limitations of previous studies like the network size, the threshold analysis, and the sensitivity to initial conditions. We presented a qualitative threshold analysis to select an appropriate value of the correlation threshold by comparing the density of the network and the corresponding scaling exponent as a function of the threshold itself. We found out that the scaling exponent stabilizes when the network threshold $\theta \ge 0.4$ confirming the results of previous works [4, 7, 8]. Then, we conducted three experiments to validate the performance of the proposed portfolio strategy. We have shown that stocks with low-degree centrality and connectedness outperform those with high-degree centrality, the Dow Jones Industrial Average, the NASDAQ and the S&P 500 indices.