Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The study of graphs, networks and particularly complex networks is a research topic which attracts broad attention of numerous scholars. The main issue in this area of research is to find suitable measures, and use them to quantify and understand the structural information of networks. Once such measures have been established, they can serve as a standard for exploring and analyzing networks or for comparing and designing new networks.

During the recent years a large variety of measures or indices have been defined as descriptors for networks [12]. They function as a universal language to describe the chemical structure of molecules, the chemical reaction networks, ecosystems, financial markets, the World Wide Web, and social networks. In chemical and biological applications these measures are referred to as topological indices [8]. The topological indices can be divided into many classes, some of them are: Distance-based measures [16], which are based on the shortest paths between pairs of vertices; Degree-based measures [5], that are computed by using vertex degree; and the measures based on both degrees and distances [1, 9].

The history of graph invariants begins in 1947, when the physical chemist H. Wiener used a descriptor called Wiener index for predicting the boiling points of paraffin [17]. Many years after its introduction and success, a large number of other topological indices have been proposed in the literature and used extensively for the development of quantitative structure-activity relationships (QSARs) and quantitative structure-property relationships (QSPRs) in which the biological activity or other properties of molecules are correlated with their chemical structure [3]. Also, they gained an interest in other fields that use network models to study complex systems.

The goal of this work is to calculate certain topological indices: the Wiener index and the generalized Terminal Wiener index, for a class of networks. The computation of this invariants identify how complex the network is and quantify its robustness [4]. We focus on a class of large networks named Hex derived Network \(HDN_n\) and Equilateral Tetra Sheet Network \(ETTS_n\). These networks have been studied in variety of context. They have been applied in chemistry to model some molecular structure [10], in Robotic [15], and in communication networks [14]. The analytical expressions for the topological indices that we aim to calculate are normally obtained from the distance matrix of the corresponding network. However, due to the complexity of networks that we want to analyze, we use a powerful approach named the cut method [11]. The objective of this method is to cut the associated network into smaller fragments and assembling the indices of fragments to generate the property of the whole structure.

This paper in organized as follows: In Sect. 2, we introduce the basic concepts and techniques employed in this work. In Sects. 3 and 4, we describe the construction method of the two networks, Equilateral Triangular Tetra Sheet \(ETTS_n\) and Hex derived network \(HDN_n\), we define some structural properties of these networks and we give there analytical expressions for the Wiener index and the generalized Terminal Wiener index. Then, we compare these topological indices using graphical representations. We summarize our findings in the section of Concluding remarks 5.

2 Background and Notation

Throughout this paper, we use the terms graph and network interchangeably.

Let \(G = (V,E)\) be a graph with vertex and edge sets are \(V = V (G) = \{v_1, ..., v_N\}\) and \(E = E(G) = \{e_1, ..., e_M\}\), respectively. The number of vertices and edges of G is denoted by N and M, respectively. The distance d(u, v) between two vertices u and v denote the length of the shortest path connecting these two vertices. The diameter D(G) of G is defined as the maximum of the shortest path between all vertices of G. We denote by deg(v) the degree of the vertex v, and the vertex \(v \in V (G)\) is said to be pendent if \(deg(v) = 1\). The number \(\delta = min\{deg(v), \forall v \in V(G)\}\) is the minimum degree of G and the parameter \(\varDelta = max\{deg(v), \forall v \in V(G)\}\) is its maximum degree. A subgraph H of a graph G is convex if for any two vertices u, v of H, any shortest path between u and v in G lies completely in H. The graph G is called a partial cube if its vertices u can be labeled with binary strings l(u) of a fixed length, such that \(d(u,v) = H(l(u),l(v))\). Holds for any two vertices u and v of G, where H(l(u), l(v)) is the Hamming distance between the binary strings l(u) and l(v), that is, the number of positions in which l(u) and l(v) differ. The edges \(e = xy\) and \(f = uv\) are in the relation Djoković-Winkler \(\theta \) if \(d(x,u)+d(y,v) \ne d(x,v)+d(y,u)\). The relation \(\theta \) is always reflexive and symmetric, and is transitive on partial cubes. Therefore, \(\theta \) partitions the edge set of a partial cube into equivalent classes \(F_1, F_2, ..., F_k\), called cuts.

Definition 1.

Let G be a graph. Then the Wiener index of G is equal to the sum of distances between all pairs of vertices of G. Mathematically:

$$\begin{aligned} W(G)= \sum _{\{u,v\}\subseteq V(G)} d(u,v) \end{aligned}$$
(1)

One of the most recent extensions of the Wiener index is the Terminal Wiener index, which was introduced by Gutman et al. [6].

Definition 2.

Let \(V_p(G)\subseteq V(G)\) be the set of pendent vertices of the graph G. Then the Terminal Wiener index is defined as the sum of distances between all pairs of pendent vertices of G.

$$\begin{aligned} TW(G)=\sum _{\{u,v\}\subseteq V_p(G)} d(u,v) \end{aligned}$$
(2)

Later, Ilic et al. [9], proposed a generalization for the Terminal Wiener index called the generalized Terminal Wiener index.

Definition 3.

Let G be a graph. For \(K \ge 1\), the generalized Terminal Wiener index is defined as the sum of the distances between all pairs of vertices of degrees K.

$$\begin{aligned} TW_K(G)= \sum _{\begin{array}{c} \{u,v\}\subseteq V(G){}\\ deg(u)=deg(v)=K \end{array}} d(u,v) \end{aligned}$$
(3)

Toward more additional references, we refer to see [7, 13, 18, 19].

The cut method is classified into two kinds based on the class of networks to which it is being applied. A standard cut method is applied to networks that fall under partial cubes and an extended cut method is applied to classes larger than partial cubes.

Theorem 1.

(Standard cut method) [11] Let G be a partial cube and let \(F_1, F_2, ..., F_k\) be its cuts. Let \(n_1(F_i)\) and \(n_2(F_i)\) be the number of vertices in the two connected components of \(G-F_i\). Then

$$\begin{aligned} W(G) = \sum _{i=1}^k n_1(F_i)n_2(F_i) \end{aligned}$$
(4)

Theorem 2.

(Extended cut method) [2] Let G be a graph larger than partial cube. Let \(E^\lambda (G), \lambda \ge 1\), denote a collection of edges of graph G with each edge in G being repeated exactly \(\lambda \) times and let \(\{F_i\}_{i=1}^k\) be the convex cuts of \(E^\lambda (G)\). Then

$$\begin{aligned} W(G) =\frac{1}{\lambda } \sum _{i=1}^k n_1(F_i)n_2(F_i) \end{aligned}$$
(5)

Note that, an edge-cut F of G is said to be a convex cut if the two components of \(G - F\) are the convex subgraphs of G.

Theorem 3.

[9] Let G be a partial cube and \(\{F_i\}_{i=1}^k\) be its cuts. Let \(n_1^K(F_i)\) and \(n_2^K(F_i)\) be the number of vertices of degree \(K \ge 1\) in the two connected components of \(G-F_i\). Then

$$\begin{aligned} TW_K(G) = \sum _{i=1}^k n_1^K(F_i)n_2^K(F_i) \end{aligned}$$
(6)

As a consequence of above theorem, we have the following result

Theorem 4.

Let G be a connected graph and let \(\{F_i\}_{i=1}^k\) be the convex cuts of \(E^\lambda (G)\). Then

$$\begin{aligned} TW_K(G) =\frac{1}{\lambda } \sum _{i=1}^k n_1^K(F_i)n_2^K(F_i) \end{aligned}$$
(7)

Proof.

For u, v \(\in V(G)\) and \(deg(u)=deg(v)=K\), let \(P_{u,v}\) be a shortest path between u, v in G. We can verify that: \(\mid E(P_{u,v}) \cap F_i \mid = 0\) if u, v belong to the same component \(G-F_i\), otherwise \(\mid E(P_{u,v}) \cap F_i \mid = 1\).

Every edge \(e \in E^\lambda (G)\) is cut by precisely \(\lambda \) convex cuts \(\{F_i\}_{i=1}^k\). Then:

$$\begin{aligned} \begin{aligned} TW_K(G)&= \sum _{\begin{array}{c} \{u,v\}\subseteq V(G){}\\ deg(u)=deg(v)=K \end{array}} d(u,v)= \sum _{\begin{array}{c} \{u,v\}\subseteq V(G){}\\ deg(u)=deg(v)=K \end{array}} \mid E(P_{u,v})\mid \\&= \frac{1}{\lambda }\sum _{i=1}^k \sum _{\begin{array}{c} \{u,v\}\subseteq V(G){}\\ deg(u)=deg(v)=K \end{array}} \mid E(P_{u,v}) \cap F_i \mid \end{aligned} \end{aligned}$$

Which gives the Eq. 7.\(\square \)

3 Equilateral Triangular Tetra Sheet Network

In this section, we discuss a kind of large networks called Equilateral Triangular Tetra Sheet Network \(ETTS_n\). We introduce the construction method of this network, analyze its structural properties and we give close formula of certain topological indices.

3.1 Construction Method

Let \(ETTS_n\) be an Equilateral Triangular Tetra Sheet of dimension n, where n denote the number of vertices in a side of this network. The \(ETSS_n\) can be built in the following iterative way. Initially, \(ETTS_2\) is composed of one tetrahedron \(K_4\) also known as a triangular pyramid. \(ETTS_3\) is obtained from \(ETTS_2\) by adding a layer of tetrahedrons around the bottom side of \(ETTS_2\). Similarly, \(ETTS_n\) is obtained from \(ETTS_{n-1}\) by adding a layer of tetrahedrons around the bottom side of \(ETSS_{n-1}\). Figure 1, illustrates some iterations of the Equilateral Triangular Tetra Sheet Network \(ETTS_n\).

Fig. 1.
figure 1

An example of Equilateral Triangular Tetra Sheet Networks, with \(n = \{2, 3, 4\}\)

Full size image

From the construction method of the Equilateral Triangular Tetra sheet Network and Fig. 1, we can extract some structural properties:

  • The order of the network \(ETTS_n\) is equal to:

    $$\begin{aligned} N = \frac{3n^2-3n+2}{2} \end{aligned}$$
    (8)

  • The number of edges of \(ETTS_n\) is equal to:

    $$\begin{aligned} M = \frac{9n^2-15n+6}{2} \end{aligned}$$
    (9)

  • The diameter of the network \(ETTS_n\) is:

    $$\begin{aligned} D = n-1 \end{aligned}$$
    (10)

3.2 Calculation of Some Topological Indices of the Network \(ETTS_n\)

In the following theorem, we use the extended edge-cut method in order to obtain exact analytical expressions for the Wiener index W and the generalized Terminal Wiener index \(TW_K\) of the structure \(ETTS_n\).

In this paper, we calculate the generalized Terminal Wiener index \(TW_K\) in the case of K equal to the maximum degree \(\varDelta \) and the minimum degree \(\delta \). From the Fig. 1, the maximum degree of the network \(ETTS_n\) is \(\varDelta = 12\) and the minimum degree is equal to \(\delta = 3\).

Fig. 2.
figure 2

Some edge cuts of Equilateral Triangular Tetra Sheet Network \(ETTS_4\)

Full size image

Theorem 5.

Let \(ETTS_n\) denote an Equilateral Triangular Tetra Sheet network of dimension n, with \(n \ge 2\). Then:

$$\begin{aligned} W(ETTS_n) = \frac{72n^5-60n^4-80n^3+60n^2+8n}{160} \end{aligned}$$
(11)
$$\begin{aligned} TW_\delta (ETTS_n) = \frac{2n^5-5n^4+20n^3-40n^2+53n}{10}-3 \end{aligned}$$
(12)
$$\begin{aligned} TW_\varDelta (ETTS_n) = \frac{8n^5-100n^4+480n^3-1100n^2+1192n}{160}-3 \end{aligned}$$
(13)

Proof.

We use horizontal, diagonal, and encircling edge cuts shown in Fig. 2.

Let \(X_i\), \(1 \le i \le n-2\), denote the horizontal edge cuts of \(ETTS_n\), as shown in the Fig. 2. Similarly, for \(1 \le i \le n-2\), let \(Y_i\) denote the diagonal edge cuts along the North-West and South-East directions and \(Z_i\) denote the diagonal edge cuts along the South-West and North-East directions as shown in the Fig. 2. Let \(E_i\), \(1 \le i \le 3+(n-1)^2\), denote the encircling edge cuts of \(ETTS_n\), as shown in the Fig. 2. We have the number of vertices of degree \(\delta = 3\) is equal to: \(N_{\{K=3\}} = 3+(n-1)^2\), and the number of vertices of degree \(\varDelta = 12\) is equal to: \(N_{\{K=12\}} = \frac{n^2-5n+6}{2}\).

Then, for \(1 \le i \le 3+(n-1)^2\):

$$\begin{aligned} \begin{aligned} n_1(E_i)&= 1\\ n_1^3(E_i)&= 1 \end{aligned} \quad \quad \begin{aligned} n_2(E_i)&= N-1\\ n_2^3(E_i)&= N_{\{k=3\}}-1 \end{aligned} \end{aligned}$$

And, for \(1 \le i \le n-2\):

$$\begin{aligned} \begin{array}{l l l l l l l l l l l} n_1(X_1) = 5 &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} n_2(X_1) = N - 5 \\ n_1(X_i) = \sum _{j=2}^i 3(j+1)-2i+7 &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} n_2(X_i) = N - n_1(X_i) \\ n_1^3(X_i) = i^2+i+1 &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} n_2^3(X_i) = N_{\{K=3\}} - n_1^3(X_i) \\ n_1^{12}(X_1) = 0 &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ n_1^{12}(X_i) = \sum _{j=2}^i(j-1) &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} n_2^{12}(X_i)= N_{\{K=12\}} - n_1^{12}(X_i) \\ \\ \end{array} \end{aligned}$$

Due to the symmetry of \(ETTS_n\) network, we have \(n_1(X_i) = n_1(Y_i ) = n_1(Z_i )\) and \(n_1^K(X_i) = n_1^K(Y_i ) = n_1^K(Z_i )\), \(1 \le i \le n - 2\).

Clearly the set \(\{X_i , Y_i , Z_i , E_i\}\) partitions the set \(E^2(ETTS_n)\) into convex cuts. By Theorems 2 and 4, we have

$$\begin{aligned} W(ETTS_n)&= \frac{1}{2} \bigg [ \sum _{i=1}^{n-2}n_1(X_i)n_2(X_i) + \sum _{i=1}^{n-2}n_1(Y_i)n_2(Y_i) + \sum _{i=1}^{n-2}n_1(Z_i)n_2(Z_i) +\\&\; \; \; \; \sum _{i=1}n_1(E_i)n_2(E_i) \bigg ]\\&= \frac{1}{2} \bigg [ 3 \sum _{i=1}^{n-2}n_1(X_i)n_2(X_i) + (N-1)(3+(n-1)^2) \bigg ] \end{aligned}$$
$$\begin{aligned} TW_{\{K=\delta \}}(ETTS_n)&= \frac{1}{2} \bigg [ \sum _{i=1}^{n-2}n_1^\delta (X_i)n_2^\delta (X_i) + \sum _{i=1}^{n-2}n_1^\delta (Y_i)n_2^\delta (Y_i) + \sum _{i=1}^{n-2}n_1^\delta (Z_i)n_2^\delta (Z_i) +\\&\; \; \; \;\sum _{i=1}n_1^\delta (E_i)n_2^\delta (E_i) \bigg ]\\&= \frac{1}{2} \bigg [ 3 \sum _{i=1}^{n-2}n_1^\delta (X_i)n_2^\delta (X_i) + (3+(n-1)^2)(2+(n-1)^2) \bigg ] \end{aligned}$$
$$\begin{aligned} TW_{\{K=\varDelta \}}(ETTS_n)&= \frac{1}{2} \bigg [ \sum _{i=2}^{n-2}n_1^\varDelta (X_i)n_2^\varDelta (X_i) + \sum _{i=2}^{n-2}n_1^\varDelta (Y_i)n_2^\varDelta (Y_i) + \sum _{i=2}^{n-2}n_1^\varDelta (Z_i)n_2^\varDelta (Z_i) \bigg ]\\&= \frac{1}{2} \bigg [ 3 \sum _{i=2}^{n-2}n_1^\varDelta (X_i)n_2^\varDelta (X_i) \bigg ] \end{aligned}$$

Which give the Eqs. 11, 12 and 13.\(\square \)

A comparison of topological indices of the Equilateral Triangular Tetra Sheet Network is given in Fig. 3. Along the horizontal line the values of dimension of \(ETTS_n\) network and along the vertical line the values of the topological indices are shown. In Fig. 3, we can see that all the topological indices are monotonically increasing and they change the monotony with a high increase in some values of dimension n. In general, the Wiener index shows a dominant change with the increasing value of the dimension of the Equilateral Triangular Tetra Sheet Network.

Fig. 3.
figure 3

Comparison of topological indices of the Equilateral Triangular Tetra Sheet Network \(ETTS_n\)

Full size image

4 Hex Derived Network

In this section, we discuss an other complex structure called Hex Derived Network \(HDN_n\). We give the construction method of this network, analyze its structural properties and evaluate its certain topological indices.

4.1 Construction Method

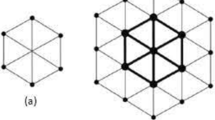
Let \(HDN_n\) be a Hex Derived Network of dimension \(n \ge 2\), such that, n denote the number of vertices in a side of this structure. The construction of \(HDN_n\) is presented in the following iterative way. At first, \(HDN_2\) is a 2-dimensional hexagonal mesh composed of six tetrahedrons \(K_4\) (Fig. 4). Then, \(HDN_3\) is obtained from \(HDN_2\) by adding a layer of tetrahedrons \(K_4\) around the boundary of \(HDN_2\). The growth process to the next generations continues in a similar way, such that, \(HDN_n\) is obtained from the previous iteration \(HDN_{n-1}\) by adding a layer of tetrahedrons \(K_4\) around the boundary of \(HDN_{n-1}\). Figure 4, illustrates some generations of the Hex Derived Network \(HDN_n\).

Fig. 4.
figure 4

An example of Hex Derived Networks \(HDN_n\), with \(n = \{2, 3\}\)

Full size image

Some structural properties of the Hex derived Network \(HDN_n\) are defined as follows:

  • The number of vertices of the network \(HDN_n\) is equal to:

    $$\begin{aligned} N = 9n^2-15n+7 \end{aligned}$$
    (14)

  • The number of edges of the network \(HDN_n\) is equal to:

    $$\begin{aligned} M = 27n^2-51n+24 \end{aligned}$$
    (15)

  • The diameter of the network \(HDN_n\) is defined as:

    $$\begin{aligned} D = 2n-2 \end{aligned}$$
    (16)

4.2 Calculation of Some Topological Indices of the Network \(HDN_n\)

In the following theorem, we obtain exact analytical expressions for the Wiener index W and the generalized Terminal Wiener index \(TW_K\) in the case of k equal to the maximum degree \(\varDelta \) and the minimum degree \(\delta \). From the Fig. 4, the maximum degree of the network \(HDN_n\) is \(\varDelta = 12\) and the minimum degree is equal to \(\delta = 3\).

Theorem 6.

Let \(HDN_n\) be a Hex Derived Network of dimension n, with \(n \ge 2\). Then

$$\begin{aligned} W(HDN_n)= \frac{1476n^5-5070n^4+6560n^3-3810n^2+844n}{40} \end{aligned}$$
(17)
$$\begin{aligned} TW_\delta (HDN_n) = \frac{82n^5-320n^4+455n^3-280n^2+63n}{5} \end{aligned}$$
(18)
$$\begin{aligned} TW_\varDelta (HDN_n) = \frac{164n^5-1230n^4+3680n^3-5490n^2+4076n}{40}-30 \end{aligned}$$
(19)
Fig. 5.
figure 5

Some edge-cuts of a Hex Derived Network \(HDN_3\).

Full size image

Proof

We use horizontal, diagonal, and encircling edge cuts shown in Fig. 5.

Let \(X_i\) and \(X_{-i}\), for \(1 \le i \le n-1\), denote the horizontal edge cuts of \(HDN_n\), as shown in the Fig. 5. Similarly, for \(1 \le i \le n-1\), let \(Y_i\), \(Y_{-i}\) denote the diagonal edge cuts along the North-West and South-East directions and \(Z_i\), \(Z_{-i}\) denote the diagonal edge cuts along the South-West and North-East directions as shown in the Fig. 5. Let \(E_i\), \(1 \le i \le 6(n-1)^2\), denote the encircling edge cuts of \(HDN_n\), as shown in the Fig. 5.

We have the number of vertices of degree \(\delta = 3\) is equal to: \(N_{\{K=3\}} = 6(n-1)^2\), and the number of vertices of degree \(\varDelta = 12\) is equal to: \(N_{\{K=12\}} = 3n^2-9n+7\).

Then, for \(1 \le i \le n-1\):

$$\begin{aligned} \begin{array}{l l l l l l l l l l l} n_1(X_1) = 2n-1 &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} n_2(X_1) = N - 2n+1 \\ n_1(X_i) = 3\sum _{j=1}^{i-1}(n+j-1)+2n+i-2 &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} n_2(X_i) = N - n_1(X_i) \\ n_1^3(X_1) = n-1 &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} n_2^(X_1) = N - n+1 \\ n_1^3(X_i) = (n-1)+2\sum _{j=1}^{i-1}(n+j-1) &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} n_2^3(X_i) =N_{\{K=3\}} - n_1^3(X_i) \\ n_1^{12}(X_1) = 0 &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} \\ n_1^{12}(X_i) = \sum _{j=1}^{i-1}(n+j-2) &{} &{} &{} &{} &{} &{} &{} &{} &{} &{} n_2^{12}(X_i)= N_{\{K=12\}} - n_1^{12}(X_i) \\ \\ \end{array} \end{aligned}$$

and, for \(1 \le i \le 6(n-1)^2\):

$$\begin{aligned} \begin{aligned} n_1(E_i)&= 1\\ n_1^3(E_i)&= 1 \end{aligned} \quad \quad \begin{aligned} n_2(E_i)&= N-1\\ n_2^3(E_i)&= N_{\{k=3\}}-1 \end{aligned} \end{aligned}$$

Using symmetry, we have \(n_1(X_i) = n_1(Y_i ) = n_1(Z_i )=n_1(X_{-i})=n_1(Y_{-i})=n_1(Z_{-i})\) and \(n_1^K(X_i) = n_1^K(Y_i ) = n_1^K(Z_i )=n_1^K(X_{-i}) = n_1^K(Y_{-i} ) = n_1^K(Z_{-i} )\), for \(1 \le i \le n - 1\).

Therefore by using Theorems 2, 4 and described cuts, we get Eqs. 17, 18 and 19.\(\square \)

Figure 6 shows the behavior of the indices for the Hex Derived Network \(HDN_n\), where along the horizontal line the values of dimension n for the network \(HDN_n\) and along the vertical line the values of topological indices are shown. Similarly, all the topological indices are increasing and change their monotony in some values of dimension n. The Wiener index shows a dominant change with the increasing value of the dimension n for the Hex Derived Network.

Fig. 6.
figure 6

Comparison of topological indices of the Hex Derived Network \(HDN_n\)

Full size image

5 Concluding Remarks

In this paper, we have given the construction method of two large networks: Equilateral Triangular Tetra Sheet \(ETTS_n\) and Hex derived network \(HDN_n\). We have obtained exact analytical expressions for the Wiener index and the generalized Terminal Wiener index in the case of K equal to the maximum and the minimum degree. We have employed a powerful approach named edge-cut method to obtain these expressions that have not been obtained before. The results found in this paper will help to figure out the properties of Equilateral Triangular Tetra Sheet \(ETTS_n\) and Hex derived network \(HDN_n\). These out-finding can also provide for opportunities to extend these networks and techniques to materials of importance in complex networks.