Capturing the Dynamics of Hashtag-Communities

Abstract

Online media have a huge impact on public opinion, economics and politics. Every day, billions of posts are created and comments are written, covering a broad range of topics. Especially the format of hashtags, as a discrete and condensed version of online content, is a promising entry point for in-depth investigations. In this work we provide a set of methods from static community detection as well as novel approaches for tracing the dynamics of topics in time dependent data. We build temporal and weighted co-occurence networks from hashtags. On static snapshots we infer the community structure using customized methods. We solve the resulting bipartite matching problem between adjacent timesteps, by taking into account higher order memory. This results in a matching that is robust to temporal fluctuations and instabilities of the static community detection. The proposed methodology, tailored to uncover the detailed dynamics of groups of hashtags is adjustable and by that broadly applicable to reveal the temporal behavior of various online topics.

1 Introduction

Networks as a representation of real-world complex systems can usually neither be uniquely classified nor do they obey a single construction rule. Functional or contextual relations lead to globally and locally heterogeneous substructures. Densely linked groups of vertices are called communities, but their structure can vary and their definition is not strict. Organizational arrangements can have various characteristics, such as overlapping, fuzziness or hierarchical structure, and require diverse detection algorithms to be uncovered [1, 12, 19, 21].

Time resolved data of online content became increasingly available in recent years and offers great possibilities for analysis. Temporality is of great importance for understanding the dynamics of content, including the emergence of topics or trends, and their lifetime. The development of methods, that capture these temporal communities is object of current research [8, 18, 25]. A meta-algorithm to track communities resulting from static snapshots through time is a promising approach [2, 4, 13, 14, 26]. This leads to a matching problem, that can reliably be solved, with a novel method, incorporating higher order memory [23].

The simplistic approach is independent from the choice of static community detection algorithm and provides a free parameter to define the timescale of a stable thread that needs to persist in order to define a topic. By that this method can reveal trajectories of content on various timescales, that can occur in the highly dynamical world of online media. Especially long term developments can be followed well by canceling out noise and by memorizing topics even with interruptions due to daily or weekly rhythms. The results allow temporal measurements like lifetime, periodicitiy or growth and decline of contextual hashtag clouds and can be used to investigate, classify or even extrapolate these developments.

2 The Networks

In order to analyze groups of related content with methods from network science, we built co-occurrence networks from empirical datasets. In this work we will focus on hashtags from the fashion platform lookbook.nu gathered from the whole year 2015.

Fig. 1.

Scheme for the construction of co-occurence networks of hashtags: Each time, two hashtags are used within the same posting, an edge with the timestamp of that post is drawn. Aggregating the edges over a window $\Delta t$, results in an undirected and weighted snapshot network. On the right, screenshots from lookbook.nu.

Nodes are labeled with corresponding hashtags and edges are realized, whenever two hashtags occur in the same posting, similar to network constructions that have been used to analyze social tagging systems [3]. These edges are undirected and timestamped. Aggregating them over a time frame $\Delta t$, results in a snapshot of the temporal network. The edges are weighted, accounting for multiple co-occurrences within that $\Delta t$. The snapshots can also be represented as weighted adjacency matrices $A_t$, with zero or positive integer elements as previously done in [9]. In Fig. 1 this procedure is schematically illustrated. Here we choose the aggregation window to be one week $\Delta t = 7\ d$ in order to avoid structural changes due to patterns within a week. As a results we obtain 52 snapshot networks for 2015. Exemplary standard measures of these networks are the mean degree $\langle k\rangle = 6.2$, the diameter $D = 5$ and the mean path length $\langle l\rangle = 3.4$ as well as the global clustering coefficient $C = 0.62$. These values are comparable to word co-occurrence networks [7] and stay stable over time.

2.1 Community Structure

In the considered co-occurrence networks we observe neither pronounced global rules like random- or preferential attachment, nor can we see any dynamical behavior in global network measures. However there is a more interesting property to look at. Since hashtags can be used on different topics by diverse communities of people, we suspect a formation of strong sub-structures in such datasets. The modularity value is quite high for all the snapshots with $Q > 0.5$, as expected and modularity maximization gives a good possibility to get a first impression of these structures [6, 17].

Fig. 2.

Two examples for different structured communities: a one strongly interconnected group of hashtags, b a more star-like and hierarchically structured community.

Zooming into the communities reveals their different characteristics. Basically two structural types can be found: The first kind is highly intra-connected as shown in Fig. 2a while the second exhibits a star-like character as shown in Fig. 2b. This might correspond to different ways of using hashtags. High numbers of hashtags in each post with low specificity form groups of the first kind. A hierarchical arrangement of few hashtags specifying a topic from general to specific on two, three, or more levels results in structures of the second type. In all the communities we found that their members characterize reasonably well certain fashion topics, something that we use as a first validation of the obtained clusters. All network visualizations were generated using gephi [5]. The structural differences can also be reflected, when comparing the degree and clustering coefficient between the subgraphs. In Fig. 3a, b these quantities are compared and almost seem inverted to each other. Members of the strongly interconnected communities show high clustering coefficients, while the most important nodes in the hierarchically structured communities have a high degree.

Fig. 3.

Values of two different local network measures reflect the structural differences between communities: a the local clustering coefficient, b the degree of the node. The darker the color and the larger the radius of a node, the higher the value of a measure. For comparison note that the two pictures show the same network, with the exact same position for each node.

2.2 A Random Walk Approach

Modularity maximization yields reasonable clustering for these networks, but their strongly weighted character as well as our knowledge about the above described structures, lead us to the assumption that a customized random walk based approach would be the best suited. More precisely, modules we are interested in finding do not have a typical structure of densely connected subgraphs that are loosely connected to the rest of the network. Instead, they are star-like and hierarchically structured (see Fig. 3) and thus, most of the common approaches would fail to identify them without including typical modules or unspecific hashtags.

To this end we adapt the clustering method developed in [11, 24]. This method uses a time-continuous random walk process for finding multi-scale fuzzy modules. We obtain clustering into m modules $M_1,\ldots , M_m$ and a transition region $T = V\setminus (\bigcup _{i=1}^m M_i)$, which consists of nodes that are not uniquely assigned to one of the modules. For each of the nodes in a transition region, we are able to calculate the affiliation probability to each of the modules. A transition region is useful for such datasets, since it can act as a filter for very unspecific hashtags by accounting for the typical fuzzy character of communities in tag co-occurrence networks and avoiding the overlapping areas at the same time [10, 20].

We define the time-continuous random walk process with the following rate matrix

$$\begin{aligned} L(x,y) = {\left\{ \begin{array}{ll} -\frac{1}{e^{\phi (1-c(x))}}, &{} x=y \\ \frac{A(x,y)}{d(x)e^{\phi (1-c(x))}}, &{} x\ne y, A(x,y)>0 \\ 0, &{} \text {else} \end{array}\right. } \end{aligned}$$

(1)

where A is the weighted adjacency matrix, d(x) is the degree and c(x) is the clustering coefficient of a node x. Off-diagonal elements of L represent the probability of the process to jump from x to y. The transition probability is positively proportional to the edge weight A(x, y). Diagonal elements of L are connected to the waiting time of the process, i.e. being in node x, the expected waiting time until the next jump from x is $\frac{1}{\Vert L(x,x)\Vert } = e^{\phi (1-c(x))}$, where $\phi$ is a free parameter to regulate the importance of c(x). Thus, the smaller the clustering coefficient of a node is, the longer a process stays in this node on average. This makes the dense groups, which are less informative, less attractive. More important nodes with regards to content have a high degree and are thereby visited more likely by the random walk process. In the next step, using the Markov state modelling approach [24], we can determine these attractive areas, and distinguish between the transition region T and the modular region $M = \bigcup _{i=1}^m M_i$. The modular region obtained in this way consists of less nodes than the original network, and clustering such a reduced network is easier as we do not consider nodes for which it is not clear where they should be affiliated. Thus, one can use any of the full/hard clustering techniques on this set of nodes. Then, for every node, we can calculate the affiliation probability to each of the modules by solving sparse, symmetric and positive definite linear systems, see [11, 16]. Here a higher threshold can be set in order to filter out unspecific hashtags. In Fig. 4 two representative snapshot and their resulting clusters are shown. Note that the community structure varies largely from summer to winter.

Fig. 4.

Two representative snapshots, with obtained clustering: a the resulting communities on a snapshot from August, b the results for a week in December. Colors correspond to different communities $M_i$ and grey nodes lie in the transition region T.

3 Seasonal Changes

The fashion world underlies strong seasonal and trend-driven influences, which we identify by analyzing the static snapshots from different times in the year. While other measures stay very stable, the communities change over time. In Fig. 4 two representative groups are marked, the one around ‘#summer’ and the counterpart for ‘#winter’, which naturally change in size and structure over the course of one year. This and many other dynamical changes in the community structure of such networks lead us to aim for a method to quantitatively capture these developments. We propose a meta-algorithm, that solves the bipartite matching problem of the previously obtained clustering. It is important to note that this method is completely independent of the algorithm used for the community detection on the snapshots. This class of matching based dynamics clustering algorithms as in [2, 13, 14, 26] offers a big advantage, since this freedom allows to tailor the analysis pipeline to the specific dataset and question (as we did in Sect. 2.1).

3.1 Matching Problem

In order to be able to measure properties like stability, the rise and descent or the lifetime of communities we aim to track their flow through the snapshot networks. Compared to an event based approach [2] our goal is to find long term developments and re-identify forgotten trends rather than observe behavioral patterns of various events. To this end we relate content of topics from adjacent timesteps, leading to a bipartite matching problem. Our aim is to maximize the flow of hashtags within one community over time. A useful target for such a maximization is the sum of Jaccard indexes J, a measure for the similarity of two sets from adjacent timesteps:

$$\begin{aligned} J(A_{t-1},B_t) = \frac{\vert A_{t-1} \cap B_t \vert }{\vert A_{t-1} \cup B_t \vert }. \end{aligned}$$

(2)

With this pairwise value one can construct weighted bipartite networks of adjacent timesteps. The obtained communities as nodes and the transitions of hashtags as edges as schematically shown in Fig. 5a. It is important to note that Jaccard indexes below a threshold $J_t = 1/10$ are not considered in that construction.

The resulting classical problem from graph theory can be solved by the Hungarian method in polynomial time [15]. In Fig. 5 one step of that procedure is drawn schematically.

Fig. 5.

One step of the matching problem, a the starting point, with calculated Jaccard indexes, b the solution obtained by the Hungarian method, with renamed communities.

In this example, the matching is simple, namely the one that results in the maximal sum of Jaccard indexes $J(A,D)+J(B,E) + J(C,F)= J_{max} = 2/2 + 3/4 + 2/4 = 9/4$, and is found by the Hungarian method. All the groups, for which a matching was found are then renamed after their match from the previous timestep. Communities which could not be matched, like $G_t$, are not renamed. This renaming procedure gives the possibility to track the development of a community over time, and measure for example its lifetime or the changes of its size.

3.2 Memory Weights

Community detection is generally very sensitive to variations in the network topology, which leads to cases as the one of group $G_t$ in our example. A community might be split up due to small temporal topological changes, but reunited after one step only. In Fig. 6a we show an example, how such a temporal splitting can be misleading. The Jaccard index would yield that J is renamed to G, while there will not be any match for C and its development would stop at $t=2$. Nevertheless hundred percent of the members in J originated from $C_{t-2}$, which makes it in our interpretation of a dynamic community, part of C.

To overcome this weakness of a pairwise overlap measure we introduce a new way to calculate the weights of the bipartite matching network. To this end we keep the same bipartite network as constructed with a pairwise similarity value in Sect. 3.1 and only change the way of calculating the weights. Namely we sum up the Jaccard indexes over n preceding steps that are weighted by the inverse temporal distance $\frac{1}{i}$ to get our new memory weights M:

$$\begin{aligned} M(A_{t-1},B_t) = \sum _{i=1}^n \frac{1}{i} \frac{\vert A_{t-i} \cap B_t \vert }{\vert A_{t-i} \cup B_t \vert }. \end{aligned}$$

(3)

In Fig. 6b the effect of this new way for calculating the weights is shown. The historical overlap of $J_t$ with $C_{t-2}$ contributes to the weight and leads to a value of $M(C_{t-1}, J_t) = 1/1 \cdot J(C_{t-1}, J_t) + 1/2 \cdot J(C_{t-2}, J_t) = 1/1 \cdot 1/3 + 1/2 \cdot 2/4 = 0.83$. By that procedure, we can cancel out temporal fluctuations in the community assignment, that can be caused by the noisy data itself as well as instabilities in the detection algorithm.

Fig. 6.

The next step of the matching process, a the splitting of the small group G from C leads to a misleading Jaccard index, b by the summation of the Jaccard values from both preceding timesteps, the choice becomes clear and leads to the desired matching.

Similar to static community detection, there is no definite solution for the problem, but incorporating extra information from previous timesteps, naturally reduces the influence of noise, which has no temporal correlation, while it captures the development of long term trends in the data.

This way of calculating the weights incorporates the ideas of considering timesteps further in the past [26] as well as a finite lengths of influence [13], motivated by the assumption that a topic can be followed over time as long as a majority of its members stays the same for a finite timespan even if members change in the long run.

3.3 Effects of Memory

The advantage of our method on the ability to find a matching in noisy data can be quantified in a constructed test case. Namely, a static partitioning is taken and uncorrelated randomized versions are created by swapping members between the communities with a fixed probability p. The obtained randomized snapshots can be assembled one after the other to construct a noisy time series with a stable underlying community structure. One can then run the matching procedure on this artificial timeseries and quantify how often the matching algorithm found the underlying (known) groups in the noisy data by the relative score s.

Fig. 7.

The resulting scores s for increasing shuffling probability p up to 1.0, when the underlying structure is completely randomized. Four different memory lengths n are compared and the increase of reliability is clearly visible.

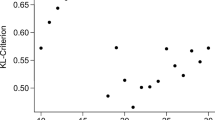
The resulting values for different shuffling probabilities p and memory lengths n are compared in Fig. 7. The case of $n=1$ corresponds to a usual Jaccard index based matching. With only a few steps of memory, the accuracy can be increased quite well, especially for relatively low shuffling probabilities. For strongly randomized matchings only high memory values can still find the underlying structure. For comparison the performance of the matching measure $match(C, C') = min(\frac{|C \cap C'|}{|C|}, \frac{|C \cap C'|}{|C'|})$ without memory, as proposed in [14] is plotted and shows low scores s for small shuffling probabilities.

The choice of the length of the memory n as well as the decay term, which is $\frac{1}{i}$ in our case is not always clear. In a realistic scenario of noisy data the corresponding p might be quite low. In Fig. 7 the area of $0.1< p < 0.4$ shows big improvement in accuracy for small memory lengths. This suggests that small orders of memory are sufficient to reduce the influence of noise. But this parameter can also be used to choose the timescale in which developments have to persist in order to stay alive, which can range from years to hours and has to be considered depending on the task.

3.4 Empirical Results

A very nice way of visualizing such complex datasets with temporal community structure was proposed in [22] under the name of ‘alluvial diagrams’. Here the communities are drawn for each snapshot with the hashtags transitions between them, shown as bands with the number of moving hashtags encoded in their thickness. In Fig. 8 one example for such a diagram is shown, where the ‘#summer’ community looses many members and the ‘#autumn’ group becomes the biggest one in the first week of September. This is just a screen-shot of our interactive online tool, which can be used to explore the full dataset (www.itp.tu-berlin.de/?lorenz).

Fig. 8.

Alluvial diagram for an exemplary part of the year, the groups in each week, their size and the number of hashtags moving between them are drawn. The number of hashtags in each group and transition is encoded in the thickness of the drawing, the groups are ordered by their size.

Fig. 9.

The lifetimes of the communities in days plotted against their mean size per shows the strong effect that even small memory lengths have, especially on small developments, which usually suffer the most from fluctuations.

As noticeable in Fig. 8 in our dataset, concerning fashion-topics, there are quite many small communities existing in parallel to the big seasonal development, exemplary labeled with ‘#gothic’ and ‘#asian’. These groups outside of the mainstream of hashtags, showed to be very stable, as shown in Fig. 9, where an interesting effect of the incorporated memory can be observed. Since small communities suffer the most from temporal fluctuations in a matching without preceding timesteps, their lifetimes are greatly increased by small orders of memory. Since small developments can be equally important, especially if they are long living, this is a desirable effect.

4 Conclusion

We presented a collection of methods to analyze the dynamical behavior of topics in online media. In this work we focused on a dataset of hashtags, which were used on the fashion platform lookbook.nu. Nevertheless the described techniques work well for various kinds of temporal content data that include discrete structures of information.

In a first step we build timestamped co-occurrence networks and aggregate them piecewise to weighted snapshot graphs. Secondly we apply a random-walk based approach for finding a transition and a modular region to obtain a reliable and meaningful clustering.

Independent from the method for community detection, we propose in a third step to construct a series of weighted bipartite networks of successive timesteps. To make the results more robust against temporal fluctuations and instabilities we extend the Jaccard index, determining the weights, to incorporate higher order memory.

The advantages of this approach can be seen in a constructed test case as well as applied on the empirical dataset.