Very High Strain Rate Range

Abstract

The classical Split Hopkinson Pressure Bar (SHPB) system is considered to be able to perform tests at strain rates ranging from 10² to 10⁴ s⁻¹ (Zhao and Gary, Mater Sci Eng A 207:46–50, [1]). However, some modifications can be carried out to extend the reachable strain rate within the specimen. The mean strain rate defined within the specimen

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

9.1 Introduction

The classical Split Hopkinson Pressure Bar (SHPB) system is considered to be able to perform tests at strain rates ranging from 10² to 10⁴ s⁻¹ [1]. However, some modifications can be carried out to extend the reachable strain rate within the specimen. The mean strain rate defined within the specimen:

$$\dot{\varepsilon}_{s}= \frac{{V_{out} - V_{in}}}{{l_{s} }},$$

(9.1)

where $V_{out}$ and $V_{in}$ stand for the velocity of output and input cross-sections of the specimen respectively, shows that the achievable strain rate varies inversely proportionally to the length of the specimen $l_{s}$, while the achievable stress is confined by the elastic limit of the bars [2], especially by the incident bar sustaining the entire impacting energy. From this viewpoint, extending the strain rate in the test can be either achieved by scaling down the size of the specimen and consequently that of the entire device, or by dispensing with the limit on the stress of the incident bar by removing it. Two modified Hopkinson devices are widely adopted to test the material at the strain rates beyond 10⁴ s⁻¹, referred to as the miniaturized Hopkinson bar and Direct-Impact (DI) devices.

9.2 Two Solutions

9.2.1 Miniaturized Hopkinson Bar Devices

Miniaturized Hopkinson devices have the same configuration than that of the classical SHPB device, but are scaled down. Thus the wave propagation in the bars and the deduction of the flow stress-strain relationship remain the same. Theoretically, the extension of the strain rate is unlimited. However, largely scaling down the equipment rises difficulties on the manufacturing of the components and on achieving a good alignment of the bars. First, the manufacturing becomes difficult with the traditional means such as turning; it can thus be replaced by Electrical Discharge Machining to get a sufficient accuracy of the geometry. Second, the specimen has to be considered as a homogeneous continuous medium, hence a characteristic length of the microstructure should remain far smaller than the length of the specimen. Lower lengths of specimen have already been experienced, Kamler et al. [3] have used a length of 0.7 mm to reach strain rates of the order of 10⁵ s⁻¹ on copper. Moreover, miniaturized Hopkinson device also rises difficulties on the strain measuring by the traditional strain gauges. The length of the gauge has to be taken into account once the dimension of the device has been decreased. However, smaller gauges need lower bridge excitations, and this decreases the sensitivity [4]. Othman [5] showed that the strain gauge length acts as a low-pass filter, and this filter effect is more important when the bar diameter is lower than 8 mm. In other words, the gauge may filter out the useful signals as the bar diameter becomes relatively small with respect to the length of the gauge. Thus smaller gauges or alternative means may be required to measure the strain in the bar. Othman’s study shows that for a specific material of the bar, the cut-off frequency introduced by the length of the gauge $l_{g}$ rises more rapidly as $l_{g}$ decreases, as shown in Fig. 9.1.

Fig. 9.1

Cut-off frequencies of gauge lengths [5]

More precisely, for a bar material with a sound speed of about 5000 m/s, the cut-off frequency of a gauge of 1 mm length reaches the large value of 2216 kHz. Jia and Ramesh [6] have used a very small strain gauge of 0.79 mm length to measure the strain in a thin bar of 3.155 mm diameter. According to Othman’s research, the signal travelling in this thin bar has a frequency not more than 1000 kHz, while the cut-off frequency of this small gauge is much higher than that of the signal. Hence the major part of the signal is not filtered. With this miniaturized device, they attained strain rates ranging from 10³ to 5 × 10⁴ s⁻¹ on an aluminium 6061-T651 specimen of 1 mm length and 1.818 mm diameter. Casem et al. [7] have also used a very small bar of 1.6 mm in diameter to test specimens made of 6061-T6 aluminium, at a very high strain rate beyond 10⁵ s⁻¹. In their research, the strain gauge measurement system is here replaced by an optical measurement techniques where the movement of the incident and transmitted bars were measured by the Transverse Displacement Interferometer (TDI) and Normal Displacement Interferometer (NDI), as shown in Fig. 9.2.

Fig. 9.2

Optical system for displacement measurement [7]

Besides the reduction of the specimen length, the Eq. (9.1) says that the strain rate can also be extended by increasing the impact velocity of the projectile. However, the increase of the impact velocity is restricted by the elastic limit of the incident bar. A direct-impact Hopkinson device can reach higher strain rate by removing the incident bar. But, the modification of the Hopkinson arrangement changes the processing of wave propagation and consequently the deduction of the stress-strain curve of the specimen as well. This point is discussed below.

9.2.2 Direct-Impact Hopkinson Bar

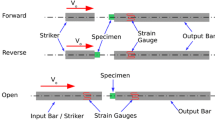
Since the incident bar has been removed in the direct-impact system, the projectile impacts the specimen directly at high velocity in order to reach a higher strain rate within the tested material. The loading pulse is generated at the impacting interface, that is the interface between the projectile and the specimen, then two waves propagate simultaneously in opposite directions in the specimen and the projectile, as shown in Fig. 9.3.

Fig. 9.3

Direct impact Hopkinson bar

On the one hand, the specimen yields under the impact loading and then the pulse is both reflected within the specimen and transmitted to the transmitted bar, owing to the mismatch of material impedance. The pulse is reflected within the specimen. On the other hand, the wave in the projectile is reflected at the free section, and then propagates back towards the impacting interface as an unloading wave. Furthermore, additional difficulties also rise in the deduction of the material behaviour. In the SHPB device, the incident bar plays the role of a load transducer and allows to check the force equilibrium of the specimen [6]. In the direct-impact system, the achievement of the force equilibrium is also usually assumed, and is used to compute the stress. However, it cannot be checked anymore. Besides, alternative techniques are requested to complete the strain and strain rate in the specimen.

Despite the difficulties induced by the absence of an incident bar, the direct-impact Hopkinson device is still of great interest for attaining higher strain rate than classical SHPB system. With such a device, Shioiri et al. [8] tested polycrystalline aluminium, iron, copper and niobium alloys at the strain rate of $2 \times 10^{4} \,{\text{s}}^{ - 1}$. Wulf [9] achieved a strain rate of about $2.5 \times 10^{4} \,{\text{s}}^{ - 1}$ on the 7039 aluminium alloy. Gorham et al. [10] extended the strain rate to $4 \times 10^{4} \,{\text{s}}^{ - 1}$ on Ti–6Al–4V and tungsten alloys. Impacting a very thin specimen of pure aluminium, Dharan and Hauser [11] have achieved strain rates up to $1.2 \times 10^{5} \,{\text{s}}^{ - 1}$. Furthermore, Kamler et al. [3] established a miniaturized direct-impact Hopkinson device where the bar diameter is just 1.5 mm. In his test, a very high strain rate of $2.5 \times 10^{5} \,{\text{s}}^{ - 1}$ was claimed on a copper specimen of 0.3 mm length and 0.7 mm diameter.

This chapter focuses on the direct impact Koslky device as used in the very high strain rate testing. A dedicated Hopkinson system allows to reach the expected levels of strain and strain rate while enforcing the basic assumptions required to deduce explicitly the stress-strain curve of the specimen. The design of such a system often relies on a set of empirical confinement equations used in order to fulfill the required assumptions. However, though it allows to restrict the range of possibilities, additional constraints built on a physical basis permit to clarify and complete these empirical bounds. Moreover, the design process should be adapted to the design of a direct impact Hopkinson system of interest here. The general design requirements set for the design are first introduced in Sect. 9.3. Next, additional criteria defined on a physical basis are introduced in Sect. 9.4 to design a direct impact Hopkinson device. Then, it is shown in Sect. 9.5 that the design process can be written as an optimization problem submitted to equality and inequality type constraints. At last in Sect. 9.6, the processing of direct-impact Hopkinson experiments is discussed.

9.3 General Design Requirements

A direct impact device consists of the projectile, the transmitted bar, the specimen and the accessory devices such as the canon, the recording device, etc. Designing a dedicated experimental device comes down to the design of the bar, the specimen, the projectile, and to determine its impact velocity. Most of the constraints used to design a conventional SHPB device are adoptable to design a direct-impact system. This leads to two topics classified as the system design and the experimental design [12]. The system design is independent of the specific experiment carried out, and involves constraints on the dimensions of the bar and the specimen by the way of three ratios: the ratio of the length of the bar to its diameter $\left( {l_{b} /\phi_{b} } \right)$, the ratio of the length of the specimen to its diameter $\left( {l_{s} /\phi_{s} } \right)$, and the ratio of the specimen diameter to that of the bar $\left( {\phi_{s} /\phi_{b} } \right)$.

These ratios will be referred in the sequel to as the first, second and third ratios of the system design respectively. The indices ($\cdot_{p}$, $\cdot_{s}$ and $\cdot_{b}$) will refer in the sequel to the projectile, the specimen and the transmitted bar respectively, as shown in Fig. 9.4. The experimental design determines the specimen dimensions $\left( {l_{s} ,\phi_{s} } \right)$, the length $\left( {l_{p} } \right)$ and the impact velocity $\left( {v_{p} } \right)$ of the projectile, to deform the specimen in such a way that a given strain rate be reached at a given level of strain.

Fig. 9.4

Geometric schema of the direct-impact Hopkinson system

9.3.1 System Design

The three ratios of the system design aim primarily to ensure the enforcement of the unidimensional wave propagation assumption, the sustainability of the system and the reduction of possible disturbances that may alter the quality of the results. This condition is of primary importance for the identification of the specimen behaviour in this test.

9.3.1.1 First Ratio $\left( {l_{b} /\phi_{b} } \right)$

The assumption of unidimensional wave propagation in the transmitted bar requires a uniform distribution of the stress throughout the entire cross-sections. Provided a given diameter $\phi_{b}$, this suggests a lower bound on the length $l_{b}$ to ensure a quasi-unidimensional wave propagation along the bar. Davies [13] proved in his work that a bar of the length $l_{b}$ being greater than $20\phi_{b}$ can satisfy this requirement. On the other hand, the diameter of the transmitted bar $\phi_{b}$ should be large enough to withstand the loading pulse without buckling or being plastically compressed. However, the errors on the stress-strain curve identification induced by dispersion and lateral effects become more important as the diameter increases. A wider range has been suggested by Ramesh [12] and is adopted in practice:

$$\frac{{l_{b} }}{{\phi_{b} }} \ge 100.$$

(9.2)

9.3.1.2 Second Ratio $\left( {l_{s} /\phi_{s} } \right)$

The design of the specimen comes down to determine its diameter $\phi_{s}$ and its length $l_{s}$. The constraint on the geometry of the specimen is usually given in the form on the length-to-diameter ratio $\left( {l_{s} /\phi_{s} } \right)$. On the one hand, a small value of this ratio leads to greater lateral inertia and friction effects. On the other hand, a too large value could lead to buckling. The restrictions on this ratio are not unique or equivalent. For instance, Ramesh [12] recommends it to be framed as follows:

$$1 \le \frac{{l_{s} }}{{\phi_{s} }} \le \frac{1}{0.6}.$$

(9.3)

Gray [14] has framed this ratio so that to minimize the lateral inertia effects and the friction effects, meanwhile to avoid the buckling of the specimen.

$$0.5 \le \frac{{l_{s} }}{{\phi_{s} }} \le 1.$$

(9.4)

The lower bound in Eq. (9.4) is determined in such a way that the lateral inertia effects be minimized. According to Gray’s work, the inertia effects are minimized for a ratio:

$$\frac{{l_{s} }}{{\phi_{s} }} = \sqrt {\frac{{3\nu_{s} }}{4}}$$

(9.5)

where $\nu_{s}$, the Poisson’s ratio, is taken equal to 1/3, yields the ratio $l_{s} /\phi_{s} = 1/2$, which is the lower bound of in Eq. (9.4). Furthermore, a ratio ranging from 1.5 to 2 permits a minimal friction at the contact interface between the bar and the specimen [2], as demonstrated in [15]. A ratio value within this range may generate buckling at high strain rate. Thus Gray suggested the value of one for the upper bound of the ratio.

Davies and Hunter [16] have used a ratio of approximately 0.5 to minimize the interface friction in their experiments. Kamler et al. [3] have impacted a copper specimen designed with a ratio $\left( {l_{s} /\phi_{s} } \right)$ slightly smaller than 0.5, around 0.43 [6]. In the limit case, a thin plate specimen is also adopted in the literature to reach higher strain rate. Dharan and Hauser [11] performed tests on aluminium workpieces with the ratio of 0.25 and achieved the strain rate of $1.2 \times 10^{5} \,{\text{s}}^{ - 1}$. Edington [17] used a thin plate of ratio 0.16 to study the dynamic behaviour of the copper. The lubrication of the interfaces and the numerical correction of lateral inertia effects are generally mandatory in the tests. For a non-cylindrical specimen, the geometry effect is studied and discussed in [18]. All these authors do not exactly agree on the allowable bounds of this ratio, but combining all these works, Guo et al. [19, 20, 25] used the in Eq. (9.4), i.e., $0.5 \le l_{s} /\phi_{s} \le 1$.

9.3.1.3 Third Ratio $\left( {\phi_{s} /\phi_{b} } \right)$

A small value of the third ratio $\left( {\phi_{s} /\phi_{b} } \right)$ enables to ensure a good contact at the specimen/bar interface even if $\phi_{s}$ dilates largely during the plastic compression of the specimen, and allows to test much more ductile materials. The decrease of this ratio is meanwhile bounded since it can lead to the punch effect. The error, between the measured strain in the specimen and the expected one, which is induced by the non-uniform distribution of the stress, increases with the decrease of this ratio.

Buchar et al. [21] indicate that the specimen diameter must be large enough compared with that of the bars and give a lower bound of this ratio of $\left( {\phi_{s} /\phi_{b} > 0.9} \right)$ [22]. Gray [14] has suggested the ratio $\left( {\phi_{s} /\phi_{b} > 0.8} \right)$ in order to minimize the mismatch of material impedance and the diameters of the bar and the specimen and consequently reduced the inertia and friction effects [2]. In order to adapt for large strain in the specimen, an empirical range can be adopted [12] as follows:

$$\frac{1}{4} \le \frac{{\phi_{s} }}{{\phi_{b} }} \le \frac{1}{2}.$$

(9.6)

9.3.2 Experimental Design

The system design has suggested a general frame for the dimension of each component of the Hopkinson device. The experimental design determines the specific dimensions of the specimen and the projectile, and the impact velocity, fulfilling the requirement to reach the expected strain rate and the allowable strain, and thus complete the dimensions of the whole device.

The achievable strain rate is related to the dimensions of the specimen, these of the projectile and its impact velocity. When the projectile impacts the specimen, a loading pulse is generated so that two waves propagate simultaneously in opposite directions within the specimen and the projectile. In the projectile, the first wave propagates to the free end and is then reflected back to the impacting interface. Likewise, the second wave propagates through the specimen and is both reflected and transmitted to the transmitted bar. When the first wave, reflected at the end side of the projectile, arrives at the projectile/specimen interface at time $\Delta t = 2l_{p} /c_{p}$, referred to as the characteristic time, the impact is considered to be terminated. In this definition, $c_{p}$ denotes the sound speed in the projectile and $l_{p}$ the projectile length. In order to achieve a high strain rate $\dot{\varepsilon}_{s}$ in the specimen, the projectile should be accelerated to a sufficient velocity $v_{p}$ to deform the specimen, though the capacity of the canon may limit it. The maximum engineering strain induced in the specimen can be estimated by:

$$\varepsilon_{s,max} = \mathop \smallint \limits_{0}^{{2l_{p} /c_{p} }} \dot{\varepsilon}_{s}\, dt$$

(9.7)

where the specimen strain rate $\dot{\varepsilon}_{s}$ can be estimated by Eq. (9.1).

The experimental design has thus to simultaneously consider the expected strain rate and the allowable strain in the specimen.

9.4 Specific Requirements of the Direct Impact Kolsky/Hopkinson Device

As mentioned above, the combination of the system design and the experimental design allows to reduce the range of possibilities for the design. Confinement criteria based on less empirical statements can be introduced to narrow down this range. These additional criteria involve quantities that either pertain to each component of the direct impact system (projectile, specimen and bar) or combine quantities related to different ones [19, 20]. They will be presented in the sequel as the criteria involving quantities relative to both the projectile and the bar, to both the specimen and the bar, and to both the projectile and the bar. Constraints on the diameter of the bar and on the projectile are also introduced.

9.4.1 Criteria Involving Quantities Relative to Both the Projectile and the Specimen

First of all, the level of strain achieved within the specimen should be bounded. A sufficient desired level of strain $\varepsilon_{s,min}^{d}$ is required to correctly characterize the dynamic behaviour of the material, whereas a maximum desired strain $\varepsilon_{s,max}^{d}$ is required to avoid to crush the specimen. Two criteria are then involved. First, these bounds on the level of strain permit to assess bounds on the length of the projectile $l_{p}$. Indeed, assuming a given average strain rate $\dot{\varepsilon}_{s,avg}$ during the characteristic time $\Delta t = 2l_{p} /c_{p}$, the maximum strain achieved in the specimen reads:

$$\varepsilon_{s,max} = \dot{\varepsilon}_{s,avg} \frac{{2l_{p} }}{{c_{p} }}$$

(9.8)

which yields the following bounds on the length of the specimen (Fig. 9.5):

Fig. 9.5

Strain assessed to derive bounds on the length of the specimen

$$\frac{{{c}_{p}}}{2}\left| \frac{\varepsilon _{s,min}^{d}}{\dot{\varepsilon} _{s,avg}} \right|\le {{l}_{p}}\le \frac{{{c}_{p}}}{2}\left| \frac{\varepsilon _{s,max}^{d}}{\dot{\varepsilon}_{s,avg}} \right|$$

(9.9)

Second, an approximate upper bound of the impact velocity of the projectile can be assessed in order to avoid to exceed the allowable level of strain. Let’s consider a system that consists of the projectile plus the specimen at two instants denoted $t_{0}$ and $t_{1}$, corresponding to their impact and depart times, as shown in Fig. 9.6.

Fig. 9.6

The unidimensional system consisting of a projectile and a specimen

Writing the conservation of energy of this system between these two instants assuming a unidimensional system, a rigid projectile, a rigid perfectly plastic behaviour of the specimen and a vanishing velocity of the projectile at the end time, yields:

$$K_{1} - K_{0} = W_{\smallint ,0 \to 1} + W_{ext,0 \to 1} ,$$

(9.10)

where $K_{1}$ and $K_{0}$ denote the kinetic energy of the projectile and specimen together at times $t_{1}$ and $t_{0}$, respectively, and $W_{\smallint ,0 \to 1}$ and $W_{ext,0 \to 1}$ are the internal and external works, respectively. Equation (9.10) leads to:

$$\frac{1}{2}\rho_{p} l_{p} A_{p} v_{p}^{2} = \sigma_{s,y} |\varepsilon_{s,max}| l_{s} A_{s} ,$$

(9.11)

where $\sigma_{s,y}$ is the yield stress of the specimen, $l_{s}$ and $A_{s}$ are the length and the cross-sectional area of the specimen, $\rho_{p}$, $A_{p}$ and $l_{p}$ the mass density, the cross-sectional area and the length of the projectile, respectively.

This leads to the following upper bound on the velocity of the projectile [20, 25]:

$$v_{p} \le \sqrt {\frac{{2\sigma_{s,y} |\varepsilon_{s,max}| l_{s} A_{s} }}{{\rho_{p} l_{p} A_{p} }}} .$$

(9.12)

Of course, a refined bound could be assessed using a more complex constitutive model to compute the strain energy of the specimen, and considering the projectile as deformable.

Afterwards, since the test is assumed to be terminated at the end of the characteristic time, the force equilibrium within the specimen should be reached before this time, so that its writing can be used in the post-processing to extract directly the stress-strain curve a posteriori. It is generally considered that a great number of round trips of the wave within the specimen should be achieved during the characteristic time:

$$\frac{{2l_{s} }}{{c_{s} }} \ll \frac{{2l_{p} }}{{c_{p} }}.$$

(9.13)

In the design, a factor n is multiplied to the left hand side of in Eq. (9.13) in order to quantify the number of these round trips needed to achieve the force equilibrium. For the value of n, Davies and Hunter [16] have proposed that the achievement of the stress equilibrium requires three reflections of the loading pulse within the specimen for ductile metal material. A greater value $n = 10$ is usually adopted to ensure the achievement of the force equilibrium.

9.4.2 Criteria Involving Quantities Relative to Both the Specimen and the Bar

During the test, the transmitted bar should remain elastic, while it has to be sufficiently strained to record a usable signal in post-processing. On the one hand, strength criteria of the bar pertain to its resistance to buckling and to plasticity. The former can be assessed in a first approximation through the critical load obtained in quasi-static:

$$F_{b} \le \frac{{\pi^{2} E_{b} I_{b} }}{{L^{2} }}$$

(9.14)

where $F_{b}$ denotes the axial force supported by a cross-section of the bar, $E_{b}$ is its Young’s modulus, $L$ is the length between two bearings (It is almost equal to $l_{b}$/2 if three bearings are used) and $I_{b}$ is the cross-section moment of inertia about the bar axis.

Since the bar should behave elastically, the stress in the bar should remain lower than the elastic yield stress of the bar material. Assuming the force equilibrium is achieved within the specimen, the axial stress in the bar should fulfill the following inequality:

$$\left| {\sigma_{b} } \right| = \left| {\sigma_{s} } \right|\frac{{A_{s} }}{{A_{b} }} \le \frac{{\left| {\sigma_{{y_{b} }} } \right|}}{\alpha }$$

(9.15)

where $\alpha$ denotes a safety factor (>1). Provided a maximum expected level of stress $\left| {\sigma_{{s_{max} }} } \right|$ within the specimen, an upper bound to the third ratio of the system design is given:

$$\left| {\frac{{\phi_{s} }}{{\phi_{b} }}} \right| \le \sqrt {\frac{{\left| {\sigma_{{y_{b} }} } \right|}}{{\alpha \left| {\sigma_{{s_{max} }} } \right|}}} .$$

(9.16)

On the other hand, a minimum signal-to-noise ratio is required in order to obtain usable signals for post-processing. This implies the normal force in the bar should most of the time be higher than a minimum value which can be roughly assessed by the force in the bar higher than the force corresponding to a stress in the specimen equal to a third of its yield stress.

$$\left| {\sigma_{{b_{min} }} } \right| \ge \frac{{A_{s} }}{{A_{b} }}\frac{{\left| {\sigma_{{y_{b} }} } \right|}}{3}.$$

(9.17)

Provided a minimum level of strain recorded by gauges on the bar $\varepsilon_{{b_{min} }}$,

$$\left| {\varepsilon_{{b_{min} }} } \right| \ge \frac{{A_{s} }}{{A_{b} }}\frac{{\left| {\sigma_{{y_{b} }} } \right|}}{{3E_{b} }}.$$

(9.18)

Thus another upper bound to the third ratio of system design can be given:

$$\left| {\frac{{\phi_{s} }}{{\phi_{b} }}} \right| \le \sqrt {\frac{{3E_{b} \left| {\varepsilon_{{b_{min} }} } \right|}}{{\left| {\sigma_{{y_{b} }} } \right|}}} .$$

(9.19)

9.4.3 Criteria Involving Quantities Relative to Both the Bar and the Projectile

The length of the bar has to be determined so that, on the one hand, a uni-dimensional propagation of the wave is ensured, which requires a minimum slenderness; the length should be at least ten times the diameter. On the other hand, no wave reflection should occur at the free end of the bar during the characteristic time. Combining both items, one gets:

$$l_{b} \ge \frac{{2l_{p} c_{b} }}{{c_{p} }} + 10\phi_{b} .$$

(9.20)

This inequality comes in addition to that of the first ratio [Inequality (9.2)] of the system design that couples the length and the diameter of the bar.

9.4.4 Diameter of the Transmitted Bar

The loading pulse propagates in the transmitted bar as a plane wave, which consists of a superposition of an infinite number of monochromatic waves with different amplitudes and frequencies:

$$u\left( {r_{b} ,z,t} \right) = \frac{1}{2\pi }\mathop \smallint \limits_{ - \infty }^{ + \infty } u\left( {r_{b} ,\omega } \right)e^{{i\left( { \pm \xi \left( \omega \right)z + \omega t} \right)}} d\omega$$

(9.21)

where $\xi \left( \omega \right)$ is the wave number, $\omega$ the angular frequency, $r_{b}$ the radius of the bar and $z$ the coordinate along axis direction. If we want to compute directly the stress in the bar from the strain which is recorded at a different position, we have to make sure that the sole first mode of the bar will be excited by the loading pulse. Thus, the profile of this loading signal has first to be assessed. Second, the spectrum of the bar is needed, and more precisely the frequency of the second mode. The well-known Pochhammer-Chree [23, 24] analytical solution enables to relate the radius of the bar to the angular frequency of a given mode. Determining an upper bound for the bar diameter thus comes down to compare the cut-off frequency of the exciting signal with respect to the frequency of the second mode of the bar.

In order to assess the profile of the loading signal that propagates within the bar, a constitutive model can be postulated to describe the behaviour of the specimen, and therefore to assess its response to the initial pulse. The cut-off frequency of this signal is then computed in the frequency space through a Fourier transform. The Johnson-Cook model has here been used in a first approximation with parameters calibrated for the Ti–6Al–4V alloy at the strain rate of 20 s⁻¹ extracted from [25] as summarized in Table 9.1. In order to convert the stress-strain curve into time space, a constant strain rate of 10⁵ s⁻¹ is chosen. According to Eq. (9.9), the total strain in the specimen can be approximately assessed by $\varepsilon = \dot{\varepsilon}_{avg} t.$ Thus a time period of 5 ms is needed to attain a strain of 0.5.

Table 9.1 Physical and mechanical properties

The unloading stage is also plotted at an arbitrary (but negative) strain rate in order to form a complete pulse. The time interval of the signal is set at 0.1 ms according to the sampling frequency of the gauges. The profile of the exciting signal is plotted in Fig. 9.7a. The exciting signal is then converted from the time space to the (angular) frequency space by the Fourier Transformation. The stress after transformation is denoted $\tilde{\sigma }$, whose profile is shown in the Fig. 9.7b. In order to determine the cut-off frequency, we define the total energy of the transformed pulse as:

$$E_{\infty } = \mathop \smallint \limits_{0}^{ + \infty } \left| {\tilde{\sigma }\left( \omega \right)} \right|^{2} d\omega$$

(9.22)

while the truncated one is:

Fig. 9.7

Exciting signal. a Exciting signal over time, b Exciting signal in frequency space

$$E_{c} = \mathop \smallint \limits_{0}^{{\omega_{c} }} \left| {\tilde{\sigma }\left( \omega \right)} \right|^{2} d\omega .$$

(9.23)

The cut-off angular frequency $\omega_{c}$ is defined as the critical frequency that allows the relative error between the total energy and the truncated one to remain within a prescribed tolerance:

$$\left| {\frac{{E_{\infty } - E_{c} }}{{E_{\infty } }}} \right| \le TOL$$

(9.24)

Consequently, the cut-off frequency $\omega_{c}$ = 1.237 × 10⁶ rad s⁻¹ is found for a tolerance of 0.1.

The Pochhammer-Chree solution is obtained by solving the set of elastodynamic equations for an infinite cylindrical bar. Non-trivial solutions are given when the Pochhammer-Chree equation [5, 23, 24] vanishes, i.e.,

$$\begin{aligned}\frac{2\alpha }{{r_{b} }}\left( {\beta^{2} + \xi^{2} } \right)J_{1} \left( {\alpha r_{b} } \right)J_{1} \left( {\beta r_{b} } \right) & - \left( {\beta^{2} - \xi^{2} } \right)^{2} J_{0} \left( {\alpha r_{b} } \right)J_{1} \left( {\beta r_{b} } \right) \\ & - 4\alpha \beta \xi^{2} J_{1} \left( {\alpha r_{b} } \right)J_{0} \left( {\beta r_{b} } \right) = 0 \end{aligned}$$

(9.25)

where $\alpha^{2} = \rho \omega^{2} /\left( {\lambda + 2\mu } \right) - \xi^{2}$ and $\beta^{2} = \rho \omega^{2} /\mu - \xi^{2}$, $J_{n} \left( . \right)$ is the Bessel function of the first kind at order n, ξ is the wave number, ω is the angular frequency, $r_{b}$ is the bar radius, and v, λ, μ, E, ρ denote the Poisson’s ratio, the Lamé’s constants, the Young’s modulus and the mass density respectively. This equation gives an implicit relation between the wave number ξ and the angular frequency ω, but also involves the radius and material properties of the bar. The first mode propagates for every frequencies. Higher modes (starting from the second one) only propagates above a critical frequency $\omega_{c}^{\left( m \right)}$. If we denote by $\xi_{m}$ the mth solution of Eq. (9.25), the displacement field reads:

$$u\left( {r_{b} ,z,\omega } \right) = \mathop \sum \limits_{m = 1}^{ + \infty } u_{m}^{ \pm } \left( {r_{b} ,\omega } \right)e^{{ \pm i\xi_{m} \left( \omega \right)z}}$$

(9.26)

where $\xi_{m} \left( \omega \right)$ is the mth solution of Eq. (9.25) and well known as the dispersion relation of the mth mode. Below these critical frequencies, the dispersion relation has no real part and is purely imaginary complex number:

$${\Re }\left( {\xi_{m} \left( \omega \right)} \right) = 0\quad if\left| \omega \right| \le \omega_{c}^{\left( m \right)} .$$

(9.27)

The limit angular frequencies $\omega_{c}^{\left( m \right)}$ of the modes are such that the wave number vanishes [5, 13]:

$$\xi \left( {\omega_{c}^{\left( m \right)} } \right) = 0.$$

(9.28)

Thus, we obtain an equation satisfied by the limit frequencies. The solution of the obtained equation allows to relate the angular frequency of the second mode to the radius of the bar. Figure 9.8 depicts an example calculated assuming a bar made of a maraging steel. The frequency of the second mode is plotted as a function of the bar radius. In the Fig. 9.8, the cut-off frequency $\omega_{c}$ is also calculated for the two strain rates 10⁴ s⁻¹ and 10⁵ s⁻¹, and is then plotted as two horizontal lines; $\omega_{c}$ increases with the targeted strain rate. With regards to the bar frequency, the second-mode frequency $\omega_{c}^{\left( 2 \right)}$ decreases as the bar radius increases. The $\omega_{c}^{\left( 2 \right)}$ curve intersects the dashed line of $\omega_{c}$ calculated with a strain rate of 10⁵ s⁻¹ at a bar radius of about $r_{b} =$ 9 mm, while it approaches the solid line of $\omega_{c}$ calculated with a strain rate of 10⁴ s⁻¹ at a bar radius of about $r_{b} = 40\,{\text{mm}}.$ Thus, 40 mm can be taken as the upper bound of the bar radius if the targeted strain rate is 10⁴ s⁻¹ or lower. However, 9 mm has to be taken as the upper bound of the bar radius if the targeted strain rate can be as high as 10⁵ s⁻¹. This ensures that the propagating frequencies of the second mode and higher are not excited. In that case, the second and higher modes can be neglected.

Fig. 9.8

Cut-off frequency of the loading pulse and angular frequency of the second mode of the bar

9.5 Design Procedure

Guo [25] summarized the constraints applied on the components of the direct impact device in the flow chart represented in Fig. 9.9. Moreover, provided some input data, the design problem of the direct-impact configuration was formulated by Guo et al. [20, 25,26,27] as an optimization problem submitted to equality and inequality constraints.

Fig. 9.9

Constraints applied on and relating the components of the direct-impact Hopkinson device

First, Guo et al. [20] assumed to be given a family of materials to be tested at a targeted strain rate $\dot{\varepsilon}_{{{s_{obj}}}}$, so that the level of strain in the specimen be framed between its given minimum $\varepsilon_{{s_{min} }}$ and maximum $\varepsilon_{{s_{max} }}$ values, and so that a minimum level of recorded bar strain $\varepsilon_{{b_{min} }}$ be reached. Second, Guo et al. [20] assumed that it is possible to choose the material of the projectile and the bar, according to the family of material to be tested, so that their Young’s modulus and mass density (and thus their sound speed), and the yield stress of the bar $\sigma_{{b_{y} }}$ are known. Finally, Guo et al. [20] assumed a coarse constitutive model of the specimen material in order to be able to assess the yield stress $\sigma_{{s_{y} }}$, the maximum level of stress reached $\sigma_{{s_{max} }}$ and the sound speed $c_{{s_{{}} }}$.

The unknown vector x associated to the optimization problem consists of the length of the projectile $l_{p}$, its impact velocity $v_{p}$, the dimensions of the specimen $\left( {l_{s} ,\phi_{s} } \right)$, and those of the bar $\left( {l_{b} ,\phi_{b} } \right)$:

$$\mathbf{x} = \left\{ {l_{p} ,v_{p} ,l_{s} ,\phi_{s} ,l_{b} ,\phi_{b} } \right\}.$$

(9.29)

A solution of x may be sought by comparing the computed value of the strain rate $\dot{\varepsilon}_{s} \left( \mathbf{x} \right)$ during the design process to the objective one $\dot{\varepsilon}_{{s_{obj}}}$. The cost function is thus defined as follows:

$$f\left( \mathbf{x} \right) = \left| \dot{\varepsilon}_{s} \left( \mathbf{x} \right) - \dot{\varepsilon}_{{s_{obj}}} \right|$$

(9.30)

where the strain rate $\dot{\varepsilon}_{s} \left( \mathbf{x} \right)$ within the specimen reads:

$$\dot{\varepsilon}_{s} = \frac{{ - v_{p} + \frac{{A_{p} + A_{b} }}{{A_{p} }}c_{b} \varepsilon_{b} }}{{l_{s} }}.$$

(9.31)

This equation allows for different diameters of the projectile and the bar and assumes that they are made of the same material. We recall that $A_{p}$ and $A_{b}$ are the cross-sectional areas of the projectile and the bar, respectively. The strain in the bar $\varepsilon_{b}$ is related to the stress in the specimen and to the second ratio of the system design through the equilibrium of the specimen/bar interface:

$$\varepsilon_{b} = \frac{{\sigma_{s} }}{{E_{b} }}\left( {\frac{{\phi_{s} }}{{\phi_{b} }}} \right)^{2} .$$

(9.32)

The optimization problem submitted to equality and inequality constraints is thus formulated as follows [20, 25]:

$$\displaystyle \min_{\mathbf{x}} f\left( \mathbf{x} \right) \, ;\mathbf{G}\left( \mathbf{x} \right) \le 0 \, ; \mathbf{h}\left( \mathbf{x} \right) = 0$$

(9.33)

where $\left( {\mathbf{h}\left( \mathbf{x} \right) = 0} \right)$ is a set of equality constraints that consists of Eqs. (9.31), (9.32) and the equality between the projectile and bar diameters. The set of inequality constraints $\left( {\mathbf{G}\left( \mathbf{x} \right) \le 0} \right)$ consists of inequalities (9.2), (9.4), (9.6), (9.9), (9.12)–(9.14), (9.16), (9.19) and (9.20). Another inequality is added to the above set of inequalities which is related to the upper bound prescribed on the bar diameter given as discussed in Sect. 9.4.4. and summarized through the following implicit relation:

$$g\left( {\phi_{b} ,\omega_{c} ,\omega_{b}^{\left( 2 \right)} } \right) \le 0$$

(9.34)

where $\phi_{b} ,\omega_{c}, \omega_{b}^{\left( 2 \right)}$ denote the bar diameter, the cut-off frequency of the loading pulse and the angular frequency of the second mode of the bar respectively. Notice also that the cost function defined by (9.30) may a priori exhibit several minima.

Guo et al. [20] used the above approach to design a direct-impact Hopkinson bar rig for testing materials at strain rates between 5000 and 30,000 s⁻¹. They were interested in characterizing Ti–6Al–4V material. To withstand the impact force required to test the titanium alloy, the high-strength maraging steel MARVAL X2NiCoMo18-8-5 is adopted to manufacture the bar and the projectile. This steel has a yield stress of 1800 MPa after sustaining an aging treatment. The diameter of the projectile is determined by that of the canon and is set at $\phi_{p} = 15.8$ mm, being given a diametral clearance of 0.2 mm. Consequently, the unknown vector $\mathbf{x} = \left\{ {l_{p} ,v_{p} ,l_{s} ,\phi_{s} ,l_{b} ,\phi_{b} } \right\}$ that consists of five parameters remains to be determined. They selected four strain rates of 5000, 10,000, 20,000 and 30,000 s⁻¹ are given as the objective strain rates. Consequently, Guo et al. [20] proposed a bar diameter, a bar length and a specimen diameter of 10, 1.2 and 5 mm, respectively. They also selected ranges for the specimen length and the impact velocity, namely, [1.5 mm, 5 mm] for the former and [15 m/s, 40 m/s] for the latter. Moreover, they selected the projectile lengths: 30, 60 and 125 mm. The shortest projectile is used for the highest strain rate.

9.6 Processing of Direct-Impact Hopkinson Bar Experiment

The common and main assumption usually performed in the post-processing of Kolsky experiments is to consider the force equilibrium achieved within the specimen. The stress is then given by:

$$\sigma_{s} \left( t \right) = \frac{{E_{b} A_{b} }}{{A_{s} }}\varepsilon_{b} \left( t \right)$$

(9.35)

where $\varepsilon_{b} \left( t \right)$, $A_{b}$ and $A_{s}$ denote the strain recorded on the bar, and the cross-sections of the projectile and the specimen respectively. The absence of the incident bar rises some difficulties on the deduction of the strain rate and thus the strain in the specimen. As a consequence, the classical equations of an SHPB do not work any more in the case of the direct-impact tests.

Alternative methods are required to bypass this difficulty. Intending to deduct the strain in the specimen, several approaches have been followed so far. A first method is to measure the strain directly during the test. A high speed camera permits to record the variation of the geometry of the specimen so that the strain can be calculated by the image processing. Gorham [10] developed an optical system for the measurement. In the optical system, he employed a refraction element. The light from the flash passes through the specimen and get refracted by the refraction element, so that the profile of the transverse edges of the specimen is shot by a high-speed camera. Thus the longitudinal strain in the specimen is deduced from the transverse deformation assuming the incompressibility of the tested material.

The calculation of the strain rate within the specimen requires the difference between the velocity of the specimen/bar $\left( {V_{out} } \right)$ and that of the projectile/specimen interface $\left( {V_{in} } \right)$ [see Eq. (9.1)], the latter being expressed as a function of the strain in the transmitted bar according to the unidimensional wave theory as:

$$V_{out} \left( t \right) = - c_{b} \varepsilon_{b} \left( t \right).$$

(9.36)

Thus the calculation of the strain and strain rate in a direct impact device comes down to approach the velocity of the projectile/specimen interface during the contact. Additional measurement/deduction techniques are proposed to obtain $\left( {V_{in} } \right)$.

Malinowski [28] used two separated light systems to measure the displacement of the projectile/specimen interface and the impact velocity of the projectile in the tests. Two laser diodes accompanied with two photodiodes are equipped close to the emitting end of the accelerating tube for the projectile with a certain distance between them. When the projectile is travelling through this distance, a time counter records the period so that the velocity of the projectile is computed by the distance over the time period. The velocity of the interface can be deduced by assuming a constant deceleration. Another setup consisting of laser diodes and a photodiode is instrumented to measure the displacement of the projectile/specimen interface at different instants, using the principle of shadow. A gap is reserved between the projectile and the deceleration tube. By scaling the light passing through the gap, the evolution in time of the displacement of the projectile/specimen interface can be deduced. Besides these experimental setups used to assess $\left( {V_{in} } \right)$, the impact velocity of the projectile $\left( {V_{p} } \right)$ can be quite easily measured, and can thus also be used to approach $\left( {V_{in} } \right)$ and hence to compute the strain rate $\left( \dot{\varepsilon}_{s} \right).$

Dharan and Hauser [11] developed a diagram method to assess the strain and the strain rate in the specimen as indicated in Fig. 9.10. In this figure, $v_{1}$, $v_{2}$ and $v_{x}$ denote the velocities on the both sides of the specimen and that of the projectile before impact, while $\varepsilon$, $\dot{\varepsilon}$, $\sigma_{x}$ and $a$ are the strain, strain rate, stress and the length of the specimen. The subscript E refers to the transmitted bar. The polygonal line starting from the original point O denotes the velocity of the projectile/specimen interface identified to ${V_{in} }$ in Eq. (9.1). It indicates that after a short constant rising time, the velocity of the projectile/specimen interface equals the impact velocity of the projectile ($v_{x}$ in Fig. 9.10), supposing that the projectile sections are rigid. The rising time is obtained from many tests by impacting the transmitted bar with the projectile directly. The segment OA represents the time period needed for the loading pulse to transmit through the specimen. Thus the curve starting from the point A denotes the stress $\sigma_{x}$ in the specimen deduced from the strain $\varepsilon_{E}$ measured in the transmitted bar. Then the velocity on the right side of the specimen is expressed as $v_{2} = \sigma_{x} /\rho_{E} c_{E}$ and plotted. Consequently, the strain in the specimen can be deduced by calculating the shaded area and then dividing by the length a. This procedure supposes a constant impact velocity since the work done to strain the specimen is negligible when compared to the kinetic energy of the comparative massive projectile.

Fig. 9.10

Determination of stress, strain and strain rate from measurements [11]

Gorham et al. [29] has used an expression proposed by Pope and Field [30], to compute the strain in the specimen from the measurements of $v_{p}$ and $\varepsilon_{b}$. Let $l_{s0}$ be the initial length of the specimen, the current length of the specimen reads at a time $t$:

$$l_{s} \left( t \right) = l_{s0} - v_{0} + x_{1} \left( t \right) + x_{2} \left( t \right),$$

(9.37)

where $v_{0}$ is the velocity of projectile, $x_{1} \left( t \right)$ and $x_{2} \left( t \right)$ are the displacement of the projectile and the transmitted bar due to elastic deformation. According to $v = c\varepsilon$, the displacement is given by the integration of the velocity with respect to time:

$$x\left( t \right) = \frac{1}{ZA}\mathop \smallint \limits_{0}^{t} f\left( \tau \right)d\tau ,$$

(9.38)

where f, $Z = \rho c$ and A are the force, the acoustic impedance and the cross-section of the bar, respectively.

Substituting Eqs. (9.38) into (9.37), the length of the specimen reads:

$$l_{s} \left( t \right) = l_{s0} - v_{0} t + \frac{{Z_{b} + Z_{p} }}{{Z_{p} Z_{b} A_{b} }}\mathop \smallint \limits_{0}^{t} f\left( \tau \right)d\tau .$$

(9.39)

The above equation assumes that the projectile and the transmitted bar have the same cross-section but different acoustic impedance. Gorham et al. [29] emphasized that, the expression (9.39) is only valid within the characteristic time, that is until the reflected wave in the projectile reaches the specimen. Moreover, Pope and Field [30] have also discussed the possible errors arisen by the propagation delay in the recorded signal and by the force rising and oscillation due to the dispersion. They clarify that, the equilibrium cannot be achieved until at least two round trips of the wave in the specimen (Fig. 9.11).

Fig. 9.11

Force (A) and calculated strain (B) curves for Ti–6Al–4V alloy [30]

Guo et al. [25] used a striker and a bar made of the same material but having different diameters. Thus Eq. (9.39) is changed to:

$$l_{s} \left( t \right) = l_{s0} - v_{0} t + \frac{1}{Z}\frac{{A_{b} + A_{p} }}{{A_{p} }}\mathop \smallint \limits_{0}^{t} E_{b} \varepsilon_{b} \left( \tau \right)d\tau ,$$

(9.40)

where $Z=Z_{b} = Z_{p} = \rho_{b} c_{b}$. Guo et al. [20, 25] used two laser diodes with photodiodes to measure the impact velocity of the projectile $v_{p}$. Thus, the strain rate in the specimen reads:

$$\dot{\varepsilon}_{s} = \frac{{ - v_{p} + \frac{{A_{p} + A_{b} }}{{A_{p} }}c_{b} \varepsilon_{b} }}{{l_{s} }}.$$

(9.41)

Guo et al. [25] proposed a second alternative for the measurement of the strain and strain rate in the specimen. The direct-impact bar is then equipped with a high-speed camera to monitor the response of the specimen. Namely, the high-speed camera allows to film the deformation of the specimen during the tests. The camera records the motion of the projectile/specimen and specimen/bar interfaces. The Fig. 9.12 presents the sequential images recorded by the high-speed camera at 1.8 × 10⁵ frames per second. A tracking technique was applied to obtain the displacement of the projectile/specimen interface $u_{in} \left( t \right)$ and that of the specimen/bar interface $u_{out} \left( t \right)$. The strain rate is estimated as

Fig. 9.12

Specimen deformation capture by the high-speed camera during the test T4 [25]

$$\dot{\varepsilon}_{s}=\frac{\dot{u}_{out}\left( t \right)-\dot{u}_{in} \left( t \right)}{{{l}_{s}}}$$

(9.42)

The Fig. 9.13 depicts a comparison between Eq. (9.41) and the strain rate deduced from high-speed images. Denoting the coordinates of the sections of the projectile and the bar as $x_{n}^{\left( p \right)}$ and $x_{n}^{\left( b \right)}$ at the instant $t = \left( {n - 1} \right)\Delta t$, then the strain rate can be assessed through the following expression:

$${\dot{\varepsilon}}_{s}= \left( {\frac{{x_{n + 1}^{\left( b \right)} - x_{n}^{\left( b \right)} }}{\Delta t} - \frac{{x_{n + 1}^{\left( p \right)} - x_{n}^{\left( p \right)} }}{\Delta t}} \right)\frac{1}{{x_{1}^{\left( b \right)} - x_{1}^{\left( p \right)} }}$$

(9.43)

where $\Delta t$ is the time interval and is a constant given by the frequency of the camera. The dots, extracted from the images, fits well the solid curve within the period 25 μs, corresponding to the characteristic time. This supports the hypothesis that Eq. (9.41) is only valid within the period of the characteristic time.

Fig. 9.13

Strain rate and strain calculated in the direct-impact tests by different manners for test T4 [25]

Integrating the strain rate over time, one gets an approximately linearly rising strain as shown in the Fig. 9.13b, that superposes well with the data extracted from the images during the characteristic time.

9.7 Conclusion

The design of direct impact Kolsky/Hopkinson bar devices for very high strain rate ranges has been presented in this chapter, as well as the processing of experimental data. It has been shown that the design of this device is constrained by a set of empirical statements supplemented by others embedding more physics, pertaining and linking quantities associated to all the components of the direct impact system. The design process can also be formulated as an optimization problem submitted to equality and inequality constraints, the solution of which can involve many projectiles of different length to span a large range of strain rate of the tested material as Guo [20, 25] did for the Ti–6Al–4V.

The removal of the input bar introduces an additional difficulty with respect to the classical SHPB device that consists in assessing the velocity of the projectile/specimen interface, in order to obtain the strain rate as well as the strain induced within the specimen. Then, two solutions have been adopted so far. Either an additional measurement technique is used (optical system for Gorham [10]) to deduce the strain within the specimen, or an additional equation based on a further assumption can be introduced (Gorham [29], Guo [20, 25]) to obtain a formulae defining the strain rate induced within the specimen during the test.