Command-Filtered Backstepping Redesign for Aerial Manipulators Under Aerodynamic and Operational Disturbances

Abstract

The complexity of autonomous Aerial Manipulators (AMs), i.e. Unmanned Aerial Vehicle (UAV) + Robot Manipulator (RM), is growing faster as per our demand of being able to perform complex tasks. This complexity makes the control system to have to take into account somehow the RM dynamics, otherwise the overall behaviour of the system could be compromised. In this work, we thoroughly analyse the overall performance of the AM with a widespread controller designed neglecting the RM dynamics. In particular, the performances under the induced forces/torques provided by a compound interaction of movements of the RM (vibrations) and aerodynamical effects. For the case of study, we consider an UAV multicopter and a generic redundant RM. A complete analysis with realistic simulations on a benchmark is reported.

1 Introduction

In the last few years, Aerial Manipulation has emerged as a special branch in Robotics with broad applications in contact inspection, maintenance, and assembling at inaccessible and/or dangerous places. Aerial Manipulators (AMs) are Unmanned Aerial Vehicle (UAVs) with mounted Robot Manipulators (RMs) Different AMs with multi-joint arms have been presented in [1,2,3]. For a detailed literature review on platforms and control systems of UAVs and RMs we refer interested readers to recent author’s work and references therein in [4,5,6,7]. In fact, interaction capabilities have been demonstrated under the framework provided by ARCAS project [8]. Moreover, the complexity of the AM is currently being increased in the AEROARMS project [9] to complete outdoor.

From a control point of view, control of AM has been almost completely devoted to the design of a controller for the UAV neglecting the RM dynamics interaction. This approach is valid for lightweight RM mounted in UAVs such that the designed controller for the UAV rejects the disturbance provided by the RM. Nevertheless, in outdoor operation and, in particular with unstructured environments, the aerodynamic effects appear to be relevant enough to even compromise the overall performance of the AM. The contribution of this paper is twofold: first, the analysis of the standard cascade and command-filtered backstepping controller designed for the UAV (see for example [10,11,12]), when the RM is present, and second, the redesign of such controller to improve the overall performance in closed loop despite of the RM dynamics. In particular, here we are devoted to thoroughly analyse the overall performance of the AM under the induced forces/torques provided by a compound interaction of movements of the RM (vibrations) and aerodynamical effects. For the case of study, we consider an UAV multicopter with rotors in cross and a dynamically equivalent model for a generic redundant RM based on its centre of gravity.

Notation: All vectors are column vectors. When clear from the context the arguments of the functions will be omitted. The $e_{(\cdot )}$ denotes the basis for the Euclidean vector space, in the direction of the unitary vector of $(\cdot )$.

Fig. 1.

AM body reference frame with reference face in red, rotor thrust criteria and generic RM characterised as its centre of gravity.

2 Framework

The full Aerial Manipulator (AM) dynamics can be described by means of the Lagrange formalism. Thus, denoting by $q=[p \ \varTheta \ \gamma ]^{\top } \in \mathbb {R}^{9}$ the AM coordinates, where p , $\varTheta$ and $\gamma$ correspond to the inertial reference frame position of the UAV, the roll, pitch, yaw attitude and the Robot Manipulator (RM) centre of gravity spherical coordinates (azimuthal angle, polar angle and radial distance), respectively, so that the whole dynamics of the AM read

$$\begin{aligned} M(q) \ddot{q} + C(q,\dot{q}) \dot{q} + \nabla V(q) = u + u_{ext} \end{aligned}$$

(1)

where $M(q) \in \mathbb {R}^{9 \times 9}$ is the symmetric and positive definite inertia matrix, $C(q,\dot{q}) \in \mathbb {R}^{9 \times 9}$ the matrix including Coriolis and centrifugal terms, $V(q) \in \mathbb {R}$ the potential function, $u_{ext} \in \mathbb {R}^{9}$ the external generalised forces vector and $u \in \mathbb {R}^{9}$ the generalised input control vector. Neglecting the RM dynamics lead to the well-known completely decoupled structure, that Newton-Euler formalism read

$$\begin{aligned} \dot{p}= & {} v , \end{aligned}$$

(2)

$$\begin{aligned} \dot{\varTheta }= & {} W \varOmega , \end{aligned}$$

(3)

$$\begin{aligned} m_{UAV} \ \dot{v}= & {} m_{UAV} \ g \ e_z - T_T R \ e_z + \mathbf {F_a} , \end{aligned}$$

(4)

$$\begin{aligned} I_{UAV} \ \dot{\varOmega }= & {} -\varOmega \times I_{UAV} \varOmega - G_a + \tau _a + \mathbf {T_a} , \end{aligned}$$

(5)

$$\begin{aligned} I_{rotor} \ \dot{\omega }= & {} \tau _{rotor} - Q_{drag} , \end{aligned}$$

(6)

where $\varOmega \in \mathbb {R}^{3}$ the angular speed in the body frame, $T_T \in \mathbb {R}$ the total thrust of the UAV, $R \in SO(3)$ the roll, pitch, yaw rotation matrix from body to inertial frame, $I_{UAV} \in \mathbb {R}^{3 \times 3}$ the inertia matrix of the UAV in the body frame, $G_a \in \mathbb {R}^{3}$ the gyroscopic torque, $\tau _a \in \mathbb {R}^{3}$ the propulsive torque produced by the differential thrust between the rotors and $\mathbf {F_a}$/$\mathbf {T_a}$ the aerodynamic drag forces/torques (see [11] and references therein). In (5) the cross product in $\mathbb {R}^{3}$ is denoted by $\times$. Finally, the rotor dynamics (6) is also considered to improve the realism of the results, where $I_{rotor} \in \mathbb {R}^{4 \times 4}$ is the inertia of the rotors, $\omega \in \mathbb {R}^{4}$ the angular speed of the rotors, $\tau _{rotor} \in \mathbb {R}^{4}$ the electric torque transmitted to the rotors and $Q_{drag}=K \omega ^2 \in \mathbb {R}^{4}$ the drag torque of the rotating blade, being $K \in \mathbb {R}^{4 \times 4}$ the drag parameters and $T_T = K_T \sum _{i=1}^{4} \omega _i$, for some constant of the propellers $K_T$.

Remark 1

In this work, we focus in the sensitivity analysis of a widespread controller for UAVs commonly used in AMs neglecting the RM dynamics. Thus, notice the there are two sources of interaction between UAV-RM that destroy the aforementioned decoupling: the own RM dynamics, in both kinematics (2)–(3), and dynamics (4)–(5) and; the aerodynamic external drag forces/torques due to the RM.

Remark 2

It is also important to highlight that the aforementioned simplistic rotating blade model has been included in the simulation model but changing the drag torques for a more accurate BEMT-based estimation of this effect.

3 Motivation

As was previously studied in [7, 13], the aerodynamic effects, and especially its vertical component, do have an important impact on the whole AM dynamics. In those works, both propulsive and flight aerodynamics effects were presented, highlighting the importance of a correct modelling in order to obtain a realistic and faithful simulation responding as expected in a real AM.

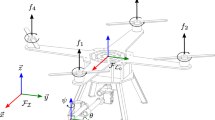
From the point of view of modelling, there are two sources of making that simplified controller perform poorly. Firstly, the commonly used propulsive model, $T_k=K_T \omega _k^2$, that oversimplifies the behaviour of rotors, being essential to trade-off between flying and hover accuracy when choosing $K_T$ in the control algorithm. If this parameter is chosen close to its hover experimental value, the permanent error is decreased but the overall flying capabilities are diminished, while if a closer to flight conditions one is taken, the flying accuracy is improved at expense of the permanent regime behaviour. Secondly, the flight aerodynamics of an UAV have a significant impact on the behaviour of AMs. Aerodynamic forces and torques are dependant not only on the flight speed and a rotating matrix, but on a set of support functions based on the aerodynamic reference frame (Fig. 1). While the advance flight components of the aerodynamic forces are mainly proportional to the flight speed, and so they would not affect the permanent regime, the vertical one produces perturbations to the AM even when it is in hovering. This is a result of the aerodynamic interferences between the propulsive system and the AM body that causes thrust losses, that is generally neglected in most studies, and whose most significant outcome is a permanent error in the vertical direction if the AM controller is not designed accordingly.

4 Cascade Nonlinear Control Strategy

In this section we briefly sketch the derivation of the aforementioned standard controller. For the position dynamics, (2) and (4), the controller is based on feedback linearisation just inverting the dynamics. For the attitude dynamics, (3) and (5), the strategy is based on command-filtered backstepping [10]. Thus, consider the dynamics of the UAV given by (2)–(6).

Position control. Let $p=(x \ y \ z)^{\top }$ be the position of the UAV and $p_{ref}=[x \ y \ z]^{\top }$ its reference, the position error is defined as $p_e=p_{ref}-p$. Thus, defining the virtual control signal as U, it is well-known that the Eq. (4) of a quadrotor-like UAV can be inverted in the following way

$$\begin{aligned} \ddot{p} = g \ e_z - \dfrac{T_T}{m_{UAV}} R \ e_z \equiv U. \end{aligned}$$

(7)

The right hand side of the latter expression that can also be rewritten, once pre and post multiplied, as

$$\begin{aligned} \dfrac{T_T}{m_{UAV}} \ e_z = R^{\top } ( g \ e_z - U ) \end{aligned}$$

(8)

which pre and post multiplying becomes

$$\begin{aligned} T_T = m_{UAV} \ ||U-g \ e_z ||_2 \end{aligned}$$

(9)

that shows the direct relation between $T_T$ and U. After some tedious but straightforward calculations from (8) the following inverted relations are also obtained

$$\begin{aligned} \tan \theta = \dfrac{U_1 \cos {\psi } + U_2 \sin {\psi }}{U_3 - g} \end{aligned}$$

(10)

$$\begin{aligned} \sin \phi = - \dfrac{U_1 \cos {\psi } - U_2 \sin {\psi }}{T_T/m} \end{aligned}$$

(11)

This step of the cascade control strategy provides the references for the attitude controller given any external yaw reference. Hence, the whole inversion of the dynamics (7) allows to prescribe any linear behaviour in closed-loop. Thus, for any positive-definite matrices $K_D$ and $K_P$ the following closed-loop is stable

$$\begin{aligned} \ddot{p}_e + K_D \ \dot{p}_e + K_P \ p_e = 0, \end{aligned}$$

corresponding to a PD-type controller. Matching the open and closed loop reads

$$\begin{aligned} \ddot{p} = \ddot{p}_{ref} - \ddot{p}_e = \ddot{p}_{ref} + K_D \ \dot{p}_e + K_P \ p_e = U, \end{aligned}$$

(12)

from where, we obtain U and with (9), (10) and (11) the actual controller inputs.

Attitude control. The attitude and angular speed errors are defined as $Z_1=\varTheta _{ref}-\varTheta$ and $Z_2=\varOmega _{ref}-\varOmega$, respectively. This controller is based on the command-filtered backstepping approach that is, in turn, a passivity-based control design technique. Thus, the following Lyapunov function can be considered

$$\begin{aligned} V_1=\frac{1}{2} Z_1^{\top } Z_1. \end{aligned}$$

Its derivative becomes

$$\begin{aligned} \dot{V}_1=Z_1^{\top } \dot{Z_1}=Z_1^{\top }(\dot{\varTheta }_{ref} - \dot{\varTheta })=Z_1^{\top }(\dot{\varTheta }_{ref} - W \varOmega ), \end{aligned}$$

where the angular speed is used as a virtual control signal. Hence, defining

$$\begin{aligned} \varOmega _d:=W^{-1} (\dot{\varTheta }_{ref} + \varGamma _1 Z_1), \end{aligned}$$

(13)

where the subscript d stands for desired, the condition of stability is met as

$$\begin{aligned} \dot{V}_1=-Z_1^{\top } \varGamma _1 Z_1<0, \end{aligned}$$

with $\varGamma _1$ a positive-definite matrix. Now the following command filter is used to make the angular speed converge to the desired one

$$\begin{aligned} \dot{\varOmega }_{ref}=-\bar{T}(\varOmega _{ref}-\varOmega _d), \end{aligned}$$

(14)

being $\bar{T}$ a positive-definite and diagonal matrix. The values of $\bar{T}$ should be large enough to assure a fast transient. However, this filter provides a mismatch in the commanded reference that has to be considered in the Lyapunov function as a tracking error. Let $\epsilon$ stands for that mismatch, and so its dynamics become

$$\begin{aligned} \dot{\epsilon }=-\varGamma _1 \epsilon - W (\varOmega _{ref}-\varOmega _d). \end{aligned}$$

Redefining the attitude error as $\bar{Z}_1:=Z_1-\epsilon$ and adding another step to the backstepping methodology the Lyapunov function reads

$$\begin{aligned} V_2=\frac{1}{2} \bar{Z}_1^{\top } \bar{Z}_1 + \frac{1}{2} Z_2^{\top } Z_2. \end{aligned}$$

Neglecting the effect on the rotating dynamics of both aerodynamic torques and the RM, its derivative becomes

$$\begin{aligned} \dot{V}_2= & {} \bar{Z}_1^{\top } \dot{\bar{Z}}_1 + Z_2^{\top } \dot{Z}_2 \\= & {} \bar{Z}_1^{\top } (\dot{\varTheta }_{ref} - W \varOmega -\dot{\epsilon }) + Z_2^{\top } (\dot{\varOmega }_{ref}-\dot{\varOmega }) \\= & {} \bar{Z}_1^{\top } (\dot{\varTheta }_{ref} - W \varOmega + \varGamma _1 \epsilon + W (\varOmega _{ref}-\varOmega _d)) \\+ & {} Z_2^{\top } (\dot{\varOmega }_{ref}+I_{UAV}^{-1}(\varOmega \times I_{UAV} \varOmega + G_a - \tau _a)) \end{aligned}$$

Using the definition of the errors the latter equation can be expressed as

$$\begin{aligned} \dot{V}_2 = -\bar{Z}_1^{\top } \varGamma _1 \bar{Z}_1 + Z_2^{\top } (W^{\top } \bar{Z}_1+\dot{\varOmega }_{ref}+I_{UAV}^{-1}(\varOmega \times I_{UAV} \varOmega + G_a - \tau _a)), \end{aligned}$$

and hence the following controller

$$\begin{aligned} \tau _a=\varOmega \times I_{UAV} \varOmega + G_a + \varGamma _2 Z_2 + I_{UAV} (W^{\top } \bar{Z}_1+\dot{\varOmega }_{ref}), \end{aligned}$$

(15)

forces the $\dot{V}_2 < 0$, as desired. $\dot{\varOmega }_{ref}$, and subsequently $\varOmega _{ref}$, is obtained from (14) and $\dot{\varTheta }_{ref}$ is estimated with a tuned linear time-derivative tracker.

Rotor control. Let $\tilde{\omega }=\omega _{ref}-\omega$ and the proposed Lyapunov function $V_3=\dfrac{1}{2} \tilde{\omega }^{\top } \tilde{\omega }$, which derivative reads

$$\begin{aligned} \dot{V}_3=\tilde{\omega }^{\top } \dot{\tilde{\omega }}=\tilde{\omega }^{\top } (\dot{\omega }_{ref}-(\tau _{rotor}-K \omega ^2)/I_{rotor}), \end{aligned}$$

and therefore, $\tau _{rotor}$ is chosen so that $\dot{V}_3=-\tilde{\omega }^{\top } K_{rotor} \tilde{\omega }<0$ as

$$\begin{aligned} \tau _{rotor}=K \omega ^2+I_{rotor}( \dot{\omega }_{ref}+K_{rotor} \tilde{\omega }), \end{aligned}$$

(16)

where $\dot{\omega }_{ref}$ is also estimated with a linear time-derivative tracker.

5 Redesign of the Control Strategy

In order to deal with the above-mentioned effects and the perturbations produced by the presence of the RM, some essential modifications are introduced. In this section the most substantial changes are presented and explained, leaving the analysis of their influence on the whole system dynamics, behaviour and operation for the next section. The stability proof of the redesigned controller mimics the one presented above for the command-filtered backstepping approach.

Feedforward position integral action. As it has been discussed in the previous section, the permanent error produced by several effects should be considered and removed. Those effects can be divided into: error in the AM mass estimation, differences between the simplistic propulsive model and the real rotor thrust and the thrust losses due to aerodynamic interferences between the rotors and the UAV rotor-arms. Thus, (12) is modified, introducing an integral action as follows

$$\begin{aligned} \ddot{p}_e + K_D \ \dot{p}_e + K_P \ p_e + K_I \int _{t_0}^{t} p_e \ d\tau = 0, \quad \ \int _{t_0}^{0} p_e \ d\tau = p_e^{I,0} \end{aligned}$$

(17)

with $p_e^{I,0}=[0 \ 0 \ z_e^{I,0}]^{\top }$ a feedforward integral action introduced to counteract the vertical forces at the beginning of the operation.

Derivative action on the attitude control. An additional derivative action is also included in the attitude control to have a better and faster estimation of the disturbances coming from the RM, like vibrations. This change is implemented by means of additional cross terms in the controllers (13) and (15), as it is shown below

$$\begin{aligned} \varOmega _d= & {} W^{-1} (\dot{\varTheta }_{ref} + \varGamma _1^P Z_1 + \varGamma _1^D \dot{Z}_1), \end{aligned}$$

(18)

$$\begin{aligned} \tau _a= & {} \varOmega \times I_{UAV} \varOmega + G_a + \varGamma _2^P Z_2 + \varGamma _2^D \dot{Z}_2 + I_{UAV} (W^{\top } \bar{Z}_1+\dot{\varOmega }_{ref}), \end{aligned}$$

(19)

where $\varGamma _1^P,\varGamma _1^D,\varGamma _2^P,\varGamma _2^D \in \mathbb {R}^{3 \times 3}$ are positive definite matrices associated to the proportional and derivative gains of the attitude and angular speed, respectively. The first recommended tuning values for both $\varGamma _1^P$ and $\varGamma _2^P$ are the ones used in the standard command-filtered backstepping controller.

Saturation and filtering. Finally, some saturation and filtering add-ons have been introduced to avoid unrealistic and/or hazardous situations and to reduce the sensitivity of the solution to noise and vibrations. The final goal is to provide the best simulation possible and to implement practical solutions in the controller to reduce unexpected responses.

On the one hand, the dynamic model has been slightly filtered so that the state signals do not show unreal behaviours, such as large accelerations or fast thrust changes. This filtering strategy has been also applied to the controller itself, being especially necessary the filtering of the position control signal, U, in (17), the differential propulsive torque, $\tau _a$, in (19) and the reference for the rotor speed, $\omega _{ref}$.

On the other hand, the introduction of saturation is completely essential in the control design to prevent references or demands not possible to meet in a real application. For example, saturations have been used to delimit the total thrust reference the control establishes for the rotors, as it is counter-productive to demand both too high or too low thrusts. Another necessary limitation has been the one of the attitude references. If not specifically avoided, these references may results in completely unsafe configurations, such as high pitch angle forward flight that would definitely end up in a catastrophic failure. Finally, the rotor angular speed references have also been saturated to prevent the same case of prejudicial thrust conditions unable to meet.

6 Simulation Results

Once the modifications of the control strategy have been presented, a simulation environment is used to compare both options and demonstrate the improvements produced by the proposed solution. In this simulation setting, the RM is considered a disturbance to the AM operation connected by the dynamic equations. However, in order to reduce the analysis complexity, the RM degrees of freedom are treated as sinusoidal signals introduced directly via acceleration instead of producing an external generalised force to control them externally. This decision provides a simplistic way of studying the influence of a generic RM, modelled as an equivalent spherical arm with the same properties at the centre of gravity, on the AM dynamics. Additionally, both aerodynamic force, torque and propulsive deviation monitoring information is presented to show the important influence these effects have on the AM dynamics and on its permanent regime errors.

6.1 RM Disturbances

The sinusoidal RM signals given (Fig. 2) are chosen to be composed by both high ($\sim$500–100 Hz), intermediate ($\sim$25–10 Hz) and low frequencies ($\sim$0.1 Hz) to simulate the real effects of a operating RM with significant noise and vibrations. The high frequency ones produce similar noise and vibrations as observed in the AM used in previous works, being the amplitude of their oscillation overestimated to analyse the problem from a conservative point of view. The same safe consideration is taken concerning mid-range oscillations, whose introduction is considered important to model small rectifications of the EE position produced by the RM controller. Finally, slow motions introduced model the overall reconfiguration of the RM in the different phases of the design mission, being the amplitude chosen less conservative in terms of order of magnitude than the previous ones.

Fig. 2.

RM disturbances, where $\gamma _1$ is the azimuth, $\gamma _2$ the polar angle and $\gamma _3$ the module of the distance between $O_B$ and the centre of gravity of the RM.

It is important to remark again that the RM signals presented are considered undesirable in a real AM operation but they are a safe simulation condition to validate the robustness of the proposed solution in substantially bad-conditioned operational environments.

6.2 Aerodynamic Influence on the AM

Before analysing the operation-focused results, the aerodynamic effects are studied in the simulation environment. Firstly, both aerodynamic forces and torques in simulation are represented to clarify the orders of magnitude of these external perturbances and their mean value (3). Both torques and horizontal forces are certainly zero-mean perturbations, as expected, being minimal when the AM is in hover (see [13] for further details). Thus, their action will definitely not have any repercussion in the permanent regime. Meanwhile, vertical aerodynamic forces tend to introduce a non-zero-mean perturbation to the system of about $3 \ N$, which causes a permanent error if not counteracted (Fig. 3).

Fig. 3.

Aerodynamic forces and torques estimation using the aerodynamic model in [13] expressed in the AM body frame (see Fig. 1).

Additionally, the thrust estimation accuracy is also studied, being its results shown in Fig. 4. As can be seen, there is an approximately constant offset between the three thrust values: the one with the advanced propulsive model (hereby called real), the $T=K_{\omega } \omega$ model and the control reference the strategy demands to the system. While on the unmodified case this offset produces permanent vertical error, a slight reduction of this deviation in the proposed modification considerably reduces the permanent error.

Fig. 4.

Comparison between the total thrust in the unmodified case and the modified one according to the BEMT model (hereby considered real as it is a much more accurate estimation) and the common proportional to quadratic rotation speed of the rotors one, being the controller references also shown as dashed lines.

6.3 Improvements of the Modified Control Strategy

Finally, the main advances obtained with the modified solution are presented. In Fig. 5 the position of the UAV is shown, being specially interesting to remark the above-mentioned reduction of the permanent error in the vertical position. On the contrary, the horizontal position of the AM seems to suffer little changes and can be considered unaffected by the improvements in the solution if only analysed by this figure. However, according to the attitude error results in Fig. 6, the modification of the controller implies a substantial decrease of noise and vibrations in attitude that produces a smoother translational motion.

Fig. 5.

AM position comparison between the modified strategy (solid) and the original cascade one (dotted), where dashed lines show the references sent as input to both position controllers.

Moreover, this decrease of attitude noise and vibrations under the significant RM perturbations introduced is considered acceptable to validate the advances to obtain a more robust solution, taking into account that not only these RM perturbations have been considered, but the aerodynamic effects have been included as well. This advance is proved to be produced by the inclusion of the term $\varGamma _2^D \dot{Z}_2$, which actually works as a filter of the RM disturbances, avoiding the over-actuation of the attitude control induced by the RM perturbations.

Fig. 6.

Attitude and motor RPM errors comparison between the modified backstepping and the unmodified one.

7 Conclusions

In this work, a modification to cope with perturbations derived from a robot manipulator and aerodynamic and propulsive effects of a cascade control strategy has been proposed and studied. This modification, consisting of the introduction of feedforward position integral action, additional derivative action in the attitude and angular speed control and some other minor changes, such as filters and saturations, has been proved to be substantially beneficial in a simulated operation mission. Although having introduced significant oscillations in the RM not considered in the model used to design the control strategy, the modified controller has shown a substantially better performance than the initial cascade controlller, based on a backstepping strategy. Moreover, the inclusion of these changes has also been demonstrated to be essential to avoid the permanent position error produced by the simplifications of a complex system needed to obtain a explicit control algorithm. Summarising, the modification significantly increases the robustness of the control solution and provides a useful controller to use in a real aerial manipulator.