Optimal Design of Disks Under Large Creep Deformation

Abstract

Optimal distribution of thickness in the class of polynomial functions for rotating axisymmetric disks with respect to the mixed creep rupture time are found. Two effects lead to damage: reduction of transversal dimensions and growth of micro-cracks are simultaneously taken into account. The former requires the finite strain analysis, the latter is described by the Kachanov’s evolution equation. Behaviour of the material is described by nonlinear Norton’s law, generalized for Cauchy true stress and logarithmic strain, and the shape change law in the form of similarity of Cauchy true stress and logarithmic strain deviators. For optimal shapes, changes of geometry of the disk and continuity function are presented. The theoretical considerations based on the perception of the structural components as some highlighted objects with defined properties are presented.

1 Introduction

For over 300 years, the optimal design problems of structural elements have been an object of interest for scientist from all over the world. It is an interdisciplinary domain combining not only mechanics and physics, but also theory of optimal design and IT. Each science domain mentioned earlier has a direct influence on the results of optimal design. Technical progress achieved in advanced technology increases growth of demands for effective tools in the range of strength of materials. Scientific research stimulates a development in this domain offering new technological opportunities making their application beneficial for industry.

The problem of structural optimization under creep conditions is a relatively young subject and offers a wide scope of investigations. Operational loadings of structural elements are usually long-lasting, quite often acting at elevated temperatures promoting large permanent deformation. Creep deformation is defined as a process carried out at long-lasting loadings at elevated temperature, during which the values of stress and strain caused by structural loadings undergo change in time. This problem is of special significance in many branches of industry, beginning from energetics (steam boilers, turbine blades), thermal power plants (pipelines) in chemical industry, defense industry (military equipment) to space research. A general approach to the creep problem, especially in multi-axial stress state was presented by Martin and Leckie [29], Hayhurst [19] and Betten [1]. Contemporary creep research is carried out for already used materials as well as for new ones such as: composites [15, 22], graded materials [25, 26, 44], intermetallic [2, 24] and many others. Among many new possible criteria of optimization, such as stiffness after given time, stress relaxation, one of the most important seems to be time to creep rupture. A broad presentation of various objective functions with division on time-dependent and time-independent was given by Życzkowski [45, 46]. Most papers on optimal structural design are based on the brittle creep rupture theory proposed by Kachanov (small deformation theory). It was due to its relative simplicity - theory based on principle rigidification. Optimal solutions with respect to brittle creep rupture often coincide with uniform strength structures. In such a way the optimal solutions have been found by: Rysz [34] for cylinders; by Ganczarski and Skrzypek [11] for prestressed disks; Gunneskov [17] for rotating disks. In the work published by Hoff [20], the moment of failure of a bar under tension is defined as the one at which the cross-sectional area becomes zero as a result of quasiviscous flow. It was shown that the calculated results are in a good agreement with the experimental data [5, 13, 14, 27, 28, 30]. Applications of the ductile rupture theory, proposed by Hoff in optimization problems are rather scarce, because they require the finite deformation theory. First time it was used by Szuwalski [36] for optimization of bars under nonuniform tension. Some problems of prismatic tension rods were discussed by Pedersen [32, 33] and Shimanovskii and Shalinskii [35]. Their approach introduces not only physical nonlinearities, connected with creep law, but also geometrical ones, resulting from the finite deformation theory. Additional time factor and presence of body forces depending on the spatial coordinate complicate analysis of the problem. The optimal full disks with respect to ductile creep rupture time were found by Szuwalski [36, 37]. The first attempts to find a solution for annular disks were made by Szuwalski and Ustrzycka [39,40,41]. Earlier, some problems of optimal design for annular rotating disks were discussed by Farshi and Bidabadi [9]. Analytical solutions for the elastic-plastic stress distribution in rotating annular disks were obtained by Çğallioğlu et al. [3], Gun [16] and Golub [12]. The ductile creep rupture analysis for the elastoplastic disks was carried by Dems and Mróz [4], Ahmet and Erslan [6], Jahed et al. [21] and Golub et al. [14]. Modifications of the Hoff’s model was proposed by Golub and Teteruk [13]. The influence of boundary conditions on optimal shape was investigated by Pedersen [33] and later by Szuwalski and Ustrzycka [38]. The elastic–plastic analysis of rotating disks was presented by Vivio and Vullo [42, 43], Eraslan [6,7,8], Gamer [10], Guven [18] and Orcan and Eraslan [31]. Hoff’s definition of rupture - reduction of transversal dimensions of structures to zero (infinite large strains) has certain limitations. It predicts, contrary to observations, that creep does not result in damage of structure. Also, his scheme does not explain fractures at small strains (brittle rupture) and the change of character of rupture (from ductile to brittle). Application of mixed rupture theory proposed by Kachanov [23] takes into account both: geometrical changes - diminishing of transversal dimensions resulting from large deformation and growth of microcracks. Theory of shape optimization was proposed currently by Szuwalski and Ustrzycka for bars under nonuniform tension (2012) and rotating full disk (2013). Problems of structural optimization under creep conditions show specific features. The constitutive equations are often strongly nonlinear. Additional time factor causes that all differential equations describing process are the partial ones. Such problems require the finite strain approach, i.e. resignation of the rigidification theorem and analysis of already deformed body using Cauchy true stress and logarithmic strain. The analytical equations describing the shapes of axisymmetric rotating discs, optimal with respect to mixed time rupture, are derived. The numerical procedure for solving these equations is proposed and same final results are presented in the form of diagrams. The problems of optimal shape are difficult, but important in view of metal structures working at elevated temperatures.

2 Optimal Design of Full Disks with Respect to Mixed Creep Rupture Time

2.1 Mathematical Model of Disk with Respect to the Mixed Creep Rupture Time

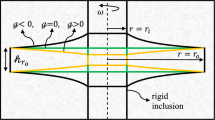
The problem of optimal shape of rotating full disk is investigated with respect to mixed creep rupture time under complex stress state. Microcracking and diminishing of transversal dimensions from the beginning of creep process is assumed. Such an approach introduces not only physical nonlinearities, connected with creep law (usually Norton’s law), but also geometrical ones, resulting from the finite deformation theory. Additional time factor leads to an increase of model complexity. The whole creep process must be analyzed from its beginning up to rupture. The concept of the mathematical description of mixed creep rupture requires examination of the entire process, taking into account geometrical changes. The problem is solved in material coordinates (Lagrangian description) and all parameters in the initial state, for time equal to zero, are denoted by capital letters, while current values of these parameters by the same small letters. Due to axial symmetry, all quantities will be functions of two independent variables: radius R and time t. The disk rotates with constant angular velocity $\omega$ and the body forces connected with own mass of the disk are taken into account, Fig. 1.

Fig. 1

Element of the deformed disk

Fig. 2

Deformed element of the disk

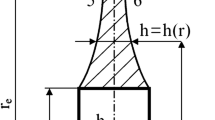
Arbitrarily chosen small element of the disk, limited previously by two cylindrical surfaces of radii R and $R+ \mathrm {d}R$, and two planes forming the angle after deformation are shown in Fig. 2. The internal equilibrium condition for plane stress state takes the form

$$\begin{aligned} {\frac{1}{hr^\prime }}{\frac{\partial }{\partial {R}}}({h\sigma _r})+{\frac{{\sigma _r}-{\sigma _\vartheta }}{r}}+{\frac{\gamma }{g}}{\omega ^2}r=0 \end{aligned}$$

(1)

where: $\sigma _r$ - current value of radial stress and $\sigma _\vartheta$ current value of circumferential stress, h - current thickness, $\gamma$ - specific weight of material and g - acceleration of gravity, $r^{'}$ - derivative of spatial coordinate r with respect to material one R. Assumption of incompressibility leads to

$$\begin{aligned} HRdR=hrdr \end{aligned}$$

(2)

where R stands for the material coordinate of the discussed point, while r for the spatial one, H for initial, and h for current thickness of the disk. Finite strain components require logarithmic measure of deformation

$$\begin{aligned} {\epsilon _r}=\ln \frac{\partial {r}}{\partial {R}}=\ln {r^{\prime }},~ \,{\epsilon _\vartheta }=\ln \dfrac{r}{R}, ~ \, {\epsilon _z}=\ln \dfrac{h}{H} \end{aligned}$$

(3)

where a prime denotes the derivative with respect to the material coordinate, and their rates denoted by overdots

$$\begin{aligned} {\dot{\epsilon }_r}=\dfrac{\dot{r}^\prime }{r^\prime }, ~ ~ \,{\dot{\epsilon }_\vartheta }=\dfrac{\dot{r}}{r},~ ~\, {\dot{\epsilon }_z}=\dfrac{\dot{h}}{h} \end{aligned}$$

(4)

Here, physical relation in the form of deviators similarity of true Cauchy stress $D_\sigma$ and logarithmic strain rate $D_{\dot{\epsilon }}$ is adopted

$$\begin{aligned} D_{\dot{\epsilon }}={\frac{3}{2}}{\frac{\dot{\epsilon _\mathrm {e}}}{\sigma _\mathrm {e}}}D_\sigma \end{aligned}$$

(5)

where $\sigma _\mathrm {e}$ denotes the effective stress, according to the Huber–Mises–Hencky hypothesis generalized to the true Cauchy stress

$$\begin{aligned} {\sigma _\mathrm {e}}=\left\{ {\frac{1}{2}\left[ {({\sigma _1}-{\sigma _2})^2}+{({\sigma _2}-{\sigma _3})^2}+{({\sigma _3}-{\sigma _1})^2}\right] }\right\} ^{\frac{1}{2}} \end{aligned}$$

(6)

and, respectively, $\dot{\epsilon _e}$ is the effective strain rate

$$\begin{aligned} {\dot{\epsilon _\mathrm {e}}}={\frac{\sqrt{2}}{3}}\left\{ \left[ ({\dot{\epsilon _1}}-{\dot{\epsilon _2})^2}+({\dot{\epsilon _2}}-{\dot{\epsilon _3})}^2+({\dot{\epsilon _3}}-{\dot{\epsilon _1}})^2\right] \right\} ^{\frac{1}{2}} \end{aligned}$$

(7)

The material of the disk fulfills Norton’s creep law:

$$\begin{aligned} {\dot{\epsilon _\mathrm {e}}}=k\sigma _{\mathrm {e}}^{n} \end{aligned}$$

(8)

Finally, taking Eq. (8) leads to the following expressions

$$\begin{aligned} {\dot{\epsilon _1}}=\frac{3}{2}k\sigma _{\mathrm {e}}^{n-1}(\sigma _1-\sigma _\mathrm {m}) \nonumber \\ {\dot{\epsilon _2}}=\frac{3}{2}k\sigma _{\mathrm {e}}^{n-1}(\sigma _2-\sigma _\mathrm {m}) \nonumber \\ {\dot{\epsilon _3}}=\frac{3}{2}k\sigma _{\mathrm {e}}^{n-1}(\sigma _3-\sigma _\mathrm {m}) \end{aligned}$$

(9)

where

$$\begin{aligned} \sigma _\mathrm {m}=\dfrac{1}{3}(\sigma _1+\sigma _2+\sigma _3) \end{aligned}$$

(10)

stands for the mean true Cauchy stress. The following compatibility equation results from definitions of logarithmic strain, cf. Eq. (3)

$$\begin{aligned} {\epsilon _r}={\epsilon _\vartheta }+\ln \left( 1+R\frac{\partial \epsilon _\vartheta }{{\partial }R}\right) \end{aligned}$$

(11)

which, after derivation with respect to time, takes the form

$$\begin{aligned} {\dot{\epsilon _r}}-{\dot{\epsilon _\vartheta }}=\frac{R\frac{\partial \dot{\epsilon _\vartheta }}{\partial {R}}}{1+R\frac{\partial \epsilon _\vartheta }{\partial {R}}} \end{aligned}$$

(12)

Substitution of the first two Eqs. (9) and (3) makes it possible to rewrite this equation in the form of the relation between stress components. Compatibility condition after some rearrangements takes the form

$$\begin{aligned} \sigma _{r}^{'}\left[ \left( n-1\right) \left( 2\sigma _{r}-\sigma _{\vartheta }\right) \left( 2\sigma _{\vartheta }-\sigma _{r}\right) -2\sigma _{\mathrm {e}}^{2}\right] +\nonumber \\ +\,\sigma _{\vartheta }^{'}\left[ \left( n-1\right) \left( 2\sigma _{\vartheta }-\sigma _{r}\right) ^{2}+4\sigma ^{4}_{\mathrm {e}}\right] = 6\sigma ^{2}_{\mathrm {e}}\frac{r^{'}}{r}\left( \sigma _{r}-\sigma _{\vartheta }\right) \end{aligned}$$

(13)

The shape change law assumed in the form of similarity of the true Cauchy stress and logarithmic strain velocity deviators leads to

$$\begin{aligned} \frac{\dot{r}}{r}=\frac{1}{2}k\sigma _{\mathrm {e}}^{n-1}\left( 2\sigma _{\vartheta }-\sigma _{r}\right) \end{aligned}$$

(14)

To find the mixed rupture time, the evolution equation proposed by Kachanov will be applied

$$\begin{aligned} \frac{\partial \Psi }{\partial {t}}=-D\left[ \frac{\sigma _\mathrm {e}}{\Psi }\right] ^m \end{aligned}$$

(15)

in which D and m are material constants. Continuity function $\Psi$ is defined by the ratio of effective cross-sectional area $a_{\mathrm {e}}$ to the total area a

$$\begin{aligned} \Psi =\frac{a_{\mathrm {e}}}{a} \end{aligned}$$

(16)

Contrary to the brittle rupture theory, $\sigma _\mathrm {e}$ denotes here the effective true Cauchy stress - related to the current cross-section a (geometrical changes are taken into account). Damage is characterized by the continuity function $0\leqslant \Psi \leqslant 1$. At the initial state (no damage): $\Psi =1$, as time goes on, it decreases. Rupture occurs when the continuity function reaches a critical value $\Psi =0$. The internal equilibrium condition Eq. (1) incompressibility condition Eq. (2), compatibility condition, in the form of the relation between stresses Eq. (13), the shape change law Eq. (14) and evolution equation Eq. (15) form the set of five equations with five unknowns: true Cauchy stress $\sigma _r$ and $\sigma {_\vartheta }$, spatial coordinate r, current thickness of the disk h, and continuity function $\Psi$.

$$\begin{aligned} {\dfrac{1}{hr^{'}}}{\dfrac{\partial }{\partial {R}}}\left( h\sigma _r\right) +{\dfrac{\sigma _{r}-\sigma {_\vartheta }}{r}}+{\dfrac{\gamma }{g}}\omega ^{2}r=0 \end{aligned}$$

$$\begin{aligned} \sigma _{\vartheta }^{'}= \dfrac{6\sigma _{\mathrm {e}}^{2} \left( {\sigma _r}-\sigma _{\vartheta }\right) \dfrac{r^{'}}{r} -{\sigma _r^{'}} \left[ \left( n-1\right) \left( 2{\sigma _r}+{\sigma _\vartheta } \right) \left( 2{\sigma _\vartheta }+{\sigma _r} \right) -2{\sigma _{\mathrm {e}}^{2}} \right] }{\left[ \left( n-1\right) \left( 2{\sigma _r}+{\sigma _\vartheta } \right) ^{2}+4{\sigma _{\mathrm {e}}^{2}} \right] } \end{aligned}$$

(17)

$$\begin{aligned} \dfrac{\dot{r}}{r}=\dfrac{1}{2}k\sigma _{\mathrm {e}}^{n-1}\left( 2\sigma _{\vartheta }-\sigma _{r}\right) \end{aligned}$$

$$\begin{aligned} HR\mathrm {d}R=hrdr \end{aligned}$$

$$\begin{aligned} {\dfrac{\partial \Psi }{\partial {t}}} =-D\left[ \dfrac{\sigma _\mathrm {e}}{\Psi }\right] ^m \end{aligned}$$

Initially, the disk remains undeformed, therefore, the initial conditions take the form

$$\begin{aligned} r\left( R,0\right) =R,\,h\left( R,0\right) =H\left( R\right) \end{aligned}$$

(18)

The boundary conditions on the disk axis are as follows

$$\begin{aligned} r\left( 0,t\right) =0, \,\dot{r}\left( 0,t\right) =0 \end{aligned}$$

(19)

$$\begin{aligned} \sigma _{r}\left( 0,t\right) =\sigma _\vartheta \left( 0,t\right) \end{aligned}$$

(20)

Further, it is assumed that the traction at the external edge of the disk results from the constant mass $M=\mathrm {const.}$ uniformly distributed throughout the whole creep process. The total radial force at the external radius is equal to

$$\begin{aligned} N_r\left( R_0\right) =M{\omega ^2}r\left( R_0,t\right) \end{aligned}$$

(21)

and the radial stress is equal to the tensile pressure

$$\begin{aligned} \sigma _{r}\left( R_0\right) =p={\dfrac{N_r\left( R_0\right) }{2\pi {r}\left( R_0\right) h\left( R_0\right) }=\dfrac{M\omega ^2}{2\pi {h}\left( R_0\right) } } \end{aligned}$$

(22)

The set of five equations Eq. (17) allows to specify the mixed creep rupture time. It is the time after which the rupture criterion adopted in the following form is fulfilled at least in one place

$$\begin{aligned} {\exists {R}}:(R\in \left\langle 0,R_0\right\rangle \wedge {\Psi }{\in }\left\langle 1,0\right\rangle {\wedge }{\Psi }{\vert _{t_{*}^{m}}}{\rightarrow }0) \end{aligned}$$

(23)

Theoretically, according to the Kachanov’s proposal, time after which the continuity function diminishes to zero is the time of mixed rupture $t_{*}^{\left( m\right) }$.

A parametric optimization, where the initial shape is defined by polynomial function, was applied. Let us consider an optimality criterion in the form

$$\begin{aligned} \left( \exists {!}H\left( R\right) \in {f}\right) t_{*}\vert _{V=const.}\longrightarrow {max} \end{aligned}$$

(24)

where functions $f:\mathbf R \longrightarrow \mathbf{R }$, $R\longrightarrow {b_{0}}+{b_{1}}R+{b_{2}}{R^2} +\cdots +{b_i}R^i$, for all arguments $R\in \left\langle A,B\right\rangle$, $i\in \mathbf{N }{\setminus }\left\{ 0\right\}$ (i is a non-negative integer) and ${b_{i}}\in \mathbf{R }$ are constant for a given and fixed volume of the structure. The latter can be treated as a limitation. The initial profile of a full disk is sought in the class of polynomial functions.

2.2 Numerical Solutions

For the sake of numerical calculations, dimensionless quantities are introduced. Both material and spatial coordinates are related to the initial external radius $R_0$

$$\begin{aligned} \hat{R}=\dfrac{R}{R_0}, \;\; \hat{r}=\dfrac{r}{R_0} \end{aligned}$$

(25)

The thickness of the disk is related to the mean thickness $h_m$ of the full disk of volume V and radius $R_0$

$$\begin{aligned} h_m=\dfrac{V}{{\pi }R_{0}^{2}} \end{aligned}$$

(26)

Dimensionless thicknesses of the initial and current disk related to the mean thickness Eq. (26), are respectively

$$\begin{aligned} \hat{H}=\dfrac{\pi {R_{0}^{2}}}{V}H, \;\; \hat{h}=\dfrac{\pi {R_{0}^{2}}}{V}h \end{aligned}$$

(27)

Dimensionless stress is referred to stress calculated using a rigidification theorem in the motionless full plane disk subject to tension with uniform pressure p Eq. (22)

$$\begin{aligned} s=\dfrac{M\omega ^2}{2{\pi }h_m}=\dfrac{M{\omega ^2}R_{0}^{2}}{2V} \end{aligned}$$

(28)

Radial loading at radius $R_0$ of the rotating disk results from mass M uniformly distributed on the external edge

$$\begin{aligned} {\sigma _{r}}\left( r\right) =p=\dfrac{M\omega ^2}{2{\pi }h\left( R_{0}\right) } \end{aligned}$$

(29)

Finally, the dimensionless stress is equal to

$$\begin{aligned} {\hat{\sigma _{i}}} =\dfrac{2V}{M{\omega ^2} R_{0}^{2} },\forall i=\left\{ r,\vartheta \right\} . \end{aligned}$$

(30)

Consequently, the dimensionless time is defined

$$\begin{aligned} {\hat{t}} =\dfrac{t}{t_{0}^{(d)}} \end{aligned}$$

(31)

where: ${t_{0}^{(d)}}$ stands for the time of ductile rupture for full plane disk. To evaluate the time of ductile rupture for full plane disk, the equation resulting from Eq. (9) may be used

$$\begin{aligned} {\dot{\epsilon _{z}}} =\dfrac{\dot{h}}{h}=\dfrac{3}{2}k\sigma _\mathrm {e}^{n-1}\left( \sigma _z-\sigma _m\right) \end{aligned}$$

(32)

where the effective stress reads

$$\begin{aligned} \sigma _\mathrm {e}=\sigma _r=\sigma _\vartheta =p \end{aligned}$$

(33)

and the mean stress can be written as

$$\begin{aligned} \sigma _m=\dfrac{2}{3}p \end{aligned}$$

(34)

Applying the above equations to Eq. (22) leads to the relationship

$$\begin{aligned} \dfrac{1}{h}\dfrac{dh}{dt}=-k\left( \dfrac{M\omega ^2}{2{\pi }h}\right) ^n \end{aligned}$$

(35)

which describes a change of thickness in time. The initial condition takes form

$$\begin{aligned} h\left( t=0\right) =h_\mathrm {m} \end{aligned}$$

(36)

The condition of ductile rupture $h{\rightarrow }0$ enables calculation of the time of ductile rupture $t_0^{(d)}$

$$\begin{aligned} t_0^{(d)}=\dfrac{1}{nk\left( \dfrac{M\omega ^2}{2{\pi }h_m}\right) ^n}=\dfrac{1}{nks^n} \end{aligned}$$

(37)

Finally, the dimensionless time Eq. (31) is defined

$$\begin{aligned} \hat{t}=nk{s^n}t \end{aligned}$$

(38)

To avoid a large number of material constants in numerical calculations, the new parameter $\Theta$ is introduced. This parameter is equal to the ratio of the brittle rupture time to the ductile rupture time for the prismatic bar subject to uniform tension under the initial stress s Eq. (28)

$$\begin{aligned} \Theta =\dfrac{t_{\mathrm {pr}}^{(K)}}{t_{\mathrm {pr}}^{(H)}}=\dfrac{nks^n}{(m+1)Ds^m} \end{aligned}$$

(39)

The parameter $\Theta$ contains four material constants: n and k in Norton’s law Eq. (8), m and D in evolution equation Eq. (15). In some way, it describes sensitivity of material to the damage type: brittle or ductile. The mathematical model of mixed creep rupture is finally described by the system of five partial differential equations in the dimensionless form

$$\begin{aligned} \hat{\sigma }_{r}^{'}=\dfrac{\hat{r}^{'}}{\hat{r}}\left( \hat{\sigma }_{r}-\hat{\sigma }_{\vartheta } \right) -2\hat{r}\hat{r}^{'}\mu -\dfrac{\hat{h}^{'}}{\hat{h}}\hat{\sigma }_r \end{aligned}$$

$$\begin{aligned} \hat{\sigma }_{\vartheta }^{'}=\dfrac{6\hat{\sigma }_{e}^{2}\left( \hat{\sigma }_{r}-\hat{\sigma }_{\vartheta } \right) \dfrac{\hat{r}^{'}}{{\hat{r}}}-\hat{\sigma }_{r}^{'}\left[ \left( n-1\right) \left( 5\hat{\sigma }_{r}\hat{\sigma }_{\vartheta }-2\hat{\sigma }_{r}^{2}-2\hat{\sigma }_{\vartheta }^{2}\right) -2\hat{\sigma }_{e}^{2} \right] }{\left( n-1\right) \left( 2\hat{\sigma }_{\vartheta }-\hat{\sigma }_{r} \right) ^2+4\hat{\sigma }_{e}^{'}} \end{aligned}$$

$$\begin{aligned} \dfrac{d\hat{r}}{d\hat{t}}=\dfrac{\hat{r}}{2n}\left( \hat{\sigma }_{r}^{2}+\hat{\sigma }_{\vartheta }^{2}-\hat{\sigma }_{r}\hat{\sigma }_{\vartheta }\right) ^{\frac{n-1}{2}}\left( 2\hat{\sigma }_{\vartheta }-\hat{\sigma }_{r}\right) \end{aligned}$$

(40)

$$\begin{aligned} \hat{h}=\dfrac{\hat{H}\hat{R}}{\hat{r}^{'}\hat{r}} \end{aligned}$$

$$\begin{aligned} \dfrac{\partial \Psi }{{\partial }{\hat{t}}}=\dfrac{-1}{\left( m+1\right) \Theta }\left[ \dfrac{\hat{\sigma }_\mathrm {e}}{\Psi }\right] ^m \end{aligned}$$

where $\mu$ is the ratio of disk’s own mass to the mass distributed at the external radius

$$\begin{aligned} \mu =\dfrac{{\gamma }V}{gM} \end{aligned}$$

(41)

The above equations set Eq. (40) contains five unknowns: true Cauchy stress components $\sigma _r$ and $\sigma _{\vartheta }$, current thickness h, spatial radial coordinate r and continuity function $\Psi$. The initial conditions Eq. (18) can be expressed in the following dimensionless form

$$\begin{aligned} \hat{r}\left( \hat{R},0\right) =\hat{R},\,\,\hat{h}\left( \hat{R},0\right) =\hat{H}\left( \hat{R}\right) \end{aligned}$$

(42)

while the boundary conditions Eqs. (19) and (20) can be described by

$$\begin{aligned} \hat{r}\left( 0,\hat{t}\right) =0,\,\hat{\dot{r}}\left( 0,\hat{t}\right) =0,\, \hat{{\sigma }_r}\left( 0,\hat{t}\right) =\hat{{\sigma }_{\vartheta }}\left( 0,\hat{t}\right) \end{aligned}$$

(43)

The condition at external radius Eq. (22), where the mass M is distributed, may be written in the dimensionless form

$$\begin{aligned} \hat{{\sigma }_r}\left( 1,\hat{t}\right) =\dfrac{1}{{\hat{h}}}\left( 1,{\hat{t}}\right) \end{aligned}$$

(44)

The function $\hat{H}(\hat{R})$ describing the initial profile of the disk is expressed by the fourth equation in set Eq. (40) and by the initial conditions Eq. (42). It is necessary to know this function in order to solve the set Eq. (40). Since this function is being sought in the optimisation process, a parametric optimisation is applied. We are looking for the best possible function $\hat{H}(\hat{R})$, leading to the longest lifetime under the mixed rupture in the class of polynomial functions assumed. In order to perform an optimisation procedure, the rupture and optimality criteria are introduced. We must follow the whole creep process step by step for each new initial geometry of the disk up to the moment of fulfilling of rupture criterion in order to establish the mixed creep rupture time. The numerical algorithm consists of two blocks, which are sequentially activated (Fig. 3).

In the first block, the stress distribution is found for a given geometry of disk. It requires integration of two first equations of set Eq. (54) and initial conditions Eq. (56). A width of the disk was divided initially into fifty parts of equal length. The program assigns a procedure using the fourth order Runge–Kutta method. The values of stresses in the middle of disk must be assumed in such a way that the result of integration satisfies the boundary condition Eq. (58) for a given accuracy. To this aim, the recurrential procedure must be applied, because initial values of stress at the external edge of the disk are unknown. In this way, the distribution of true Cauchy stress components with help of the evolution equation may be found (the last one in the set Eq. (54). This makes it possible to establish the distribution of continuity function $\Psi$. Subsequently, the rupture criterion is checked, and a new geometry of the disk is calculated.

Fig. 3

Numerical algorithm for the finite creep deformation analysis and optimization procedure

In the second block, for already known distribution of stress the integration with respect to time is made, and the new geometry of the disk is calculated. The third equation in set Eq. (54) is integrated with respect to time using Euler’s method. The time step varies, at the beginning of the creep process it may be larger (slow geometry changes), it must be small for time close to the rupture time, since process accelerates significantly. The new spatial coordinates of the knot points are found (third equation in set Eq. (54), after that the current thickness h is calculated from the incompressibility condition (fourth equation in set Eq. (54). In this way, the new geometry of deformed disk is found, stress distribution may be calculated repeating the procedure of part I. All time steps are summarized giving the total time of the work for a given disk. The calculations are carried out until the mixed rupture condition is satisfied, i.e. the continuity function reaches the critical value 0.001. As a consequence, the creep process can be treated as finished and the time to mixed rupture determined.

Among the results obtained for many initial shapes of the disk described by the assumed polynomial function one can indicate the best solution leading to the longest time to mixed creep rupture. This is the optimal disk.

For the arbitrary chosen initial geometry: $\hat{H}( \hat{R}) =0.8-\hat{R}+2.1{\hat{R}}^2$, an influence of parameters m and $\Theta$ on time to the mixed rupture $t^{(m)}$ can be investigated (see Fig. 4).

Fig. 4

Influence of parameters m and $\Theta$ on time to mixed rupture $t^{(m)}$

The $\Theta$ parameter Eq. (53) characterizes sensitivity of a material to a type of rupture Fig. 4. As the $\Theta$ parameter increases, the material sensitivity to cracking decreases and geometrical variation decides when time to rupture is achieved. Above the critical value of $\Theta$ parameter, the material can be treated as destroyed due to diminishing of transversal dimensions, and as a consequence, time to rupture is equal to that for ductile rupture obtained.

2.3 Optimal Solutions

2.3.1 Uniparametric Optimization

Firstly, the optimal solutions for the problem of rotating full disk with respect to mixed creep rupture time are sought in the class of linear functions:

$$\begin{aligned} \hat{H}\left( \hat{R}, u_0, u_1\right) =u_0+u_1{\hat{R}} \end{aligned}$$

(45)

Parameters $u_0$ and $u_1$ (uniparametric optimisation), which optimal values are sought, are linked together by the condition of given volume V:

$$\begin{aligned} u_1 =\dfrac{3}{2}\left( 1-u_0\right) \end{aligned}$$

(46)

Parameter $u_0$ is treated as a free steering one (uniparametric optimisation). Values of it are limited by the condition of nonnegative thickness at the external edge:

$$\begin{aligned} \hat{H}\left( 1\right) >1{\rightarrow }1\le {u_0}\le 3 \end{aligned}$$

(47)

An influence of two important parameters is investigated: $\mu$ as the ratio of own mass of the disk to mass uniformly distributed at the external edge, and $\Theta$ ratio of the brittle rupture time and ductile rupture time of the prismatic bar subject to uniform tension under the stress expressed by Eq. (28).

Profiles of optimal disks for uniparametric optimization are shown in Table 1 as a function of the parameter $\mu$ for three different values of parameter $\Theta$.

Table 1 Profiles of optimal disks for $n=3$ and $m=2$ and for three different values of parameter $\Theta$ and $\mu$

Fig. 5

Profiles of the optimal disks for $n=3$ and $m=2$ and for three different values of parameter $\Theta$

The solutions strongly depend on the ratio $\Theta$ and $\mu$ (Fig. 5). When the mass M is very large in comparison to the disk’s own mass (small values of $\mu$), optimal disks are close to flat ones. For larger values of parameter $\Theta$ (ductile materials), the thickness of optimal disks in the vicinity of external edge grows. For larger values of parameters $\mu$ (small mass M at the external radius), the mass of the disk is distributed as close to the rotation axis as possible.

2.3.2 Biparametric Optimization

Better results may be obtained for disks, that initial shape is defined by quadratic function:

$$\begin{aligned} \hat{H}\left( \hat{R}, b_0, b_1, b_2\right) =b_0+b_{1}\hat{R}+b_{2}\hat{R^{2}}, \;\;b_2\ne 0 \end{aligned}$$

(48)

In the case of quadratic functions, three parameters are considered. Finding the optimal values for these parameters takes much more time than for the uniparametric optimization. From three parameters in this function, only two of them may be treated as free ones, the third one results from the given volume of disk:

$$\begin{aligned} \hat{V}={\int _{0}^{1}}2{\pi }\left( b_0+b_1{\hat{R}}+b_2{\hat{R}^2}\right) \hat{R}d\hat{R}=\pi \end{aligned}$$

(49)

Including Eq. (49), one can obtain the following formula:

$$\begin{aligned} b_2=2-2b_0-\dfrac{4}{3}b_1 \end{aligned}$$

(50)

In the process of biparametric optimization, we look for such parameters $b_0$ and $b_1$, that give the longest values of the time to ductile creep rupture. Some limitations may be imposed on these parameters. One may expect that for the rotating disk with centrifugal forces, its thickness should diminish with an increase of radius (although sometimes this limitation may be violated). It leads to:

$$\begin{aligned} \dfrac{d\hat{H}(\hat{R)}}{d\hat{R}}\,\,{\le }\,\,0\;{\longrightarrow }\;{b_0}<2-\dfrac{1}{3}b_1 \end{aligned}$$

(51)

Obviously, the thickness at the external radius (and on the whole width of the disk) must be positive, that means:

$$\begin{aligned} \hat{H}(1)>0\;{\longrightarrow }\; b_0<1-\dfrac{5}{12}b_1 \end{aligned}$$

(52)

Finally, in the plane of free parameters $b_0$ and $b_1$, the search range at the beginning of numerical calculation will be restricted to the triangle area designated by continuous lines shown in Fig. 6.

Fig. 6

Range of the expected $b_0$ and $b_1$ optimal parameters for $n=6$, $\beta =0.5$, $\mu =1$

Profiles of optimal disks for the biparametric optimization are shown in Fig. 7. For smaller parameter $\mu$ (the own mass almost neglected), the growth of thickness at the external edge was observed. The optimal solutions have minimum inside the disk width.

The larger thickness at the external edge works as some kind of reinforcement, which slows down the creep process, and thanks to it, the time to mixed rupture may be longer. For larger parameter $\Theta$ (brittle materials), this effect is weaker.

Fig. 7

Optimal shapes of the disks for biparametric optimisation

Fig. 8

Time to mixed rupture for the disks with optimal biparametric shapes in terms of $\mu$ and $\Theta$

Fig. 9

Creep process for selected time intervals

The time to mixed rupture for optimal shapes of the disks with the same volume, as a function of the parameters $\mu$ and $\Theta$ for biparametric optimisation is shown in Fig. 8. The longest time to mixed creep rupture for optimal disks is observed for larger parameter $\Theta$ (brittle materials) and smaller $\mu$ (the own mass almost neglected). Increase of $\mu$, for all kind of materials (brittle and ductile) leads to decrease of the lifetime of the full disks. Changes of a profile for the optimal disk are shown in Fig. 9a, while in Fig. 9b the corresponding distribution of the continuity function is illustrated for the same time intervals. The results are presented for optimal disks using the following parameters: $\mu =0.1$, $n=3$, $\Theta =3$, where an initial shape is described by function $\hat{H}(\hat{R})=2-3\hat{R}+2\hat{R}^2$. It was observed, that despite the strengthening of the external edge of the disk, the rupture criterion for the continuity function is fulfilled. Inside the disk the values of function are quite large. This effect is only achieved for the disks of initial profile described by the quadratic function Eq. (48).

2.3.3 Modified Disk of Uniform Strength

One may expect that disks of uniform initial strength, in which both radial and circumferential stresses are the same for $0\,{\le }\,{R}\,{\le }\,{B}$ and close to optimum with respect to mixed rupture time. Such disks are described by formula:

$$\begin{aligned} {{\hat{H}}_\mathrm {us}}(\hat{R})=\dfrac{1}{\hat{\Sigma }}\exp \left[ \dfrac{\mu }{\hat{\Sigma }}\left( 1-{\hat{R}}^2\right) \right] \end{aligned}$$

(53)

where: $\hat{\Sigma }$ - dimensionless equalized initial stress, calculated under assumption of the constant volume:

$$\begin{aligned} \hat{\Sigma } =\dfrac{\mu }{\ln (1+\mu )} \end{aligned}$$

(54)

It may be slightly corrected in order to obtain the longest creep lifetime. Correction may be adopted in the form of the third degree polynomial function:

$$\begin{aligned} \hat{H}_{\mathrm {cor}}=p_0+{p_2}{\hat{R}}^2+{p_3}{\hat{R}}^3 \end{aligned}$$

(55)

without the linear element. As a consequence, the thickness derivative in the middle of the disk is equal to zero.

As the correction cannot change the total volume of the bar, only two coefficients in Eq. (55) may be treated as free, while the third one can be determined from the constant volume condition:

$$\begin{aligned} p_3=-\dfrac{5}{2}{p_0}-\dfrac{5}{4}p_2 \end{aligned}$$

(56)

An initial shape of the disk was proposed for different values of these parameters using expression

$$\begin{aligned} {{\hat{H}}}(\hat{R})={{\hat{H}_{us}}}(\hat{R})+{{\hat{H}_{cor}}}(\hat{R}) \end{aligned}$$

(57)

and then carrying out integration of the set of equations Eq. (40). Calculations were carried for $\mu =0.1,\; \Theta =3$, exponent in Norton’s law $n=3$ and exponent in Kachanov’s law $m=2$. The comparison between the optimal shapes of the uniform strength disk and uni- and biparametric optimisation is presented in Fig. 10.

Fig. 10

Optimal shape of the corrected uniform initial strength disks compared to the uni- and biparametric optimisation

The optimal solution of the disks are presented on the time axis. As expected, the corrected shape of uniform initial strength disk provides the longest time of mixed creep rupture. The parabolic disk enlarges this time around 14%. The lifetime of corrected disk of uniform strength is 70% longer than that of conical disk.

Fig. 11

Model of the annular rotating disk

3 Optimal Design of Annular Disks with Respect to Mixed Creep Rupture Time

3.1 Mathematical Model of Annular Disk with Respect the Mixed Creep Rupture Time

The initial shape of rotating annular disk is sought for the given internal and external radii A and B and given volume V (Fig. 11), ensuring the longest time to mixed creep rupture. In the case of the annular disk (volume V and initial radii A and B are given) rotating with constant angular velocity $\omega$, (the properties of material are known, mass M is uniformly distributed at the external edge), the optimization problem can be formulated in the following way:

• for given V, A, B, $\omega$, $\gamma$, M

• we look for such $H(R,b_0, b_1, b_2)=b_0+b_1R+b_2R^2$

• that $t_{*}^{(m)}\;\longrightarrow \; \mathrm {max}$

The problem seems to be of great importance for rotors of jet engines and power plant turbines working at high temperatures. In such cases the creep effects must be taken into account. Also, the body forces are of great importance. The axially symmetric problem (all variables depend on the single material coordinate only, a radius) is described using material Lagrangean coordinate denoted by capital R. Corresponding spatial coordinate r may be treated as a measure of deformation. The external loading of the disk results from centrifugal force acting on the blades of total mass M put at the external edge of the disk, under assumption that they are uniformly distributed. Moreover, the body forces connected with the own mass of the disk are taken into consideration. Both types of loading depend on the spatial coordinate, and change according to the disk deformation within the creep process. The mathematical model of mixed creep rupture is finally described by the system of five partial differential equations in the dimensionless form:

$$\begin{aligned} \hat{\sigma }_{r}^{'}=\dfrac{\hat{r}^{'}}{\hat{r}}\left( \hat{\sigma }_{r}-\hat{\sigma }_{\vartheta } \right) -2\hat{r}\hat{r}^{'}\mu -\dfrac{\hat{h}^{'}}{\hat{h}}\hat{\sigma }_r \end{aligned}$$

(58)

$$\begin{aligned} {\sigma _{\vartheta }^{'}}=\dfrac{6\sigma _{e}^{2}\left( {\sigma _r}-\sigma _\vartheta \right) \dfrac{r^{'}}{r} -{\sigma _r^{'}}\left[ \left( n-1\right) \left( 2{\sigma _r}+{\sigma _\vartheta } \right) \left( 2{\sigma _\vartheta }+{\sigma _r} \right) -2{\sigma _{e}^{2}}\right] }{\left[ \left( n-1\right) {\left( 2{\sigma _r}+{\sigma _\vartheta } \right) ^{2}}+4{\sigma _{e}^{2}} \right] } \end{aligned}$$

(59)

$$\begin{aligned} \dfrac{d\hat{r}}{d\hat{t}}=\dfrac{\hat{r}}{2n}\left( \hat{\sigma }_{r}^{2}+\hat{\sigma }_{\vartheta }^{2}-\hat{\sigma }_{r}\hat{\sigma }_{\vartheta }\right) ^{\frac{n-1}{2}}\left( 2\hat{\sigma }_{\vartheta }-\hat{\sigma }_{r}\right) \end{aligned}$$

(60)

$$\begin{aligned} \hat{h}=\dfrac{\hat{H}\hat{R}}{\hat{r}^{'}\hat{r}} \end{aligned}$$

(61)

$$\begin{aligned} \dfrac{\partial \Psi }{{\partial }{\hat{t}}}=\dfrac{-1}{\left( m+1\right) \Theta }\left[ \dfrac{\hat{\sigma }_e}{\Psi }\right] ^m \end{aligned}$$

(62)

In the case of annular disk an additional parameter is used:

$$\begin{aligned} \beta =\dfrac{A}{B} \end{aligned}$$

(63)

where: $\beta$ is the ratio of internal and external radii. A set of equations Eqs. (58)–(62) written in the above form is convenient for numerical calculations.

3.2 Influence of Boundary Conditions

3.2.1 Disk Clamped on a Rigid Shaft

At the beginning of creep process (for $t=0$), the disk remains undeformed, therefore, the initial conditions take the form:

$$\begin{aligned} \hat{r}\left( \hat{R},0\right) =\hat{R},\;\;\hat{h}\left( \hat{R},0\right) =\hat{H}\left( \hat{R}\right) \end{aligned}$$

(64)

Boundary conditions at internal radius may be written:

$$\begin{aligned} \hat{h}\left( \beta ,\hat{t}\right) =\hat{H}(\beta ,0),\;\;\hat{r}\left( \beta ,\hat{t}\right) =\beta \end{aligned}$$

(65)

Since we are looking for the stress distribution, this boundary condition should be rewritten in terms of stress. Taking advantage of shape change law Eq. (60), the condition at the internal edge can be written as follows:

$$\begin{aligned} \dot{{\hat{r}}}(\beta , \hat{t})=0 \end{aligned}$$

(66)

It leads to relation of stress at the internal edge

$$\begin{aligned} \hat{{\sigma }}_r(\beta , \hat{t})=2\hat{{\sigma }}_{\vartheta }(\beta , \hat{t}) \end{aligned}$$

(67)

By introduction of dimensionless parameters into the condition at external radius Eq. (65), where the mass M is distributed:

$$\begin{aligned} \dfrac{\hat{{\sigma }}_r(b)M\omega ^2b^2}{2V}=\dfrac{M\omega ^2b^2}{2V\hat{h}(b)} \end{aligned}$$

(68)

one can get a condition at the external radius B in the following form:

$$\begin{aligned} \hat{{\sigma }}_r(1,t)=\dfrac{1}{\hat{h}(1,t)} \end{aligned}$$

(69)

The numerical algorithm consists of three steps:

The first step – for given geometry of the disk, the true Cauchy stress distribution is established from Eqs. (58) and (59). We don’t know values of stress at the internal edge of the disk, so it is necessary to assume them arbitrarily, remmembering that the boundary condition at the external edge of the disk must be fulfilled.

The second step – distribution of the Cauchy stress found in the first step, makes it possible to establish a new geometry of the disk from Eqs. (60) and (61).

The third step – from Eq. (62) a distribution of continuity function $\Psi$ is calculated. If its minimum value satisfies the rupture criterion, the creep process is finished – the time to mixed rupture is found. Due to the inability in order to write the objective function (mixed rupture time) as an explicit function of the optimization parameters (initial profile of the disk) the parametric optimization is applied (search method). To establish the range of parameter $\Theta$ arbitrary taken the disk described by the equation $\hat{H}(\hat{R})=0.8-\hat{R}+2.1\hat{R}^{2}$, was investigated. The parameter $\Theta$ is defined here identically as for full disks, Eq. (39), where it has significant influence on the time to rupture. The results are presented in Fig. 12.

Fig. 12

Influence of parameter $\Theta$ on the time to rupture for the disk clamped on the shaft

By increasing of $\Theta$, the time to rupture becomes longer for the disk clamped on the rigid shaft. This is observed up to the values of $\Theta$ equal to 11 approximately. For higher values of $\Theta$, the influence of brittle rupture becomes so small in comparison to ductile effect, that rupture effects result almost from geometrical variations only. Time to rupture for $\Theta \ge 11$ coincides with that for ductile rupture obtained. For numerical calculations three values $\Theta =0.4, \Theta =3$ and $\Theta =10$ were taken into account. Initially, the optimal solution was sought among the conical disks which initial shape is described by the formula:

$$\begin{aligned} \hat{H}\left( \hat{R};u_0, u_1\right) =u_0+u_1{\hat{R}} \end{aligned}$$

(70)

Using condition of constant volume leads to:

$$\begin{aligned} u_1 =\dfrac{3}{2}\left( 1-u_0\right) \end{aligned}$$

(71)

and as a consequence, only one free parameter $u_0$ remains. Optimal solutions for the disks clamped on the rigid shaft for various $\Theta$ are presented in Fig. 13 for $\beta =0.1$ and $\mu =0.1$.

Fig. 13

Optimal profiles of conical disk clamped on the rigid shaft, $\beta =0.1$, $\mu =0.1$

For $\Theta =0.4$, the optimal profile of the conical disk becomes almost flat. For higher $\Theta$, the mass moves toward the internal edge. It was expected that the results presented earlier can be improved by expanding the class of functions, in which the optimal solution is sought. In the next step the biparametric optimization was used.

An initial shape is defined by quadratic function:

$$\begin{aligned} \hat{H}\left( \hat{R}, b_0, b_1, b_2\right) =b_0+b_{1}\hat{R}+b_{2}\hat{R^{2}}, \;\;b_2{\ne }0 \end{aligned}$$

(72)

From three parameters in this function, only two of them may be treated as free ones, the third results from the given volume of disk:

$$\begin{aligned} \hat{V}={\int _{0}^{1}}2{\pi }\left( b_0+b_1{\hat{R}}+b_2{\hat{R}^2}\right) \hat{R}d\hat{R}=\pi \end{aligned}$$

(73)

in which:

$$\begin{aligned} b_2=\dfrac{2-\dfrac{4}{3}b_1(1-\beta ^3)-2b_0(1-\beta ^2)}{1-\beta ^4} \end{aligned}$$

(74)

The search process for biparametric optimisation is much more time consumable. For determined values of $b_0$, the time to mixed rupture is calculated for various $b_1$. In such a way, parameter $b_1$ leading to the longest lifetime may be found. This procedure is repeated for subsequent values of $b_0$. Finally, the optimal solution is established as “maximum maximorum” of all disks investigated (sometimes almost hundred). Optimal shapes of the disks for biparametric optimisation are shown in Fig. 14.

Fig. 14

Optimal shapes of the disks clamped on the rigid shaft, $\beta =0.5, \mu =0.1$

The optimal shape of disk for $\Theta =0.4$ is characterized by the large increase of thickness at the external edge. In spite of larger centrifugal forces, the external edge works as a kind of reinforcement slowing down the creep process. For larger $\Theta$ such effect does not occur.

The creep process of the optimal disk with initial profile described by the function:

$$\begin{aligned} \hat{H}\left( \hat{R}\right) =3.51-5\hat{R}+2.76\hat{R^{2}} \end{aligned}$$

(75)

is presented in Fig. 15, showing changes of shape (A) and continuity function distribution (B) in terms of time. A distribution of the continuity function at rupture is not uniform, criterion of rupture is fulfilled inside the disk at single point. For other radii the values of function are non-zero and at the internal and external edges they are quite large. This effect is attributed only to the disks of initial profile described by the quadratic function, Eq. (72).

Fig. 15

Time intervals of creep process for $\beta =0.5$, $\mu =0.1$ and $\Theta =3$

One may expect that disks of uniform initial strength, in which the radial and circumferential stress components are equal and independent of the radius, will be close to the optimal profiles with respect to the mixed rupture time.

3.2.2 Disk Fastened on the Rigid Shaft, with Changing Thickness in the Place of Joint

Analysis of the disk fastened to the rigid shaft is carried out in such a way that enables displacement on the one hand and variation of thickness in this place (e.g. spline joint) on the other. The boundary and initial conditions are the same as in Sect. 4.2.1, Eqs. (65), (67) and (69). Only the condition represented by Eq. (66) is eliminated, what means that thickness of the disk at the joint with the shaft will diminish throughout the creep process. An influence of the parameter $\Theta$ on the time to rupture of disk fastened to the rigid shaft, with possible change of thickness was investigated for the annular disk described by the equation $\hat{H}(\hat{R}) =0.8-\hat{R}+2.1\hat{R^{2}}$. The results are presented in Fig. 16.

Fig. 16

Influence of parameter $\Theta$ on the time to rupture of disk fastened to the rigid shaft, with possible thickness variation in the place of joint

Taking advantage of these results the following values of $\Theta$ were chosen for numerical calculations: $\Theta =0.4, \Theta =3$ and $\Theta =10$. It turned out, that parameter $\Theta$ has no influence on the optimal shape of conical disk (due to small width of the disk, Fig. 17), which is described by the equation:

$$\begin{aligned} \hat{H}\left( \hat{R}\right) =1.87-0.74\hat{R} \end{aligned}$$

(76)

The optimal shapes of disks fastened to the rigid shaft with possible thickness variation are shown in Fig. 18 for the biparametric optimisation. For $\Theta =0.4$ and $\Theta =3$ the optimal shapes of disk have a reinforcement of the external edge (an increase of the thickness). For larger $\Theta$, the effect vanishes.

Fig. 17

The optimal shapes of disks fastened to the rigid shaft - uniparametric optimisation, $\beta =0.5, \mu =0.1$

Fig. 18

The optimal shapes of disks fastened to the rigid shaft - biparametric optimisation, $\beta =0.5, \mu =0.1$

Figure 19 elaborated for the optimal disk:

$$\begin{aligned} \hat{H}(\hat{R})=4.39-8\hat{R}+5.05{\hat{R}}^2 \end{aligned}$$

(77)

shows the time intervals of the optimal profile for the annular disk fastened to the rigid shaft (Fig. 19a) and the continuity function (Fig. 19b).

The geometrical variations of a disk profile are not significant in the creep process. Due to small width of the disk, the thickness variation at the internal edge is not too large, although possible.

3.2.3 Disk with Free Inner Edge

Boundary condition at the internal radius is described by the following expression:

$$\begin{aligned} {\hat{\sigma }}_{r}\left( {\beta }, \hat{t}\right) =0 \end{aligned}$$

(78)

and at the external radius by the following equations:

$$\begin{aligned} \hat{{\sigma }}_r(1,t)=\dfrac{1}{\hat{h}(1,t)} \end{aligned}$$

(79)

The optimal profiles for the conical disk are plotted in Fig. 20 as a function of parameter $\Theta$ for the boundary conditions defined.

Fig. 19

Time intervals of the optimal profile and the continuity function for $\beta =0.5, \mu =0.1, \Theta =3$

Fig. 20

The optimal profiles of the conical disk with free internal edge, $\beta =0.1, \mu =0.1$

The optimal profiles for the conical disks with free internal edge are characterized by significant reduction of thickness at the external radius, even larger than for the disk clamped to the rigid shaft. The optimal shapes of the free disks are shown in Fig. 21 for the biparametric optimization.

Fig. 21

The optimal shape for the disk with free internal edge, $\beta =0.5, \mu =0.1$

The reinforcement of the disk external edge is observed for $\Theta =0.1$. In the case of $\Theta =0.2$ and $\Theta =0.3$ the optimal shapes are characterized by reduction of the disk thickness toward the external edge. An example of the optimal profiles can be expressed as follows:

$$\begin{aligned} \hat{H}\left( \hat{R}\right) =4.09-5.01\hat{R}+1.79{\hat{R}} \end{aligned}$$

(80)

The time intervals of the disk profile and continuity function are shown in Fig. 22a, b, respectively.

Fig. 22

Time intervals of the optimal profile for free edge and the continuity function, $\beta =0.5, \mu =0.1, \Theta =0.2$

Time intervals of the optimal profile and the continuity function indicate, that the rupture criterion of the disk is fulfilled at the internal edge, despite of the significant reinforcement of the thickness at this point.

4 Conclusions

Time-dependent properties of materials make it possible to formulate various problems of structure optimization under creep conditions. The problem of optimal design with respect to ductile and mixed creep rupture time turns out to be a very complicated one. In spite of physical nonlinearites (Norton’s creep law), also geometrical nonlinearities are introduced, due to necessity of finite deformation theory application. Moreover, additional time factor causes that all differential equations describing process are the partial ones.

All these complications caused, that the parametric optimization was applied – the initial shape of the disk was described by polynomial function. The best solution was sought among disks with initial shape described by linear (one free parameter), or quadratic (two free parameters) functions. Better result, longer times to mixed creep rupture were obtained for biparametric optimization.

Significant influence on optimal solution of parameter $\Theta$ describing sensitivity of material on brittle, or ductile rupture was observed. Also ratio of own mass of the disk and mass placed at the external edge $\mu$ is of great importance.