1 Introduction

Smart composite structures have attracted a great deal of attention in the last few decades due to their significant potential applicability in various industrial and research areas. Piezocomposites constitute a significant class of smart structures and have been studied extensively. Dealing with smart composite structures requires the possibility of modelling and simulation of their behavior. Stress and strain distribution within a multilayer composite may require careful approximation that deviates from classical thin plate theories. This is mainly due to the higher contribution of shear and the effect of weak points like glue layers and interfaces. It is widely accepted that higher-order shear deformation theory (HSDT) is essentially required for the accurate modelling of thick plates. If one uses the classical plate theory for modelling of thick laminated structures made of advanced composites (e.g. graphite/epoxy, boron/epoxy) whose elastic to shear modulus ratios are very large, the errors in deflections, stresses, natural frequencies and buckling loads become higher. Reddy [1] also showed that HSDT improves the in-plane response even in the case of thin laminated composite structure. Thus, if the substrate of a smart structure is a multilayered laminated composite structure, one should consider the effect of transverse shear deformation to obtain an accurate response. A variety of higher order lamination theories has been proposed in order to improve the transverse shear stress calculation. Kant and Manjunatha [2] developed a nine-node finite element (FE) having seven degrees of freedom per node to perform free vibration analysis of unsymmetrically laminated multilayered plates. Goswami [3] presented a simple \(C^0\) FE formulation for nine-node FE with six degrees of freedom based on HSDT. Lee and Kim [4] developed a four-node laminated plate element by using a higher order shear deformation theory and assumed strains to perform the FE analysis of laminated composite plate structures.

The recent advances in smart structures have prompted interest in more accurate modelling and simulation of their coupled electro-mechanical behavior for active control applications. FE models for piezoelectric composite beams and plates have been reported in Refs. [5]–[12]. Ray et al. [13] developed a two-dimensional eight-noded isoparametric finite element for modelling the distributed coupled electromechanical behavior of smart structures using higher-order displacement theory. In Ref. [14] a higher-order, shear-flexible piezolaminated \(C^1\) QUAD 8 multi-layer composite plate finite element with 48 elastic degrees of freedom per element and 9 electric degrees of freedom per element per piezoelectric layer has been presented for the analysis of multi-layer smart composite structures. The electric potential is assumed to vary quadratically over the thickness, following [15], representing the potential induced due to bending deformation more accurately, by interpolating using nodal mid-plane electric potentials and one electric degree of freedom representing the potential difference between the top and bottom surfaces of the piezoelectric layer. Phung–Van et al. [16] presented a simple and effective formulation to investigate static, free vibration and dynamic control of piezoelectric composite plates integrated with sensors and actuators, based on isogeometric analysis and higher order shear deformation theory. Recently, the static behavior of a laminated composite flat panel, surface bonded with and without piezoelectric and/or magnetostrictive layers, have been analyzed in [17]. The plate has been modeled in the framework of the HSDT mid-plane kinematics discretised using suitable FEM with sixteen degrees of freedom.

Additionally, several other analytical and numerical methods [18,19,20] are promising to solve various piezoelectric structures.

The objective of this work is to develop a finite element model for active control of multilayer piezocomposite plates using higher order shear deformation displacement theory. The core elastic part of the smart plate is a laminate made of several plies with different material orientations. The plate is integrated with piezoelectric layers or patches polarized in the thickness direction. The overall structure is considered as a laminated plate with the integrated piezoelectric and sensor layers as the bounding plies of the laminated plate. In order to create a flexible model, suitable for both classical (statics, dynamics, control) as well as advanced applications (delamination, damage, consideration of glue material), a nine-node quadrilateral finite element is developed. The formulation is based on the third order shear deformation theory that accounts for parabolic distribution of the transverse shear strains through the thickness of the plate and rotary inertial effects [2] and has been extended to incorporate the piezoelectric sensors and actuators layers. To illustrate the accuracy of the present finite element model, a comparison of results with published ones is presented. Moreover, the shape control and active vibration suppression of a cantilever composite plate are studied, in order to demonstrate some of the capabilities of the model.

Fig. 1
figure 1

Geometry of the smart piezocomposite plate

Full size image

2 Governing Equations

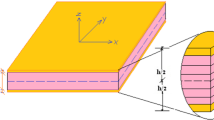
Consider a piezocomposite plate structure consisting of several layers, including piezoelectric layers, as shown in Fig. 1. All layers are perfectly bonded. The plate has length a, width b, total thickness h and consists of N layers with the principal material coordinates of the k -th lamina oriented at an angle \({\theta _k}\) to the laminate coordinate x. The xy plane coincide with the midplane of the plate, with the z-axis being normal to the midplane. The piezoelectric layers are much thinner than the host structure and they have poling direction along z-axis. For simplicity of the notation, all the layers of the laminate will be considered as piezoelectric. Elastic layers are then obtained by making their piezoelectric constants vanish.

2.1 Mechanical Displacement and Strains

The mechanical behaviour of the structure is modelled by the 3rd order displacement theory developed by Kant et al. [2] as follows

$$\begin{aligned} u_1(x,y,z,t)= & {} u(x,y,t)+z\theta _x(x,y,t)+z^3\theta ^*_x(x,y,t)\nonumber \\ u_2(x,y,z,t)= & {} v(x,y,t)+z\theta _y(x,y,t)+z^3\theta ^*_y(x,y,t) \nonumber \\ u_3(x,y,z,t)= & {} w(x,y,t) \end{aligned}$$
(1)

where, \(u_1\), \(u_2\), \(u_3\) are the displacements at any point of the plate along the (x, y, z) coordinates, u, v, w are the displacements associated with a point on the mid-plane of the plate and \(\theta _x\), \(\theta _y\) are the normal rotations about the y and x -axes, respectively. The functions \(\theta ^*_x\), \(\theta ^*_y\) are the higher order terms of Taylor series expansion defined at the mid-surface.

The in-plane strains are thus expressed by the following equation

$$\begin{aligned} \{\varepsilon _b\}= \{\varepsilon _{xx}, \varepsilon _{yy}, \gamma _{xy}\}^T =\{\varepsilon _{b0}\} +z \{k\}+z^3 \{k^*\} \end{aligned}$$
(2)

where

$$ \{\varepsilon _{0b}\} = \left\{ \frac{\partial u}{\partial x}, \frac{\partial v}{\partial y}, \left( \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right) \right\} ^T, \{k\} = \left\{ \frac{\partial \theta _x}{\partial x}, \frac{\partial \theta _y}{\partial y}, \left( \frac{\partial \theta _x}{\partial y}+\frac{\partial \theta _y}{\partial x} \right) \right\} ^T, $$
$$ \{k^*\} = \left\{ \frac{\partial \theta ^*_x}{\partial x}, \frac{\partial \theta ^*_y}{\partial y}, \left( \frac{\partial \theta ^*_x}{\partial y}+\frac{\partial \theta ^*_y}{\partial x}\right) \right\} ^T, $$

The transverse shear strains are given by

$$\begin{aligned} \{\varepsilon _s\}= \{\gamma _{yz}, \gamma _{xy}\}^T =\{\varepsilon _{0s}\} +z^2 \{k_s\} \end{aligned}$$
(3)

where

$$ \{\varepsilon _{0s}\} = \left\{ \psi _x, \psi _y \right\} ^T =\left\{ \theta _y+\frac{\partial w}{\partial y}, \theta _x+\frac{\partial w}{\partial x}\right\} ^T, \{k_s\} = \left\{ \psi _x^*, \psi _y^* \right\} ^T =\left\{ 3\theta _y^*, 3\theta _x^*\right\} ^T. $$

2.2 Constitutive Equations of Piezoelectric Lamina

The linear constitutive equations for the k -th piezoelectric lamina with reference to its principal axes are given by:

$$\begin{aligned} \{\hat{\sigma }\}_k= & {} [\bar{Q}]_k \{\hat{\varepsilon }\}-[\bar{e}]_k^T \{E\}_k \nonumber \\ \{ \hat{D}\}_k= & {} [\bar{e}]_k \{\hat{\varepsilon }\}+[\bar{\xi }]_k \{E\}_k \end{aligned}$$
(4)

where \(\{\hat{\sigma }\}\),\(\{\hat{\varepsilon }\}\), \(\{ \hat{D}\}\) and \(\{E\}\) are stress, strain, electric displacement and electric field vector, respectively. \([\bar{Q}]\), \([\bar{e}]\) and \([\bar{\xi }]\) are plane-stress reduced stiffness coefficients, the piezoelectric coefficients and the permittivity constant matrices, respectively. In the above equations, a superscript T denotes the transpose of a matrix. Equation (4a) describes the inverse piezoelectric effect and Eq. (4b) describes the direct piezoelectric effect. Next, we assume that the piezoelectric material exhibits orthorhombic 2 mm symmetry. After transforming Eq. (4) to the global coordinate system (x, y, z) and separating the bending and shear related variables, the constitutive Eq. (4) becomes

$$\begin{aligned} \{ \sigma _b\}= & {} [Q_b] \{\varepsilon _b\}-[e_b]^T \{E\} \nonumber \\ \{ \sigma _s\}= & {} [Q_s] \{\varepsilon _s\}-[e_s]^T \{E\}\nonumber \\ \{ D\}= & {} [e_b] \{\varepsilon _b\}+[e_s] \{\varepsilon _s\}+[\xi ] \{E\} \end{aligned}$$
(5)

where \(\{ \sigma _b\}=\{ \sigma _{xx},\sigma _{yy}, \tau _{xy}\}^T,\{ \sigma _s\}=\{ \tau _{yz},\tau _{xz}\}^T \) and

$$\begin{aligned}{}[Q_b]_k= \begin{bmatrix} Q_{11}&Q_{12}&Q_{16} \\ Q_{21}&Q_{22}&Q_{26} \\ Q_{16}&Q_{26}&Q_{66} \end{bmatrix},&[Q_s]_= \begin{bmatrix} Q_{44}&Q_{45} \\ Q_{45}&Q_{55} \end{bmatrix} \end{aligned}$$
$$\begin{aligned}{}[e_b]= \begin{bmatrix} 0&0&0 \\ 0&0&0 \\ e_{31}&e_{32}&e_{36} \end{bmatrix},&[e_s]_= \begin{bmatrix} e_{14}&e_{15} \\ e_{25}&e_{25} \\ 0&0 \end{bmatrix},&[\xi ]= \begin{bmatrix} \xi _{11}&\xi _{12}&0 \\ \xi _{21}&\xi _{22}&0 \\ 0&0&\xi _{33} \end{bmatrix} \end{aligned}$$
(6)

In Eq. (6), \(Q_{kl}\), \(e_{kl}\) and \(\xi _{kl}\) are the transformed reduced elastic, piezoelectric and permittivity constants of the kth lamina, respectively. The detailed expressions for transformed material constants can be obtained from [21]. For non-piezoelectric layer the material constants \(e_{kl}\) and \(\xi _{kl}\) should be zero.

2.3 Electric Field

It is assumed that the electric field acts in the thickness direction. Also, this paper considers piezoelectric elements with electrodes on the top and bottom surfaces and poled in the thickness direction. Thus, for most of the typical piezoelectric laminate structures with relatively small thickness of the piezolayers in comparison to the overall laminate thickness, the electric field inside the k-th piezoelectric layer can be expressed as

$$\begin{aligned} \{E\}_k = [B_{\phi }]_{p_k}\phi ^{p_k} \end{aligned}$$
(7)

where

$$ [B_{\phi }]_{p_k}= \begin{bmatrix} 0&0&-\frac{1}{h^{p_k}} \end{bmatrix} $$

and \(h^{p_k}\), \(\phi ^{p_k}\) are the thickness and the difference of electric potential between the electrodes covering the surface on each side of the piezoelectric layer \(p_k\). It should be noted that such formulation gives one electric degree of freedom per layer per element of the electric field.

2.4 Finite Element Formulation

It is well known that the analytical solutions of laminated composite structure bonded with and without functional materials are very tough due to their material and geometrical complexities. However, FEM has been proved to be a robust numerical tool for such kind of complex analysis. In this present study, the smart plate model has been discretized using a nine nodded isoparametric quadrilateral Lagrangian element with seven degrees of freedom (DOF) per node. The element is developed to include the stiffness and the electromechanical coupling of the piezoelectric sensor/actuator layers. The generalized displacement vector for any point within a typical element e may be expressed as:

$$\begin{aligned} \{\bar{u}(x,y,t)\} \equiv \{u,v,w,\theta _x, \theta _y, \theta _x^*, \theta _y^*\}^T=[N_u]\{d\}_e=\sum _{i=1}^{9} {(N_i[I]_{7\times 7}\{d_i\}_e)} \end{aligned}$$
(8)

where \(\{d_i\}_e=\{u_i, v_i, w_i, \theta _{xi}, \theta _{yi}, \theta _{xi}^*, \theta _{yi}^*\}^T\) corresponding to the i-th node of the element and \(N_i\) are the shape functions.

Substituting (8) into Eqs. (2) and (3) gives:

$$\begin{aligned} \{\varepsilon (x,y,t)\} = [B]\{d\}_e=\sum _{i=1}^{9} {([B_i]\{d_i\}_e)} \end{aligned}$$
(9)

or equivalent:

$$ \{\bar{\varepsilon }\}= \left\{ \begin{array}{ccc} \{\varepsilon _{b0}\} \\ \{k\} \\ \{k^*\} \\ \{\varepsilon _{s0}\} \\ \{k_s\} \end{array} \right\} = \begin{bmatrix} [B_b]\\ [B_k]\\ [B_{k^*}]\\ [B_s]\\ [B_{ks}]\\ \end{bmatrix}\{d\}_e= \sum _{i=1}^{9} \left( \begin{bmatrix} [B_b]_i\\ [B_k]_i\\ [B_{k^*}]_i\\ [B_s]_i\\ [B_{ks}]_i\\ \end{bmatrix}\{d_i\}_e \right) $$

where

$$\begin{aligned}{}[B_b]_i= \begin{bmatrix} \partial _x&0&0&0&0&0&0\\ 0&\partial _y&0&0&0&0&0\\ \partial _y&\partial _x&0&0&0&0&0 \end{bmatrix}N_i,&[B_k]_i= \begin{bmatrix} 0&0&0&\partial _x&0&0&0\\ 0&0&0&0&\partial _y&0&0\\ 0&0&0&\partial _y&\partial _x&0&0 \end{bmatrix}N_i \end{aligned}$$
$$\begin{aligned}{}[B_{k^*}]_i= \begin{bmatrix} 0&0&0&0&0&\partial _x&0\\ 0&0&0&0&0&0&\partial _y\\ 0&0&0&0&0&\partial _y&\partial _x \end{bmatrix}N_i,&[B_{s}]_i= \begin{bmatrix} 0&0&\partial _x&1&0&0&0\\ 0&0&\partial _y&0&1&0&0 \end{bmatrix}N_i \end{aligned}$$
$$\begin{aligned}{}[B_{k_s}]_i= \begin{bmatrix} 0&0&0&0&0&3&0\\ 0&0&0&0&0&0&3 \end{bmatrix}N_i \end{aligned}$$

and \(\partial _x=\frac{\partial }{\partial {x}}\), \(\partial _y=\frac{\partial }{\partial {y}}\).

In general, piezocomposite structures may comprise more than one piezoelectric layer, e.g. a number of \(N_{pe}\) piezoelectric layers. Therefore, electrical quantities are observed layerwise, and in the finite element model they are given in the condensed form of vectors \(\{E\}_e\) and \(\{\phi \}_e\) defined on the element level.

Thus after the discretization of the structure, the differences of electric potentials of all piezoelectric layers across the thickness of the element can be expressed as:

$$\begin{aligned} \{\phi \}_e = \{\phi ^1, \phi ^2, \dots , \phi ^{N_{pe}}\}^T \end{aligned}$$
(10)

where \(N_{pe}\) is the number of the piezoelectric layers of the \(e^{th}\) element. The electric field distribution can be written as:

$$\begin{aligned} \{E\}_e=[B_\phi ]\{\phi \}_e \end{aligned}$$

where \([B_\phi ]=diag([B_\phi ]_1, [B_\phi ]_2, \dots , [B_\phi ]_{N{pe}})\) is the electric field-electric potential matrix, which has a diagonal form since the difference of electric potentials of a piezo-layer affects the electric field only of the very same layer.

2.5 Variational Principle

This formulation will be based on the Hamilton variational principle in which the strain potential energy, kinetic energy and work are considered for the entire structure. Since we are dealing with the piezoelectric continuum, the Lagrangian will be properly adapted in order to include the contribution from the electrical field besides the contribution from the mechanical field. The most general form of this variational principle is stated as:

$$\begin{aligned} \int \limits _0^T (\delta T - \delta U + \delta W) \, \mathrm {d} t \end{aligned}$$
(11)

where T is the total kinetic energy, U is the total strain energy and W is the work done by the loads.

The strain energy of a piezocomposite element is given by:

$$\begin{aligned} U= & {} \frac{1}{2}\int \limits _{V_e} (\{\varepsilon _b\}^T\{\sigma _b\}+\{\varepsilon _s\}^T\{\sigma _s\}) \, \mathrm {d} V \nonumber \\= & {} \frac{1}{2}\int \limits _{V_e} (\{\varepsilon _{b0}\}^T[Q_b]\{\varepsilon _{b0}\}+\{\varepsilon _{b0}\}^Tz[Q_b]\{k\}+\{\varepsilon _{b0}\}^Tz^3[Q_b]\{k^*\} \nonumber \\&\quad \quad +\{k\}^Tz[Q_b]\{\varepsilon _{b0}\}+\{k\}^Tz^2[Q_b]\{k\}+\{k\}^Tz^4[Q_b]\{k^*\} \nonumber \\&\quad \quad +\{k^*\}^Tz^3[Q_b]\{\varepsilon _{b0}\}+\{k^*\}^Tz^4[Q_b]\{k\}+\{k^*\}^Tz^6[Q_b]\{k^*\} \nonumber \\&\quad \quad +\{\varepsilon _{s0}\}^T[Q_s]\{\varepsilon _{s0}\}+\{\varepsilon _{s0}\}^Tz^2[Q_s]\{k_s\} \nonumber \\&\quad \quad +\{k_s\}^Tz^2[Q_s]\{\varepsilon _{s0}\}+\{k_s\}^Tz^4[Q_s]\{k_s\} \nonumber \\&\quad \quad -\{\varepsilon _{b0}\}^T[e_b]^T\{E\}-\{k\}^Tz[e_b]^T\{E\}-\{k^*\}^Tz^3[e_b]^T\{E\} \nonumber \\&\quad \quad -\{\varepsilon _{s0}\}^T[e_s]^T\{E\}-\{k_s\}^Tz[e_s]^T\{E\} )\, \mathrm {d} V\nonumber \\= & {} \frac{1}{2}\int \limits _{V_e} \begin{bmatrix} \{\varepsilon _{b0}\} \\ \{k\} \\ \{k^*\}\\ \{\varepsilon _{s0}\}\\ \{k_s\} \end{bmatrix}^T \begin{bmatrix} [Q_b]&z[Q_b]&z^3[Q_b]&0&0 \\ z[Q_b]&z^2[Q_b]&z^4[Q_b]&0&0 \\ z^3[Q_b]&z^4[Q_b]&z^6[Q_b]&0&0 \\ 0&0&0&[Q_s]&z^2[Q_s] \\ 0&0&0&z^2[Q_s]&z^4[Q_s] \end{bmatrix}\quad \begin{bmatrix} \{\varepsilon _{b0}\} \\ \{k\} \\ \{k^*\}\\ \{\varepsilon _{s0}\}\\ \{k_s\} \end{bmatrix} \mathrm {d} V\nonumber \\&\quad \quad -\frac{1}{2}\int \limits _{V_e} \begin{bmatrix} \{\varepsilon _{b0}\} \\ \{k\} \\ \{k^*\}\\ \{\varepsilon _{s0}\}\\ \{k_s\} \end{bmatrix}^T \begin{bmatrix} [\varepsilon _b]^T \\ z[\varepsilon _b]^T \\ z^3[\varepsilon _b]^T \\ [\varepsilon _s]^T \\ z^2[\varepsilon _s]^T \end{bmatrix} \{E\} \mathrm {d} V \nonumber \\= & {} \frac{1}{2}\int \limits _{V_e}(\{\bar{\varepsilon }\}^T[\mathscr {D}(z)]\{\bar{\varepsilon }\}-\{\bar{\varepsilon }\}^T[\mathscr {E}(z)]\{E\}) \mathrm {d} V \end{aligned}$$
(12)

where \(V_e\) is the volume of an element. Substituting for \(\{\varepsilon _{b0}\}, \{k\}, \{k^*\}, \{\varepsilon _{s0}\}, \{k_s\}\) and \(\{E\}\) in Eq. (12), U can be written as:

$$\begin{aligned} U=\frac{1}{2}\{d\}_e^T[K_{uu}]_e\{d\}_e-\frac{1}{2}\{d\}_e^T[K_{u\phi }]_e\{\phi \}_e \end{aligned}$$
(13)

where

$$\begin{aligned}{}[K_{uu}]_e=\sum _{k=1}^{N}\left[ \int \limits _{V_k}([B]^T[\mathscr {D}(z)]_k[B] \mathrm {d} V_k\right] \end{aligned}$$
$$\begin{aligned} {[K_{u\phi }]_e}&=\left[ \int \limits _{V_{p_1}}[B]^T[\mathscr {E}(z)]_{p_1}[B_\phi ]_{p_1}\mathrm {d} V_{p_1} \int \limits _{V_{p_2}}[B]^T[\mathscr {E}(z)]_{p_2}[B_\phi ]_{p_2}\mathrm {d} V_{p_2}\dots \right. \\&\qquad \qquad \qquad \qquad \quad \left. \dots \int \limits _{V_{p_{N_e}}}[B]^T[\mathscr {E}(z)]_{p_{N_e}}[B_\phi ]_{p_{N_e}}\mathrm {d} V_{p_{N_{e}}}\right] \end{aligned}$$

and \(V_k\) is the volume of the k-th layer, \(V_{p_k}\) is the volume of the \(p_k\)-th piezoelectric layer inside an element and N is the number of lamina.

The element kinetic energy is given by:

$$\begin{aligned} T=\frac{1}{2}\sum _{i=1}^{N}\int \limits _{V_k}\rho _k\left[ \{\dot{u_1}\}^2 + \{\dot{u_1}\}^2 + \{\dot{u_1}\}^2\right] \mathrm {d} V_k \end{aligned}$$
(14)

where \(\rho _k\) is the density of the k-th layer. Substituting the displacements relations (1), Eq. (14) becomes:

$$\begin{aligned} T= & {} \frac{1}{2}\sum _{i=1}^{N}\int \limits _{V_k}\rho _k[{\dot{u}}^2+2z{\dot{u}}{\dot{\theta }}_x+2z^3{\dot{u}}{\dot{\theta }}_x^*+{\dot{v}}^2+2z{\dot{v}}{\dot{\theta }}_y+2z^3{\dot{v}}{\dot{\theta }}_y^*+{\dot{w}}^2\nonumber \\&\quad \quad +z^2{\dot{\theta }}_x^2+2z^4{\dot{\theta }}_x{\dot{\theta }}_x^*+z^6({\dot{\theta }}_x^{*})^2+z^2{\dot{\theta }}_y^2+2z^4{\dot{\theta }}_y{\dot{\theta }}_y^*+z^6({\dot{\theta }}_y^*)^2] \mathrm {d} V_k\nonumber \\= & {} \frac{1}{2}\sum _{k=1}^{N}\int \limits _{V_k}\rho _k \left\{ \begin{array}{ccc} u \\ v \\ w \\ \theta _x \\ \theta _x^{*} \\ \theta _y \\ \theta _y^{*} \end{array} \right\} ^T \begin{bmatrix} 1&0&0&z&0&z^3&0 \\ 0&1&0&0&z&0&z^3 \\ 0&0&1&0&0&0&0 \\ z&0&0&z^2&0&z^4&0 \\ 0&z&0&0&z^2&0&z^4 \\ z^3&0&0&z^4&0&z^6&0 \\ 0&z^3&0&0&z^4&0&z^6 \end{bmatrix} \left\{ \begin{array}{ccc} u \\ v \\ w \\ \theta _x \\ \theta _x^* \\ \theta _y \\ \theta _y^* \end{array} \right\} \mathrm {d}V\nonumber \\= & {} \frac{1}{2}\sum _{k=1}^{N}\int \limits _{V_k}\{{\dot{\bar{u}}}\}^T[I(z)]_k\{{\dot{\bar{u}}}\}\mathrm {d}V \end{aligned}$$
(15)

Substituting Eq. (8) in the relation (15), one obtains:

$$\begin{aligned} T=\frac{1}{2}\{\dot{d}\}_e^T[M]_e\{\dot{d}\}_e \end{aligned}$$
(16)

where

$$\begin{aligned}{}[M]_e=\int \limits _{A_{e}}\sum _{k=1}^{N}\int \limits _{z_{k-1}}^{z_k}[N]^T[I(z)]_k[N]\mathrm {d}z\mathrm {d}A \end{aligned}$$

where \(A_e\) is the area of the element and \(z_{k-1}\), \(z_k\) are the z coordinates of laminates corresponding to the top and bottom surface of the k-th layer.

The total work W is the sum of the work done by the electrical forces \(W_E\) and the work done by the mechanical forces \(W_m\). Using constitutive relations, strain displacement and electric field-electric potential relations, the element electrical energy can be written as:

$$\begin{aligned} W_E= & {} \frac{1}{2}\sum _{k=1}^{N_{pe}}\int \limits _{V_{p_k}}\{E\}_k^T\{D\}_k \mathrm {d}V=\frac{1}{2}\sum _{k=1}^{N_{pe}}\int \limits _{V_{pk}}\{E\}_k^T([e_b]_k\{\varepsilon _b\}+[e_s]_k\{\varepsilon _s\}+[\xi ]_k\{E\}_k) \mathrm {d}V\nonumber \\= & {} \frac{1}{2}\{\phi \}_e^T \int \limits _{V_{p}}[B_\phi ]^T[\xi ][B]\mathrm {d}V \{d\}_e+\frac{1}{2}\{\phi \}_e^T \int \limits _{V_{p}}[B_\phi ]^T[\xi ][B_\phi ] \mathrm {d}V \{\phi \}_e\nonumber \\= & {} \frac{1}{2}\{\phi \}_e^T[K_{\phi u}]_e\{d\}_e+\frac{1}{2}\{\phi \}_e^T[K_{\phi \phi }]_e\{\phi \}_e \end{aligned}$$
(17)

where

$$\begin{aligned}{}[K_{\phi \phi }]_e&=diag\left( \int \limits _{V_{p_1}}[B_\phi ]_{p_1}^T[\xi ]_{p_1}[B_\phi ]_{p_1} \mathrm {d}V_{p_1}, \int \limits _{V_{p_2}}[B_\phi ]_{p_2}^T[\xi ]_{p_2}[B_\phi ]_{p_2} \mathrm {d}V_{p_2}, \dots ,\right. \\&\qquad \qquad \qquad \qquad \quad \left. \dots ,\int \limits _{V_{p_{N_{e}}}}[B_\phi ]_{p_{N_{e}}}^T[\xi ]_{p_{N_{e}}}[B_\phi ]_{p_{N_{e}}} \mathrm {d}V_{p_{N_{e}}} \right) \end{aligned}$$

\([K_{\phi u}]_e=[K_{\phi \phi }]_e^T\) and \(V_p\) is the volume of the piezoelectric layer.

The work done by the mechanical forces is given by:

$$\begin{aligned} W_m= & {} \{\bar{u}\}^T\{f_c\}+\int \limits _{S_{1}}\{\bar{u}\}^T\{f_s\}\mathrm {d}S+\int \limits _V\{\bar{u}\}^T\{f_v\}\mathrm {d}V-\int \limits _{S_{2}}\{E\}^T\{f_\phi \}\mathrm {d}S\nonumber \\= & {} \{d\}_e^T[N]^T\{f_c\}+\{d\}_e^T\int \limits _{S_{1}}[N]^T\{f_s\}\mathrm {d}S+\{d\}_e^T\int \limits _V [N]^T\{f_v\}\mathrm {d}V-\nonumber \\- & {} \{\phi \}_e^T\int \limits _{S_{2}}[B_{\phi }]^T\{f_\phi \} \mathrm {d}S\nonumber \\= & {} \{d\}_e^T\{F_m\}_e+\{\phi \}_e^T\{F_\phi \}_e \end{aligned}$$
(18)

In Eq. (18), \(\{f_c\}\) denotes the concentrated forces intensity, \(\{f_s\}\) and \(\{f_v\}\) denote the surface and volume force intensity, respectively and \(\{f_\phi \}\) denotes the surface charge density. \(S_1\) and \(S_2\) are the surface areas where the mechanical forces and electrical charge are applied, respectively. \(\{F_m\}_e\) are the applied mechanical forces at each element and \(\{F_\phi \}_e\) are the applied electrical charges at each element.

2.6 Equations of Motion

Using Hamilton s principle (11) the resultant global FE spatial model, governing the motion and electric charge equilibrium, is given by:

$$\begin{aligned} \left[ M \right] \left\{ \ddot{d} \right\} + \left[ K_{uu} \right] \left\{ d \right\} +\left[ K_{u\phi } \right] \left\{ \phi \right\}= & {} \left\{ F_m \right\} \nonumber \\ \left[ K_{\phi u} \right] \left\{ d \right\} + \left[ K_{\phi \phi } \right] \left\{ \phi \right\}= & {} \left\{ F_\phi \right\} \end{aligned}$$
(19)

where \(\left\{ d \right\} \) and \(\left\{ \phi \right\} \) are the global mechanical and electrical DoFs vectors, [M] is the global mass matrix, \(\left[ K_{uu} \right] \), \(\left[ K_{u\phi } \right] = \left[ K_{u\phi } \right] ^T\) and \(\left[ K_{\phi \phi } \right] \) are the global mechanical stiffness, mechanical-electrical coupling stiffness and dielectric stiffness matrices respectively. \(\left\{ F_m \right\} \) and \(\left\{ F_\phi \right\} \) are the respective global mechanical and electrical loading vectors.

Next we assume that the electrical DoFs vector in Eq. (19) can be divided into the actuating and sensing DoFs, \(\left\{ \phi \right\} _e=\left\{ \phi _a,\phi _s \right\} ^T\), where the subscripts a and s denote the actuating and sensing capabilities. Hence, considering open-circuit electrodes, and in that case \(\left\{ F_\phi \right\} = 0\), the non-specified potential differences in (19) can be statically condensed and the equations of motion and charge equilibrium become:

$$\begin{aligned} \left[ M \right] \left\{ \ddot{d} \right\} + \left[ K_{uu}^* \right] \left\{ d \right\}= & {} \left\{ F_m \right\} - \left[ K_{u\phi } \right] _a \left\{ \phi \right\} _a \nonumber \\ \left\{ \phi \right\} _s= & {} - \left[ K_{\phi \phi } \right] ^{-1}_s \left[ K_{\phi u} \right] _s \left\{ d \right\} \end{aligned}$$
(20)

where \( \left[ K_{uu}^* \right] = \left[ K_{uu} \right] - \left[ K_{u\phi } \right] _s \left[ K_{\phi \phi } \right] ^{-1}_s \left[ K_{\phi u} \right] _s\).

Equation (20) can be used in smart structures applications such as vibration control, static or dynamic shape control, etc. In shape control applications, the piezoelectric layers are used as actuators. In addition the time-dependent momentum forces become zero. Thus, all the electrical degrees are considered as known quantities and the coupled equations (20) reduce to pure mechanical ones:

$$\begin{aligned} \left[ K_{uu} \right] \left\{ d \right\} = \left\{ F_m \right\} - \left\{ F_{el} \right\} \end{aligned}$$
(21)

where \(\left\{ F_{el} \right\} = \left[ K_{u\phi } \right] \left\{ \phi \right\} \) is the electrical force vector due to the actuation.

2.7 Modal Model in Terms of State Space

The application of the active control methods in dynamic structural problem requires the use of a state space model. Before we obtain this kind of equations, a mode superposition method is adopted to obtain an approximate reduced-order dynamic model of the system with uncoupled equations of motion in the modal coordinates. Hence \(\left\{ d(t) \right\} \) can be approximated by:

$$\begin{aligned} \left\{ d \right\} \approx \sum _{i=1}^r\Phi _j\eta _j = \left[ \Phi \right] \left\{ \eta \right\} \end{aligned}$$
(22)

where \(\left[ \Phi \right] = \left[ \Phi _1, \Phi _2,\cdots , \Phi _r \right] \) is the truncated modal matrix and \(\{ \eta \}= \{\eta _1, \eta _2,\cdots , \eta _r \}\) is the modal coordinate vector. Substituting Eq. (22) into Eq. (20) leads to:

$$\begin{aligned} \left\{ \ddot{\eta } \right\} + \left[ \Omega ^2 \right] \left\{ \eta \right\} = \left[ \Phi \right] ^T \left\{ F_m \right\} - \left[ \Phi \right] ^T \left[ K_{u\phi } \right] _\alpha \left\{ \phi \right\} _\alpha \end{aligned}$$
(23)
$$\begin{aligned} \left\{ \phi \right\} _s = - \left[ K_{\phi \phi } \right\} _s^{-1}\left[ K_{u\phi } \right] _s \left[ \Phi \right] ^T \left\{ \eta \right\} \end{aligned}$$
(24)

Also, using the modal approach, structural damping can be easily introduced as:

$$\begin{aligned} \left\{ \ddot{\eta } \right\} + \left[ \Lambda \right] \left\{ \dot{\eta } \right\} + \left[ \Omega \right] \left\{ \eta \right\} = \left[ \Phi \right] ^T \left\{ F_m \right\} - \left[ \Phi \right] ^T \left[ K_{u\phi } \right] _\alpha \left\{ \phi \right\} _\alpha \end{aligned}$$
(25)

where \(\left[ \Lambda \right] \) is a diagonal modal damping matrix with the generic term \(2\xi _i\omega _i\), where \(\xi _i\) is the modal damping ratio and \(\omega _i\) the undamped natural frequency of the i-th mode.

For control design, the Eqs. (25) and (24) are transformed into state-space form as follows:

$$\begin{aligned} \left\{ \dot{x} \right\} = \left[ A \right] \left\{ x \right\} + \left[ B \right] \left\{ u_\phi \right\} + \left\{ f \right\} \end{aligned}$$
(26)
$$\begin{aligned} \left\{ \phi \right\} _s = \left\{ y \right\} = \left\{ C \right\} \left\{ x \right\} \end{aligned}$$
(27)

where \(\left\{ x \right\} = \left\{ \eta , \dot{\eta } \right\} ^T\) is the state vector, \(\left[ A \right] \) is the system matrix, \(\left[ B \right] \) is the control matrix, \(\left\{ f \right\} \) is the disturbance input vector and \(\left\{ u_\phi \right\} = \left\{ \phi \right\} _\alpha \) is the control input to the actuator.

These matrices are given by

$$\begin{aligned} \left[ A \right]= & {} \begin{bmatrix} \left[ 0 \right]&\left[ I \right] \\ \left[ -\Omega ^2 \right]&\left[ \Lambda \right] \end{bmatrix} \quad \quad \left[ B \right] = \begin{bmatrix} \left[ 0 \right] \\ -\left[ \Phi \right] ^T \left[ K_{u\phi } \right] _a \end{bmatrix} \nonumber \\ \left\{ f \right\}= & {} \begin{bmatrix} \left[ 0 \right] \\ \left[ \Phi \right] ^T \left\{ F_m \right\} \end{bmatrix} \quad \quad \left[ C \right] = \begin{bmatrix} -\left[ K_{\phi \phi } \right] _s^{-1} \left[ K_{\phi u} \right] _s \left[ \Phi \right] \left[ 0\right] \end{bmatrix} \end{aligned}$$
(28)

2.8 Control Law

The state-space system Eq. (26) is now applied to the design of an optimal controller. The control algorithm considered here is the linear quadratic regulator (LQR) controller. The control voltage in this case is given by:

$$\begin{aligned} \{u_\phi \} = [G]\{x\} \end{aligned}$$
(29)

in which the feedback control gain [G] is obtained so as to minimize the quadratic cost function of the form:

$$\begin{aligned} J=\frac{1}{2}\int \limits _0^{\infty }\left( \{x\}^T[Q]\{x\}+\{u\}^T[R]\{u\}\right) \mathrm {d}t \end{aligned}$$
(30)

subjected to system equation (26). [Q] and [R] are the semi-positive-definite and positive-definite weighting matrices on the outputs and control inputs, respectively. In our case higher values in [Q] mean that we demand more vibration suppression ability from the controller, while larger values in [R] put more interest in limiting the control effort. Assuming infinite optimization horizon and full state feedback, the control gain [G] in (29) is given by:

$$\begin{aligned}{}[G]=-[R]^{-1}[B]^T[P] \end{aligned}$$
(31)

where [P] is a solution of the Riccati equation.

$$\begin{aligned}{}[A]^T[P]+[P][A]-[P][B][R]^{-1}[B]^T[P]+[Q]=0 \end{aligned}$$
(32)

An advantage of the linear quadratic formulation of the problem is the linearity of the control law, which leads to easy analysis and practical implementation. Another advantage is that the values of the gain and phase margins imply stability, good disturbance rejection and good tracking.

A computer program has been developed in MATLAB to perform all the necessary computations. Reduced integration technique is adopted to avoid shear and membrane locking during computation.

3 Numerical Applications

In this section, the formulation and finite element code developed in the present work is validated with existing results documented in the literature. For static deflection, a piezoelectric bimorph cantilever beam is considered and for dynamic analysis a cantilever piezocomposite plate is considered. After the validation work, shape control and vibration suppression of piezocomposite multilayer plate is investigated.

3.1 Validation Example 1

To validate the static analysis, a piezoelectric bimorph cantilever beam (\(100 \times 5 \times 1\) mm) constructed of two layers of PVDF bonded together and polarized in opposite directions is considered. The total height or thickness is 0.001 m, the length is 0.1 m and the width is 0.005 m. The cantilever is fixed on the left end and electric potential is applied such that the top layer is 0.5V and the bottom layer is 0.5 V. The material properties of the PVDF material are given as: \(E_1= E_2= 2.0 ~E^9 \mathrm{N/m}^2\), \(G_{12} = G_{13} = G_{23} = 7.75~ E^9 \mathrm{N/m}^2\) and \(e_{31} = 0.046~ \mathrm{N/Vm}\). The bimorph beam is modelled using five beam elements of equal length. This particular example has been considered by several researchers (see e.g. [5,6,7]). The numerical results for the present method are compared with results from other methods in Table 1. Veley and Rao [6] used a 2D plane stress element modified with pseudo-nodes to include the electric potential DOF. Tzou and Ye [7], using triangular shell elements which have both mechanical (using FOSDT) and electrical DOFs, showed that they produced better results than the thin solid linear elements used by Tzou [7]. Chee et al. [10] used a mixed finite element model, which uses Hermitian beam elements with electric potential incorporated via the layerwise formulation. The present results fit exactly with those of Chee et al. and has a high correlation with Tzou ’s theoretical shell solutions and the results of Veley and Rao. This comparison suggests that the developed finite element code is capable of analyzing cases where piezoelectric material in the structures is used for actuation.

Table 1 Transverse Displacement w (m) of the bimorph beam
Full size table
Fig. 2
figure 2

The cantilever piezocomposite plate

Full size image

3.2 Validation Example 2

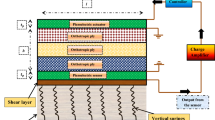
To validate the dynamic analysis, a cantilever composite plate (\(20 \times 20\) cm) with continuous piezoceramic layers bonded to the surface (top and bottom) is considered (Fig. 2). The stacking sequence the composite is antisymmetric angle-ply ([\(-45^o/45^o/-45^o/45^o\)]). The plate is made of T300/976 graphite-epoxy composite and the piezoceramic is PZT G1195N. The material properties are given in Table 2. The total thickness of the composite is 1 mm and each layer has the same thickness (0.25 mm); the thickness of each PZT is 0.1 mm. The plate is modelled using the present nine-node elements with a mesh size of \(6 \times 6\). The first ten circular frequencies based on the present element are compared with those obtained by Lam et al., [8] in Table 3. Lam et al. [8] used a rectangular nonconforming plate bending element based on classical plate theory. It can be easily observed that the present values are showing good agreement with the results of Lam et al. and the difference between the results are within the expected line. The minor difference was expected because the model of Ref. [8] used low order classical displacement field.

Table 2 Material properties of T300/976 graphiteepoxy composites and PZT G1195N piezoceramics
Full size table
Table 3 Natural frequencies (in Hz) for the piezocomposite plate
Full size table

3.3 Shape Control Applications

Having validated the model and finite element method code, we present a numerical example to demonstrate the use of this code for the simulation of the response of laminated composite plates with integrated piezoelectric sensor and actuator in active deformations and vibration control. The physical model is the same as in the previous dynamic study.

First, the static analysis and deformation control of the composite plate are presented. In the static analysis, all the piezoceramics on the upper and lower surfaces of the plate are used as actuators. Equal voltages with opposite signs are applied across the thickness of the upper and lower piezoelectric layer, respectively. Figure 3 shows the corresponding displacements at the tip point A for different applied actuator voltages under different symmetric angle-ply lay up \([p/ \theta / \theta / \theta / \theta /p]\) and antisymmetric angle-ply layup \([p/ \theta / \theta / \theta / \theta /p]\). It can be concluded from Fig. 3 that there is a linear relationship between the plate s centerline deflection and the actuator ’s input voltage. Also, it is observed that with an increase in the angle \(\theta \), an increase of tip deflection is obtained under same applied actuator voltage in both type of layup. However, deflection is more in case of the symmetric angle-ply lay up than the antisymmetric angle-ply lay up.

Fig. 3
figure 3

Effect of symmetric and asymmetric ply orientation on the deflection of point A for different applied voltage

Full size image

For practical applications one would like to know the optimal actuation value with respect to a given shape control task. A first attempt has been done here by classical trial and error techniques. After some numerical experiments the more satisfactory results are shown in Fig. 4.

The centerline deflection under the action of a uniform distributed load of \(100\, \mathrm{N\,m}^{-2}\) for different values of the actuation is shown in Fig. 3. The task has been the reduction of plate’s deflections due to loading. The results are directly comparable with that published in paper [8].

Fig. 4
figure 4

The centerline deflection under uniform load and different actuator input voltages

Full size image

3.4 Vibration Control Applications

In order to investigate the active vibration control of the composite plate, the same structure as in validation example 2 is considered again except that the piezoelectric layers are not located on the entire top and bottom faces of the plate. In the present case, only the first six elements near the clamped edge are covered (on the top and bottom) by piezoelectric patches. In vibration control, the upper piezoceramics serve as sensors and the lower ones as actuators. The first six modes are used in the modal space analysis and an initial modal damping ratio for each of the modes is assumed to be \(0.4\%\). The plate is subjected to a vertical impulse at its tip and the disturbance in a structure is suppressed by using the linear quadratic regulator (LQR) as a control measure.

To design the feedback control using LQR, the appropriate selection of the weighting matrices [Q] and [R] plays a vital role. To estimate the weighting matrices and provide an insight into weighting matrices on structural response and actuator voltage, the effect of [Q] and [R] on vibration response and control voltage is investigated in the following.

The value of the [Q] matrix is changed as \((10^5, 10^6, 10^7)~I_{12\times 12}\) in the LQR procedure given by Eqs. (29) and (31), while the value of [R] is kept constant as \([R] = \gamma ~ I_{36\times 36}\) with \(\gamma =1\). One should note that the order of matrix [Q] is determined according to the number of state variables, \(\{x\}\), which is defined by the number of vibration modes considered in the control system. Here, the first six modes the vibration control is considered. Similarly, the order of matrix [R] is determined according to the number of actuators of the system. In the present example, each finite element is assumed to covered by an actuator requiring a dimension of \(36 \times 36\) for matrix [R]. The LQR function in MATLAB is used to find the optimal gain, which decides the gain based on the system matrix, disturbance matrix and control matrix as explained in Eq. (29). Using the determined feedback control, the tip displacement and the control voltage for the first mode of the smart laminated plate are obtained as shown in Fig. 5. It is observed that the higher value of [Q] results in lower settling time but higher applied voltage (Fig. 5).

Fig. 5
figure 5

Effect of the [Q] matrix coefficient on a tip displacement and b applied voltage

Full size image

In another investigation, the coefficient \(\gamma \) of the [R] matrix is changed from 1 to 3 in the LQR procedure, while the value of [Q] is kept constant as \([Q] = 10^5~ I_{12\times 12}\). Next, the feedback gain is determined according to each [R] value. Using the determined feedback control, the tip displacement and control voltage of the first actuator are obtained as shown in Fig. 6. It is observed that increasing the value of the [R] matrix decreases the required electric voltage but, on the other hand, it increases the settling time.

Fig. 6
figure 6

Effect of the [R] matrix coefficient on a tip displacement and b applied voltage

Full size image

4 Conclusion

In this work, a theoretical and FE formulation for the analysis of anisotropic piezocomposite laminated plates was presented. The formulation was based on the third order shear deformation theory that accounts for parabolic distribution of the transverse shear strains through the thickness of the plate and rotary inertial effects and has been extended to incorporate the piezoelectric sensors and actuators layers. To implement the model, a nine-noded isoparametric element with seven degree of freedom per node and one electric degree of freedom per element per piezoelectric layer has been proposed. The element was developed to include stiffness and the electromechanical coupling of the piezoelectric sensor/actuator layers. Numerical experiments using a computer code, whose algorithm is based on the present finite element model, produced results that correlated well with other published results. After the validation work, numerical illustrations have been presented to study shape and vibration control of a cantilever piezocomposite plate. The effects of laminate configuration and applied voltage on shape control of the smart system have been investigated in this simulation study. Finally, the active vibration control performance of the piezocomposite plate was studied by applying LQR optimal control based on full state feedback assumption. The effects of weighting matrices on controlled response of the smart system have also been investigated.

More complicated adaptive fuzzy and neurofuzzy controllers have been recently studied by the authors [22]–[25] and can be used for control applications of the created model. Furthermore, extension to geometric or material nonlinearity is possible, within classical Newton–Raphson approaches.