Abstract
Correlation filter-based trackers (CFTs) with multiple features have recently achieved competitive performance. However, such conventional CFTs simply combine these features via a fixed weight. Likewise, these trackers also utilize a fixed learning rate to update their models, which makes CFTs easily drift especially when the target suffers heavy occlusions. To tackle these issues, we propose a dynamic decision fusion strategy to automatically learn the weight from the corresponding response map, and accordingly, models are adaptively updated based on a reliability metric. Moreover, a novel kernelized scale estimation scheme is proposed by exploiting the nonlinear relationship over targets of different sizes. Qualitative and quantitative comparisons on the benchmark have demonstrated that the proposed approach significantly outperforms other state-of-the-art trackers.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Visual tracking is one of the most important research topics in computer vision. It aims to locate a given target in each frame of a video sequence. Although significant progress has been made over the decades, many challenging problems still remain due to several factors, such as illumination variations, background clutter and occlusions.
In general, tracking methods can be either generative or discriminative. Generative methods tackle the tracking problem as finding the best image candidate with minimal reconstruction error [1, 14, 17]. Comparably, discriminative methods train a classifier to distinguish the target from the background. The representative discriminative methods are the Correlation Filter-based Trackers (CFTs) [2, 4, 7, 10, 11]. They aim to learn a correlation filter from a set of training image patches, and then efficiently locate the target position in a new frame by utilizing the Discrete Fourier Transform (DFT). Bolme et al. [4] firstly introduce the correlation filter method into visual tracking. Henriques et al. [11] propose a Kernelized Correlation Filter (KCF) approach by exploiting the circulant structure of training samples. Based on [7], Bertinetto et al. [2] simply combine the scores of template and color distribution, which has achieved excellent results.
Despite their promising tracking performance, there still exist several problems within the CFTs. First, since the scale space consists of patches of different sizes, such nonlinear classification issue cannot be tackled well by linear correlation filters in [2, 7]. It not only results in inaccurate target position, but also contaminates the training set during updating, which easily leads the tracker to drift. Second, although the fusion strategy of multiple models is incorporated in [2], estimations are roughly combined by a fixed fusion weight regardless of each reliability. Such fusion scheme does not make full use of each feature, and is not robust to drastic appearance variations either. Third, these former CFTs [2, 4, 7, 10, 11] utilize a fixed learning rate to update the filter coefficients and appearance models, which makes trackers unable to recourse to samples accurately tracked long before to help resist accumulated drift error, especially when the target suffers heavy occlusions.
To tackle the above issues, we attempt to build a novel correlation filter-based tracker, which investigates a kernelized scale estimation strategy, learns adaptive memories, and incorporates a dynamic fusion scheme into the tracking framework. First, we propose a novel scale estimation scheme with kernel trick to search in the scale space by exploiting the nonlinear relationship over targets of different sizes. Second, we design a dynamic decision fusion scheme based on Peak-to-Sidelobe Ratio (PSR) [12], which takes color distributions of the target into account to remedy the weaknesses of the Histogram of Oriented Gradients (HOG) [9] features. Third, different from existing CFTs above, an adaptive online learning scheme with PSR as the criterion is proposed to update the models, which helps to decontaminate the training set.
Experiments on Object Tracking Benchmark (OTB) [15] with 51 sequences demonstrate that the proposed tracker achieves superior performance when compared with other state-of-the-art trackers, especially on illumination variation, scale variation, and rotation attributes.
2 Related Work
The CFTs share the similar framework [6]. In this section, we briefly introduce the KCF method [11], which is closely related to the proposed approach.
Given the training samples \(\lbrace \mathbf {x}_i\rbrace _{i=1}^m\), the KCF tracker aims to train a classifier \(f(\mathbf {z})=\mathbf {w}^{\top } \mathbf {z}\) that minimizes the squared error between \(f(\mathbf {x}_i)\) and the corresponding function label \(y_i\), i.e.,
where \(\lambda >0\) is a regularization parameter. According to the Representer Theorem [13], the optimal weight vector \(\mathbf {w}\) can be represented as \(\mathbf {w}=\sum _{i=1}^m \alpha _i \varphi (\mathbf {x}_i)\), where \(\varphi \) is the mapping to a high-dimensional space with the kernel trick, and \(\varvec{\alpha }\) is the dual conjugate of \(\mathbf {w}\) in the dual space, which can be calculated as
where \(\mathcal {F}\) and \(\mathcal {F}^{-1}\) denote the DFT and its inverse, respectively. Given a new patch \(\mathbf {z}\) from the search window in the next frame, the target location can be obtained by searching for the maximal value in response \(\mathbf {\bar{y}}\), namely,
where \(\odot \) denotes element-wise product, and \(\mathbf {\bar{x}}\) is the learned target appearance model.
3 Proposed Approach
In this following section, we detail the proposed approach. The flowchart of the overall estimation and learning procedure is shown in Fig. 1. The proposed method is incorporated with the color information and the HOG features to comprehensively depict the target appearance. In frame t, we first obtain the filter response \(\mathbf {\bar{y}}_{pf} ^{t}\) based on the learned HOG models and filter coefficient, as well as the color scores \(\mathbf {\bar{y}}_{ph} ^{t}\) by utilizing the learned color histogram models respectively. A dynamic decision fusion is then proposed to merge these two estimations to derive the final position response \(\mathbf {\bar{y}}_{p} ^{t}\). Meanwhile, all models are updated adaptively with PSR as a criterion. The final result is obtained by the translation and the scale estimation.
3.1 Translation Estimation
Filter Response via HOG Features. The filter response yielded by the proposed approach in Flow-HOG process is similar to that of KCF. The filter coefficient \(\varvec{\alpha }_{p}^{t}\) can be derived based on 2-dimensional Gaussian-shaped function labels \(\mathbf {y}_{p}\) using Eq. (2). Given the learned target appearance model \(\mathbf {\bar{x}}_{p}^{t-1}\), the filter response \(\mathbf {\bar{y}}_{pf} ^{t}\) of the image patch \(\mathbf {z}_{p}^{t}\) in the new frame is then calculated as in Eq. (3).
Color Scores via RGB Histograms. In Flow-color process, the search window is partitioned into the object region \(\mathcal {O}\) and the background region \(\mathcal {B}\). Similar to [3], we learn two models \(P({\mathbf \Omega }|M_{\mathcal {O}}^{t-1})\) and \(P({\mathbf \Omega }|M_{\mathcal {B}}^{t-1})\) represented by RGB histograms with 32 bins in frame \(t-1\). They correspond to the color distributions of \(\mathcal {O}\) and \(\mathcal {B}\) respectively, and \({\mathbf \Omega }\) denote pixel values.
Subsequently, the pixel-wise posteriors of the object \(P(M_{\mathcal {O}}^t|{\mathbf \Omega })\) in frame t can be calculated using the Bayes’ theorem as
Note that the model priors \(P(M_{\mathcal {O}}^{t})\) and \(P(M_{\mathcal {B}}^{t})\) are given by \(P(M_{\mathcal {O}}^{t})=\frac{N_{\mathcal {O}}^{t}}{N^{t}}\) and \(P(M_{\mathcal {B}}^{t})=\frac{N_{\mathcal {B}}^{t}}{N^{t}}\), where \(N_{\mathcal {O}}^{t}\), \(N_{\mathcal {B}}^{t}\) and \(N^{t}\) denote the pixel numbers of object region, background region and search window, respectively. Finally, the color scores \(\mathbf {\bar{y}}_{ph}^{t}\) in frame t can be calculated using an integral image based on the pixel-wise probabilities \(P(M_{\mathcal {O}}^{t}|{\mathbf \Omega })\).
Dynamic Decision Fusion. We propose the final position response as a linear combination of the kernelized correlation response and the color scores, which arrives at
where \(\xi ^{t}\) is a fusion weight associated with the current PSR value of the filter response. The PSR value is defined as \(\mathrm {psr} (\mathbf {R})=\frac{\max (\mathbf {R})- \mu _\mathrm{{\Theta }}(\mathbf {R})}{\sigma _\mathrm{{\Theta }}(\mathbf {R})}\), where \(\mathbf {R}\) is a response map, and \(\mathrm {\Theta }\) denotes the part of \(\mathbf {R}\) except the sidelobe area around the peak, the mean value and standard deviation of which are \(\mu _\mathrm{{\Theta }}\) and \(\sigma _\mathrm{{\Theta }}\), respectively. Since the color information resists on the target appearance variations, we associate the fusion weight \(\xi ^{t}\) in each frame with the PSR value of current response \(\mathbf {\bar{y}}_{pf} ^{t}\) as \(\xi ^{t}=\varPsi \big (\frac{psr(\mathbf {\bar{y}}_{pf}^{t})}{psr(\mathbf {\bar{y}}_{pf}^{1})}\big )\). Herein, the function \(\varPsi \) which ensures both smoothness and boundness is defined as
where \(\kappa \) and \(\tau \) are tuning parameters of the logistic function.
3.2 Robust Scale Estimation with Kernel Trick
In our approach, a novel robust scale estimation is proposed by learning an extra 1-dimensional scale KCF to search in the scale space. Suppose that the current target size is \(M \times N\). We extract S patches centered at the position obtained in Eq. (5) and at sizes of \(\rho ^n M \times \rho ^n N, n\in \lbrace \lfloor -\frac{S-1}{2} \rfloor , \lfloor -\frac{S-3}{2} \rfloor ,\dots , \lfloor \frac{S-3}{2} \rfloor , \lfloor \frac{S-1}{2} \rfloor \rbrace \), where \(\rho \) is a scale factor. These patches are resized to the same size and vectorized to make up the scale sample \(\mathbf {x}_{s}\). The coefficient of the proposed scale KCF is then trained as
where \(\mathbf {y}_{s}\) are \(1 \times S\) Gaussian-shaped function labels. The test sample \(\mathbf {z}_{s}^t\) is obtained in the similar way of the training sample. The corresponding scale responses \(\mathbf {\bar{y}}_{s} ^{t}\) can be calculated as
where \(\mathbf {\bar{x}}_{s}^{t-1}\) is the learned target scale model, and the current scale is the one which maximizes \(\mathbf {\bar{y}}_{s} ^{t}\).
3.3 Adaptive Updating Scheme
This section introduces an adaptive model learning strategy, which aims to consider different reliable degrees of models via PSR [12] in each frame. A high PSR value of the response map usually implies that the corresponding sample suffers casual occlusion or illumination variations with a low probability. Similar to Sect. 3.1, the updating weight \(\eta _{i}^{t}\) in each frame can be calculated as \(\eta _{i}^{t}=\varPhi _{i}\big (\frac{psr(\mathbf {\bar{y}}_{pf}^{t})}{psr(\mathbf {\bar{y}}_{pf}^{1})}\big ), i\in \lbrace f, h\rbrace \). The function \(\varPhi _{i}\) is defined as
where \(\sigma _i\) and \(\upsilon _i\) are tuning parameters. Accordingly, we update the filter coefficient \(\varvec{\alpha }_{p}^{t}\) and target appearance model \(\mathbf {\bar{x}}_{p}^{t}\) as
where the apostrophe denotes that the model is estimated from frame t alone. The histogram models can be updated similarly as
Considering the fact that the scale difference is usually quite small between two adjacent frames, we use a constant learning weight \(\eta _{s}\) (\(0<\eta _{s}<1\)) to update the scale KCF model as
which also helps to cut down the computational cost. Finally, the process of the proposed method is summarized in Algorithm 1.

4 Implementation and Experiments
4.1 Experimental Setup
The proposed tracker was implemented in MATLAB on a PC with Intel Xeon E5506 CPU (2.13 GHz) and 16 GB RAM. The parameters in our implementation were set as follows. The regularization parameter \(\lambda =0.0001\); the Gaussian kernel was chosen to calculate the kernelized correlation in Eqs. (3) and (8), with the kernel width = 0.5; the size S of the proposed scale KCF was set to 33 and the scale factor \(\rho =1.02\); the parameters of the logistic function were set as \(\kappa =0.3\), \(\sigma _f=0.01\), \(\sigma _h=0.04\), and \(\tau =\upsilon _f=\upsilon _h=6\); the scale learning weight \(\eta _{s}=0.025\). All these parameters were fixed for all sequences.
4.2 Visual Benchmark
We test the proposed approach on OTB [15], compared with 35 state-of-the-art trackers such as Staple [2], BIT [5], CNT [16], RPT [12], KCF [11], DSST [7], CSK [10], and CN [8]. The datasets of OTB contain 51 sequences annotated with different attributes including fast motion (FM), background clutter (BC), motion blur (MB), deformation (DEF), illumination variation (IV), in-plane rotation (IPR), occlusion (OCC), out-of-plane rotation (OPR), out of view (OV), and scale variation (SV).
The precision to evaluate a tracker on a sequence is associated with the Center Location Error (CLE). It denotes the average Euclidean distance between the center locations of \(r_T\) and \(r_G\), where \(r_T\) denotes the tracked bounding box and \(r_G\) denotes the ground truth. The final precision score is chosen from the precision plot for the threshold = 20 pixels. The accuracy metric of a tracker is the overlap score, which is defined as \(\frac{|r_T \cap r_G |}{|r_T \cup r_G|}\), where \(|\cdot |\) represents the number of pixels in this region. The success rate denotes the ratio of the number of successful frames (whose overlap scores are larger than a given threshold \(\varepsilon _0\)) to the total frame number. Trackers are ranked by the Area Under Curve (AUC) of each success plot.
4.3 Qualitative Comparisons
Overall Performance. The overall performance of One Pass Evaluation (OPE) is shown in Fig. 2(a) and (b). Note that only the top 10 trackers are listed. The proposed method ranks first in both precision and success plots. It achieves an 8.1% improvement in mean CLE and 10.1% improvement in success rate over KCF [11], and achieves a 3.9% improvement in mean CLE and 2.2% improvement in success rate over a recent state-of-the-art tracker Staple [2]. Besides, the proposed approach is able to run up to 40 frames per second.
Attribute-Based Comparison. Table 1 shows the attribute-based comparison between different methods, which demonstrates that our tracker outperforms others especially in case of illumination variations, scale variations, and rotations. The tracking results of the five trackers are illustrated directly in Fig. 3. Specifically, the DSST and Staple methods do not perform well in soccer sequence, of which the challenging issues are illumination variations and rotations. The proposed tracker accurately tracks the woman while the CN and KCF methods drift in walking2 sequence with the target undergoing significant scale variations. Since the proposed method updates the models adaptively, our tracker outperforms others in girl sequence when the girl’s face is severely occluded by the man’s.
 ,
,  and
and  performance are indicated by colors.
performance are indicated by colors.Ablation Analysis. In order to validate the effectiveness of the key components of our approach, the comparison between the following variants is shown in Fig. 2(c): (i) the proposed method; (ii) the setting without scale estimation scheme like that in [4, 11]; (iii) the setting using the linear scale estimation scheme which is applied in [2, 7]; (iv) the setting without color information, similar to [4, 7, 11]; (v) the setting without dynamic decision fusion, similar to [2]; (vi) the setting using multi-channel filters, which is applied in [2, 7]; (vii) the setting without adaptive memories, which is similar to [2, 4, 7, 11]. The result demonstrates that each key component of the proposed approach is significantly conducive to the improvement of final tracking performance, especially the kernelized scale estimation scheme.
5 Conclusion
In this paper, we propose a novel scale estimation scheme with kernel trick by exploiting the nonlinear relationship over targets of different sizes. Besides, a dynamic decision fusion strategy is proposed to combine the color information with the HOG features, which makes the translation estimation more robust to both deformations and color changes. Moreover, we design an adaptive online learning scheme in order to decontaminate the training set, which efficiently prevents the tracker from drifting. The proposed tracker has achieved encouraging empirical performance in comparison to other state-of-the-art trackers on OTB, especially on conditions of scale variations, illumination variations, and rotations of the target.
References
Bao, C., Wu, Y., Ling, H., Ji, H.: Real time robust L1 tracker using accelerated proximal gradient approach. In: Computer Vision and Pattern Recognition (CVPR), pp. 1830–1837 (2012)
Bertinetto, L., Valmadre, J., Golodetz, S., Miksik, O., Torr, P.H.: Staple: complementary learners for real-time tracking. In: Computer Vision and Pattern Recognition (CVPR), pp. 1401–1409 (2016)
Bibby, C., Reid, I.: Robust real-time visual tracking using pixel-wise posteriors. In: Forsyth, D., Torr, P., Zisserman, A. (eds.) ECCV 2008. LNCS, vol. 5303, pp. 831–844. Springer, Heidelberg (2008). doi:10.1007/978-3-540-88688-4_61
Bolme, D.S., Beveridge, J.R., Draper, B.A., Lui, Y.M.: Visual object tracking using adaptive correlation filters. In: Computer Vision and Pattern Recognition (CVPR), pp. 2544–2550 (2010)
Cai, B., Xu, X., Xing, X., Jia, K.: BIT: biologically inspired tracker. Trans. Image Process. (TIP) 25(3), 1327–1339 (2016)
Chen, Z., Hong, Z., Tao, D.: An experimental survey on correlation filter-based tracking. Comput. Sci. 53(6025), 68–83 (2015)
Danelljan, M., Häger, G., Khan, F.S., Felsberg, M.: Accurate scale estimation for robust visual tracking. In: British Machine Vision Conference (BMVC), pp. 65.1–65.11 (2014)
Danelljan, M., Khan, F.S., Felsberg, M., Weijer, J.V.D.: Adaptive color attributes for real-time visual tracking. In: Computer Vision and Pattern Recognition (CVPR), pp. 1090–1097 (2014)
Felzenszwalb, P.F., Girshick, R.B., McAllester, D., Ramanan, D.: Object detection with discriminatively trained part-based models. Trans. Pattern Anal. Mach. Intell. (TPAMI) 32(9), 1627–1645 (2010)
Henriques, J.F., Caseiro, R., Martins, P., Batista, J.: Exploiting the circulant structure of tracking-by-detection with kernels. In: Fitzgibbon, A., Lazebnik, S., Perona, P., Sato, Y., Schmid, C. (eds.) ECCV 2012. LNCS, vol. 7575, pp. 702–715. Springer, Heidelberg (2012). doi:10.1007/978-3-642-33765-9_50
Henriques, J.F., Caseiro, R., Martins, P., Batista, J.: High-speed tracking with kernelized correlation filters. Trans. Pattern Anal. Mach. Intell. (TPAMI) 37(3), 583–596 (2015)
Li, Y., Zhu, J., Hoi, S.C.H.: Reliable patch trackers: robust visual tracking by exploiting reliable patches. In: Computer Vision and Pattern Recognition (CVPR), pp. 353–361 (2015)
Schölkopf, B., Smola, A.J.: Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. MIT press, Cambridge (2002)
Wang, N., Wang, J., Yeung, D.Y.: Online robust non-negative dictionary learning for visual tracking. In: International Conference on Computer Vision (ICCV), pp. 657–664 (2013)
Wu, Y., Lim, J., Yang, M.H.: Online object tracking: a benchmark. In: Computer Vision and Pattern Recognition (CVPR), pp. 2411–2418 (2013)
Zhang, K., Liu, Q., Wu, Y., Yang, M.H.: Robust visual tracking via convolutional networks without training. Trans. Image Process. (TIP) 25(4), 1779 (2016)
Zhang, T., Liu, S., Ahuja, N., Yang, M.H., Ghanem, B.: Robust visual tracking via consistent low-rank sparse learning. Int. J. Comput. Vis. (IJCV) 111(2), 171–190 (2015)
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Grant 61572315, Grant 6151101179, in part by 863 Plan of China under Grant 2015AA042308.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Peng, C., Liu, F., Yang, H., Yang, J., Kasabov, N. (2017). Correlation Filters with Adaptive Memories and Fusion for Visual Tracking. In: Liu, D., Xie, S., Li, Y., Zhao, D., El-Alfy, ES. (eds) Neural Information Processing. ICONIP 2017. Lecture Notes in Computer Science(), vol 10636. Springer, Cham. https://doi.org/10.1007/978-3-319-70090-8_18
Download citation
DOI: https://doi.org/10.1007/978-3-319-70090-8_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70089-2
Online ISBN: 978-3-319-70090-8
eBook Packages: Computer ScienceComputer Science (R0)



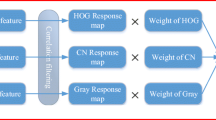


 and the color scores from
and the color scores from  . After that, the current scale is then obtained by the proposed scale estimation with kernel trick to achieve the final result. (Color figure online)
. After that, the current scale is then obtained by the proposed scale estimation with kernel trick to achieve the final result. (Color figure online)
