Steady and Unsteady Shock Interactions by Shock Fitting Approach

Abstract

The numerical solution of shock interactions has been a challenge since the beginning of the computational fluid dynamics age. Different approaches have been introduced with the goal of making the approach either a general purpose one or suitable to solve a specific family of problems. Among them Moretti’s floating shock fitting approach has played an important role, especially for unsteady problems, where the mesh resolution needed to accurately solve the problem with other approaches was rather difficult to obtain. In this paper the authors present a review of steady and unsteady problems with shock interactions they have computed using a floating shock fitting approach.

1 Introduction

In the last decades computational fluid dynamics (CFD) has grown its predicting capabilities becoming more and more an indispensable design tool. The most successful numerical approaches have undergone both a refining process, eventually leading to robust codes able to treat a wide range of complex problems, and an analysis of the limits connected to their own nature, that continues to encourage the study of less popular approaches. One of them is the shock fitting technique, left aside after its success in the sixties and seventies [8], and being still considered as an option by a few researchers [14, 24, 25]. The main merit of shock fitting is its capability of considering shocks as discontinuities, that is as they actually are in all scales larger than the molecular scale. Moreover, it allows discretizing the equations without passing through the formulation in “conservation” variables. The latter merit greatly reduces the numerical error because of the “quasi-linear” form of the equations and especially because of the possibility of naturally describing wave propagation phenomena, respecting the domains of dependence. These merits yielded the solution of the inviscid blunt body flows by just a few dozens of cells [10].

While shock fitting was considered the best approach to solve blunt body flows, where the shock was taken as a boundary of the computational domain, it enjoyed less success for complex problems featuring multiple shocks. Nevertheless, attempts were done to make the approach as general as possible for two-dimensional problems including inviscid and viscous flows in both steady-state and unsteady regimes, and also to solve specific three-dimensional problems [2]. The most general technique was that of letting shocks move over a fixed grid: it was referred to as floating shock fitting [6]. In this paper results obtained by using the floating shock fitting technique for steady and unsteady shock interactions are presented. The technique is coupled with a solver of governing equations for the “continuous” regions of the flow. The solver is an extension to viscous flow of the “lambda-scheme” introduced by Moretti [4]. Further extension to more complex problems has been made on the basis of a multi-block procedure introduced in [15].

2 Governing Equations

The governing equations for the present study of steady and unsteady turbulent compressible flows are the two-dimensional (linear and axisymmetric) Reynolds-Averaged Navier-Stokes equations (RANSE), written in nonconservative form. They are integrated by an explicit second-order time and space accurate scheme that follows Moretti’s “lambda” formulation for the convective terms, and uses central differencing for the viscous terms [13]. Turbulence is treated according to the one-equation model of Spalart and Allmaras, including a correction that takes into account the effect of compressibility in shear-layers [23, 26]. The present technique features less nonlinearity than the conservative form and thus it yields the same error with less cells in the inviscid regions of the flow field. Moreover, it does not require any flux limiter like those needed in conservative approaches to capture shocks, provided that shocks are treated as discontinuities by shock-fitting.

Following the approach proposed in [3], which analyzes the mathematical properties of the non-conservative form of Navier-Stokes equations written in terms of speed of sound a, velocity v, and entropy s, the equation set is considered here in nondimensional variables as:

$$\displaystyle \begin{aligned} \frac{1}{\delta} \frac{Da}{Dt} + a \nabla \cdot \mathbf{v} - a \frac{Ds}{Dt} = 2 \delta a V_s \end{aligned} $$

(1)

$$\displaystyle \begin{aligned} \frac{D \mathbf{v}}{D t} + \frac{a} {\delta} \nabla a - a^2 \nabla s = \mathbf{V}_m \end{aligned} $$

(2)

$$\displaystyle \begin{aligned} \frac{Ds}{Dt} = V_s \end{aligned} $$

(3)

where t denotes time, γ the ratio of specific heats, δ = (γ − 1)/2, and the nondimensional viscous terms V _s , V _m are:

$$\displaystyle \begin{aligned} \begin{array}{rcl} V_s &=& (\nabla \cdot \mathbf{q} + \nabla \mathbf{v} : \mathbf{T} ) /( \gamma p) \end{array} \end{aligned} $$

(4)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathbf{V}_m &=& (\nabla \cdot \mathbf{T})/(\rho) \end{array} \end{aligned} $$

(5)

where p denotes pressure, ρ density, T the stress tensor and q the heat flux.

The numerical integration of (1)–(3) is based on the separation of the role of the viscous terms, whose derivatives are discretized by central differencing [13], from the convective terms, which are treated following the λ-scheme [6] by upwind differences, to emphasize the effect of the propagation of signals.

As a consequence, the left-hand sides of the Eqs. (1)–(3) are reformulated following [6]. The propagation phenomenon is simulated by signals running along four bicharacteristic lines and the streamline direction. In particular, assuming an orthogonal grid and two unit vectors i, j, orthogonal to each other and parallel to the coordinate lines at each point, the equations are recast, using the two velocity components u = v ⋅i, and v = v ⋅j, as:

$$\displaystyle \begin{aligned} \begin{array}{ccl} a_t\hspace{-0.15em}\hspace{-0.15em} &=& \hspace{-0.15em}\hspace{-0.15em}\delta (f_1^x+f_2^x+f_1^y+f_2^y+2\delta a V_s+as_t) \\ u_t\hspace{-0.15em}\hspace{-0.15em} &=& \hspace{-0.15em}\hspace{-0.15em}f_1^x-f_2^x+f_3^y+\mathbf{V}_m \cdot \mathbf{i} \\ v_t\hspace{-0.15em}\hspace{-0.15em} &=& \hspace{-0.15em}\hspace{-0.15em}f_1^y-f_2^y+f_3^x+\mathbf{V}_m \cdot \mathbf{j} \\ s_t\hspace{-0.15em}\hspace{-0.15em} &=& \hspace{-0.15em}\hspace{-0.15em}f_4^x+f_4^y+V_s \end{array}\end{aligned} $$

(6)

where the subscript () _t denotes the time derivative and the terms $f_p^q$ indicate the convective contributions along each bicharacteristic line. For instance, $f_1^x$ is the contribution carried along the bicharacteristic $\lambda _1^x$ to the propagating signal, $f_2^x$ is the contribution along the bicharacteristic $\lambda _2^x$, and so on. In particular, they are:

$$\displaystyle \begin{aligned} \begin{array}{ccl} f_1^x&=&-{\mit 0.5} \lambda_1^x[(R_1^x)_X-v\alpha_X-as_X]\\ f_2^x&=&-{\mit 0.5} \lambda_2^x[(R_2^x)_X+v\alpha_X-as_X]\\ f_3^x&=&-\lambda_3^x(v_X+u\alpha_X)\\ f_4^x&=&-\lambda_3^x s_X \end{array} \end{aligned} $$

(7)

$$\displaystyle \begin{aligned} \begin{array}{ccl} f_1^y&=&-{\mit 0.5} \lambda_1^y[(R_1^y)_Y+u\alpha_Y-as_Y]\\ f_2^y&=&-{\mit 0.5} \lambda_2^y[(R_2^y)_Y-u\alpha_Y-as_Y]\\ f_3^y&=&-\lambda_3^y(u_Y-v\alpha_Y)\\ f_4^y&=&-\lambda_3^y s_Y \end{array} \end{aligned} $$

(8)

where the subscripts () _X and () _Y denote space derivatives in the X and Y directions, respectively, and α in the above equations and G in the following are the metric coefficients of the mapping between the computational (X,Y ) and the physical (x,y) planes, as defined in [6]. The other terms appearing in (7)–(8) are defined as:

$$\displaystyle \begin{aligned} \lambda_1^x=G(u+a), \; \; \; \; \lambda_2^x=G(u-a), \; \; \; \; \lambda_3^x=G u \end{aligned} $$

(9)

$$\displaystyle \begin{aligned} \lambda_1^y=G(v+a), \; \; \; \; \lambda_2^y=G(v-a), \; \; \; \; \lambda_3^y=G v \end{aligned} $$

(10)

$$\displaystyle \begin{aligned} R_1^x=a/\delta+u, \; \; \; \; R_2^x=a/\delta-u \end{aligned} $$

(11)

$$\displaystyle \begin{aligned} R_1^y=a/\delta+v, \; \; \; \; R_2^y=a/\delta-v \end{aligned} $$

(12)

The integration of (6) is performed following the two level explicit scheme, having second-order accuracy, described in detail in [6], and extended to viscous flows in [13].

3 Floating Shock-Fitting

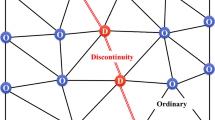
In the framework of shock-fitting, an important step towards a technique capable of handling complex flow configurations, including shock interactions, was undertaken by Moretti with the development of the floating shock-fitting, which led to the outstanding results presented in [7] and relevant to typical shock interaction test cases. Some details of the technique were only published in [5], whereas more details are presented now in [9]. In the floating shock-fitting the discontinuities are allowed to move (float) freely over a fixed background structured grid. A shock front is described by its intersections with grid lines, which give rise to shock points, as shown in Fig. 1.

Fig. 1

Shock points: (open circle) x-shock, (filled circle) y-shock

Moretti’s claim was that shock fitting codes were simple and provided fast and accurate solutions if coupled with a suitable solver of Euler equations, as the λ-scheme proposed by himself. He started from the assumption that shock-fitting simplicity was obvious in 1D problems, where the shock depends on its environment through a Riemann variable which can be correctly computed on both sides of the shock. In a one-dimensional problem, the values of the variables in the mesh node on the low pressure side of the shock () _A and the value of one Riemann variable (R = 2a/(γ − 1) ± u, where a is the local speed of sound and u the local velocity) in the mesh node on the high pressure side are correctly computed by λ-scheme [6]. On the other hand, the values on the high pressure side of the shock () _B will be updated by means of the Rankine-Hugoniot relations once the shock strength M _s , defined as:

$$\displaystyle \begin{aligned} M_s= \frac{|{u}_A-W_s|}{a_A} \end{aligned} $$

(13)

has been computed. To evaluate M _s , a new variable Σ is introduced [11], computed from the variables on the low pressure side and the Riemann variable on the high pressure side of the shock as:

$$\displaystyle \begin{aligned} {\mit \varSigma} = ( a_B + \delta |{u}_A-{u}_B | )/a_A \end{aligned} $$

(14)

Since Σ can also be expressed as a monotonic increasing function of M _s :

$$\displaystyle \begin{aligned} {\mit \varSigma}=\frac{ \left[\sqrt{(\gamma M_s^2 - \delta) (1+\delta M_s^2)} +\delta(M_s^2-1) \right]} {(1+\delta)M_s} \end{aligned} $$

(15)

the shock strength M _s is obtained by inverting (15).

According to Moretti, simplicity is not lost in two dimensions, where the equations are only slightly altered by a slope factor and one more Rankine Hugoniot condition. The topological problem of evaluation of shock slope was solved by suitably analyzing the shock point neighborhood. Before looking to neighbors let us consider first with a closer attention what is a shock point and how it can be classified and used in numerical simulations. When a shock occurs in a two-dimensional field it can cross one or both families of coordinate lines. Therefore we can identify x and y shocks accordingly. Moreover, for each of them one can identify the high pressure side of the shock. The solution of the topological problem of shock slope evaluation was found storing information relevant to shock points in single arrays without ordering them in any particular way. Shock slope was therefore obtained looking to the immediate neighborhood of the shock point. Let us consider, for instance, the x shock point J sketched in Fig. 2. Its neighborhood is made by the two cells surrounding it. The task of identifying which is a neighboring shock point of a given shock point as J in Fig. 2, if any exist, is carried out as follows. In case of ordinary shock points, which are defined as shock points J with no more than two shock points in their neighborhood, one (J _i , i = 1, 3, 5) in the mesh above (right) and/or one (J _j , j = 2, 4, 6) in the mesh below (left). In the general case, the connection of the shock points around J used to compute θ _s (the shock angle with respect to coordinate line directions) has to be carried out according to a physical criterion based on the domain of dependence. From this point of view, two cases are possible:

• 1. sup-shock when the velocity component along the shock direction ($\tilde {v}$) is such that $|\tilde {v}_A|>a_A$ and $|\tilde {v}_B|>a_B$ (note that $\tilde {v}_A=\tilde {v}_B$). In this case no signal can propagate upstream in the direction tangential to the shock, being the flow supersonic in that direction at both sides of the shock. As a consequence, no J _i which is downstream of J along the shock can affect the computation of θ _s in J. Therefore, only the shock point located upstream of J is used to compute θ _s , and the direction J-J _i is taken as the shock direction.

  Fig. 2

  

  Possible shock points around: (a) an x-shock; (b) a y-shock

• 2. sub-shock when $|\tilde {v}_A|<a_A$ or $|\tilde {v}_B|<a_B$ ($\tilde {v}_A=\tilde {v}_B$). In this case θ _s is computed taking the direction J _i -J _j .

The technique is also able to deal with shock interaction so also triple or multiple shock points may occur. A shock point is defined as a triple shock point if either two of J₁, J₃ and J₅ or two of J₂, J₄ and J₆ exist (Fig. 2). Let us consider the example of an x-shock in Fig. 3. If J, J₄, and J₃ have the high pressure side on the right, and J₁ on the upper side, then J is actually a triple point and requires a specific treatment, whereas J₁ and J₃ are ordinary shock points. θ _s is computed taking the direction J_P-J₄ as the shock direction, where J_P is the middle point of the line J₁-J₃. During the computation, particularly in the case of transient flows, it may happen that many shock points are close to each other. If there are both two or three compatible shock points above J and two or three compatible shock points below J (Fig. 2a), θ _s is obtained with a procedure similar to that used for triple points, considering a suitable averaging of compatible shock point positions. The floating shock-fitting technique is completed by specific procedures able to move shock points along the grid according to computed shock velocity, detect the formation of new shocks [12, 17] and the possible weakening of shocks up to disappear.

Fig. 3

Triple shock point

The procedure can also include fitting of contact-discontinuities as can be of interest for specific problems. Procedure is not much different than for shocks. Contact discontinuities (CD) are fitted following a procedure similar to the shock fitting, but only those existing at the beginning of the computation have been considered in this floating shock fitting approach, without performing any detection. A set of indices and variables identical to that for a shock point is introduced for a CD point, and the calculation of the local slope, the displacement, and the introduction of connecting points follow the same procedure as for the shocks. The main difference concerns the enforcement of the relations across the CD. Only two kinds of CD are defined: x-CD, and y-CD. Moreover, () _A denotes the left (lower) side and () _B the right (upper) side.

The value of variables at the mesh nodes near a CD computed in the first integration step are not correct on either side of the discontinuity. But, in a frame of reference moving with the CD, the variables $R_1^x$ in the mesh node at the left side of an x-CD and $R_2^x$ in the mesh node at its right side (see Eq. 11) are computed correctly. Let us now introduce the components of flow velocity in the direction normal to local CD direction, $\tilde {u}$, and in the direction parallel to local CD direction, $\tilde {v}$. The CD relations

$$\displaystyle \begin{aligned} \tilde{u}_A=\tilde{u}_B=W_c \end{aligned} $$

(16)

$$\displaystyle \begin{aligned} p_A=p_B \end{aligned} $$

(17)

along with the definitions

$$\displaystyle \begin{aligned} a_A+\delta \tilde{u}_A = \delta (R_1^x)_A \end{aligned} $$

(18)

$$\displaystyle \begin{aligned} a_B-\delta \tilde{u}_B = \delta (R_2^x)_B \end{aligned} $$

(19)

provide the equations for the calculation of the unknowns $\tilde {u}_A$, $\tilde {u}_B$, a _A , a _B , and W _c . The mesh nodes on the left and right side of the discontinuity are updated with the values of variables resulting from interpolation between their values in () _A and () _B , respectively, and their values at the next nodes (for instance, interpolation for node N, on the left side of an x-CD lying between N and N + 1 is made using the values in node N − 1 and the values in () _A ). The values $\tilde {v}_A$, s _A , and $\tilde {v}_B$, s _B are independent of each other. They are correctly computed in the first step of the integration, since they are not affected by signals propagating across the CD.

Summarizing, each time iteration of the integration process can be organized in six main steps to be considered in any computations that may include shocks:

• 1. Integration of the equations over all the mesh nodes, according to the λ-scheme.

• 2. Detection of the formation of new shocks.

• 3. Calculation of the local slope of the shocks.

• 4. Enforcement of the Rankine-Hugoniot jump conditions between the two sides of each shock point.

• 5. Displacement of the shock points, according to the velocity of propagation of the shock front.

• 6. Check of crossing of shock and grid lines introducing markers [5, 7, 9] or connecting shock points [17].

Four more steps have to be added to the above six steps of the integration technique if also contact discontinuities are fitted:

• 7. Calculation of the local slope of the CD.

• 8. Enforcement of the CD relations across the discontinuity.

• 9. Displacement of the CD.

• 10. Introduction of connecting CD points.

4 Multi-Block Approach

The approach described in the foregoing sections is extended to overlapping multi-block mesh structures, that permit a suitable distribution of cells throughout the computational domain while preserving a structured distribution and reasonable cell aspect ratio. The equations are treated at the block boundary as in the inner nodes by introducing ghost nodes and by using bilinear interpolation, whereas a peculiar interpolation procedure is introduced to correctly treat shocks.

4.1 Governing Equations

At boundaries some of the spatial derivatives cannot be computed by differences among values at nodes inside the block, because some signal will propagate from outside the block, except for the case of supersonic outflow. In general, signals propagating from outside can be obtained by enforcing the proper boundary condition, whereas in case of boundary between blocks the missing derivatives must be inferred from the solution in the neighboring block. An approach that preserves the accuracy of the method, while maintaining a general easy-to-implement coding, is that of using two rows of ghost nodes outside the block. In general, considering all of the boundaries of the block, two rings of ghost nodes are defined as shown in Fig. 4, whose position is obtained by smoothly prolonging outside of the block the inner node distribution.

Fig. 4

Ghost points

To make it possible that the solution at the ghost nodes is interpolated from that of the neighboring block, such nodes are required to lie inside the neighboring block, or in other words, they have to be such that there are no mesh-size holes between neighboring blocks. A possible configuration is drawn in Fig. 5, where only the ghost nodes of the left block (block 1) are displayed for the sake of clarity. The generic ghost point A lies inside a real cell BCED of the neighboring block (block 2) and the solution of the generic function $\mathcal {F}_A$ at the point A is obtained by the bilinear interpolation

$$\displaystyle \begin{aligned} \mathcal{F}_A=\mathcal{A} + \mathcal{B} \hat{x}_A + \mathcal{C} \hat{y}_A + \mathcal{D} \hat{x}_A \hat{y}_A \end{aligned} $$

(20)

where the coordinates of the node A in the frame of reference $(\hat {x}, \hat {y})$ having origin in B and axes directed as BC and BD are known, whereas $\mathcal {A}$, $\mathcal {B}$, $\mathcal {C}$, and $\mathcal {D}$ are computed by solving at each step and for each variable the 4 × 4 linear system obtained applying (20) in B, C, D, and E, respectively.¹ Then, at the next iteration, the solution in the boundary nodes can be updated as done in the inner nodes because the missing derivatives are obtained from the solution in the inner and ghost nodes, the latter bringing information from the neighboring blocks.

Fig. 5

Interpolation at ghost points

4.2 Shock-Fitting

The use of ghost nodes allows introducing also ghost shock points needed to follow the general shock fitting procedure to transfer information between blocks. In particular, the introduction of ghost shock points is necessary to compute the local shock slope of real shock points at the block boundary and to avoid interpolating across shocks. The procedure used to find ghost shock points is illustrated by the example shown in Fig. 6, where the problem is to find the ghost shock points in the prolongation of block 1, when the shock position is known by the real shock points in block 2. A possible approach is to consider for each ghost cell A₁A₂A₄A₃ a quadrilateral B₁C₂ED, that is the smallest group of cells large enough to include the whole ghost cell. Once the quadrilateral is defined, it is possible to look for shock points along its boundaries, and, in case some are found, connect them by straight lines and find the intersection of these lines with the boundaries of the ghost cell. In the example of Fig. 6 the procedure finds the shock points S₁ and S₄, and the intersection of S₁S₄ with A₁A₃ and A₃A₄ provides the ghost shock points T₁ and T₂, respectively.

Fig. 6

Ghost shock points

5 Steady Interactions

The approach described in the foregoing sections is suited to time-accurate computations of unsteady problems. However, it can also be used to solve problems having a steady state solution through a numerical transient in time. A bunch of solutions for steady state problems is therefore reported first to show the capability of the technique to solve problem with shock reflections and interactions.

5.1 Regular Reflection

The first case of shock interaction that is analyzed here is the regular reflections occurring in a planar converging channel. A supersonic flow with a Mach number M = 3 enters a 2D plane duct, whose geometry displays two regions with constant area sections joined through a ramp of 10^∘ slope, and having a contraction ratio of 0.65. Mach number flowfield computed with a 70 × 20 grid is shown in Fig. 7. The straight shock wave originated at the first concave corner reaches the lower wall. A suitable boundary condition has to be considered for shock points moving along walls, as can occur for inviscid problems, or also on symmetry lines of viscous problems. This boundary condition must allow the shock to be such to keep the flow tangential to the wall. Two possible options exist: the shock is perpendicular to the wall or a regular reflection occurs. Basing on shock relations it can be identified which of the two solutions takes place during the numerical transient, up to the final steady solution. In the test case shown in Fig. 7, regular reflection occurs. Then, the reflected shock propagates back towards the upper wall, is bent while crossing the expansion fan generated at the convex corner, and eventually reaches the upper wall where it experiences a second regular reflection.

Fig. 7

Steady inviscid regular reflection of an oblique shock computed by floating shock fitting

Another example of regular reflection computation is that relevant to a confined jet as shown in Fig. 8. A supersonic plane jet at M = 1.5 expands from a nozzle in a wider channel. The supersonic jet is uniform and the expansion pressure ratio (jet total pressure over ambient pressure) is PR = 7.82, that yields an expansion from M = 1.5 to M = 2. The shear layer between jet and external ambient is simulated under the inviscid hypothesis by a contact discontinuity line. As shown in Fig. 8, the jet expands by a fan centered at the nozzle lip, and the flow takes the outward direction. As a consequence, the flow impinges on the channel wall at an angle, and at that location an oblique shock takes place. Figure 8a shows the Mach number contour lines of the computed flowfield: the expansion waves are reflected on the symmetry axis as expansion waves, that turn the flow toward the axial direction. More downstream, the reflected expansion waves and the shock interact with each other, and are then both reflected on the upper and lower boundaries respectively, as waves of the same family. The computed flowfield includes also a second shock reflection on the upper wall.

Fig. 8

M = 1.5 confined jet test case simulation. (a) Numerical solution of the Mach number flowfield. (b) Numerical (line) and semi-analytical (spaced line) characteristic lines, and numerical slip line (line with dot) and shocks (thick line)

From the point of view of the numerical implementation it is worth to note that because the nozzle lip is a singular point, a specific treatment is needed to handle the discretized form of a finite-differences method. This is achieved here by enforcing the solution of the two-dimensional Riemann problem at that point and at its three closer neighboring points.

The precision of the solution can be assessed close to the nozzle exit section, where the semi-analitical solution of the expansion fan and of its reflection can be easily achieved through a characteristic based computation. Figure 8b shows the comparison of the characteristic lines obtained by the numerical and semi-analytical solutions.

5.2 Mach Reflection

A steady Mach reflection test case has been obtained by simulating a M = 5 flow over a ramp followed by a convex corner. This result is part of a study made to understand the capability of the shock fitting approach to reproduce the hysteresis phenomenon occurring when the free stream Mach number is changed cyclically. In fact, the Mach number for transition from regular to Mach reflection changes depending on the direction of Mach number change: it is higher when Mach number is increasing, lower when transition occurs for decreasing Mach number [22]. More specifically, results reported in [22] are referred to a fluid featuring ratio of specific heats γ = 1.4, to a ramp angle is θ = 26.565, and to a cyclic variation of free stream Mach number between 2.7 and 12.3. The solution obtained at M = 5 shows an example of Mach reflection and the capability to handle this kind of reflection and the triple point by the floating shock fitting approach (Fig. 9).

Fig. 9

Steady inviscid Mach reflection of an oblique shock computed by floating shock fitting

5.3 Overexpanded Jet

A peculiar test case is that of the exhaust of an overexpanded supersonic jet in a quiescent ambient, because of the particular interaction between the shock and the jet boundary, computed as a contact discontinuity. The present test case concerns the exhaust of a supersonic jet at M = 2 in a quiescent ambient. The stagnation to ambient pressure ratio is PR = 5, and therefore the jet to ambient pressure ratio is PR = 0.634. Also in this case the two-dimensional Riemann problem is used to solve the singularity at the nozzle lip, from where a shock and the contact discontinuity introduced to simulate the jet boundary, emanate.

The computed flowfield is shown in Fig. 10 by the Mach number and pressure contour lines. The dashed line indicates the position of the jet boundary. It is worth to remark that the solution of both the shock emanating from the nozzle lip and the reflected shock is superimposed to the analytical solution. It is also interesting to notice the accurate solution of the interaction between shock and contact discontinuity and between expansion waves and contact discontinuity, and the resulting sequence of expansions and compressions due to the external constant pressure ambient.

Fig. 10

M = 2 overexpanded jet test case. (a) Mach number flowfield. (b) Pressure flowfield and slip line (dashed line)

5.4 Interaction of Two Supersonic Jets

The next test aims to show the result of the interaction between a nozzle jet and a supersonic external flow. Two parallel uniform supersonic jets with different Mach numbers and static pressures interacting with each other are considered. The lower (“nozzle”) jet exhausts at M = 2 and at a static pressure lower than the external free jet, that features a flow with M = 4. The internal to external jet pressure ratio is PR = 0.383. The upper boundary features conditions of an unconfined jet, whereas a symmetry line is enforced at the lower boundary. From the nozzle lip a shock, a contact discontinuity, and an expansion fan emanate, and therefore this singular point is treated according to the analytical approach illustrated for the foregoing test cases.

The solution of this test case is shown in Fig. 11, and should be compared with the previous one (Fig. 10). In fact, when compared to the preceding test case, the interaction of the reflected shock wave with the contact discontinuity line shows a different effect on the evolution of the jet structure. The higher external pressure deviates both the streams towards the lower wall, increasing the lower jet pressure through a shock and decreasing that of the upper flow through a centered expansion. The shock is reflected on the lower wall, and the reflected shock deviates the jet streamlines upwards, in direction parallel to the lower wall. As this reflected shock reaches the jet boundary a two-dimensional Riemann problem takes place. In particular, downstream the interaction point the contact discontinuity, even if it is still directed towards the lower wall, deviates upwards such to yield a weaker shock in the upper flow and a reflected shock in the lower jet.

Fig. 11

Interaction of two supersonic jets. (a) Mach number flowfield. (b) Pressure flowfield and slip line (dashed line)

More downstream, when this new reflected shock—further reflected at the lower wall—reaches again the jet boundary, the phenomenon will repeat itself with lower intensity. The final consequence is that the presence of the external flow changes the characteristics of the internal jet, that does not display the typical sequence of compression and expansion waves shown in the foregoing test case. On the contrary the nozzle jet experiences a sequence of compressions of decreasing intensity, that gradually increase its pressure value, until a uniform pressure is achieved in both flows. The profile of the jet boundary behaves accordingly, with the height decreasing by steps, but practically constant downstream the first two reflected compressions.

5.5 Shock Boundary Layer Interaction

If shocks are able to reach walls and reflect in the inviscid flow theory, this is no longer true in case of viscous flows where a boundary layer develops along the walls. Basic studies of shock boundary layer interaction solutions obtained by floating shock fitting were carried out in [13]. As an example, the supersonic flow over a flat plate followed by a wedge is considered (Fig. 12a). The Mach number of the supersonic stream is M _∞  = 3 and the wedge has a 20^∘ slope. Figure 12a shows the generation of three shocks. The fitting technique allows to solve all of them as shown by the shock points in the figure. Note that the first shock, originating from the flat plate leading edge, starts in a singular point of the computation and its position is known a priori providing a boundary condition for the shock. Inviscid flow solution would show a single shock generated by the concave corner. In the viscous case, besides the flat plate leading edge shock, the concave corner should generate a shock similarly to that of the inviscid case. However, this shock generates an adverse pressure gradient in the boundary layer that consequently separates from the wall. The result is that the boundary layer separation generates a shock before the wedge. Flow reattachment follows with a further change of flow direction and a third shock. Note that, theoretically the two shocks originated at the wedge are slightly converging such to lead, far enough from the wall to the single shock solution foreseen in the inviscid case. This is correctly obtained and shown in Fig. 12a with the present shock fitting approach.

Fig. 12

Shock boundary layer interactions in supersonic flows (adapted from [13]). (a) Flat plate followed by a wedge. (b) Shock impinging on a flat plate

Another example is the reflection of an oblique shock from a rigid wall (Fig. 12b). The free-stream Mach number is M _∞  = 2 and the impinging shock is a shock produced by a 3^∘ deflection. The same mechanism generating two shocks instead of a single one at the wedge occurs in this case. The adverse pressure gradient caused by the impinging shock thickens the boundary layer before the impinging point and yielding a reflected shock anticipating shock impingement. Then, downstream the flow direction is redirected towards the wall by a centered expansion and eventually realigns with the horizontal direction through a second shock wave. Again, the two reflected shocks will eventually merge far from the wall to yield the inviscid solution. Figure 12b shows the fitting of the impinging and of the two reflected shocks that can be easily identified as discontinuities in the flowfield rather than as thick change of property regions that would be shown by shock capturing approaches (unless order of magnitude higher number of cells is considered). These two results show the capabilities of shock fitting to manage the challenging transition from the shock discontinuity, typical of the inviscid region, to the smooth pressure variation in the viscous region where the shock discontinuity vanishes.

5.6 Examples of Application

Steady state solutions of flows with shocks and contact discontinuities have been obtained for different applications. A few examples are reported here. The first one is the case of an unstarted supersonic air intake. The case shown in Fig. 13 is relevant to a mixed external-internal compression air intake operating at M _∞  = 2.25 and whose behavior is discussed in detail in [27]. Being unstarted, some of the incoming mass flow has to be spilled out before entering the air intake duct. This can only occur because of the presence of a strong shock ahead of the intake. A complex shock structure results, as shown in Fig. 13, with the shock fitting technique able to correctly compute both oblique shocks starting at concave corners of the external compression ramp, the strong shock, and the interactions between each oblique shock and the strong shock.

Fig. 13

Shock interaction ahead of an unstarted supersonic air intake

Another application is that of the exhaust jet from a plug nozzle operating in quiescent air. In this case it is advantageous, even in a RANSE simulation, to consider the jet boundary (where mixing with the quiescent air occurs) as a slip line that is fitted as a contact discontinuity. An example of the solution obtained for overexpanded operation is reported in Fig. 14. More examples and details are presented in [20].

Fig. 14

Fitted contact discontinuity in the simulation of overexpanded jet in a plug nozzle

6 Unsteady Shock Interactions

One of the most important properties of shock fitting is its capability to deal with transient flows without requiring local grid refinements moving in time. Examples are reported in the following.

6.1 Unsteady Mach Reflection

An example of computation of unsteady inviscid flows, with shock interaction is that of the unsteady Mach reflection that occurs when a planar moving shock reaches a concave corner. Figure 15 shows the results obtained considering a plane shock (M _s  = 6.69) followed by an inviscid supersonic flow (M = 1.75) which moves from the left in quiescent air towards a concave corner of 10^∘. As the shock enters the ramp a simple Mach reflection occurs. The solution is pseudo-stationary, i.e. similar to itself in time, with the triple point moving along a straight line. The shock evolution in time is shown in Fig. 15. The straight line overlapping the computed triple point trajectory is drawn according to the experimental measure fit reported in [1]. Details of the position of computed shock points at a given time are shown in Fig. 16.

Fig. 15

Unsteady inviscid Mach reflection: comparison of experimental data fit line for triple point evolution and computed shock at different times (shock lines are obtained connecting shock points)

Fig. 16

Unsteady inviscid Mach reflection: computed shock points and the underlying grid lines

6.2 Inviscid Nozzle Flow Transient

The impulsive startup of an overexpanded nozzle has been computed assuming inviscid flow [16]. At the diaphragm rupture a shock wave followed by a contact discontinuity moves inside the converging diverging nozzle. At the first time shown in Fig. 17a three different discontinuities can be identified. From right to left the first one is the front shock which has already propagated from the inlet to the diverging section. It appears as a discontinuity extended from the axis to the wall. Because of the converging-diverging channel it has changed its shape, and its local and average intensity, with respect to the planar uniform shape it had at starting time (when it was placed at the left inlet). The second discontinuity also appears in the divergent section, and it is a shock of the other family. It is only extended a few cells from the upper wall and occurs because of the overexpansion generated by the convex wall. Finally, the contact discontinuity generated at the diaphragm rupture is still in the converging section, and is characterized by a lower propagation speed than the front shock. Note CD bending due to the different flow velocity if one moves from the wall to the axis. The next three time instants (Fig. 17b–d) show the slow propagation and the effect of the overexpansion shock, which now covers the whole cross section. More specifically, in Fig. 17b, the contact discontinuity has reached the divergent section and has passed the overexpansion shock, continuing to follow the front shock which is approaching the divergent section exit. The next two times show that vorticity is being generated behind the quasi-steady overexpansion shock. This vorticity is affecting the contact discontinuity shape that is no longer smooth, and its central part is being significantly slowed down by the peculiar flow generated downstream the overexpansion shock. This solution shows the reliability of fitting both shock and contact discontinuities in impulsive startup problems, provided that this assumption is justified by the problem physics. In fact, when a vortical region affects the contact discontinuity, mixing becomes no longer negligible and, accordingly, the assumption of modeling the original contact discontinuity with a discontinuous front is no longer valid.

Fig. 17

Impulsive startup of an inviscid overexpanded converging-diverging nozzle

6.3 Viscous Nozzle Flow Transient

The viscous nozzle startup of Vulcain engine was one of the most successful applications of the technique from an application point of view, leading to the identification of the phenomenon referred to as “inviscid flow separation”[18] with a modest computational cost as compared to the other attempts made in the 1990s to compute the same phenomenon with software based on shock-capturing schemes. The results shown in the following are relevant to a computational campaign made after the study published in [19]. More specifically, a series of steady-state simulations was carried out because of the slow variation of combustion chamber condition in time, that allowed to neglect time-dependent phenomena. Solutions are relevant to non-reacting RANSE, for prescribed chamber (total pressure and temperature) and ambient (ambient pressure) conditions. Each simulation is identified by the corresponding chamber to ambient pressure ratio (PR). This quasi-steady simulation is started from the less overexpanded conditions (referred to as in the figure as PR = 130, note that the adaptation condition is about PR = 500) and then the solution for PR = 100 is obtained starting from that at PR = 130 and changing the chamber conditions. The same procedure is repeated for the other chamber conditions, that is for PR = 40 the initial condition is the steady state solution for PR = 100, for PR = 30 the initial condition is the steady state solution for PR = 40 and so on. After reaching the minimum PR = 10 the pressure ratio is increased again to show the possible occurrence of hysteresis (i.e., in this case solutions which depend on the initial conditions). Results show that starting from an operating condition with a conventional Mach reflection generated by supersonic nozzle overexpansion, increasing the degree of overexpansion moves towards a peculiar shock structure that the floating shock-fitting approach is able to correctly capture despite the different shock interactions and vortical structures that take place and while keeping always the same grid. The most peculiar shape is that leading to the flow structure known as “restricted-shock-separation” (Fig. 18c–e). In this case an upstream bent shock generates a big vortex which confines the jet in a narrow region close to the wall where a shock boundary layer interaction similar to that shown in Fig. 12b occurs [21]. Note that different solutions can occur at the same PR (see PR = 20) depending on the initial conditions, or in other words on the direction of PR change. This hysteresis phenomenon is confirmed experimentally.

Fig. 18

Mach number flowfield, streamlines, and shock points (filled circle) for the steady-state solutions at varying PR: each solution is taken as initial condition for the next. (a) PR=130. (b) PR=100. (c) PR= 40. (d) PR= 30. (e) PR= 20. (f) PR= 10. (g) PR= 20

7 Conclusions

A floating shock fitting technique following the approach introduced by Moretti has been used to compute different flowfield including fitting of shocks and contact discontinuities as well as shock interactions. Fitting of discontinuities in two-dimensional flows showed to be successful for a high number of problems, especially because of its efficiency in terms of computational cost for the study of flow transients. Some of the results obtained by the authors in a couple of decades have demonstrated the versatility and reliability of the technique.