Two Effective Algorithms for Color Image Denoising

Abstract

We present two effective algorithms for removing impulse noise from color images. Our proposed algorithms take a two-step approach: in the first step, noise color pixel candidates are identified by an impulse detector, and in the second step, only those identified noise candidates in the image are restored by using a modified weighted vector median filter. Extensive experiments indicate that our proposed algorithms have good performance, and are more effective than most of the existing algorithms in removing impulse noise from color images.

1 Introduction

Removing impulse noise is an import and challenging problem in image processing. A lot of researches have been done for this problem. For example, nonlinear filters such as median filter are successfully applied to impulse noise removal in scalar valued images [6]. For a color image, its pixel has three scalar values. Suppose it is encoded by red, green and blue values in RGB color space. Then it is natural to apply the traditional nonlinear filtering techniques to each channel separately [2]. However, such technique does not use the correlation exists among the three different color channels, and therefore may lead to problems that are not present in scalar valued images [1]. Therefore vector processing techniques for color image denoising are desirable.

To our knowledge, vector median filter (VMF) [1] may be the first and the best-known vector filtering technique for its simplicity, robustness and impulse noise removing ability [13]. Since the development of VMF, many vector filtering techniques are proposed. For example, the vector directional filters (VDF) which consider the vectors’ direction is proposed [17]. In [10], the directional-distance filters (DDF) is developed. In [7], a hybrid directional filter (HDF) is proposed by using the output of the VDF and the VMF. Similar to the scalar median filter, the above mentioned vector filters have some undesirable side effects that tend to smear sharp edges and fine details of an image [8]. In order to eliminate such defects, some new vector processing techniques have been developed, see for example [11, 12] and references therein. We remark here that, relaxation Labeling [4] may also be applied to solving color image denoising problem.

Recently, a two-step approach for removing impulse noise from scalar valued images was developed [3, 5]. In this work, we present two effective algorithms for removing impulse noise from color images. Our proposed algorithms take a two-step approach. In the first step, noise color pixel candidates are identified by an impulse detector, and then in the second step, only those identified noise candidates in the image are restored by using a modified weighted vector median filter. Extensive experiments indicate that our proposed algorithms have good performance, and are more effective than most of the existing algorithms in removing impulsive noise from color images.

The remainder of the paper is organized as follows. In Sect. 2, we clarify the problems we are considered. In Sect. 3, we present our denoising algorithms. Experimental results are presented in Sect. 4 and Sect. 5 concludes the paper.

2 Problem Setting

The problem we are considered is the impulse noise removal in color images. Given an M by N noisy image, let $x_{ij}$ be the vector of the given image, let $v_{ij}$ be the impulse noise vector, and let $z_{ij}$ be the noise-free color pixel, for $(i, j)\in \mathcal {I} \equiv \{1, \cdots , M\}\times \{1, \cdots , N\}$, and let p be impulse noise probability. Then impulse noise model is described as,

$$\begin{aligned} x_{ij} = \left\{ \begin{array}{ll} v_{ij} &{}\text {with probability}~ p\\ z_{ij} &{}\text {with probability}~ 1-p\\ \end{array} \right. \end{aligned}$$

(1)

The model (1) gives many kinds of impulse noise for color images. Depending on the type of vector $v_{ij}$, we consider two impulse noise models, called salt-and-pepper noise model, and random-valued impulse noise model. See [9] for example.

For salt-and-pepper noise model, $v_{ij}$ is characterized by the following expression,

$$\begin{aligned} v_{ij} = \left\{ \begin{array}{ll} (d_1, v^G_{ij}, v^B_{ij}) &{}\text {with probability}~ p_1\\ (v^R_{ij}, d_2, v^B_{ij}) &{}\text {with probability}~ p_2\\ (v^R_{ij}, v^G_{ij}, d_3) &{}\text {with probability}~ p_3\\ (d_4, d_5, d_6) &{}\text {with probability}~ p_4\\ \end{array} \right. \end{aligned}$$

(2)

where $d_k$ takes an extreme value for $k = 1,2, \cdots , 6$, and $p_1+p_2+p_3+p_4=1$. In the remainder of the paper, the two extreme values are denoted by $x_{\min }$ and $x_{\max }$, respectively.

In the case of random-valued impulse noise model, we define $v_{ij}$ by using the following model:

$$\begin{aligned} v_{ij} = \left\{ \begin{array}{ll} (r_1, v^G_{ij}, v^B_{ij}) &{}\text {with probability}~ p_1\\ (v^R_{ij}, r_2, v^B_{ij}) &{}\text {with probability}~ p_2\\ (v^R_{ij}, v^G_{ij}, r_3) &{}\text {with probability}~ p_3\\ (r_4, r_5, r_6) &{}\text {with probability}~ p_4\\ \end{array}\right. \end{aligned}$$

(3)

where $r_k$ is independent uniformly distributed random numbers for $k = 1,2, \cdots , 6$, and $p_1+p_2+p_3+p_4=1$.

In the following, we will design two denoising algorithms based on the presented noise models.

3 Our Proposed Method

As we have known, it should consider the correlations that exists among the different color channels in the processing of color image data [1, 8, 14]. However, this correlation property does not need to be considered when detecting impulses in color images. Since for a color vector $X_i=(X^R_i, X^G_i, X^B_i)$, if one of its components is corrupted by impulse, then the whole vector would be contaminated by the impulse. Therefore we can detect impulses in color images by using impulse detection algorithms for scalar valued images.

In the following, we first present the adaptive median filter (AMF) [6], which will be used to identify salt-and-pepper noise in scalar valued images. Then we present our denoising algorithm.

Let $W^s_{ij}$ be a window of size $(2s+1)\times (2s+1)$ centered at location (i, j). More definitely, $W^s_{ij} = \{(k, l) |~ (k,l)\in \mathcal {I}, |k - i| \le s ~ \text {and} ~|l - j| \le s \}$. The observed color image vectors in this window consisting of samples denoted by $X = \{X_1, X_2, \cdots , X_S\}$, with $x_{ij} = X_{(S+1)/2}$, and $S = (2s+1)^2$. The corresponding three individual color channel are denoted as $X^R = \{X^R_1, X^R_2, \cdots , X^R_S\}$, $X^G = \{X^G_1, X^G_2, \cdots , X^G_S\}$ and $X^B = \{X^B_1, X^B_2, \cdots , X^B_S\}$, respectively. We use $X^C$ to represent either of the $X^R, X^G, X^B$.

Algorithm 1

(AMF for scalar valued images)

Initialize $s = 1$, and set the maximum window size be $s_{\max }$. For all pixel location (i, j), do

• 1. Compute $x^C_{\max }$, $x^C_{{med}}$, $x^C_{\min }$, which are respectively the maximum, median and minimum of the pixel values in $W^s_{ij}$.

• 2. If $x^C_{{med}} = x^C_{\max }$ or $x^C_{{med}} = x^C_{\min }$, set $s = s + 1$; otherwise, go to step 4.

• 3. If $s > s_{\max }$, replace $x^C_{ij}$ by $x^C_{{med}}$; otherwise, go to step 1.

• 4. If $x^C_{\min }< x^C_{ij} < x^C_{\max }$, then $x^C_{ij}$ is noise-free; replace $x^C_{ij}$ by $x^C_{{med}}$, otherwise.

Based on the color image noise model (1)(2), we can identify salt-and-pepper noise in color images by using Algorithm 1.

Algorithm 2

(Noise identification)

Let $y^C$ be the image obtained by applying Algorithm 1 to the channel $x^C$. Since noisy pixels take only extreme values $x_{\min }$ or $x_{\max }$, the noise candidate set can be obtained by

$$ \mathcal {N} = \{(i, j) |~ (i,j)\in \mathcal {I}, y^C_{ij}\ne x^C_{ij} ~ \text {and} ~ x^C_{ij} = x_{min}, \text {or} ~ x^C_{ij} = x_{max}\}.$$

We use

$$\mathcal{{N}}^c = \{(i, j)|~ (i,j)\in \mathcal {I},~ \text {and} ~ (i,j) \notin \mathcal {N}\},$$

to denote the set of noise-free pixels.

By using Algorithm 2, we now present our denoising algorithm for removing salt-and-pepper noise from color images.

Algorithm 3

(Denoising algorithm for color images corrupted by salt-and-pepper noise)

1. (Noise identification): Dividing the image vectors into noise-free set $\mathcal{{N}}^c$ and noise corrupted set $\mathcal {N}$ by using Algorithm 2.

2. (Restoration): Let the observed image vectors in $S^w_{ij}$ consisting of samples denoted by $X = \{X_1, X_2, \cdots , X_S\}$, with $x_{ij} = X_{(S+1)/2}$. If $x_{ij} \in \mathcal{{N}}^c$, the output is $x_{ij}$ itself. Otherwise, the output is defined as,

$$ X_{(1)} = \arg \displaystyle \min _{X_k\in X}\displaystyle \sum ^W_{{l = 1}\atop {l \in \mathcal{{N}}^c}} \Vert X_k - X_l\Vert _2,$$

where $l \in \mathcal{{N}}^c$ denotes that $(i,j) \in \mathcal{{N}}^c$ for some $x_{i,j} = X_l$,

$$\Vert X_k - X_l\Vert _2 = \sqrt{(X_k^R - X_l^R)^2 + (X_k^G - X_l^G)^2 + (X_k^B - X_l^B)^2},$$

and $\arg \displaystyle \min$ is argument of the minimum, that is,

$$ \displaystyle \sum ^S_{{l = 1}\atop {l \in \mathcal{{N}}^c}} \Vert X_{(1)} - X_l\Vert _2 = \displaystyle \min _{X_k\in X}\displaystyle \sum ^S_{{l = 1}\atop {l \in \mathcal{{N}}^c}} \Vert X_k - X_l\Vert _2.$$

We can easily see that our proposed algorithm (Algorithm 3) is easy to implement. In the used distance measure, we give zeros weights on the noise color pixels. This strategy ensures more effective impulse removal than other methods in the literature such as VMF.

We now consider to remove random-valued impulse noise from color images. Here we use the rank-ordered logarithmic difference (ROLD) algorithm developed in [5] to identify noise color pixels.

Algorithm 4

(ROLD algorithm)

Let the observed color image vectors in $W^s_{ij}$ consisting of samples denoted by $X = \{X_1, X_2, \cdots , X_S\}$, with $x_{ij} = X_{(S+1)/2}$. Let $D_j(X^C_{(S+1)/2}) = 1 + \displaystyle \max \{\log _2|X^C_j - X^C_{(S+1)/2}|, -5\}/5, ~ \text {for}~ j = 1, 2, \cdots , S, j\ne (S+1)/2.$ Arrange all $D_j$ in an increasing order,

$$ D_{(1)}\le D_{(2)} \le \cdots \le D_{(S-1)}.$$

Define local image order statistics as

$$ \text {ROLD}_l(X^C_{(S+1)/2}) = \displaystyle \sum ^l_{k = 1}D_{(k)}(X^C_{(S+1)/2}).$$

We then identify random-valued impulse noise candidates by using ROLD with threshold $T^C$: a color vector $X_{(S+1)/2}$ or equivalently, $x_{ij}$ is corrupted with impulse noise if one of its component $X^C_{(S+1)/2}$ satisfies $\text {ROLD}_l(X^C_{(W+1)/2}) > T^C$, and it is noise free otherwise.

Now we present our denoising algorithm for color images contaminated by random-valued impulse noise.

Algorithm 5

(Denoising algorithm for color images contaminated by random valued impulse noise.)

1. (Noise identification): Dividing the image vectors into noise free set $\mathcal{{N}}^c$ and noise corrupted set $\mathcal {N}$ by using Algorithm 4.

2. (Restoration): Let the observed image vectors in $W^s_{ij}$ consisting of samples denoted by $X = \{X_1, X_2, \cdots , X_S\}$, with $x_{ij} = X_{(S+1)/2}$. If $x_{ij} \in \mathcal{{N}}^c$, the output is $x_{ij}$ itself. Otherwise, the output is given by,

$$ X_{(1)} = \arg \displaystyle \min _{X_k\in X}\displaystyle \sum ^S_{{l = 1}\atop {l \in \mathcal{{N}}^c}} \Vert X_k - X_l\Vert _2.$$

4 Experimental Results

We conduct two experiments in this section, to exam the noise removal ability of our proposed algorithms. Three $512\times 512$ color images are used in our experiments. These three images are “Lena", “Mandril", and “Lake”, which are shown in Fig. 1. We also compared performance of our algorithms with many other algorithms in the literature, including VMF [1], AVMF [12], MAVMF [12], quaternion based algorithm, denoted by QVMF [8], VDF [17], AVDF [15], DDF [10] and HDF [7].

In the experiments, $3 \times 3$ filter window is used for all above-mentioned techniques. For AVMF, we set $\lambda _1 = 4$, and for MAVMF, we set $\lambda _2 = 12$ [12]. For QVMF, we set the parameter Tol to be 22 as it was set in [8]. For DDF, we set $p = 0.75$ [10]. For AVDF, we use AVDF2, since it performances best in all AVDFs proposed in [15].

We use AMF of maximum size 13 to identify salt-and-pepper noise for Algorithm 3,.

For Algorithm 5, we use ROLD algorithm to identify noise as described. We set $l=4$ and set the window size to be $3\times 3$, and the threshold is set to be $T = s\cdot q$ with $s = 1.9$ if noise ratio is equal or less than 25%; we set $l = 12$, and set the window size to be $5\times 5$, and the threshold is set to be $T = s\cdot q$ with $s = 5.4$ if noise ratio is greater than 25%. Where q is the fraction of the pixels in each color channel whose ROLD values are less than s.

Fig. 1.

Original images. (a) Lena, (b) Mandril, (c) Lake.

To get quantitative measure for the noise removal ability of above mentioned algorithms, the normalized color difference (NCD) and the normalized mean square error (NMSE) are used in this section. Let M, N be the image dimensions, and $x_{ij}$ and $\tilde{x}_{ij}$ be the original image vector and its filtered image vector at location (i, j), respectively. Let $L^*$ and $(u^*, v^*)$ be lightness values and chrominance values corresponding to $x_{ij}$ and $\tilde{x}_{ij}$ samples encoded in CIE $L^*u^*v^*$ color space, respectively. Then NCD is defined as [16],

$$\text {NCD} = \frac{\displaystyle \sum ^M_{i=1}\displaystyle \sum ^N_{j=1} \sqrt{(L^*_{x_{ij}} - L^*_{ \tilde{x}_{ij}})^2 + (u^*_{x_{ij}} - u^*_{ \tilde{x}_{ij}})^2 + (v^*_{x_{ij}} - v^*_{ \tilde{x}_{ij}})^2}}{\displaystyle \sum ^M_{i=1}\displaystyle \sum ^N_{j=1} \sqrt{(L^*_{x_{ij}})^2 + (u^*_{x_{ij}})^2 + (v^*_{x_{ij}})^2}},$$

and NMSE is defined as

$$\text {NMSE} = \frac{\displaystyle \sum ^M_{i=1}\displaystyle \sum ^N_{j=1} \Vert x_{ij} - \tilde{x}_{ij}\Vert ^2_2}{\displaystyle \sum ^M_{i=1}\displaystyle \sum ^N_{j=1} \Vert x_{ij}\Vert ^2_2}.$$

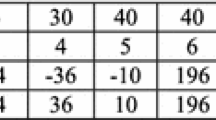
Experiment 1. In this experiment, we test the salt-and-pepper noise removal ability of the above mentioned algorithms. To this end, we use the noise model (1)(2) to corrupt the three original test images by salt-and-pepper noise. In the corruption, different noise levels ranging from 5% to 35% with increments of 10% are carried out. Tables 1, 2 and 3 show respectively, the values of NCD and NMSE for the restored images “Lena”, “Mandril” and “Lake”. Where “Alg3” denotes our proposed algorithm (Algorithm 3). In Fig. 2, we show the restored images by applying VMF, AVMF and Alg5 to the 25% noise corrupted Lena image.

Table 1. Values of NCD and NMSE obtained by different algorithms applied to salt-and-pepper noise corrupted Lena image.

Table 2. Values of NCD and NMSE obtained by different algorithms applied to salt-and-pepper noise corrupted Lena image.

Table 3. Values of NCD and NMSE obtained by different algorithms applied to salt-and-pepper noise corrupted Lena image.

From the Tables 1, 2 and 3 and Fig. 2, we see that Algorithm 3, has lowest NCD and NMSE values and good subjective performance. Moreover, our algorithm is easy to implement. Based on the given results, we draw a conclusion that our proposed algorithm, Algorithm 3, is competitive with most existing algorithms when applied to salt-and-pepper noise removal.

Fig. 2.

Restored images by using different algorithms. (a) 25% salt-and-pepper noise corrupted Lena image, (b) VMF, (c) AVMF, (d) Alg3.

Experiment 2. In this experiment, we test the random-valued impulse noise removal ability of the above mentioned algorithms. To this end, we use the noise model (1)(3) to contaminate the three original test images by random-valued impulse noise. In the corruption, different noise levels ranging from 5% to 35% with increments of 10% are carried out. Tables 4, 5 and 6 show the values of NCD and NMSE for the restored images “Lena”, “Mandril” and “Lake”, respectively. Where “Alg5” denotes our proposed algorithm, Algorithm 5. In Fig. 3, we show the restored image by applying VMF, AVMF and Alg5 to the 25% noise corrupted Lena image.

Table 4. Values of NCD and NMSE obtained by different algorithms applied to random-valued impulse noise corrupted Lena image.

Table 5. Values of NCD and NMSE obtained by different algorithms applied to random-valued impulse noise corrupted Lena image.

Table 6. Values of NCD and NMSE obtained by different algorithms applied to random-valued impulse noise corrupted Lena image.

Fig. 3.

Restored images by using different methods. (a) 25% random-valued impulse noise corrupted Lena image, (b) VMF, (c) AVMF, (d) Alg5.

From the Tables 4, 5 and 6 and Fig. 3, we see that Algorithm 5, has lowest NCD and NMSE values and good subjective performance. Moreover, our algorithm is easy to implement. Based on the above results, we conclude that our proposed algorithm, Algorithm 5, is competitive with the most of other existing algorithms in removing random-valued impulse noise.

5 Conclusions

We present two classes of effective approaches for removing impulse noise from color images. Our proposed algorithms are effective and performance good. Experimental results show that our proposed algorithms have improvements in NCD and NMSE over most of the existing algorithms.