Optimization of Oriented and Parametric Cellular Structures by the Homogenization Method

Abstract

We present here a topology optimization method based on a homogenization approach to design oriented and parametrized cellular structures. The present work deals with 2-D square cells featuring a rectangular hole, because their structure is close to that of rank-2 sequential laminates, which are optimal for compliance optimization. For several cells, the value and the parametric sensitivities of their effective elastic tensor can easily be computed, by the resolution of a cell problem. The obtained results can be used to build a surrogate model for the homogenized constitutive law. Moreover, we add the local orientation of the cells to our problem. Then, an optimal composite shape is computed thanks to an alternate directions algorithm. The crucial ingredient of the methodology is the extraction of a quasi-periodic and additive manufacturable structure from the previously obtained composite shape, based on the introduction of a space transformation.

1 Introduction

We present here a topology optimization method based on a homogenization approach to design oriented and parametrized cellular structures. On one hand, for a large class of shape optimization problems, composite structures, which are mathematically the limits of classical micro-perforated shapes, are known to reach the optimum [1]. On the other hand, the improvement of additive manufacturing (AM) technologies makes possible to manufacture structures with very complex topologies, like periodic cellular structures [14].

The choice of the periodic cells is not trivial and there is a large literature [7] about optimization of periodic cells to achieve some mechanical properties. However, graded cellular structures can be more efficient than periodic cellular structures, since mechanical properties can be locally adjusted to the needs. Several approaches have been explored to optimize such structures. Geihe et al. [10] work on the set of square cells with parametrized elliptic holes and rewrite the topology optimization problem as a parametric one. Other methods are based on the Simplified Isotropic Material with Penalization (SIMP) method [6]. After the selection of a set of density- parametrized cells, an optimal density is computed and then is used to define the final design of each cell which composed the global structure [16]. An alternative consists of optimizing locally the design of each cell, with the constraint that its density is equal to the previously computed optimal density [12]. Wang et al. [18] present a multiscale design method: the microstructure of the cells, parametrized by the density, and the macro distribution of material are both simultaneously optimized.

In the present study, our approach is close to the one developed by Cramer et al. [8, 9], or likewise, by Zhang et al. [19]. A set of parametrized cells is previously fixed. We introduce their effective elastic properties, which are computed by homogenization method and which vary smoothly with the design variables. Then an optimal composite shape, defined by the optimal homogenized fields of parameters is computed thanks to an alternate directions algorithm. One of the originalities of our work is that we do not consider only the density as design variables, but more parameters, whose the cell orientation. In that way, we enlarge greatly the set of reachable elastic tensors.

The main originality of our work is to propose a deshomogenization method, which yields to a smooth and well-connected structure. Indeed, the question of the connectivity between neighbors cells is crucial. Several methods have been developed to take account this constraint, during the cell design optimization [20], or during the multiscale design optimization [18]. Here, thanks to the design of our cells, we do not face this issue. But our method is also generalizable to other kind of cells, without any further limitation. Indeed, we compute optimal continuous fields of design variables (the final size of the cells is not a priori fixed) and the connectivity is ensured by the smoothness of the design parameters.

Otherwise, to deshomogenize a composite structure with isotropic cells, the direct projection of the optimal density on each cell is a natural approach [19]. However, here the optimal cell orientation has to be considered. We introduce a space transformation for this purpose [13]. To prevent a significant distortion of cells during the projection, we regularize the optimal orientation, so that the previous transformation is conformal (i.e. angle-preserving). Thus, the respective elastic behaviors of the projected structure and the optimal composite it is based on remain close to each other.

2 Square Cells

A classical optimization problem in elasticity involves the minimization of the compliance under a volume constraint.

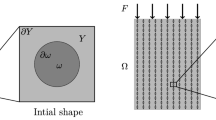
Let D be the optimization domain and $\Omega \subset D$ the reference configuration of an isotropic elastic body. The structure $\Omega$ is clamped on $\Gamma _D \subset \partial \Omega$, and submitted to surface loads g on $\Gamma _N \subset \partial \Omega$. Let u be the displacement in the structure, $\sigma$ the constraint tensor and A the elastic tensor of the material phase:

$$\begin{aligned} \left\{ \begin{array}{l l } div( \sigma ) = 0 &{} \text{ in }\,\, \Omega \\ \sigma = A e(u) &{} \text{ in }\,\,\Omega \\ e(u) = \frac{1}{2} (\nabla u + \nabla u ^T) \\ u=0 &{} \text{ on } \,\, \Gamma _D, \\ \sigma \cdot n = g &{} \text{ on }\,\, \Gamma _N, \\ \sigma \cdot n = 0 &{} \text{ on }\,\, \Gamma = \partial \Omega \setminus (\Gamma _D \cup \Gamma _N) \\ \end{array} \right. \end{aligned}$$

(1)

Given V a target value for the volume, we are interested in the following compliance minimization problem:

$$\begin{aligned} \min _{\begin{array}{c} |\Omega | = V \\ \Gamma _D \cup \Gamma _N \subset \partial \Omega \\ \end{array} } \int _{\Gamma _N} g \cdot u \, ds \end{aligned}$$

(2)

Robust approaches, for instance the level-set method [3] or SIMP [6], are really efficient to find an optimal distribution of material in the design space D. However, they do not consider the option to adapt locally the microstructure of the medium to design a better performing structure. Indeed, the global optimum is known to be reached by composite materials, in particular by laminates of rank-2 (respectively rank-3) laminates in 2D (respectively, in 3D) [1, 4].

Let $G_{\theta }$ be the set of effective elastic tensors for composites structures of density $\theta$ (composed of a void phase and an isotropic elastic phase) and $CD$ be the set of composite designs:

$$ CD =\{ (\theta , A^*) \in L^\infty (D;[0,1] \times \mathscr {M}^4_N) \, | \, A^*(x) \in G_{\theta (x)} \quad \text {a.e. in D} \} $$

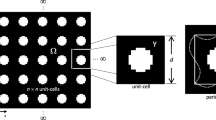
The optimisation problem could be reformulated as a minimization problem on $CD$, however this is not appropriate since the set $G_{\theta }$ is not explicitly known. Thus, we use a subset of $G_{\theta }$, namely the homogenized elastic tensors of a particular class of composites. Even if the laminates are known to be optimal and their elastic tensors have explicit expressions, they are excluded from the admissible set. Indeed they present several scales of material, putting them out of reach of traditional and additive manufacturing processes. Instead, we retain a simple composite already used in the seminal paper [5]: square cells with a rectangular central hole (see Fig. 1). We will denote them by $Y_{sq}(l_1,l_2)$ where $l_1, l_2 \in [0;1]$ are the relative linear dimensions of the hole. The structure of those cells is close to the one of rank-2 laminates with orthogonal lamination directions, which are optimal for compliance minimization problems. Moreover, they do not feature several embedded material scales: a structure made of this composite is more likely to be additive manufacturable. We emphasize the fact that the global optimum can be reached only by multi-scale design cells [2], and consequently no manufacturable structures.

Fig. 1.

Square cell and hole parametrization

Because the considered cell is not isotropic, its effective elastic behavior is orientation-dependent. Hence, there are three optimization variables for the optimization problem (2), namely the functions $l_1(x), l_2(x) \in L^{\infty }(D,[0;1])$ and $\alpha (x) \in L^{\infty }(D,\mathbb {R})$ the angle of rotation of the cells.

The compliance minimization problem (2) does not consist anymore in capturing an optimal shape $\Omega$, but in finding the most efficient microstructure on the whole domain D, with $(\Gamma _N \cup \Gamma _D) \subset \partial D$.

Let $S_{sq} = \{ (l_1, l_2, \alpha ) \in L^{\infty } (D, [0;1]^2 \times \mathbb (R) | \int _D (1-l_1(x)l_2(x)) dx = V\}$ the set of admissible designs. The minimization problem becomes:

$$\begin{aligned} \min _{(l_1,l_2,\alpha ) \in S_{sq} } \int _{\Gamma _N} g \cdot u \, ds \end{aligned}$$

(3)

where u is the solution of (1) with $\Omega = D$ and $A = A^*$.

3 Homogenized Elastic Tensor

3.1 Homogenization Method

The homogenization method has been used in many scientific disciplines, in particular for shape optimization. For the sake of completeness and brevity, only a few important results are recalled here, the interested reader will find more details and proofs in [1]. Let $\Omega$ be a periodic medium of period $\epsilon$, constituted of an isotropic elastic solid phase, with constant Hooke’s tensor A, and a void phase. The distribution is given through the characterisitic function $\chi (y) \in L^\infty _\#(Y,\{0,1\})$. Let $Y = (0,1)^N$ be the rescaled unit periodic cell, where N is the space dimension.

When $\epsilon \rightarrow 0$, the medium can be considered homogeneous, with an effective constant elastic tensor $A^*$. To compute this homogenized tensor $A^*$, we introduce correctors $w_{ij}$ corresponding to the local displacement in the cell Y, defined for each pair $(i,j) \in \{1,...,N\}^2$ by the solutions of the following cell problems [1]:

$$\begin{aligned} \left\{ \begin{array}{ccc} div(A \chi (e_{ij} + e( w_{ij})) ) = 0 \\ y \mapsto w_{ij} \quad \text{ Y-periodic } \\ \end{array} \right. \end{aligned}$$

(4)

where $e_{ij} = \frac{1}{2} (e_i \otimes e_j +e_j \otimes e_i)$ is a basis of the symmetric tensors of order 2. It can be shown that the tensor $A^*$ depends on the solutions $w_{ij}$ of the cell problems:

$$\begin{aligned} A^*_{ijkl} = \int _Y \chi _A(y) \, A (e_{ij} +e(w_{ij})): (e_{kl} +e(w_{kl})) dy \quad \forall i,j,k,l \in \{1,..,N\} \end{aligned}$$

(5)

Because the set of periodic composites is dense in the set of all composites [17], this method can be used to compute the homogenized elastic properties of any composite materials.

3.2 Homogenized Elastic Tensor of $Y_{sq}$ cells

Thanks to homogenization, the effective elastic tensors $A^*(l_1,l_2)$ of the cells $Y_{sq}$ can be computed. The considered cells are orthotropic: $A^*$ is fully characterized by only four of its components, namely $A^*_{1111}, A^*_{1122},A^*_{2222},A^*_{1212}$ in the basis $(y_1,y_2)$.

Let $(l_1,l_2)$ be the sizing parameters of the cell $Y_{sq}$. We solve the three cell problems (4) on $Y_{sq}$, to determine the correctors $w_{11},w_{22}, w_{12}$. The four independent coefficients of the elastic tensor can be calculated using the Eq. (5).

3.3 Parametric Sensitivities of the Homogenized Tensor

Let $Y_{sq}$, and $l_1$ and $l_2$ its sizing parameters. Let $\Gamma _{int}$ be the internal boundary of $Y_{sq}$, separated it in two parts according to the direction of the normal: $\Gamma _{int,m}$ of normal colinear to $y_m$ with $m \in \{1,2\}$, and $\Gamma _{int} = \Gamma _{int,1} \cup \Gamma _{int,2}$. The derivatives of the homogenized elastic tensor of $Y_{sq}$ with respect to $l_m$ is:

$$\begin{aligned} \forall i,j,k,l \in \{1,2\} \quad \frac{\partial A^*_{ijkl}}{\partial l_m} = - \frac{1}{2} \int _{\Gamma _{int,m}} (A(e_{ij} + e(w_{ij})): (e_{kl} + e(w_{kl}))) ds \end{aligned}$$

(6)

3.4 Interpolation of the Homogenized Elastic Tensors and Its Derivatives

Thanks to the previous method, we are able to compute the elastic tensor and its derivatives for any arbitrary set of sizing parameters $(l_1,l_2)$, even if we can not establish a closed-form expression when $(l_1,l_2)$ vary. The proposed strategy consists in computing the material properties for a discrete sample of parameters values and using the collected data to construct a surrogate model for the constitutive law.

The compliance of the cell grows with the size of the hole: the four homogenized coefficients are strictly decreasing, with respect to $l_1$ and $l_2$. This property must be preserved during the interpolation of the elastic tensor. Among the several interpolation methods that were investigated, namely linear interpolation, plines, Kriging, only the linear interpolation ensures the strict monotonicity of the functions. However, using a linear interpolation, the derivatives of the tensor with respect to $l_1$ and $l_2$ can not be properly computed directly from the interpolated coefficients. So the sensitivities have been interpolated separately them likewise. This strategy makes the values of coefficients and their sensitivities inconsistent. However, in practice, this approximation leads to consistent results and so is admissible.

3.5 Cell Orientation

As mentioned in Sect. 4, the considered cells are not isotropic but orthotropic, in other words their elastic behavior depends on their orientation $\alpha$. Let $R(\alpha )$ be the rotation matrix of angle $\alpha$, and $A^*(l_1,l_2,\alpha )$ the effective elastic tensor of a cell $Y_{sq}$ rotated by the angle $\alpha$:

$$\begin{aligned} A^*_{ijkl}(l_1,l_2,\alpha ) = R_{ip}(\alpha ) R_{jq}(\alpha ) R_{kr}(\alpha ) R_{ls}(\alpha ) \, A^*_{pqrs}(l_1,l_2) \quad \quad i,j,k,l,p,q,r,s \in \{1,..,N\} \end{aligned}$$

(7)

Unlike the parameters $l_1$ and $l_2$, the dependency on the orientation $\alpha$ can be written as an explicit expression: the derivatives of the elastic tensor according to $\alpha$ are also formally known. We notice that a rotation of angle $\pi$ yields an equivalent cell: the optimal orientation is so defined modulo $\pi$.

4 Topology Optimization

The optimization problem (3) defined in Sect. 4 is self-adjoint. The associated Lagrangian is:

$$\begin{aligned} \mathscr {L}(l_1,l_2,\alpha , \eta ) = \frac{1}{2} \int _{\Omega } A^{*-1}(l_1,l_2,\alpha ) \sigma : \sigma dx + \eta \int _{\Omega } ((1-l_1l_2) - V_0) dx \end{aligned}$$

(8)

where $\eta$ is the Lagrange multiplier associated with the volume constraint.

We use the projected gradient algorithm to find a stationary point of (8). The descent directions are given by the derivatives of $\mathscr {L}$ with respect to $l_1$, $l_2$ and $\alpha$ (the projection part comes from the box constraints $l_1, l_2 \in [0;1]$). The value of $\eta$ is updated at each iteration by a dichotomy process, to respect the volume constraint.

In practice, the gradient descent method is not really efficient to compute the optimal orientation. Pedersen proved that the optimal orientation of an orthotropic cell for a given displacement field is the one where the cell is aligned with the principal directions of the stress tensor [15]. First, we solve the elasticity problem, which means we minimize with respect to the stress. Second, for the computed stress field, we update the orientation in order that the cells are aligned with the principal directions of the stress tensor. We reiterate this process until convergence, alternating with the usual gradient descent on $l_1$ and $l_2$.

This approach is more efficient that the gradient descent method, especially because the optimal orientation is exactly known at each iteration. However, for multiple loads cases, the optimal orientation is no longer explicitly defined. Nevertheless, the optimal orientation at one point only depends on the value of the local stress field and is solution of a one dimensional minimization problem.

However, this method can not be straightforwardly generalized to other objective functions. For other objective functions, like point-wise displacement, there is no such local formulation.

5 Results

5.1 Homogenized Elastic Tensor

To interpolate the effective elastic tensor, we have to solve the cell problems for differents pairs of sizing parameters $(l_1,l_2)$. We chose a regular grid of samples: $(l_1,l_2) \in \{ (\frac{i}{n}, \frac{j}{n}) \, | \, i,j \in \{0,1, .., n\} \}$, with $n=20$. All our computations have been performed with FreeFem++ [11].

5.2 Numerical Results of Topology Optimization

The methodology is applied to the bridge case, see Fig. 2. The width of the design domain is twice its height, a vertical load is applied on a central segment, and sliding conditions are applied on low external segments (each segment is $10\%$ of the total length). The constraint volume is $30\%$ of the total available volume. The Lamé coefficients of the solid material are $\lambda = 7.5$ and $\mu =5.5$.

We run five test cases: in case A, we optimized on the three design variables, while in cases B and C, we optimized respectively only on the dimensions of the holes, and only on the orientation $\alpha$. Results are summarized in Table 1. Cases D and E differ from cases A and B because of the constraint $l_1 = l_2$: we restrict the subset of considered cells to square cells with square holes, and consequently the subset of admissible effective elastic tensors to $\{ A^* | A^*_{1111} = A^*_{2222}\}$. Even if those cells are not isotropic, they are less anisotropic due to the fact that they are symmetric under a $\frac{\pi }{2}$ rotation.

Fig. 2.

Bridge load case

Table 1. Test cases

The lower compliance is reached when all microstructural parameters are actually used as design variables: taken separately, the orientation and the sizing parameters of the holes alone do not allow to reach the minimal compliance. Note that between cases A and B, the compliance improvement is about $25\%$. The anisotropy of the cells is efficiently used. This is supported by a comparison of cases A and B with cases D and E: the loss of anisotropy leads to a suboptimal design. Furthermore, the final compliances in cases B and E differ only by $4\%$. Indeed, in those cases, orientation is fixed, so to withstand the load in regions where the principal directions of the stress tensor are not aligned with the principal axes of the cell, the best option is to have an isotropic material, and so intermediate densities are unfavourable. This is the only way to maximize the strength of the material in the directions of the stress (Fig. 3). Consequently, the optimal density is automatically penalized to 0 and 1 in large areas, see Fig. 4, case E leads to similar results.

Fig. 3.

Numeric results for case A: optimal $l_1$ (a), $l_2$ (b) and density (c)

Fig. 4.

Numeric results for case B: optimal density

6 Projection of the Optimal Homogenized Design

To project our optimal homogenized design, we use the deshomogenization proposed by Pantz and Trabelsi [13]. They introduce the set of Y-periodic open subset of $\mathbb {R}^2$: $\mathscr {U}_{\#}$. Let $\omega : \mathbb {R}^2 \mapsto \mathscr {U}_{\#}$ and $\epsilon \in \mathbb {R}^{+*}$ a scale parameter. They can then define a locally periodic composite:

$$\begin{aligned} \omega _{\epsilon } = \{x \in \mathbb {R}^2: x \in \epsilon \omega (x)\} \end{aligned}$$

(9)

First, if we consider the test case B, the orientation is fixed to 0 in D: we can produce a sequence of shapes $\omega _{\epsilon }$, with $\epsilon \mapsto 0$, where the function $\omega$ depends only on $l_1$ and $l_2$. This sequence converges then to the optimal shape. To take account the local rotation $\alpha (x)$ of the cells, they introduce $\varphi : \mathbb {R}^2 \mapsto \mathbb {R}^2$ a regular local diffeormorphism and the sequence of composites:

$$\begin{aligned} \Omega _{\varphi ,\epsilon } = \{ x \in D \quad : \quad x \in \varphi ^{-1}( \epsilon \omega (x)) \} \end{aligned}$$

(10)

The components of its gradient $D\varphi = (u_1,u_2)$ have to be colinear respectively to $v_1 =R(\alpha )e_1$ and $v_2 = R(\alpha )e_2$ where $(e_1,e_2)$ is the canonical basis of $\mathbb {R}^2$:

$$\begin{aligned} u_1 = e^r v_1 \quad \text{ and } \quad u_2 = e^r v_2 \end{aligned}$$

(11)

with $r:\mathbb {R}^2 \mapsto \mathbb {R}$, local dilatation factor. Note that the condition we imposed here means that the diffeomorphism $\varphi$ preserves locally the angles, since it preserves the orthogonality of the canonical basis: it is a conformal map. Consequently, the square cells are not too much distorted by the projection, and their effective elastic tensors are closed to the ones previously computed and used during the optimization process. Moreover, the lower $\epsilon$ is chosen, the less the cells are deformed and the closer the effective tensors are to computed ones.

Pantz et al. proved that r depends only on $v_1$ and $v_2$ up to a constant:

$$\begin{aligned} \nabla r = (\nabla \wedge v_1)v_2 - (\nabla \wedge v_2)v_1 \end{aligned}$$

(12)

and

$$\begin{aligned} \forall p:D \mapsto \mathbb {R}, p=0 \text{ on }\,\, \partial D, \quad \int _D \nabla r \wedge \nabla p dx = 0 \end{aligned}$$

(13)

Since $v_1= (cos(\alpha ), sin(\alpha ))^T$ and $v_2 = (-sin(\alpha ),cos(\alpha ))^T$, (11) and (12) we can conclude:

$$\begin{aligned} \nabla r = (-\frac{\partial \alpha }{\partial y},\frac{\partial \alpha }{\partial x})^T\quad \text{ and } \quad \Delta \alpha = 0 \end{aligned}$$

(14)

To compute the diffeomorphism $\varphi$, we first have to regularize the optimized orientation $\alpha$. In practice, we define a new optimization problem, similar to the previous one, defined in Sect. 4. We simply add the constraint $\Delta \alpha = 0$, and minimize the compliance on the variables $l_1$ and $l_2$. We initialize $l_1$, $l_2$ and $\alpha$ with the optimal fields previously computed. The constraint is imposed with an Uzawa algorithm. The optimal orientation field (so before regularization) presents a singularity in the center of the low border of D, but in practice, the density is equal to 1 in its neighborhood, which means the cells are full, hence their orientation is irrelevant. The optimal orientation field seems also arbitrary in the upper corners, where the density is close to 0. In these areas, it is almost void, so that the orientation is meaningless as well. Consequently, in the both extreme cases, orientation can be adjusted, without significantly deteriorating the solution. Indeed, during the regularization phase, orientation is mainly revised in these three areas, see Fig. 5. The singularity is pushed outside the design domain D: there is no problem to apply the above method. We observe on Fig. 5 a jump of the sign of the orientation, even after the regularization. This is not a theoritical limitation, since the angle $\alpha$ is defined modulo $\pi$. We take into account this observation in our algorithm to compute $\varphi$ by introducing a manifold on which $\alpha$ and $\alpha + \pi$ coexist and where the diffeomorphism is defined and continuous.

After the orientation regularization phase, we can compute r up to a constant, which corresponds to a global dilation of the cells, and the diffeomorphism $\varphi$, also up to a constant corresponding to a phase difference and which can be chosen to adjust, for example, the symmetry of the projected shape. Projections of the optimal design are shown on Fig. 6 for two different values of $\epsilon$. In practice, $\epsilon$ has to be chosen according to the resolution of the additive manufacturing process.

Fig. 5.

(left) Optimal orientation - (right) Regularised orientation

Fig. 6.

Projection of case A optimal design - (a) $\epsilon = 1$, (b) $\epsilon = 2$

7 Conclusion and Perspectives

The optimization strategy based on homogenization method developed in the present work allows to design anisotropic cellular structures. A manufacturable shape is then computed by post-processing the homogenized optimal results, thanks to the introduction of a diffeomorphism.

However, an additional cleanup step is necessary to improve the final design. For example, low densities could be penalized where they are not required (here, above the bridge for example). The question of high density is more complex: we would like to force high densities to 1, in order to limit details too thin for the AM process. But in 3D, we would prefer to exclude high density to avoid any inclusions where some material could be trapped during the fabrication, like unfused metal powder in selective laser melting (SLM).

Our method can be extended to 3D and to more complex parametrized designs of cells. Hence, the set of reachable elastic tensors will be greatly enlarged. More results will be available in a future paper.