Keywords

1 Introduction

Optimization is a subset of mathematics that deals with determining system parameters that minimizes or maximizes one or more functions under certain conditions. The optimization problem is often bounded by constraints. The constraints can be explicit, such as by a restriction of the parameter range, or implicit by functions, which may not leave a certain range of values depending on the parameters. In engineering or economics, objectives and constraints are often determined by non-linear functions. These non-linearities yield a parameter response with multi-modal landscape. For such an optimization problem, local search algorithms, like hill climbing or Nelder-Mead downhill simplex methods are usually not able to determine a global optimum. Therefore, global optimization algorithms like stochastic methods are appropriate. [1, 2]

Stochastic methods are randomized search methods, which are usually based on no mathematical foundation. They represent iterative methods whose course is determined by certain stochastics in addition to logical conditions. Because these iterative optimization algorithms are independent of the system to be optimized, they are eligible for optimization problems in which the objective function or constraints are mathematically decoupled from the decision variables. Most stochastic procedures are inspired and abstracted by nature, like the Genetic Algorithm (GA) [3], the Ant Colony Optimization (ACO) [4] or the Particle Swarm Optimization (PSO) [5].

Another frequently used stochastic algorithm is the swarm-intelligence-based Firefly Algorithm (FA), developed in 2008 by Xin-She Yang [6]. The FA is used successfully in a wide range of fields like economic dispatch problems [7, 8], scheduling problems [9] and structural optimization problems [10, 11]. Preliminary studies show that the FA outperforms existing algorithms in many test cases with multi-modal landscape [12, 13].

In this paper, we first give a brief outline of the basic Firefly Algorithm. Then, we introduce the implicit movement within the Firefly Algorithm to enhance its convergence behavior and solution quality. Afterwards, the modified algorithm is applied to continues benchmark optimization functions as well as to a discrete parameter optimization of a ten-bar truss in the sense of a weight reduction. Finally, we will validate the performance of the Firefly Algorithm with implicit movement and propose topics for further research.

2 Basic Firefly Algorithm

The Firefly Algorithm (FA) by Yang [6] is inspired by the characteristic behavior of fireflies. The specific feature of these insects is the ability to glow, with which they attract their conspecific. The FA transfers the demand of fireflies to move toward bright glowing mates in a swarm-intelligence-based optimization algorithm. The \( d \) to be optimized parameters form a hyperspace \( {\mathbb{R}}^{d} \) in which the \( n \) individuals are located. According to the position vector \( \varvec{x}_{i} \), an individual \( i \) has an objective function value \( f \) whose quality determines the brightness \( I_{i} \) of the individual. In terms of a maximization problem, the brightness \( I_{i} \) can simply be chosen as

$$ I_{i} \left( {\varvec{x}_{i} } \right) \propto f\left( {\varvec{x}_{i} } \right) . $$
(1)

During the optimization process, each individual \( i \) moves within the solution space toward every brighter (by means of \( I_{j} > I_{i} \)) individual \( j \), with the intention to improve their own objective function value. The step size toward another individual is up to the attractiveness of this individual. The attractiveness \( \beta_{ij} \) of the individual \( j \) for the individual \( i \) depends on the distance \( r_{ij} \) of the two individuals and is determined by

$$ \beta_{ij} = \beta_{0} e^{{ - \gamma r_{ij}^{2} }} . $$
(2)

The parameter \( \beta_{0} \) corresponds to the attractiveness at a distance of \( r_{ij} = 0 \) and \( \gamma \) is the light absorption coefficient. The distance is commonly the Cartesian distance

$$ r_{ij} = \left| {\left| {\varvec{x}_{i} - \varvec{x}_{j} } \right|} \right|. $$
(3)

For an individual \( i \), its movement toward a brighter individual is determined by

$$ \varvec{x}_{i}^{t + 1} = \varvec{x}_{i}^{t} + \beta_{0} e^{{ - \gamma r_{ij}^{2} }} \left( {\varvec{x}_{j}^{t} - \varvec{x}_{i}^{t} } \right) + \alpha_{t} \varepsilon_{i}^{t} $$
(4)

The third term corresponds to a random movement in space with the step size \( \alpha_{t} \) and a vector \( \epsilon_{i}^{t} \) with random numbers drawn from a Gaussian or uniform distribution. The pseudo-code of the basic Firefly Algorithm is given in Table 1.

Table 1. Pseudo code: Firefly Algorithm [6]
Full size table

3 Firefly Algorithm with Implicit Movement

The Firefly Algorithm without random movement correlates to a diffusion process of the form

$$ \frac{\partial X}{\partial t} = \beta L\left( X \right) $$
(5)

with \( L\left( {\varvec{x}_{i} } \right) = \left( {\varvec{x}_{j}^{t} - \varvec{x}_{i}^{t} } \right) \). The diffusion Eq. (5) can be integrated with an explicit Euler scheme, yielding:

$$ X^{t + 1} = X^{t} + \beta dtL\left( {X^{t} } \right), $$
(6)

which corresponds to the movement Eq. (4) in the basic Firefly Algorithm without random movement:

$$ \varvec{x}_{i}^{t + 1} = \varvec{x}_{i}^{t} + \beta \left( {\varvec{x}_{j}^{t} - \varvec{x}_{i}^{t} } \right). $$
(7)

The position of an individual at iteration \( t + 1 \) is therefore dependent on the positions of the other individuals at iteration \( t \). To improve the convergence behavior of the FA, Eq. (5) is now solved by an implicit integration. The position of an individual at iteration \( t + 1 \) thus depends on the positions of the other individuals at iteration \( t + 1 \). The integration of Eq. (5) by the implicit backward Euler method is \( X^{t + 1} = X^{t} + \beta dtL\left( {X^{t + 1} } \right) \), which leads to the linear system of equation (LSE):

$$ \begin{aligned} \left( {E - \beta dtL} \right)X^{t + 1} & = X^{t} \\ KX^{t + 1} & = X^{t} \\ \end{aligned} $$
(8)

with the identity matrix \( E \). The size of the matrix \( K = E - \beta dtL \) equals \( {\mathbb{R}}^{{\left( {n \cdot d} \right) \times \left( {n \cdot d} \right)}} \), with the number of individuals \( n \) and the number of the to be optimized parameters \( d \). After solving the LSE, a random movement of the individuals takes place:

$$ \varvec{x}_{i} = \varvec{x}_{i} + \alpha \varepsilon $$
(9)

The pseudocode of the Firefly Algorithm with implicit movement is given in Table 2.

Table 2. Pseudo code: implicit Firefly Algorithm
Full size table

4 Experiments and Results

In the following, the Firefly Algorithm with an implicit movement is evaluated using benchmark optimization problems. Each optimization is carried out fifty times and the average (AVG) value are formed from these to take account of fluctuations in the course. On the one hand, the Ackley’s function, the Sphere function, the Rosenbrock function and the Lévi#13 function given in Table 3 are optimized. The results are compared with the classical FA in order to determine the impact of the implicit position determination. Furthermore, a discrete parameter optimization of a ten-bar truss shown in Fig. 5 regarding to a weight reduction is carried out. The optimization results are compared to the basic FA and furthermore to the optimization results of the Particle Swarm Optimization (PSO) algorithm, the Ant Colony Optimization (ACO) algorithm, the Artificial Bee Colony (ABC) algorithm and a Genetic Algorithm (GA) adapted from [14,15,16,17,18].

Table 3. The function test bed
Full size table

The basic FA as well as the implicit FA are implemented with a population size of \( n = 25 \). The parameters are set to \( \beta_{0} = 1.0 \), \( \gamma = 0.0001 \) and \( \alpha = 0.1 \). Thus, the basic FA and the implicit FA only differ in the sense of explicit and implicit movement. The algorithms are implemented in MATLAB R2016b. The calculations are done on an intel® core™ i5-6200U CPU with 2.40 GHz. The evaluation of the LSE in each iteration of the implicit Firefly Algorithm are done with the standard mldivide-operator in MATLAB. The calculation time of the LSE is between 4.50e-06 s and 6.36e-04 s in all optimizations carried out in this study.

4.1 Optimization Results of Benchmark Test Functions

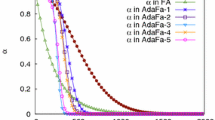
The optimization results of the test functions given in Table 3 are shown in Figs. 1, 2, 3 and 4. In order to obtain representative results, the best objective function values found within the respective iteration are averaged over the fifty optimization runs. The results show that the Firefly Algorithm with implicit movement has a superior convergence behavior. Especially in the first iterations, the objective function value is minimized significantly faster. Table 4 shows the averaged values (AVG) and the standard deviations (STD) of the optimizations in the last iteration. The Firefly Algorithm achieves better mean objective function values, whereby on the average a better optimization result is achieved. The lower standard deviation for all four test functions verifies the superior reliability of the FA with implicit movement. Note from Figs. 1, 2, 3 and 4 that in every iteration, the Firefly Algorithm with implicit movement provides a superior averaged best objective function value.

Fig. 1.
figure 1

Comparison of convergence rates for Ackley’s Function of FA and implicit FA

Full size image
Fig. 2.
figure 2

Comparison of convergence rates for Sphere Function of FA and implicit FA

Full size image
Fig. 3.
figure 3

Comparison of convergence rates for Rosenbrock Function of FA and implicit FA

Full size image
Fig. 4.
figure 4

Comparison of convergence rates for Lévi#13 Function of FA and implicit FA

Full size image
Table 4. Comparison of FA and implicit FA optimization results of the test functions
Full size table

4.2 Optimization Results of a Planar 10-Bar Truss

For the evaluation of the developed optimization algorithm, a discrete parameter optimization problem of a planar 10-bar truss is carried out. This test problem has already been used in different studies and, accordingly, there are comparative values for other optimization algorithms. The planar structure to be optimized is shown in Fig. 5. The parameters to be optimized are the ten bar cross sections with regard to a weight reduction while maintaining the restrictions defined by a maximum permissible stress of \( 172.369 \) MPa and by a maximum node deflection in the vertical and horizontal direction of \( \pm 50.8 \) mm. The structure is subjected by the external force \( F = 444.82 \) kN at node 2 and 4. The bar cross-sectional areas are selected from a set of 42 discrete predefined values given in Table 5. The density of the material is \( 2767.99 \) kg/mm 3 and the modulus of elasticity is \( 68947.6 \) MPa.

Fig. 5.
figure 5

Schematic of the planar 10-bar truss structure

Full size image
Fig. 6.
figure 6

Schematic of the optimized planar 10-bar truss structure

Full size image
Table 5. Predefined set of possible cross-sectional areas for the 10-bar-truss [mm2]
Full size table

The averaged optimization processes out of 50 optimizations of the Firefly Algorithm and the implicit Firefly Algorithm are shown in Fig. 7. The corresponding courses of the standard deviations of the weight are shown in Fig. 8. To compare the optimization results with other algorithms, the optimization processes in Figs. 7 and 8 are indicated by the number of performed calculations. One calculation corresponds to a stress and deformation calculation of the truss. It can be seen from Figs. 7 and 8 that the implicit movement provides a much better convergence behavior. The averaged best weights obtained after 2500 performed calculations are \( 2504 \) kg by the implicit Firefly Algorithm and \( 2556 \) kg by the basic Firefly Algorithm respectively. Including the standard deviation after 2500 performed calculations of \( 11.48 \) Kg and \( 65.71 \) kg as shown in Fig. 8, the Firefly Algorithm with implicit movement achieves a distinctly better reliability.

Fig. 7.
figure 7

Comparison of convergence rates for ten-bar truss of FA and implicit FA

Full size image
Fig. 8.
figure 8

Comparison of standard deviation for ten-bar truss of FA and implicit FA

Full size image

The best permissible parameter combination found within the 50 optimizations compared to the results of state-of-the art algorithms are given in Table 6. The number of calculations corresponds to the number of stress and deformation calculations necessary to reach the indicated weight. The calculation numbers are to be interpreted in such a way that no improvement to the listed weight was possible in subsequent iterations. It can be seen in Table 6 that both, the basic Firefly Algorithm and the implicit Firefly Algorithm, outperform the reviewed state-of-the-art algorithms. The implicit Firefly Algorithm achieves the best weight of \( 2490.55 \) kg within \( 2125 \) calculations and is therefore superior to the basic Firefly Algorithm where \( 3750 \) calculations are necessary. The truss structure corresponding to the weight of \( 2490.55 \) kg is shown in Fig. 6.

Table 6. Comparison of FA and implicit FA optimization results with literature for the ten-bar-truss problem
Full size table

5 Conclusion

The Firefly Algorithm is an optimization algorithm, which is typically applied to global optimization problems. We successfully improved the Firefly Algorithm by using an implicit determination of the changes in individual positions. The system of equations that must be solved for the implicit position determination is efficiently solvable due to its sparseness. The proposed modification therefore has no remarkable effect on the runtime.

The implicit Firefly Algorithm has been tested by means of test functions and has also been validated by a discrete optimization of a ten-bar truss. Compared to the basic Firefly Algorithm, the implicit Firefly Algorithm showed a much better convergence behavior and better reliability. In addition, the optimization of the ten-bar-truss showed that the implicit Firefly Algorithm outperforms state-of-the-art methods reviewed in this study both in calculation time and quality.

The proposed algorithm presents an easy to implement and mathematically intuitive modification of the basic Firefly Algorithm. Due to its generality, the proposed implicit movement can be implemented to several swarm-intelligence-based algorithms and offers a promising universal approach for enhancement. Within the scope of this study no disadvantages of the implicit movement could be identified. In addition to the implementation in further swarm-intelligence-based algorithms, supplementary optimization problems should be investigated in order to ensure the validity of the statements made.