Abstract
Many supertree estimation and multi-locus species tree estimation methods compute trees by combining trees on subsets of the species set based on some NP-hard optimization criterion. A recent approach to computing large trees has been to constrain the search space by defining a set of “allowed bipartitions”, and then use dynamic programming to find provably optimal solutions in polynomial time. Several phylogenomic estimation methods, such as ASTRAL, the MDC algorithm in PhyloNet, and FastRFS, use this approach. We present SIESTA, a method that allows the dynamic programming method to return a data structure that compactly represents all the optimal trees in the search space. As a result, SIESTA provides multiple capabilities, including: (1) counting the number of optimal trees, (2) calculating consensus trees, (3) generating a random optimal tree, and (4) annotating branches in a given optimal tree by the proportion of optimal trees it appears in. SIESTA is available in open source form on github at https://github.com/pranjalv123/SIESTA.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Phylogeny estimation is generally approached as a statistical estimation problem, and finding the best tree for a given dataset is typically based on methods that are computationally very intensive; for example, maximum likelihood phylogeny estimation is NP-hard [19] and Bayesian MCMC methods require a long time to converge. For this reason, among others, the calculation of very large phylogenies is often enabled by divide-and-conquer methods that use “supertree methods” to combine smaller trees into larger trees. A more common use of supertree methods is to combine trees computed by independent research groups on different datasets into a single tree on a large dataset. Supertree methods are very popular and an area of active research in the computational phylogenetics community [3].
Species tree estimation, even for small numbers of species, is also difficult because of multiple processes that create differences in the evolutionary history across the genome; examples of such processes include incomplete lineage sorting (ILS), gene duplication and loss (GDL), and horizontal gene transfer (HGT) [12]. Species tree estimation is therefore performed using multiple loci from throughout the genomes of the different organisms, and is referred to as “phylogenomics”. One of the standard approaches for species tree estimation is to compute gene trees (i.e., trees on different genomic regions) and then combine the trees together into a species tree under statistical models of evolution, such as the multi-species coalescent (which models ILS), that allow for gene tree heterogeneity. Examples of methods that construct species trees by combining gene trees and that are statistically consistent under the multi-species coalescent model include ASTRAL [15, 16], GLASS [17], the population tree in BUCKy [8], MP-EST [10], NJst [9], and a modification of NJst called ASTRID [29].
This approach, called “summary methods”, shares algorithmic features in common with supertree methods in that both construct trees on the set of species by combining trees on subsets of the species set; the difference between the two types of methods is that in the supertree context, the assumption is that the heterogeneity observed between these “source trees” is due only to estimation error, while in the phylogenomic context the assumption is that source trees can differ from the species tree due to a combination of estimation error and true heterogeneity resulting from ILS, GDL, HGT, or some other causes.
Summary methods and supertree methods are often based on attempts to solve NP-hard problems, and so typically use heuristics (a combination of hill-climbing and randomization) to search for optimal trees. While these heuristics can be highly effective on small datasets, they are often very slow and there are no guarantees about the solutions they find.
An alternative approach to the use of heuristic searches is constrained exact optimization, whereby the solution space is first constrained using the input source trees, and then an exact solution to the optimization problem is found within that constrained space. This approach can lead to polynomial time methods (where the running time depends on the size of the constraint space as well as on the input) that can have outstanding accuracy. The first use of this approach was presented in Hallet and Lagergren [7], which provided a method to find a species tree minimizing the duplication-loss reconciliation cost given a set of estimated gene trees. Since then, many other constrained exact optimization methods have been developed in phylogenomics for different purposes, including species tree estimation from sets of gene trees under gene duplication and loss models or under the multi-species coalescent model, or improving gene trees given a species tree [2, 4, 15, 16, 26, 27, 30, 31].
Most of these approaches constrain the search space using a set of “allowed bipartitions”, which we define here. Each edge e in an unrooted tree T on a set S of species defines a bipartition \(\pi _e\) of S (also called a “split”), obtained by deleting e but not its endpoints from T; hence, every tree T can be defined by its set of bipartitions \(C(T) = \{\pi _e: e \in E(T)\}\). The constraints imposed by these algorithms are obtained by specifying a set X of allowed bipartitions so that the returned tree T must satisfy that \(C(T) \subseteq X\). The set X is used to define a set of “allowed clades” (comprised of the halves of the bipartitions, plus the full set of species), and dynamic programming is then used on the set of allowed clades to find an optimal solution to the optimization problem. The set X has an impact on the empirical performance, but even simple ways of defining X can result in very good accuracy and provide guarantees of statistical consistency under statistical models of evolution [16, 30].
The constrained exact optimization approach has multiple advantages over heuristic search techniques. From an empirical perspective, the dynamic programming approach is frequently faster, and if the constraint space is selected well it is often more accurate than alternative approaches that typically use heuristic searches for optimal solutions. From a theoretical perspective, the ability to provably find an optimal solution within the constraint space is often sufficient to prove statistical consistency under a statistical model of evolution (e.g., under the multi-species coalescent model); hence, many of the methods that use constrained exact optimization can be proven statistically consistent, even for very simple ways of defining the constraint set.
These constrained exact optimization methods typically have excellent accuracy in terms of scores for the optimization problems they address (established on both biological and simulated datasets) and topological accuracy of the trees they compute (as established using simulated datasets). A basic limitation of these methods, however, is that they return a single optimal tree, even though there can be multiple optima on some inputs. This limitation reduces the utility of the methods.
We present SIESTA (Summarizing Implicit Exact Species Trees Accurately), an algorithmic tool that can be used to enhance these dynamic programming methods for finding optimal trees. The input to SIESTA is the set \(\mathcal {T}\) of source trees, the constraint set X of allowed bipartitions, and a scoring function w that assigns scores to tripartitions of the taxon set (and which is derived from the optimization function F that assigns scores to trees and the set \(\mathcal {T}\), as we show later); SIESTA returns a data structure \(\mathcal {I}\) that represents the set \(\mathcal {T}^*\) of trees that optimize the function F subject to the constraint that every bipartition in every tree in \(\mathcal {T}^*\) is in X. This data structure \(\mathcal {I}\) enables the user to explore the set of optimal trees in various ways. In this study, we use SIESTA to compute consensus trees and the maximum clade credibility (MCC) tree, to count the number of optimal trees, and to report the frequency of each bipartition in the set of optimal trees. We explore the impact of using SIESTA with two methods that use the dynamic programming method for constrained exact optimization: the supertree method FastRFS [30] and the species tree estimation method ASTRAL [16], which addresses gene tree heterogeneity due to ILS.
The remainder of the paper is organized as follows. The performance study is described in Sect. 2, and the results of that study are presented in Sect. 3. We discuss the trends observed in our experiment, and the impact of using SIESTA in supertree estimation and multi-locus species tree estimation, in Sect. 4. The conclusions are presented in Sect. 5. Details of SIESTA’s algorithm design and running time analysis are provided in Sect. 6. The simulated datasets analyzed in this paper are available on FigShare at [28].
2 Experiments
2.1 Overview
We tested SIESTA in conjunction with the supertree method FastRFS (using the enhanced version) and the coalescent-based species tree estimation method ASTRAL on 2 biological and 1765 simulated datasets. For each dataset we examined, we used SIESTA to compute the set of optimal solutions, and then computed consensus trees for these trees. We computed the strict consensus tree, which is the unique tree whose bipartitions appear in every optimal tree. We report the average of the FN and FP error rates.
2.2 Methods
Standard Methods. We report results for FastRFS v2.0 (using the enhanced variant, as described in [30]) on the supertree datasets, since this technique gave the best performance, and improved on MRL [18], a leading supertree method, as well as on ASTRAL-II. We also report results for ASTRAL-II (ASTRAL v4.11.1) on the phylogenomic datasets using default settings. We used RAxML v8.2.4 [23] to estimate gene trees (using options -m GTRGAMMA -p 12345) and to run MRL within FastRFS (using options -m BINGAMMA -p 12345).
ASTRAL-SIESTA. The use of SIESTA to process ASTRAL trees is called ASTRAL-SIESTA: this is the algorithm that computes the data structure for the optimal trees computed by ASTRAL, and then returns the strict consensus of the optimal trees as well as the Maximum Clade Credibility (MCC) tree. The output of ASTRAL-SIESTA can also be used for other explorations of the set of optimal trees, including annotating edges in a given candidate species tree with branch support based on the frequency of the edge appearing in the set of optimal trees. ASTRAL-SIESTA uses ASTRAL v4.11.1 (with the -q option) to compute the Maximum Clade Credibility (MCC) tree, which is based on the ASTRAL-II posterior support values [21].
FastRFS-SIESTA. The use of SIESTA to process FastRFS trees is called FastRFS-SIESTA: this is the algorithm that computes the data structure for the optimal trees computed by FastRFS, and then returns the strict consensus of the optimal trees. The output of FastRFS-SIESTA can also be used for other explorations of the set of optimal trees, including annotating edges in a given candidate supertree with branch support based on the frequency of each edge appearing in the set of optimal trees. FastRFS-SIESTA uses ASTRAL v4.7.8 to compute the set X of allowed bipartitions (using the option -k searchspace_norun).
Simulated Supertree Datasets. The simulated supertree datasets were originally provided in [25], and have been used to explore the accuracy of several supertrees methods [18, 30]. We explore the results on the datasets with 1000 taxa, which are the hardest datasets in this collection; results on 100 and 500 taxa are shown in the supplement. Each replicate contains one “scaffold” tree and several clade-based trees. The scaffold tree is based on a random sample of the species, and contains \(20\%, 50\%, 75\%\), or \(100\%\) of the taxa sampled uniformly at random from the leaves of the tree. The clade-based trees are based on a clade and then a birth-death process within the clade (and hence may miss some taxa). The original 100-taxon, 500-taxon, and 1000-taxon datasets had 6, 16, and 26 source trees respectively; the number of source trees was reduced to 6, 11, and 16 for the 500-taxon datasets, and 6, 11, 16, 21, and 26 for the 1000-taxon datasets. Sequences evolved down each scaffold and clade-based source tree under a GTR+Gamma model (selected from a set of empirically estimated parameters) with branch lengths that are deviated from the strict molecular clock. Maximum likelihood trees were estimated on each sequence alignment using RAxML under the GTRGAMMA model (with numeric parameters estimated by RAxML from the data), and used as source trees for the experiment. 10 replicates were analyzed for each scaffold factor of the 1000-taxon model condition.
Simulated Phylogenomic Datasets. The simulated phylogenomic datasets are from [16]; the gene trees were generated by SimPhy [14] and the sequences evolved down the gene trees using Indelible [5]. The species trees are randomly generated, and gene trees evolve within the species trees under the multi-species coalescent model; hence there is gene tree heterogeneity resulting from ILS in these datasets. Three levels of ILS were generated, characterized by the average normalized bipartition distance (AD) between true gene trees and true species trees: a moderate ILS condition (AD = 12%), a high ILS condition (AD = 31%), and a very high ILS condition (AD = 68%). These datasets have a speciation rate of \(10^{-6}\), resulting in speciation close to the tips of the model trees (recent divergence). Sequences evolved down each gene tree under a GTR+Gamma model with branch lengths that are deviated from the strict molecular clock.
These datasets were then modified for the purposes of this study. These datasets originally had 200 taxa each, but were randomly reduced to 50 taxa each to reduce the running time. The original datasets had variable length loci between 300 and 1500 bp, and were truncated for this experiment to 150 bp to produce datasets with properties that are consistent with empirical phylogenomic datasets (which frequently have very low phylogenetic signal). Each replicate was evaluated with 5, 10, and 25 loci. We evaluated model conditions where each gene contained all 50 taxa, as well as model conditions where each gene contained 10, 20, or 30 taxa chosen at random from the taxon set.
Gene trees were estimated on each sequence alignment using RAxML [23] under the GTRGAMMA model (with numeric parameters estimated by RAxML), and we analyzed 25 replicates for each model condition (defined by the ILS level, number of loci, and amount of missing data).
Overall, we examined 900 simulated phylogenomic datasets and 600 simulated supertree datasets.
Biological Phylogenomic Datasets. We analyzed two phylogenomic datasets on which ASTRAL had at least two optimal trees: a Sigmontidine rodent dataset [13] with 285 species and 11 genes, and a Hymenoptera dataset [22] with 21 species and 24 genes. The Sigmontidine rodent dataset has 72 optimal ASTRAL trees and the Hymenoptera dataset has 4 optimal ASTRAL trees.
Performance Criteria. For the simulated datasets, we evaluate accuracy of the strict consensus trees in comparison to the accuracy of a single optimal tree returned by the default usage of either FastRFS or ASTRAL. We report both the false negative (FN) rate and the false positive (FP) rate, with respect to the model tree; the FN rate is the number of bipartitions in the model tree that are missing from the estimated tree and the FP rate is the number of bipartitions in the estimated tree that are not in the model tree, each divided by \(n-3\) where n is the total number of leaves in the model tree. For each tree estimation method (i.e., ASTRAL and FastRFS), we report Delta-Error, which is the difference between the average of its FN and FP error rates, and the error rate of the strict consensus of the optimal trees. Hence, when Delta-Error is negative, the strict consensus has overall lower error than a single optimal tree. For the biological datasets, since topological accuracy cannot be assessed completely, we describe differences between the consensus trees we compute using SIESTA and trees computed using other techniques. We report the number of optimal trees for the optimization problems on all the datasets we examine. DendroPy [24] was used to measure tree error.
3 Results
3.1 Simulated Supertree Data
Topological Accuracy of Estimated Supertrees. Figure 1 shows a comparison on 1000-taxon simulated supertree datasets between the strict consensus tree computed by FastRFS-SIESTA and a single best FastRFS tree; note the FastRFS-SIESTA is more accurate than FastRFS for all scaffold factors, with the largest improvements when the scaffold factor is the smallest. The same trends hold on the 100- and 500-taxon datasets, as seen in Supplementary Fig. 7.
Figure 2 shows FN and FP rates separately for the 1000-taxon supertree datasets, and how they are impacted by the number of optimal trees. As expected, the FP rates decrease and the FN rates increase using the strict consensus tree as the number of optimal trees increases. However, as the number of optimal trees increases, the decrease in FP rate is substantially larger than the increase in FN rate. As a result, while there is generally a benefit in using FastRFS-SIESTA, the benefit increases with the number of optimal trees. The same trends hold on the 100- and 500-taxon datasets, as seen in Supplementary Figs. 7 and 8.
FastRFS-SIESTA is more accurate than FastRFS. We show Delta-error (change in mean topological error between FastRFS and the strict consensus of FastRFS trees) on simulated supertree datasets with 1000 species; values below 0 indicate that the strict consensus FastRFS is more accurate (i.e., it has lower error) than FastRFS. The figure shows how the percentage of taxa in the scaffold source tree impact accuracy, averaged over 10 replicates. Error bars indicate the standard error; the topological error is the average of the FN and FP error rates. Results on other numbers of species show the same trends.
Mean error rates for a single FastRFS tree and the strict consensus of all FastRFS trees on the supertree datasets with 1000 species, compared to the number of optimal trees. We show FP and FN rates (maximum error rate is 1.0) for each method; these are equal for default FastRFS (because it is always binary), but can be different for the strict consensus of the FastRFS trees. The decrease in the FP rate is larger than the increase in the FN rate for the strict consensus of the FastRFS trees, as the number of optimal trees increases, explaining why the average error for the strict consensus of the FastRFS trees is lower than for a single FastRFS tree (as shown in Fig. 1). Results for 193 replicates are shown.
The strict consensus of ASTRAL trees is more accurate than ASTRAL. We show Delta-error (change in mean topological error between FastRFS and the strict consensus of FastRFS trees) on simulated phylogenomic datasets with 25 incomplete gene trees with three different ILS levels; values below 0 indicate that the strict consensus ASTRAL is more accurate (i.e., it has lower error) than ASTRAL. Note how the percentage of taxa in each gene tree impact accuracy. We show results for 25 replicates. Error bars indicate the standard error; topological error is the average of the FN and FP error rates.
Number of Optimal FastRFS Trees. Both variants of FastRFS (the enhanced and basic forms) have a large number of optimal trees on these supertree datasets, as seen in Table 4. Datasets with 100 taxa typically have tens or hundreds of optimal solutions, but the number of optimal trees increases with the number of species, so that with 1000 species there are up to \(10^{18}\) optimal trees. Most of the supertree datasets have a sparse scaffold and not too many source trees, and these factors generally (but not always) increase the number of optimal trees.
3.2 Simulated Phylogenomic Data
We examined two types of simulated datasets: the first type is where all the gene trees are complete (i.e., all species are present in all the genes), and the other type is where we deleted random species from the genes, so that all genes are missing the same number of species.
As shown in Supplementary Tables 1, 2 and 3, when all the gene trees are complete, nearly all the analyses produced only one optimal ASTRAL tree, and when more than one tree was produced it was typically a very small number (often just two). For these datasets, there was essentially no difference between the strict consensus and a single ASTRAL tree, as the strict consensus tree usually lost only one edge, and whether it was a false positive or a true positive the error rate was changed only slightly.
The situation changes for the datasets with incomplete gene trees: there are many optimal ASTRAL trees (see Supplementary Tables 1, 2 and 3). Furthermore, when there are many optimal trees, the average error rates for the strict consensus of the ASTRAL trees are lower than the error rate for a single ASTRAL tree: Fig. 3 shows results under the highest ILS condition as a function of the amount of missing data, and Fig. 4 shows this as a function of the number of optimal trees. The trends are the same under lower ILS conditions (Supplementary Figs. 9 and 10).
Mean change in error between the strict consensus of the ASTRAL trees compared to a single ASTRAL tree on the 50-taxon phylogenomic datasets with high ILS and varying degrees of missing data, as a function of the number of optimal trees. Values below zero indicate that the strict consensus tree has better accuracy (lower error) than a single ASTRAL tree. We show the change in FP rates (blue, solid line) and in FN rates (red, dashed); the black line represents the baseline. This figure shows that the strict consensus has lower false positives than a single ASTRAL tree and higher false negative, but also that the reduction in false positives is larger than the increase in false negatives. The figure also shows that the reduction in false positives increases with the number of optimal trees. (Color figure online)
3.3 Biological Datasets
Hymenoptera Dataset. There are four optimal ASTRAL trees on this dataset (shown in Fig. 5). The differences between these four trees are restricted to two clades with three species each: (1) Solenopsi, Apis, and Vesputal_C, and (2) Acyrthosi, Myzus, and Acyrthosp. The strict and majority consensus trees (Fig. 6) on these four ASTRAL trees are identical, and present these two groups as completely unresolved. The MCC tree on this set of four ASTRAL trees matches one of the four trees with respect to topology, but has different branch support on the edges, so that the branch support for the two clades in question are halved in comparison to the four ASTRAL trees; thus, the MCC tree correctly identifies these clades as having very low support.
The ASTRAL MCC (left) and strict consensus (right) trees on the Hymenoptera dataset. The ASTRAL MCC tree is topologically identical to one of the four ASTRAL trees, but has different branch support; in particular, the branch support on the clades in question is half the branch support in the original ASTRAL trees on these clades. The ASTRAL strict consensus tree makes these two clades into polytomies.
Sigmontidine Rodent Dataset. The species tree computed on this dataset in [13] was a concatenated Bayesian tree using MrBayes [20], with branch support based on posterior probabilities. We used the approach detailed in Sect. 6.3 to further analyze the Sigmontidine rodent dataset [13], which had 72 optimal ASTRAL trees. The ASTRAL MCC tree is highly unresolved after collapsing edges with less than \(75\%\) support. This dataset has 285 taxa, meaning that a fully resolved tree would have 282 internal edges; the collapsed ASTRAL MCC tree has only 74 internal nodes. By comparison, the MrBayes tree has 223 internal nodes after collapsing edges with less than \(75\%\) support.
Comparing the MrBayes tree with the ASTRAL MCC tree, we find that 64 bipartitions are present and highly supported in both trees. After collapsing the edges with lower support, we are left with only the high support edges. Six highly supported bipartitions are present in the ASTRAL MCC tree and compatible with the collapsed MrBayes tree, and three bipartitions are present in the ASTRAL MCC tree and incompatible with the collapsed MrBayes tree. 153 highly supported bipartitions are present in the MrBayes tree and compatible with (but not present in) the collapsed ASTRAL MCC tree, and 5 highly supported bipartitions in the MrBayes tree are incompatible with the collapsed ASTRAL MCC tree. The highly supported conflicts between the trees occur in three locations:
-
1.
The MrBayes tree has Akodon Mimus as the root of the Akodon genus, while the ASTRAL MCC tree has it internal to Akodon (the root of Akodon is not resolved with greater than 75% support).
-
2.
The MrBayes tree and the ASTRAL MCC tree swap the locations of the Holochilus and Sooretamys clades, with ASTRAL putting Holochilus as the basal clade and MrBayes putting Sooretamys as the basal clade.
-
3.
The ASTRAL MCC tree and the MrBayes tree disagree about some resolutions within the Oligoryzomys clade.
These placements are in general not well established in the literature [1, 6, 11], and so it is not clear which of the two trees is more likely to be correct.
4 Discussion
We studied SIESTA in conjunction with ASTRAL and FastRFS on a collection of biological and simulated datasets, mainly focusing on using SIESTA to compute the strict consensus of the set of optimal trees. This study showed that using SIESTA to compute the strict consensus produced a benefit for some methods in some cases, but not in all. The trends we observed clearly indicate that when there are many optimal trees, the use of the strict consensus tree results in a substantial reduction in the false positive rate and a lesser increase in the false negative rate, for an overall reduction in topological error. Conversely, when there are only a small number of optimal trees, there is little change between the strict consensus tree and any single optimal tree. Thus, the impact of using the strict consensus depends on the number of optimal solutions. We also saw that the number of optimal trees depends on the amount of missing data, so that the benefit of using SIESTA to compute the strict consensus seems to be reliable only when there is missing data.
The study also showed that FastRFS typically benefited from using the strict consensus tree, while ASTRAL’s benefit varied with the dataset. To some extent this is a natural consequence of using FastRFS on the supertree datasets, all of which have substantial amounts of missing data, and we used ASTRAL on the phylogenomic datasets, most of which had no missing data. However, a comparison of ASTRAL and FastRFS on the same datasets shows that ASTRAL tends to have fewer optimal trees than FastRFS (Table 4).
The reason that FastRFS tends to have more optimal solutions than ASTRAL, even on the same datasets, is probably that the number of possible FastRFS scores is substantially smaller than the number of possible ASTRAL scores. Specifically, if n is the number of species and k is the number of source trees, the FastRFS scores are all integers in the range \([0,(n-3)k]\), while the possible ASTRAL scores are integers in the range \([0,k{n \atopwithdelims ()4}]\). Therefore, the frequency of multiple trees with the same optimal score is higher for FastRFS than for ASTRAL.
5 Conclusions
SIESTA is a simple technique for computing a data structure that implicitly represents a set of optimal trees found during the dynamic programming algorithms used by ASTRAL and FastRFS, but SIESTA is generalizable to any algorithm that uses the same basic dynamic programming structure. Once the data structure is computed, it can be used in multiple ways to explore the solution space. In particular, it can be used to count the number of optimal solutions and determine the support for a particular bipartition, thus enabling the estimation of the support on branches for a given optimal tree that takes into account the existence of other optimal trees. This study showed that SIESTA generally improves topological accuracy when the number of optimal trees is not too small, and that otherwise it allows the user to confirm that the solution that is returned is highly supported.
An interesting application of SIESTA is to produce better statistical support values on the edges of ASTRAL trees. In the current implementation of ASTRAL, the support values are obtained using posterior probabilities based on quartet trees around an edge in a single optimal tree. However, a simple example can explain why this can be misleading. Suppose \(T_1\) and \(T_2\) are the only trees that are optimal for ASTRAL, and that \(T_1\) has a split \(\pi \) that \(T_2\) does not have. Then under the assumption that \(T_1\) and \(T_2\) are both equally likely to be the true species tree, the maximum probability that \(\pi \) can be a true split is 0.5 – since it is in only one optimal tree. It is easy to see that any support value greater than 0.5 produced when \(T_1\) is examined is inflated, and that a correction must be made that takes into consideration that \(T_2\) is also an optimal tree. SIESTA’s way of calculating support explicitly enables this correction, since it explicitly considers the support of each bipartition obtained from the entire set of optimal trees.
6 The SIESTA Algorithm
6.1 The Dynamic Programming Approach to Constrained Optimization
We begin with a review of the fundamentals of the dynamic programming algorithms for the constrained optimization problems. Recall that in the constrained optimization approach, the input is a set of source trees (estimated gene trees in the case of ASTRAL, generic source trees in the case of FastRFS) as well as a set X of allowed bipartitions of the set S of species. Given this set X of allowed bipartitions, we define a set \(\mathcal {C}\) of “allowed clades” by taking the two halves of each bipartition, and we also include the set S; thus, \(\mathcal {C} = \{A: [A|S \setminus A] \in X \} \cup \{S\}\).
We also form a set TRIPS of “allowed tripartitions”, as follows. TRIPS contains all ordered 3-tuples (A, B, C) of allowed clades that are pairwise disjoint, that union to S, and where \(A \cup B\) is also an allowed clade. We require that A and B be non-empty, but we allow C to be empty.
The purpose of creating this set is that it allows us to perform the dynamic programming algorithm to find optimal solutions for some optimization problems. To see this, consider an unrooted binary tree T that is a feasible solution to the constrained optimization problem under consideration. Now root the tree T arbitrarily and pick some internal node v defining clade c. Since T is a feasible solution to the optimization problem, all the clades in \(T^{(r)}\) (the rooted version of T) are allowed clades, and every vertex v defining clade c that is not a leaf has two major subclades A and B defined by its two children. The 3-tuple (A, B, C) where \(C= S \setminus (A \cup B)\) is the tripartition associated to node v (equivalently, associated to clade c). If v is the root of T, then C will be empty. The set of “allowed tripartitions” is defined to ensure that it includes all 3-tuples that could be formed in this way. Finally, by construction, we consider (A, B, C) and (B, A, C) to be equivalent tripartitions.
Similarly, given a rooted binary tree \(T^{(r)}\) on leafset S, each non-leaf node v in \(T^{(r)}\) defines a tripartition (A, B, C) where A and B are the clades (i.e., leafsets) below the two children of v, and \(C = S \setminus (A \cup B)\). We refer to the set of tripartitions of a rooted binary tree \(T^{(r)}\) by \(trips(T^{(r)})\).
Hence, the objective of the constrained optimization problems is to find an unrooted tree \(T^*\) on leafset S that optimizes a function \(F(\cdot )\) defined on unrooted trees, subject to \(T^*\) drawing its bipartitions from X. Hence, if we root \(T^*\), we obtained a rooted tree \(T^{*(r)}\) in which the non-leaf nodes define allowed tripartitions.
ASTRAL and FastRFS are each algorithms that find optimal binary trees for some optimization problem, subject to the constraint that the tree draw its bipartitions from a set X of allowed bipartitions. These algorithms reframe the problem by seeking a rooted tree that draws its clades (i.e., subsets of leaves defined by internal nodes) from the set \(\mathcal {C}\) of allowed clades, and use the dynamic algorithm design that we will now describe.
For both ASTRAL and FastRFS, it is possible to define a function w on allowed tripartitions such that for any unrooted binary tree T on leafset S, letting \(T^{r}\) denote a rooted version of T (obtained by rooting T on any edge),
where F(T) is the optimization score for tree T.
The existence of a function w that is defined on tripartitions and that satisfies Eq. 1 is the key to these dynamic programming algorithms. Given function w that is defined on tripartitions, we define a recursive function f that is defined on clades that we can then use to find optimal solutions. We show how to define f for a maximization problem; defining it for a minimization problem is equivalently easy.
The calculation of f(c) for a given allowed clade c given w and X uses the following recursion (phrased here in terms of maximization):
By Eq. 1, \(f(S) = F(T^*)\), where \(T^*\) is the optimal solution to the constrained optimization problem.
Hence, we can solve the optimization problem using dynamic programming. We compute all the f(c) from the smallest clades to the largest clade S. To construct the optimal solution \(T^*\), when we compute f(c) for a clade c, we record how we obtained this best score (i.e., we record the unordered pair (a, b) of clades whose union is c achieving this optimal score), and we use backtracking to construct the rooted version of \(T^*\). Then we unroot the rooted tree.
6.2 The SIESTA Data Structure
SIESTA modifies these algorithms so they output a set containing all the optimal trees that contain only clades in \(\mathcal {C}\). When computing f(c), instead of recording a single split of the clade c into two subclades that generates an optimal score, we record every such split of c. To achieve this, we show how we can represent the entire set of optimal trees computed during the algorithm with a novel data structure.
A rooted binary tree can be stored as a collection of nodes, where each node contains either two pointers (one to each of its two children, if it is an internal node) or a taxon label (if it is a leaf node). Since each node in a rooted binary tree with leaves labelled by S can be represented by a clade, this representation of a tree can be seen as having pointers from each clade c (with at least two species) to a pair of disjoint clades \(c_1\) and \(c_2\), whose union is c.
We modify this representation to compactly represent a set of rooted binary trees, using the correspondence between nodes in rooted trees and clades, as follows. Instead of having each clade have a pair of pointers to two sub-clades, we have each clade have a set of pairs of pointers to a potentially large number of sub-clades. We denote the set of pairs of pointers for clade c by \(\mathcal {I}[c]\). Thus, the entire data structure is the array \(\mathcal {I}\) indexed by the clades in \(\mathcal {C}\).
Given such a representation, it is easy to generate any single tree by following a path from the entry \(\mathcal {I}[S]\) down to the leaves, and at each clade corresponding to a non-leaf node, choosing one of the pairs of pointers in its set.
The asymptotic running time of this phase is equal to the asymptotic running time of the original DP algorithm, which is \(O(|X|^2 \alpha )\), where \(\alpha \) is the time required to calculate w for a single tripartition [15]. Storing the entire data structure requires \(O(|X|^2)\) space in the extreme case where every tree has the same score, but in many real-world cases will require less.
6.3 Using SIESTA
We show how we can use SIESTA in various ways, including counting the number of optimal trees, generating greedy, strict, and majority consensus trees, and computing the maximum clade credibility tree.
Counting the Number of Optimal Trees. We traverse the collection of allowed clades from smallest to largest, calculating for each allowed clade c the number of optimal rooted binary trees that contain exactly the taxa in c. Obviously, clades of size 1 have exactly one optimal rooted binary tree. For larger clades c, the following expression gives the number of optimal subtrees:
The number of optimal rooted binary trees is optimalsubtrees(S), where S is the entire set of species. For the algorithms we consider (ASTRAL and FastRFS), all rootings of a particular unrooted tree have the same criterion score, and so this quantity should be divided by \(2n - 3\), where \(n=|S|\) is the number of species, to get the number of optimal unrooted trees.
Calculating Consensus Trees. A particular clade c is present in fraction \(A_c\) of the optimal trees, where
For \(\alpha \ge 0.5\), the \(\alpha \)-consensus tree is the unique tree that contains exactly those bipartitions that occur in more than fraction \(\alpha \) of the optimal trees. For smaller values of \(\alpha \), we can still construct a consensus tree, but the set of bipartitions that appear with frequency greater than \(\alpha \) may not form a tree. To construct the \(\alpha \)-consensus tree, we sort the clades in descending order by \(A_c\), restricted only to those clades c with \(A_c> \alpha \), and construct a greedy consensus tree using this ordering. The asymptotic running time of this phase is \(O(|X| \log |X|)\).
The ASTRAL Maximum Clade Credibility Tree. ASTRAL-2 uses a quartet-based local posterior probability (PP) measure [21] to assign support values to edges. We can enhance this technique by outputting every tree in the space of optimal trees, assigning support local PP values to their edges using ASTRAL-2, then computing the average support of each clade (where a tree without a certain clade contributes a support of zero), and taking a greedy consensus of the resulting clades ranked by their average support over all optimal trees. In other words, we greedily compute a maximum clade credibility tree over all optimal trees, and we refer to this as the ASTRAL MCC tree.
References
Alvarado-Serrano, D.F., D’Elía, G.: A new genus for the Andean mice Akodon latebricola and A. bogotensis (Rodentia: Sigmodontinae). J. Mammal. 94(5), 995–1015 (2013)
Bayzid, M.S., Mirarab, S., Warnow, T.J.: Inferring optimal species trees under gene duplication and loss. In: Pacific Symposium Biocomputing, vol. 18, pp. 250–261 (2013)
Bininda-Emonds, O.R.: Phylogenetic Supertrees: Combining Information to Reveal the Tree of Life, vol. 4. Springer Science & Business Media, Dordrecht (2004). doi:10.1007/978-1-4020-2330-9
Bryant, D., Steel, M.: Constructing optimal trees from quartets. J. Algorithms 38(1), 237–259 (2001)
Fletcher, W., Yang, Z.: INDELible: a flexible simulator of biological sequence evolution. Mol. Biol. Evol. 26(8), 1879–1888 (2009). http://mbe.oxfordjournals.org/content/26/8/1879.abstract
González-Ittig, R.E., Rivera, P.C., Levis, S.C., Calderón, G.E., Gardenal, C.N.: The molecular phylogenetics of the genus Oligoryzomys (Rodentia: Cricetidae) clarifies rodent host-hantavirus associations. Zool. J. Linn. Soc. 171(2), 457–474 (2014)
Hallett, M.T., Lagergren, J.: New algorithms for the duplication-loss model. In: Proceedings of the Fourth Annual International Conference on Computational Molecular Biology (RECOMB), pp. 138–146. ACM (2000)
Larget, B.R., Kotha, S.K., Dewey, C.N., Ané, C.: BUCKy: gene tree/species tree reconciliation with Bayesian concordance analysis. Bioinformatics 26(22), 2910–2911 (2010)
Liu, L., Yu, L.: Estimating species trees from unrooted gene trees. Syst. Biol. 60(5), 661–667 (2011)
Liu, L., Yu, L., Edwards, S.V.: A maximum pseudo-likelihood approach for estimating species trees under the coalescent model. BMC Evol. Biol. 10(1), 1–18 (2010). doi:10.1186/1471-2148-10-302
Machado, L.F., Leite, Y.L., Christoff, A.U., Giugliano, L.G.: Phylogeny and biogeography of tetralophodont rodents of the tribe Oryzomyini (Cricetidae: Sigmodontinae). Zoolog. Scr. 43(2), 119–130 (2014)
Maddison, W.: Gene trees in species trees. Syst. Biol. 46(3), 523–536 (1997). doi:10.1093/sysbio/46.3.523
Maestri, R., Monteiro, L.R., Fornel, R., Upham, N.S., Patterson, B.D., Freitas, T.R.O.: The ecology of a continental evolutionary radiation: is the radiation of sigmodontine rodents adaptive? Evolution 71(3), 610–632 (2017)
Mallo, D., Martins, L.D.O., Posada, D.: SimPhy: phylogenomic simulation of gene, locus, and species trees. Syst. Biol. 65(2), 334–344 (2016). doi:10.1093/sysbio/syv082
Mirarab, S., Reaz, R., Bayzid, M.S., Zimmermann, T., Swenson, M.S., Warnow, T.: ASTRAL: genome-scale coalescent-based species tree estimation. Bioinformatics 30(17), i541–i548 (2014)
Mirarab, S., Warnow, T.: ASTRAL-II: coalescent-based species tree estimation with many hundreds of taxa and thousands of genes. Bioinformatics 31(12), i44–i52 (2015)
Mossel, E., Roch, S.: Incomplete lineage sorting: consistent phylogeny estimation from multiple loci. IEEE/ACM Trans. Comput. Biol. Bioinform. (TCBB) 7(1), 166–171 (2010)
Nguyen, N., Mirarab, S., Warnow, T.: MRL and SuperFine+MRL: new supertree methods. Algorithms Mol. Biol. 7(1), 3 (2012)
Roch, S.: A short proof that phylogenetic tree reconstruction by maximum likelihood is hard. IEEE/ACM Trans. Comput. Biol. Bioinform. (TCBB) 3(1), 92 (2006)
Ronquist, F., Teslenko, M., Van Der Mark, P., Ayres, D.L., Darling, A., Höhna, S., Larget, B., Liu, L., Suchard, M.A., Huelsenbeck, J.P.: MrBayes 3.2: efficient Bayesian phylogenetic inference and model choice across a large model space. Syst. Biol. 61(3), 539–542 (2012)
Sayyari, E., Mirarab, S.: Fast coalescent-based computation of local branch support from quartet frequencies. Mol. Biol. Evol. 33(7), 1654–1668 (2016)
Sharanowski, B.J., Robbertse, B., Walker, J., Voss, S.R., Yoder, R., Spatafora, J., Sharkey, M.J.: Expressed sequence tags reveal Proctotrupomorpha (minus Chalcidoidea) as sister to Aculeata (Hymenoptera: Insecta). Mol. Phylogenet. Evol. 57(1), 101–112 (2010)
Stamatakis, A.: RAxML version 8: a tool for phylogenetic analysis and post-analysis of large phylogenies. Bioinformatics 30(9) (2014). doi:10.1093/bioinformatics/btu033
Sukumaran, J., Holder, M.T.: Dendropy: a python library for phylogenetic computing. Bioinformatics 26(12), 1569–1571 (2010)
Swenson, M.S., Barbançon, F., Warnow, T., Linder, C.R.: A simulation study comparing supertree and combined analysis methods using SMIDGen. Algorithms Mol. Biol. 5, 8 (2010)
Szöllősi, G.J., Rosikiewicz, W., Boussau, B., Tannier, E., Daubin, V.: Efficient exploration of the space of reconciled gene trees. Syst. Biol. 62, 901–912 (2013)
Than, C., Nakhleh, L.: Species tree inference by minimizing deep coalescences. PLoS Comput. Biol. 5(9), e1000501 (2009). doi:10.1371/journal.pcbi.1000501.g016
Vachaspati, P.: Simulated data for siesta paper (2017). doi:10.6084/m9.figshare.5234803.v1. Accessed 21 July 2017
Vachaspati, P., Warnow, T.: ASTRID: accurate species TRees from internode distances. BMC Genom. 16(10), 1–13 (2015). doi:10.1186/1471-2164-16-S10-S3
Vachaspati, P., Warnow, T.: FastRFS: fast and accurate Robinson-Foulds Supertrees using constrained exact optimization. Bioinformatics 33(5), 631–639 (2017)
Yu, Y., Warnow, T., Nakhleh, L.: Algorithms for MDC-based multi-locus phylogeny inference: beyond rooted binary gene trees on single alleles. J. Comput. Biol. 18(11), 1543–1559 (2011)
Acknowledgments
We thank the anonymous reviewers for their helpful criticisms on an earlier draft, which greatly improved the manuscript. We also thank Erin Molloy, Sarah Christensen, and Siavash Mirarab, for feedback on the initial results.
Funding. This study made use of the Illinois Campus Cluster, a computing resource that is operated by the Illinois Campus Cluster Program in conjunction with the National Center for Supercomputing Applications and which is supported by funds from the University of Illinois at Urbana-Champaign. This work was partially supported by U.S. National Science Foundation Graduate Research Fellowship Program under Grant Number DGE-1144245 to PV and U.S. National Science Foundation grant CCF-1535977 to TW.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Supplementary Materials
Supplementary Materials
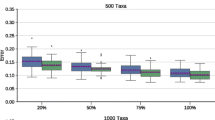
The strict consensus of FastRFS trees is more accurate than FastRFS. We show Delta-error (change in mean topological error between FastRFS and the strict consensus of FastRFS trees) on simulated supertree datasets with 100, 500, and 1000 species; values below 0 indicate that the strict consensus FastRFS is more accurate (i.e., it has lower error) than FastRFS. The figure shows how the percentage of taxa in the scaffold source tree impact accuracy, averaged over 10 replicates for 1000-taxon data and 25 replicates for 100- and 500-taxon data. Error bars indicate the standard error; the topological error is the average of the FN and FP error rates.
Mean error rates for a single FastRFS tree and the strict consensus of all FastRFS trees on the supertree datasets with 100, 500, and 1000 species, compared to the number of optimal trees. We show FP rate and FN rates for each method; these are equal for default FastRFS (because it is always binary), but different for the strict consensus of the FastRFS trees. As the number of optimal trees increases, the decrease in the FP rate is larger than the increase in the FN rate for the strict consensus of the FastRFS trees, explaining why the average error for the strict consensus of the FastRFS trees is lower than for a single FastRFS tree (as shown in Fig. 7). Results for 193 replicates are shown on 1000-taxon data, results for 312 replicates are shown on 500-taxon data, and results for 104 replicates are shown on 100-taxon data.
The strict consensus of ASTRAL trees is more accurate than ASTRAL when gene trees are incomplete. We show Delta-error (change in mean topological error between FastRFS and the strict consensus of FastRFS trees) on simulated phylogenomic datasets with varying numbers of incomplete gene trees on 50-species datasets with three different ILS levels; values below 0 indicate that the strict consensus ASTRAL is more accurate (i.e., it has lower error) than ASTRAL. Note that there is a big advantage in computing the strict consensus tree of the optimal ASTRAL trees instead of a single ASTRAL tree under the highest amount of missing data, and that the advantage decreases as the amount of missing data decreases. We show results for 25 replicates. Error bars indicate the standard error; topological error is the average of the FN and FP error rates.
Mean change in error between the strict consensus of the ASTRAL trees compared to a single ASTRAL tree on the 50-taxon phylogenomic datasets with varying degrees of missing data and ILS, as a function of the number of optimal trees. Values below zero indicate that the strict consensus tree has better accuracy (lower error) than a single ASTRAL tree. We show the change in FP rates (blue, solid line) and in FN rates (red, dashed); the black line represents the baseline. This figure shows that the strict consensus has lower false positives than a single ASTRAL tree and higher false negatives, but also that the reduction in false positives is larger than the increase in false negatives. The figure also shows that the reduction in false positives increases with the number of optimal trees. (Color figure online)
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Vachaspati, P., Warnow, T. (2017). Enhancing Searches for Optimal Trees Using SIESTA. In: Meidanis, J., Nakhleh, L. (eds) Comparative Genomics. RECOMB-CG 2017. Lecture Notes in Computer Science(), vol 10562. Springer, Cham. https://doi.org/10.1007/978-3-319-67979-2_13
Download citation
DOI: https://doi.org/10.1007/978-3-319-67979-2_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-67978-5
Online ISBN: 978-3-319-67979-2
eBook Packages: Computer ScienceComputer Science (R0)