Reparameterization and Adaptive Quadrature for the Isogeometric Discontinuous Galerkin Method

Abstract

We use the Poisson problem with Dirichlet boundary conditions to illustrate the complications that arise from using non-matching interface parameterizations within the framework of Isogeometric Analysis on a multi-patch domain, using discontinuous Galerkin (dG) techniques to couple terms across the interfaces. The dG-based discretization of a partial differential equation is based on a modified variational form, where one introduces additional terms that measure the discontinuity of the values and normal derivatives across the interfaces between patches. Without matching interface parameterizations, firstly, one needs to identify pairs of associated points on the common interface of the two patches for correctly evaluating the additional terms. We will use reparameterizations to perform this task. Secondly, suitable techniques for numerical integration are needed to evaluate the quantities that occur in the discretization with the required level of accuracy. We explore two possible approaches, which are based on subdivision and adaptive refinement, respectively.

1 Introduction

Isogeometric Analysis (IgA) [5, 6] uses the same spaces of spline functions for representing the geometry of a physical domain and for performing a discretization in the context of a PDE-based numerical simulation. This method is based on a parameterization of the physical domain, i.e., on a geometry map that relates the physical domain and the parameter domain.

Many approaches rely on tensor product parameterizations, where the domain is a unit square or a unit cube. Consequently, more complex domains have to be divided into several single patches, forming a multi-patch representation. There exist several methods for coupling the discrete discontinuous Galerkin IgA patch wise solution across the interfaces between single patches and enhancing global continuity of the solution. These include Nitsche’s [16] method and mortar techniques [2] as well as the discontinuous Galerkin (dG) approach, which is the focus of the present paper.

DG methods discretize the variational form of a partial differential equation taking into account the discontinuity of the finite dimensional discretization spaces. The publications [4, 17] provide a general description of dG techniques in the context of finite elements, which have been transferred to the isogeometric setting in [3, 12,13,14].

So far, only matching interface parameterizations have been studied in the context of dG-IgA methods. More precisely, whenever two patches meet in an interface, then the parameterizations restricted to these interfaces are assumed to be identical (possibly after affine transformations of the parameter domains), see [12,13,14, 18]. On the one hand, this limitation provides the advantage that the elements of the patches on both sides of the interface are perfectly matching, which significantly simplifies the implementation of such methods. On the other hand, it complicates substantially the creation of multi-patch parameterizations.

As notable exceptions we mention the recent publications [10, 11], where the authors study gaps and overlaps at the interfaces. While the theory presented in these papers does not require any assumptions regarding matching interfaces, such conditions are assumed to be satisfied in all the computational examples. More precisely, the meshes of the considered domains fulfill restrictive correspondence conditions, which are quite similar to the matching case. This is due to the lack of an implementation for the non-matching case [9].

This recent work has motivated us to investigate the effect of non-matching interface parameterizations in the context of dG-IgA in the present paper. We aim to give a complete description of the necessary computational steps for applying the theoretical results of [10,11,12,13,14, 18] to the case of non-matching parameterizations at the interfaces. In order to keep the presentation simple, we restrict ourselves to planar two-patch domains and we assume that the interfaces are geometrically matching, thus they have neither overlaps nor gaps. However, it is clear that the results from [10, 11] apply to the non-matching case also, as the theory presented there is sufficiently general.

More precisely, the assembly of the local stiffness matrices derived from the dG bilinear form requires the computation of integrals of the type

$$\begin{aligned} \int _{e} D\,b^k_i(\varvec{x}) D'\,b^{\ell }_j(\varvec{x}) d\varvec{x}, \end{aligned}$$

(1)

where e is an interface between $\varOmega ^k$ and $\varOmega ^{\ell }$ in the physical domain, $\varvec{x} \in e$ is a point on the interface, $b^k_i,\, b^{\ell }_j$ are isogeometric basis functions defined on patches $\varOmega ^k,\, \varOmega ^{\ell } \subset \varOmega$ of the multi-patch domain $\varOmega \subseteq \mathbb {R}$, and $D, D'$ are differential operators. As we shall see, non-matching interface parameterizations give rise to two problems that need to be treated separately.

The first one concerns the evaluation of $b^k_i(\varvec{x})$ and $b^{\ell }_j(\varvec{x})$ at the same position $\varvec{x}$ on the interface. Due to the use of non-matching parameterizations, a point $\varvec{x}$ will have two possibly different preimages in the parameter domains of the two patches joined by the interface respectively. To identify pairs of corresponding preimages we use reparameterizations of the preimages of the interface. We also investigate the influence of the quality of the reparameterization on the accuracy of the overall result.

The second problem is related to the use of numerical integration methods. We need to find a quadrature method whose exactness does not depend on the smoothness of the integrands. We present different approaches, one resulting from dividing the element on which quadrature is performed and another one making use of automatized element splitting. The performance of both approaches is explored in numerical experiments.

The remainder of this paper is structured as follows: We establish the notation and describe the example problem we will focus on in the next section. We then state the two issues of evaluation and numerical integration, as described above. Section 3 treats the first problem of finding suitable reparameterizations, while Sect. 4 is devoted to the different quadrature techniques. Results of numerical experiments are presented in Sect. 5. Finally we conclude the paper.

2 Preliminaries

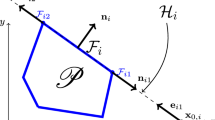
We recall the discontinuous Galerkin isogeometric (dG-IgA) discretization of a given model problem and discuss the computation of the stiffness matrix elements in the case of non-matching interface parameterizations. Hereby, we restrict ourselves to the two-patch case shown in Fig. 1 due to better readability. All observations generalize directly to domains with more than two patches.

Fig. 1.

Multi-patch domain with two patches $\varOmega ^1, \varOmega ^2$, one interface e and geometry mappings $G^1$, $G^2$. The mappings L and R will be introduced later.

2.1 The Model Problem and the Multi-patch Discretization

Given a domain $\varOmega \subseteq \mathbb {R}^2$, we consider the Poisson problem

$$\begin{aligned} \mathrm {Find} \; u: \quad {\left\{ \begin{array}{ll} -\nabla \cdot (\alpha \nabla u) &{}= f \quad \text {on } \varOmega \\ u &{}= 0 \quad \text {on } \partial \varOmega , \end{array}\right. } \end{aligned}$$

(2)

where f is given and $\alpha > 0$ is the known diffusion coefficient. We allow $\alpha$ to be piecewise constant, i.e. $\alpha$ may take different values on every single patch (see below).

More precisely, we consider a multi-patch domain $\varOmega \subseteq \mathbb {R}^2$ that consists of 2 non-overlapping single patches $\varOmega ^1, \, \varOmega ^2$ such that $\bar{\varOmega }^1 \, \cup \, \bar{\varOmega }^2 = \bar{\varOmega }$. We use upper indices to refer to the number of the patch, and thus $\alpha ^k$ denotes the value of the diffusion coefficient on the k-th patch, $k = 1, 2$.

An interface e between the two patches is the intersection $e = \bar{\varOmega }^1 \cap \bar{\varOmega }^2$. We consider interfaces that are curve segments only and ignore the remaining ones.

Each physical patch $\varOmega ^k$ is parameterized by an associated geometry mapping $G^k$ with parameter domain $\hat{\varOmega }^k = [0,1]^2$, $k = 1, 2$. These mappings are tensor product spline functions

$$\begin{aligned} G^k (\varvec{\xi }) = \sum _{i \in \mathcal {R}^k} P_i^k \beta _i^k(\varvec{\xi }) \, , \, \varvec{\xi } \in \hat{\varOmega }^k, \end{aligned}$$

(3)

which are defined by control points $P_i^k\in \mathbb {R}^2$ and tensor product B-splines $\beta _i^k$, where $\mathcal {R}^k$ is the index set of the k-th patch. The lower index i identifies the i-th degree of freedom of the k-th patch.

We do not assume that the knot vectors of the patches are identical. These knot vectors split each parameter domain into elements. We will use open knot vectors which implies that the boundaries of the patches are B-spline curves.

An isogeometric basis function $b_i^k$ on the physical patch $\varOmega ^k$ is the push-forward of a B-spline $\beta ^k$ defined on the parameter domain $\hat{\varOmega }^k$,

$$\begin{aligned} b_i^k ( \varvec{x} ) = {\left\{ \begin{array}{ll}\left( \beta _i^k \circ \left( G^k \right) ^{-1} \right) ( \varvec{x} ) &{} \text { if } \varvec{x} \in \varOmega ^k \\ 0 &{} \text { otherwise.} \end{array}\right. } \end{aligned}$$

(4)

These functions span the space which is used to derive the dG-IgA discretization.

For later reference we define the set of all edges

$$\begin{aligned} \varGamma = \bigcup _{k=1}^2 \{G^k([0,1],0),\, G^k([0,1],1),\, G^k(0,[0,1]),\, G^k(1,[0,1]) \} \end{aligned}$$

(5)

of the multi-patch domain. It is the disjoint union of the set of the interface edges

$$\begin{aligned} \varGamma _C = \{ e\in \varGamma : e \subseteq \bar{\varOmega }^1 \cap \bar{\varOmega }^2 \} \end{aligned}$$

(6)

and the set of boundary edges

$$\begin{aligned} \varGamma _D = \{ e \in \varGamma : e \subseteq \bar{\varOmega }^k \cap \partial \varOmega \, , \, k = 1, 2\, \}. \end{aligned}$$

(7)

2.2 DG-IgA Discretization

The discontinuous Galerkin isogeometric (dG-IgA) discretization space considers the subspace

$$\begin{aligned} \mathcal {V}_h = {{\mathrm{span}}}\, \{ b_i^k \, : \, i \in \mathcal {R}^k, \, k = 1, \ldots , n \} \subseteq \prod _{k = 1}^2 \mathcal {H}^1 \left( \varOmega ^k \right) , \end{aligned}$$

(8)

of the broken Sobolev space, see [17]. Functions in $\mathcal {V}_h$ are continuously differentiable on the interior of the single patches but not necessarily smooth across interface edges. This smoothness of the solution is achieved approximately by introducing a penalty term that considers the jump of the solution across the interface. Before stating the final variational formulation we need to define averages and jumps, see [4, 17].

For each patch index k, any function $v \in \prod _{k = 1}^2 \mathcal {H}^1 \left( \varOmega ^k \right)$ has a well-defined trace along any edge $e\subset \partial \varOmega ^k$. Thus, any such function v defines two traces on the interface $e\in \varGamma _C$, which we denote as $v|_{\varOmega ^{1_e}}$ and $v|_{\varOmega ^{2_e}}$, respectively. We use them to define the average

$$\begin{aligned} \{v\}^e = \frac{1}{2} \left( v |_{\varOmega ^{1_e}} + v |_{\varOmega ^{2_e}} \right) \end{aligned}$$

(9)

and the jump

$$\begin{aligned}{}[v]^e = v |_{\varOmega ^{1_e}} - v |_{\varOmega ^{2_e}} \end{aligned}$$

(10)

across the interface $e\in \varGamma _C$.

These definitions are further extended to boundary edges $e\in \varGamma _D$,

$$\begin{aligned} \{v\}^e = v |_{\varOmega ^k} \text { and } [v]^e = v |_{\varOmega ^k }, \, k = 1,2. \end{aligned}$$

(11)

The dG-IgA discretization

$$\begin{aligned} \mathrm {Find}\; u \in \mathcal {V}_h: \quad a(u,v) = F(v) \quad \forall v\in \mathcal {V}_h \end{aligned}$$

(12)

of the Poisson problem (2) uses the bilinear form

$$\begin{aligned} a(u,v) = \sum _{k=1}^2 a_1^k(u,v) - \frac{1}{2} \sum _{e \in \varGamma _C\cup \varGamma _D } \left( a_{2,1}^e (u,v) + a_{2,2}^e (u,v) \right) + \sum _{e \in \varGamma _C\cup \varGamma _D } a_3^e(u,v) \end{aligned}$$

(13)

with

$$\begin{aligned} a_1^k(u,v)&= \int _{\varOmega ^k} \alpha ^k \nabla u \cdot \nabla v \mathrm {d}\varOmega , \end{aligned}$$

(14)

$$\begin{aligned} a_{2,1}^e(u,v)&= \int _{e} \{ \nabla u \cdot n \}^e [v]^e de,&a_{2,2}^e(u,v)&= \int _e \{ \nabla v \cdot n \}^e [u]^e \mathrm {d}e,\end{aligned}$$

(15)

$$\begin{aligned} a_3^e(u,v)&= \int _{e} \frac{\delta }{h} [u]^e[v]^e \mathrm {d}e&\end{aligned}$$

(16)

and the linear form

$$\begin{aligned} F(v) = \int _{\varOmega } f v d\varOmega . \end{aligned}$$

(17)

The second group of terms $a_{2,1}^e$ and $a_{2,2}^e$ considers normal vectors $n=n_e$ of the interface e, which need to comply with the chosen orientation of the edges (determined by the patch numbering). The last terms $a_3^e$ in the bilinear form are the penalty terms mentioned before, which involve the sufficiently large parameter $\delta$. They depend on the element size h, i.e. on the length of the knot spans¹.

A detailed derivation of the dG discretization is given in [17]. The adaptation to the isogeometric setting is discussed in the thesis [3], which also comments on the choice of the $\delta$, and in the recent article [12].

The discretization (12) defines the associated dG norm

$$\begin{aligned} \Vert u \Vert _{dG}^2 = \sum _{k=1}^2 a_1^k(u,u) + \sum _{e \in \varGamma _C \cup \varGamma _D} a_3^e(u,u), \end{aligned}$$

(18)

where in $a_1(u,u)$ the gradient of u is restricted to $\varOmega ^k$, see again [12].

The coefficients $u_i^k$ of the approximate solution

$$\begin{aligned} u_h = \sum _{k=1}^2 \sum _{i \in \mathcal {R}_k} u_i^k b_i^k \end{aligned}$$

(19)

are found by solving the linear system $Su = b$ with

$$\begin{aligned} S&= \left( s_{(i,k),(j, \ell )}\right) _{(i,k),(j, \ell )}, \\ b&= \left( b_{(j, \ell )} \right) _{(j, \ell )}, \\ u&= \left( u_i^k\right) _{(i,k)}, \end{aligned}$$

where

$$\begin{aligned} s_{(i,k),(j, \ell )}&= a \left( b_i^k, b_j^{\ell } \right) , \, i \in \mathcal {R}^k, \, j \in \mathcal {R}^{\ell }, \, k, \ell = 1, 2, \text { and} \\ b_{(j, \ell )}&= F \left( b_j^{\ell } \right) , \, j \in \mathcal {R}^{\ell }, \, \ell = 1, 2.\\ \end{aligned}$$

2.3 Integrals Along Interfaces

Evaluating the forms in (13) involves integrals along interfaces, which pose considerable difficulties. We discuss the evaluation of these quantities in more detail, considering again the domain shown in Fig. 1. As a representative example we shall focus on $a_{2,1}^e$. All observations generalize directly to other terms.

In this situation we obtain

$$\begin{aligned} a_{2,1}^e(u,v) = \int _e \left( \nabla u |_{\varOmega ^1} \cdot n \right) v |_{\varOmega ^1} + \left( \nabla u |_{\varOmega ^2} \cdot n \right) v |_{\varOmega ^1} \\ - \left( \nabla u |_{\varOmega ^1} \cdot n \right) v |_{\varOmega ^2} - \left( \nabla u |_{\varOmega ^2} \cdot n \right) v |_{\varOmega ^2} \mathrm {d}e. \end{aligned}$$

The stiffness matrix is a combination of several matrices, each of which is contributed by one of the four forms in (13) defining it. In particular we focus on the contribution of $a_{2,1}^e$.

Taking into account that

$$\begin{aligned} b_i^2 |_{\varOmega ^1} = 0 , \,&\nabla b_i^2 |_{\varOmega ^1} = 0 \quad \forall i \in \mathcal {R}^2,\\ b_i^1 |_{\varOmega ^2} = 0 , \,&\nabla b_i^1 |_{\varOmega ^2} = 0 \quad \forall i \in \mathcal {R}^1, \end{aligned}$$

we find that only the expressions

$$\begin{aligned} a_{2,1}^e \left( b_i^k, b_j^{\ell } \right) = (-1)^{\ell +1} \int _e \left( \nabla b_i^k |_{\varOmega ^k} \cdot n \right) b_j^{\ell }|_{\varOmega ^{\ell }} \mathrm de \end{aligned}$$

(20)

contribute to the element $s_{(i,k),(j,\ell )}$ of the stiffness matrix.

In order to compute these values we use an appropriate numerical quadrature rule, which means that we have to evaluate these products on the interface e. This is no major problem if $k = \ell$ since the integral involves only one trace in this case. However, the situation is more complicated if $k\ne \ell$ since the (possibly different) parameterizations of the interface need to be taken into account. In the remainder of this section we discuss the evaluation of $a_{2,1}^e \left( b_i^1, b_j^2 \right)$ in more detail.

The interface

$$\begin{aligned} e = G^1( [0,1]^2 ) \cap G^2( [0,1]^2) = G^1 (1, [0,1]) = G^2(0, [0,1]) \end{aligned}$$

(21)

is parameterized by the restrictions

$$\begin{aligned} L = G^1|_{ (G^1)^{-1}(e)} \text { and } R = G^2|_{(G^2)^{-1}(e)}, \end{aligned}$$

(22)

see Fig. 1. These two different representations of the same interface are related by the reparameterizations

$$\begin{aligned} \lambda : [0,1] \rightarrow \{1\} \times [0,1] \end{aligned}$$

(23)

and

$$\begin{aligned} \varrho : [0,1] \rightarrow \{0\} \times [0,1] \end{aligned}$$

(24)

via

$$\begin{aligned} L \circ \lambda = R \circ \varrho . \end{aligned}$$

(25)

The construction of suitable reparameterizations $\lambda$ and $\varrho$ is the first major problem related to the evaluation of this term. We will discuss it in the next section.

These parameterizations will be used to represent the edge as

$$\begin{aligned} e = (L \circ \lambda ) ([0,1]) = (G^1 \circ \lambda ) ([0,1]) = (G^2 \circ \varrho ) ([0,1]) = (R \circ \varrho ) ([0,1]). \end{aligned}$$

(26)

Finally we define $P=L\circ \lambda =R\circ \varrho$ and arrive at

$$\begin{aligned}&-a_{2,1}^e \left( b_i^1, b_j^2 \right) = \int _e \left( \nabla b_i^1 (\varvec{x})|_{\varOmega ^1} \cdot n (\varvec{x}) \right) b_j^2 (\varvec{x} ) |_{\varOmega ^2} \mathrm {d} \varvec{x}\\&= \int _e \left[ \left( \nabla G^1 (\varvec{x}) \right) ^{-1} \nabla \beta _i^1 \left( (G^1)^{-1} (\varvec{x}) \right) |_{\varOmega ^1} \cdot n (\varvec{x}) \right] \beta _j^2 \left( (G^2)^{-1} (\varvec{x}) \right) |_{\varOmega ^2} \mathrm {d} \varvec{x}\\&= \int _0^1 \left[ \left( \nabla G^1 \left( P(t) \right) \right) ^{-1} \nabla \beta _i^1 \left( L^{-1} \left( P(t) \right) \right) \cdot n \left( P(t) \right) \right] \beta _j^2 \left( R^{-1} \left( P(t) \right) \right) \Vert \dot{P}(t) \Vert \mathrm {d}t\\&= \int _0^1 \left[ \left( \nabla G^1 \left( P(t) \right) \right) ^{-1} \nabla \beta _i^1 \left( \lambda (t) \right) \cdot n \left( P(t) \right) \right] \beta _j^2 \left( \varrho (t) \right) \Vert \dot{P}(t) \Vert \mathrm {d}t. \end{aligned}$$

The integral in the last line is evaluated by a quadrature rule. However, the choice of the quadrature rule, which is the second major problem related to the evaluation of this term, is nontrivial and will be discussed further in Sect. 4. In fact, the choice of the rules needs to take the different knots of the functions $\beta _i^1$, $\beta _j^2$, $\lambda$ and $\varrho$ into account. While one will generally choose the same knots for $\lambda$ and $\varrho$, the knots of $\beta _i^1$ and $\beta _j^2$ are subject to a non-linear transformation and cannot be assumed to be identical.

3 Finding the Reparameterizations

It is quite common in the literature to assume matching parameterizations or almost matching ones, see [5, p. 4148], [6, p. 87], [12,13,14, 18]. In this situation, the choice of the reparameterizations $\lambda$ and $\varrho$ is trivial, as they are simply linear parameterizations (possibly reversing the orientation) of the preimages of the interface in the parameter domains. However, the restriction to matching parameterizations poses constraints on the construction of multi-patch parameterizations, making it essentially impossible to parameterize the individual patches separately. This fact motivates us to study the non-matching case.

More precisely, we consider situations where the condition (25) cannot be satisfied by considering linear reparameterizations $\lambda$ and $\varrho$. Clearly, the condition does not determine $\lambda$ and $\varrho$ uniquely. We fix one of the mappings, say $\lambda$, and compute the remaining one, $\varrho$. Figure 2 visualizes the relations between the mappings.

Fig. 2.

Multi-patch domain with geometry maps $G^1$ and $G^2$, their restrictions L and R to the preimages of the interface and reparameterizations $\lambda$ and $\varrho$

The unknown mapping $\varrho$ satisfies $\varrho = R^{-1} \circ L \circ \lambda$. We compute it by least-squares approximation of point samples, as follows:

• 1. For a given number N of samples, we evaluate

  $$\begin{aligned} \varrho _i = R^{-1} \circ L \circ \lambda \left( \frac{i}{N} \right) \end{aligned}$$

  (27)

  by performing the closest point computations

  $$\begin{aligned} \varrho _i = \mathop {{{\mathrm{argmin}}}}_{\varvec{\xi } \in \{0\} \times [0,1]} \left\| L \circ \lambda \left( \frac{i}{N} \right) - R(\varvec{\xi }) \right\| , \, i = 0, \ldots , N, \end{aligned}$$

  (28)

  where $\Vert \cdot \Vert$ is the Euclidean norm. This formulation also applies to the case of geometrically inexact interfaces (cf. [10, 11]).

• 2. We choose a suitable spline space (e.g. linear, quadratic or cubic splines with a few uniformly distributed inner knots) and find the control points $c_j\in \{0\}\times [0,1]$ of the associated B-splines $N_j$, $j = 1, \ldots , m$, by solving the linear least-squares problem

  $$\begin{aligned} \sum _{i=1}^N \left( \sum _{j=1}^m c_j N_j \left( \frac{i}{N} \right) - \varrho _i\right) ^2 \, \longrightarrow \text {min}, \end{aligned}$$

  (29)

cf. [7]. The influence of the choice of the spline space for $\varrho$ will be discussed later in Sect. 5. The given reparameterization $\lambda$ is chosen as a linear polynomial.

We will refer to the case where at least one of the mappings $\lambda$ and $\varrho$ is different from the identity as non-matching parameterizations at the interface.

4 Numerical Integration

The evaluation of

$$\begin{aligned} a_{2,1}^e \left( b_i^1, b_j^2 \right) = \int _0^1 \left[ \left( \nabla G^1 \left( P(t) \right) \right) ^{-1} \nabla \beta _i^1 \left( \lambda (t) \right) \cdot n \left( P(t) \right) \right] \beta _j^2 \left( \varrho (t) \right) \Vert \dot{P}(t) \Vert \mathrm {d}t \end{aligned}$$

(30)

requires integration with respect to the parameter t, which varies in the parameter domain [0, 1]. This is done by applying numerical quadrature and we present several strategies for doing so.

4.1 Gauss Quadrature with Exact Splitting

Gauss quadrature can be applied to segments of analytic functions. Consequently, we split the parameter domain [0, 1] into segments (separated by junctions) where the integrand satisfies this requirement. Three types of junctions arise:

• the inverse images $\lambda ^{-1}(\kappa _i^1)$ of the knots $\kappa _i^1$ that were used to define the B-splines $\beta ^1_j$,

• the inverse images $\varrho ^{-1}(\kappa _i^2)$ that were used to define the B-splines $\beta ^2_j$, and

• the knots $\tau _i$ that were used to define the B-splines $N_j$ in (29).

These types are visualized in Fig. 3.

Fig. 3.

Exact splitting of a knot span and application of a quadrature rule to each subsegment

Consequently we perform Gauss quadrature with exact splitting by applying the following algorithm:

• Compute all junction points (all three types) in [0, 1],

• sort the junction points, subdivide the domain into segments accordingly,

• subdivide the resulting segments if they are too long,

• apply a Gauss quadrature rule to each segment and sum up the contributions.

As a disadvantage, the inversion of $\lambda$ and $\varrho$ is costly and has to be done with high accuracy, as the sorting depends on it. Furthermore, the method may result in many segments of varying lengths.

We use Gauss quadrature with $p+1$ nodes per element (which exactly integrates polynomials of degree $2p+1$), where p is the degree used for defining the dG-IgA discretization, cf. [15].

4.2 Gauss Quadrature with Uniform Splitting

A computationally simpler approach is to use uniform subdivision, as follows:

• Split the domain [0, 1] uniformly into M segments, where M is a multiple of the number of knot spans used to define the B-splines $N_j$ in (29),

• apply a Gauss quadrature rule to each segment and sum up the contributions.

As we shall see later, it is mandatory to use large values of M in order to reach the desired level of accuracy. This is due to the fact that the junctions of the first two types listed in the previous section may still be located within the segments obtained by uniform splitting. On the other hand, the use of uniform refinement also creates many small segments that could be merged into larger ones without compromising the accuracy. This can be exploited by using adaptive quadrature.

4.3 Adaptive Gauss Quadrature

We recall the main idea of adaptive quadrature, cf. [8]. In order to evaluate the integral

$$\begin{aligned} I = \int _a^b f(x) \mathrm {d}x \end{aligned}$$

(31)

of an integrable function f over an interval [a, b] adaptively one computes two different estimates $I_1$ and $I_2$ of I by using two different integration methods. One assumes that one of these estimates, say $I_1$, is more accurate than the other. Next, one computes the relative distance between $I_1$ and $I_2$ taking into account a given (or chosen) tolerance ${{\mathrm{tol}}}$, e.g. machine precision. If the difference is small enough, one chooses $I_1$ as the value of the integral $\int _a^b f(x)\mathrm {d}x$. If this is not the case one splits the interval [a, b] into two subintervals,

$$\begin{aligned}{}[a,b] = \left[ a, m\right] \cup \left[ m, b\right] , \quad \text{ where } \quad m = \frac{a+b}{2}, \end{aligned}$$

and evalues I by summing up the two contributions. This means that one applies the procedure of computing two different estimates and checking their relative difference to both subintervals. Adaptive quadrature is therefore a recursive procedure, which is summarized in Algorithm 1.

Note that the stopping criterion has to be chosen with care and in fact line 6 in the algorithm is a slight oversimplification of it. See [8] for further information.

We apply this procedure to the knot spans that were used to define the B-splines $N_j$ in (29). Therefore we choose $I_1$ as a Gauss quadrature rule with $p+1$ quadrature knots, where again p is the degree of the basis functions in the dG-IgA discretization space. For the computation of $I_2$ we split the interval manually into two halves, apply a Gauss quadrature rule of the same order on both halves, and sum up. The tolerance ${{\mathrm{tol}}}$ is set to machine precision.

As an advantage, adaptive quadrature can be performed without inverting the reparameterizations. Moreover, it avoids the oversegmentation problem that was present for the previous approach. We observed experimentally that the adaptive procedure accurately detects the junction points and subdivides the domain accordingly. Clearly, the implementation is more costly and requires a recursive algorithm.

5 Numerical Results

We examine the performance of the quadrature methods presented in Sect. 4 as well as the influence of the accuracy of the reparameterization. All experiments were performed using G+Smo², an object-oriented C++ IgA library named “Geometry + Simulation Modules”.

5.1 Reference Results

As a reference we will first show the convergence plot of the solution of the Poisson equation in the case of matching parameterizations, i.e. for $\lambda = \varrho = \text {id}$. In this case we can restrict ourselves to a simple quadrature rule. There is no need for using more elaborate versions of numerical integration. Furthermore, since $\lambda = \varrho = \text {id}$, we do not need to consider the influence of the quality of the reparameterization. More precisely, we consider the two-patch domain with biquadratic matching interface parameterizations shown in Fig. 4, left.

Fig. 4.

Patch and its control net. Left: matching parameterizations at the interface. Right: non-matching parameterizations at the interface.

Figure 5 demonstrates the convergence behaviour of the numerical solutions that were obtained for various values of the element size h that was used to define the dG-IgA discretization. We consider a problem with a known solution and measure the error as the difference to it. The quadrature method we used is Gauss quadrature with three quadrature knots. A convergence rate of three for the L2 error and of two for the dG error is clearly visible. This is in accordance with the theoretical predictions, see [1, 6].

Fig. 5.

Matching parameterizations at the interface, convergence behaviour of error in different norms: L2 norm (blue curve), dG norm (red curve). (Color figure online)

5.2 Influence of the Quadrature Rule

We now consider a different parameterization of the same computational domain, with non-matching parameterizations of the interface, see Fig. 4, right. Again we use biquadratic patches. Now we need to use a more complicated integration technique, and we consider the three approaches that were described in Sect. 4.

Figure  6, top and bottom, visualizes the convergence behaviour measured in the L2 and dG norms respectively. Each plot contains four curves, corresponding to four different numerical quadrature techniques. More precisely, we consider Gauss quadrature with exact splitting (yellow), Gauss quadrature with uniform splitting into 10 (blue) and into 30 (red) segments, and adaptive Gauss quadrature (purple). We observe that the first and the last method perform better than the results based on uniform splitting and they achieve the optimal convergence rates (compare with Fig. 5). In particular we note that using uniform quadrature leads to a reduced order of convergence for smaller mesh sizes h. Even the use of a very fine but uniform segmentation (30 (red) instead of 10 (blue) segments) does not improve this significantly.

Fig. 6.

Influence of the quadrature rule. Top: Convergence behavior of the error in L2 norm. Bottom: Convergence behavior of the error in dG norm. Blue and red curves: 10 and 30 uniform segments per t-knot span. Yellow curves: exact splitting of the knot spans. Purple curves: adaptive quadrature. Note that the yellow curve coincides with the purple one for smaller values of h. Exact representation of the reparameterizations $\lambda$ and $\varrho$. (Color figure online)

Based on these observations we decided to use solely adaptive and exact Gauss quadrature in the remaining example.

5.3 Influence of the Reparameterization

Next we analyse the influence of the quality of the representation of the reparameterization. Consider again the parameterization of the domain in Fig. 4, right, with non-matching parameterizations of the interface. We compare three different choices of the reparameterizations $\lambda$ and $\varrho$.

For the first reparameterization, which generates the results represented by the blue curve in Fig. 7, we choose polynomials $\lambda$ and $\varrho$ such that the equation $L \circ \lambda = R \circ \varrho$ is exactly satisfied. In this case it was possible to find such polynomials, due to the particular construction of the example. However, this would be impossible in general and it is used here to generate a reference result.

The second and third reparameterizations (red and yellow curves) were obtained using the Algorithm from Sect. 3 to find $\varrho$, while $\lambda$ was chosen as a linear polynomial. The second reparameterization uses a linear spline with 8 segments and has an L2 error of $1.3 \cdot 10^{-2}$, and the third reparameterization uses a cubic spline with 4 segments and has an L2 error of $3.1 \cdot 10^{-15}$.

Figure 7 compares the errors in the L2 (top) and dG norms (bottom) for the three reparameterizations. We observe that using a high quality reparameterization is essential for the convergence of the method. Depending on the accuracy of the reparameterization, h-refinement only works until it reaches a critical mesh size, where further refinement does not have any effect.

The plots show the results obtained by using adaptive Gauss quadrature. The exact method gives virtually identical results.

Fig. 7.

Influence of the reparameterization. Adaptive quadrature on interface integrals. Top: Convergence behaviour of the error in L2 norm. Bottom: Convergence behaviour of the error in dG norm. Blue curves: Exact representation of $\lambda$ and $\varrho$. Red curves: Approximation error of $\varrho$ $\approx 0.0131167$. Yellow curves: Approximation error of $\varrho$ $\approx$ $3.10616 \cdot 10^{-15}$ (Color figure online)

5.4 Comparison of Exact and Adaptive Quadrature

We perform an experimental comparison of the computational complexity of exact and adaptive quadrature for the domain in Fig. 4, right.

First we demonstrate the effect of using adaptive quadrature, by showing the automatically created splitting points in Fig. 8. We used an accuracy of $10^{-6}$ instead of machine precision for this picture to obtain a clearer image. Both patches were uniformly refined into $4\times 4$ elements by knot insertion. The mappings $\lambda$ and $\varrho$ are cubic splines on [0, 1] with four knot spans of equal length. Their knots $\tau _i$ coincide with the inverse images $\lambda ^{-1}(\kappa ^1_i)$, as the first mapping is simply the identity. The adaptive quadrature, which is applied to the knot spans $[\tau _i,\tau _{i+1}]$, thus creates additional splitting points around the inverse images $\varrho ^{-1}(\kappa ^2_i)$, as shown in the Figure. In this particular case, only one splitting point (at 0.5625) is created near $\varrho ^{-1}(\kappa ^2_2)=0.5615$ since this suffices to reach the desired accuracy.

Fig. 8.

Splitting points created by adaptive quadrature - see text for details.

These results indicate that, unlike uniform Gauss quadrature, adaptive quadrature avoids over-segmentation of the integration domains. Still, it splits the knot spans more often than exact Gauss quadrature, which also results in a higher number of quadrature knots and thus evaluations.

In order to analyze this effect, Fig. 9 compares the number of evaluations (i.e., quadrature knots) used by exact and adaptive Gauss quadrature for increasing numbers of elements. In addition, we also show the number of root finding operations (which are more expensive than evaluations) needed to compute the splitting points of exact Gauss quadrature. Clearly, adaptive quadrature requires more evaluations than exact splitting. However, for sufficiently fine discretizations, the number of evaluations in the interior of the patches dominates the total effort.

Fig. 9.

Number of quadrature knots and root finding operations needed by exact and adaptive quadrature for increasingly finer discretizations.

6 Conclusion

We used a simple model problem to investigate the complications that arise from using non-matching interface parameterizations within the framework of Isogeometric Analysis on a multi-patch domain, using discontinuous Galerkin techniques to couple terms across the interfaces. More precisely, we studied two particular problems. Firstly, we explored the use of reparameterizations to identify pairs of associated points on the common interface. This was found to be useful for correctly evaluating certain terms in the dG discretization. Secondly, we addressed the construction of a suitable procedure for numerical integration. As demonstrated in our numerical experiments, both problems are important for ensuring the optimal rate of convergence for the numerical simulation based on the isogeometric dG discretization.

Future work may be devoted to the extension of the adaptive quadrature-based approach to the three-dimensional case. Moreover, we are currently studying dG-type techniques for performing multi-patch spline surface fitting with approximate geometric smoothness across patch interfaces.