Towards Subdivision Surfaces C2 Everywhere

Abstract

The conditions for subdivision surfaces which are piecewise polynomial in the regular region to have continuity higher than C1 were identified by Reif [7]. The conditions are ugly and although schemes have been identified and implemented which satisfy them, those schemes have not proved satisfactory from other points of view. This paper explores what can be created using schemes which are not piecewise polynomial in the regular regions, and the picture looks much rosier. The key ideas are (i) use of quasi-interpolation (ii) local evaluation of coefficients in the irregular context. A new method for determining lower bounds on the Hölder continuity of the limit surface is also proposed.

1 Motivation

There is a myth among commercial CAD system suppliers that “Subdivision surfaces are adequate for animation, but they can’t be used for serious CAD because they are not C2 at extraordinary points.”

Although this myth cannot be completely discounted (like most myths there is some truth hidden underneath), in this raw form it is false.

• 1. There are subdivision surface schemes which are C2 at extraordinary vertices (see [9, 18, 19] and several others). They may all have other problems, but they are C2.

• 2. Lack of C2 at isolated points does not matter. The ideas of [18] could be applied after a few hundred iterations of a standard method. This would make the limit C2 everywhere, but it would be totally indistinguishable from the raw limit surface. Also, there is a bivariate interpolation technique which minimises the bending energy of the surface. This is widely regarded as good, but the second derivatives are unbounded at the data sites.

• 3. The ‘raw’ forms of popular subdivision surfaces [2, 4, 5] are not merely not C2. They actually have unbounded curvature at extraordinary points, and because the unboundedness accelerates at different rates for positive and negative Gaussian curvatures, this can force regions of the limit surface close to an extraordinary point to have the wrong sense of curvature [15, 16]. Such extreme behaviour can be eliminated easily [23, 24] by tuning of the coefficients in extraordinary regions, but this does not cure the lack of C2, and is not widely cited.

The truth underneath is that the raw forms of the popular schemes, and even tuned versions to a lesser extent, suffer from local distortion of the surface over non-infinitesimal regions. It is these artifacts which are visible and objectionable in the reflection line plots, and it is these which need to be eliminated. The basic cause of these turns out to be the same as the cause of our inability to tune these schemes to perfection: the inability to achieve quadratic generation in any simple uniform stationary scheme which gives bi-polynomial pieces in the regular regions. This was understood nearly twenty years ago [7, 9, 10] and that understanding has deepened since [17].

This paper explores the idea of using schemes with fractal limit surfaces, the analog of the quasi-spline curves of [20, 21] to give the kind of behaviour which serious CAD needs. [25] has already explored the quad grid case, and so the focus here is on surfaces where the regular part of the mesh contains triangles.

Any full coverage of this will require many more years of work, and so this paper merely sets out the territory and provides some initial results and some ideas for directions which need to be explored. The exploration here is of surfaces with a quasi-interpolating degree of three.

2 Definitions

A scheme is said to generate polynomials of degree d if for any bivariate polynomial of degree d we can find a control polyhedron for which that function is the limit.

A scheme is said to reproduce polynomials of degree d if for any bivariate function of degree d we can find a control polyhedron for which that function is the limit, and for which the control points all lie on the function. The limit has to interpolate them.

The distinction between these two was not emphasised in the early papers, but it turns out to be fairly important. Over regular grids, most subdivision schemes can generate polynomials of low degree. Those which are B-spline based do not reproduce them for degrees above 1.

A scheme can reproduce polynomials without being an interpolating scheme for arbitrary data. Such a scheme is called a quasi-interpolating scheme of degree d where d is the highest degree of polynomial which it can reproduce.

A scheme is called a stable generator of degree d if it generates polynomials of degree d and if the maximum change of $d^{th}$ derivative with respect to addition of perturbations of maximum amplitude $\epsilon$ is continuous with respect to $\epsilon$ with Hölder exponent greater than 1, 0. The issue of stability is critical. The four-point scheme is a quasi-interpolant of degree 3, but not a stable one, because for any sequence of six data points which do not all lie on a cubic, the second derivatives at dyadic points within the central span diverge at a rate depending on the fourth differences of the local control points.

3 Quadratic and Cubic Reproduction in Functional Subdivision over a Regular Triangulation of the Domain

This section exemplifies an approach. It does not preclude further work on higher quasi-interpolation degrees, on different regular connectivities or on higher arities.

3.1 Stencil Sizes

A quasi-interpolating functional subdivision scheme has the property that if the values at all the old vertices lie on a polynomial, then new vertices will also get vertices on that polynomial. If this property holds at every step, then the limit surface will reproduce that polynomial, which we take as a condition for continuity of the relevant degree, and for avoiding certain artifacts.

In order for a new vertex to have that property, the value has to be chosen to match all polynomials of the target degree, d, which means that unless the scheme is actually interpolating, there is a number n of conditions to be fulfilled equal to the number of independent polynomials of that degree. These are tabulated in Table 1.

Table 1. Stencil sizes

Table 2. Number of available vertices

We get the new value by taking a linear combination of the values at the vertices in the stencil of the new point, and in order to be able to satisfy all these conditions, we need to have at least as many independent coefficients in those linear combinations. This leads to the unwelcome conclusion that high degrees of polynomial reproduction will require very large stencils, involving a number of rings varying at least linearly with the degree. See Table 2. Quadratics and cubics remain (just) within sensible reach.

We can have more coefficients (i.e. more old vertices in the footprint of the stencil) than conditions to satisfy, and in this case the choice of the values of those coefficients is underdetermined. This can be demanded by symmetry, since the number of vertices in a rotationally symmetric stencil goes up with the number of rings included.

However, in the case of the completely regular domain, symmetry also provides a way of resolving the extra freedom.

3.2 Construction of Cubic Quasi-interpolant

We know that each of the stencils must contain at least 10 entries for cubic quasi-interpolation. There are three e-vertex stencils as well as the v-vertex stencil, and so the total number of entries in the mask must be at least 40. We need some understanding in order to be able to construct such a beast.

This understanding comes from two sources: the first is that the v-vertex stencils must have 6-fold rotational symmetry, and that the e-vertex stencils must have two mirror symmetry axes. The second is that we cannot have good behaviour for general data if we do not have good behaviour for extruded data, in which each mesh direction has the same value at all points along each edge in that direction.

If the data is extruded, then the shape of a cross-section limit curve will be given by a univariate refinement scheme whose mask is given by the row-sums of the bivariate scheme. Further, factorisation of the mask is preserved under the taking of row-sums. Because there are three directions for the row sums, the desired symmetries come out in the wash.

We know a univariate scheme with cubic quasi-interpolation. This was described by Hormann and Sabin [20]. Its mask is

$$\begin{aligned} 2\left( {{[1,1]}\over {2}}\right) ^6 {{[-3,10,-3]}\over {4}} \end{aligned}$$

To map this to a triangular grid we need to take the $[1,1]{\slash }2$ factors in pairs, replacing each pair by

and finding a kernel which, when multiplied by the cube of this, gives the required row sums.

This is easily found to be

which has the correct row sums to match $[-3,10,-3]/4$, giving a final mask¹ of $4S^3K$.

From this we can extract the stencils

and

There are enough entries in these stencils (19 and 14 respectively) to give cubic precision, which requires 10 points, but not quite quartic, which requires 15. In any case there is no reason why these coefficients should satisfy the quartic quasi-interpolation conditions. Three of the four cubics and all lower degrees are satisfied because cubic extruded data is matched for three extrusion directions (by symmetry). The fourth cubic condition is based on a linearly varying quadratic, and this is satisfied by mirror symmetry. We therefore assert that this set of stencils satisfies all of the constant, linear, quadratic and cubic quasi-interpolation conditions.

The question remains whether the resulting scheme is stable in the sense that the eigenvalues behave.

3.3 The Basis Function

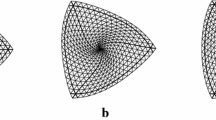
The basis function is the effect on the surface when one control point is moved. If we start the refinement process itself with a single unit valued control point and all the rest with value zero (cardinal data), successive refinements converge towards the basis function. We can get tesselations of the basis function by convolving each of these with the unit row stencil (the row (left) eigenvector of the component with unit eigenvalue and column (right) eigenvector of all 1s) to get the vertices at limit points. These are shown in Fig. 1. The last of these can be compared with the basis functions of the Butterfly [5] and Loop [4] schemes in regular regions in Fig. 2. Our scheme has significantly smaller wriggles than Butterfly, and is narrower than Loop. In all of these figures, the basis function is shown as far out as the first zero entries. Note that these are not control polyhedra, as the scheme is only quasi-interpolating and the basis function is not a polynomial.

Fig. 1.

The first four iterations, in which there is refinement, but no alteration of existing limit points.

Fig. 2.

The basis functions of the butterfly scheme and of Loop in regular regions. (also drawn at four iterations.)

3.4 Continuity Analysis

We can address the determination of lower bounds on the Hölder continuity by three routes. The first approach is to apply the bivariate approach of Cavaretta et al. [6], which is capable of showing that whatever the data, a norm of the first difference of the second or third divided difference contracts with each refinement. This is capable of putting a lower bound on the continuity of the limit surfaces. Unfortunately I have not been able to formulate this approach and have not therefore been able to apply this test.

The second is that of Kobbelt [11], which applies difference operators to the powers of the refinement operation.

I suggest here that a simpler approach may be to check whether the contractivity is true for the basis function. Any other data has its limit surface expressed at any point as a finite weighted sum of basis functions, and so if the basis function is continuous in derivative to a certain degree, then so must any other limit surface. This can be done numerically and is covered in Sect. 3.5 below.

We can also determine upper bounds by checking the magnitudes of the eigenvalues, which can put upper bounds on the level of continuity, by measuring the actual continuity at specific mark points of the surface. This can also be done numerically and is covered in Sect. 3.6 below. Sharper bounds can in principle be determined by eigenanalysis at more mark points. Here only the triangle vertices and triangle centres are considered.

3.5 Contractivity of Differences of the Basis Function

Because we have tesselations of the basis function at different levels, we can, merely by convolving with appropriate difference stencils, determine how the various differences vary from level to level.

Because it is easiest to implement, the tables below are derived by taking the appropriate differences (up to 4th) over the entire domain and then extracting norms. We show here the max-norm and the average absolute value.

Because of the symmetry of the basis, we need only take the first differences in one direction giving Table 3. Similarly the three second differences are just symmetric versions of a single one giving Table 4. We can get the four 3rd differences just by evaluating two of them giving Table 5. The same is true of the 4th differences giving Table 6.

In each table are five columns. The second is the sum of the absolute values of the relevant difference, taken over the tesselations of the basis function shown in Fig. 1. The third is the ratio between each such value and the one above. The fourth column is the maximum absolute value of the relevant difference, and again the fifth holds the ratio between successive refinements.

Table 3. First differences: Because the entries in the second column are sums, the ratios need to be divided by 4 to get the actual ratio of norms. (There are four times as many triangles and therefore four times as many difference entries in each row compared with the previous.) With this correction, both ratios are converging nicely to 1/2, which, because it is less than one indicates that the scheme is convergent, with a continuous limit.

Table 4. Differences of first divided differences: The ratios in the third column now need to be divided by 4, but also multiplied by 2, because the raw figures are differences rather than divided differences. Those in the fifth column now need to be multiplied by 2. Again, the ratios are nicely converging to 1/2 which is well below 1, and so we can deduce that the scheme is C1.

Table 5. Differences of second divided differences: We have two different third differences in use here. The ratios in the third column now need to be divided by 4, but also multiplied by 4, because the raw figures are differences rather than divided differences. Those in the fifth column now need to be multiplied by 4. Yet again, the ratios are nicely converging to 1/2 which is well below 1, and so we can deduce that the scheme is C2.

Table 6. Differences of third divided differences: We have three different fourth differences in use here. The ratios in the third column now need to be divided by 4, but also multiplied by 8, because the raw figures are differences rather than divided differences. Those in the fifth column now need to be multiplied by 8. It looks as though we can infer C3.

3.6 Eigenvalue Analysis

This is very straightforward, as we can work solely with the kernel, which is very simple.

The stencils are

The subdivision matrix at vertices for the zero frequency Fourier component becomes

whose only non-zero eigenvalues are 26/2 and $-3/2$. Those of higher frequency Fourier components are never larger.

We may therefore determine the Hölder continuity at vertices to be

$$\begin{aligned} 6-log_2(13) = 6-3.7004 = 2.2996, \end{aligned}$$

because each S factor increases the Holder continuity by 2.

The subdivision matrix at triangle centres for the zero frequency Fourier component becomes

$$\begin{aligned} \left[ \begin{matrix}-6/2\\ 26/2&{}0\\ -3/2&{}-3/2&{}0\\ -3/2&{}0&{}-3/2&{}\ddots \end{matrix}\right] \end{aligned}$$

whose only nonzero eigenvalue is $-3$. Those of higher frequency Fourier components are never larger.

The Hölder continuity here is $6-log_2(3) = 4.41$

In fact the continuity might be less than 2.2996, because this analysis only tells us about the continuity at the dyadic points, giving upper bounds on the level of continuity. Other mark points might have different (worse) behaviour. There are an infinite number of them and this is why the joint spectral radius calculation is such a lot of work. However, getting two upper bounds on the right side of 2 means that the method has not failed this test.

4 Triangulations with Extraordinary Vertices

The handling of extraordinary vertices requires amazingly little additional analysis. If a scheme has quadratic or cubic precision, it will have linear precision. We can therefore choose a desired natural configuration, for example by taking that of any C2 scheme, and the coefficients computed to give the reproduction properties will automatically make that natural configuration a self-fulfilling prophecy.

We have three types of stencil to determine:

• (i) That of the EV itself.

  Here use of symmetry resolves the underdeterminedness.

• (ii) Those of new vertices² lying within the support of the EV: i.e. whose stencils contain the EV in their interior, so that the topology of the stencil is affected asymmetrically by the presence of the EV.

  This is where most of the work lies, in that the vertices which need to be taken into account have to be chosen. The EV spoils the regularity of the topology. Calculating the coefficients to give the required reproduction properties applies as in the regular case.

• (iii) Those of vertices lying further out, in what we can term the ‘far field’. Here the topology of the stencil is regular, but the geometry is influenced by the natural configuration. Thus the actual coefficients will differ from the regular case. This effect propagates unboundedly, although hopefully reducing with distance. However, we can choose to resolve the underdeterminedness by minimising the difference from the regular case. Because of the regress of regularity around the extraordinary vertices, if the stencils converge fast enough towards the regular case, we do not have to worry about continuity at any points other than the extraordinary vertices themselves. This means that eigenanalysis at the EVs is a sufficient tool. Thus most of the really hard work is done in the regular case.

In fact at large distances from an EV we have two possible strategies

• (iii.i) to be pure, and insist that all stencils are determined correctly.

  In fact, if we are careful, the perturbation of the coefficients from the regular case reduces fast enough with distance that after a certain distance it can be approximated accurately enough (to machine precision) by some simple form, which can be combined when more than one EV is present in the control polyhedron.

• (iii.ii) just to revert to the regular stencil for all new vertices whose support does not touch the EV.

  This avoids a lot of implementation problems, and will not spoil the continuity at the EV, because only control points within, or on the boundary of, the support of the EV influence the shape of the limit surface in the immediate neighbourhood of the EV. It will not spoil the continuity anywhere else either, because everywhere outside that neighbourhood has its continuity governed by the regular case.

  However, we can expect something to go wrong, and an obvious symptom to be expected will be the appearance of artifacts in the region between the two regimes.

A practical resolution might well be to use (iii.ii) to avoid overlapping influences from more than one EV. In regions where more than one EV has a significant effect, who can say what the desired surface should be? As refinement proceeds, the threshold between the two regimes can move in more slowly than the refinement rate, and the artifacts should therefore be spread out and diluted.

4.1 Conformal Characteristic Map

In [13] David Levin conjectured that a stationary subdivision scheme giving the characteristic map

$$u+iv = (s+it)^{6/n}$$

would require a EV mask of unbounded size. Here we have a non-stationary scheme, because the stencils depend on the local layout of control points in the domain, and the corresponding conjecture is that the influence of the presence of the extraordinary point extends unboundedly, even though the EV itself is only accessed by the stencils of a finite number of nearby new vertices.

In the far field we find that the rate of convergence to the regular case turns out to be significantly slower if we enforce cubic reproduction than if we only enforce quadratic, despite the fact that what we are trying to be close to does have cubic precision when the geometry is regular. The Tables 7, 8, 9 and 10 in Annex 2 report $E1=\varSigma _i \delta _i^2$ and $E2=max_i |\delta _i|$ for reproduction of degrees 2 and 3, for v-vertices along rays from the EV of valencies 5 and 7.

4.2 Other Characteristic Maps

The choice of the conformal characteristic map is entirely an aesthetic one. It would be equally possible to choose as arbitrary natural configuration that of Loop or of the Butterfly scheme. Anything, in fact, which can be shown to be 1:1 and have its characteristic map join smoothly enough to its scaled instance under the next ring.

4.3 Moving Least Squares

Since presentation of the paper I have seen the recent work of Ivrissimtzis. This uses a combination of a standard subdivision scheme (in this Loop, Butterfly or even the degree 1 box-spline) to determine approximate new vertex positions, which are then refined by projection on to a local least squares fit to some subset of the old vertices. This work is following a line which can be traced back through the work of Boyé, Guennebaud and Schlick [22], Levin [14] and McLain [1]. It looks to be almost equivalent to the above ideas, in that it gives a quasi-interpolant (if enough local points lie on a polynomial, the new point will lie on that polynomial), but goes, apparently, more directly to the new points (projecting rather than first computing coefficients).

5 Directions Still Needing Exploration

5.1 Stronger Proof of Degree of Continuity

The analysis of the regular case above is unsatisfactory, with different approaches giving different opinions. The method of chapter seven in Cavaretta et al. [6] needs to be made to work.

5.2 End and Edge Conditions

Before these ideas can be applied to practical situations, the detail of what to do at the edges of the domain of interest needs to be articulated. Unfortunately we do not yet even have end conditions adequately explored for univariate quasi-splines, and this must obviously come first.

5.3 Extension to Higher Degrees

In principle exactly similar constructions can be made, choosing coefficients to give any desired quasi-interpolation degree. Because the stencils for higher degrees become large quadratically with degree, it is unlikely that higher degrees will be of more than academic interest, but the academic interest is there. It seems likely that the extension in this direction will not expose new problems significantly different from those already seen.

5.4 Extension to Solids and Higher Dimensions

Although regular triangular grids do not have completely regular analogues in higher dimensions, the ideas of using subdivision basis functions which reproduce low degree polynomials without being interpolating for general data must be relevant to IsoGeometric Analysis, overcoming the current disadvantage of subdivision that the lack of polynomial generation gives excessive stiffness because the artifacts contribute spurious energy to the solution.

Appendices

Annex 1: Computation of Stencil Nearest to a Regular Stencil

In the topologically regular but geometrically irregular case, I suggest that the nearest solution to the regular one should be chosen. This gives some measure of continuity with respect to changing layouts in the abscissa plane. The metric for ‘nearest’ might be chosen by more sophisticated arguments later³, but for the moment I just use the euclidean distance in coefficient space.

Call the number of coefficients c and the number of quasi-interpolation conditions n.

The quasi-interpolating conditions define a linear subspace of dimension $c-n$ in the space of dimension $c-1$ of sets of coefficients: nearness to the regular coefficients defines a complementary subspace orthogonal to it, and the solution can be found in that subspace by solving a linear system of size $n\times n$.

Let the set of coefficients be $a_i,\ i\in 1..c$, and let the quasi-interpolation conditions be

$$\begin{aligned} \forall j\in 1..n\quad \varSigma _i a_if_j(v_i) = 0 \end{aligned}$$

If the regular coefficients are $\bar{a}_i$, then we can set up the system

$$\forall i\ a_i = \bar{a}_i + \varSigma _{k\in 1..n}\,\delta _k f_k(v_i)$$

and solve for the $\delta _j$.

$$\begin{aligned} \forall j\in 1..n\quad 0= & {} \varSigma _i a_if_j(v_i) \\= & {} \varSigma _i\, \left( \bar{a}_i + \varSigma _{k}\,\delta _k f_k(v_i)\right) f_j(v_i) \\= & {} \varSigma _i\, \bar{a}_if_j(v_i) + \varSigma _i \,\varSigma _{k}\,\delta _k f_k(v_i)f_j(v_i) \\= & {} \varSigma _i\, \bar{a}_if_j(v_i) + \varSigma _{k}\,\varSigma _i\,\delta _k f_k(v_i)f_j(v_i) \\= & {} \varSigma _i\, \bar{a}_if_j(v_i) + \varSigma _{k}\,\delta _k\varSigma _i\, f_k(v_i)f_j(v_i) \\\left[ \begin{matrix}\ddots &{}&{}\\ &{}\varSigma _i\, f_k(v_i)f_j(v_i)&{}\\ &{}&{}\ddots \end{matrix}\right] \left[ \begin{matrix}\vdots \\ \delta _k\\ \vdots \\ \end{matrix}\right]= & {} -\left[ \begin{matrix}\vdots \\ \varSigma _i\, \bar{a}_if_j(v_i)\\ \vdots \\ \end{matrix}\right] \\\end{aligned}$$

The actual coefficients can then be determined from these $\delta _j$ values.

$$\begin{aligned} \forall i\ a_i:= & {} \bar{a}_i + \varSigma _{k}\,\delta _k f_k(v_i) \end{aligned}$$

The rate of convergence with distance from the EV in an interesting natural configuration can be measured by how $\varSigma _j \delta _j^2$ varies with distance.

Annex 2: Convergence for Conformal Characteristic Map

Table 7. Valency = 5, reproduction degree = 2

Table 8. Valency = 5, reproduction degree = 3

Table 9. Valency = 7, reproduction degree = 2

Table 10. Valency = 7, reproduction degree = 3

These figures in Tables 7, 8, 9 and 10 ($E1=\varSigma _i \delta _i^2$ and $E2=max_i |\delta _i|$) are disappointing in that the convergence is so slow. A conjecture that the rate of convergence would be $d^{-6}$ has been soundly disproved by these calculations.