Image Denoising Using Backward Stochastic Differential Equations

Abstract

In this paper we explore the problem of reconstruction of RGB images with additive Gaussian noise. In order to solve this problem we use backward stochastic differential equations. The reconstructed image is characterized by smoothing noisy pixels and at the same time enhancing and sharpening edges. This novel look on the reconstruction is fruitful, gives encouraging results and can be successfully applied to denoising of high ISO images.

1 Introduction

The backward stochastic differential equations (BSDEs) were introduced by Pardoux and Peng [14] who proved the existence and uniqueness of their adapted solution under suitable assumptions. Independently, Duffie and Epstein [9, 10] considered stochastic differential utilities in economics models, as solution of certain BSDEs. Since then, it has been widely recognized that BSDEs provide a useful framework for formulating many problems in mathematical finance [11]. These equations have also appeared to be useful for problems in stochastic control and differential games [13]. Many papers (for instance [15]) show the connections between BSDEs driven by a diffusion process and solutions of a large class of quasilinear parabolic and elliptic partial differential equations (PDEs). These results may be seen as a generalization of the celebrated Feynman-Kac formula. Through all these results, a formal dictionary between BSDEs and PDEs can be established, which suggests that existence and uniqueness results obtained on the one side should have their counterparts on the other side. In our case, we treat BSDEs as a starting point in the creation of reconstruction model of the noisy image. In our opinion a stochastic description is more intuitive than PDEs description. Moreover in order to solve the BSDE model we use tools of stochastic analysis giving us completely new methodology.

In image processing one can find some practical aspects [1,2,3,4] of BSDE-based applications. In [1] the problem of reconstruction of the noisy chromaticity is considered. Presented model of denoising is expressed in terms of Skorokhod problem associated with the solution of BSDE and an epsilon neighbourhood of two dimensional sphere. In that paper BSDE is driven by a trivial drift function ($f\equiv 0$). This means that presented equation is a model of forward filtering and has properties of smoothing filters. In [2] problems of reconstruction of the noisy grayscale image (smoothing filters) and enhancing of the blurred grayscale image (enhancing filters) are presented. Smoothing filter, similarly as in [1], models on anisotropic forward diffusion with BSDEs with $f\equiv 0$. Enhancing filters presented in [2] are driven by BSDEs with non trivial drift function and correspond to inverse heat equation. This equation is a model of backward filtering (not forward) and in consequence this model fails to edge enhancing of the noisy image. The paper [4] is a generalisation of [2] to images with values in $\mathbf R^n$. In papers [2, 4] smoothing and enhancing filters were considered as two separable models while in [3] authors proposed the model of image reconstruction using backward stochastic diffusion associated with forward stochastic diffusion. This method combines forward anisotropic filtering in perpendicular to gradient direction and inverse anisotropic filtering in gradient direction, where effects of smoothing, enhancing and sharpening join. The article [3] focuses only on images with values in $\mathbf {R}^1$ (greyscale images).

In this paper we generalise the results from [3] to $\mathbf {R}^n$ valued images, in particular to colour images and apply the proposed method to denoising of high ISO images taken from digital cameras.

The paper is constructed as follows. Sections 2 and 3 contain basic ideas of filtering in terms of BSDEs taken from [3]. Section 4 provides new results to reconstruction of colour images. In Sect. 5 we give details of numerical approximation of the proposed method. Finally, in Sect. 6 experimental results to denoising of high ISO images taken from digital cameras are presented.

2 Continuous Model

A general model of the image reconstruction in terms of BSDE is the following [3]:

$$\begin{aligned} \left\{ \begin{array}{ll} X_t=x+\displaystyle \int _0^t\sigma (s,X_s)\,dW_s+K_t^{\overline{D}},\quad t\in [0,T]\\ \\ Y_t=\xi +\displaystyle \int _t^Tf(s,Y_s,X_s)ds-\displaystyle \int _t^T Z_s\,dW_s,\quad t\in [0,T] \end{array} \right. \end{aligned}$$

(1)

where $\xi$ is some random variable which depends on the noisy image $u_0: \overline{D} \rightarrow \mathbf {R}^n$ and $\{W_t\}_{t\in [0,T]}$ is two-dimensional Wiener process. $\{X_t\}_{t\in [0,T]}$ is a stochastic diffusion process with reflection with values in the domain of the image $\overline{D}$ and is driven by some function $\sigma$. The function $\sigma$ is called the diffusion coefficient. The process X characterizes the behaviour of the continuous time stochastic process X as an Itö integral. A heuristic interpretation is that in a small time interval of length $\sigma$ the stochastic process X changes its value by an amount that is normally distributed with variance $\sigma (t,X_t)$ and is independent of the past behaviour of the process. This is so because the increments of a Wiener process are independent and normally distributed. The term $\{K_t^{\overline{D}}\}_{t\in [0,T]}$ is the minimal push needed to keep process X in $\overline{D}$. $\{Y_t\}_{t\in [0,T]}$ (the first component of the solution to the BSDE) is a backward stochastic diffusion process with values in the codomain of the image $\mathbf {R}^n$ and is driven by some function f. $\{Z_t\}_{t\in [0,T]}$, the second component of the solution to the BSDE determines the measurability of the process Y. The process Y is constructed so that it starts at $t=T$ until $t=0$. A drift function f causes the correction of values of Y in expected strength and direction. The value of the process Y at time $t=0$ is the reconstructed pixel u(x). Note that $Y_0$ is a deterministic value.

In the case of image processing we have the following interpretation of this BSDE equation. For a fixed pixel x we consider a certain BSDE equation. The values of the process X determines pixels from domain of the image $\overline{D}$ which we will use in process reconstruction. We can say that this process determines neighbourhood of the pixel x (with irregular shape). The reconstructed value u(x) is the sum of pixels from its neighbourhood multiplied by some weights. The weight values are determined by the process Y, a more specifically by the function f. Appropriate definition of the function f allows as to give weight values (also negative) which depend on direction and distance from reconstructed pixel.

Fig. 1.

Results of the reconstruction using [3] of grayscale Lenna image ($512 \times 512$ pixels) for different values of the parameter c. Standard deviation of the noise is 10. The time of the reconstruction is 8 s (CPU: $2\times 2.5$ GHz).

3 Grayscale Images

In [3] the authors proposed the following method of the reconstruction ofgrayscale images:

$$\begin{aligned} \left\{ \begin{array}{ll} X_t=x+\displaystyle \int _0^t\sigma (s,X_s)\,dW_s+K_t^{\overline{D}},\quad t\in [0,T],\\ Y_t=u_0(X_S)+\displaystyle \int _t^Tc(s)(Y_s-u_0(X_s))ds-\displaystyle \int _t^T Z_s\,dW_s,\quad t\in [0,T], \end{array} \right. \end{aligned}$$

(2)

where $S<T$,

$$\begin{aligned} \sigma (s,X_s)=\left[ \begin{array}{ll} -\left( 1-\frac{c(s)}{c}\right) \frac{(G_{\gamma }*u_0)_{x_2}(X_s)}{|\nabla (G_{\gamma }*u_0)(X_s)|},&{}\frac{c(s)}{c}\frac{(G_{\gamma }*u_0)_{x_1}(X_s)}{|\nabla (G_{\gamma }*u_0)(X_s)|}\\ \\ \left( 1-\frac{c(s)}{c}\right) \frac{(G_{\gamma }*u_0)_{x_1}(X_s)}{|\nabla (G_{\gamma }*u_0)(X_s)|},&{}\frac{c(s)}{c} \frac{(G_{\gamma }*u_0)_{x_2}(X_s)}{|\nabla (G_{\gamma }*u_0)(X_s)|} \end{array} \right] \end{aligned}$$

$$\begin{aligned} c(t)=\left\{ \begin{array}{llll} 0\quad \quad \mathrm{if}&{}t<S&{} \quad \mathrm{or}&{}|\nabla (G_{\gamma }*u_0)(x)|<d,\\ c\quad \quad \mathrm{if}&{}t\ge S&{} \quad \mathrm{and}&{}|\nabla (G_{\gamma }*u_0)(x)|\ge d , \end{array} \right. \end{aligned}$$

$u_{x_i}(y)=\frac{\partial u}{\partial x_i}(y)$ and by $*$ we denote a convolution operation.

The Eq. (2) is a particular case of (1) for given specific functions $\sigma$ and f. In this model we deblur in gradient direction from time T to S and smooth out in perpendicular to gradient direction from S to 0. To avoid false detections due to noise, $u_0$ is convolved with a Gaussian kernel $G_{\gamma }$ (in practice $3\times 3$ Gaussian mask). Parameter T defines the size of the neighbourhood used in the reconstruction procedure. The parameter d determines which pixels will be reconstructed with using smoothing model (only in gradient direction) and which with using enhancing model (in gradient and in perpendicular to gradient direction). The parameter c is responsible for effect of sharpening of edges (see Fig. 1).

Fig. 2.

Example of a trajectory of the process X defined by (2) which starts from the edge of the image.

If reconstructed pixel x belongs to the edge (the condition $|\nabla (G_{\gamma }*u_0)(x)|\ge d$ is true) the process X has values as in Fig. 2 and we will use pixels along edges (from time 0 to S) and pixels in gradient direction (from time S to T). The final value u(x) is the sum of the pixel given by $X_S$ multiplied by positive weight and pixels from time S to T multiplied by negative weights. If the condition $|\nabla (G_{\gamma }*u_0)(x)|\ge d$ is false then we explore only pixels along edges with positive weights and resign from sharpening effect.

4 Vector Valued Images

Now we concentrate on images with values in $\mathbf R^n$. A very common idea to restore vector-valued images is to use scalar diffusion on each channel of a noisy image. But one may quickly notice that this scheme is useless, since each image channel evolves independently with different smoothing geometries. To avoid this blending effect, the regularization process has to be driven in a common and coherent way for all vector image channels. In order to execute that we use Di Zenzo geometry [7, 8]. Let $u:D \rightarrow \mathbf R^n$ be a vector valued image and $x \in D$ be fixed. Consider the function $F_x: V \rightarrow \mathbf {R}$, $F_x(v)=\left| \frac{\partial u}{\partial v}(x)\right| ^2,$ where $V=\{v\in ~\mathbf {R}^2; |v|=~1\}$. We are interested in finding the arguments $\theta _{+}(u,x), \theta _-(u,x)$ and corresponding values $\lambda _+(u,x)=F_x(\theta _+(u,x))$, $\lambda _-(u,x)=F_x(\theta _-(u,x))$ which maximize and minimize the function $F_x$, respectively. Note that $F_x$ can be rewritten as $F_x(v)=F_{x}([v_1,v_2]^T)=v^T\mathbf G(x)v$. In the useful case of colour RGB images $\mathbf G$ is defined by the following [7]

$$\begin{aligned} \mathbf G(x)=\left[ \begin{array}{lr}\displaystyle \sum _{i=1}^3\left( \frac{\partial u_i}{\partial x_1}(x)\right) ^2,&{} \displaystyle \sum _{i=1}^3 \frac{\partial u_i}{\partial x_1}(x)\frac{\partial u_i}{\partial x_2}(x)\\ {} &{}\\ \displaystyle \sum _{i=1}^3\frac{\partial u_i}{\partial x_1}(x)\frac{\partial u_i}{\partial x_2}(x),&{} \displaystyle \sum _{i=1}^3\left( \frac{\partial u_i}{\partial x_2}(x)\right) ^2\end{array}\right] . \end{aligned}$$

(3)

The interesting point about $\mathbf G(x)$ is that its positive eigenvalues $\lambda _{+}(u,x)$,$\lambda _{-}(u,x)$ are the maximum and the minimum of $F_x$ while the orthogonal eigenvectors $\theta _+(u,x)$ and $\theta _-(u,x)$ are the corresponding variation orientations. Three different choices of vector gradient norms N(u, x) have been proposed in the literature: $\sqrt{\lambda _+(u,x)}$, $\sqrt{\lambda _+(u,x) - \lambda _{-}(u,x) }$ and $\sqrt{\lambda (u,x) + \lambda _{-}(u,x) }$. In this paper we have used $N(u,x)=\sqrt{\lambda _+(u,x)}$ as a natural extension of the scalar gradient norm viewed as the value of maximum variations.

Fig. 3.

Results of the reconstruction using Eq. (4) of RGB Lenna image ($512 \times 512$ pixels) for different values of the parameter c. Standard deviation of the noise is 10 (independently added to all coordinates). The time of the reconstruction is 19 s (CPU: $2\times 2.5$ GHz).

Replacing in Eq. (2) $|\nabla (u,x)|$ and $[u_{x_1}(x),u_{x_2}(x)]^T$ by N(u, x) and $\theta _+(u,x), \theta _{-}(u,x)$ respectively, we obtain the following model for vector-valued images:

$$\begin{aligned} \left\{ \begin{array}{ll} X_t&{}=x+\displaystyle \int _0^t\sigma (s,X_s)\,dW_s+K_t^{\overline{D}},\quad t\in [0,T],\\ Y_t&{}=u_0(X_S)+\displaystyle \int _t^Tc(s)(Y_s-u_0(X_s))ds-\displaystyle \int _t^T Z_s\,dW_s,\quad t\in [0,T], \end{array} \right. \end{aligned}$$

(4)

where $S<T$,

$$\begin{aligned} \sigma (s,X_s)=\left[ \begin{array}{ll} \left( 1-\frac{c(s)}{c}\right) \theta _-(G_{\gamma }*u_0,X_s),&\frac{c(s)}{c}\theta _+(G_{\gamma }*u_0,X_s) \end{array} \right] \end{aligned}$$

$$\begin{aligned} c(t)=\left\{ \begin{array}{llll} 0\quad \quad \mathrm{if}&{}t<S&{} \quad \mathrm{or}&{}N(G_{\gamma }*u_0,x)<d,\\ c\quad \quad \mathrm{if}&{}t\ge S&{} \quad \mathrm{and}&{}N(G_{\gamma }*u_0,x)\ge d. \end{array} \right. \end{aligned}$$

In Fig. 3 we can see similar as before results of the reconstruction using (4) for RGB Lenna image and different values of the parameter c. The parameter d depends on the noise of the image, and it can be set as the standard deviation of the noise.

5 Approximation

The following theorem allows us to transition from a continuous model to the discrete model.

Theorem 1

Let $S<T$, $u_0:\overline{D} \rightarrow \mathbf R^n$, $x\in \overline{D}$. Assume that $f(t,y)=c(t)(y-u_0(X_t))$, $c(t)=0$ for $t<S$ and $\xi = u_0(X_S)$, where X is two-dimensional diffusion process with reflection with values in $\overline{D}$ and starting from x. If (Y, Z) is a solution to BSDE

$$\begin{aligned} Y_t=\xi +\int _t^Tf(s,Y_s)ds-\int _t^TZ_s\,dW_s,\,\,\,\,t \in [0,T], \end{aligned}$$

then

$$\begin{aligned} \lim _{m\rightarrow +\infty }Y_0^m= Y_0, \end{aligned}$$

where

$$\begin{aligned} Y_0^m=\sum _{k=j}^{m-1} a_k \mathbf E\left[ u_0(X_{t_k})\right] , \end{aligned}$$

(5)

and j is a index of discretisation, such that

$$\begin{aligned} 0=t_0<t_1<\dots< t_j\le S< t_{j+1}<\dots <t_m=T,\quad t_{i+1}-t_i=\frac{T}{m}, \end{aligned}$$

$$\begin{aligned} \displaystyle a_j= & {} \prod _{r=j}^{m-1}\left( 1+\frac{c(t_r)T}{m}\right) -\frac{c(t_j)T}{m},\end{aligned}$$

(6)

$$\begin{aligned} \displaystyle a_k= & {} -\frac{c(t_k)T}{m}\prod _{r=j}^{k-1}\left( 1+\frac{c(t_r)T}{m}\right) , k=j+1,j+2,...,m-1, \end{aligned}$$

(7)

and by $\mathbf {E}$ we denote the expected value.

The coefficients $a_k$, $k=j,j+1,...,m-1$ define the weights used in the process reconstruction and satisfy the useful condition $\sum _{k=j}^{m-1}a_k=1$. The proof of the above theorem is analogous to the proof of Theorem 5.1 in [3]. Repeating arguments from the work [3] and using the above theorem we obtain the following discrete inverse formula for RGB images.

$$\begin{aligned} u(x)\approx \left\{ \begin{array}{ll} \displaystyle \frac{1}{N_0}\sum _{n_0=1}^{N_0}u_0(X^x_{t_j}(\omega _{n_0})) &{}\mathrm{if}\,N(G_{\gamma }*u_0,x)<d,\\ \frac{1}{N_0}\sum \nolimits _{n_0=1}^{N_0}\left[ a_ju_0\left( X^x_{t_j}(\omega _{n_0})\right) \right. \\ \left. +\frac{1}{N_1} \sum \nolimits _{n_1=1}^{N_1}\sum \nolimits _{k=j+1}^{m-1}a_ku_0\left( X^{X^x_{t_j}(\omega _{n_0})}_{t_k}(\omega _{n_1})\right) \right] &{}\mathrm{if}\,N(G_{\gamma }*u_0,x)\ge d \end{array} \right. \end{aligned}$$

(8)

where $X^a_t(\omega )$ is the value at time t of $\omega$-trajectory of the process X starting from a point a.

6 Experimental Results

Measure of quality for our evaluation experiments regarding the new method and other classic methods: total variation [12] and non local means [6] for colour images are presented in Table 1. The results refer to RGB image Lenna corrupted (channels independently) with the Gaussian noise with standard deviation $\rho$. Noisy images have been reconstructed with vector analysis in RGB space. The maximum values of Peak Signal to Noise Ratio (in short PSNR) is given in the table. The analysis of PSNR measure shows that the new method performs better then PDE approach and is comparable to the method based on non-local similarity of patches.

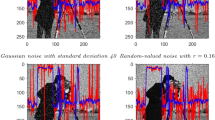
Note that the type of high ISO noise generated by a typical digital camera sensor can be modelled as an additive white Gaussian distribution with standard deviation proportional to the value of the ISO [5]. In Fig. 4 we present the images taken with high ISO value and the result of the reconstruction using the new algorithm, non local means [6] and total variation [12]. Parameters of all methods were set to the default values as recommended by [3, 6, 12]. It should be noted that we have one unknown parameter: standard deviation of the noise. This parameter is determined from the background of the image and set to 5. Looking (carefully) at the images you can observe that the image created by the new method is visually more sharp and therefore all the details are more visible (see Fig. 4).

Table 1. Lenna (PSNR)

Fig. 4.

(a) Input high ISO image (b) Result of reconstruction using total variation [12] (c) Result of reconstruction using non local means [6] (d) Result of reconstruction using the new method

7 Conclusion

In this paper we proposed a new method of colour image denoising. The obtained results demonstrate that proposed approach can be used successfully to reconstruction of high ISO images and can provide a good alternative to other methods.