A Distance Measure Between Fuzzy Variables

Abstract

This paper shows some distance measures based on memberships and centroids for comparing fuzzy variables which are commonly used in fuzzy logic systems and rule-based models. An application example is provided, and some interpretation issues are explained.

Juan Carlos Figueroa-García is Assistant Professor of the Universidad Distrital Francisco José de Caldas, Bogotá - Colombia.

Eduyn López-Santana is Assistant Professor of the Universidad Distrital Francisco José de Caldas, Bogotá - Colombia.

Carlos Franco-Franco is Professor of the Universidad del Rosario, Bogotá - Colombia.

1 Introduction and Motivation

Fuzzy logic systems (FLS) relate multiple inputs composed by multiple fuzzy sets (usually fuzzy numbers) in order to represent a desired output. An FLS is based on human-like information which contains imprecision/uncertainty, and there is no a single way to define the shapes and parameters of every fuzzy set, so there is a need for defining a distance measure between two FLSs to establish how far/close they are.

An FLS is composed by three components: a set of inputs, a rule base, and a desired output. A fuzzy variable is defined by a finite number of fuzzy sets whose shapes and parameters can be defined by different methods such as machine learning, experts opinions, data driven regressions, etc., with different results.

A fuzzy variable is composed by a crisp set of possible values X, a universe of discourse often called $\varOmega$, and a set of primary fuzzy terms (a.k.a linguistic labels/partitions) that should be used when describing specific fuzzy concepts associated to the fuzzy variable. Then, the main problem is how to compare two fuzzy variables whose linguistic labels are associated to Fuzzy Numbers (FN).

This paper focuses on defining some distances to compare fuzzy variables (FV) in order to identify differences using a single measure involving all its individual fuzzy sets (which is useful in decision making, fuzzy logic systems, fuzzy algebras, etc.). An example is provided and its results are discussed. The paper is divided into five sections. Section 1 introduces the problem. In Sect. 2, some basic definitions about FNs are provided; in Sect. 3, some distance measures for FVs are presented. Section 4 presents an application example; and finally in Sect. 5, the concluding remarks of the study are presented.

2 Basics on Fuzzy Sets

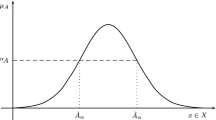
A fuzzy set (FS) is denoted by capital letters e.g. A with a membership function $\mu _A(x)$ defined over $x\in X$. A membership function $\mu _A$ measures affinity of a value $x\in X$ to a linguistic label/partition A (A is then a word/concept such as high, medium, low etc.), so A measures imprecision around X (see Fig. 1).

$$\begin{aligned}\begin{gathered} A: X \rightarrow [0,1], \\ A = \{ (x, \mu _A(x)) \; | \; x \in X \}. \end{gathered}\end{aligned}$$

where x is the primary variable, and $\mu _A(x)$ is the membership function of A.

2.1 Fuzzy Numbers

A fuzzy number (FN) is a fuzzy set whose membership function is normal and convex (a fuzzy subset of $\mathbb {R}$, Zadeh [1]). Thus, $^\alpha \!A$ is a closed interval for all $\alpha \in [0,1]$, and its support supp(A) is defined over $x\in X$, as shown as follows (the set A in Fig. 1 is also a Fuzzy Number (FN)).

Definition 1

(Fuzzy Number). Let $\tilde{A} \in \mathcal {F}(X)$. Then, A is a Fuzzy Number (FN) iff there exists a closed interval $[a,b]\ne 0$ such that

$$\begin{aligned} \mu _{\tilde{A}}(x)=\left\{ \begin{array}{cl} 1 &{} \text { for } x\in [a,b], \\ l(x) &{} \text { for } x\in [-\infty ,a], \\ r(x) &{} \text { for } x\in [b,\infty ] \end{array}\right. \end{aligned}$$

(1)

where $l:(-\infty ,a)\rightarrow [0,1]$ is monotonic non-decreasing, continuous from the right, and $l(x)=\emptyset$ for $x<\omega _1$, and $r:(b,\infty )\rightarrow [0,1]$ is monotonic non-increasing, continuous from the left, and $r(x)=\emptyset$ for $x>\omega _2$.

Fig. 1.

Fuzzy sets A, B, C

Figure 1 shows three FSs associated to three linguistic labels A, B, C whose universe of discourse is the set X. Since S is characterized by different linguistic labels and their associated membership functions, then we can call it fuzzy variable. Note that every fuzzy number is associated to a linguistic label.

A widely used method to represent a fuzzy set A is through $\alpha$-cuts. The $\alpha$-cut of a A, namely $^\alpha \!A$, is defined as:

$$\begin{aligned} ^\alpha \!A=\{x\, | \, \mu _A(x) \geqslant \alpha \}, \end{aligned}$$

(2)

where $^\alpha \!A$ for a fuzzy number is:

$$\begin{aligned} ^\alpha \!A= \Bigl [\inf _{x\in X}\{\mu _A(x)\ge \alpha \}, \sup _{x\in X} \{\mu _A(x)\ge \alpha \}\Bigr ]= \bigl [\check{A}_{\alpha }, \hat{A}_{\alpha }\bigr ]. \end{aligned}$$

(3)

Thus, a fuzzy set A is the union of its $\alpha$-cuts, $\bigcup _{\alpha \in [0,1]}\alpha \cdot \,\!^\alpha \!A,$ where $\cup$ denotes union (Klir and Yuan [2]).

3 Distance-Based Similarity Between Two FVs

An FV is used to represent perceptions of people about a variable X. While some distance measures between two FNs have been proposed by Chaudhuri and RosenFeld [3], Nguyen and Kreinovich [4], Zheng et al. [5], Xuechang [6], and Hung and Yang [7], Figueroa-García et al. [8], and Figueroa-García and Hernández-Pérez [9], there is no a distance measure between two FVs. The problem of comparing fuzzy partitions has been extensively treated by Anderson et al. [10] and Hüllermeier et al. [11] who were focused to clustering problems where the idea is to measure similarity of elements of a cluster regarding different partitions. This way, our approach goes to compare two FVs using distances to establish if they are either equal or not. To do so, we use the classical axiomatic definitions of distance since every $^\alpha \!A$ can be seen as a crisp set over X.

Let $\mathbb {R}$ be the set of real numbers, and $\mathbb {R}_+$ be its non-negative orthant. X is the universal set; $\mathcal {F}_1(X)$ is the class of all FNs of X; $\mathcal {P}(X)$ is the class of all crisp sets of X, then the distance between A and B namely d(A, B) is called to be a metric (or simply distance) if $d(A,B)\in \mathbb {R}_+$ and satisfies the following three axioms:

D1: :

$d(A,B)=d(B,A),$

D2: :

$d(A,A)=0,$

D3: :

$d(A,C)\leqslant d(A,B)+d(B,C),$

 

Now, in the p-dimensional Euclidean space $\mathbb {R}^p$, the family of $L_m$ Minkowski distances is defined as:

$$\begin{aligned} d_m(A,B)=\left\{ \sum _{i=1}^p|x_i-y_i|^m \right\} ^{1/m}, \end{aligned}$$

(4)

where A, B are two points in $\mathbb {R}^p$ with coordinates $x_i$ and $y_i$.

Now, some useful definitions of distances between intervals, FNs, and the centroids of two FNs are presented. In this paper we adopt the following definition of distance among two interval sets:

Definition 2

Let $A\in [\underline{a}, \overline{a}]$ and $B\in [\underline{b}, \overline{b}]$ two interval sets defined over $\mathbb {R}_+$, the $L_1$ distance between A and B is defined as follows:

$$\begin{aligned} d(A,B)= \left| \underline{a}-\underline{b}\right| +\left| \overline{a}-\overline{b}\right| . \end{aligned}$$

(5)

Kosko [12], and Nguyen and Kreinovich [4] defined the index $A\cap B \subseteq A \cup B$ for crisp/interval sets to evaluate whether $A=B$ or not, so $A = B$ if and only if $A \cap B = A \cup B$. Hence, for crisp (or interval) finite sets. Then, we can establish differences between A and B using the following ratio:

$$ R_{A,B}=\dfrac{|A\cap B|}{|A\cup B|}.$$

If $R_{A,B}=1$ then $A=B$, so if $R_{A,B}<1$ then $A\ne B$. As $R_{A,B}\rightarrow 0$ as less elements from $A\cup B$ are into $A\cap B$, this is:

$$A=B \Leftrightarrow \mu _{A}(x)=\mu _{B}(x) $$

Ramík and R̆imánek [13] defined that two fuzzy sets A and B are equal iff $^\alpha \!A=\,\!^\alpha B \,\,\forall \,\,\alpha \in [0,1]$, $^{\alpha }\!A := [\inf \,\!^{\alpha }\!A, \sup \,\!^{\alpha }\!A]$ and $^{\alpha }\!B := [\inf \,\!^{\alpha }\!B, \sup \,\!^{\alpha }\!B]$, this is:

$$A=B \Leftrightarrow \dfrac{|^\alpha \!A\cap \,\!^\alpha \!B|}{|^\alpha \!A\cup \,\!^\alpha \!B|}=1, \,\,\forall \,\, \alpha \in [0,1] ,$$

Now, the distance between two FNs can be defined as follows:

Definition 3

Let $A,B\in \mathcal {F}_1(X)$ be two FNs. The distance (metric) $d_{\alpha }$ between A and B given a set of n $\alpha$-cuts, $\{\alpha _1,\alpha _2,\cdots ,\alpha _n\}$ and $\varLambda =\sum _{i=1}^n\alpha _i$, is:

$$\begin{aligned} d_{\alpha }(A,B)\triangleq \dfrac{1}{\varLambda } \sum _{i=1}^N \alpha _i\left[ \left| \check{A}_{\alpha _i}-\check{B}_{\alpha _i}\right| + \bigl |\hat{A}_{\alpha _i}-\hat{B}_{\alpha _i}\bigr | \right] , \end{aligned}$$

(6)

for continuous $\alpha$ we have that $\varLambda =\int _0^1 \alpha \, d\alpha =1/2$, so $d_\alpha$ is defined as:

$$\begin{aligned} d_{\alpha }(A,B)\triangleq 2 \int _0^1 \alpha \left[ \left| \check{A}_{\alpha }-\check{B}_{\alpha }\right| + \bigl |\hat{A}_{\alpha }-\hat{B}_{\alpha }\bigr | \right] d\alpha . \end{aligned}$$

(7)

The centroid of A, C(A) is a crisp number that measures the central trend of A. Now, two FNs A and B are centroid equal if their centroids are equal, this is $C(A)=C(B)$, so the $L_1$ distance between C(A), C(B) is:

$$\begin{aligned} d_c(C(A),C(B))= |C(A)-C(B)|. \end{aligned}$$

(8)

We recall that ; and $A=B \Rightarrow C(A)= C(B)$. This means that A and B could be different, this is $d_{\alpha }>0$ (see Definition 3) while having equal centroids $C(A)= C(B)$.

3.1 Distances Between FVs

An FLS relates fuzzy variables using different linguistic labels/partitions and a rule base. We address a case where two FVs defined over the same variable X are to be compared; for instance, two FLSs synchronized by machine learning techniques, clustering, genetic optimized methods, etc. To do so, some theoretical definitions about fuzzy variables are provided.

Definition 4

A linguistic variable S is a triplet $(s,X,\varOmega )$ where $s=\{A, B,\cdots , K\}$ is a set of linguistic labels defined over a subset X of a universe of discourse $\varOmega$, this is $X\in \varOmega$. It is said S to be a fuzzy variable if $\{\mu _A, \mu _B, \cdots , \mu _K\}\in \mathcal {F}_1(X)$.

In this paper, we do not make a distinction between a linguistic label A and its associated fuzzy set $\mu _A$. Figure 1 shows a variable S conformed by three labels $s=\{A, B, C\}$ whose fuzzy sets are FNs $\{A, B, C\}\in \mathcal {F}_1(X)$.

Comparability: Comparability between two FVs $S_1, S_2$ is an interesting concept. Two sets A, B are comparable if there is a total order relation between both, but when comparing two FVs we have that they can be composed by different linguistic labels and/or over different $X\in \varOmega$. Now, we focus on comparing two FVs with the same linguistic labels and defined over the same universe $X\in \varOmega$.

Definition 5

Let $S_1, S_2$ be two FVs, then they are pairwise comparable $S_1\bot _p\,S_2$ only if: (i) they are composed by the same partition $s_1=s_2=s=\{A, B, \cdots , K\}$, (ii) its associated fuzzy sets are defined over the same variable $X\in \varOmega$, and iiii) the memberships $\mu _{S_{1,j}}, \mu _{S_{2,j}}$ are totally ordered.

This means that $S_1\bot _p\,S_2$ only if $S_1, S_2$ are equally labeled no matter its membership functions e.g. $s_1=\{A_1, B_1, \cdots , K_1\}, s_2=\{A_2, B_2, \cdots , K_2\}$, they are defined over the same universe $X\in \varOmega$, and there is a total order for every pair of labels $j\in s$, this is $\mu _{S_{1,j}} \leqslant ,\geqslant \mu _{S_{2,j}}\,\forall \, j\in s$.

Conversely, two FVs $S_1, S_2$ are not pairwise comparable $S_1\Vert _p\,S_2$ if they are composed by different linguistic labels/partitions, they are defined over different universes of discourse $X\in \varOmega$, or there exists only a partial order between $S_1, S_2$. If $\mu _{S_{1,j}}, \mu _{S_{2,j}}$ for some $j\in s$ are partially ordered then we propose to compute a distance measure between $S_1, S_2$ to see how different they are.

Now, the distances $d_\alpha , d_c$ are metrics that helps to see how different $S_1\bot _p\,S_2$ or $S_1\Vert _p\,S_2$ are, so the idea is to aggregate all distances between pairs of fuzzy sets using its sum. This way, we propose the following distances between FVs. First, the Minkowski distance between $S_1, S_2$ is as follows:

Proposition 1

Let $S_1, S_2$ be two FVs. The distance $d_{\alpha }$ between $S_1,S_2$ given $\{A_1, A_2, B_1, B_2, \cdots , K_1, K_2\} \in \mathcal {F}_1(X)$, a set of n $\alpha$-cuts $\{\alpha _1,\alpha _2,\cdots ,\alpha _n\}$, and $\varLambda =\sum _{i=1}^n\alpha _i$, is:

$$\begin{aligned} {d_{\alpha }(S_1,S_2)\triangleq \sum _{j\in \{s\}} d_{\alpha }(S_{1,j},S_{2,j})= d_{\alpha }(A_1,A_2)+\cdots +d_{\alpha }(K_1,K_2),} \end{aligned}$$

(9)

where $j\in \{s\}$ is the set of linguistic labels of $S_1$ and $S_2$.

Now, the centroid-based $L_1$ distance between centroids $C(S_1), C(S_2)$ is:

Proposition 2

Let $S_1, S_2$ be $S_1\bot _p\,S_2$. The centroid-based $L_1$ distance d between $S_1, S_2$ given $\{C(A_1), C(A_2), \cdots , C(B_1), C(B_2), \cdots ,C(K_1),$ $C(K_2)\} \in \mathcal {P}(\mathbb {R})$ is:

$$\begin{aligned}&d_c(S_1,S_2)\triangleq \sum _{j\in \{s\}} d_c(C(S_{1,j}),C(S_{2,j}))\nonumber \\&\qquad \quad = |C(A_1)-C(A_2)| + |C(B_1)-C(B_2)| + \cdots + |C(K_1)-C(K_2)|\}, \end{aligned}$$

(10)

where $j\in \{s\}$ is the set of linguistic labels of $S_1$ and $S_2$.

Note that $d_{\alpha }(S_1,S_2)>0$ does not imply $C(S_{1,j})\ne C(S_{2,j})$. It is also clear that if $S_{1,j}=S_{2,j}$ then $C(S_{1,j})=C(S_{2,j})$, and conversely $C(S_{1,j})=C(S_{2,j})$ does not mean that $S_{1,j}=S_{2,j}$, in other words:

Conversely, $d_\alpha =0$ implies $C(S_{1,j})=C(S_{2,j})$. It is possible to have $C(A)=C(B)$ while $d_\alpha \ne 0$ since the axiomatic idea that $\mu _{A_1}\ne \mu _{A_2}$ can lead to equal centroids.

Fig. 2.

Fuzzy variables $S_1, S_2$

4 Application Example

In this example, we compare two FVs $S_1$ and $S_2$ composed by three linguistic labels $s=\{A, B, C\}$ defined over the reals $X\in \mathbb {R}$ where B and C are linear sets $L(\check{x},\bar{x},\hat{x})$, and A is a triangular set $T(\check{x},\bar{x},\hat{x})$ (see Fig. 2 and Table 1). All centroids were computed using the proposal of Figueroa-García [14] (other efficient methods for type reduction were proposed by Melgarejo [15, 16], and Wu and Mendel [17, 18]).

Table 1. Parameters and centroids for $S_1,S_2$

Note that the pairs $A_1, A_2$ and $C_1, C_2$ are totally ordered pairs while the pair $B_1, B_2$ is only partially ordered, this means $S_1\Vert _p S_2$. To establish the difference between $S_1,S_2$ we apply the proposed distances $d_\alpha$ and $d_c$ (see Propositions 1 and 2). We recall that as smaller $d_\alpha$ and d, as closer $S_1$ to $S_2$. The obtained results are shown as follows:

$$\begin{aligned}&d_{\alpha }(B_{1},B_{2})=0.666, \,\, d_{\alpha }(A_{1},A_{2})=1, \,\, d_{\alpha }(C_{1},C_{2})=0.505, d_{\alpha }(S_{1},S_{2})=2.171, \\&d_c(B_{1},B_{2})=1, \,\, d_c(A_{1},A_{2})=0.5, \,\, d_c(C_{1},C_{2})=0.5, d_c(S_{1},S_{2})=2. \end{aligned}$$

4.1 Discussion of the Results

The distance $d_{\alpha }(S_{1},S_{2})=2.171$ shows us that $S_{1}\ne S_{2}$, even when they are graphically similar (see Fig. 2). The only case in which $S_{1}=S_{2}$ is when all fuzzy sets are equal.

Fig. 3.

Ordering of centroids

Regarding $C(S_{i,j})$, we computed $d_c(S_{1},S_{2})=3.035$ which means there are some differences between $S_{1},S_{2}$, so we can conclude that its centroids are different. Figure 3 shows the exact location of $C(S_{1,j}), C(S_{2,j})$ and also shows that even if the shapes of every set seem to be similar, its centroids can be different.

Conversely, two partially ordered sets could have similar centroids, note that $B_2$ seems to be on the left of $B_1$, but clearly $C(B_1)<C(B_1)$. Also note that $S_{1},S_{2}$ are centroid totally-ordered since $C(S_{1,j})\leqslant C(S_{2,j}) \, \forall \, j\in {s}$.

After computing all distances, there is a clear idea about the distance between $S_{1},S_{2}$: they are not similar, and its centroids are different. This leads us to think that if both sets $S_{1},S_{2}$ are used in an FLS or a rule-based model, they should produce different results since they are different. If all distances were close to zero then we can assert that $S_{1},S_{2}$ are similar/equal, so no difference would be detected when using any of them.

5 Concluding Remarks

The proposed distance measures for FVs provide a base for comparing fuzzy logic systems (or rule-based models) which are popular in practice. We also have provided some conditions to establish if two FVs are equal or not by using an $L_1$ Minkowski crisp distance.

We proposed an $L_1$ Minkowski distance to compare the centroids of two FVs as well. This helps to measure differences among its centroids (which are widely used defuzzification measures). Also we point out that our proposal does not need big computational efforts and it can be easily implemented.

The membership functions used in the example are trapezoidal and triangular FNs since they are popular in practice. The obtained results are satisfactory since we identified some differences between $S_1, S_2$, and how distant they are. The same concept was applied to its centroids for which the distance between them was computed.

5.1 Further Topics

The definition of distance measures for Type-2 fuzzy variables is a natural step in the analysis. On the other hand, the application of our proposal to decision making problems, including fuzzy differential equations, fuzzy linear programming, among others, appears as an interesting field to be covered in the future (see Chalco-Cano and Román-Flores [19, 20]), Figueroa-García and Pachon-Neira [21, 22], and Wu and Mendel [23], etc.).