Abstract
SMT solvers have become de rigueur in deductive verification to automatically prove the validity of verification conditions. While these solvers provide an effective support for theories—such as arithmetic—that feature strongly in program verification, they tend to be more limited in dealing with first-order quantification, for which they have to rely on special annotations—known as triggers—to guide the instantiation of quantifiers. Writing effective triggers is necessary to achieve satisfactory performance with SMT solvers, but remains a tricky endeavor—beyond the purview of non-highly trained experts.
In this paper, we experiment with the idea of using first-order provers instead of SMT solvers to prove the validity of verification conditions. First-order provers offer a native support for unrestricted quantification, but have been traditionally limited in theory reasoning. By leveraging some recent extensions to narrow this gap in the Vampire first-order prover, we describe a first-order encoding of verification conditions of programs written in the Boogie intermediate verification language. Experiments with a prototype implementation on a variety of Boogie programs suggest that first-order provers can help achieve more flexible and robust performance in program verification, while avoiding the pitfalls of having to manually guide instantiations by means of triggers.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 The Trouble with Triggers
Deductive verification reduces the problem of assessing the correctness of a program to checking the validity of logic formulas known as verification conditions (VCs). VCs normally include both first-order quantification and theory-specific fragments: quantifiers naturally express specification properties of the program under verification—such as its heap-based memory model, or an inductive definition of “sortedness”; logic theories, on the other hand, are needed to reason efficiently about basic data types—most notably, integers. Having both kinds of logic in the same formulas aggravates the already challenging problem of automated reasoning.
SMT solvers are the tools of choice to check the validity of VCs, and in this role they are part of nearly every verification toolchain. Such solvers expressly target combinations of decidable logic theories (the “T” in SMT is for “theory”) on which they achieve a high degree of automation; in contrast, they tend to struggle with handling the complex usages of quantification that are often necessary for expressing VCs but render logic undecidable. The practical solution that has been adopted in most SMT solvers is to use triggers [7]—heuristics that guide the instantiation of quantifiers. Triggers are specific to the axioms that define the predicates used in a formal specification; as such, they are additional annotations that must be provided for verification. Writing triggers that achieve good, predictable performance remains a highly specialized skill—a bit of a black art that only few researchers are fluent in.Footnote 1
In contrast to SMT solvers, first-order theorem provers support, as the name suggests, first-order quantification natively and without particular restrictions. First-order provers have not been often used in program verification for a number of reasons, including the more spectacular performance improvements of SAT/SMT solvers, and the lack of out-of-the-box support for theory-specific reasoning. More recently, however, these limitations have started to mollify, and the best first-order provers have become flexible tools with some effective support for arithmetic and other commonly used theories. Encouraged by these improvements, in this paper we probe the feasibility of using first-order provers in lieu of SMT solvers to check the validity of VCs for the deductive verification of programs.
To make our contributions applicable to the verification of a variety of programming languages, we target the popular intermediate verification language Boogie—which we outline in the motivating examples of Sect. 2. Boogie is both a language and a tool: Boogie the language combines an expressive typed logic and a simple imperative procedural programming language, and Boogie the tool generates VCs from Boogie programs in a form suitable for SMT solvers; the Boogie language also includes syntax for triggers, which are passed on to the back-end solver to help handle quantifications.
We developed a technique and a tool called blt (Boogie less triggers), which inputs Boogie programs and generates VCs in a subset of the TPTP (Thousands of Problems for Theorem Provers) format [23] that is suitable for first-order provers. In Sect. 3 we describe the salient features of the first-order encoding, and the key challenges we addressed to produce VCs that are tractable. To this extent, we specifically took advantage of some recent features of TPTP supported by the Vampire prover [12, 13] to encode imperative code effectively. Based on experiments involving 126 Boogie programs, in Sect. 4 we demonstrate how blt can achieve better stability and flexibility in a variety of situations that depend on triggers when analyzed using the SMT solver Z3 (Boogie’s default back-end solver).
The main advantage of using a first-order prover is that complex quantifications are handled by the prover without requiring trigger annotations—thus helping increase the degree of automation, and reduce the expertise required to use verification technology proficiently. In Sect. 6 we discuss some outstanding challenges of improving the flexibility of deductive verification that we intend to address to extend the present paper’s work in this direction.
In the paper, “Boogie” refers to the behavior of the Boogie tool with its standard back-end Z3, whereas “blt ” refers to the behavior of the blt tool, which also inputs Boogie programs but feeds VCs to the Vampire first-order prover. To simplify the presentation, we often attribute to Boogie qualities that more properly belong to Boogie used in combination with Z3—namely, the effect of triggers.
Tool availability. The tool blt and the examples used in the paper are available as open source at: https://emptylambda.github.io/BLT/.
2 Motivating Examples
This section discusses examples of programs where the outcome of verification using Boogie (with Z3 as back-end solver) crucially depends on triggers; blt, which generates VCs for the Vampire first-order prover, is not affected by triggers, and thus behaves in a more predictable and robust way on such examples. Section 4 discusses a more extensive experimental evaluation.
Matching triggers. Boogie dispatches VCs to an SMT solver, which may need help to decide how to instantiate universally quantified variables while searching for a proof. A trigger (also called matching pattern) is a directive to the SMT solver on how to instantiate quantifiers to create new terms based on the terms that are already in the proof space. A trigger  , associated with a universally quantified variable x, instructs the SMT solver to instantiate x with the value E whenever the ground term f(E) is in the proof state. Picking suitable triggers is not trivial, as it risks introducing problems in opposite directions: triggers that are too permissive generate otiose terms that may slow down a proof, or even set off an infinite loop of term generation; triggers that are too specific miss terms that are necessary for a proof, and thus ultimately reduce the level of proof automation. To make things even more complicated, SMT solvers introduce their own default triggers when no user-supplied triggers are available, which renders the whole business of understanding and selecting triggers a mighty tricky one.
, associated with a universally quantified variable x, instructs the SMT solver to instantiate x with the value E whenever the ground term f(E) is in the proof state. Picking suitable triggers is not trivial, as it risks introducing problems in opposite directions: triggers that are too permissive generate otiose terms that may slow down a proof, or even set off an infinite loop of term generation; triggers that are too specific miss terms that are necessary for a proof, and thus ultimately reduce the level of proof automation. To make things even more complicated, SMT solvers introduce their own default triggers when no user-supplied triggers are available, which renders the whole business of understanding and selecting triggers a mighty tricky one.
Linked lists. In the example of Fig. 1a, inspired by one of Boogie’s online examplesFootnote 2, next is a map from nodes of type ref to their successors in a chain of linked nodes—a straightforward model of a heap-allocated linked list. Function dist defines that the distance between two nodes from and to is the number of hops following next from one node to the other. Procedure length computes such distance with a simple loop that starts from a given node head and follows next until it reaches a nil node—indicating the end of the list. If the list is acyclic—an assumption we encode with the invariant  (declared as
(declared as  , and thus assumed without checking it)—length satisfies its specification that it returns the value dist(head,nil). Still, without trigger
, and thus assumed without checking it)—length satisfies its specification that it returns the value dist(head,nil). Still, without trigger  , Boogie fails to verify the procedure; precisely, it cannot prove that the loop invariant holds initially—that is, that 0 == dist(head, head)—even if this is a mere application of the base case in dist’s axiomatic definition.
, Boogie fails to verify the procedure; precisely, it cannot prove that the loop invariant holds initially—that is, that 0 == dist(head, head)—even if this is a mere application of the base case in dist’s axiomatic definition.
For a successful correctness proof, Boogie requires either that the axiom defining dist be split into two axioms—one for the base case and one for the inductive case—or that the trigger  be added to dist’s definition. Even this simple example indicates that predicting the behavior of quantifier instantiation, and the need for triggers, imposes an additional burden to users, and renders the verification process less robust. In contrast, blt verifies the very same example without any user-provided suggestions about how to instantiate quantifiers, and without depending on the axioms being in a specific form.
be added to dist’s definition. Even this simple example indicates that predicting the behavior of quantifier instantiation, and the need for triggers, imposes an additional burden to users, and renders the verification process less robust. In contrast, blt verifies the very same example without any user-provided suggestions about how to instantiate quantifiers, and without depending on the axioms being in a specific form.
Hash functions and sortedness. Using quantified formulas with SMT solvers often leads to brittle behavior: changes to a formula that do not affect its semantics may make it significantly less effective in proofs. Take the example of Fig. 1b, where map a models an unbounded integer array whose elements are sorted in strictly increasing order. Function hash has the property that the hash of an integer x is greater than any integer smaller than x. By combining these two properties, it should be possible to verify procedure ah, which inputs a nonnegative integer k and returns the hash of a[k + 1]—which has to be greater than a[k]. Boogie, however, fails verification of ah’s postcondition.
In an attempt to help the SMT solver, we may try to add triggers to the axioms in the example. However, we cannot add triggers to the axiom about hash: in order to be sufficiently discriminating [2, 7], a trigger must mention all quantified variables (x and y in this case), cannot use theory-specific interpreted symbols (such as  ), because matching does not know about function symbols interpreted by some theory, and cannot mention variables by themselves (such as
), because matching does not know about function symbols interpreted by some theory, and cannot mention variables by themselves (such as  ), because a variable by itself would match any ground term. Since y only appears by itself or in arithmetic predicates, no valid user-provided trigger involving y can be written. What about adding triggers to the axiom that declares a sorted? Here the only sensible trigger is a[i], which however results in a matching loop: an infinite chain of instantiations that quickly saturate the proof space.
), because a variable by itself would match any ground term. Since y only appears by itself or in arithmetic predicates, no valid user-provided trigger involving y can be written. What about adding triggers to the axiom that declares a sorted? Here the only sensible trigger is a[i], which however results in a matching loop: an infinite chain of instantiations that quickly saturate the proof space.
As observed elsewhere [17, 18] and part of the folklore, an equivalent definition of sortedness that works much better with SMT solvers uses two quantified variables:

Boogie can verify ah if we use the definition of sortedness in (1) instead of the one in Fig. 1b. Somewhat surprisingly, Boogie can also verify ah if we use the same definition as in Fig. 1b but we add it as a precondition to ah rather than as an axiom. In contrast, blt easily verifies any of these semantically equivalent variants: while first-order theorem provers are not immune from generating infinite fruitless instantiations, their behavior does not incur the brittleness that derives from depending on suitable triggers—that are neither too permissive nor too constraining.
3 Encoding Boogie in TPTP
In order to use first-order provers to verify Boogie programs, we define a semantic-preserving translation \(\mathcal {T}\) of the Boogie language into TPTP—the standard input format of first-order theorem provers.
As a result of continuous evolution, TPTP has become a sizable language that aggregates several different logic fragments, going well beyond classic first-order predicate calculus. We loosely use the name TPTP to refer to the specific subset targeted by our translation, which mainly consists of a monomorphic many-sorted first-order logic, augmented with the so-called FOOL fragment: a first-class Boolean sort and polymorphic arrays. Our translation is informed by the recent support for FOOL [13] added to the Vampire automated theorem prover, so that we can use it in our experiments as an effective back-end to verify Boogie programs.
Boogie combines a typed logic and a simple imperative programming language; Sect. 3.1 discusses the translation of the former, and Sect. 3.2 the translation of the latter. We outline the essential features of Boogie and TPTP as we describe the translation \(\mathcal {T}\).
3.1 Declarative Constructs
Types. Boogie’s primitive types include  (mathematical integers) and
(mathematical integers) and  (Booleans), which naturally translate to TPTP’s integer type
(Booleans), which naturally translate to TPTP’s integer type  and Boolean type
and Boolean type  . Vampire reasons about terms of type
. Vampire reasons about terms of type  using an incomplete first-order axiomatization of Presburger arithmetic, sufficient to handle common usages in program analysis.
using an incomplete first-order axiomatization of Presburger arithmetic, sufficient to handle common usages in program analysis.
A Boogie user-defined type declaration  introduces an uninterpreted type t, expressed in TPTP by a type entity t of type
introduces an uninterpreted type t, expressed in TPTP by a type entity t of type  , which represents the type of all primitive uninterpreted types.
, which represents the type of all primitive uninterpreted types.
A Boogie map type  corresponds to a mapping
corresponds to a mapping  , which translates to a curried array type
, which translates to a curried array type  in TPTP:
in TPTP:

We currently do not support other Boogie types—notably, reals, bitvectors, and polymorphic types and type constructors.
Declarations. TPTP declarations are expressions of the form \(\ell (I, K, D)\), where \(\ell \) denotes a specific subset of TPTP, I is an identifier of the declaration, K is the kind of declaration ( ,
,  , or
, or  ), and D is the actual declaration. Here we simply write
), and D is the actual declaration. Here we simply write  for \(\ell \) and omit the identifier I—which is not used anyway. Then, a constant declaration
for \(\ell \) and omit the identifier I—which is not used anyway. Then, a constant declaration  in Boogie translates to the TPTP declaration
in Boogie translates to the TPTP declaration  . An axiom
. An axiom  in Boogie translates to a TPTP axiom
in Boogie translates to a TPTP axiom  . Section 3.2 describes other kinds of declarations, used to translate imperative constructs.
. Section 3.2 describes other kinds of declarations, used to translate imperative constructs.
Functions. Mathematical functions are part of both Boogie and TPTP; thus the translation is straightforward: function declarations translate to function declarations

and function definitions are axiomatized.
Expressions. Boolean connectives translate one-to-one from Boogie to TPTP. The integer operators \(+\) and − translate to built-in binary functions  and
and  ; similarly, integer comparison uses built-in functions such as
; similarly, integer comparison uses built-in functions such as  and
and  , with obvious meaning. The equality and non-equality symbols have the same meaning in Boogie and in TPTP: x = y iff x and y have the same type and the same value.
, with obvious meaning. The equality and non-equality symbols have the same meaning in Boogie and in TPTP: x = y iff x and y have the same type and the same value.
Boogie map expressions translate to nested applications of TPTP’s  and
and  , which behave according to the axiomatization of FOOL [13]:
, which behave according to the axiomatization of FOOL [13]:

where m is an entity of type  .
.
Quantifiers. Quantified logic variables must have identifiers starting with an uppercase letter in TPTP, and thus \(\mathcal {T}\) may rename logic variables. As we repeatedly mentioned, triggers (associated with quantifiers) have no use in TPTP and thus the translation drops them.
3.2 Imperative Constructs
Variables. Program variables encode state, which is modified by computations. In the logic representation, a Boogie program variable  translates to the TPTP declaration
translates to the TPTP declaration  , which corresponds to a free logic variable of given type. Indeed, constants and program variables have the same TPTP representation, with VCs encoding the effects of computations in a purely declarative way.
, which corresponds to a free logic variable of given type. Indeed, constants and program variables have the same TPTP representation, with VCs encoding the effects of computations in a purely declarative way.
Procedures. Boogie’s imperative constructs define procedures, each consisting of a signature, a specification, and an implementation, as shown in Fig. 2a. Each procedure determines a set of VCs that encode the correctness of the procedures’s implementation against its specification.
Figure 2b shows the TPTP translation  of p, which consists of three parts:
of p, which consists of three parts:
-
1.
The input/output arguments of p, which are encoded as if they were global program variables; since each procedure is translated independent of the others, there is no risk of interference.
-
2.
The precondition of p (
 ), which is encoded as an axiom.
), which is encoded as an axiom. -
3.
The actual VCs of p, which are encoded as a TPTP conjecture expressing that the implementation B determines a sequence of states that end in a state satisfying p’s postcondition (
 ). In the rest of this section, we define the predicate transformer
). In the rest of this section, we define the predicate transformer  , which behaves like a weakest precondition calculation [11] of predicate Q through Boogie statement S.
, which behaves like a weakest precondition calculation [11] of predicate Q through Boogie statement S.
If a theorem prover can prove the conjecture from the given axioms, the implementation of p is (partially) correct against its specification.Footnote 3 Figure 3b shows the complete translation of the example in Fig. 1b, including functions, axioms, arrays, and assignments.
Sequential composition. The encoding of statements is naturally compositional:

Assignments. The encoding of assignments uses the let-in construct:

which roughly corresponds to introducing a fresh variable v’, defining its value according to  , and replacing every free occurrence of
, and replacing every free occurrence of  in Q by v’.
in Q by v’.
The encoding of nondeterministic assignments (“havoc”) uses the derived scheme  , where v’ is a locally fresh variable—introduced by the translation—of the same type as v without other constraints on its value.
, where v’ is a locally fresh variable—introduced by the translation—of the same type as v without other constraints on its value.
Passive statements. The encoding of assertions and assumptions follows the standard weakest precondition rules:

Procedure calls. A call  to procedure p in Fig. 2a desugars the call using standard modular verification semantics, where the callee’s effects within the caller are limited to what the callee’s specification declares:
to procedure p in Fig. 2a desugars the call using standard modular verification semantics, where the callee’s effects within the caller are limited to what the callee’s specification declares:

Loops. Encoding a loop  involves three logically conjoined conditions:
involves three logically conjoined conditions:
-
1.
Initiation checks that the invariant holds upon entering the loop:
 .
. -
2.
Consecution checks that the invariant is maintained by the loop:
 where
where  are the targets of the loop body—variables that may be modified by L; these are just the variables that appear as targets of assignments, as arguments of
are the targets of the loop body—variables that may be modified by L; these are just the variables that appear as targets of assignments, as arguments of  statements, or in the
statements, or in the  clauses of procedures called in L.
clauses of procedures called in L. -
3.
Closing checks that the invariant establishes Q (the loop’s postcondition):
 .
.
The tool blt generates a TPTP conjecture for each of these conditions, which are proved independently; thus, in case of failed verification, we know which VC failed verification. Figure 3a shows the VC corresponding to closing of procedure length’s loop from Fig. 1a.
Abrupt termination. Statements such as  and
and  make imperative code less structured, and complicate the encoding of VCs. We currently do not support
make imperative code less structured, and complicate the encoding of VCs. We currently do not support  and
and  , whereas we handle
, whereas we handle  statements: for every simple path \(\pi \) on the control-flow graph of the procedure p being translated that goes from p’s entry to a
statements: for every simple path \(\pi \) on the control-flow graph of the procedure p being translated that goes from p’s entry to a  statement, we generate the additional VC
statement, we generate the additional VC  —where E is p’s postcondition and \(\widetilde{\pi }\) is the sequence of statements on \(\pi \), suitably modified to account for conditional branches and loops. For brevity we omit the uninteresting details.
—where E is p’s postcondition and \(\widetilde{\pi }\) is the sequence of statements on \(\pi \), suitably modified to account for conditional branches and loops. For brevity we omit the uninteresting details.
Excerpts of blt ’s TPTP encoding of the examples in Fig. 1.
Conditionals. TPTP includes the conditional expression  —which evaluates to then if b evaluates to true, and to else otherwise. Using
—which evaluates to then if b evaluates to true, and to else otherwise. Using  and first-order Booleans, we could encode the VC for a Boogie conditional statement as:
and first-order Booleans, we could encode the VC for a Boogie conditional statement as:

As noted elsewhere [16], (3) tends to be inefficient because it duplicates formula Q, so that the generated VC is worst-case exponential in the size of the input program.
Instead of following [9, 16]’s approach, based on passivization, we leverage another feature of FOOL, namely tuples, to build a VC whose size does not blow up. A code block is purely active if every statement it contains is an assignment or a conditional whose branches are purely active. Given a purely active code block B,  denotes the variables assigned to anywhere in B. Given a purely active conditional statement, we encode it using TPTP tuples and conditional expressions as:
denotes the variables assigned to anywhere in B. Given a purely active conditional statement, we encode it using TPTP tuples and conditional expressions as:

Operator \(\oplus \) denotes a kind of tuple concatenation where variables that appear in both tuples only appear once in the concatenation; for example  . In the right-hand side of (4), \( \tau \) applies to the assignments in the then and else branches of the conditional and, recursively, to nested conditionals. Expressions of the form
. In the right-hand side of (4), \( \tau \) applies to the assignments in the then and else branches of the conditional and, recursively, to nested conditionals. Expressions of the form  indicate the formal application of the predicate transformer \( \tau \) on a tuple of variables instead of a proper predicate;Footnote 4 the semantics of let-in with tuples is such that every variable that is not explicitly assigned a value in the let part stays the same:
indicate the formal application of the predicate transformer \( \tau \) on a tuple of variables instead of a proper predicate;Footnote 4 the semantics of let-in with tuples is such that every variable that is not explicitly assigned a value in the let part stays the same:  is equivalent to
is equivalent to  .
.
Finally, let us outline how to transform any conditional into purely active code. Since structured imperative Boogie code can be desugared into assignments (including the nondeterministic assignment  ), passive statements, and conditionals, we only need to explain how to handle passive statements. The idea is to introduce a fresh Boolean variable \(\alpha \) for every passive statement
), passive statements, and conditionals, we only need to explain how to handle passive statements. The idea is to introduce a fresh Boolean variable \(\alpha \) for every passive statement  : set \(\alpha \) to
: set \(\alpha \) to  before the conditional; replace
before the conditional; replace  by
by  ; and add
; and add  after the conditional. Since \(\alpha \) is fresh, it can be tested after the conditional in any order; since it is initialized to
after the conditional. Since \(\alpha \) is fresh, it can be tested after the conditional in any order; since it is initialized to  it does not interfere with the other branch (where the assumption or assertion does not appear). The same approach works for
it does not interfere with the other branch (where the assumption or assertion does not appear). The same approach works for  passive statements. Overall, this encoding generates VCs of size linear in the size of the input program.
passive statements. Overall, this encoding generates VCs of size linear in the size of the input program.
4 Implementation and Experiments
Implementation. We implemented the translation described in Sect. 3 as a command-line tool blt. blt is written in Haskell and reuses parts of Boogaloo’s front-end [21] to parse and typecheck Boogie code. The translation is implemented as the composition of a collection of functions, each taking care of the encoding of one Boogie language features; this facilitates extensions and modifications in response to language and translation changes.
blt inputs a Boogie file, generates its VCs in TPTP, feeds them to Vampire, and reports back the overall outcome. An option is available to choose between the tuple-based (4) and the duplication-based (3) encoding of conditionals; some experiments, which we describe later, compared the performance of these two encodings.
4.1 Experimental Subjects
The experiments target Boogie programs in groups demonstrating different traits of the TPTP encoding of VCs and of blt:
-
Group E consists of examples selected to demonstrate the impact of using triggers, and thus blt ’s capability of handling quantifiers without triggers.
-
Group A is a selection of algorithmic problems (such as searching and sorting), which demonstrates to what extent blt measures up to Boogie on problems in the latter’s natural domain.
-
Group T is a selection of programs from Boogie’s test suite,Footnote 5 which demonstrate blt ’s applicability to a variety of features of the Boogie language.
-
Group S consists of few Boogie programs with a fixed structure and increasingly larger size, used to assess blt ’s scalability and the efficiency of its generated VCs.
We wrote the programs in group E based on examples in the Boogie tutorial and in papers discussing trigger design [2, 17, 18, 22]. We took the programs in group A from our previous work [10], with small changes to fit blt ’s currently supported Boogie features. We retained in group T all test programs that only use language features currently fully supported by blt, and do not target options or features of the Boogie tool—such as assertion inference or special type encoding—other than vanilla deductive modular verification. We constructed the programs in group S by repeating conditional assignments according to different, repetitive patterns (for example as a sequence of conditional increments to the same variable); the resulting programs allow us to empirically evaluate the size of the VCs generated by blt, and to what extent Vampire can handle them efficiently. Table 1 shows some statistics about the size of the programs in each group, as well as that of the VCs generated by Boogie in SMT-LIBFootnote 6 and by blt in TPTP. blt ’s repository (https://emptylambda.github.io/BLT/) includes all Boogie programs used in the experiments.
4.2 Experimental Setup
All the experiments ran on a Ubuntu 14.04 LTS GNU/Linux box with Intel 8-core i7-4790 CPU at 3.6 GHz and 16 GB of RAM, with the following tools: Boogie 2.3.0.61016, Z3 4.3.2, and Vampire 4.0.
Each experiment targets one Boogie program and runs four verification attempts: (i) Boogie runs on b (\(\checkmark _t\)); (ii) Boogie runs on b with all prover annotations (in particular, triggers) removed (\(\checkmark _0\)); (iii) blt runsFootnote 7 on b, encoding conditionals using tuples (\(\checkmark \)); (iv) blt runs on b, encoding conditionals using duplication (\(\checkmark _d\)). We always used Boogie with the /noinfer option, which disables inference of loop invariants; since blt does not have any inference capabilities, this ensures that we are only comparing their performance of VC generation and checking. We used different timeouts per verification condition in each group—E: 30 s; A: 180 s; T: 30 s; S: 300 s—while capping the memory to the available free RAM; blt may use up to 30 s to generate VCs in each problem, although this time is measurable only in group S’s scalability experiments.
Except to specify timeouts and the input format, we always ran Vampire with default options; in particular, we did not experiment with its numerous proof search strategies: while users familiar with Vampire’s internals may be able to tweak them to get better performance in some examples, we want to focus on assessing the predictability of behavior when we use the first-order prover as a black box—in contrast to through lower-level annotations and directives.
4.3 Experimental Results
Table 2 shows the number of successful verification attempts in each case, as well as statistics on the wall-clock running time. The most direct comparison is between \(\checkmark _0\) and \(\checkmark \), which shows how blt compares to Boogie without the help of triggers.
The experiments in group E highlight five cases where Boogie’s effectiveness crucially depends on triggers; thus, blt outperforms Boogie since it can prove all 19 VCs independent of triggers or other quirks of the encoding. The experiments in group A indicate that there remains a considerable effectiveness gap between Boogie and blt when it comes to algorithmic reasoning, which is mainly due to first-order provers’ still limited capabilities of reasoning about arithmetic and other theories that feature strongly in program correctness; the gap of performance (that is, running time) is instead mainly due to the fact that Vampire continues a proof attempt until reaching the given timeout, whereas Z3 normally terminates quickly. The experiments in group T indicate that blt provides a reasonably good coverage of the Boogie language, but is sometimes imperfect in reasoning about some features. Note that several of the programs in T are supposed to fail verification, and we observed that blt ’s behavior is consistent on these—that is, it does not produce spurious proofs.Footnote 8
Scalability. Let us look more closely into the experiments in group S, which assess the scalability of blt, and compare its two encodings—tuple-based (4) and duplication-based (3)—of conditionals. Boogie scales effortlessly on these examples, so we focus on blt ’s performance.
First, note that the two encodings yield similar performance in the program groups other than S, which do not include long sequences of conditional statements. More precisely, group S includes four families of programs; programs in each family have identical structure and different size, determined by a size parameter that grows linearly. Family \(S_v\) performs simple assignments on a growing number of variables; family \(S_a\) performs a growing number of assignments on a fixed number of variables; families \(S_i\) and \(S_n\) perform conditional assignments following different patterns—sequential and nested conditionals.
blt scales as well as Boogie when we increase the number of variables or assignments (\(S_v\) and \(S_a\)): the verification time with both tools is essentially insensitive to input size and under one second per input program. In contrast, blt ’s performance degrades significantly when we increase the number of conditionals, so that group S’s numbers in Table 2 are dominated by the experiments in \(S_i\) and \(S_n\). Figure 4 illustrates the different behavior of the two encodings in \(S_i\) (the results in \(S_n\) are qualitatively similar). As expected (Fig. 4, left), the tuple-based encoding scales with the input program size, whereas the duplication-based encoding blows up exponentially—and in fact the largest example in this group can only be generated with the tuple-based encoding within 30 s. The verification time (Fig. 4, right) shows a somewhat more unexpected picture: Vampire can digest very large input files, and is generally faster on the wasteful duplication-based encoding; in contrast, reasoning about tuples requires much memory and is quite slow in these conditions. Extrapolating the trends in Fig. 4, it seems that the verification time of tuple-based VCs may eventually reach a plateau—even though is currently too large in absolute value to be practical.
We plan to experiment with different encodings of conditional statements to investigate ways of assuaging the current scalability limitations of blt. It is however encouraging that blt ’s performance on the smaller, yet more logically complex, examples in the other groups is often satisfactory.
5 Related Work
Triggers were first proposed by Greg Nelson in his influential PhD work [20]. Simplify [7] was the first SMT solver implementing those ideas; today, most widely used SMT solvers—including Z3 [6] and CVC4 [3]—support trigger annotations and include trigger-selection heuristics for when the input does not include such annotations.
As we repeatedly argued in this paper, triggers are indispensable as they increase the flexibility of SMT solvers—especially for program proving—but also introduce an additional annotation burden, and reduce the predictability and stability of provers. A key challenge in developing program provers based on SMT solvers is designing suitable triggers, but few publications deal explicitly with the problem of trigger selection—which thus remains a skill prohibitively difficult to master. Among these works, Spec# generates special triggers to support list comprehensions in specifications [17]; the Dafny verifier includes flexible strategies to generate triggers that avoid matching loops while also supporting calculations of ground facts from recursive definitions [2]; recently, Dafny has been extended with a mechanism that helps users design triggers in their verified programs [18]. The behavior of triggers has also been analyzed in the context of the VCC [5] and Why3 [8] verifiers.
First-order theorem provers approach the problem of checking validity using techniques, such as saturation, quite different from those of SMT solvers. As a result, they fully support complex usage of quantifiers, but they tend to struggle dealing with theories that are not practical to axiomatize—which has restricted their usage for program verification, where theory reasoning is indispensable for dealing with basic types. The results of the present paper rely on recent developments of the Vampire theorem prover [15], which have significantly extended the support for theory reasoning with a first-class Boolean sort and polymorphic arrays [13].
Others have used the Boogie language as input to tools other than the Boogie verifier, to extend the capabilities of verifiers using Boogie as intermediate representation. HOL-Boogie [4] uses a higher-order interactive prover to discharge Boogie’s verification conditions; Boogaloo [21] and Symbooglix [19] support the symbolic execution of Boogie programs; Boogie2Why [1] translates Boogie into Why3, to take advantage of the latter’s multi-prover support.
6 Discussion and Future Work
The experimental results detailed in Sect. 4 show the feasibility of using a first-order prover for program verification. The gap between blt and Boogie is still conspicuous—both in applicability and in performance—but we must also bear in mind that most programs used in the experimental evaluation have been written expressly to demonstrate Boogie’s capabilities, and thus it is unsurprising that Boogie works best on them. In Sect. 2, however, we have highlighted situations where Boogie’s behavior becomes brittle and dependent on low-level annotations such as triggers; it is in these cases that a different approach, such as the one pursued by blt, can have an edge—if not yet in overall performance at least in predictability and usability at a higher level.
blt remains quite limited in scalability and theory reasoning compared to approaches using SMT solvers. Progress in both areas depends on improvements to the Boogie-to-TPTP encoding, as well as to the back-end prover Vampire. Only recently has Vampire been extended with support [13, 14] for some of the TPTP features that the encoding described in Sect. 3 depends on; hence, blt will immediately benefit from improvements in this area—in particular in the memory-efficiency of rules for tuple reasoning. As future work, we plan to fine-tune the TPTP encoding for performance; the experiments of Sect. 4 suggest focusing on finding a scalable encoding of conditionals. There is also room for improving the encoding based on static analysis of the source Boogie code—a technique that is used in different modules of the Boogie tool but not in any way by the current blt prototype. Finally, we will extend the TPTP encoding to cover the features of the Boogie language currently unsupported—most notably, type polymorphism and gotos.
This paper’s research fits into a broader effort of integrating different verification techniques and tools to complement each other’s shortcoming. Our results suggest that it is feasible to rely on first-order provers to discharge verification conditions in cases where the more commonly used SMT solvers are limited by incompleteness and exhibit brittle behavior, so as to make verification ultimately more flexible and with a higher degree of automation.
Notes
- 1.
Section 5 outlines the relatively few works that deal with trigger selection explicitly.
- 2.
- 3.
The typechecker establishes the correctness of a procedure’s
 clause, so that the prover can just rely on it. This is possible because Boogie’s variables cannot be aliased.
clause, so that the prover can just rely on it. This is possible because Boogie’s variables cannot be aliased. - 4.
Since \(\tau \) is applied recursively as usual, consecutive assignments to the same variable translate to nested let-ins (see sequential composition and assignments rules).
- 5.
- 6.
The size of the SMT-LIB encoding gives an idea of the size of the generated VCs, but in the experiments we used Boogie in its default mode where it feeds VCs directly through Z3’s API.
- 7.
Remember that blt always ignores triggers and other prover annotations in the Boogie input.
- 8.
While the total number of VCs verified by Boogie in group T (137) is the same with (\(\checkmark _t\)) and without (\(\checkmark _0\)) prover-specific annotations, the two sets are different: 13 VCs verify without annotations but do not verify with annotations because they correspond to tests that should fail with the annotations; another 13 VCs verify with annotations but not without them.
References
Ameri, M., Furia, C.A.: Why just Boogie? Translating between intermediate verification. In: Ábrahám, E., Huisman, M. (eds.) IFM 2016. LNCS, vol. 9681, pp. 79–95. Springer, Cham (2016). doi:10.1007/978-3-319-33693-0_6
Amin, N., Leino, K.R.M., Rompf, T.: Computing with an SMT solver. In: Seidl, M., Tillmann, N. (eds.) TAP 2014. LNCS, vol. 8570, pp. 20–35. Springer, Cham (2014). doi:10.1007/978-3-319-09099-3_2
Barrett, C., Conway, C.L., Deters, M., Hadarean, L., Jovanović, D., King, T., Reynolds, A., Tinelli, C.: CVC4. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 171–177. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22110-1_14
Böhme, S., Leino, K.R.M., Wolff, B.: HOL-Boogie — an interactive prover for the boogie program-verifier. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) TPHOLs 2008. LNCS, vol. 5170, pp. 150–166. Springer, Heidelberg (2008). doi:10.1007/978-3-540-71067-7_15
Böhme, S., Moskal, M.: Heaps and data structures: a challenge for automated provers. In: Bjørner, N., Sofronie-Stokkermans, V. (eds.) CADE 2011. LNCS (LNAI), vol. 6803, pp. 177–191. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22438-6_15
Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78800-3_24
Detlefs, D., Nelson, G., Saxe, J.B.: Simplify: a theorem prover for program checking. J. ACM 52, 365–473 (2005)
Dross, C., Conchon, S., Kanig, J., Paskevich, A.: Reasoning with triggers. In: SMT. EPiC Series, pp. 22–31. EasyChair (2012)
Flanagan, C., Saxe, J.B.: Avoiding exponential explosion: generating compact verification conditions. In: POPL, pp. 193–205. ACM (2001)
Furia, C.A., Meyer, B., Velder, S.: Loop invariants: analysis, classification, and examples. ACM Comp. Sur. 46(3) (2014)
Gries, D.: The Science of Programming. Springer, New York (1981)
Kaliszyk, C., Sutcliffe, G., Rabe, F.: TH1: the TPTP typed higher-order form with rank-1 polymorphism. In: PAAR at IJCAR. CEUR Workshop Proceedings, vol. 1635, pp. 41–55. CEUR-WS.org (2016)
Kotelnikov, E., Kovács, L., Reger, G., Voronkov, A.: The Vampire and the FOOL. In: SIGPLAN CPP, pp. 37–48. ACM (2016)
Kotelnikov, E., Kovács, L., Suda, M., Voronkov, A.: A clausal normal form translation for FOOL. In: GCAI. EPiC, vol. 41, pp. 53–71. EasyChair (2016)
Kovács, L., Voronkov, A.: First-order theorem proving and Vampire. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 1–35. Springer, Heidelberg (2013). doi:10.1007/978-3-642-39799-8_1
Leino, K.R.M.: Efficient weakest preconditions. Inf. Process. Lett. 93(6), 281–288 (2005)
Leino, K.R.M., Monahan, R.: Reasoning about comprehensions with first-order SMT solvers. In: SAC, pp. 615–622. ACM (2009)
Leino, K.R.M., Pit-Claudel, C.: Trigger selection strategies to stabilize program verifiers. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9779, pp. 361–381. Springer, Cham (2016). doi:10.1007/978-3-319-41528-4_20
Liew, D., Cadar, C., Donaldson, A.F.: Symbooglix: a symbolic execution engine for Boogie programs. In: ICST, pp. 45–56. IEEE Computer Society (2016)
Nelson, C.G.: Techniques for program verification. Ph.D. thesis, Xerox PARC (1981). CSL-81-10
Polikarpova, N., Furia, C.A., West, S.: To run what no one has run before: executing an intermediate verification language. In: Legay, A., Bensalem, S. (eds.) RV 2013. LNCS, vol. 8174, pp. 251–268. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40787-1_15
Rümmer, P.: E-matching with free variables. In: Bjørner, N., Voronkov, A. (eds.) LPAR 2012. LNCS, vol. 7180, pp. 359–374. Springer, Heidelberg (2012). doi:10.1007/978-3-642-28717-6_28
Sutcliffe, G.: The TPTP problem library and associated infrastructure. J. Autom. Reason. 43(4), 337–362 (2009)
Acknowledgments
We thank Evgenii Kotelnikov for helping us understand the latest features of Vampire’s support for FOOL.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Chen, Y., Furia, C.A. (2017). Triggerless Happy. In: Polikarpova, N., Schneider, S. (eds) Integrated Formal Methods. IFM 2017. Lecture Notes in Computer Science(), vol 10510. Springer, Cham. https://doi.org/10.1007/978-3-319-66845-1_19
Download citation
DOI: https://doi.org/10.1007/978-3-319-66845-1_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-66844-4
Online ISBN: 978-3-319-66845-1
eBook Packages: Computer ScienceComputer Science (R0)


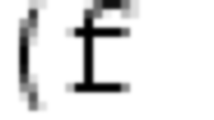



 in the axiomatic definition of function
in the axiomatic definition of function  ), which is encoded as an axiom.
), which is encoded as an axiom. ). In the rest of this section, we define the predicate transformer
). In the rest of this section, we define the predicate transformer  , which behaves like a weakest precondition calculation [
, which behaves like a weakest precondition calculation [
 .
. where
where  are the targets of the loop body—variables that may be modified by
are the targets of the loop body—variables that may be modified by  statements, or in the
statements, or in the  clauses of procedures called in
clauses of procedures called in  .
.

 encoding (
encoding ( encoding (
encoding ( clause, so that the prover can just rely on it. This is possible because Boogie’s variables cannot be aliased.
clause, so that the prover can just rely on it. This is possible because Boogie’s variables cannot be aliased.