Introduction to Competitive Graph Coloring

Abstract

We consider a collection of coloring games played on finite graphs. These games all involve two players, Alice and Bob, alternating coloring the vertices (or edges or both) from a finite set of colors. At each step, the players must use legal colors, where the definition of legal depends on which variation of the game is being considered. The first player, Alice, wants to ensure that all relevant elements (vertices and/or edges) are colored. The second player, Bob, wants to force a situation in which there is an uncolored element that cannot be legally colored. For each version of the game the parameter of interest finds the least number of colors that must be available so that Alice has a winning strategy for the game. We examine this game for a number of classes of graphs, including trees, forests, outerplanar graphs, and planar graphs. We also note a number of unexpected interesting properties these parameters have and highlight how rich these games can be to explore for undergraduate researchers and their mentors.

FormalPara Suggested Prerequisites.

Ideally a first course in Graph Theory or Discrete Mathematics. However, mathematical maturity and experience writing proofs will suffice.

1 Introduction

The map-coloring game was first presented in Martin Gardner’s “Mathematical Games” column in Scientific American in 1981 [24]. Invented by Steven J. Brams, the game involves two players, Alice and Bob, alternating coloring the countries on a map such that two countries that share a nontrivial border must receive different colors. The first player, Alice, wants to ensure that the map eventually gets colored with the finite set of colors with which the players begin. The second player, Bob, however, wants to ensure that there comes a time in the game when there is an uncolored country for which none of the existing colors can be used. The interesting question is then, for a given map what is the least number of colors necessary such that Alice has a winning strategy? Unfortunately, this game did not receive any attention from the graph theory community at the time. Ten years later, Bodlaender reintroduced the r-coloring game [4] within the broader context of graphs. In the original formulation of the game on graphs, we begin with a finite graph, G, and a set X of r colors. Two players, Alice and Bob, alternate coloring the uncolored vertices of G using colors from X. At each step of the game, the players must choose to color an uncolored vertex with a legal color. Alice goes first. In the basic formation of the game, a color α ∈ X is legal for an uncolored vertex u if u has no neighbors already colored α. Alice wins the game if all vertices of the graph are colored; otherwise, Bob wins. Although both players must use a legal color, Alice is trying to ensure that at every stage of the game all vertices have a legal color available, while Bob would like to force a situation in which an uncolored vertex exists for which there is no legal color.

For example, suppose Alice and Bob are playing the game on the graph G in Figure 1 with two colors which we will call α and β. If u is colored α, then only β is legal for v. However, if u is colored α and w is colored β, then v will have no legal color.

Fig. 1

Alice and Bob playing with two colors on G.

Notice, on this small example, we can see that if Alice first colors v, with α, then β is always legal for u and w. Thus Alice wins on G. However, if Alice first colors u with α, then Bob can color w with β, leaving v with no legal color. Hence Bob wins.

The least r such that Alice has a winning strategy for this game on G is called the game chromatic number of G, denoted χ _g(G). The game chromatic number was first introduced by Bodlaender in [4]. It has since been studied extensively, including in [11, 23, 27].

In our example, it should be clear that Bob will win the 1-coloring game on G. We have demonstrated a strategy for Alice to win the 2-coloring game on G. Thus, χ _g(G) = 2.

1.1 Trees and Forests

We begin by looking at the game chromatic number for trees and forests and comparing it to the usual chromatic number of a graph, denoted χ(G).

Consider the rooted tree T in Figure 2. The chromatic number of T, χ(T), is 2 since we can alternate colors on each level. In particular, each vertex will have a different color from its parent and from its children. All children of a vertex v can have the same color since no children of v are adjacent to each other.

Fig. 2

Tree T.

Since every tree can be represented by a rooted tree, we can generalize the method in the example to show that for any tree, T, χ(T) ≤ 2.

Now consider the game chromatic number of a tree T. If Bob is always able to color two children of a vertex, v, different colors, then Alice cannot color T with two colors, since v will have no legal color. The reader can check that the tree in Figure 2 has game chromatic number greater than 2. No matter what Alice does, Bob is able to force a vertex to have no legal color.

The following theorems give some known results for the game chromatic number of trees and forests, which will be explored in more detail in Section 2.

Theorem 1 (Faigle, et al. [23]).

If F is a forest, then χ _g (F) ≤ 4. Moreover, there exists a forest F with χ _g (F) = 4.

Theorem 2 (Dunn et al. [18]).

Let F be a forest and let ℓ(F) be the length of the longest path in F. Then χ _g (F) = 2 if and only if:

• 1. 1 ≤ ℓ(F) ≤ 2, or

• 2. ℓ(F) = 3, | V (F) | is odd, and every component with diameter 3 is a path.

Consider the tree in Figure 3. It is the smallest tree T with χ _g(T) = 4.

Fig. 3

The smallest tree T with χ _g(T) = 4.

Theorem 3 (Dunn et al. [18]).

If F is a forest with | V (F) | ≤ 13 then χ _g (F) ≤ 3.

Although we know a bound for the game chromatic number of trees and forests, classifying trees with game chromatic number 3 or 4 remains open.

It has been well established that the parameter χ _g(G) has some interesting and possibly unexpected properties. For example, while it is true that if H is a subgraph of G then χ(H) ≤ χ(G), it is not necessarily the case that χ _g(H) ≤ χ _g(G). For example, as discussed in [3], if G = K _n, n and n ≥ 2 we have that χ _g(G) = 3. However, if M is any perfect matching in G, then χ _g(G − M) = n. So for n ≥ 4, χ _g(G − M) > χ _g(G).

We now briefly look at some variations of the coloring game.

1.2 The (r, d)-Relaxed Coloring Game

Let r be a positive integer, d be a nonnegative integer, and G be a finite graph. Two players, Alice and Bob, play a game on G by coloring the uncolored vertices with colors from a set X of r colors. At all times, the subgraph induced by a color class must have maximum degree at most d. Alice wins the game if all vertices are eventually colored; otherwise, Bob wins. We call this the (r, d)-relaxed coloring game. In particular, we have modified the original coloring game by changing the definition of a legal color. At any point in the game for any α ∈ X, let C _α be the set of vertices colored α at that point. We say that a color α ∈ X is legal for the uncolored vertex u, if after u is colored α we have that Δ(G[C _α ]) ≤ d, where G[C _α ] is the subgraph of G induced by the vertices in C _α .

The least r for which Alice has a winning strategy for this game on G is called the d-relaxed game chromatic number of G, denoted^d χ _g(G). When d = 0, we have the usual coloring game and the game chromatic number of G, χ _g(G). The relaxed game chromatic number has been considered in [6, 14,15,16, 26]. We will examine the d-relaxed game chromatic number further in Section 3.

Suppose that Alice and Bob are playing the (r, d)-relaxed coloring game on a graph G. For the purposes of analyzing strategies for Alice or Bob, we note that a color α is legal for an uncolored vertex u if the following two conditions hold:

• 1. The vertex u has at most d neighbors already colored α.

• 2. If v is a neighbor of u and v is already colored α, then v has at most d − 1 neighbors already colored α.

It might seem that if we increase the defect, then Alice could more easily win with fewer colors. It is known that if G = K _n, n with n ≥ 2, then¹ χ _g(G) = n. But as we saw in Section 1.1, if G = K _n, n and n ≥ 2 we have that χ _g(G) = 3. Thus, for n ≥ 4, there is a class of graphs for which⁰ χ _g(G) = 3 but¹ χ _g(G) ≥ 4.

Although the (r, d)-relaxed game is a common way to change the definition of a legal color, there are many other ways to relax the conditions of the game. For example, we also explore the notion of a clique-relaxed game in Section 4. In the k-clique-relaxed r-coloring game on a finite graph G, a color α is legal for an uncolored vertex u if coloring u with α does not result in a monochromatic (k + 1)-clique. As before, we can find the least number of colors required for Alice to have a winning strategy on G. We call this the k-clique-relaxed game chromatic number of G, denoted χ _g ^(k)(G).

1.3 Edge Coloring and Total Coloring

Another variation of the coloring game is to consider the game on edges rather than vertices. The rules are similar to the vertex coloring game. We begin with a finite graph, G, and a set X of r colors. Two players, Alice and Bob, alternate coloring the uncolored edges of G using colors from X. At each step of the game, the players must choose to color an uncolored edge with a legal color. Alice goes first. A color α ∈ X is legal for an uncolored edge e if e has no incident edges already colored α. Alice wins the game if all edges of the graph are colored; otherwise, Bob wins. The least number of colors required for Alice to have a winning strategy on G is called the game chromatic index of G, denoted χ _g′(G). This is explored in Section 5.

Once we have considered edge coloring and vertex coloring, a natural extension might be to consider total coloring. In a total coloring game, explored in Section 6, Alice and Bob alternate coloring vertices and edges.

2 Classifying Forests by Game Chromatic Number

In this section we examine the classic coloring game played on forests and trees. In [23], it was shown that the game chromatic number of a forest is at most 4. In this section, we focus on the question “Do there exist simple criteria for determining the game chromatic number of a forest?”

It is trivial to see that only edgeless forests have game chromatic number 1. Further exploration of this question is in the paper [18]. We will prove some results from the paper to highlight strategies which are helpful in exploring game coloring problems. First, we show that forests with game chromatic number 2 have determining criteria. We also demonstrate how a separator strategy is used to prove that small trees have game chromatic number at most 3. There is not any known criteria for differentiating between forests with game chromatic number 3 and 4.

2.1 Forests with Game Chromatic Number 2

We begin by showing the proof of Theorem 2, restated below.

Theorem 2 (Dunn et al. [18]).

Let F be a forest and let ℓ(F) be the length of the longest path in F. Then χ _g (F) = 2 if and only if:

• 1. 1 ≤ ℓ(F) ≤ 2, or

• 2. ℓ(F) = 3, | V (F) | is odd, and every component with diameter 3 is a path.

Proof.

Suppose that the condition is not met by some forest F. If ℓ(F) < 1, then it is easy to see that χ _g(F) = 1. Thus ℓ(F) ≥ 3. First, assume that ℓ(F) > 3 and that Alice colors x with α as her first move. If there is a vertex y at distance 2 from x then Bob can color y with β. The common neighbor of x and y has no legal color available, so Bob wins. Thus we assume that there is no such y. Then, some component of F not containing x must contain a path subgraph with 5 vertices, P ₅. Let v ₁, v ₂, v ₃, v ₄, v ₅ be the vertices of this P ₅. Bob will color v ₃ with α on his first turn, and on his second he can color either v ₁ or v ₅ with β and win the 2-coloring game on F.

Now assume that ℓ(F) = 3 and that Alice colors x with α as her first move; if there is a vertex y at distance 2 from x, then Bob will win the 2-coloring game as above. Thus x is not in a component with diameter 3. If there is a component with diameter 3 that is not a path, then this component has a vertex, u, of degree 3 or more that is adjacent to at least two leaves, v ₁ and v ₂. Bob colors v ₁ with α. Unless Alice colors u with β, Bob will win on his second move by coloring an uncolored neighbor of u with β. If Alice colors u with β, then because the component has diameter 3, there exists a vertex at distance 2 from u. Bob colors this with α and wins the 2-coloring game on F.

Thus every component with diameter 3 is a path, but | V (F) | is even. Let T ₁ be a path component with diameter 3. Because | V (F) | is even Bob can play so that Alice is the first to color a vertex in T ₁ (unless Bob wins the game before that point). When Alice colors a vertex x in T ₁, Bob immediately colors a vertex at distance 2 from x with a different color and wins the 2-coloring game on F.

Now suppose that a forest F satisfies the condition of the theorem. We will show that Alice can win the 2-coloring game on F. If diam(F) ≤ 2 then note that Bob can only win if, in a component of diameter 2, two leaves are colored using different colors before the central vertex is colored. Therefore, Alice will win the 2-coloring game by using the following strategy. (1) If possible, color the central vertex in the component Bob most recently played in. (2) Otherwise, color the central vertex in a component with no colored vertices. (3) If neither of those are possible, color any uncolored vertex.

If there are components of diameter 3, then they are all paths and | V (F) | is odd. By parity, Alice can always choose a vertex to color so that either it is not in a P ₄ component or it is in the same P ₄ component that Bob just played in. Alice’s strategy is as follows: if Bob colors x in a P ₄ component using color α, Alice colors the unique vertex at distance 2 from x with α. If it is Alice’s first turn, or if Bob did not color in a P ₄ component, then she follows her strategy from the case where diam(F) ≤ 2 with the additional restriction that she does not choose a vertex from a P ₄ component. Using this strategy, no uncolored vertex will ever have two differently colored neighbors. Therefore, Alice will win the 2-coloring game on F.

In the proof above, we identify configurations which allow Bob to win the r-coloring game (in this case, an uncolored vertex with two differently colored neighbors), and implement a strategy for Bob (or Alice) which forces (or avoids) these configurations. These two methods are at the heart of many proofs in game coloring, so finding such configurations is both a tractable and useful exercise for students.

2.2 Smallest Tree with Game Chromatic Number 4

Now that forests with game chromatic number 2 are classified, the investigation turns to the differences between forests with game chromatic numbers 3 and 4. Some simple observations can be made: in order for Bob to win the 3-coloring game on a forest F there must be a vertex of degree 3 or more. Thus linear forests have game chromatic number at most 3. It is a natural question to ask how small a forest with game chromatic number 4 can be.

Using small configurations on which Bob can win the 3-coloring game, we show that the graph T′ in Figure 4 is the smallest tree with game chromatic number 4.

Fig. 4

The tree T′ has game chromatic number 4 by Theorem 4

Lemma 1.

Let T ₀ be the partially colored tree shown in Figure  5 . Bob can win the 3-coloring game on T ₀ .

Fig. 5

The tree T ₀; the two shaded vertices have color α and unshaded vertices are uncolored.

Proof.

Suppose it is Alice’s turn. If she colors x ₁ or x ₂, or if she colors any uncolored leaf with a color other than α, Bob can immediately color so that either x ₁ or x ₂ has no legal color available. Therefore, we may assume without loss of generality that Alice colors x ₁ ^′ with α. Bob will color x ₂ ^′ with β. Now if Alice colors x ₂ with γ, then Bob can color x ₁ ^″ with β and win. If Alice does not color x ₂ with γ, then Bob will color either x ₁ or x ₂ ^″ with γ and win because x ₂ has no legal color available.

Suppose instead that it is Bob’s turn. He colors x ₂ ^′ with β. Exactly as above, Bob has a winning response to any move Alice can make.

Theorem 4 (Dunn et al. [18]).

The tree T′ (Figure  4 ) has game chromatic number 4.

Proof.

We show that χ _g(T′) = 4 by showing that Bob has a winning strategy when playing the 3-coloring game on T′. Bob’s goal is to attain the configuration T ₀ from Lemma 1. If Alice colors (with α) one of x ₁, x ₂, x ₃, x ₄ or a leaf adjacent to either x ₁ or x ₄, then Bob colors one of the x _i at distance 3 away from Alice’s move using α. By Lemma 1, Bob will win the 3-coloring game. Otherwise, we may assume without loss of generality that Alice colors a leaf adjacent to x ₂ with α; Bob responds by coloring the other leaf adjacent to x ₂ with β. Unless Alice now colors x ₂, Bob can make it uncolorable on his next turn. However, if Alice colors x ₂ (necessarily with γ), then Bob can color a leaf of x ₄ with γ and win by Lemma 1.

The proof of Theorem 4 highlights some of the potential difficulty in using partially colored subgraphs in a larger graph. When creating a strategy for one player that focuses on a subgraph, an opponent can either color a vertex in that subgraph, a vertex that is not on that subgraph but affects color choices for uncolored vertices in the subgraph, or a vertex that has no effect on the subgraph in question.

To show that trees with fewer vertices than T′ have game chromatic number at most 3, we need some lemmas regarding small trees. More detailed proofs can be found in [18].

Lemma 2.

If T is a tree with | V (G) | ≤ 13, then there exists a vertex v ∈ V (T) such that every component of T − v has at most 6 vertices.

Proof.

Choose v so that the order of the largest component in T − v is minimized.

Lemma 3.

If T is a tree on at most 7 vertices, then T has at most two vertices of degree 3 or more and at most one vertex of degree 4 or more.

Proof.

This can be shown by examining the degree sum of a counterexample.

In order to prove Theorem 3, it is useful to describe a separator strategy. At any point in the game, the forest F will be partially colored. Using the partial coloring, we define a collection of trunks as follows. For each colored vertex x with degree d, split x into d colored vertices, say x ₁, x ₂, …, x _d , so that each x _i is colored the same as x and is adjacent to exactly one neighbor of x. After each colored vertex is split in this fashion, the resulting graph will be a collection of trees, called trunks. Any colored vertex in a trunk must be a leaf of that trunk; if every vertex in a trunk is colored then it is a K ₂ component. Defined a different way, given a forest F and a partial coloring, a trunk R is a maximal connected subgraph of F such that every colored vertex in R is a leaf of R. It is important to note that coloring a vertex in one trunk has no effect on available colors in another trunk. We now restate and prove Theorem 3.

Theorem 3 (Dunn et al. [18]).

If F is a forest with | V (F) | ≤ 13 then χ _g (F) ≤ 3.

Proof.

Let F be a forest with | V (F) | ≤ 13 and let T be the component with the most vertices. By Lemma 2, there exists a vertex v ∈ V (T) such that every component of T − v has size at most 6. Alice colors this vertex, and now each trunk of F has order at most 7 and at most 1 colored vertex.

We call a vertex v dangerous if v has at least as many uncolored neighbors as legal colors available for it. Alice will win the 3-coloring game if there are no dangerous vertices in F. We show that Alice has a strategy which eliminates dangerous vertices in each trunk of F, and therefore has a strategy that will win the 3-coloring game on F. Alice will always play in the same trunk as Bob; if there are no uncolored vertices in that trunk Alice will play in a new trunk as if Bob just colored v.

Let R be the trunk of F where Bob just played. By Lemma 3, R has at most 2 dangerous vertices. If there are fewer than 2 dangerous vertices then Alice will color any remaining dangerous vertex on her turn, and then no dangerous vertices exist in R. If there are two dangerous vertices in R, then we consider the following cases:

Case 1

Some dangerous vertex x has no colored neighbors.

Alice colors the other dangerous vertex with any legal color. After Bob’s next move in this trunk, Alice colors x if it is still uncolored.

Case 2

Some dangerous vertex x has two colored neighbors.

Alice colors x with any available color. Since the colored vertices of R lie on a path, the other dangerous vertex x′ has at most one colored neighbor. After Bob’s next move in this trunk, Alice colors x′ if it is still uncolored.

Case 3

Each dangerous vertex has exactly one colored neighbor.

By Lemma 3 at least one dangerous vertex, say x, has degree 3; let the other dangerous vertex be x′. If x and x′ are not adjacent then Alice can color x first and then x′ later, as in Case 2. If x and x′ are adjacent, then x must have an uncolored neighbor u distinct from x′. Alice colors u with the same color as the previously colored neighbor of x. Therefore, x is no longer a dangerous vertex, and x′ has only 1 colored neighbor. After Bob’s next move in this trunk, Alice can color x′ if it is still uncolored.

In all cases, Alice is able to eliminate the dangerous vertices before Bob is able to surround any vertex with 3 distinct colors. Therefore, Alice can win the 3-coloring game on F.

By using this trunk coloring strategy and considering the different cases on maximum degree and diameter, it can be shown that T′ is in fact the unique forest on 14 vertices with game chromatic number 4 [18]. A main idea in this proof is that if there are few dangerous vertices, then Alice will have an easier time creating a winning strategy. Further utilizing this idea, one can prove some conditions under which a forest F has χ _g(F) ≤ 3.

Theorem 5 (Dunn et al. [18]).

A forest F has game chromatic number at most 3 if there exists a vertex b such that, if Alice starts by coloring b, every trunk R of F either

• 1. has no neighboring vertices whose degrees are both 3 or more, or

• 2. has a vertex v ∈ R with degree 3 or more which is adjacent to every vertex in R with degree 3 or more, and v is not adjacent to a colored vertex.

In fact, [18] proves something slightly stronger, but we omit that statement here in order to avoid a technical definition.

The proofs of Theorems 4 and  :ref T:Tree13 might lead one to believe that, if we can restrict the maximum degree of a forest, then Bob will not have the flexibility required to win the 3-coloring game. However, the following result shows that this is false.

Theorem 6 (Dunn et al. [18]).

There exists a tree T with Δ(T) = 3 and χ _g (T) = 4.

When outlining a strategy for Alice in the 3-coloring game on trees with maximum degree 3, the authors of [18] found a partially colored subgraph for which the strategy did not work. In fact, Bob could win the 3-coloring game on this subgraph. Working backwards, the authors pieced together a tree on which Bob can force this partially colored subgraph to occur.

As an aside, this is not an uncommon path towards interesting results. Recently, Steinberg’s Conjecture (every planar graph without 4-cycles and 5-cycles is 3-colorable) was proven to be false [7] using this “method”. As a team of mathematicians were working on a lemma needed to prove the conjecture, a gap in the proof turned into a counterexample to that lemma, which led to a counterexample to the entire conjecture!

Every known example of trees with Δ(T) = 3 and χ _g(T) = 4 have even order; the proof of Theorem 6 relies on the fact that Alice cannot avoid coloring first in a particular subgraph. One unanswered question regarding forests with game chromatic number 3 and 4 is if it is possible that maximum degree 3 implies χ _g(T) ≤ 3 for trees with odd order.

3 Relaxed-Coloring Games

In this section we will consider a variation of the game in which the subgraphs induced by each color class must satisfy the condition of having maximum degree bounded by a predetermined constant d. In this version of the game, the players are in the process of creating a defect coloring or relaxed coloring of the graph. Such colorings have been examined in [8,9,10, 21]. To highlight some of the strategies that have been employed to provide upper bounds on the associated parameter, we will provide results with trees. However, these strategies have been useful with many classes of graphs.

First we will define the game, which we will refer to as the (r, d)-relaxed coloring game. Let G be a finite graph and let X be a set of r colors, for some positive integer r. Let d be a nonnegative integer. We call d the defect. For each α ∈ X, we call the set of all vertices colored α the color class of α, denoted C _α . In this version of the game, a color α ∈ X is legal for an uncolored vertex u if, after u has been colored α, the subgraph induced by color class C _α must have maximum degree at most d. More succinctly, at every point in the game, for every α ∈ X, it must be true that Δ(G[C _α ]) ≤ d. Note that if d = 0, this is the original version of the coloring game. For a fixed d, the least r such that Alice has a winning strategy for this game is called the d-relaxed game chromatic number of G and is denoted by^d χ _g(G). For a fixed r, the least d for which Alice has a winning strategy for this game is called the r-game defect of G and is denoted by $\mathop{\mathrm{def}}\nolimits _{\mathrm{g}}(G,r)$.

At any time in the game, we define the defect of a colored vertex x ∈ C _α to be the number of neighbors of x already colored α. We denote this value by $\mathop{\mathrm{def}}\nolimits (x)$.

In terms of the analysis of a strategy, one must evaluate two things when considering the color α for the uncolored vertex u:

• 1. the vertex u must be adjacent to at most d vertices already colored α; and

• 2. if v is adjacent to u and v has already been colored α, then v can be adjacent to at most d − 1 vertices already colored α.

Theorem 7 (Chou et al. [6]).

If T is a tree, then ¹ χ _g (T) ≤ 3.

We will present two proofs of this theorem. First, we will provide the argument used by Chou, Wang, and Zhu in [6]. This uses a separator strategy as introduced in Section 2. The second result uses an activation strategy. Activation strategies have proven to be quite useful for many classes of graphs, and can be seen as the culmination of the work in a number of papers [11, 23, 27, 28, 30, 31]. We will present a number of activation strategies in later sections.

Proof.

(Separator Argument) Suppose in the process of the game, the tree T is partially colored. We obtain a collection of subtrees as follows: for each colored vertex x with degree d, we split x into d colored vertices, say x ₁, x ₂, …, x _d , so that each x _i is colored the same color as x and is incident with exactly one of the original edges incident to x in T. After splitting each of the colored vertices of T, we obtain a collection of smaller partially colored trees, say T ₁, T ₂, …, T _m , which we will call trunks, such that ∪ _{i = 1} ^m E(T _i ) = E(T). Note that in each T _i , it is the case that only some of the leaves may be colored.

Alice’s goal in selecting the vertices to color is simply to ensure that after she has colored her chosen vertex, each of the trunks of the partially colored T has at most two colored leaves. Suppose Alice can achieve this goal. Then after Bob colors a vertex, each trunk T _i has at most two colored vertices, with the exception of one trunk which may have three colored vertices. Moreover, if the trunk T _i has three colored leaves, then one of those leaves was just colored by Bob. We will call this the new colored leaf of T _i .

It is easy to prove inductively that Alice can achieve her goal. If after Bob’s move there is a trunk T _i containing three colored leaves, then Alice will choose the vertex that lies at the intersection of the paths joining these three colored vertices. Suppose Alice has chosen vertex u ∈ V (T _i ) by this process. She will then choose a color for u as follows: if the colored leaves of T _i use at most two colors, Alice will choose a color that has not been used on T _i . Otherwise, T _i has three distinctly colored leaves. Alice will color u with the color of the new colored leaf, v, of T _i .

To show that this works, it suffices to show that in the case that T _i has three distinctly colored leaves, then the color of v is legal for u. This is obvious as v has no other colored neighbors. Thus, Alice can color u with the color assigned to v. This will affect the defect of at most two vertices: u and v. Each will then have defect of at most 1. Thus, following this strategy, all vertices of T will be colored and Alice will win.

For the second proof of this result, we will define what we will call the Tree Strategy for Alice. Suppose Alice and Bob are playing the coloring game on the tree T = (V, E). Alice picks a vertex r and orients all edges in the tree toward r. The resulting orientation on T has the property that every vertex v ∈ V ∖{ r } has a unique outneighbor which we denote p(v). We call p(v) the parent of v and refer to v as a child of p(v). Continuing this notation, let p ²(v) = p(p(v)). Inductively, if p ⁱ(v) is defined, let p ⁱ⁺¹(v) = p(p ⁱ(v)). We define the set of descendants of a vertex v by

$$\displaystyle{G(v):=\{\, w \in V \mid v = p^{k}(w)\text{ for some }k\,\}.}$$

We then define G[v]: = G(v) ∪{ v }.

Throughout the game, vertices go from uncolored to colored. At any time in the game, let U be the set of uncolored vertices and C be the set of colored vertices. Alice will maintain a set A of active vertices. One way of viewing the notion of an active vertex is to think of it like a post-it note that Alice places on vertices that are becoming dangerous, yet not requiring immediate attention. When her strategy leads her to consider a vertex that already has such a post-it note, she knows that it is now time to color this vertex. Alice will only color vertices that are active; however, she may activate a vertex and color it on the same turn. For simplicity, we will assume that any vertex that Bob colors also becomes active; thus C ⊆ A. Whenever a vertex is colored it is added to C, and whenever a vertex is activated it is added to A. When a vertex v is colored, let c(v) be that color. For any color α ∈ X, we say that α is eligible for a vertex v if either p(v) ∈ U or c(p(v)) ≠ α. Note that if $\left \vert X\right \vert \geq 2$, every uncolored vertex must have at least one eligible color.

Tree Strategy

On her first move, Alice will color the vertex r with any color. Suppose Bob has just colored vertex b. Alice’s strategy will have two stages: a search stage and a coloring stage. In the search stage, she seeks the vertex u that she will color. In the coloring stage, she selects the color for u.

Search Stage

• Initial Step

  • If p(b) ∈ U, then set x: = p(b) and move to the recursive step.

  • If p(b) ∈ C, c(b) = c(p(b)), and p ²(b) ∈ U, then set u: = p ²(b) and move to the coloring stage.

  • Otherwise, let u be any uncolored vertex such that p(u) ∈ C and move to the coloring stage, activating u if u is inactive.

• Recursive Step

  • If x ∉ A and p(x) ∈ U, then activate x, set x: = p(x) and repeat the recursive step.

  • Otherwise, activate x if it is inactive, set u: = x, and move to the coloring stage.

Coloring Stage

• Choose an eligible color for u which minimizes $\mathop{\mathrm{def}}\nolimits (u)$.

We are now ready to provide our second proof of Theorem 7.

Proof.

(Activation Argument) Let T be a tree and let $\left \vert X\right \vert = 3$. Alice will employ the Tree Strategy defined above. Suppose u = p(v) and u is uncolored. Then the first time a vertex in G[v] is activated, necessarily by Bob, Alice will take action at u by coloring (if u is already active) or by activating.

Suppose that Alice has chosen to color vertex u. Suppose x and y are the first two children of u to be activated, and x is activated first. Note that on the turn that x is activated, Alice takes action at u by activating it. Assuming that she does not also color u on this turn, suppose that w is the first vertex in G[y] to be activated. Then when w is activated (by Bob coloring it), y is activated and Alice moves to color u.

Now suppose that Alice is choosing a color for u. First note that u has at most three colored neighbors: p(u) and at most two children, again say x and y. If the number of colors used on these three neighbors is at most two, then Alice’s strategy dictates that she will use a color not used in the set of neighbors of u, N(u). Otherwise, it must be the case that p(u), x, and y are all colored distinctly. Since there is only one vertex in G[y] colored, then Alice can safely color u with c(y) as this results in $\mathop{\mathrm{def}}\nolimits (u) =\mathop{ \mathrm{def}}\nolimits (y) = 1$, with the defect of no other vertex affected. We note that Bob can borrow this strategy at any time. So at any time in the game, it is possible to color any uncolored vertex with a legal color. Thus, all vertices of T will eventually be colored, and Alice will win.

We note that while the bound in Theorem 7 is known to be sharp [6], we do not know the necessary and sufficient characteristics of a tree T to determine whether¹ χ _g(T) = 3 or¹ χ _g(T) = 2.

4 The Clique-Relaxed Game

Earlier, we examined the graph coloring game using d-relaxed coloring rules on vertices and on edges. Exploring different modifications to standard coloring rules can open up a wide range of interesting competitive coloring problems. Another relaxation of standard coloring rules is clique-relaxed coloring, where the aim is to avoid large monochromatic cliques (complete subgraphs).

In this section, we examine the game coloring version of clique-relaxed coloring; we focus on planar and outerplanar graphs. A planar graph is a graph that can be drawn in the plane such that no edges cross each other. Each region bounded by the edges is called a face and the infinitely large unbounded face is called the outer face. One specific type of planar graph is an outerplanar graph, which is a planar graph that can be drawn so that every vertex belongs to the outer face.

Recall that ω(G) denotes the size of the largest clique in G. We say that a vertex coloring of a graph G is a proper k-clique-relaxed coloring if ω(H) ≤ k for each subgraph H induced by one of the color classes. The k-clique-relaxed chromatic number of G, denoted χ ^(k)(G), is the smallest k such that G has a proper k-clique-relaxed coloring.

Although there appears to be very little proven about this parameter in the literature, it seems like a natural variation of other coloring relaxations and has interesting properties with regards to competitive graph coloring. Notice that for any graph G, we get χ ⁽¹⁾(G) =⁰ χ _g(G) = χ(G) and that χ ^(k)(G) ≤ χ ^(k−1)(G) for every positive integer k. The following theorem gives an upper bound for χ ^(k)(G) in terms of the standard chromatic number χ(G).

Theorem 8 (Dunn et al. [17]).

Let G be a graph. Then $\chi ^{(k)}(G) \leq \left \lceil \frac{\chi (G)} {k} \right \rceil$ for any positive integer k.

Proof.

Let G be a graph where χ(G) = r. Color the vertices of G properly with r colors which we denote α ₁, …, α _r . We divide the r colors into $s:= \left \lceil \frac{r} {k}\right \rceil$ groups, all of size exactly k except possibly the last group. We label these groups A ₁, …, A _s and recolor all vertices in A _i with color β _i . There are s colors used in this new coloring. Suppose, for the sake of contradiction, that H ⊆ G is a (k + 1)-clique where each vertex of H receives color β _i . Then by the pigeonhole principle, at least two vertices x and y in A _i were colored α _j originally for some j. Thus xy cannot be an edge of G, which contradicts the fact that H is a (k + 1)-clique.

Using this theorem we are able to give bounds for χ ^(k)(G) for some classes of graphs. The Four Color Theorem [2] shows that χ(G) ≤ 4 for all planar graphs G. Also, it is also easy to show that χ(G) ≤ 3 for outerplanar graphs G. These observations lead to the following corollary.

Corollary 1.

If G is a planar graph, then χ ^(k)(G) ≤ 2 when 2 ≤ k ≤ 3 and χ ^(k)(G) = 1 when k ≥ 4. Moreover, if G is an outerplanar graph, then χ ⁽²⁾(G) ≤ 2 and χ ^(k)(G) = 1 when k ≥ 3.

These bounds are sharp as K ₄ is a planar graph with χ ^(k)(K ₄) = 2 when 2 ≤ k ≤ 3 and K ₃ is an outerplanar graph with χ ⁽²⁾(K ₃) = 2.

To play the k-clique-relaxed r-coloring game on a graph G, two players (Alice and Bob) will take turns coloring uncolored vertices of G with legal colors coming from a fixed set X of r colors. A color α ∈ X is legal for an uncolored vertex u if coloring u with α does not create a monochromatic (k + 1)-clique. Said another way, α is not a legal color for u if G[N(u)] contains a k-clique H where each vertex of H is colored α. Alice always colors first, and she wins the game when all the vertices are colored. Therefore, Bob will win if there is at least one uncolored vertex u in G whose neighborhood contains monochromatic k-cliques in each of the r colors. The k-clique-relaxed game chromatic number of G, denoted χ _g ^(k)(G), is the least r such that Alice has a winning strategy in the k-clique-relaxed r-coloring game.

The first observation is that χ _g ⁽¹⁾(G) =⁰ χ _g(G). In [17], the authors investigate the k-clique-relaxed game chromatic number on outerplanar graphs. Because the maximum clique size in an outerplanar graph is 3, it follows that χ _g ^(k)(G) = 1 when G is an outerplanar graph and k ≥ 3. Therefore, the focus is on the 2-clique-relaxed coloring game. In the following result, Alice’s strategy is to use a vertex ordering given by Guan and Zhu [25] to implement a separator strategy similar to the one used on trees (see Section 3).

Theorem 9 (Dunn et al. [17]).

Let G be an outerplanar graph. Then χ _g ⁽²⁾(G) ≤ 4.

Proof.

Let G be an outerplanar graph. Alice’s strategy is to define auxiliary graphs G′ and T, and to use these graphs to choose which vertex to color. First, let G′ be the graph obtained by adding edges to G until the graph is maximally outerplanar. Guan and Zhu [25] showed that for every maximally planar graph, there is a linear ordering L: = v ₁, …, v _n of the vertices of H such that v ₁ v ₂ is on the outer face and, for all i ≥ 3, the vertex v _i is adjacent to exactly two vertices v _a(i) and v _b(i) such that a(i) < b(i) < i. We call v _a(i) and v _b(i) the major parent and minor parent (respectively) of v _i .

To create the graph T, Alice deletes from G′ all the edges of the form v _i v _b(i). Note that v ₁ v ₂ is still an edge and for each i ≥ 3 the vertex v _i is adjacent to exactly one vertex with lower index; thus, T must be a tree. As in the separator strategy of Section 3, Alice can ensure that after her turn each trunk of T has at most two colored vertices. Bob may possibly color a third vertex in a trunk, so each uncolored vertex v _i that Alice chooses has at most 3 colored neighbors in T. It is possible that v _i has more colored neighbors in G, as v _i v _b(i) could be an edge in G. Further, [25] showed that each vertex in G′ is the minor parent to at most two vertices. Therefore v _i is adjacent to at most six colored vertices in the original graph G. In the 2-clique relaxed 4-coloring game, a vertex will have a legal color unless it is adjacent to monochromatic K ₂ subgraphs in each of the 4 colors. Because v _i is adjacent to at most 6 colored vertices, there is a legal color for Alice to use.

Bob will also always have a legal move, because Alice’s strategy leaves at most two colored vertices in each trunk of T. Therefore, uncolored vertices have at most 5 colored neighbors in G on Bob’s turn.

The bound in Theorem 9 has no sharpness example; in [17] an example is given where Bob has a winning strategy for the 2-clique-relaxed 2-coloring game on an outerplanar graph. Bob’s strategy uses the symmetry of the graph to create a particular partially colored subgraph on which an uncolored vertex can be made uncolorable. It remains open whether or not there exists an outerplanar graph where Bob has a winning strategy for the 2-clique-relaxed 3-coloring game.

Theorem 10 (Dunn et al. [17]).

There exists an outerplanar graph G with χ ⁽²⁾(G) ≥ 3.

Figure 6 provides an example of an outerplanar graph with χ ⁽²⁾(G) ≥ 3. The proof can be found in [17].

Fig. 6

An outerplanar graph with χ ⁽²⁾(G) ≥ 3.

This raises the question of whether there exists an outerplanar graph G such that χ _g ⁽²⁾(G) = 4. Further results in [17] show a subclass of outerplanar graphs in which no such example can be found.

The question of clique-relaxed coloring games on planar graphs also remains open. Because the maximum clique size in a planar graph is four, the games of interest on planar graphs are the 2- and 3-clique-relaxed games.

5 Edge Coloring

The focus of this section is a variation of the game in which Alice and Bob alternate coloring edges rather than vertices. The most obvious consequence of analyzing this version of the game is that the maximum degree of the graph becomes an important component of the upper bounds for the corresponding parameters.

Let G be a finite graph and let r be a positive integer and d be a nonnegative integer. As used before, d is the defect and X is a set of r colors. The players alternate coloring, with Alice coloring an edge first. We say that a color α ∈ X is legal for an uncolored edge e if the following conditions are satisfied:

• 1. the edge e is incident with at most d edges already colored α; and

• 2. if e′ is an edge incident to e and e′ has already been colored α, then e′ is adjacent to at most d − 1 edges already colored α.

Note that if e is colored α, then at this point in the game, every edge has at most d neighbors colored α. Alice wins if every edge is eventually legally colored. Bob wins if there comes a time in the game when there is an uncolored edge for which no legal color exists. For a fixed defect d, the least r such that Alice has a winning strategy for this game is called the d-relaxed game chromatic index of G, denoted^d χ _g′(G). Similarly, for a fixed r, the r-edge-game defect of G, denoted $\mathop{\mathrm{def}}\nolimits _{\mathrm{g}}'(G,r)$, is the least d such that Alice has a winning strategy. This game was first introduced in [13].

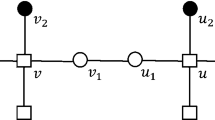
We will present some of the work done in [19] restricted to trees, which generalized the results in [13]. Further work in this area can be seen in [1, 5, 22, 29]. We begin by defining terminology and notation, and by providing a winning strategy for Alice in the edge coloring game on trees. Let T be a tree with Δ(T) = Δ for some positive integer Δ. For her strategy, Alice chooses an arbitrary leaf r ∈ V (T) at which she roots T. She then regards all edges in T as oriented toward r. Let e ₀ be the unique edge in T that is incident to r. For each vertex v ∈ V ∖{ r }, define p(v) to be the unique outneighbor of v. Then for each edge e ∈ E, there is a unique vertex x ∈ V such that e = xp(x). We now introduce some terminology, as illustrated in Figure 7.

Fig. 7

For an edge e = xp(x), the vertex p(p(x)) = p ²(x), the edge p(e), and the sets B(e) and S(e).

For every edge e = xp(x) with e ≠ e ₀, define the parent of e, denoted p(e), to be the edge p(x)p ²(x), where p ²(x) = p(p(x)). We say that e is a child of p(e). Note that, because p(x) is well defined, p(e) is also well defined. Whenever p ⁱ(e) is defined and p ⁱ(e) is not incident with the root, define p ⁱ⁺¹(e) = p(p ⁱ(e)). As in the second (activation) proof of Theorem 7, we define the descendants of e to be

$$\displaystyle{G(e) =\{ e' \in E\mid e = p^{k}(e')\mbox{ for some positive integer }k\}.}$$

For each edge e = xp(x), define the siblings of e to be

$$\displaystyle{B(e) =\{ yp(y) \in E\mid p(y) = p(x)\mbox{ and }y\neq x\}}$$

and B[e] = B(e) ∪{ e}. Define the children of e to be

$$\displaystyle{S(e) =\{ yp(y) \in E\mid x = p(y)\}.}$$

We call the set of all edges incident to an edge e the neighborhood of e, denoted N(e).

Fix j ∈ [Δ − 3] and let X be a set of Δ − j colors. Note that $\left \vert X\right \vert \geq 3$. At any point in the game, let C and U be the set of colored and uncolored edges, respectively. For each α ∈ X, we call the set of all edges colored α the color class of α, denoted C _α . For a colored edge e, denote the color of e by c(e).

Similar to the notion with vertices, for each colored edge e, define the defect of e to be the number of neighbors of e colored with c(e). If e is uncolored, we set the defect of e to be zero. We denote the defect of e by $\mathop{\mathrm{def}}\nolimits (e)$. Thus

$$\displaystyle{ \mathop{\mathrm{def}}\nolimits (e) = \left \{\begin{array}{@{}l@{\quad }l@{}} \left \vert N(e) \cap C_{c(e)}\right \vert,\quad &\text{if }e \in C; \\ 0, \quad &\text{otherwise.} \end{array} \right. }$$

We say that color α ∈ X is eligible for edge e if p(e) ∉ C _α . We denote the set of eligible colors for e by X(e). When coloring an edge e, Alice always chooses an eligible color. Note that since $\left \vert X\right \vert \geq 3$, this is always possible.

In most strategies for vertex-coloring games, Alice avoids increasing the defect of a vertex when she can. The interesting aspect of this edge strategy is that in some cases, it will be necessary for her to do just the opposite. She will attempt to reach a minimum threshold for the defect of some edges. For any edge e, we say that B[e] is secure if there exist edges e ₁, e ₂, …, e _j+1 ∈ B(e) and a color α such that c(e _i ) = α for i ∈ [j + 1]. In other words, B[e] is secure if e has j + 1 siblings colored with the same color. Note that if B[e] is secure, then the number of distinctly colored siblings of e is at most

$$\displaystyle{\left \vert B(e)\setminus \{e_{1},e_{2},\ldots,e_{j}\}\right \vert \leq \varDelta -j - 2.}$$

As $\left \vert X(e)\right \vert \geq \varDelta -j - 1$, there is always a legal eligible color for an uncolored edge e when B[e] is secure.

We will now define the strategy that Alice will use for this game with trees. This strategy is a modification of the activation strategy developed in [13]. In response to Bob’s moves, Alice designates certain edges active, as above in the second proof of Theorem 7; precisely how she chooses these edges will be explained below. When an edge e becomes active, we say that e has been activated. In addition, all colored edges are active. We denote the set of active edges by A, and note that C ⊆ A. This set has the property that once an edge e is in A, e will remain active for the remainder of the game.

Tree Strategy for Edges

Alice begins the game by coloring e ₀ with any color. Suppose now that Bob has just colored edge b = xp(x) in T for some x ∈ V ∖{ r } and some i ∈ [n]. Alice’s response has two stages: a Search Stage and a Coloring Stage. In the Search Stage, Alice finds an edge e to color. In the Coloring Stage, Alice chooses a color for e.

Search Stage

• If p(b) ∈ U, then activate each edge along the (x, r)-path until reaching an edge g with p(g) ∈ A. [Note that this includes Alice activating the edge b.] If p(g) ∈ C, set e: = g. Otherwise, set e: = p(g).

• If p(b) ∈ C with c(p(b)) = c(b) and p ²(b) ∈ U, then set e: = p ²(b).

• If p(b) ∈ C with c(p(b)) = c(b), p ²(b) ∈ C, and B(p(b)) ∩ U ≠ ∅, then set e to be any uncolored sibling of p(b).

• Otherwise, set e to be any uncolored edge whose parent is colored.

Coloring Stage

• If B[e] is secure, then color e with an eligible color for e that does not appear among the siblings of e.

• Otherwise, B[e] is not secure. Let f be the last edge to be colored with a color eligible for e such that c(f) = c(p(f)) and p(f) ∈ B(e). If such an edge exists, then color e with c(f). If no such edge exists, then color e with any eligible color for e that minimizes $\mathop{\mathrm{def}}\nolimits (e)$.

We now present the theorem and proof from [19] for trees.

Theorem 11 (Dunn et al. [19]).

Let T be a tree and Δ(T) = Δ for some positive integer Δ. Let j be an integer with 0 ≤ j ≤ Δ− 1, and define h(j) = 2j + 2. Then $\mathop{\mathrm{def}}\nolimits _{\mathrm{g}}'(T,\varDelta -j) \leq h(j)$ . Moreover, if d ≥ h(j) then ^d χ _g ′(T) ≤ Δ− j.

Proof.

Suppose that Alice and Bob are playing the (Δ − j, d)-relaxed edge coloring game on T for some d ≥ h(j). Note that when either j = Δ − 1 or j = Δ − 2, the result is immediate. Hence, it will suffice to consider the game with color set X with $\left \vert X\right \vert \geq 3$. We will assume that Alice uses the Tree Strategy for Edges.

Claim.

If e ∈ U, then e has at most two active children. Furthermore, when e has two active children, Alice colors e.

Proof.

Let f be the first active child of e. When Alice activates f, she also activates e. Note that while e is uncolored, Alice never colors an edge in G(e)∖G(f) before Bob. If Bob colors an edge b ∈ G(e)∖G(f), Alice activates p(b), p ²(b), …, and so on, until she reaches e. Since e is active, Alice colors e.

Claim.

Suppose that Alice has chosen to color edge e with α ∈ X. Then at the end of Alice’s turn, $\mathop{\mathrm{def}}\nolimits (e) \leq j + 2$.

Proof.

Since α ∈ X(e), then p(e) does not contribute to the defect of e. By Claim 5, e has at most two active children; hence, e has at most two children colored α. If B[e] is secure, then Alice would have chosen a color that does not appear among the siblings of e. In this case, $\mathop{\mathrm{def}}\nolimits (e) \leq 2$. Otherwise, when B[e] is not secure, there are at most j siblings of e colored α. Thus, $\mathop{\mathrm{def}}\nolimits (e) \leq j + 2$.

Claim.

Suppose that e is about to be colored α and p(e) ∈ U. Then e has at most one child colored α. Furthermore, if e has a child colored α, then Bob colors e and Alice colors p(e).

Proof.

If some sibling f ∈ B(e) is the first active child of p(e), then Alice colors p(e) when the first edge in G(p(e))∖G(f) is activated. Since p(e) is uncolored and e is to be colored, we conclude that e has no active children and hence no children colored. So assume that e is the first active child of p(e). Note that p(e) ∈ A. If an edge in G(p(e))∖G(e) is then activated, Alice colors p(e). Otherwise, we may assume that e has no colored siblings at the time when e is colored. Before e is colored, it is incident with at most two colored edges, which are children of e. Since $\left \vert X\right \vert \geq 3$, there is a color that does not appear on any child of e. Then, because Alice will choose a color to minimize $\mathop{\mathrm{def}}\nolimits (e)$, Alice never chooses to color e with α if a child of e has already been colored α. So, if e has two active children before e is colored, then Alice colors e with α only when neither child is colored α. Thus, if e has a child colored α, then Bob must be coloring e with α, and since p(e) ∈ A, Alice responds by coloring p(e).

Suppose f ∈ S(e) ∩ C _α . By Claim 5, if f has a child colored α before f is colored, then Bob must have colored f and Alice responds by coloring e. Thus $\mathop{\mathrm{def}}\nolimits (f) = 2$ once e is colored. Otherwise, f has no children colored α before f is colored. Since e has at most two active children before e is colored, f has at most one sibling colored α before e is colored. Then $\mathop{\mathrm{def}}\nolimits (f) \leq 2$ once e is colored.

Now consider the siblings of e. If B[e] is secure, since Alice is choosing to color e with α, then α does not appear among the siblings of e. Hence, coloring e with α does not affect the defect of any edge in B(e).

Finally, we consider the case where B[e] is not secure.

Claim.

Suppose Alice has chosen to color edge e with α ∈ X and B[e] is not secure. If there exists an edge f ∈ B(e) ∩ C _α , then $\mathop{\mathrm{def}}\nolimits (f) \leq 2j + 2$ once e is colored.

Proof.

Let E′ = B(e) ∩ C _α . Since B[e] is not secure, we have that $\left \vert E'\right \vert \leq j$. Let f ∈ E′ such that $\left \vert S(f) \cap C_{\alpha }\right \vert$ is maximal, and let

$$\displaystyle{S(f) \cap C_{\alpha } =\{ s_{1},s_{2},\ldots,s_{m}\},}$$

where i < j implies that s _i is colored before s _j . We show that $m \leq \left \vert E'\right \vert + 2$. By Claim 5, f has at most two active children before it is colored. Hence, f has at most two children colored α before f is colored. So only the following cases need be considered:

Case 1

The edge f is colored before s ₁.

Since p(s _i ) = f for each i ∈ [n] and c(f) = α, Alice does not color any s _i . For each s _i that Bob colors, Alice then colors p(e) if p(e) ∈ U, an edge in E′∖{f} if p(e) ∈ C, or e if E′ ∩ U = ∅. Then at most $\left \vert E'\right \vert + 1$ children of f are colored α before Alice colors e. Hence, $m \leq \left \vert E'\right \vert + 1$.

Case 2

The edge f is colored after s ₁ and before s ₂.

Alice does not color s _i for any i ≥ 2. As in the previous case, when Bob colors s _i with i ≥ 2, Alice then colors p(e), an edge in E′∖{f}, or e. Thus, once f ∈ C, at most $\left \vert E'\right \vert + 1$ children of f are colored α. Including s ₁, we have that $m \leq \left \vert E'\right \vert + 2$.

Case 3

The edge f is colored after s ₂.

If p(e) ∈ U, then Claim 5 implies that f has at most one child colored α before f is colored. Since f has two children colored α before f is colored, p(e) must be colored before f. Furthermore, Alice colors f immediately after s ₂ is colored, as s ₁ and s ₂ must be the first two active children of f. Once f is colored, each time Bob colors a child of f with α, Alice colors an edge in E′∖{f}. Therefore, once f is colored, Bob can color at most $\left \vert E'\right \vert$ children of f with α before e is colored. So $m \leq \left \vert E'\right \vert + 2$.

Thus, in all cases, we have that

$$\displaystyle{m = \left \vert S(f) \cap C_{\alpha }\right \vert \leq \left \vert E'\right \vert + 2 \leq j + 2}$$

once e is colored. Since f was chosen to maximize $\left \vert S(f) \cap C_{\alpha }\right \vert$ and each f′ ∈ E′ has at most j siblings colored α before e is colored, we have that

$$\displaystyle{\mathop{\mathrm{def}}\nolimits (f') \leq \left \vert S(f) \cap C_{\alpha }\right \vert + j \leq 2j + 2}$$

for all f′ ∈ E′.

Note now that if Alice is coloring edge e with α, according to the Tree Strategy for Edges, Claim 5 guarantees that $\mathop{\mathrm{def}}\nolimits (e) \leq h(j)$. We have also shown that for any edge f ∈ N(e) ∩ C _α , immediately after e is colored, $\mathop{\mathrm{def}}\nolimits (f) \leq h(j)$. As Bob may adopt Alice’s strategy at any point in the game, every edge is eventually colored, and Alice wins the game. Thus

$$\displaystyle{\mathop{\mathrm{def}}\nolimits _{\mathrm{g}}'(T,\varDelta -j) \leq 2j + 2 = h(j).}$$

Moreover, if the game is being playing with some defect d > 2j + 2, and an edge e eventually has defect at least d, then it must be through the actions of Bob that this occurs. At the time that e is uncolored, the above arguments show that it is possible to color e with an eligible color α such that coloring e does not increase the defect of any edge e′ with $\mathop{\mathrm{def}}\nolimits (e')> 2j + 2$. Thus, for any d ≥ h(j), we have that

$$\displaystyle{^{d}\chi _{ \mathrm{g}}'(T) \leq \varDelta -j,}$$

as desired.

In addition to possible improvements to the above bounds, there are many properties of χ _g′(G) and^d χ _g′(G) that remain to be studied. This variation of the coloring game would be ideal for asking additional questions and examining additional classes of graphs. While the above result is generalized in [19] to a larger class of graphs (k-degenerate), no other classes have yet been considered.

6 Total Coloring

The total coloring game is a variation of the original coloring game in which Alice and Bob are free to color vertices or edges on their turns. For the remainder of this section, we will refer to vertices and edges as elements of the graph. The components of the game are a finite graph G and a finite set of colors X with $\left \vert X\right \vert = r$. At any point in the game, a color α ∈ X is legal for an uncolored vertex u if u has no neighbors colored α and is incident with no edges colored α. Similarly, α is legal for an uncolored edge e if e is not incident with any edges colored α and neither endpoint of e is colored α. Alice wins the game if all of the elements of G are colored. Bob wins otherwise. In other words, Bob wins if there comes a time in the game when there is an uncolored element for which no legal color exists. The least r such that Alice has a winning strategy is called the total game chromatic number of G and is denoted χ _g″(G).

The following work is currently in preparation [20]. To prove the following theorem, we will again have Alice employ an activation strategy, which we will refer to as the Total Activation Strategy. Let G = (V, E) be a graph and fix a linear ordering L of V. Note that L lexicographically induces a linear ordering $\overline{L}$ of E. For any element a we use L and $\overline{L}$ to separate N(a) into two sets, N ⁺(a) and N ⁻(a); an element b ∈ N(a) is only in N ⁺(a) if b < a. Let N ⁺[a]: = N ⁺(a) ∪{ a} and N ⁻[a]: = N ⁻(a) ∪{ a}. At any time in the game, let U _v and U _e be the sets of uncolored vertices and edges of G, respectively. Alice will maintain two sets, A _v and A _e of active vertices and edges, respectively. Once an element has become active, it will remain active for the remainder of the game. For a given vertex v, at any given time in the game let $m(v) =\min _{L}\left (N^{+}[v] \cap U_{\mathrm{v}}\right )$ be the mother of v. Similarly, for a given edge e, we define $m(e) =\min _{L}\left (N^{+}[e] \cap U_{\mathrm{e}}\right )$ to be the mother of e. We note that the mother of any uncolored element must exist, as the element itself is a candidate.

Total Activation Strategy

On Alice’s first turn, she activates and colors the first vertex in L. Now suppose that Bob has just colored element b of type t, where t ∈ { v, e } and $\{\,t,\overline{t}\,\} =\{\, v,e\,\}$. (We again assume that Bob also activates b if it is not already active.) Alice must now search for the element she will color and choose a color for this element.

Search Stage

• Initial Step

  • If m(b) exists, then set x: = m(b) and move to the recursive step.

  • If m(b) does not exist and U _t ≠ ∅, let u be the least element of U _t and move to the coloring stage.

  • Otherwise, let u be the least element of $U_{\overline{t}}$ and move to the coloring stage.

• Recursive Step

  • If x is active, set u: = x and move to the coloring stage.

  • Otherwise, activate x, set x: = m(x), and repeat the recursive step.

Coloring Stage

• Color u with any color legal for u.

Theorem 12 (Dunn et al. [20]).

If F is a forest with Δ(F) = Δ, then χ _g ″(F) ≤ Δ + 4.

Proof.

Suppose Alice and Bob are playing the total coloring game on F with color set X where $\left \vert X\right \vert =\varDelta +4$. We will assume that Alice will use the activation strategy outlined above. We will now show that for any uncolored element, there is always a legal color available at any point in the game.

Suppose v is an uncolored vertex. At any time in the game, v is incident with at most Δ edges, possibly all distinctly colored before v is activated. Additionally, at most one vertex in N ⁺(v) can be colored before v becomes active. Finally, at most two vertices in N ⁻(v) can be activated (or colored) before v is colored: one which activates v, and one which forces Alice to immediately color v. Thus, v is incident or adjacent to at most Δ + 3 uniquely colored elements before v is colored.

Now suppose that e = xy is an uncolored edge and x > y in L. At any point in the game, e can be incident with at most two distinctly colored vertices before e becomes active. In addition, at most Δ − 1 edges in P(e) ∪ B(e) can be distinctly colored before e becomes active. Finally, two children of e can be activated (or colored) before e is colored: one to activate e and one to trigger the coloring of e. Thus, e is incident with at most Δ + 3 colored elements before it is colored.

Since Δ + 4 colors are available, and given that Bob may utilize Alice’s strategy, Alice will win. Thus, χ _g″(F) ≤ Δ + 4.

A chordal graph is a graph in which every cycle subgraph with 4 or more vertices has a chord; in other words, a chordal graph does not have C _n as an induced subgraph for any n ≥ 4.

Theorem 13 (Dunn et al. [20]).

If G is a chordal graph with Δ(G) = Δ and ω(G) = k + 1, then χ _g ″(G) ≤ Δ + 3k + 2.

Proof.

Let X be a set of colors with $\left \vert X\right \vert =\varDelta +3k + 2$ and suppose that Alice and Bob are playing the total coloring game on G with X. We will assume that Alice employs the Total Activation Strategy defined above. We will show that at any time in the game, any uncolored element has an eligible legal color available.

Suppose that v is an uncolored vertex. First, it is clear that there are at most Δ edges incident with v that could be colored before v is activated (or colored). Also, every vertex in N ⁺(v) may be colored before v is colored. Let S ⊆ N ⁻(v) be the set of all children of v that are activated before v is colored. Note that for any vertex w ∈ S, it must be the case that m(w) ∈ N ⁺[v] since G is a chordal graph. Thus, every time a vertex in S is activated, Alice will respond by either activating or coloring a vertex in N ⁺[v]. So initially, this yields $\left \vert S\right \vert \leq 2\left \vert N^{+}[v]\right \vert \leq 2(k + 1) = 2k + 2$. However, we can improve this bound slightly by considering the turn on which Alice activates v. Suppose that Alice activates v in response to an action taken at w ∈ S. Alice will then take another action in N ⁺[v]. So Alice has responded with two actions in N ⁺[v] due to the action taken at w. Thus, $\left \vert S\right \vert \leq 2k + 1$. So we have that before v is colored, the number of distinctly colored elements to which v may be adjacent or incident is at most

$$\displaystyle{\varDelta +\left \vert N^{+}(v)\right \vert + \left \vert S\right \vert \leq \varDelta +3k + 1.}$$

Now suppose that e = xy is an uncolored edge with x < y in L. At any point in the game e can be incident to at most two colored vertices before e is activated. Additionally, at most Δ − 1 edges in P(e) ∪ B(e) can be colored before e becomes active. Similar to the argument above for vertices, let S ⊆ S(e) be the set of children of e that are activated before e is colored. Note that each time an edge in S is activated or colored, Alice will take action at an edge in H[e]. Thus, $S \leq 2\left \vert H[e]\right \vert \leq 2k$. Thus, before e is colored, the number of distinctly colored elements to which e may be incident is at most

$$\displaystyle\begin{array}{rcl} \varDelta -1 + \left \vert \{\,x,y\,\}\right \vert + \left \vert H(e)\right \vert + \left \vert S\right \vert & \leq & \varDelta -1 + 2 + (k - 1) + 2k {}\\ & =& \varDelta +3k. {}\\ \end{array}$$

We note that there are multiple avenues for creating “defect” versions of this game, depending on whether you allow for adjacent vertices to receive the same color (or not), and similarly for edges. Each of these variations can lead to different results for different classes of graphs.

7 Conclusions and Problems to Consider

The area of competitive graph coloring is rich with open problems. We have presented the standard vertex coloring game along with variations in the definition of a legal color. Additionally, we have presented variations in which the players color edges. Each of these variations still have problems to consider, but we have also given a framework which invites researchers to consider their own variations of a legal color.

Questions in competitive graph coloring are ideally suited to undergraduate research. Not only are there many interesting open questions, but students can begin exploring these questions with very little background. For many questions, students need only to be introduced to basic definitions in graph theory, the rules of the game and the relevant parameters, along with strategies for Alice and Bob. Experimentation with game variations and specific classes of graphs can lead students to ask their own questions. We would note that the work in each of papers in [17,18,19,20] was done with undergraduates and each paper has undergraduates listed as coauthors.

We summarize some open questions stemming from the games presented above, but we also expect this paper to provide a model for asking and answering additional questions in the area of competitive graph coloring.

Regarding the standard vertex coloring game, a number of problems still remain open.

Research Project 1.

Find criteria which differentiates between forests with game chromatic numbers 3 and 4.

Research Project 2.

Does there exists a forest F of odd order with Δ(F) = 3 where χ _g(F) = 4?

The game chromatic number has also been studied on other common classes of graphs, and there are many open questions coming from this.

Research Project 3.

For planar graphs G, the best known upper [32] and lower [28] bounds show that 8 ≤ χ _g(G) ≤ 17. For outerplanar graphs G, the current bounds are 6 ≤ χ _g(G) ≤ 7 [25]. Progress for either class would be of interest.

Research Project 4.

Another interesting question, asked by Zhu [30], is whether χ _g(G) = k implies that Alice has a winning strategy for the (k + 1)-coloring game on G.

Regarding the d-relaxed chromatic number^d χ _g(G), Theorem 7 has been shown to be sharp, and it was shown in [26] that if d ≥ 2 then for any tree T,^d χ _g(T) ≤ 2. However, similar to the classification problem discussed in Section 2, we do not know criteria to distinguish those trees T for which¹ χ _g(T) = 3 and those for which¹ χ _g(T) = 2.

Research Project 5.

Find criteria to distinguish trees where¹ χ _g(T) = 3 from those where¹ χ _g(T) = 2.

Chou et al. [6] also showed that, where G is an outerplanar graph and d ≥ 1,^d χ _g(G) ≤ 6.

Research Project 6.

Improve this bound, or provide an example which shows that it is sharp. This has not been done for any d.

Clique-relaxed game chromatic number has not been as widely studied. In particular, there are no current results for planar graphs. For outerplanar graphs G, Theorems 9 and 10 show that 3 ≤ χ _g ⁽²⁾(G) ≤ 4.

Research Project 7.

Determine bounds for the clique-relaxed game chromatic number for planar graphs. Once a sharp upper bound is known, the question of classifying graphs with particular clique-relaxed game chromatic number arises.

The edge coloring game also has many open questions. For forests F with maximum degree Δ, it has been shown in [1, 22] that χ _g′(F) ≤ Δ + 1 except when Δ = 4, where the best result shows χ _g′(F) ≤ 6. Lam et al. [29], who showed that χ _g′(F) ≤ Δ + 2 for forests, also asked if there could be a constant c such that χ _g′(G) ≤ Δ + c for all graphs.

Research Project 8.

Is there a constant c such that χ _g′(G) ≤ Δ + c for all graphs? A similar question can be asked of the d-relaxed edge coloring game, or for the total coloring game.

Finally, in [12] it is shown that for every $m \in \mathbb{N}$, there exists a graph G such that m ≤ χ _g(G) <¹ χ _g(G), which seems counterintuitive.

Research Project 9.

Is it true that for every nonnegative integer d, there exists a graph G such that^d χ _g(G) <^d+1 χ _g(G)? This question was first proposed by Kierstead and would seem an interesting one to settle.