Keywords

1 Bootstrap Percolation Models

Bootstrap percolation models (also known in the literature as k-core percolation [1], neuropercolation [2, 3], jamming percolation [4], quorum percolation [5] or diffusion percolation [6]) are Cellular Automata, with a deterministic discrete-time dynamics. Often, however, probability is brought in, as one considers probabilistic initial conditions. Although bootstrap percolation models are not PCA in the proper sense, as CA combined with probability, they are close relations of PCA.

Bootstrap percolation models describe the growth of sets of occupied vertices (or sites) of a graph. At all vertices of a graph (whether finite or infinite), one places at an initial time with probability p a particle. The bootstrap percolation rule then requires each occupied vertex to stay occupied, and each empty vertex to become occupied whenever sufficiently many vertices in its neighbourhood are occupied. The choice of graph, the choice of “sufficiently many” and the choice of the neighbourhood determine the model. One is interested whether after sufficiently many iterations each vertex gets occupied or not, and how this depends on the value of p. In particular, one wants to know what happens for infinite graphs, or for sequences of increasing graphs. One also can consider more general rules, where an empty site gets occupied once a particular configuration, or one out of a particular set of configurations, in some neighbourhood is occupied. For example, the “modified” bootstrap percolation model requires that one neighbouring site along each lattice axis is occupied. The bootstrap percolation models have some obvious monotonicity properties, in particular the number of occupied vertices is growing in time, and there is stochastic monotonicity, in the sense that the occupation number of each vertex of one evolving configuration is always larger or equal than that of a second evolving configuration once this holds at the beginning.

Bootstrap percolation models have been applied in a variety of contexts, e.g. for the study of metastability [7] and for magnetic models [8], for the glass transition [4] and for capillary fluid flow [9], for study of neural networks [10, 11], rigidity [12], contagion [13], and they have also been studied for purely mathematical interest, including recreational mathematics [14,15,16,17].

Most interest is in the so-called critical models, in which the growth rule is such that a finite set of occupied sites (\(=\) vertices) cannot fill the infinite lattice, and at the same time all finite empty sets in an infinite occupied environment will be filled.

The simplest such models on (hyper-)cubic lattices are those where one considers the nearest neighbours of each site and requires half of them to be occupied to get occupied at the next step, or where one requires at least one occupied site among the neighbours along every axis (modified bootstrap percolation). In these models the most detailed results are known. In particular, it is known that on infinite lattices the percolation threshold is trivial (\(p_c=0\)), that is, for every positive p every vertex of the infinite lattice will in the end be occupied with probability one [18, 19].

Moreover, on finite volumes the percolation threshold (now defined as the smallest value of p above which the volume will be occupied with probability above one half) scales as a \(d-1\)-repeated logarithm of the size of the volume (i.e. \(p_c = O(\frac{1}{\ln V})\) in \(d=2\), \(p_c =O(\frac{1}{\ln \ln V})\) in \(d=3\), etc.). Such behaviour, with different constants for lower and upper bounds, was proven in [7, 20, 21], and with coinciding lower and upper bounds in [22,23,24,25]. These last types of results (i.e. \( p_c = C \frac{1}{\ln V} + o(\frac{1}{\ln V})\) in \(d=2\), or \( p_c = C \frac{1}{\ln \ln V}+o(\frac{1}{\ln \ln V})\) in \(d=3\), and similarly in general d with \(d-1\) times repeated logarithms for higher dimensions) have been called “sharp thresholds”.

As for lower-order corrections, (estimates on those are also called “sharper” thresholds in the literature), in \(d=2\) the \(o(\frac{1}{\ln V})\) terms were shown to be of order \(O( \frac{1}{(\ln V)^{\frac{3}{2}}})\), see [26]. This strengthened earlier results of [27, 28]. For higher-dimensional results about “sharper” thresholds, see [29]. These sharper thresholds describe the systematic error which computational physicists in the past have run into, as is discussed e.g. in [30, 31].

However, another notion of sharp thresholds, based on a sharp-threshold theorem of Friedgut and Kalai, was presented in [32]. This \(\varepsilon \)-window—the window within which with large probability one will find the answer—provides an estimate for the statistical error, which is of order \(O( \frac{\ln \ln V}{\ln ^2 V})\) and hence much smaller than the systematic error. The statistical error being small with respect to the systematic error has been a source for various erroneous numerical estimates of percolation thresholds and their numerical precision in the past, as errors tended to be substantially underestimated.

In this contribution, I plan to describe to what extent the behaviour of bootstrap models is modified once the model becomes anisotropic, and in particular “unbalanced” (compare [33]). In particular, I will concentrate on the \((1,2)-\)model, introduced in [34], in which one considers an anisotropic neighbourhood consisting of the nearest neighbours along one axis, and the nearest and next-nearest neighbours along the other axis. The distinction between balanced and unbalanced rules is that in balanced cases the growth occurs with the same speed in different directions, whereas in unbalanced cases there are easy and hard directions for growth. It appears to be the case that in \(d=2\) a wide class of growth models is either balanced or unbalanced and that both classes display a characteristic scaling behaviour [35].

In higher dimensions, it turns out that the leading behaviour is ruled by the two “easiest” growth directions [36].

2 A Tractable Example: The (1, 2)-Model

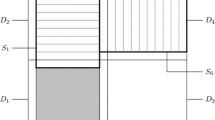
In the (1, 2)-model, the neighbourhood of each site in \(\mathbb {Z}^2\) consists of 2 sites in the east and west directions, and one site in the north and south directions. In picture form:

$$\begin{aligned} \begin{array}{ccccccc} \, &{} \, &{} \, &{} \, &{} \bullet &{} \, &{} \, \\ \mathcal {N} &{} = &{} \bullet &{} \bullet &{} 0 &{} \bullet &{} \bullet \\ \, &{} \, &{} \, &{} \, &{} \bullet &{} \, &{} \, \end{array} \end{aligned}$$

At every step, each empty site which has 3 of its neighbours (out of the 6 possible ones) occupied, becomes itself occupied, and every occupied site stays occupied forever. As an initial condition, we take a percolation configuration with initial occupation probability p. This model, which is critical, was introduced by Gravner and Griffeath [34], and they looked at its finite-size behaviour. The model is similar to, but somewhat easier to analyse than, the north-east-south model of Duarte [37], for which related but somewhat weaker results are known [38, 39].

The fact that \(p_c=0\) in the infinite lattice follows from an argument due to Schonmann, first given for Duarte’s model [38, 40].

Indeed, let a \(2 \times n\) rectangle be occupied, then the probability that this rectangle grows both eastwards and westwards is larger than the probability that at least 1 site in the columns east and west of this rectangle is occupied, which is \([1 - (1-p)^n]^2\). The probability that this occurs in each column in a rectangle of size \(l \times n\) we bound from below by \([1 - (1-p)^n]^l\). Choose \(n= \frac{C}{p} \ln \frac{1}{p}\), then this probability can be bounded by \((1-p^C)^l\); once \(C \ge 2\) and \(l \ge \frac{1}{p^C}\), such a rectangle keeps growing in both directions with large probability; the fact that such an occupied and growing rectangle can occur with positive probability implies that somewhere in an infinite lattice such a nucleation centre will occur, and it will then fill up the whole lattice.

The question after this is how big a square volume should be for such a nucleation centre to occur with large probability (e.g. probability a half). The argument given above predicts that a \(2 \times n\) rectangle occurs at some fixed location with probability at least \(p^{2n} = e^{-O(\frac{1}{p} \ln ^2 \frac{1}{p})}\) and that therefore the size of the square volume \(V= N \times N\) should be the inverse of that probability, that is, if N (or \(V) \ge e^{+O(\frac{1}{p} \ln ^2 \frac{1}{p})}\), it can be filled with large probability. Inverting the argument implies an upper bound for the rate at which the percolation threshold decreases as a function of V, of the form

$$\begin{aligned} p_c \le C_1 \frac{\ln ^2 \ln V}{\ln V}. \end{aligned}$$
(5.1)

An argument providing a lower bound for \(p_c\) of the same order, that is,

$$\begin{aligned} p_c \ge C_2 \frac{\ln ^2 \ln V}{\ln V} \end{aligned}$$
(5.2)

was developed in [41], using and correcting the analysis of [34].

In fact, one can improve the on above strategy, as follows (see [42], following [43]). One starts with a \(2 \times \frac{2}{p} \ln \ln \frac{1}{p}\) rectangle, which has all its even (or odd) sites occupied, then at the next step, the whole rectangle is filled. After that, one grows with vertical steps of size 1 and horizontal steps of increasing size, through a sequence of rectangles \(R_n\), which in the y-direction have size n and in the x-direction have size \( \frac{1}{3p} \exp 3np \). This goes on until we reach the size \(n= \frac{1}{3p} \ln \frac{1}{p}\). With this choice, the probability for a rectangle \(R_n\) to grow a step in the x-direction equals the probability to grow a step in the y-direction.

The probability of growing a step in the vertical direction from a rectangle \(R_n\) is approximately \(8p^2 x_n\) (one needs two occupied sites close enough, the factor 8 here is of combinatorial origin) which equals \(\frac{8p}{3} \exp 3np\). The probability of growing in the horizontal direction, over a distance \(x_{n+1} -x_n\) equals a constant term \(\frac{1}{e}\), for every n.

One thus needs to compute the product from \(n_0= \frac{2}{p} \ln \ln \frac{1}{p}\) to \(n_f= \frac{1}{3p} \ln \frac{1}{p}\) over these probabilities. The result is

$$\begin{aligned} \begin{aligned} \prod _{n=n_0}^{n=n_f} \frac{8p}{3e} \exp (3np)&= {\frac{8p}{3e}}^{(n_f- n_0)} \exp \biggl ( 3p \sum \limits _{n=n_0}^{n=n_f} n\biggr ) \\&= {\frac{8p}{3e}}^{ (n_f- n_0)} \exp \biggl ( 3p \biggl [\frac{1}{2} n_f(n_f-1) - \frac{1}{2}n_0(n_0 -1) \biggr ] \biggr ) \\&= \exp \biggl (-\frac{1}{6p} \ln ^2 \frac{1}{p} + \frac{1}{3} \ln \frac{8}{3p} \ln \frac{1}{p} + o\biggl (\frac{1}{p}\ln \frac{1}{p}\biggr ) \biggr ) . \end{aligned} \end{aligned}$$
(5.3)

This is our main result, for the detailed proof that this strategy indeed provides the best estimate, see [42].

3 Inversion

If the probability for a nucleation centre to occur at a fixed location is given by an expression of the form \(P= \exp (-\frac{C}{p})\), the necessary volume size to see such a nucleation centre with substantial probability in that volume, that is the “critical volume”, will be \(V_c = \exp (+ \frac{C}{p})\), which is easily inverted, resulting in an expression of the form \(p_c = C \frac{1}{\ln V}\) for the critical percolation threshold as a function of the volume.

However, if there are logarithmic corrections and subdominant terms as above, that is

$$\begin{aligned} V_c = \exp \biggl ( \frac{C}{p} \ln ^2 \frac{1}{p} + \frac{C'}{p} \ln \frac{1}{p} \biggr ), \end{aligned}$$
(5.4)

to invert such expressions we need to perform some extra steps. We observe the following:

$$\begin{aligned} p_c = \frac{1}{\ln V} \biggl (C \ln ^2\frac{1}{p_c} +C' \ln \frac{1}{p_c}\biggr ). \end{aligned}$$
(5.5)

We also notice that in the limit of V large and hence \(p_c\) small it holds that

$$\begin{aligned} \frac{1}{p_c} \le \ln V \le \frac{1}{p_c^{1+ \varepsilon }} \end{aligned}$$
(5.6)

and (by taking logarithms)

$$\begin{aligned} \ln \frac{1}{p_c} \le \ln \ln V \le (1 + \varepsilon )\ln \frac{1}{p_c} \end{aligned}$$
(5.7)

and

$$\begin{aligned} \ln \ln \frac{1}{p_c} \le \ln \ln \ln V \le \ln \ln \frac{1}{p_c} + \varepsilon . \end{aligned}$$
(5.8)

Thus asymptotically, by substitution plus using the above estimates

$$\begin{aligned} p_c&= \frac{1}{\ln V} \biggl (C \ln ^2\frac{1}{p_c} +C' \ln \frac{1}{p_c} \biggr )\nonumber \\&= \frac{1}{\ln V} \biggl (C (\ln \ln V - 2 \ln \ln \ln V - \ln C +O(\varepsilon ))^2 +C' \ln \ln V + O(\varepsilon ) \biggr )\nonumber \\&= \frac{1}{\ln V} \biggl (C (\ln ^2 \ln V - 4 \ln \ln \ln V \ln \ln V- 2\ln C \ln \ln V) + +C' \ln \ln V + O(\ln ^2 \ln \ln V) \biggr ). \end{aligned}$$
(5.9)

Hence knowing the second term in the critical volume provides a third term in the critical probability, and we also notice that the second term in the critical probability does not depend on the constant \(C'\) of this second critical-volume term.

A related argument was used in [44] to estimate the \(\varepsilon \)-window. This analysis extended the analysis of [32], applying the sharp-threshold theorem of Friedgut and Kalai, and the \(\varepsilon \)-window turns out to have width \(O(\frac{\ln ^3 \ln V}{\ln ^2 V})\).

Numerically, that is for computational physicists, e.g., these results are totally discouraging. Whereas in standard bootstrap percolation to obtain a 99% accuracy in \(p_c\) the order of magnitude of a square already needs to be of order \(O(10^{3000})\) [27], in the (1, 2)-model one needs to go even higher, namely to a doubly exponential size of order \(O(10^{10^{1400}})\). These findings illustrate the point made in [45] that Cellular Automata, despite being discrete in state, space and time, may still be ill-suited for computer simulations.

4 Generalisations: Related Models, Higher Dimensions and Other Graphs

In ordinary and modified bootstrap percolation, we have quite precise results. There is a variety of related models with similar behaviour, e.g. [46,47,48,49]. In particular, it is remarkable that the model of [47] is anisotropic, but nonetheless scales in the same way as ordinary bootstrap percolation; in the terms of [33], it is “balanced”. A much wider class of models was recently considered in [50], in which some general order-of-magnitude results were derived for critical models. More recently [35], it was shown that this class consists of two subclasses, either the balanced ones, such as ordinary bootstrap percolation, which display similar asymptotic behaviour, or the unbalanced ones, in which logarithmic corrections of the type displayed in the (1, 2)-model occur. The essential distinction is that balanced models grow at the same rate in two different directions, whereas unbalanced models have an easy and a hard growth direction.

There exist also some results on bootstrap percolation in higher dimensions. In the anisotropic case, for the time being we only know order-of-magnitude results for (a, b, c)-models, in which neighbourhoods are considered which consist of neighbours at distances a, b and c (\(a \le b\le c\)) along the different axes [36] (of which again half the sites need to be occupied to occupy an empty site). The result is that the scaling becomes doubly exponential, or, for the inverse quantities, doubly logarithmic, similarly to the isotropic models [20, 21], but with the behaviour controlled by the two-dimensional (a, b)-model. One bound is based on a variation of Schonmann’s [19] induction-on-dimension argument, the other direction follows a similar strategy as [20]. To establish any form of a sharp threshold, however, is open for the time being.

In two dimensions, the (1, b)-models can be analysed along similar lines as the (1, 2)-model, which results in the same asymptotics, but with the (sharp and computable) constant \(C=\frac{(b-1)^2}{2(b+1)}\), rather than \(C=\frac{1}{6}\), as the leading term. For the sharp constant in the Duarte model, see [35].

A quite different family of results, in which there is a transition at a finite threshold p, occurs for bootstrap percolation models on either trees [51,52,53,54], random graphs [55, 56], or hyperbolic lattices [57]. Such transitions have a “hybrid” (mixed first-second order) character, in the sense that on the one hand, one finds that at the threshold the infinite cluster has a minimum density (so it jumps from zero, just as one expects at a first-order phase transition), while at the same time there are divergent correlation lengths and non-trivial critical exponents, which are characteristic for second-order (critical) phase transitions. Such hybrid “random first-order” transitions have been proposed to be characteristic for glass transitions. See, e.g. [58]. On regular lattices, models with this kind of behaviour cannot be constructed via the type of bootstrap percolation rules discussed above, but more complicated Cellular Automaton growth rules with this type of behaviour have been studied in [59, 60].