Basic Ideas to Approach Metastability in Probabilistic Cellular Automata

Abstract

Cellular Automata are discrete-time dynamical systems on a spatially extended discrete space, which provide paradigmatic examples of nonlinear phenomena. Their stochastic generalizations, i.e., Probabilistic Cellular Automata, are discrete-time Markov chains on lattice with finite single-cell states whose distinguishing feature is the parallel character of the updating rule. We review the some of the results obtained about the metastable behavior of Probabilistic Cellular Automata, and we try to point out difficulties and peculiarities with respect to standard Statistical Mechanics Lattice models.

1 Introduction

Cellular Automata are discrete-time dynamical systems on a spatially extended discrete space. They are well known for being easy to implement and for exhibiting a rich and complex nonlinear behavior as emphasized for instance in [22] for Cellular Automata on one-dimensional lattice. For the general theory of deterministic Cellular Automata, we refer to the recent paper [12] and references therein

Probabilistic Cellular Automata (PCA) are Cellular Automata straightforward generalization where the updating rule is stochastic. They are used as models in a wide range of applications. From a theoretic perspective, the main challenges concern the nonergodicity of these dynamics for an infinite collection of interacting cells.

Strong relations exist between PCA and the general equilibrium statistical mechanics framework [14, 21]. Important issues are related to the interplay between disordered global states and ordered phases (emergence of organized global states, phase transition) [19]. Although PCA initial interest arose in the framework of Statistical Physics, in the recent literature many different applications of PCA have been proposed. In particular, it is notable to remark that a natural context in which the PCA main ideas are of interest is that of evolutionary games [20].

In this paper, we shall consider a particular class of PCA, called reversible PCA, which are reversible with respect to a Gibbs-like measure defined via a translation invariant multi-body potential. In this framework, we shall pose the problem of metastability and show its peculiarities in the PCA world.

Metastable states are ubiquitous in nature and are characterized by the following phenomenological properties: (i) The system exhibits a single phase different from the equilibrium predicted by thermodynamics. The system obeys the usual laws of thermodynamics if small variations of the thermodynamical parameters (pressure, temperature, $\ldots$) are considered. (ii) If the system is isolated, the equilibrium state is reached after a very large random time; the lifetime of the metastable state is practically infinite. The exit from the metastable state can be made easier by forcing the appearance large fluctuations of the stable state (droplets of liquid inside the super-cooled vapor, $\ldots$). (iii) The exit from the metastable phase is irreversible.

The problem of the rigorous mathematical description of metastable states has long history which started in the 70s, blew up in the 90s, and is still an important topic of mathematical literature. Different theories have been proposed and developed, and the pertaining literature is huge. We refer the interested reader to the monograph [18]. In this paper, we shall focus on the study of metastability in the framework of PCA.

In [1, 5, 8, 9, 16], the metastable behavior of a certain class of reversible PCA has been analyzed. In this framework, it has been pointed out the remarkable interest of a particular reversible PCA (see Sect. 3.3) characterized by the fact that the updating rule of a cell depends on the status of the five cells forming a cross centered at the cell itself. In this model, the future state of the spin at a given cell depends also on the present value of such a spin. This effect will be called self-interaction, and its weight in the updating rule will be called self-interaction intensity.

The paper is organized as follows. In Sect. 3.2, we introduce reversible Probabilistic Cellular Automata and discuss some general properties. In Sect. 3.3, we introduce the model that will be studied in this paper, namely the nearest neighbor and the cross PCA, and discuss its Hamiltonian. In Sect. 3.4, we pose the problem of metastability in the framework of Probabilistic Cellular Automata and describe the main ingredients that are necessary for a full description of this phenomenon. In Sect. 3.5, we finally state our results.

2 Reversible Probabilistic Cellular Automata

We shall first briefly recall the definition of Probabilistic Cellular Automata and then introduce the so-called Reversible Probabilistic Cellular Automata.

Let $\varLambda \subset {\mathbb {Z}}^d$ be a finite cube with periodic boundary conditions. Associate with each site $i\in \varLambda$ (also called cell) the state variable $\sigma _i\in X_0$, where $X_0$ is a finite single-site space and denote by $X:=X_0^\varLambda$ the state space. Any $\sigma \in X$ is called a state or configuration of the system.

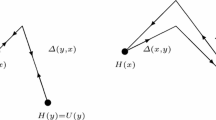
We introduce the shift $\varTheta _i$ on the torus, for any $i\in \varLambda$, defined as the map $\varTheta _i:X\rightarrow X$ shifting a configuration in $X$ so that the site i is mapped onto the origin 0, more precisely such that (see Fig. 3.1)

$$\begin{aligned} (\varTheta _i\sigma )_j=\sigma _{i+j}. \end{aligned}$$

(3.1)

The configuration $\sigma$ at site j shifted by i is equal to the configuration at site $i+j$. For example, (see Fig. 3.1) set $j=0$, then the value of the spin at the origin 0 will be mapped onto site i.

Fig. 3.1

Schematic representation of the action of the shift $\varTheta _{i}$ defined in (3.1)

We consider a probability distribution $f_{\sigma }:X_0\rightarrow [0,1]$ depending on the state $\sigma$ restricted to $I\subset \varLambda$. A Probabilistic Cellular Automata are the Markov chain $\sigma (0),\sigma (1),\dots ,\sigma (t)$ on $X$ with transition matrix

$$\begin{aligned} p(\sigma ,\eta )=\prod _{i\in \varLambda }f_{\varTheta _{i}\sigma } (\eta _i) \end{aligned}$$

(3.2)

for $\sigma ,\eta \in X$. We remark that f depends on $\varTheta _{i}\sigma$ only via the neighborhood $i+I$. Note that the character of the evolution is local and parallel: The probability that the spin at the site i assumes at time $t+1$ the value $s\in X_0$ depends on the value of the state variables at time t (parallel evolution) associated only with the sites in $i+I$ (locality).

A class of reversible PCA can be obtained by choosing $X=\{-1,+1\}^\varLambda$, and probability distribution

$$\begin{aligned} f_{\sigma }(s)=\frac{1}{2}\Big \{ 1+s\tanh \Big [\beta \Big (\sum _{j\in \varLambda }k(j)\sigma _j+h\Big )\Big ]\Big \} \end{aligned}$$

(3.3)

for all $s\in \{-1,+1\}$ where $T\equiv 1/\beta >0$ and $h\in \mathbb {R}$ are called temperature and magnetic field. The function $k:{\mathbb {Z}}^2\rightarrow {\mathbb {R}}$ is such that its support¹ is a subset of $\varLambda$ and $k(j)=k(j')$ whenever $j,j'\in \varLambda$ are symmetric with respect to the origin. With the notation introduced above, the set I is the support of the function k. We shall denote by $p_{\beta ,h}$ the corresponding transition matrix defined by (3.2).

Recall that $\varLambda$ is a finite torus, namely periodic boundary conditions are considered throughout this paper. It is not difficult to prove [10, 13] that the above-specified PCA dynamics is reversible with respect to the finite-volume Gibbs-like measure

$$\begin{aligned} \mu _{\beta ,h}(\sigma ) = \frac{1}{Z_{\beta ,h}} \,e^{-\beta G_{\beta ,h}(\sigma )} \end{aligned}$$

(3.4)

with Hamiltonian

$$\begin{aligned} G_{\beta ,h}(\sigma ) = -h\sum _{i\in \varLambda }\sigma _i -\frac{1}{\beta }\sum _{i\in \varLambda } \log \cosh \Big [\beta \Big (\sum _{j\in \varLambda }k(j-i)\sigma _j+h\Big )\Big ] \end{aligned}$$

(3.5)

and partition function $Z_{\beta ,h}= \sum _{\eta \in X} \exp \{-\beta G_{\beta ,h}(\eta )\}$. In other words, in this case the detailed balance equation

$$\begin{aligned} p_{\beta ,h}(\sigma ,\eta ) e^{-\beta G_{\beta ,h}(\sigma )} =e^{-\beta G_{\beta ,h}(\eta )} p_{\beta ,h}(\eta ,\sigma ) \end{aligned}$$

(3.6)

is satisfied thus the probability measure $\mu _{\beta ,h}$ is stationary for the PCA.

Note that different reversible PCA models can be specified by choosing different functions k. In particular, the support I of such a function can be varied. In the next section, we shall introduce two common choices, the nearest neighbor PCA [5] obtained by choosing the support of k as the set of the four sites neighboring the origin and the cross PCA [9] obtained by choosing the support of k as the set made of the origin and its four neighboring sites (see Fig. 3.2).

Fig. 3.2

Schematic representation of the nearest neighbor (left) and cross (right) models

The stationary measure $\mu _{\beta ,h}$ introduced above looks like a finite-volume Gibbs measure with Hamiltonian $G_{\beta ,h}(\sigma )$ (see (3.5)). It is worth noting that $G_{\beta ,h}$ cannot be thought as a proper statistical mechanics Hamiltonian since it depends on the temperature $1/\beta$. On the other hand, the low-temperature behavior of the stationary measure of the PCA can be guessed by looking at the energy function

$$\begin{aligned} H_h(\sigma ) = \lim _{\beta \rightarrow \infty }G_{\beta ,h}(\sigma ) = -h\sum _{i\in \varLambda }\sigma _i -\sum _{i\in \varLambda } \Big |\sum _{j\in \varLambda }k(j-i)\sigma _j+h\Big | \end{aligned}$$

(3.7)

The absolute minima of the function $H_h$ are called ground states of the stationary measure for the reversible PCA.

3 The Tuned Cross PCA

We consider, now, a particular example of reversible PCA. More precisely, we set $k(j)=0$ if j is neither the origin nor one of its nearest neighbors, i.e., it is not in the five-site cross centered at the origin, $k(0)=\kappa \in [0,1]$, and $k(j)=1$ if j is one of the four nearest neighbors of the origin; we shall denote by J the set of nearest neighbors of the origin. With such a choice, we have that

$$\begin{aligned} f_{\sigma }(s)=\frac{1}{2}\Big \{ 1+s\tanh \Big [\beta \Big ( \kappa \sigma _0+\sum _{j\in J}\sigma _j+h \Big )\Big ]\Big \} = \frac{1}{1+e^{-2\beta s (\kappa \sigma _0+\sum _{j\in J}\sigma _j+h)}} \end{aligned}$$

(3.8)

We shall call this model the tuned cross PCA. The self-interaction intensity $\kappa$ tunes between the nearest neighbor $(\kappa =0)$ and the cross $(\kappa =1)$ PCA.

Note that for this model, the Hamiltonian $G_{\beta ,h}$ defining the stationary Gibbs-like measure is given by

$$\begin{aligned} G_{\beta ,h}(\sigma ) = -h\sum _{i\in \varLambda }\sigma _i -\frac{1}{\beta ,h}\sum _{i\in \varLambda } \log \cosh \Big [\beta \Big ( \kappa \sigma _i+\sum _{j\in i+J}\sigma _j +h \Big )\Big ] \end{aligned}$$

(3.9)

while the corresponding energy function, see (3.7), is

$$\begin{aligned} H_h(\sigma ) = -h\sum _{i\in \varLambda }\sigma _i -\sum _{i\in \varLambda } \Big |\kappa \sigma _i+\sum _{j\in i+J}\sigma _j+h\Big | \end{aligned}$$

(3.10)

In Statistical Mechanics Lattice systems, the energy of a configuration is usually written in terms of coupling constants. We could write the expansion of the energy $H_h$ in (3.10), but, for the sake of simplicity, we consider the nearest neighbor PCA [5], namely we set $\kappa =0$. We get

$$\begin{aligned} \begin{array}{ll} {\displaystyle { H_h(\sigma )=}} &{} {\displaystyle {-J_{.} \sum _{x\in \varLambda }\sigma (x) -J_{_{\langle \langle \rangle \rangle }} \sum _{\langle \langle x y\rangle \rangle }\sigma (x)\sigma (y) -J_{_{\langle \langle \langle \rangle \rangle \rangle }} \sum _{\langle \langle \langle x y\rangle \rangle \rangle }\sigma (x)\sigma (y) }}\\ &{} {\displaystyle { \!\!\! -J_{_{\triangle }} \sum _{\triangle _{xyz}}\sigma (x)\sigma (y)\sigma (z) -J_{_{\diamondsuit }} \sum _{\diamondsuit _{xywz}}\sigma (x)\sigma (y)\sigma (w)\sigma (z) }} \\ \end{array} \end{aligned}$$

where the meaning of the symbols $\cdot$, $\langle \langle \rangle \rangle$, $\langle \langle \langle \rangle \rangle \rangle$ $\triangle$, and $\diamondsuit$ is illustrated in Fig. 3.3 and the corresponding coupling constants are

$$\begin{aligned} J_{.} = \frac{5}{2} h, \, J_{_{\langle \langle \rangle \rangle }}= 1-\frac{1}{4}h,\, J_{_{\langle \langle \langle \rangle \rangle \rangle }} =\frac{1}{2}-\frac{1}{8}h,\, J_{_{\triangle }} = -\frac{1}{8}h,\, \text { and } J_{_{\diamondsuit }} = -\frac{1}{2}+\frac{3}{8} h \end{aligned}$$

It is interesting to note that the coupling constant $J_\diamondsuit$ is negative (antiferromagnetic coupling), and this will give a physical meaning to the appearance of checkerboard configurations in the study of metastability for the nearest neighbor PCA.

Fig. 3.3

Schematic representation of the coupling constants: from the left to the right and from the top to the bottom the couplings $J_{.}$, $J_{\langle \langle \langle \rangle \rangle \rangle }$, $J_{\langle \langle \rangle \rangle }$, $J_{\triangle }$, and $J_{\diamondsuit }$ are depicted

The coupling constants can be computed by using [4, Eqs. (6) and (7)] (see also [11, Eqs. (3.1) and (3.2)] and [7]). More precisely, given $f:\{-1,+1\}^V\rightarrow {\mathbb {R}}$, with $V\subset {\mathbb {Z}}^2$ finite, we have that for any $\sigma \in \{-1,+1\}^V$

$$\begin{aligned} f(\sigma ) = \sum _{I\subset V} C_I\prod _{i\in I}\sigma _i \end{aligned}$$

(3.11)

with the coefficients $C_I$’s given by

$$\begin{aligned} C_I = \frac{1}{2^{|V|}} \sum _{\sigma \in \{-1,+1\}^V}f(\sigma )\prod _{i\in I}\sigma _i \end{aligned}$$

(3.12)

We refer to [6] for the details. We note that in that paper, the couplings have been computed for a more general model than the one discussed here.

Now, we jump back to the tuned cross PCA and we discuss the structure of the ground states, that is to say, we study the global minima of the energy function $H_h$ given in (3.10). Such a function can be rewritten as

$$\begin{aligned} H_h(\sigma ) = \sum _{i\in \varLambda } H_{h,i}(\sigma ) \end{aligned}$$

with

$$\begin{aligned} H_{h,i}(\sigma ) = -\Big [\frac{1}{5}h\Big (\sigma _i+\sum _{j\in i+J}\sigma _j\Big ) +\Big |\kappa \sigma _i+\sum _{j\in i+J}\sigma _j+h\Big | \Big ] \end{aligned}$$

(3.13)

We also note that

$$\begin{aligned} H_h(\sigma )=H_{-h}(-\sigma ) \end{aligned}$$

(3.14)

for any $h\in {\mathbb {R}}$ and $\sigma \in X$, where $-\sigma$ denotes the configuration obtained by flipping the sign of all the spins of $\sigma$. By (3.14), we can bound our discussion to the case $h\ge 0$ and deduce a posteriori the structure of the ground states for $h<0$.

The natural candidates to be ground states are the following configurations: $\mathbf{u }\in X$ such that $\mathbf{u }(i)=+1$ for all $i\in \varLambda$, $\mathbf {d}\in X$ such that $\mathbf {d}(i)=+1$ for all $i\in \varLambda$, $\mathbf {c}_\text {e}$, and $\mathbf {c}_\text {o}$ with $\mathbf {c}_\text {e}$ the checkerboard configuration with pluses on the even sub-lattice of $\varLambda$ and minuses on its complement, while $\mathbf {c}_\text {o}$ is the corresponding spin-flipped configuration. Indeed, we can prove that the structure of the zero-temperature phase diagram is that depicted in Fig. 3.4.

Fig. 3.4

Zero-temperature phase diagram of the stationary measure of the tuned cross PCA. On the thick lines, the ground states of the adjacent regions coexist. At the origin, the listed four ground states coexist

Case $h>0$ and $k_0\ge 0$. The minimum of $H_{h,i}$ is attained at the cross configuration having all the spins equal to plus one. Hence, the unique absolute minimum of $H_h$ is the state $\mathbf{u }$.

Case $h=0$ and $k_0>0$. The minimum of

$$\begin{aligned} H_{0,i}(\sigma ) =-\Big |\kappa \sigma _i+\sum _{j\in i+J}\sigma _j\Big | \end{aligned}$$

is attained at the cross configuration having all the spins equal to plus one or all equal to minus one. Hence, the set of ground states is made of the two configurations $\mathbf{u }$ and $\mathbf {d}$.

Case $h=0$ and $k_0=0$. The minimum of $H_{0,i}$ is attained at the cross configuration having all the spins equal to plus one or all equal to minus one on the neighbors of the center and with the spin at the center which can be, in any case, either plus or minus. Hence, the set of ground states is made of the four configurations $\mathbf{u }$, $\mathbf {d}$, $\mathbf {c}_\text {e}$, and $\mathbf {c}_\text {o}$.

Case $h<0$. The set of ground states can be easily discussed as for $h>0$ by using the property (3.14).

4 Main Ingredients for Metastability

At $\kappa >0$, the zero-temperature phase diagram in Fig. 3.4 is very similar to that of the standard Ising model, which is the prototype for the description of phase transitions in Statistical Mechanics. So we expect that even in the case of the tuned cross PCA, the equilibrium behavior could be described as follows: (i) At positive magnetic field h, there exist a unique phase with positive magnetization²; (ii) the same it is true at negative h but with negative magnetization; (iii) at $h=0$, the equilibrium behavior is more complicated: There exists a critical value of the temperature such that at temperatures larger than such a value there exists a unique phase with zero magnetization, while at temperatures smaller than the critical one there exists two equilibrium measures with opposite not zero magnetization, called the residual magnetization.

This scenario has proven to be true in the case of the two-dimensional standard Ising model, but in the context of the tuned cross PCA, the problem is much more difficult due to the complicated structure of the energy function (3.9). The validity of such a scenario has been checked via a mean-field computation in [6].

From now on, for technical reasons, we shall assume that the magnetic field satisfies the following conditions

$$\begin{aligned} 0<h<4 \;\;\;\text { and }\;\;\; h\ne \kappa ,2-\kappa ,2+\kappa ,4-\kappa ,4+\kappa \end{aligned}$$

(3.15)

Since $h>0$, the equilibrium is characterized by positive magnetization. The question is: Is it possible to investigate the possibility of the existence of metastable states? In other words, is it possible to show that there exist not equilibrium phases in which the system is trapped in the sense described in the introduction (see Sect. 3.1)?

This question has a very long history: In some sense, it arose with the van der Waals theory of liquid–vapor transition and began to find some mathematically rigorous answer only in the 80s. We just quote [17] for the pathwise approach and [2] for the potential theoretic one, and we refer to [18] for the full story and for complete references.

According to the rigorous theories of metastability, the problem has to be approached from a dynamical point of view. Namely, we shall consider the evolution of the tuned cross PCA started at the initial configuration $\zeta \in X$ and study the random variable

$$\begin{aligned} \tau ^\zeta _\mathbf{u }:=\inf \{t>0,\,\sigma (t)=\mathbf{u }\} \end{aligned}$$

(3.16)

called the first hitting time to $\mathbf{u }$. The state $\zeta$ will be called metastable or not depending on the properties of the random variable $\tau ^\zeta _\mathbf{u }$ in the zero-temperature limit³ ($\beta \rightarrow \infty$). In the framework of different approaches to metastability, different definitions of metastable states have been given, but they are all related to the properties of the hitting time $\tau ^\zeta _\mathbf{u }$. In particular, it has to happen that the mean value of $\tau ^\zeta _\mathbf{u }$ has to be large, say diverging exponentially fast with $\beta \rightarrow \infty$.

As remarked above, for $h>0$ small, natural candidates to be metastable states for the tuned cross PCA are the configurations $\mathbf {d}$, $\mathbf {c}_\text {e}$, and $\mathbf {c}_\text {o}$. But, imagine to start the chain at $\mathbf {d}$: Why should such a state be metastable? Why should the chain take a very long time to hit the “stable” state $\mathbf{u }$? The analogous question posed in the framework of the two-dimensional Ising model with Metropolis dynamics has an immediate qualitative answer: In order to reach $\mathbf{u }$ starting from $\mathbf {d}$, the system has to perform, spin by spin, a sequence of changes against the energy drift. Indeed, plus spins have to be created in the starting sea of minuses, and those transitions have a positive energy cost if the magnetic field is small enough, indeed the interaction is ferromagnetic and pairs of neighboring opposite spins have to be created.

But in the case of the tuned cross PCA, recall (3.10) and recall we assumed $h<4$, see (3.15), the starting $\mathbf {d}$ and the final $\mathbf{u }$ configurations have energy

$$\begin{aligned} H_h(\mathbf {d})=-|\varLambda |(4+\kappa -2h) \;\;\text { and }\;\; H_h(\mathbf{u })=-|\varLambda |(4+\kappa +2h) \end{aligned}$$

So that $H_h(\mathbf {d})>H_h(\mathbf{u })$, as it is obvious since $\mathbf{u }$ is the ground state. Moreover, the dynamics is allowed to jump in a single step from $\mathbf {d}$ to $\mathbf{u }$ by reversing all the spins of the system. A naive (wrong) conclusion would be that $\mathbf {d}$ cannot be metastable because the jump from $\mathbf {d}$ to $\mathbf{u }$ can be performed in a single step by decreasing the energy.

The conclusion is wrong because in reversible PCA the probability to perform a jump is not controlled simply by the difference of energies of the two configurations involved in the jump. Indeed, in the example discussed above, recall (3.2) and (3.8), and we have that

$$\begin{aligned} p_{\beta ,h}(\mathbf {d},\mathbf{u })= \Big [\frac{1}{1+e^{2\beta (4+\kappa -h)}}\Big ]^{|\varLambda |} {\mathop {\sim }\limits ^{\beta \rightarrow \infty }} e^{-2|\varLambda |\beta (4+\kappa -h)} \end{aligned}$$

which proves that the direct jump from $\mathbf {d}$ to $\mathbf{u }$ is depressed in probability when $\beta$ is large.

This very simple remark shows that the behavior of the PCA cannot be analyzed by simply considering the energy difference between configurations. It is quite evident that a suitable cost function has to be introduced.

From (3.15), the local field $\kappa \sigma _0+\sum _{j\in J}\sigma _j+h$ appearing in (3.8) is different from zero. Thus, for $\beta \rightarrow \infty$,

$$\begin{aligned} p_{\beta ,h}(\sigma ,\eta ) \rightarrow \left\{ \begin{array}{l} {\displaystyle 1\;\;\;\; \text { if } \eta (i)\big [\kappa \sigma _i+\sum _{j\in i+J}\sigma _j+h\big ]>0 \;\;\forall i\in \varLambda }\\ 0\;\;\;\; \text { otherwise } \end{array} \right. \end{aligned}$$

where we have used (3.2). Hence, given $\sigma$, there exists a unique configuration $\eta$ such that $p_{\beta ,h}(\sigma ,\eta )\rightarrow 1$ for $\beta \rightarrow \infty$ and this configuration is the one such that $\eta (i)$ is aligned with the local field $\kappa \sigma _i+\sum _{j\in i+J}\sigma _j+h$ for any $i\in \varLambda$. Such a unique configuration will be called the downhill image of $\sigma$. This property explains well in which sense PCA are the probabilistic generalization of deterministic Cellular Automata: Indeed, in such models each configuration is changed deterministically into a unique image configuration. This property is recovered in probability in reversible PCA in the limit $\beta \rightarrow \infty$.

We now remark that if $\eta$ is different from the downhill image of $\sigma$, we have that $p_{\beta ,h}(\sigma ,\eta )$ decays exponentially with rate

$$\begin{aligned} \varDelta _h(\sigma ,\eta )= -\lim _{\beta \rightarrow \infty }\frac{1}{\beta }\log p_{\beta ,h}(\sigma ,\eta ) = \!\!\!\!\!\!\!\!\! \sum _{\genfrac{}{}{0.0pt}{}{i\in \varLambda :}{\eta (i)[\kappa \sigma _i+\sum _{j\in i+J}\sigma _j+h]<0}} \!\!\! 2\Big |\kappa \sigma _i+\sum _{j\in i+J}\sigma _j+h\Big | \end{aligned}$$

(3.17)

Note that if $\eta$ is the downhill image of $\sigma$, then $\varDelta _h(\sigma ,\eta )=0$. More precisely, we have

$$\begin{aligned} e^{-\beta \varDelta _h(\sigma ,\eta )-\beta \gamma (\beta )} \le p_{\beta ,h}(\sigma ,\eta ) \le e^{-\beta \varDelta _h(\sigma ,\eta )+\beta \gamma (\beta )} \end{aligned}$$

with $\gamma (\beta )\rightarrow 0$ for $\beta \rightarrow \infty$. This property is known in the literature as the Wentzel and Friedlin condition.

Since from (3.6) and (3.17), it follows that the following reversibility condition

$$\begin{aligned} H_h(\sigma )+\varDelta _h(\sigma ,\eta ) = H_h(\eta )+\varDelta _h(\eta ,\sigma ) \end{aligned}$$

(3.18)

is satisfied for any $\sigma ,\eta \in X$; we have that the function $\varDelta _h(\sigma ,\eta )$ can be interpreted as the energy cost that must be paid in the transition $\sigma \rightarrow \eta$.

We are now ready to give a precise definition of metastable states in the framework of reversible Probabilistic Cellular Automata. We shall follow the approach in [15] which is based on the analysis of the energy landscape of the system. Note that in our setup, the energy landscape is not only given by the energy function $H_h$, but it is also decorated by the energy cost function $\varDelta _h$. It is important to remark that, for the sake of clearness, we shall give the definition having in mind the specific case we are considering, namely the tuned cross PCA with $0<h<\kappa$, but the definition we shall can give can be easily generalized to the broad context of reversible PCA.

A sequence of configurations $\omega =\{\omega _1,\dots ,\omega _n\}$, with $\omega _i\in X$ for $i=1,\dots ,n$, is called path. The height of the path $\omega$ is defined as

$$\begin{aligned} \varPhi _\omega =\max _{i=1,\dots ,n-1}[H_h(\omega _i)+\varDelta _h(\omega _i,\omega _{i+1})] \end{aligned}$$

(3.19)

see Fig. 3.5 for a graphic illustration.

Fig. 3.5

Graphic representation of the definition of height of a path

Given two sets of configurations $A,A'\subset X$, the communication height $\varPhi (A,A')$ between $A,A'$ is defined as

$$\begin{aligned} \varPhi (A,A')=\min _{\omega :A\rightarrow A'}\varPhi _\omega \end{aligned}$$

(3.20)

where the minimum is taken on the set of paths starting in A and ending in $A'$. Given $\sigma \in X$, we define the stability level of $\sigma$ as

$$\begin{aligned} V_\sigma =\varPhi (\sigma ,\{\text {states with energy smaller than }\sigma \}) -H_h(\sigma ) \end{aligned}$$

(3.21)

That is to say, $V_\sigma$ is the height of the most convenient path that one has to follow in order to decrease the energy starting from $\sigma$.

Finally, we define the maximal stability level as the largest among the stability levels, i.e.,

$$\begin{aligned} \varGamma _\text {m} =\max _{\sigma \in X\setminus \{\mathbf{u }\}}V_\sigma >0 \end{aligned}$$

(3.22)

and the set of metastable states

$$\begin{aligned} X_{\text {m}}= \{\eta \in X\setminus \{\mathbf{u }\}:\,V_\eta =\varGamma _\text {m}\} \end{aligned}$$

(3.23)

This definition of metastable states is particularly nice, since it is based only on the properties of the energy landscape. In other words, in order to find the metastable states of the tuned cross PCA, one “just” has to solve some variational problems on the energy landscape of the model. This is, unfortunately, a very difficult task that has been addressed mainly in [5, 8].

Why is this definition of metastable states satisfying? Because, given $\zeta \in X_\text {m}$, for the chain started at $\zeta$, we can prove properties of the random variable $\tau ^\zeta _\mathbf{u }$ characterizing $\zeta$ as a metastable state in the physical sense outlined in the introduction. Indeed, if we let ${\mathbb {P}}_\sigma$ and ${\mathbb {E}}_\sigma$, respectively, the probability and the average computed along the trajectories of the tuned cross PCA started at $\sigma \in X$, we can state the following theorem.

Theorem Let $\zeta \in X_{ \text {m}}$. For any $\varepsilon >0$ we have that

$$\begin{aligned} \lim _{\beta \rightarrow \infty } \mathbb {P}_\zeta ( e^{\beta (\varGamma _{ \text {m}}-\varepsilon )}<\tau ^\zeta _\mathbf{u }< e^{\beta (\varGamma _{ \text {m}}+\varepsilon )} ) =1 \end{aligned}$$

Moreover,

$$\begin{aligned} \lim _{\beta \rightarrow \infty } \frac{1}{\beta } \log {\mathbb {E}}_\zeta [\tau ^\zeta _\mathbf{u }] =\varGamma _{ \text {m}} \end{aligned}$$

This theorem has been proven in [15] in the framework of Statistical Mechanics Lattice systems with Metropolis dynamics. Its generalization to the PCA case has been discussed in [8].

The physical content of the two statements in the theorem is that the first hitting time of the chain started at a metastable state $\zeta \in X_\text {m}$ is of order $\exp \{\beta \varGamma _\text {m}\}$. The first of the two statements ensures this convergence in probability and the second in mean.

It is important to remark that it is possible to give a more detailed description of the behavior of the chain started at a metastable state. In particular, it can be typically proven a nucleation property, that is to say, one can prove that before touching the stable state $\mathbf{u }$ the chain has to visit “necessarily” an intermediate configuration corresponding to a “critical” droplet of the stable phase (plus one) plunged in the sea of the metastable one. By necessarily, above, we mean with probability one in the limit $\beta \rightarrow \infty$. For a wide description of the results that can be proven, we refer the interested reader, for instance, to [15, 18].

5 Metastable Behavior of the Tuned Cross PCA

The metastable behavior of the tuned cross PCA has been studied extensively in [5] (nearest neighbor PCA, i.e., $\kappa =0$), [1, 8] (cross PCA, i.e., $\kappa =1$), and [9] (tuned cross PCA with $0<\kappa <1$). In the extreme cases, i.e., $\kappa =0$ and $\kappa =1$, rigorous results were proved, while in the case $0<\kappa <1$ only heuristic arguments have been provided. In this section, we shall review briefly the main results referring the reader to the quoted papers for details. We shall always assume that h satisfies (3.15) and 2 / h not integer; moreover, we note that the result listed below are proven for $\varLambda$ large enough depending on h.

In the cross case ($\kappa =1$), it has been proven [8] that the metastable state is unique, and more precisely, with the notation introduced above, it has been shown that $X_\text {m}=\{\mathbf {d}\}$. Moreover, it has also been proven that the maximal stability level is given by

$$\begin{aligned} \varGamma _\text {m} =H_h(\mathbf p _{\ell _{\text {c},1}}) +\varDelta _h(\mathbf p _{\ell _{\text {c},1}}, \mathbf p _{\ell _{\text {c},2}})-H_h(\mathbf {d}) {\mathop {\sim }\limits ^{\beta \rightarrow \infty }} \frac{16}{h} \end{aligned}$$

(3.24)

where⁴ $\ell _\text {c}=\lfloor 2/h\rfloor +1$ is called critical length, $\mathbf p _{\ell _{\text {c},1}}$ is a configuration characterized by a $\ell _\text {c}\times (\ell _\text {c}-1)$ rectangular droplet of plus spins in the sea of minuses with a single-site protuberance attached to one of the two longest sides of the rectangle, and $\mathbf p _{\ell _{\text {c},2}}$ is a configuration characterized by a $\ell _\text {c}\times (\ell _\text {c}-1)$ rectangular droplet of plus spins in the sea of minuses with a two-site protuberance attached to one of the two longest sides of the rectangle (see Fig. 3.6).

Fig. 3.6

Graphical description of $\varGamma _\text {m}$ for the cross PCA

Once the model dependent problems have been solved and the metastable state found, the properties of such a state are provided by the general theorem stated in Sect. 3.4. We just want to comment that the peculiar expression of the maximal stability level that, we recall, gives the exponential asymptotic of the mean exit time has a deep physical meaning. Indeed, it is also proven that during the escape from the metastable state $\mathbf {d}$ to the stable one $\mathbf{u }$, the chain visits with probability tending to one in the limit $\beta \rightarrow \infty$ the configuration $\mathbf p _{\ell _{\text {c},1}}$ and, starting from such a configuration, it performs the jump to $\mathbf p _{\ell _{\text {c},2}}$. From the physical point of view, this property means that the escape from the metastable state is achieved via the nucleation of the critical droplet $\mathbf p _{\ell _{\text {c},2}}$.

In the nearest neighbor case ($\kappa =0$) it has been proven [5] that the set of metastable states is $X_\text {m}=\{\mathbf {d},\mathbf {c}_\text {e},\mathbf {c}_\text {o}\}$. It is important to note that the two states $\mathbf {c}_\text {e}$ and $\mathbf {c}_\text {o}$ are essentially the same metastable state; indeed, it can be easily seen that $\mathbf {c}_\text {e}$ is the downhill image of $\mathbf {c}_\text {o}$ and vice versa. So that, when the system is trapped in such a metastable state, it flip-flops between these two configurations. Moreover, it has also been proven that the maximal stability level is given by

$$\begin{aligned} \varGamma _\text {m} =H_h(\mathbf c _{\ell _{\text {c}}}) +\varDelta _h(\mathbf c _{\ell _{\text {c}}}, \mathbf c _{\ell _{\text {c},1}})-H_h(\mathbf {d}) {\mathop {\sim }\limits ^{\beta \rightarrow \infty }} \frac{8}{h} \end{aligned}$$

(3.25)

where $\ell _\text {c}=\lfloor 2/h\rfloor +1$ is called critical length, $\mathbf c _{\ell _{\text {c}}}$ is a configuration characterized by a $\ell _\text {c}\times (\ell _\text {c}-1)$ rectangular checkerboard droplet in the sea of minuses, and $\mathbf p _{\ell _{\text {c},1}}$ is a configuration characterized by a $\ell _\text {c}\times (\ell _\text {c}-1)$ rectangular checkerboard droplet in the sea of minuses with a single-site plus protuberance attached to one of the two longest sides of the rectangle (see Fig. 3.7). It is worth noting that, comparing (3.24) and (3.25), the exit from the metastable state is much slower in the case of the cross PCA with respect to the nearest neighbor one.

Even in this case, the properties of the metastable states are an immediate consequence of the theorem stated above. But also for the nearest neighbor PCA, the nucleation property is proven: During the transition, during the escape from the metastable state $\mathbf {d}$ to the stable one $\mathbf{u }$, the chain visits with probability tending to one in the limit $\beta \rightarrow \infty$ the configuration $\mathbf c _{\ell _{\text {c}}}$ and, starting from such a configuration, it performs the jump to $\mathbf c _{\ell _{\text {c},1}}$. From the physical point of view, this property means that the escape from the metastable state is achieved via the nucleation of the critical checkerboard droplet $\mathbf c _{\ell _{\text {c}}}$.

Fig. 3.7

Graphical description of $\varGamma _\text {m}$ for the nearest neighbor PCA

Moreover, in the nearest neighbor case, it has been proven that during the escape from $\mathbf {d}$ to $\mathbf{u }$, the system has also to visit the checkerboard metastable states $\{\mathbf {c}_\text {e},\mathbf {c}_\text {o}\}$. Starting from such a metastable state, the system performs the final escape to $\mathbf{u }$ with an exit time controlled by the same maximal stability level $\varGamma _\text {m}$ (3.25).

Finally, we just mention the heuristic results discussed in [9] for the tuned cross PCA with $0<\kappa <1$. There is one single metastable state, i.e., $X_\text {m}=\{\mathbf {d}\}$, but, depending on the ration $\kappa /h$, the system exhibits different escaping mechanisms. In particular, for $h<2\kappa$ the systems perform a direct transition from $\mathbf {d}$ to $\mathbf{u }$, whereas for $2\kappa <h$ the system “necessarily” visits the not metastable checkerboard state before touching $\mathbf{u }$. In [9], it has been pointed out the analogies between the behavior of the tuned cross PCA and the Blume–Capel model [3]. The metastable character of the two models is very similar with the role of the self-interaction parameter $\kappa$ played by that of the chemical potential in the Blume–Capel model.