Econometric Genetic Programming in Binary Classification: Evolving Logistic Regressions Through Genetic Programming

Abstract

Logistic Regression and Genetic Programming (GP) have already been compared to each other in classification tasks. In this paper, Econometric Genetic Programming (EGP), first introduced as a regression methodology, is extended to binary classification tasks and evolves logistic regressions through GP, aiming to generate high accuracy classifications with potential interpretability of parameters, while uses statistical significance as a feature-selection tool and GP for model selection. EGP-Classification (or EGP-C), the name of this proposed EGP’s extension, was tested against a large group of algorithms in three cross-sectional datasets, showing competitive results in most of them. EGP-C successfully competed against highly non-linear algorithms, like Support Vector Machines and Multilayer Perceptron with Back Propagation, and still allows interpretability of parameters and models generated.

1 Introduction

Logistic Regression (LR or logit regression) and Genetic Programming (GP) have already been compared to each other in classification tasks [1,2,3].

The work on [4] is pioneer in evolving LR models through GP. As they state, their approach merges the ability of LR to deal with dichotomous data and provide quantitative results with the optimization characteristic of GP to search the entire hypothesis space for the “most fit” hypothesis. GP modifies, using an iterative trial and error process, LR models formed by vegetation indices built from basic function blocks defined in the function and terminal sets. Each candidate model is refined with a stepwise backward elimination using the level of significance associated with Chi-square test of each term and then evaluated based on the fitness function which is defined by the model’s Kappa statistics and the number of terms in the model. Figure 1 shows a possible individual generated by its algorithm.

Fig. 1.

(Source: [4])

Example of a proposed candidate model representation for the GP and LR integrated model.

Kaizen Programming (KP) [18] is an interesting evolutionary tool based on concepts of continuous improvement from Kaizen methodology, which was successfully tested against traditional SR benchmark functions. In [19], KP was coupled with LR models to extract useful features from a widely studied credit scoring dataset, aiming at improving the prediction performance of LR.

EGP, which was first introduced in [5] for regression tasks and tested against traditional feature-selection econometric algorithms, is carefully constructed considering econometric theory on cross-sectional datasets, aiming to generate high accuracy regressions with potential interpretability of parameters.

EGP is now extended to binary classification tasks, evolving logistic regressions through GP, aiming to improve the approach proposed by its predecessors, [4, 19], particularly on interpretation of parameters. Predictors 1, 2 and 3, in Fig. 1, when components in a logit model, offer just a few or even none interpretation of parameters. To perceive this, it is sufficient to try an interpretation on $\left( {{\text{B}}_{5} {\text{B}}_{3} } \right)/\left( {{\text{B}}_{3} + {\text{B}}_{1} } \right)$, a coefficient in a LR model of [4]. EGP-C uses just polynomials in the $X\beta$ part of LR and to see why this kind of approach is beneficial to parameter interpretation, see [6]. EGP-C is interpretation-oriented and also aims to generate high accuracy models.

This paper is organized as follows: Sect. 2 describes the elements of econometrics used by EGP-C: there is no intention to fully exhaust the theme; justification on these elements is presented when necessary. Section 3 succinctly describes EGP-C. Sections 4 proposes experiments and discuss results. Conclusion is done in Sect. 5, with mention to future work.

2 Econometrics

2.1 Logistic Regression, Maximum Likelihood, Newton’s Method

The Logistic Regression (LR) aims to model $P_{t}$, the conditional probability of $y_{t} = 1$ to $\varvec{X}$, with $t \in \left[ 1 \right.,\left. n \right]$. Only possible outcomes for $y_{t}$ are $0$ or $1$. The matrix $\varvec{X} = \left[ {\varvec{x}_{1} \ldots \varvec{x}_{i} \ldots \varvec{x}_{k} } \right]$ is constructed by $\varvec{x}_{i}$ $n \times 1$ vectors, $i \in \left[ 1 \right.,\left. k \right]$. Mathematically:

$$ P_{t} \equiv \,\Pr \left( {y_{t} = 1 |\varvec{X}} \right) = E\left( {y_{t} |\varvec{X}} \right) $$

(1)

Multiple linear regressions are inadequate to model (1) and [7] shows the reason. Logit or probit models [8] are well recognized methods for binary classification tasks. Both methods consist of modelling $E\left( {y_{t} |\varvec{X}} \right)$ with a transformation function, $F\left( x \right)$, applied to an index function, $h\left( {\varvec{X}_{t} ,\varvec{\beta}} \right)$:

$$ E\left( {y_{t} |\varvec{X}} \right) = F\left( {h\left( {\varvec{X}_{t} ,\varvec{\beta}} \right)} \right) = F\left( {\varvec{X}_{t}\varvec{\beta}} \right) $$

(2)

with $h\left( {\varvec{X}_{t} ,\varvec{\beta}} \right) = \varvec{X}_{t}\varvec{\beta}$. The expected value $E\left( {y_{t} |\varvec{X}} \right)$ is a typical cumulative probability distribution, a monotonically growing linear transformation that maps from the real line to $\left[ {0,1} \right]$, with properties $F\left( { - \infty } \right) = 0$, $F\left( \infty \right) = 1$ and $\left( {\partial F\left( x \right)/\partial x} \right) > 0$.

Logit and probit models are usually preferred over other econometric classification models mainly due linearity on $h\left( {\varvec{X}_{t} ,\varvec{\beta}} \right)$. For probit regressions, $E\left( {y_{t} |\varvec{X}} \right) =\upphi\left( {\varvec{X}_{t}\varvec{\beta}} \right)$, the cumulative normal probability distribution, which has not closed formula but is easily calculated numerically. For the logit regression:

$$ E\left( {y_{t} |\varvec{X}} \right) =\Lambda \left( {\varvec{X}_{t}\varvec{\beta}} \right) = \frac{{e^{{\varvec{X}_{t}\varvec{\beta}}} }}{{1 + e^{{\varvec{X}_{t}\varvec{\beta}}} }} $$

(3)

which has closed formula. $\Lambda \left( {\varvec{X}_{t}\varvec{\beta}} \right)$ is called logistic function.

Maximum Likelihood (ML) is commonly used to estimate $\widehat{\varvec{\beta}}$ on (3) [9]. ML estimation proposes the maximization of the ML function, which gives the likelihood of the sample $\varvec{y}$ to be observed as realizations of $n$ independent Bernoulli random variables. The vector $\widehat{\varvec{\beta}}$ is the solution of this maximization, which usually occurs on the logarithm of ML function, because it involves a sum instead of a product:

$$ l\left( {\varvec{y},\varvec{\beta}} \right) = \sum\nolimits_{t = 1}^{n} {[y_{t} \log \left( {\Lambda \left( {\varvec{X}_{t}\varvec{\beta}} \right)} \right) + \left( {1 - y_{t} } \right)\log \left( {1 -\Lambda \left( {\varvec{X}_{t}\varvec{\beta}} \right)} \right)]} $$

(4)

which is globally concave whenever $\log \left( {\Lambda \left( {\varvec{X}_{t}\varvec{\beta}} \right)} \right)$ and $\log \left( {1 -\Lambda \left( {\varvec{X}_{t}\varvec{\beta}} \right)} \right)$ are concave functions of $\varvec{X}_{t}$: in such case, $\widehat{\varvec{\beta}}$ is unique. However, [10] states that the presence of non-linear elements, crossed feature terms (like $x_{3} x_{11}^{2}$), will not permit oneness of $\widehat{\varvec{\beta}}$. First order conditions of (4) are:

$$ \sum\nolimits_{t = 1}^{n} {(y_{t} -\Lambda \left( {\varvec{X}_{t} \widehat{\varvec{\beta}}} \right))X_{ti} } $$

(5)

Conditions in (5) are just solved numerically, due non-linearity in parameters $\widehat{\varvec{\beta}}$, and Newton’s Method (NM) is an interactive method that possibly solves it, performing as follows:

$$ \varvec{\beta}^{{\left( {s + 1} \right)}} =\varvec{\beta}^{\left( s \right)} - \varvec{H}^{ - 1} \left( {\varvec{\beta}^{\left( s \right)} } \right)\nabla l\left( {\varvec{\beta}^{\left( s \right)} } \right) $$

(6)

with $\varvec{H}$ the Hessian Matrix and $\nabla l$ the gradient of $l\left(\varvec{\beta}\right)$. Even if there is no global maximum for $l\left(\varvec{\beta}\right)$, [11] guarantees it always increases by NM.

2.2 Hypothesis Test

Hypothesis Test (HT) is applied in EGP-C in the same way it is applied in EGP and it is only possible due satisfiability of three regularity conditions, as described in [12]. Under these conditions and $n$ sufficiently large, the following verifies:

$$ \widehat{\varvec{\beta}}\mathop \to \limits^{d} N\left( {\varvec{\beta},\left[ {I\left(\varvec{\beta}\right)} \right]^{ - 1} } \right) $$

(7)

$$ \frac{{\widehat{\beta }_{i} - \beta_{i} }}{{SE\left( {\widehat{\beta }_{i} } \right)}} \sim N\left( {0,1} \right) $$

(8)

with $I\left(\varvec{\beta}\right)$, the Fisher Information, equals to $\varvec{\sigma}_{\varvec{\beta}}^{2}$, the asymptotic variance. For a brief review on HT and how it is applied in EGP, see [5].

3 Econometric Genetic Programming – Classification: EGP-C

EGP-C is the EGP algorithm applied to classifications tasks, when logit models are evolved. The main difference between EGP and EGP-C lies in Accuracy and related metrics, showed in Sect. 3.3.

EGP-C evolves models in format of (3) through GP, which is responsible for model selection. GP is mainly based in [13] configuration.

3.1 Representation

Individuals are multigenic. Any constant in any program comes from NM in (6), i.e. there are no ephemeral constants. The terminal set, namely $\Omega$, is purely composed by variables. The primitive set, namely ϑ, is composed just by variables and operations of sum and multiplication, due $X\beta$ format.

Search space for EGP-C is the number of models, $n_{mod}$, which is function of the number of regressors created for an individual, $n_{reg}$.

$$ n_{reg} = \sum\nolimits_{{q_{var} = 1}}^{K} {\frac{{\left( {K - 1 + q_{var} } \right)!}}{{\left( {K - 1} \right)!q_{var} !}}} $$

(9)

$$ n_{mod} = \sum\nolimits_{{q_{reg} = 1}}^{{n_{reg} }} {\frac{{n_{reg} !}}{{\left( {n_{reg} - q_{reg} } \right)!}}} $$

(10)

In (9), $q_{var}$ is the number of variables on $\Omega$ necessary to create a regressor; in (10), $q_{reg}$ is the number of regressors required to build a model. (9) is the sum of possible combinations with repetitions, $q_{var}$ to $q_{var}$. (10) is the sum of possible arrangements of $n_{reg}$ regressors, $q_{reg}$ to $q_{reg}$. Supposing $K = 3$ for a particular dataset, $n_{mod}$ rounds $10^{17}$.

3.2 Initial Population

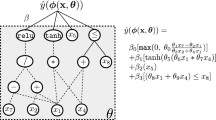
EGP-C uses a probabilistic version of ramped half-and-half method. Figure 2 shows a possible individual generated by EGP-C.

Fig. 2.

A possible individual generated by EGP-C.

Set $\Omega$ is composed by $K$ features (independent variables). Every individual has its own set of regressors, forming its own $\varvec{X}$, composed by simple or combined elements of $\Omega$. As an example, it is possible that $x_{1}$, $x_{3} x_{11}^{2}$ and $x_{3} x_{4} x_{6}$ are regressors of a particular individual, formed by features $x_{1}$, $x_{3}$, $x_{4}$, $x_{6}$ and $x_{11}$.

3.3 Accuracy

In EGP, RMSE is the objective function and $\overline{\text{R}}^{2}$ is used to compare models. In EGP-C, the percentage of correctly classified instances (“$\% \_corr$”) has been chosen as objective function (accuracy measure), due benchmarks were evaluated using such metric. Experiments and Results will fully describe the comparison methodology.

To calculate accuracy in an EGP-C individual, the following procedure needs to be done (Fig. 3).

Fig. 3.

The multigenic individual is written as a set of regressors. Repetitions will be discarded.

EGP-C will solve (5) for $X\beta = \beta_{1} x_{7} + \beta_{2} x_{9} x_{12} + \beta_{3} x_{18} x_{25}$. If any of the regressors are not statistically significant, they will be removed from (5). In sequence, (6) is recalculated just with statistically significant regressors from (5). $\% \_corr$ is finally calculated using $\widehat{\varvec{\beta}}$ after these steps. This routine is traditional in econometric studies, ensuring statistical significance over a determined significance level $\alpha$. Modifications described are necessary just for accuracy calculation, therefore individuals will keep their multigene structure to mutation, crossover and elitism (Fig. 4).

Fig. 4.

Individual ready for accuracy calculation.

EGP-C does not estimate on genes, just on regressors, by two main reasons: possible multicollinearity problem, interfering on HT for $\beta_{i}$, and lack of interpretation for $\widehat{\beta }_{i}$ when it is related to a gene.

3.4 Selection

Tournament selection with $n_{tourn} = 7$ and repetitions allowed, with a variation on lexicographic parsimony pressure of [14], is used. Individuals with a large number of statistically significant regressors will be preferred over others with a few number, in the same range of fitness. Therefore, EGP-C is parsimonious in its nature, because it avoids the individuals with a large amount of introns (in this case, non statistically significant regressors).

3.5 Mutation, Crossover and Elitism

Types of mutation used: traditional mutation proposed by [15] and mutation by regressors’ substitution. Types of crossover used: intergenic and intragenic crossovers. Mutation and crossover rates vary through evolution following automatic adaptation of operators as described in [16]. Elitism rate is set to 5% of individuals by generation.

3.6 Tools and Parameters

EGP-C is implemented through a modification on GPTIPS, a Matlab toolbox, presented in [17]. Information on EGP-C parameters are shown in Table 1.

Table 1. EGP-C Parameters

4 Experiments and Results

EGP-C can be used in different forms, e.g. for model selection or interpretation of parameters. For the reasoning of this article, EGP-C was submitted to generate high accuracy models, with potential interpretability of parameters, and tested against a large group of algorithms in three classification cross-sectional datasets, namely: “Breast Cancer Wisconsin (Original) Data Set”; “Pima Indians Diabetes Data Set”; “Ionosphere Data Set”. All information on datasets can be found in UCI Machine Learning Repository [20].

To fully test EGP-C’s capability to generate high accuracy models, a generous list of algorithms to compare it was required. The Computational Intelligence Laboratory in Informatics’ Department of Nicolaus Copernicus University holds results on a list of algorithms for datasets used in this article. Their comparison methodology is based on a 10-fold cross validation on the entire dataset and that is the reason EGP-C is evaluated in the same manner. Authors of each algorithm are responsible for every result divulgated at Computational Intelligence Laboratory in Informatics’ Department of Nicolaus Copernicus University domain [21].

Tables 2, 3 and 4 present the results. Results for EGP-C are identified as “EGP-Classification” in Tables. Algorithms are ordered by $\% \_corr$, the percentage of correct hits, while standard deviation works as the next sorting criteria.

Table 2. Results for Wisconsin Dataset

Table 3. Results for Diabetes Dataset

Table 4. Results for Ionosphere Dataset

EGP-C was competitive in Wisconsin and Diabetes datasets, performing in 14^th (40 algorithms in total) and 7^th (49 in total), respectively. Support Vector Machines (SVMs) and Multilayer Perceptron with Back Propagation (MLP + BP), which are highly non-linear in structure, using more complex non-linear functions like trigonometric ones, presented results just a little better than EGP-C (in average, 0.5% above). Additionally, SVMs and MLP + BP permits low or none interpretability of parameters.

In logit models, the coefficient $\widehat{\beta }_{i}$ can be interpreted as the effect of a unit of change in $x_{i}$ on the predicted logits with other regressors considered constants in the model. (11) is a model generated by EGP-C.

$$ \frac{{e^{{ - 7.12 + 0.14x_{4} - 0.25x_{6} }} }}{{1 + e^{{ - 7.12 + 0.14x_{4} - 0.25x_{6} }} }} $$

(11)

with $X\beta = - 7.12 + 0.14x_{4} - 0.25x_{6}$. The effect on the odds of a 1-unit increase in $x_{4}$ is $e^{0.14} = 1.15$, meaning the odds of an instance to be classified as $y_{t} = 1$ increase approximately $15\%$ when $x_{4}$ is added by one unit (of $x_{4}$), regardless of the $x_{6}$ value.

In Ionosphere dataset, EGP-C was not competitive. Ionosphere has a binary attribute with 89.17% of its values equals to 1 and the rest, 10.83%, equals 0. When combining features to generate regressors, this attribute (suppose it is $x_{1}$) can easily form a regressor that is collinear with other. For example, $x_{1}$ and $x_{1}^{2}$ composing the same individual. In such cases, $\varvec{X}$ has not full rank and thus the variant of NM used to solve (5) will fail to find a maximum (even it is local) to (4), because this version of NM has not a protection against linear dependent columns. That is why EGP-C, in some circumstances like highly unbalanced datasets, is purposely set to do not generate too large individuals, consequently compromising accuracy. EGP-C controls individuals’ growth by parsimoniously regulating GP parameters as population size, number of generations or maximum gene height for trees.

5 Conclusion and Future Work

EGP-C was successful in achieving its objective of generating high accuracy logit models. Although non-linear, logit models generated by EGP-C hold a linear portion on its structure, $X\beta$, which permits potential interpretability of parameters.

Future work points out in designing EGP for time series forecast. High collinearity between columns of $\varvec{X}$ requires a distinct approach to prediction, depending on the model someone is interested in.