Keywords

1 Introduction

The technology of taking off from the lunar is the key for lunar exploration project, which is of great importance for the returning of spacecraft from lunar. To verify the stability of spacecraft when taking off lunar, the force state of the spacecraft needs to be simulated accurately, which is the key of the takeoff from lunar. Traditional simulation methods, such as computer simulation and rocket-propelled experiment, are too expensive or too complex for lunar takeoff simulation. In order to implement lunar takeoff simulation in an efficient way, a cable-driven parallel mechanism has been built [1]. Lunar takeoff simulation has high requirements on the acceleration and workspace of cable-driven parallel mechanism. In this paper, the installation positions of cables will be optimized based on the acceleration requirements and workspace requirements of simulation mechanism. It should be noted that in this paper, the layout of installation points on moving platform is “6–3”.

Owing to the advantages of simple configuration, large workspace and high speed, cable-driven parallel mechanisms has been widely used [2,3,4]. However, the fact that cable can only bear tension but not compression, the installation positions of cables and the acceleration of moving platform all have effect on the dynamic workspace of cable-driven parallel mechanisms [5,6,7]. Lunar takeoff simulation requires the quality, the vertical and horizontal acceleration of moving platform are 15 kg, 2.4 m/s2 and ±1.1 m/s2 respectively. Therefore, the purpose of this paper is to optimize installation points of cables to maximize dynamic workspace of constraint condition in terms of cable tensions.

So far, great progress has been made in this field. Landsberger [8], studied the feasible workspace of cable-driven parallel mechanism. Barrette and Gosselin [9], carried out that the acceleration of moving platform will influence workspace and introduced the concept of dynamic workspace. Agrawal [10], introduced a cable driven upper arm exoskeleton and optimized the connection points of cables. Ouyang [11], maximum the wrench-feasible workspace of a parallel mechanism driven by 8 cables by optimizing the dimension of its frame. Rui [12], optimized a 3T cable-driven parallel mechanism with constraint condition in terms of cable force and stiffness.

The existing research results are lack of the study of the mathematic relationship between structural parameters and the volume of workspace. Response surface method (RSM) is a multi-parameter optimization method [13]. The main idea of RSM is establishing and analyzing the surrogate mathematical model between optimization variables and optimization index. This paper employs latin-hypercube sampling method to select experimental points and establishes surrogate mathematical model by RSM to achieve optimization results. The virtual prototype experiment is taken to verify the accuracy of the optimized results.

2 Kinematics and Force Equilibrium

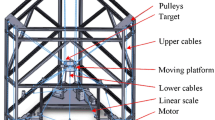
The nine-cable parallel mechanism is shown in Fig. 1. The device is called cable-driven parallel simulator for lunar takeoff, CDPSL for short. CDPSL consists of a base frame equipped with motors and winches and a moving platform connected together with 9 cables, and the layout of cables is “6–3”. The lower 3 cables are connected to the winches directly, while the upper 6 cables go through pulleys to be connected to the winches on the bottom. The length of cable and cable tension are controlled by winches driven by motors.

Fig. 1.
figure 1

CDPSL with nine cables.

Full size image

Figure 2 shows the mechanism model of CSPSL. In Fig. 2, two coordinates are defined as follow, the global frame K b is fixed at the base frame, the moving frame K p is connected to the moving platform. B i ( i = 1,2,…,9) represent the cable installation positions on the base frame and P i (i = 1,2,…,9) denote the cable installation positions on moving platform. The platform-fixed vectors to the connecting points in K p , the vectors to the fixed point on winches in K b and the cable tension vectors are described by p i (i = 1,2,…,9), b i (i = 1,2,…,9) and f i (i = 1,2,…,9) respectively. f p and \( {\varvec{\uptau}}_{\text{p}} \) represent extern forces and torques acting on the platform except for gravity. The position of origin of K p in the fixed base frame K b is defined as op = (x, y, z) and the posture of platform in K b is defined as (Ψ, Φ, γ). Define R as the transformation matrix from K p to K b .

Fig. 2.
figure 2

The mechanism model of CDPSL

Full size image

According to the vector loop method, the kinematics of each cable can be established in (1) with i = 1, 2, 3, …, 9

$$ {\mathbf{l}}_{i} = {\mathbf{b}}_{i} - {\mathbf{o}}{\text{p}} - {\mathbf{Rp}}_{i} $$
(1)

The unit vector of cable could be calculated by

$$ {\mathbf{u}}_{i} = \frac{{{\mathbf{l}}_{i} }}{{\left| {{\mathbf{l}}_{i} } \right|}} = \frac{{{\mathbf{b}}_{i} - {\mathbf{op}} - {\mathbf{Rp}}_{i} }}{{\left| {{\mathbf{b}}_{i} - {\mathbf{op}} - {\mathbf{Rp}}_{i} } \right|}} $$
(2)

The force and torque equilibrium for the platform could be derived

$$ \begin{aligned} \sum\limits_{i = 1}^{9} {{\mathbf{f}}_{i} + {\mathbf{f}}_{{\mathbf{p}}} + {\text{m}}{\mathbf{g}} = {\mathbf{0}}} \hfill \\ \sum\limits_{i = 1}^{9} {{\mathbf{p}}_{i} } \times {\mathbf{f}}_{{\mathbf{i}}} + {\varvec{\uptau}}_{{\mathbf{p}}} = {\mathbf{0}} \hfill \\ \end{aligned} $$
(3)

Then, the force and torque equilibrium could be rewritten into matrix form, where A T is the transpose of the inverse Jacobian, m indicates the mass of moving platform, g is the acceleration of gravity and g = 9.8 m/s2.

$$ \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{u}}_{1} } \\ {{\mathbf{p}}_{1} \times {\mathbf{u}}_{1} } \\ \end{array} } & {\begin{array}{*{20}c} \ldots \\ \ldots \\ \end{array} } & {\begin{array}{*{20}c} {{\mathbf{u}}_{9} } \\ {{\mathbf{p}}_{9} \times {\mathbf{u}}_{9} } \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {t_{1} } \\ \vdots \\ {t_{9} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{f}}_{\text{p}} } \\ {{\varvec{\uptau}}_{\text{p}} } \\ \end{array} } \right] = 0 $$
(4)
$$ {\mathbf{A}}^{{\mathbf{T}}} \cdot {\mathbf{T}} + {\mathbf{w}} = 0 $$
(5)

In this paper, f p is defined as f p  = [ma 2, ma 2, mg + ma 1]T, where a 1 and a 2 represent the maximum vertical acceleration and the maximum horizontal acceleration respectively. In this article, on the basis of the simulation requirements of lunar takeoff, m = 15 kg, a 1 = 2.4 m/s2 and a 2 = ±1.1 m/s2. The method proposed by Lafourcade [14], is adopted in this paper in order to obtain a solution with continuous cable tension.

The solution of cable tension consists of two parts, T eff shown in (7) and T null shown in (8).

$$ {\mathbf{T}} = {\mathbf{T}}_{\text{eff}} + {\mathbf{T}}_{\text{null}} $$
(6)
$$ {\mathbf{T}}_{\text{eff}} = - \left( {{\mathbf{A}}^{\text{T}} } \right)^{ + } \cdot {\mathbf{w}} $$
(7)
$$ {\mathbf{T}}_{\text{null}} = \left( {{\mathbf{I}}_{{{\text{m}} \times {\text{m}}}} - \left( {{\mathbf{A}}^{\text{T}} } \right)^{ + } {\mathbf{A}}^{\text{T}} } \right) \cdot {\mathbf{t}}_{{\mathbf{d}}} $$
(8)

where, (A T)+ is the M-P inverse of A T , t d  = [t d t d t d t d t d t d t d t d t d]T is a desired value of f i . t d is utilized to improve the performance of CDPSL as a control variable. The value of each element in t d is identical because it is beneficial to simplify the control system and CDPSL is designed into modular part.

3 Workspace Determination and Single-Factor Test

3.1 Workspace Determination

For cable-driven parallel mechanism, the tension t i (i = 1, 2, …, 9) (N) should be limited between the maximum tension t max(N) and the minimum tension t min(N), which is required to keep the cable tight. Thus, a condition shown in (9) should be added to (6).

$$ t_{\hbox{max} } \ge t_{i} \ge t_{\hbox{min} } > 0 $$
(9)

The dimension of base frame is 3 × 3 × 4 m. The space occupied by CDPSL is well-distributed into 562400 small cubes. Take the coordinate of the body-center of each cube as sample point, thus obtaining 562400 sample points.

The algorithm based on Monte-Carlo method can be used to analyze the workspace of CDPSL.

  • Give a sample point and its position belonging to the convex set of fixed points;

  • Calculate structure matrix A T

  • \( {\mathbf{T}}_{{e{\text{ff}}}} \text{ = } - \left( {{\mathbf{A}}^{{\mathbf{T}}} } \right)^{{\mathbf{ + }}} { \cdot }{\mathbf{w}} \)

  • Choose a desired tension t d

  • \( {\mathbf{T}}_{{\text{null}}} \text{ = }\left( {{\mathbf{I}}_{{\text{m} \times m}} - \left( {{\mathbf{A}}^{{\mathbf{T}}} } \right)^{ + } {\mathbf{A}}^{{\mathbf{T}}} } \right){ \cdot }{\mathbf{t}}_{{\mathbf{d}}} \)

  • Calculate T = T eff +T null

  • If min(T) ≥ t min and max(T) ≤ t max, the sample point belongs to the workspace. Otherwise, the sample point does not belong to the workspace.

  • Repeat the above process until all the sample points belonging to the convex set of fixed points are calculated.

The variable SUM is introduced to represent the number of sample points belonging to the workspace. Furthermore, SUM could be used to indicate the volume of workspace. Thus, we can optimize the structure of CDPSL by trying to find the maximum value of SUM.

3.2 Single-Factor Test

Lunar takeoff simulation requires the workspace of cable-driven parallel mechanism as large as possible. Hence, the target of structure optimization is set as following:

Maximize the value of SUM under the condition that the quality, the vertical and horizontal acceleration of moving platform are set as 15 kg, 2.4 m/s2 and ±1.1 m/s2 respectively.

In this paper, B i (i = 1, 2, …, 9) are distributed around a circle with radius of 2 m, P i (i = 1, 2, …, 9) are distributed around a circle with radius of 0.25 m and the height of moving platform is 0.75 m. B i are y axial symmetry in K b and P i are y axial symmetry in K p . The circle made up by B i and the circle made up by P i are in similarity relation. To optimize the installation positions of cables, θ i (i = 1, 2, 3) are chosen as optimal variables. Optimal variables are shown in Fig. 3 and the range of optimal variables are shown in Table 1.

Fig. 3.
figure 3

Optimal variables

Full size image
Table 1. Variable name and their lower and upper limits
Full size table

Before optimizing structure, single-factor tests are taken to analyze the relationship between optimal variables and SUM qualitatively. Results of single-factor tests are shown in Fig. 4 and the meaning of each curve is illustrated in Table 2. It should be noted that only 8000 sample points are chosen to calculate SUM in this part. And in Table 2, “+” means taking a number of values in the range.

Fig. 4.
figure 4

Results of single-factor test

Full size image
Table 2. The optimal variables corresponding to each curve in Fig. 4
Full size table

Figure 4 indicates that all optimal variables have influence on the workspace of CDPSL. With θ1 increases, the values of SUM increases gradually, then decreases rapidly. With θ2 increases, the values of SUM increases gradually. With θ3 increases, the value of SUM increases gradually, then decreases gradually. Optimal variables are coupled to each other. Thus, it is necessary to use the optimal design method to optimize the value of optimal variables.

4 Optimal Design

4.1 Design of Experiment

In this paper, latin-hypercube method is taken to select experimental points. Response surface method is taken to optimize the installation positions of cables.

The latin-hypercube method is based on the principle of random probability orthogonal distribution principle. Thus, the response surface model with high precision is obtained by using fewer experimental points [15, 16]. The selected experimental points are shown in Fig. 5.

Fig. 5.
figure 5

Selected experimental points

Full size image

4.2 Response Surface Model

Quadratic polynomial response surface model shown in (10) is taken to establish the surrogate mathematical model between optimization variables and optimization index.

$$ y\left( x \right) = \beta_{0} + \sum\limits_{i = 1}^{n} {\beta_{i} x_{i} } + \sum\limits_{i = 1}^{n} {\beta_{ii} x_{i}^{2} } + \sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\beta_{ij} x_{i} x_{j} } } $$
(10)

where, y(x) is the predictive value of response surface model, x i is the i-th component of the n-dimensional independent variable.β 0, β i , β ii , β ij are the coefficients of the polynomial, which are calculated by least square method.

In this article, θ1, θ2 and θ3 are set as independent variables, SUM is set as output response. Determinant coefficients R2 and multiple fitting coefficient \( R_{adj}^{2} \) are chosen to verify the surrogate mathematical model. The surrogate mathematical model is shown in (11) and calibration results are indicated in Table 2. It should be noted that all 562400 sample points are chosen to calculate SUM in this part.

$$ \begin{aligned} {\text{SUM}} & = 13800.76 + 1554.15\uptheta_{1} + 149.15\uptheta_{2} - 628.51\uptheta_{3} - 73.96\uptheta_{1}\uptheta_{2} - 8.79\uptheta_{1}\uptheta_{3} \\ & \quad + 54.95\uptheta_{2}\uptheta_{3} - 19.09\uptheta_{1}^{2} - 0.12\uptheta_{2}^{2} + 36.38\uptheta_{3}^{2} \\ \end{aligned} $$
(11)

From Table 3, the response surface model meets the accuracy requirements.

Table 3. Calibration results
Full size table

The response surface is shown in Fig. 6.

Fig. 6.
figure 6

Response surface

Full size image

Figure 6 illustrates that the relationship between optimal variables and SUM can be approximated by established surrogate mathematical model. To maximize SUM, θ1 and θ2 should be close to 0 or 60 synchronously. θ3 should be in the vicinity of 60.

Based on the above-mentioned results, multiple sets of optimal solutions could be obtained. Then, we obtain the optimized results while taking some restrictions on production, processing and installation into consideration. One of the solutions and the optimized results are indicated in Table 4.

Table 4. Optimal solution and optimized results
Full size table

5 Virtual Prototype Experiment

Due to the disadvantages of physical prototype, such as high cost, long experimental cycle and the difficulty of structure adjustment, the virtual prototype experiment is utilized to verify the accuracy of the optimized results.

The virtual prototype model of CDPSL, shown in Fig. 7, is established using multi-body dynamics software ADAMS. The workspace of CDPSL could be determined through the analysis of each cable’s tension condition when the moving platform are set at different positions under the condition that the vertical force and the horizontal force are 186 N and ±16.5 N respectively.

Fig. 7.
figure 7

Virtual prototype model

Full size image

Figure 8 shows the workspace calculated by MATLAB according to Sect. 3.1 and Fig. 9 shows the workspace calculated by ADAMS.

Fig. 8.
figure 8

Workspace calculated by MATLAB

Full size image
Fig. 9.
figure 9

Workspace calculated by ADAMS

Full size image

The comparison between the optimal variables and the value of SUM before and after the optimization are shown in Table 5. And Table 5 indicates that the volume of workspace increased by 46% by optimizing the installation positions of cables.

Table 5. Comparison of variables before and after optimization
Full size table

6 Conclusion

In this paper, a cable-driven parallel mechanism with nine cables for lunar takeoff simulation (CDPSL) is presented and optimized. First, the workspace of CDPSL is calculated using the static equations. Then, latin-hypercube method and response surface method are taken to optimize the installation positions of cables with the goal of maximizing workspace. Finally, virtual prototype is established using multi-body dynamics software ADAMS to validate the final optimization results. The relationship between the angle between cables and workspace, which under the condition that the quality, the vertical acceleration and the horizontal acceleration are 15 kg, 2.4 m/s2 and ±1.1 m/s2 respectively, could be described by quadratic polynomial approximatively. For cable driven parallel mechanism with “6–3” layout, the installation positions of lower cables should exactly like a triangle and the installation positions of upper cables should be similar to triangle, while the angles between the odd cable and the even cable of upper cable should remain between 10° to 20°. Then, it could be guaranteed that CDPSL has a large workspace. Ongoing work is to build this device and implement the real-time control.