Using Dynamics to Analyse Time Series

Abstract

We present a review of recent work to analyze time series in a robust manner using Wasserstein distances which are numerical costs of an optimal transportation problem. Given a time series, the long-term behavior of the dynamical system represented by the time series is reconstructed by Takens delay embedding method. This results in probability distributions over phase space and to each pair we then assign a numerical distance that quantifies the differences in their dynamical properties. From the totality of all these distances a low-dimensional representation in a Euclidean space is derived. This representation shows the functional relationships between the time series under study. For example, it allows to assess synchronization properties and also offers a new way of numerical bifurcation analysis. Several examples are given to illustrate our results. This work is based on ongoing joint work with Michael Muskulus [19, 20].

Dedicated to Bernold Fiedler on the occasion of his sixtieth birthday.

1 Introduction

In nonlinear time series analysis the center of attention is not at predicting single trajectories, but rather on estimating the totality of possible states a system can attain and their statistical properties. Of particular importance is the long-term behavior of the system described by the the attractor [1, 8, 17], and the notion of an invariant measure on the attractor that captures the statistical properties of a dynamical system. Qualitative changes in the long-term dynamical behavior can then be detected by comparing properties of the corresponding attractors and invariant measures. Unfortunately, many of the present methods are based on the assumption that the dynamics is given by a deterministic (possibly chaotic) process, and this usually unverifiable assumption can lead to doubts about the validity of the analysis. Moreover, commonly used measures such as Hausdorff dimension and Lyapunov exponents are notoriously difficult to estimate. For this reason, Murray and Moeckel [18] introduced the so-called transportation distance between attractors, which is a single number that expresses how closely the long-term behavior of two dynamical systems resembles each other. In contrast to general divergences such as the Kullback-Leibler divergence, mutual information or the Kolmogorov-Smirnov statistic, the advantage of the transportation distance is that it is a metric on the space of (reconstructed) dynamical systems. The transportation distance is based on a convex optimalization problem that optimally matches two invariant measures, minimizing a cost functional. Mathematically, it is an example of a Wasserstein distance between probability measures [26]. Although computationally involved, Wasserstein distances are much more robust than, for example, Hausdorff distance. Furthermore, these distances have interesting theoretical features, for example interpolation properties that allow to reconstruct dynamical behaviors in between two invariant measures.

Following the idea of Murray and Moeckel, a theory of distance based analysis of dynamical systems was developed in the PhD thesis of Micheal Muskulus which let to a number of applications, see [19, 20] and the references given there. Applications of our work are given in [10, 21], and a related approach to compare dynamical systems directly is given in [29]. In this paper we will review our approach and demonstrate the feasibility by both using synthetic time series obtained from a reference dynamical system and real time series derived from measurements. Ongoing work is devoted to a rigorous foundation of our approach for synthetic time series generated by an Axiom A dynamical system, we also hope to use ideas from Benedicks and Carleson [3] to extend our rigorous analysis to the Hénon map.

1.1 Time Series and Discrete Dynamical Systems

Let $X \subset \mathbb R^d$ and $f : X \rightarrow X$ be a given map. Consider the discrete dynamical system

$$\begin{aligned} x_{n+1} = f(x_n)\qquad \hbox {for } n =0,1,\ldots \end{aligned}$$

(1)

starting from an initial point $x_0 \in X$. The trajectory $x = (x_0, x_1, \cdots , x_N)$ generated by the discrete dynamical system modeled by f can be viewed as a (synthetic) time series. A set ${\mathscr {A}}$ is called attracting with respect to a subset $U \subset X$ if for every neighborhood V of ${\mathscr {A}}$, there exists a $K=K(V)$ such that $f^k(U) \subset V$ for all $k \ge K$. The basin of attraction of ${\mathscr {A}}$ is defined by

$$\begin{aligned} B({\mathscr {A}}) = \cup _{k \ge 0}\ f^{-k}(U). \end{aligned}$$

(2)

If $B({\mathscr {A}}) = X$, then we call ${\mathscr {A}}$ a (global) attractor.

In this paper we will consider time series generated by the Hénon map [9] to obtain synthetic time series. The Hénon map is defined by $H : \mathbb R^2 \rightarrow \mathbb R^2$

$$\begin{aligned} \left( \begin{matrix}x \\ y\end{matrix}\right) \mapsto \left( \begin{matrix}1+y-ax^2 \\ bx\end{matrix}\right) . \end{aligned}$$

(3)

Here a and b are real parameters and the corresponding discrete dynamical system is given by

$$\begin{aligned} \left( \begin{matrix}x_{n+1} \\ y_{n+1}\end{matrix}\right) = H\left( \begin{matrix}x_n \\ y_n\end{matrix}\right) ,\qquad n \ge 0, \end{aligned}$$

(4)

where $x_0 \in \mathbb R$ and $y_0 \in \mathbb R$ are given initial conditions.

1.2 Attractor Reconstruction by Delay Embedding and Subdivision

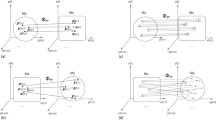
Given a time series $x = (x_1, \cdots , x_N)$ of N measurements of a single observable ${\mathbf x}$, a trajectory of a dynamical system is reconstructed by mapping each consecutive block

$$\begin{aligned} x_{[i]}=(x_i, x_{i+q}, \cdots , x_{i+(k-1)q}) \end{aligned}$$

(5)

of k values, sampled at discrete time intervals q, into a single point $x_{[i]}$ in the reconstructed phase space $\varOmega = \mathbb R^k$.

The intuitive idea is that the information contained in the block $x_{[i]}$ fully describes the state of the dynamical system at time i, albeit in an implicit fashion. From a statistical point of view, the reconstructed points in $\varOmega$ capture higher-order correlations in the time series. This procedure defines the so-called delay-coordinate map $F : \mathbb R^N \rightarrow \mathbb R^k$. In [22] Sauer, Yorke and Casdagli showed, under mild assumptions extending work by Takens [26], that almost every delay-coordinate map $F : \mathbb R^N \rightarrow \mathbb R^k$ is one-to-one on ${\mathscr {A}}$ provided that the embedding dimension k is larger than twice the box counting dimension of ${\mathscr {A}}$. Also, any manifold structure within ${\mathscr {A}}$ will be preserved in $F({\mathscr {A}})$. The optimal value of the lag q and of the embedding dimension k can be estimated from the data [11] (Fig. 1).

The result of the embedding process is a discrete trajectory in reconstructed phase space $\varOmega = \mathbb R^k$ and this trajectory is interpreted as a probability measure $\mu$ on $\varOmega$, where

$$\begin{aligned} \mu [A] = \frac{1}{N'} \sum _{i=1}^{N'} \delta _{x_{[i]}}[A], \quad A \subseteq \varOmega , \end{aligned}$$

(6)

is the time average of the characteristic function of the points in phase space visited; here $\delta _{x_{[i]}}$ is the Dirac measure of the block $x_{[i]}$ and $N' = N-(k-1)q$ is the length of the reconstructed series.

In the limit $N' \rightarrow \infty$ the measure $\mu$ is invariant under the dynamics and assuming that the system is subject to small random perturbations leads to the uniqueness of the invariant measure under mild assumptions [12], which is then called the natural invariant measure. If the time series is synthetic and the underlying discrete dynamical system is available, subdivision methods allow to approximate the attractor and its natural measure with arbitrary precision [6].

Fig. 1.

The methodology of attractor reconstruction via delay embeddings. The true attractor is projected into a time series by some measurement function

We shall illustrate the procedure for the Hénon map (3). For the parameter values $a=1.0$ and $b=0.54$ and for the initial condition $x_0=0.1$ and $y_0=0.0$, the time series for the x-coordinate is given by (Fig. 2).

Fig. 2.

Time series of the x-coordinate with $x_0=0.1$ and $y_0=0.0$

The time series consists of 3000 iterations and is relatively short as this is the situation one often encounters in practice, and the attractor reconstruction using Takens delay embedding is based on the entries [1000–3000]. In Fig. 3 we give the reconstructed attractor.

Fig. 3.

The measure $\mu$ for, respectively, $a=1.0$, $b=0.54$ and $a=1.0$, $b=0.5065$. Note that the chaotic behavior disappears for the last set of parameter values and that we have periodic behavior

The subdivision algorithm to approximate the attractor

Since the time series is synthetic and the underlying discrete dynamical system is given by the Hénon map (3), we can use subdivision methods to approximate the attractor and its natural measure. We recall the algorithm from Dellnitz and Junge [6]:

Let $Q \subset X$ be a compact set and let ${\mathscr {B}}_j$, $j=0,1,2,\ldots$, be a finite of compact subsets of Q with ${\mathscr {B}}_0 = \{Q\}$. Given the collection ${\mathscr {B}}_{k-1}$, the will be constructed in two steps:

• 1. Choose a refinement ${\widetilde{{\mathscr {B}}}}_k$ of ${\mathscr {B}}_{k-1}$ such that both collections of subsets of Q have the same covering.

• 2. Let ${{\mathscr {B}}}_{k} = \{B \in {\widetilde{{\mathscr {B}}}}_{k} \mid f(B') \cap B \not = {\emptyset } \, \text { for certain }\, B' \in {\widetilde{{\mathscr {B}}}}_{k}\}$.

Put

$$\begin{aligned} Q_k = \cup _{B\in {\mathscr {B}}_k} B, \end{aligned}$$

(7)

then $Q_k$ approximates the attractor with precise error estimates [6].

The result of the subdivision algorithm applied to the Hénon map in given in Figs. 4 and 5. Note that in the case of synthetic time series, we can use the attractor produced by the subdivision method as a benchmark for the quality of the reconstructed attractor using Takens delayed embedding.

Fig. 4

Subdivision algorithm: iteration steps 4 and 6 for the Hénon map

Fig. 5.

Subdivision algorithm: iteration steps 8 and 18

2 The Wasserstein Distance

In the sequel we consider two time series $x = (x_1, \cdots , x_N)$ and $y = (y_1, \cdots , y_N)$ of N measurements of a single observables ${\mathbf x}$ and ${\mathbf y}$, and assume that the delay-coordinate map $F[x] : \mathbb R^N \rightarrow \mathbb R^k$ and $F[y] : \mathbb R^N \rightarrow \mathbb R^k$ have been constructed. In order to compare the long-term behavior of dynamical systems that correspond to ${\mathbf x}$, respectively, ${\mathbf y}$, we compute the Wasserstein distances of the natural invariant measures corresponding to ${\mathbf x}$ and ${\mathbf y}$.

Given two probability measures $\mu$ and $\nu$ on $\varOmega$, the Wasserstein distance $W(\mu ,\nu )$ is defined as the solution of an optimal transportation problem in the sense of Monge-Kantorovich [26]. The functional to be optimized is the total cost

$$\begin{aligned} C[\pi ] = \int _{\varOmega \times \varOmega } ||x-y||_2 \, \; \mathrm {d}\pi [x,y], \end{aligned}$$

over the set $\varPi (\mu ,\nu )$ of all probability measures on the product $\varOmega \times \varOmega$ with prescribed marginals $\mu$ and $\nu$, such that

$$\begin{aligned} \int _\varOmega \, \; \mathrm {d}\pi [U,y] = \mu [U], \qquad \int _\varOmega \, \; \mathrm {d}\pi [x,V] = \nu [V] \end{aligned}$$

for all measurable $U, V \subset \varOmega$ and all $\pi \in \varPi (\mu ,\nu )$. Each measure $\pi \in \varPi (\mu ,\nu )$ is interpreted as a transportation plan that specifies how much probability mass $\pi [x,y]$ is transferred from each location $x \in \varOmega$ to each location $y \in \varOmega$, incurring a contribution $d_2(x,y)\cdot \mathrm {d}\pi [x,y]$ to the total cost.

The Wasserstein distance is now defined by

$$\begin{aligned} W(\mu ,\nu ) = \inf _{\pi \in \varPi (\mu ,\nu )} \int _{\varOmega \times \varOmega } ||x-y||_2 \, \; \mathrm {d}\pi [x,y] \end{aligned}$$

(8)

and defines a metric on the space of probability measures, see [5] for simple proof that W defines a metric. For self-similar measures aspects of Wasserstein distances can be computed explicitly [7].

Note that the cost per unit mass is given by a metric on the phase and that there are many choices for this metric. Here we only consider the Euclidean metric because of equivariance under rotations

$$\begin{aligned} d_2(x,y) = ||x-y||_2 = \left( \sum _{i=1}^k |x_i-y_i|^2 \right) ^{1/2}. \end{aligned}$$

(9)

Although all metrics on $\varOmega$ are topologically equivalent, other metrics emphasize different aspects of the statistical properties of the invariant measures. In ongoing work, we are studying various properties and merits of different metrics.

Optimal transport problems arise in a number of applications in image analysis, shape matching, and inverse modeling in physics, see [28] for references. The measure theoretic Wasserstein formalism allows a unified treatment, but more importantly in the present setting the natural measures correspond to finite sum of Dirac measures. In this case the optimal transportation problem reduces to a convex optimalization problem between two weighted point sets and can be calculated by standard methods.

Following early work of Hitchcock [20, 28], suppose discrete measures are given by

$$\begin{aligned} \mu = \sum _{i=1}^{n_1} \alpha _i \delta _{x_i}, \qquad \nu = \sum _{j=1}^{n_2} \beta _j \delta _{y_j}, \end{aligned}$$

(10)

where the supplies $\alpha _i \in (0,1]$ and the demands $\beta _j \in (0,1]$ are normalized such that $\sum _i \alpha _i = \sum _j \beta _j = 1$.

Any measure in $\varPi (\mu ,\nu )$ can then be represented as a nonnegative that is feasible, which is to say that it fulfills the source and sink conditions

$$\begin{aligned} \sum _j f_{ij} = \alpha _i, \quad i=1,2,\cdots ,n_1 \quad \text {and}\quad \sum _i f_{ij} = \beta _j, \quad j=1,2,\cdots ,n_2. \end{aligned}$$

(11)

In this case the optimal transportation problem reduces to a special case of a minimum cost flow problem, the so-called transportation problem

$$\begin{aligned} W(\mu ,\nu ) = \min \sum _{ij} f_{ij} c_{ij}, \end{aligned}$$

(12)

over all feasible flows $f_{ij}$, where $c_{ij} = ||x_i-y_j||_2$.

This minimization problem can in principle be solved using a general linear programming solver [2, 23], and in the examples in this paper we have used an implementation by Löbel [13]. See Fig. 6 for an example.

Fig. 6.

Open circles correspond to the first measure, filled circles correspond to the second measure. Left panel Initial configuration. Numbers indicate probability mass at each point. Right panel An optimal transportation plan with Wasserstein distance $W \approx 3.122$. The numbers next to the arrows indicate how much probability mass is transported from the first measure to the second measure

Since the algorithms for the transportation problem have at least a cubic dependence on sample size. A practical solution is to resample smaller subseries from the reconstructed trajectory and to estimate the Wasserstein distances multiple times, bootstrapping its expected value. This reduces the computational load [20].

3 Distance Matrices

The statistical analysis of distance matrices is a well developed topic in analysis [4]. We give a short overview of techniques that are particularly useful in the analysis of Wasserstein distances. We assume that the distance information is presented in the form of a single matrix M whose entries $M_{ij} = W(\mu _i,\mu _j)$ represent the distance between two dynamical systems (which are calculated from their invariant measures $\mu _i$ and $\mu _j$, as discussed before). The actual distance being used is left unspecified.

3.1 Reconstruction by Multidimensional Scaling

Multi-Dimensional Scaling (MDS) is the generic name for a number of techniques that model distance data as points in a geometric (usually Euclidean) space. In the application to dynamical systems, each point in this space represents a single dynamical system and the space can be interpreted as the space of their possible dynamical behavior. We therefore call this space the behavior space. It should not be confused with the k-dimensional reconstruction space $\varOmega$ used for each single dynamical system in the calculations of the Wasserstein distances.

Classical (also called metric) MDS is similar to principal component analysis (PCA) and has been pioneered by Torgerson and Gower (see [4] for references). Here we focus on classical MDS and refer to the Appendix of [20] for more recent developments and variations.

Let us assume a priori that the distances $M_{ij}$, $1 \le i,j \le n$, are the distances between n points (representing n dynamical systems) in a m-dimensional Euclidean space with $m \le n$. Denote the coordinates of the i-th point by $x_{i1}, x_{i2}, \cdots , x_{im}$. In the following, we want to determine the $n \times m$ matrix $X=(x_{ij})$ of the totality of these coordinates from the distances in $M_{ij}$.

The squared distances $M_{ij}^2$, $1 \le i,j \le n$, can be expanded as

$$\begin{aligned} M_{ij}^2 = \sum _{l=1}^m \left( x_{il}^2 + x_{jl}^2 - 2 x_{il} x_{jl} \right) , \end{aligned}$$

(13)

which results in the matrix equation $D^2 = c1^T_n + 1_nc^T - 2 XX^T$. Here $D^2$ represents the matrix with elements $D^2_{ij} = M_{ij}^2$, the vector $c = (c_1, \cdots , c_n)^T$ consists of the norms $c_i = \sum _{l=1}^m x_{il}^2$, and $1_n$ is an $n \times 1$ unit vector. Therefore, the scalar product matrix $B = XX^T$ is given by

$$\begin{aligned} B = -\frac{1}{2}JD^2J, \end{aligned}$$

(14)

where $J = I - \frac{1}{n}1_n 1^T_n$ and I denotes the $n \times n$ identity matrix. To find the classical MDS coordinates from B, we factor B by its eigendecomposition (Singular Value Decomposition):

$$\begin{aligned} B = Q \varLambda Q^T = (Q \varLambda ^{1/2})(Q \varLambda ^{1/2})^T = XX^T. \end{aligned}$$

(15)

Here $\varLambda$ is the diagonal matrix with the eigenvalues of B on the diagonal. In general, the dimension m is not known in advance, and has to be interpreted as a parameter. Let the eigenvalues of B be ordered by decreasing size, and denote by $Q_m$ the matrix of the first m columns of Q; these correspond to the first m eigenvalues of B, in decreasing order. The coordinate matrix of classical MDS is then given by

$$\begin{aligned} X = Q_m \varLambda ^{1/2}_m. \end{aligned}$$

(16)

The distances in the matrix M can now be represented as points in a Euclidean space if X is real, or equivalently if the first m eigenvalues of B are nonnegative. In that case, the coordinates in X are found up to a rotation.

The optimal maximal dimension m of the reconstruction can be determined by considering the strain,

$$\begin{aligned} S = ||XX^T - B||^2 = \sum _{ij} |(XX^T)_{ij} - B_{ij}|^2. \end{aligned}$$

(17)

The strain quantifies the error made by projecting the distances to the subspace, and decreases monotonously as the reconstruction dimension m is increased, as long as no negative eigenvalues are encountered under the m eigenvalues used in the reconstruction. However, the speed of decrease varies with the dimensionality. A rapid fall in the beginning usually turns into a much slower decrease above a certain dimensionality $m^*$ (see for example in Figs. 14 and 15). The dimension $m^*$ so obtained is the choice for m used in this paper.

Note that the primary use of the MDS reconstruction is dimension reduction. This is particularly useful in exploratory data analysis. In the Hènon example, we use a number of two-dimensional reconstructions of the behavior space for visualization purposes (as more than two dimensions are obviously difficult to assess visually). A different application of the MDS reconstruction is the classification of time series by their dynamical properties (see Sect. 5), and in this case we determine the optimal dimension of the behavior space by cross-validation of the accuracy of Linear Discriminant Analysis (LDA).

3.2 Classification and Discriminant Analysis

Assume a number of points $x_i \in \mathbb R^m$ are given, where $1 \le i \le n$. Consider a partition of the index set $I=(1, \cdots , n)$ into the indices $I_1$ belonging to the first class, and the remaining indices $I_2 = I \setminus I_1$. The weighted class means (also called centroids) are

$$\begin{aligned} c_1 = \frac{1}{n_1} \sum _{i \in I_1} x_i, \qquad c_2 = \frac{1}{n_2} \sum _{i \in I_2} x_i, \end{aligned}$$

(18)

with corresponding intra-class variances

$$\begin{aligned} \sigma ^2_1 = \sum _{i \in I_1} (x_i - c_1)(x_i - c_1)^T, \qquad \sigma ^2_2 = \sum _{i \in I_2} (x_i - c_2)(x_i - c_2)^T. \end{aligned}$$

(19)

The overall mean is

$$\begin{aligned} \bar{x} = \frac{1}{n} \sum _i x_i = \frac{n_1 c_1 + n_2 c_2}{n}. \end{aligned}$$

(20)

The goal of LDA is to find a vector $w \in \mathbb R^m$ that maximizes the generalized Rayleigh quotient

$$\begin{aligned} J(w) = \frac{w^T(c_1-c_2)(c_1-c_2)^Tw}{w^T (\sigma ^2_1 + \sigma ^2_2) w}. \end{aligned}$$

(21)

The motivation to do this is that the optimal direction maximizes the separation (or inter-class scatter) of the means, scaled by the variances in that direction (the corresponding sum of intra-class scatter), and which can, in some sense, be considered the signal-to-noise ratio of the data.

The direction w is easily found by a spectral technique [24], and the method is implemented in standard software packages (for example, see [15]). Points are then classified by their nearest neighbour in the projection onto the direction of $\omega$. Application of LDA to point coordinates in behavior space allows to classify dynamical systems.

Note that it is not possible to apply LDA directly on distance matrices since these are collinear. This is the main reason to adopt as a principle underlying distance-based analysis of dynamical systems:

Principle 1.

The reconstructed behavior space, i.e., the MDS coordinates derived from a distance matrix, is the object at which all (statistical) analysis starts.

In the statistical analysis we follow this principle and only consider points in behavior space and no longer consider distance matrices directly.

3.3 Cross-Validation

In the case of LDA in behavior space, increasing the dimensionality m of the behavior space inevitably improves the accuracy of classification (as long as no negative eigenvalues are encountered). However, this does not usually tell us more about the accuracy obtained when faced with the classification of an additional data item of unknown class. The usual solution to assess predictive accuracy in a useful way is to partition the available data into a training and a test set of about the same size. After setting up the discrimination method on the former, its accuracy is then tested on the latter. However, for small datasets this is usually not feasible, so that we have to use cross-validation.

In leave-one-out cross-validation, the i-th data point is removed from the n points available, the discriminant function is set up, and the i-th point classified, for all possible values of $i \le n$. The average accuracy of all these classifications is the (leave-one-out) cross-validated predictive accuracy of the classification.

Cross-validation of LDA in behavior space seems straightforward: first the behavior space is constructed by the classical MDS solution, then the classification of points in this space is cross-validated. Note however that a (often significant) bias is introduced, if the MDS reconstruction makes use of the distance information of each point that is left out in the cross-validation step. Ideally, when classifying the i-th point as an “unknown data item” we would like to construct behavior space from a submatrix of the distance matrix, with the i-th row and column removed, classifying the i-th point in this space. For simplicity, let $i=n$, such that the coordinates of the last point need to be found in the behavior space defined by the first $n-1$ points. The idea is instead of deriving the scalar product matrix by the usual definition (14), the scalar product is computed using

$$\begin{aligned} B = -\frac{1}{2}\left( I-\frac{1}{n-1}1_{n-1} 1^T_{n-1}\right) D^2\left( I-\frac{1}{n-1}1_{n-1} 1_{n-1}^T\right) , \end{aligned}$$

(22)

where $1^T_{n-1}$ is used instead of $1^T_{n}$. Denote by b the fallible scalar products of the cross-validated item with the others, and by $\beta$ its squared norm. The coordinates $y \in \mathbb R^m$ of the last item are then given as the solution of the following nonlinear optimization problem:

$$\begin{aligned} \min _{y \in \mathbb R^m} \;\;(\beta - y^T y)^2 + 2 \sum _{i=1}^n (b_i - x^T_i y)^2, \end{aligned}$$

(23)

which can be solved by standard methods [20].

3.4 Statistical Significance by Permutation Tests

Given a partition of time series into two or more classes, we quantify the significance of the separation between the classes by using the Multiple Response Permutation Procedure (MRPP), see [16]. Assuming two classes of systems as before, the usual MRPP statistic is given by

$$\begin{aligned} \delta = \sum _{i=1}^2 \frac{n_i}{n_1+n_2} \varDelta _i,\quad \hbox { where }\, \varDelta _i = \left( {\begin{array}{c}n_i\\ 2\end{array}}\right) ^{-1} \sum _{k,l \in I_i} M_{kl}, \quad i = 1, 2. \end{aligned}$$

(24)

Here $\varDelta _i$ is the average distance of the i-th class.

Under the null hypothesis that the classes of dynamical systems arise from the same (unknown) distribution of systems in behavior space, we can reassign their class labels arbitrarily. For each of these $\left( {\begin{array}{c}n_1+n_2\\ n_1\end{array}}\right)$ labelings, the MRPP is calculated. The distribution of values of $\delta$ under all possible relabelings is (for historical reasons) called the permutation distribution. The (P-value) of this statistical test is given by the fraction of labelings of the permutation distribution with a smaller value of $\delta$ than the one obtained by the original class labels. Note that the $\delta$ statistic itself is generally not scale-invariant, but that the P-value derived from it can be used to compare the quality of separation across different datasets. In practice the number of possible labelings to consider is usually too large, so the results in the example sections are based on $10^5$ randomly generated labelings, as is common practice in statistics.

4 Example: The Hénon System

In this section we use the proposed approach to the synthetic time series generated by the Hénon map. As discussed before, bootstrapping the Wasserstein distances leads to an error which is a combination of simulation error, due to the finite number of bootstraps, plus a statistical error, due to the finite number of points from the invariant measures sampled and the finite length of the time series. Fortunately, the estimation of the self-distances $W(\mu ,\mu )$ allows to assess these errors.

The left panel of Fig. 7 shows the self-distances against the sample size used for bootstrapping in a double logarithmic plot. Observe that the simulation error is much smaller than the statistical error, so bootstrapping the Wasserstein distances with the low number of 25 realizations seems sufficient in the present setting.

Fig. 7.

Dependence of Wasserstein self-distances on sample size. Left panel Wasserstein distances for embedding dimensions 1 (lowest curve) to 6 (highest curve). The deviation from the true value of zero is an indication of the statistical error. The slope of the regression lines is roughly $-1/2$, which is the typical scaling behavior of Monte-Carlo simulation. Right panel CPU time needed for these calculations showing quadratic dependence on sample size

The lowest line in Fig. 7 corresponds to a one-dimensional (trivial) embedding. Increasing the embedding dimension leads to the lines above it, with the highest one corresponding to a six-dimensional delay embedding. As expected, the self-distances decrease with increasing sample size. Interestingly, the slope of this decrease is $-0.53 \pm 0.03$ ($R^2=0.989$, P-value $4.4 \times 10^{-6}$), in the double-logarithmic plot (for embedding dimension $k=3$, with similar values for the other dimensions), which is consistent with the typical scaling behavior of Monte-Carlo simulation. In other words, the error is mainly statistical, which is evidence for the robustness of the Wasserstein distances. From the above we see that self-distances can be used to assess errors in embeddings, and that they can also provide an alternative way to estimate the optimal embedding dimension in nonlinear time series analysis.

Fig. 8.

Dependence of Wasserstein self-distances on noise. Left panel Wasserstein distances for embedding dimensions 1 (lowest curve) to 6 (highest curve) and fixed sample size $N=512$. Right panel Wasserstein distances for sample sizes $N \in \{64,128,256,512\}$ (from top to bottom) and fixed embedding dimension $k=3$

4.1 Influence of Noise

To study the influence of additive noise, normally distributed random variates were added to each point of the time series prior to reconstruction of the invariant measures. The mean of the noise was zero, and the standard deviation a fixed fraction of the standard deviation of the signal over time. Figure 8 shows the dependence of the Wasserstein self-distances for different noise levels. In the left panel, the embedding dimension was varied from one (lowest line) to six (highest line), for a fixed sample size $N=512$ and 25 bootstraps. The effect of noise is higher for larger embedding dimensions, with a linear change in the slope of the regression lines of $0.15\pm 0.01$ ($R^2=0.99$, P-value $8.0\cdot 10^{-5}$). The error can partially be compensated by increasing the sample size, as can be seen in the right panel of Fig. 8, for the case of a three-dimensional embedding. For $N=512$ sample points, the slope of the Wasserstein distances is $2.02 \pm 0.03$ (with similar values for other sample sizes), i.e., the statistical error doubles for noise on the order of the original variability in the signal. This shows the robustness Wasserstein distances with respect to noise, since the statistical error is of the order of the signal-to-noise ratio, and not higher.

Fig. 9.

Invariant measures of the x-variable in the Hénon system, for different values of the parameters. Left panel Variation in parameter a, with constant $b=0.3$. Right panel Variation in parameter b, with constant $a=1.4$

4.2 Visualizing Parameter Changes

A main goal of the distance analysis presented in Sect. 3 is the possibility to visualize changes in dynamical behavior with respect to parameter changes, similar to a bifurcation analysis. However, whereas in the usual bifurcation analysis only regions of phase space are identified where the qualitative behavior of a dynamical system changes, in the distance-based analysis of dynamical systems these changes are quantified. This has not only potential applications in numerical bifurcation analysis, but also aids in quickly identifying interesting atypical) regions of parameter space. We demonstrate this approach using the synthetic time series generated by the Hénon map and vary the parameters a, b of the Hénon map as follows

$$\begin{aligned} (a,b) = (a_i,0.3)\qquad \hbox { and }\quad (a,b)=(1.4,b_j), \end{aligned}$$

(25)

where $a_i = 1.4 - 0.05 i$, for $0 \le i \le 14$, and $b_j = 0.3 + 0.02 j$, for $-14 \le j \le 0$. In Fig. 9 the invariant measures of the x-variable, corresponding to the embedding dimension $k=1$ are shown. Dark areas correspond to large time averages, and light areas to low time averages. On the top of the plots, the indices of the corresponding parameter values are indicated.

Fig. 10.

Two-dimensional MDS representation of Wasserstein distances for the Hénon system under parameter variation. Parameter values are shown in Fig. 9. Squares correspond to variation in the first parameter, triangles to variation in the second parameter. Numbers next to the symbols correspond to the indices of the dynamical systems introduced in the top axes of Fig. 9. The circles around the points corresponding to $a=1.4$, $b=0.3$ have radius 0.091 and 0.118, which are the mean self-distances

Bootstrapping all mutual distances, again under 25 bootstraps with 512 sample points each, is used in the left panel of Fig. 10 to obtain a two-dimensional projection of behavior space. Larger deviations of the parameters from $(a_0,b_0)=(1.4,0.3)$ result in points that are farther away from the point 0 corresponding to $(a_0,b_0)$. Summarizing, the points are well-separated, although quite a few of their distances are smaller than the mean self-distance $0.091 \pm 0.005$(indicated by a circle in the left panel of Fig. 10). Note that the triangle inequality was not violated, but subtracting more than 0.030 will violate it. Only the self-distances have therefore been adjusted, by setting them to zero.

Theoretically, as the Wasserstein distances are true distances on the space of (reconstructed) dynamical systems, it is clear that the points corresponding to changes in one parameter only lie on a few distinct piecewise continuous curves in behavior space. At a point where the dynamical system undergoes a bifurcation, these curves are broken, i.e., a point past a bifurcation has a finite distance in behavior space from a point before the bifurcation. The relatively large distance of point 10 (with parameter $a_{10}=0.9$) from the points with indices larger than 11 as seen in Fig. 10 corresponds to the occurrence of such a bifurcation.

The right panel of Fig. 10 shows a two-dimensional reconstruction of the Hénon system on a smaller scale, where the parameters were varied as $a_i = 1.4 - 0.0125 i$, for $0 \le i \le 14$, and $b_j = 0.3 + 0.005 j$, for $-14 \le j \le 0$. Even on this smaller scale, where the mean self-distances were $0.118 \pm 0.003$, the points are relatively well separated and there are indications for bifurcations. Note that the triangle inequality again holds, with a threshold of 0.070 before it is violated.

4.3 Coupling and Synchronization

Wasserstein distances also allow to quantify the coupling between two or more dynamical systems, for example, to analyse synchronization phenomena in dynamical systems. In this section we consider two unidirectionally coupled chaotic Hénon maps similar to the example discussed in [25]. The systems are given by the following equations

$$\begin{aligned} x_{n+1}&= 1 + y_n - 1.4 x_n^2,&y_{n+1}&= 0.3 x_n, \end{aligned}$$

(26)

$$\begin{aligned} u_{n+1}&= 1 + v_n - 1.4 (C x_n + (1-C) u_n) u_n&v_{n+1}&= B v_n, \end{aligned}$$

(27)

and we call the (x, y) system the master and the (u, v) system the slave system. The strength of the coupling is given by the coupling parameter C, which can be varied from 0 (uncoupled systems) to 1 (strongly coupled systems) in steps of size 0.05. The parameter B is either $B=0.3$ (equal systems) or $B=0.1$ (distinct systems).

Fig. 11.

Distances for coupled Hénon systems. Coupling strength varied from $C=0.0$ to $C=1.0$ in steps of 0.05. Left panel Equal Hénon systems ($B=0.3$). Right panel Distinct Hénon systems ($B=0.1$). Top curves are uncorrected distances, the lower curves are corrected by subtracting the minimum distance encountered. Only the mean curve is depicted at the bottom

Fig. 12.

Two-dimensional MDS representation of Wasserstein distances for coupled Hénon systems. Coupling strength varied as in Fig. 11. Left panel Equal Hénon systems ($B=0.3$). Right panel Distinct Hénon systems ($B=0.1$)

In Fig. 11 Wasserstein distances between the dynamics reconstructed from the variables x and u, respectively, against coupling strength C are shown. The initial conditions of the two Hénon systems were chosen uniformly from the interval [0, 1] and the results for ten such randomly chosen initial conditions are depicted in Fig. 11 as distinct lines (top). The dots correspond to the mean of the distances over the ten realizations. The variation over the ten different initial conditions is considerably small, as expected. This shows that the approximations of the invariant measures are considerably close to the true invariant measure which does not depend on the initial condition. The bottom lines display corrected distances, where the minimum of all distances has been subtracted. This seems appropriate in the setting of synchronization analysis, and does not violate the triangle inequality.

A further important feature of the Wasserstein distances can be seen in the left panel of Fig. 11, where the distances for the two Hénon systems with equal parameters (but distinct, randomly realized initial conditions) are depicted. As the distances are calculated from (approximations of) invariant measures, these equivalent systems are close in behavior space either when (i) they are strongly coupled, but also (ii) when the coupling is minimal. In between, for increasing coupling strengths the distances initially rise to about the four-fold value of the distance for $C=0$, and then fall back to values comparable to the uncoupled case, from about $C=0.7$ on.

The right panel of Fig. 11 shows the case of two unequal Hénon systems, where the initial distances ($C=0$) are positive and eventually decrease for stronger coupling. Interestingly, also in this case one sees the phenomenon that increasing coupling first results in a rise of the distances, that only decrease after a certain threshold in coupling is crossed. This can be interpreted as follows: Weak forcing by the master system does not force the behavior of the slave system to be closer to the forcing dynamics, rather the nonlinear slave system offers some “resistance” to the forcing (similar to the phenomenon of compensation in physiology). Only when the coupling strength is large enough to overcome this resistance does the slave dynamics become more similar to the masters’ (decompensation).

In Fig. 12 this phenomenon is illustrated in behavior space, reconstructed by multidimensional scaling from the distances between the dynamics in the u-variables (the slave systems) only. The left panel, for equal systems, shows a closed curve, i.e., the dynamics of the slave systems is similar for both small and large coupling strengths. The right panel, for unequal systems, shows the occurrence of the compensation/decompensation phenomenon in the curves of the right panel of Fig. 11.

5 Example: Classification of Lung Diseases Asthma and COPD

An interesting concept to connect dynamical systems and physiological processes is the notion of a dynamical disease, which was defined in a seminal paper [14] as a change in the qualitative dynamics of a physiological control system when one or more parameters are changed.

5.1 Background

Both asthma and the condition known as chronic obstructive pulmonary disease (COPD) are obstructive lung diseases that affect a large number of people worldwide, with increasing numbers expected in the future. In the early stages they show similar symptoms, rendering correct diagnosis difficult. As different treatments are needed, this is of considerable concern.

Fig. 13.

Example time series of respiratory resistance R(8) (upper curves) and respiratory reactance X(8) (lower curves) by forced oscillation technique during thirty seconds of tidal breathing. Left panel A patient with mild asthma. Right panel A patient with mild to severe chronic obstructive pulmonary disease. The horizontal lines indicate the mean values used routinely in clinical assessment

An important diagnostically tool is the forced oscillation technique (FOT), as it allows to assess lung function non-invasive and with comparatively little effort [19]. By superimposing a range of pressure oscillations on the ambient air and analyzing the response of the airway systems, a number of parameters can be estimated that describe the mechanical properties of airway tissue. In particular, for each forcing frequency $\omega$, transfer impedance $Z(\omega )$ can be measured. This is a complex quantity consisting of two independent variables. The real part of $Z(\omega )$ represents airway resistance $R(\omega )$, and its imaginary part quantifies airway reactance $X(\omega )$, i.e., the elasticity of the lung tissue. Both parameters are available as time series, discretely sampled during a short period of tidal breathing. The dynamics of $R(\omega )$ and $X(\omega )$ are influenced by the breathing process, anatomical factors and various possible artifacts (deviations from normal breathing, movements of the epiglottis, etc.). Clinicians usually only use the mean values $\bar{R}(\omega )$ and $\bar{X}(\omega )$ of these parameters, averaged over the measurement period, but clearly there is a lot more dynamical information contained in the time series, see Fig. 13 for example time series of these fluctuations for two patients.

Fig. 14.

Results for distances in means (see text for details). Panel A Two dimensional MDS reconstruction for patients suffering from asthma (open circles) and COPD (filled squares). The patient number is shown below the symbols. Panel B Strain values against reconstruction dimension. Panel C MRPP statistic for the two classes. The value of $\delta$ for the labeling in panel A is indicated by the vertical line. The P-value is shown in the upper left corner

5.2 Discrimination by Wasserstein Distances

The main motivation for the application of Wasserstein distances to this dataset is the assumption that the two lung diseases affect the temporal dynamics of transfer impedance in distinct ways, and not only its mean value. Considering asthma and COPD as dynamical diseases, we assume an underlying dynamical systems with different parameters for the different diseases. Although these parameters are not accessible, it is then possible to discriminate the two diseases, with the Wasserstein distances quantifying the differences in the shape of their dynamics.

Fig. 15.

Results for Wasserstein distances. Panel A Two dimensional MDS reconstruction for patients suffering from asthma (open circles) and COPD (filled squares). The patient number is shown below the symbols. Panel B Strain values against reconstruction dimension. Panel C MRPP statistic for the two classes. The value of $\delta$ for the labeling in panel A is indicated by the vertical line. The P-value is shown in the upper left corner

For simplicity, we only consider a two-dimensional reconstructing, where the time series of R(8) and X(8) were combined into a series of two-dimensional vectors with trivial embedding dimension $k=1$, trivial lag $q=1$, and a length of about 12000 values (recorded at 16 Hz, the Nyquist frequency for the 8 Hz forced oscillation, concatenating all 12 measurements into one long series per patient). A more elaborated analysis will be presented elsewhere. Here we consider the distribution of these points in $\varOmega =\mathbb R^2$ an approximation of the invariant measure of the underlying dynamical system.

The results for the squared sum of differences

$$\begin{aligned} d_{ij} = \left( (\bar{X}_i(8)-\bar{X}_j(8))^2 + (\bar{R}_i(8)-\bar{R}_j(8))^2 \right) ^{1/2} \end{aligned}$$

(28)

in means (not the Wasserstein distances), are shown in Fig. 14 and the results for the Wasserstein distance are shown in Fig. 15. Panel A on the left shows a two-dimensional reconstruction of their behavior space by metric MDS. The strain plot in Panel B suggests an optimal reconstruction occurs in two dimensions, and indeed the classification confirms this. Although the maximal accuracy of classification is 0.88 in a 11-dimensional reconstruction (i.e., 88% of the patients could be correctly classified), this drops to 0.72 in two dimensions when cross-validated. The separation of the two classes is significant at the 0.033 level, as indicated by the MRPP statistic in Panel C. Note that these distances violated the triangle inequality by 0.23, with mean self-distances of about 0.12. The results for the Wasserstein distances W shown in Fig. 15 are much more pronounced, significant at the 0.0003 level. The classification is even perfect in a 12-dimensional reconstruction, with a maximal accuracy of 0.88 in a 9-dimensional reconstruction when cross-validated. Although the information about the means and their variance has been removed, the classification by Wasserstein distances is actually better. From this we conclude that the dynamical information contained in the fluctuations of respiratory impedance contains valuable clinical information. Moreover, these distances respect the triangle inequality (with a mean self-distance of about 0.25). See [19] for details and further information.

In ongoing work we are further improving the analysis by approximating the nonlinear dynamics by a Markov process. In particular, we first describe the FOT dynamics locally by a Fokker-Planck equation estimating the drift and diffusion coefficients directly from the time series, and then use the improved dynamical description to quantify differences between the FOT dynamics of different patient groups, and between individual days for each patient separately.