Understanding Entrainment Processes in the Atmosphere: The Role of Numerical Simulation

Abstract

Turbulent entrainment is a process of primary importance in the atmospheric boundary layer; however despite several decades of intense study much remains to be understood. Direct Numerical Simulation (DNS) and Large-Eddy Simulation (LES) have a tremendous potential to improve the understanding of turbulent entrainment, particularly if combined with theory. We discuss a recently developed framework for turbulent jets and plumes to decompose turbulent entrainment in various physical processes, and modify it for use in a stably stratified shear driven (nocturnal) boundary layer. The decomposition shows that inner layer processes become negligible as time progresses and that the entrainment coefficient is determined by turbulence production in the outer layer only.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Turbulent entrainment plays a central role in the evolution of the atmospheric boundary layer, the life cycle of clouds, katabatic winds and many other physical processes in the atmosphere [13]. Turbulent entrainment occurs on the interface of two fluid layers with differing turbulence intensity and entails the incorporation of fluid from the relatively quiescent layer into the turbulent layer. One of the canonical examples in the atmosphere is the entrainment of fluid from the free troposphere (which is relatively quiescent) into the atmospheric boundary layer (ABL), which is the turbulent fluid layer closest to the earth’s surface. Turbulent entrainment will cause the ABL of thickness h to increase in time at a rate

$$\begin{aligned} w_e = \frac{\text {d} h}{\text {d} t}, \end{aligned}$$

(1)

where $w_e$ is referred to as an entrainment velocity.

Restricting attention to dry conditions, the (potential) temperature $\theta$ in the ABL is relatively uniform due to the turbulent mixing and the quiescent layer overhead is warmer; a relatively sharp temperature jump of magnitude $\varDelta \theta$ is present at the interface of the two layers. Turbulent entrainment will be inhibited by the temperature jump as the turbulence will need to perform work to pull the warm fluid down, causing an increase in the potential potential energy of the ABL. Introducing a typical turbulent velocity scale $\mathscr {U}$, it is thus expected that (assuming very high Reynolds and Péclet numbers)

$$\begin{aligned} E \equiv \frac{w_e}{\mathscr {U}} = f(\text {Ri}),\quad \quad \text {where} \quad \quad \text {Ri} = \frac{\varDelta b h}{\mathscr {U}^2}. \end{aligned}$$

(2)

Here, $\text {Ri}$ is a bulk Richardson number and $\varDelta b = (g / \theta _0) \varDelta \theta$ is the buoyancy jump between the two layers, g is the gravitational acceleration and $\theta _0$ is a reference temperature.

Entrainment laws are important in numerical weather prediction because three-dimensional turbulence is not resolved. For example, the UK Unified Model currently employs a horizontal resolution of 1.5 km, insufficient to resolve any of the turbulence which has scales as small as 1 mm in a typical daytime ABL. Hence, finding the appropriate function f has received significant attention over the last half century [5]. However, turbulent entrainment velocities $w_e$ are usually very small compared to the other velocity scales (wind, turbulence) and its measurement is a formidable challenge. Consequently, experiments and observations sometimes report a factor 5 difference in the measured entrainment velocities [5].

The tremendous increase in computational power has enabled significant progress to be made in understanding entrainment via the turbulence-resolving methods of large-eddy simulation and direct numerical simulation, in the context of daytime boundary layers [7, 8, 14], nocturnal boundary layers [2, 9] and clouds [1, 4]. The turbulence community has made substantial progress in understanding entrainment from a small-scale perspective, e.g. [3, 16]. However, the understanding remains fragmented and case-specific, with an overarching theory being absent.

Recently, a framework was developed for turbulent jets and plumes which enables turbulent entrainment to be decomposed into different physical processes [15]. The framework relies on the internal consistency of the continuity, momentum and mean kinetic energy equations. For jets and plumes, it was shown that the dimensionless turbulence production is practically identical in jets and plumes, which implied that the Priestley and Ball entrainment model [6, 12, 15] is the appropriate model for jets and plumes in a neutral environment. In this contribution, this framework will be extended to a wall-bounded flow, specifically the nocturnal boundary layer discussed in [9].

2 Sheared Nocturnal Boundary Layer

Consider an idealised sheared nocturnal boundary layer with an initially linear stratification $b_0 = N^2 z$ and a uniform wall shear stress $\tau _w \equiv \rho u_*^2$ as discussed in [9, 10] and schematically shown in Fig. 1. This problem has two homogeneous directions and is mathematically described after Reynolds-averaging by

$$\begin{aligned} \frac{\partial \overline{u}}{\partial t} + \frac{\partial \overline{w'u'}}{\partial z}&= \nu \frac{\partial ^2 \overline{u}}{\partial z^2},&\frac{\partial \overline{b}}{\partial t} + \frac{\partial \overline{w'b'}}{\partial z}&= \kappa \frac{\partial ^2 \overline{b}}{\partial z^2}, \end{aligned}$$

(3)

$$\begin{aligned} \left. \frac{\partial \overline{u}}{\partial z} \right| _w&= \frac{u_*^2}{\nu },&\left. \frac{\partial \overline{b}}{\partial z} \right| _w&= 0, \end{aligned}$$

(4)

$$\begin{aligned} \overline{u}(z, t=0)&=0,&\overline{b}(z, t=0)&= N^2 z. \end{aligned}$$

(5)

We performed Direct Numerical Simulation with our in-house code SPARKLE of a domain of $1024 \times 1024 \times 256$ m and a constant (eddy) viscosity $\nu =0.046$ m$^2$s$^{-1}$. Further simulation details are provided in Table 1. Here, $h_*=u_*/N$ is the buoyancy length scale and $\text {Re}_N=u_* h_* / \nu$ is the buoyancy Reynolds number, which were shown in [9] to be fundamental quantities for this problem.

Fig. 1

Schematic of the idealised sheared nocturnal boundary layer simulation setup

Table 1 DNS cases; the domain size is $4H\times 4H \times H$ with $\text {Pr}=1$ and $\nu = 0.046~$m$^2$/s

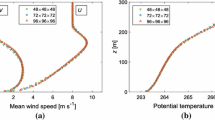
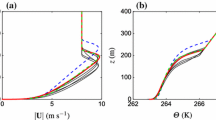
The system (3–5) evolves in a self-similar manner and has an inner and outer layer structure (Fig. 2). The characteristic scales of the inner layer are the classical shear length scale $\nu /u_*$, velocity scale $u_*$ and buoyancy scale $u_*^3/\nu$. The middle panels of Fig. 2 show a collapse of the velocity and buoyancy profiles for all three simulations for $z u_* / \nu < 150$.

Fig. 2

Velocity and buoyancy profiles for simulations 1a–c. Left panel unnormalised variables. Middle panel normalised by inner scales. Right panel normalised by outer scales

The outer length and velocity scales will be denoted by h and $u_T$, respectively. In [9] we diagnosed h based on the location of the inflection point in $\overline{b}$ [14], but in order to decompose entrainment we will need an estimate of h based on integral quantities. We choose the scales

$$\begin{aligned} h = \frac{Q^2}{M}, \quad \quad u_T = -\frac{M}{Q}, \quad \quad b_T = N^2 h, \end{aligned}$$

(6)

where the volume flux Q [L$^2$T$^{-1}$] and specific momentum flux M [L$^3$T$^{-2}$] are defined as, respectively

$$\begin{aligned} Q = \int _0^\infty \overline{u} \text {d} z, \quad \quad M = \int _0^\infty \overline{u}^2 \text {d} z. \end{aligned}$$

(7)

Here we note that the minus sign in the definition of $u_T$ is present to make this quantity positive. The definition of $b_T$ ensures that the self-similarity solution remains consistent with the stratification in the ambient. The self-similar profiles in the outer layer scales are shown in the right panels of Fig. 2. An excellent collapse can be observed, except very near the surface.

The dependence of $(h/h_*)^2$ on Nt is shown in the left panel of Fig. 3 for all three cases under consideration and displays almost perfect linear scaling with time, which implies that $h/h_* \sim (N t)^{1/2}$ [9]. For the case under consideration, $\mathscr {U} = u_*$ and $\varDelta b = N^2 h / 2$ (Fig. 1), implying that Eq. (2) becomes

$$\begin{aligned} E = \frac{1}{u_*} \frac{\text {d} h}{\text {d} t}, \quad \quad \text {Ri}= \frac{N^2 h^2}{2 u_*^2}. \end{aligned}$$

(8)

Noting that $\text {Ri} = (h/h_*)^2 / 2$, it is clear that $\text {Ri}$ will increase linearly with time. In the right panel of Fig. 3, the entrainment coefficient E is plotted as a function of $\text {Ri}(t)$, together with the power law $E=0.26 \text {Ri}^{-1/2}$. The proportionality constant is lower than in [9] because of the different definition of h in this paper.

Fig. 3

a The layer thickness h as a function of Nt. b The entrainment coefficient E as a function of $\text {Ri}$

3 Entrainment Decomposition

By substituting the the definition of h in Eq.  (6) into the definition of E in Eq.  (8) it follows that [15]

$$\begin{aligned} E = \frac{1}{u_*} \frac{\text {d}}{\text {d} t} \left( \frac{Q^2}{M}\right) = -\frac{2}{u_* u_T} \frac{\text {d} Q}{\text {d} t} - \frac{1}{u_* u_T^2} \frac{\text {d} M}{\text {d} t}. \end{aligned}$$

(9)

This provides important information as it reveals that an explicit equation for the entrainment law can be obtained by combining the integral momentum and mean energy equations. Taking the time-derivative of Q and M results in

$$\begin{aligned} \frac{\text {d} Q}{\text {d} t} = - u_*^2, \quad \quad \frac{\text {d} M}{\text {d} t} = 2 \int _0^\infty \overline{w'u'} \frac{\partial \overline{u}}{\partial z} \text {d} z - 2 \nu \int _0^\infty \left( \frac{\partial \overline{u}}{\partial z}\right) ^2 \text {d} z - 2 \overline{u}_w u_*^2, \end{aligned}$$

(10)

where $\overline{u}_w = \overline{u}(z=0, t)$. Substitution of Eq. (10) into Eq. (9) leads to

$$\begin{aligned} E = \underbrace{- \frac{2}{u_* u_T^2} \int _0^\infty \overline{w'u'} \frac{\partial \overline{u}}{\partial z} \text {d} z}_{E_{\text {prod}}} + \underbrace{\frac{2 \nu }{u_* u_T^2} \int _0^\infty \left( \frac{\partial \overline{u}}{\partial z}\right) ^2 \text {d} z + \frac{2 u_*}{u_T} \left( 1+\frac{\overline{u}_w}{u_T}\right) }_{E_{\text {dis}}}. \end{aligned}$$

(11)

The first term is the turbulent production contribution $E_{\text {prod}}$, which is the prime contributor to turbulent entrainment. The second term $E_{\text {dis}}$ includes contributions of the dissipation rate of mean kinetic energy and friction.

Fig. 4

Entrainment decomposition for simulation 1a: a in terms of $E_{prod}$ and $E_{dis}$ and compared with the direct definition (E); b in terms of inner and outer layer contributions $E_\chi ^+$ and $E_\chi ^-$, respectively

The top panel of Fig. 4 shows the individual terms of the decomposition and their sum. Here, E has been corrected for the expected powerlaw-dependence on $\text {Ri}$, and it can indeed be observed that all quantities become constant with time, demonstrating once more the robustness of the $E\sim \text {Ri}^{-1/2}$ relation. The correspondence between E calculated directly from the definition of Eq. (8) and from the decomposition (11) are within 10% of each other. Clearly, $E_{prod}$ has a positive contribution and $E_{dis}$ a negative contribution; $E_{prod}$ is about a factor two larger than E.

It is useful to be able to distinguish inner layer contributions to E from outer layer contributions. To this end, we split the integrals in Eq. (11) into two parts:

$$\begin{aligned} \int _0^{\infty } \text {d} z = \underbrace{\int _0^{h/2} \text {d} z}_{\text {inner}} + \underbrace{\int _{h/2}^\infty \text {d} z}_{\text {outer}} \end{aligned}$$

(12)

and denote inner and outer layer contributions by $E_\chi ^+$ and $E_\chi ^-$, respectively; these are displayed in the bottom panel of Fig. 4. The inner layer contributions vanish over time; this because in the inner layer, production and dissipation are in equilibrium so that the difference will come from the boundary terms which reduce to zero due to the factor $u_*/u_T$. Hence, outer layer processes are solely responsible for the observed entrainment coefficient E (consistent with [11]). Furthermore, the outer layer term $E_{dis}^-$ is negligible, implying that

$$\begin{aligned} E \approx E_{prod}^{-} = -\frac{2}{u_* u_T^2} \int _{h/2}^\infty \overline{w'u'} \frac{\partial \overline{u}}{\partial z} \text {d} z. \end{aligned}$$

(13)

This is a remarkably simple expression. Using the gradient-diffusion hypothesis $\overline{w'u'} = - \nu _T \partial \overline{u} / \partial z$, noting that $\nu _T \sim h_* u_*$ [9], and using the outer layer scaling suitable for the integral under consideration, it follows directly that

$$\begin{aligned} E \approx \frac{2}{u_* u_T^2} \int _{h/2}^\infty \nu _T \left( \frac{\partial \overline{u}}{\partial z} \right) ^2 \text {d} z \sim \frac{h_*}{h} \sim \text {Ri}^{-1/2}. \end{aligned}$$

(14)

4 Conclusions

Large-eddy Simulation and Direct Numerical Simulations are important numerical techniques for understanding turbulent entrainment. The availability of noise-free fully resolved data under “ideal” circumstances allows one to systematically diagnose the small but important signals that comprise turbulent entrainment. Particularly in combination with theory, DNS and LES provide a unique tool to probe deeply into what causes turbulent entrainment, often at Reynolds numbers equal or exceeding those from the canonical laboratory experiments carried out in the seventies and eighties [5] (although not in terms of their Prandtl/Schmidt number, as most experiments were carried out using salt).

In this paper, we decomposed entrainment into contributions from distinct physical processes. The method, originally developed for free-shear layers [15], was extended to wall-bounded flows which have both an inner and outer layer structure. An analysis of an idealised sheared nocturnal boundary layer revealed that the inner layer contributions provide a negligible contribution to E provided enough time has passed. In the outer layer, the dissipation is negligible, implying that the turbulent entrainment coefficient E is determined primarily by the production of turbulence kinetic energy.