Nanoelectronic Coupled Problem Solutions: Uncertainty Quantification of RFIC Interference

Abstract

Due to the key trends on the market of RF products, modern electronics systems involved in communication and identification sensing technology impose requiring constraints on both reliability and robustness of components. The increasing integration of various systems on a single die yields various on-chip coupling effects, which need to be investigated in the early design phases of Radio Frequency Integrated Circuit (RFIC) products. Influence of manufacturing tolerances within the continuous down-scaling process affects the output characteristics of electronic devices. Consequently, this results in a random formulation of a direct problem, whose solution leads to robust and reliable simulations of electronics products. Therein, the statistical information can be included by a response surface model, obtained by the Stochastic Collocation Method (SCM) with Polynomial Chaos (PC). In particular, special emphasis is given to both the means of the gradient of the output characteristics with respect to parameter variations and to the variance-based sensitivity, which allows for quantifying impact of particular parameters to the variance. We present results for the Uncertainty Quantification of an integrated RFCMOS transceiver design.

1 Introduction

Modern mixed-signal and radio frequency (RF) integrated circuits (ICs) increasingly show the integration of various systems on a singe die [4, 5]. The integration involves both noisy parts, the so-called aggressors, and sensitive parts, the so-called victims and thus challenge the intellectual property blocks (IPs) to provide their proper and interference-free functioning. The integration goes hand in hand with progressive down scaling with impact on various parameters. The statistical variations, resulting from manufacturing tolerances of industrial processes, could lead to the acceleration of migration phenomena in semiconductor devices and finally can cause a thermal destruction of devices due to thermal runaway [7, 9, 10, 12].

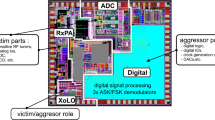
Moreover, unintended RF coupling, which can occur both as a result of industrial imperfections and as a consequence of the integration process, might additionally downgrade the quality of products and their performance or even be dangerous for safety of both environment and the end users [2]. Meeting the specification requirements for electromagnetic compatibility standards and issues related to interference between IPs at early design stages allows for avoiding expensive re-spins and for the consecutive decrease of the time-to-market cycle. In this phase proper floorplanning and grounding strategies are studied [5]. It allows for the identification, quantification and prediction of cross-domain coupling. Figures 1 and 2 show a floorplan setup and a testbench model, which includes the key elements. Among the coupling paths investigated in [5] were (i) the exposed diepad and downbonds, (ii) the splitter cells, (iii) the substrate, and (iv) the air. We analyze the exposed diepad vias and downbonds paths with respect to a number of model parameter variations including the number of downbonds, the number of ground pins, and the number of exposed diepad vias. Cross-domain transfer functions y from the digital to the analogue RF domain are studied with respect to input variations. We have a sinusoidal component of |X|, an angular frequency ω := 2πf and a phase ϕ := arg(X) as input to a linear time-invariant system and, with corresponding output as |Y | and ϕ _Y  := arg(Y ), the frequency response of the transfer function and the phase shift are defined by G(ω) = |Y |/|X| =: |H(iω)| and ϕ(ω) := ϕ _Y  − ϕ _X  = arg(H(iω)), respectively.

Fig. 1

Chip architecture with domains indicated [5]: Floorplan model for isolation and grounding strategies [2]

Fig. 2

Chip architecture with domains indicated [5]: Testbench model for an RFIC isolation problem

2 Stochastic Modeling

We apply stochastic modeling for a floorplan model with grounding strategies. The physical design, shown in Fig. 2, involves on-chip coupling effects, chip-package interaction, substrate coupling, leading to co-habitation issues. Consequently, a direct problem is governed by a system of time-harmonic random-dependent Partial Differential Equations, derived from Maxwell’s equations

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l l} \nabla\cdot\left[ \epsilon\left( \boldsymbol\chi\right) \nabla \varPhi \left( \boldsymbol\chi\right) + {\mathrm{i}}\,\epsilon\left( \boldsymbol\chi\right)\,\omega \textbf{A}\left( \boldsymbol\chi\right)\, \right]=\rho\left( \boldsymbol\chi\right)\\[0.5ex] \nabla \times \left(\nu\left( \boldsymbol\chi\right) \nabla \times \textbf{A}\left( \boldsymbol\chi\right)\right) = {\mathbf{J}\left( \boldsymbol\chi\right)} + \omega^2\,\epsilon\left( \boldsymbol\chi\right)\left(\textbf{A}\left( \boldsymbol\chi\right) - \frac{{\mathrm{i}}}{\omega} \nabla \varPhi \left( \boldsymbol\chi\right) \right)\\[0.5ex] \nabla \cdot \textbf{A}\left( \boldsymbol\chi\right) + {\mathrm{i}} \omega k \varPhi \left( \boldsymbol\chi\right) = 0 \\[0.5ex] \nabla \cdot \textbf{J}\left( \boldsymbol\chi\right) + {\mathrm{i}} \omega \rho\left( \boldsymbol\chi\right) = 0, \\[0.5ex] \end{array} \right. \end{aligned} $$

(1)

equipped with suitable initial and boundary conditions. Here, χ := (x, f, ξ) is defined on D × D _F × Ξ with D = D ₁ ∪ D ₂ ∪ D ₃ being a bounded domain in $\mathbb {R}^3$, composed of regions such as metal, insulator and semiconductor, respectively. D _F represents the frequency spectrum and Ξ is a multidimensional domain of physical parameters. The charge density ρ is represented by ${\rho } = q\left (n - p -N_{\mathrm {D}}\right )~\mathrm {on}\,~D_{3}$ and 0 otherwise (on D _1,2); the current density J is defined as $\textbf {J}_{D_{1}} = -\sigma \left (\nabla \varPhi + {\mathrm {i}}\,\epsilon \,\omega \textbf {A} \right )$, $\textbf {J}_{D_{2}} = 0$ and $\textbf {J}_{D_{3}} = {\textbf {J}_{n} + \textbf {J}_{p}}$. Here, σ and 𝜖 are the electric conductivity and the permittivity. Φ is the scalar electric potential, while A is the magnetic vector potential. J _n and J _p denote electron and hole current densities, whereas n and p represent electron and hole concentrations. N _D refers to the doping concentration, k is a constant that depends on the scaling scenario. In order to obtain the solution of an integral equation formulation of (1), ADS/MomentumⒸ from Keysight Technologies, http://www.keysight.com, has been used. Therein, Green’s functions are applied to model the proper behavior of the substrate [3]. In our simulations, the Quasi-Static Mode is used, which provides accurate electromagnetic simulation performance in RF for the geometrically complex and electrically small designs.

3 Uncertainty Quantification

For Uncertainty Quantification (UQ), a type of SCM compound with the PC expansion has been used. In this respect, some parameters z(ξ) ∈ Ξ in the model (1) have been modified by random variables

$$\displaystyle \begin{aligned} {\boldsymbol z}({\boldsymbol \xi})=[z_{\mathrm{dwnbond}}(\xi_{1}),\;z_{\mathrm{exp}}(\xi_{2}),\;z_{\mathrm{Xolo}}(\xi_{3}),\;z_{\mathrm{RxPa}}(\xi_{4})], \end{aligned} $$

(2)

where ξ is defined on the probability triple $\left ({\Omega }, \mathscr {F},\mathbb {P}\right )$ [13]. We assume a joint (uniform) probability density function $g: \varXi \rightarrow \mathbb {R}$ associated with $\mathbb {P}$ and that y is a quadratically integrable function. Then, a response surface model of y, in the form of a truncated series of the PC expansion [13], reads as

$$\displaystyle \begin{aligned} y \left({f , {\boldsymbol z} } \right) \doteq \sum\limits_{i=0}^N { {{v}}_{i} \left( f \right) } {{ {\varPsi}_i}} \left( {\boldsymbol z} \right), \end{aligned} $$

(3)

with a priori unknown coefficient functions v _i and predetermined basis polynomials Ψ _i with the orthogonality property $\mathbb {E}\left [{\varPsi }_i {\varPsi }_j \right ]=\delta _{ij}$. Here, $\mathbb {E}$ is the expected value, associated with $\mathbb {P}$. Specifically, for the calculation of the unknown coefficients v _i , we applied a pseudo-spectral approach with the Stroud-3 formula [10, 12, 14]. Within SCM, first the solution at each (deterministic) quadrature node z ^(k), k = 1, …, K of the system (1) is determined, resulting in approximations for the v _i in the form of

$$\displaystyle \begin{aligned} {{v}}_{i} (f) \doteq \sum\limits_{k=1}^K y \left({f,\,{\boldsymbol z}^{(k)}} \right)\varPsi_{i} \left( { {\boldsymbol z}}^{(k)} \right) {w_{k}} , \;\; w_{k} \in \mathbb{R}. \end{aligned} $$

(4)

Finally, the moments are approximated by, cf. [13],

$$\displaystyle \begin{aligned} \mathbb{E}_{} \left[ {{ {y}}\left({f,\;{{\boldsymbol z}}} \right)} \right]\;\doteq\;{ { v}}_{0} (f),\quad \mbox{Var}\left[ {{{y}}\left( {f,\;{{\boldsymbol z}}} \right)} \right]\;\doteq\sum\limits_{i=1}^N {\left| {{ { v}}_{i} (f)} \right|{}^{2}} \end{aligned} $$

(5)

assuming Ψ ₀ = 1. In order to investigate the impact of each uncertain parameter on the output variation, we performed a variance-based sensitivity analysis. The Sobol decomposition yields normalized variance-based sensitivity coefficients [6, 11]

$$\displaystyle \begin{aligned} S_{j}: = \frac{\mbox{V}_{j}^d}{\mbox{Var}(y)} \quad {\mathrm{with}} \quad \mbox{V}_{j}^d:= \sum_{i \in \mathit{I}_{j}^{d}}\,|v_{i}|{}^2, \;\;j=1,\ldots,q, \end{aligned} $$

(6)

with sets $\mathit {I}_{j}^{d}:=\{j \in \mathbb {N}: \varPsi _j(z_1,\ldots ,z_q)\; \text{is not constant in}\; z_j\; \text{and degree} (\varPsi _i) \leq d \}$, where d is the maximum degree of the polynomials. We will have d = 3 and q = 4. Note that 0 ≤ S _j  ≤ 1. A value close to 1 means a large contribution to the variance. Differentiating (3) with respect to z _k gives ∂y/∂z _k at any value of z. The z _k -th mean sensitivity is obtained by integrating over the whole parameter space [13].

4 Numerical Example and Conclusions

The model, shown schematically in Fig. 2, has been simulated within the frequency range from 1 MHz to 10 GHz. We performed UQ analysis using [1] for the frequency response functions y ₂ and y ₃,¹ which have been defined as (see also Fig. 2)

$$\displaystyle \begin{aligned} \begin{array}{l l} y_2 = |{\mathrm{CplXolo}}|:=\frac{|\mathrm{gnd}{\_}\mathrm{xolo} - \mathrm{PCBgnd}|}{|\mathrm{Vdd}{\_}\mathrm{dig} - \mathrm{gnd}{\_}\mathrm{dig}|}, \;\;\; y_3 = |{\mathrm{CplRx}}|:=\frac{|\mathrm{gnd}{\_}\mathrm{rx} - \mathrm{PCBgnd}|}{|\mathrm{Vdd}{\_}\mathrm{dig} - \mathrm{gnd}{\_}\mathrm{dig}|}. \end{array} \end{aligned} $$

(7)

The results in terms of statistical moments have been depicted in Fig. 3. Here, we assumed that the input variations are described by a joint uniform discrete distribution, which describes numbers of parallel connected impedances. Therefore, in this case, the particular numbers of connected branches are generated using the range of discrete random variables as: $N_{\mathrm {downbonds}} \in \left \langle 1, 10 \right \rangle$, $N_{\mathrm {exp}}\in \left \langle 1, 20 \right \rangle$, $N_{\mathrm {XoLO}} \in \left \langle 1, 8 \right \rangle$, $N_{\mathrm {RxPA}} \in \left \langle 1, 12 \right \rangle$, thus N := (N _downbonds, N _exp, N _XoLO, N _RxPA), R := (R _downbonds, R _exp, R _XoLO, R _RxPA), L := (L _downbonds, L _exp, L _XoLO, L _RxPA). Consequently, the particular impedances z are defined as follows: z(ω) = [(R ₁ + iωL ₁)/N ₁, (R ₂ + iωL ₂)/N ₂, (R ₃ + iωL ₃)/N ₃, (R ₄ + iωL ₄)/N ₄], where R ₁ = 50.0[m Ω] and L ₁ = 0.1[nH]; R ₂ = 1.0[m Ω] and L ₂ = 0.1[nH]; R ₃ = 100.0[m Ω] and L ₃ = 2.0[nH]; R ₄ = 100.0[m Ω] and L ₄ = 2.0[nH]. The variance-based sensitivity coefficients, shown in Fig. 4, allow to find the most influential parameters contributing to the variance, whereas the mean gradients of y are presented in Fig. 5. Based on this analysis we further developed a regularized Gauss-Newton algorithm, which allows for finding robust optimized values of the considered parameters with minimum variation around the mean of an appropriate objective function [8].

Fig. 3

Mean and standard deviation values of the modulus of the cross-domain frequency response transfer functions y ₂ and y ₃, calculated for the testbench model under input uncertainties

Fig. 4

Variance-based sensitivity performed for the testbench model. Due to the normalization, a value close to 1 means a large (‘dominant’) contribution to the variance

Fig. 5

Mean gradient sensitivity analysis performed for the testbench model. Shown are the means of the coordinates of the gradient of y with respect to z