Eddy Current Testing Models for the Analysis of Corrosion Effects in Metal Plates

Abstract

Direct method for the solution of eddy current testing problem for the case where an air core coil is located above a conducting two-layer plate with a flaw in the form of a cylindrical inclusion with reduced electrical conductivity is presented in the paper. Semi-analytical approach (the TREE method) is used to construct the solution of the system of equations for the components of the vector potential. The flaw is assumed to be symmetric with respect to the coil. Numerical calculations are performed using the proposed model and Comsol Multiphysics software. The obtained values of the change in impedance of the coil for both methods are found to be in a good agreement. The proposed model can be used for the assessment of the effect of corrosion in metal plates.

1 Introduction

Eddy current methods are widely used to analyze the effect of corrosion in metal plates [2]. Mathematical methods that are used to analyze such problems can be divided into two broad categories: (a) numerical methods and (b) analytical and semi-analytical methods. Methods from category (a) include, for example, finite element methods or finite difference methods (see [4, 9]). Analytical methods can be used for the cases where conducting medium is unbounded with respect to one or two spatial coordinates. Such models are discussed in detail in [1, 7]. Corroded samples have finite sizes so that truly analytical approach cannot be used. However, the domain of applicability of analytical methods can be extended using the following idea described in [8]: it is assumed that the electromagnetic field is exactly zero at a sufficiently large distance from the source of alternating current. In this case the domain where the problem has to be solved becomes finite and method of separation of variables can be used to solve the system of equations for the vector potential in each of the regions of interest. Examples where such an approach (known as the TREE method in the literature) is used for solution of eddy current testing problems with asymmetric flaws can be found in [5, 6]. In the present paper we present semi-analytical solution of direct eddy current testing problem for a two-layer plate. The plate contains a flaw in the form of a cylindrical inclusion with reduced electrical conductivity. The axis of the inclusion coincides with the axis of an air core coil. The formula for the change in impedance of the coil is derived. Numerical computations show good agreement of the proposed model with the computations performed using Comsol Multiphysics software.

2 Mathematical Analysis

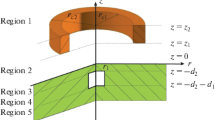
Suppose an air core coil carrying alternating current of frequency f is located above a conducting nonmagnetic two-layer plate. The conductivites of the upper and lower layers are σ ₁ and σ ₂, respectively. The lower layer is infinite in the vertical direction.The upper layer has a flaw in the form of a circular cylinder of radius c. The flaw has the two layers in the vertical direction: the upper layer where − d ₁ < z < 0 and the lower layer where − d ₁ < z < −d ₂. The upper layer of the flaw has zero conductivity while the lower layer has a reduced electrical conductivity σ ₃ < σ ₁. This is a typical situation in corroded samples [2]. It is assumed that the axis of the flaw coincides with the axis of the coil. The geometrical parameters of the coil are as follows: the inner and outer radii are r ₁ and r ₂, respectively, z ₁ is the distance from the bottom of the coil to the upper layer of the conducting plate, z ₂ − z ₁ is the height of the coil and N is the number of turns. Due to axial symmetry only the azimuthal component of the vector potential is not equal to zero. Thus, in the system of cylindrical polar coordinates (r, φ, z) centered at the axis of the coil at the point located on the upper surface of the plate we have

$$\displaystyle \begin{aligned} \mathbf{{A}}=A(r,z)\exp(j\omega t)\mathbf{e}_{\boldsymbol{\varphi}}, {} \end{aligned} $$

(1)

where ω = 2πf, $j=\sqrt {-1}$ and e _φ is the unit vector in the azimuthal direction. We denote by R ₀, R ₁, R ₂ and R ₃ the regions where z > 0, − d ₁ < z < 0, − d ₁ − d ₂ < z < −d ₁ and z < −d ₁ − d ₂, respectively. The component of the vector potential in region R _i is denoted by A _i , i = 0, 1, 2, 3. All the components of the vector potential are equal to zero at r = b:

$$\displaystyle \begin{aligned} A_i(b,z)=0,\quad i=0,1,2,3. {} \end{aligned} $$

(2)

Since the problem is linear it is natural to use the superposition principle. First, we consider a single-turn coil of radius r ₀ located at distance h above the conducting plate. The problem is solved for the case of the single-turn coil and then the solution is integrated over the cross-section of the coil in order to find the vector potential for the coil of finite dimensions.

The system of equations for the components of the vector potential in regions R _i has the form

$$\displaystyle \begin{aligned} \frac{\partial^2 A_0}{\partial r^2}+\frac{1}{r}\frac{\partial A_0}{\partial r}-\frac{A_0}{r^2}+\frac{\partial^2 A_0}{\partial z^2}=-\mu_0I\delta(r-r_0)\delta(z-h), {} \end{aligned} $$

(3)

$$\displaystyle \begin{aligned} \frac{\partial^2 A_1}{\partial r^2}+\frac{1}{r}\frac{\partial A_1}{\partial r}-\frac{A_1}{r^2}-j\omega\sigma_1(r)\mu_0A_1+\frac{\partial^2 A_1}{\partial z^2}=0, {} \end{aligned} $$

(4)

$$\displaystyle \begin{aligned} \frac{\partial^2 A_2}{\partial r^2}+\frac{1}{r}\frac{\partial A_2}{\partial r}-\frac{A_2}{r^2}-j\omega\sigma_2(r)\mu_0A_2+\frac{\partial^2 A_2}{\partial z^2}=0, {} \end{aligned} $$

(5)

$$\displaystyle \begin{aligned} \frac{\partial^2 A_3}{\partial r^2}+\frac{1}{r}\frac{\partial A_3}{\partial r}-\frac{A_3}{r^2}-j\omega\sigma_3\mu_0A_3+\frac{\partial^2 A_3}{\partial z^2}=0, {} \end{aligned} $$

(6)

where δ(x) is the Dirac delta function, μ ₀ is the magnetic constant, σ ₁(r) = σ ₁ if c < r < b and σ ₁(r) = 0 if 0 < r < c. Similarly, σ ₂(r) = σ ₁ if c < r < b and σ ₂(r) = σ ₃ if 0 < r < c. The current in the coil is given by

$$\displaystyle \begin{aligned} \mathbf{{I}}^e=I\exp(j\omega t)\mathbf{{e}}_{\varphi}. {} \end{aligned} $$

(7)

The boundary conditions are

$$\displaystyle \begin{aligned} A_0\mid_{z=0}=A_1^{air}\mid_{z=0},\quad\frac{\partial A_0}{\partial z}\mid_{z=0}=\frac{\partial A_1^{air}}{\partial z}\mid_{z=0},\quad 0<r<c, {} \end{aligned} $$

(8)

$$\displaystyle \begin{aligned} A_0\mid_{z=0}=A_1^{con}\mid_{z=0},\quad\frac{\partial A_0}{\partial z}\mid_{z=0}=\frac{\partial A_1^{con}}{\partial z}\mid_{z=0},\quad c<r<b, {} \end{aligned} $$

(9)

$$\displaystyle \begin{aligned} A_1^{air}\mid_{z=-d_1}=A_2^{red}\mid_{z=-d_1},\quad\frac{\partial A_1^{air}}{\partial z}\mid_{z=-d_1}=\frac{\partial A_2^{red}}{\partial z}\mid_{z=-d_1},\quad 0<r<c, {} \end{aligned} $$

(10)

$$\displaystyle \begin{aligned} A_1^{con}\mid_{z=-d_1}=A_2\mid_{z=-d_1},\quad\frac{\partial A_1^{con}}{\partial z}\mid_{z=-d_1}=\frac{\partial A_2}{\partial z}\mid_{z=-d_1},\quad c<r<b, {} \end{aligned} $$

(11)

$$\displaystyle \begin{aligned} A_2^{red}\mid_{z=-d_1-d_2}=A_3\mid_{z=-d_1-d_2},\quad\frac{\partial A_2^{red}}{\partial z}\mid_{z=-d_1-d_2}=\frac{\partial A_3}{\partial z}\mid_{z=-d_1-d_2},\quad 0<r<c, {} \end{aligned} $$

(12)

$$\displaystyle \begin{aligned} A_2\mid_{z=-d_1-d_2}=A_3\mid_{z=-d_1-d_2},\quad\frac{\partial A_2}{\partial z}\mid_{z=-d_1-d_2}=\frac{\partial A_3}{\partial z}\mid_{z=-d_1-d_2},\quad c<r<b. {} \end{aligned} $$

(13)

Here the notations $A_1^{air}$ and $A_1^{con}$ are used to denote the vector potentials in region R ₁ where 0 < r < c and c < r < b, respectively. Similar notation is used for the region of reduced electrical conductivity: $A_2^{red}$ in the region 0 < r < c. The vector potential and its derivative with respect to r are continuous at r = c:

$$\displaystyle \begin{aligned} A_1^{con}\mid_{r=c}=A_1^{air}\mid_{r=c},\quad\frac{\partial A_1^{con}}{\partial r}\mid_{r=c}=\frac{\partial A_1^{air}}{\partial r}\mid_{r=c}, {} \end{aligned} $$

(14)

$$\displaystyle \begin{aligned} A_2^{red}\mid_{r=c}=A_2\mid_{r=c},\quad\frac{\partial A_2^{red}}{\partial r}\mid_{r=c}=\frac{\partial A_2}{\partial r}\mid_{r=c}. {} \end{aligned} $$

(15)

In addition, the vector potential is assumed to be bounded at infinity in the vertical direction:

$$\displaystyle \begin{aligned} A_0\mid_{z\rightarrow+\infty}=0, \quad A_3\mid_{z\rightarrow-\infty}=0. {} \end{aligned} $$

(16)

The solution in region R ₀ has the form

$$\displaystyle \begin{aligned} A_0(r,z)=\sum_{i=1}^{\infty}D_{1i}e^{-\lambda_iz}J_1(\lambda_ir)+\frac{\mu_0Ir_0}{b^2}\sum_{i=1}^{\infty}\frac{J_1(\lambda_ir_0)}{\lambda_iJ_0^2(\lambda_ib)}e^{-\lambda_i|z-h|}J_1(\lambda_ir), {} \end{aligned} $$

(17)

where λ _i  = α _i /b, α _i , i = 1, 2, … are the roots of the equation J ₁(α) = 0, J ₀ and J ₁ are the Bessel functions of the first kind of orders 0 and 1, respectively. The solution in region R ₁ is

$$\displaystyle \begin{aligned} A_1^{con}(r,z)=\sum_{i=1}^{\infty}[D_{2i}e^{p_iz}+D_{3i}e^{-p_iz}]J_1(q_ir), {} \end{aligned} $$

(18)

$$\displaystyle \begin{aligned} A_1^{air}(r,z)=\sum_{i=1}^{\infty}[(D_{4i}J_1(p_ir)+D_{5i}Y_1(p_ir))e^{p_iz}+(D_{6i}J_1(p_ir)+D_{7i}Y_1(p_ir))e^{-p_iz}], {} \end{aligned} $$

(19)

where q _i is the separation constant, $p_i=\sqrt {q_i^2+j\omega \sigma _1\mu _0}$ and Y ₁ is the Bessel function of the second kind of order 1. Similarly, the solution in region R ₂ is

$$\displaystyle \begin{aligned} A_2(r,z)=\sum_{i=1}^{\infty}[D_{8i}e^{s_iz}+D_{9i}e^{-s_iz}]J_1(q_ir), {} \end{aligned} $$

(20)

$$\displaystyle \begin{aligned} A_2^{red}(r,z)=\sum_{i=1}^{\infty}[(D_{10i}J_1(s_ir)+D_{11i}Y_1(s_ir))e^{s_iz}+(D_{12i}J_1(s_ir)+D_{13i}Y_1(s_ir))e^{-s_iz}], {} \end{aligned} $$

(21)

where $s_i=\sqrt {q_i^2+j\omega \sigma _3\mu _0}$. Finally, the solution in region R ₃ has the form

$$\displaystyle \begin{aligned} A_3(r,z)=\sum_{i=1}^{\infty}D_{14i}e^{u_iz}J_1(q_ir), {} \end{aligned} $$

(22)

where $u_i=\sqrt {q_i^2+j\omega \sigma _2\mu _0}$.

Using the boundary conditions (8)–(13) we obtain the unknown coefficients D _1i − D _14i. The interface conditions (14)–(15) give the equation for the unknown complex eigenvalues p _i :

$$\displaystyle \begin{aligned} p_iJ_1^{\prime}(p_ic)T^{\prime}(q_ic)=q_iJ_1(p_ic)T^{\prime}(q_ic), {} \end{aligned} $$

(23)

where T(p _i r) = J ₁(p _i r)Y ₁(p _i b) − J ₁(p _i b)Y ₁(p _i r). The technical details of the derivation are not shown here for brevity and can be found, for example, in [3] where a similar problem with two cylindrical flaws is solved. The induced vector potential in air due to the presence of the conducting plate is

$$\displaystyle \begin{aligned} A_0^{ind}(r,z,r_0,h)=\sum_{i=1}^nD_{1i}e^{-\lambda_iz}J_1(\lambda_ir), {} \end{aligned} $$

(24)

where only the first n terms of the series are taken into account.

Using the superposition principle we obtain the induced vector potential in air due to currents in the whole coil:

$$\displaystyle \begin{aligned} A_{0coil}^{ind}(r,z)=\int_{r_1}^{r_2}\int_{z_1}^{z_2}A_0^{ind}(r,z,r_0,h)dr_0dh. {} \end{aligned} $$

(25)

The change in impedance of the coil is computed as follows (see [8]):

$$\displaystyle \begin{aligned} Z^{ind}=\frac{i\omega}{I^2}\int\limits_V\mathbf{{A}}_{0coil}^{ind}\cdot\mathbf{{I}}\,dV. {} \end{aligned} $$

(26)

Using (24)–(26) we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} Z^{ind}&\displaystyle =&\displaystyle \frac{2j\omega\pi\mu_0N^2}{(r_2-r_1)^2(z_2-z_1)^2}\sum_{m=1}^n\frac{(e^{-\lambda_mz_2}-e^{-\lambda_mz_1})}{\lambda_m^3} \int_{\lambda_mr_1}^{\lambda_mr_2}\xi J_1(\xi)\,d\xi\\ &\displaystyle &\displaystyle \times\sum_{i=1}^nY_{mi}\frac{(e^{-\lambda_iz_2}-e^{-\lambda_iz_1})}{\lambda_i^3}\int_{\lambda_ir_1}^{\lambda_ir_2}\eta J_1(\eta)\,d\eta. {} \end{array} \end{aligned} $$

(27)

(the formulas for the elements of the matrix Y  are bulky and are not shown here).

3 Numerical Results

Formula (27) is used to compute the change in impedance of the coil for the following parameters of the problem: r ₁ = 2.5 mm, r ₂ = 5.5 mm, z ₁ = 0.3 mm, z ₂ = 2.6 mm, d ₁ = 1 mm, d ₂ = 1 mm, b = 55 mm, σ ₁ = 0.5 Ms/m, σ ₂ = 7 Ms/m, c = 3 mm. Nine frequencies are used for the calculations: from 1 to 9 kHz with the stepsize of 1 kHz. The results of computations are shown in Fig. 1. The solid curve represents theoretical calculations with the TREE method. In addition, the problem is solved using Comsol Multiphysics software. The points on the graph represent the values computed using Comsol Multiphysics. As can be seen from the graph, both calculations are in a good agreement.

Fig. 1

The change in impedance of the coil for the nine frequencies