Answer Set Programming and Its Applications in Planning and Multi-agent Systems

Abstract

The paper presents some applications in planning and multi-agent systems of answer set programming. It highlights the benefits of answer set programming based techniques in these applications. It also describes a class of multi-agent planning problems that is challenging to answer set programming.

1 Introduction

The invention of answer set programming (ASP) [18, 20] and the development of efficient answer set solvers such as smodels [24], dlv [5], and clingo [8] enable the use of logic programming under answer set semantics in several practical applications [6]. The fundamental idea of ASP is to represent solutions to a problem by answer sets of a logic program. That is, to solve a problem, one first represents it as a logic program whose answer sets correspond one-to-one to its solutions; next, to find a solution, one computes an answer set of that program and extracts the solution from the answer set.

Formally, a logic program $\varPi$ is a set of rules of the form

$$\begin{aligned} c_1 \mid \ldots \mid c_k \leftarrow a_1,\ldots ,a_m, not \,a_{m+1},\ldots , not \,a_n \end{aligned}$$

(1)

where $0 \le m \le n, \, 0 \le k$, each $a_i$ or $c_j$ is a literal of a propositional language¹ and $not \,$ represents default negation. Both the head and the body can be empty. When the head is empty, the rule is called a constraint. When the body is empty, the rule is called a fact. The semantics of a program $\varPi$ is defined by a set of answer sets [10]. An answer set is a distinguished model of $\varPi$ that satisfies all the rules of $\varPi$ and is minimal and well-supported.

To increase the expressiveness of logic programs and simplify its use in applications, the language has been extended with several features such as weight constraints or choice atoms [24], or aggregates [7, 21, 25]. Standard syntax for these extensions has been proposed and adopted in most state-of-the-art ASP-solvers such as clingo and dlv.

In recent years, attempts have been made to consider continuously changing logic programs or external atoms. For example, the system clingo enables the multi-shot model as oppose to the traditional single-shot model. In this model, ASP programs are extended with Python procedures that control the answer set solving process along with the evolving logic programs. This feature provides an effective way for the application of ASP in a number of applications that were difficult to deal with previously.

This paper describes the application of ASP in planning in the presence of incomplete information and sensing actions (Sect. 2), in goal recognition design (Sect. 3), and in various settings of multi-agent planning (Sect. 4). It highlights the advantage of ASP in these researches and, when possible, identifies the challenging issues faced by ASP.

2 Planning with Incomplete Information and Sensing Actions

Answer set planning was one of the earliest applications of answer set programming [3, 16, 32]. The logic program encoding proposed in these papers are suitable for classical planning problems with complete information about the initial state and deterministic actions. In a series of work, we applied ASP to conformant planning and conditional planning (e.g., [30, 31, 34, 35]). The former refers to planning with incomplete information about the initial state whose solutions are action sequences that achieve the goal from any possible initial state (and hence, the terms comformant planning). The latter refers to planning with incomplete information and sensing actions whose solutions often contain branches in the form of conditional statements (e.g., if-then-else or case-statement) that leads to the terms conditional planning.

Conditional planning is computationally harder than conformant planning which, in turn, is computationally harder than classical planning. When actions are deterministic and the plan’s length is polynomially bounded by the size of the problem, the complexity of conditional and comformant planning are PSPACE-complete and $\varSigma _2^P$-complete, respectively, [1]. As such, there are problems that has conditional plan as solution but does not have conformant plan as solution. The following example highlights this issue.

Example 1

(From [34]). Consider a security window with a lock that can be in one of the three states opened, closed ² or locked ³. When the window is closed or opened, pushing it up or down will open or close it respectively. When the window is closed or locked, flipping the lock will lock or close it respectively.

Suppose that a robot needs to make sure that the window is locked and initially, the robot knows that the window is not open (but whether it is locked or closed is unknown).

No conformant plan can achieve the goal. Instead, the robot needs a conditional plan consisting of the following steps: (1) checks the window to determine the window’s status; if the window is closed, (2.a) locks the window; otherwise (i.e., the window is already locked), (2.b) does nothing.     $\square$

The proposed ASP-based systems for conditional and conformant planning in [30, 31, 34, 35] show that ASP-based planners performed well comparing to state-of-the-art planning systems of the same kind in several domains. Their performance can be attributed to the following key ideas:

• The use of an input language that allows for the representation and reasoning with static causal laws (a.k.a. axiom or domain constraints). It should be noted that the original specification of the Planning Domain Description Language (PDDL) – a language frequently used for the specification of planning problems by the planning community – includes axioms⁴ which correspond to non-recursive static causal laws in our terminology [11]. However, the conformant planning benchmarks designed by the planning community do not use static causal laws.

• The employment of an approximation semantics that reduces the computational complexity of planning with incomplete information to NP-complete.

The next example highlights the advantage of directly dealing with static causal laws.

Example 2

(Dominos Domain [31]). Suppose that we have n dominos standing on a line in such a way that if one domino falls then the domino on its right also falls. There is also a ball hanging close to the leftmost domino. Swinging the ball will cause the leftmost domino to fall. Initially, the ball stays still and whether or not the dominos are standing is unknown. The goal is to have the rightmost domino to fall. Obviously, swinging the ball is the only plan to achieve this goal, no matter how big n is.

The problem can be easily expressed by a theory with a set of objects $1,\ldots ,n$ denoting the dominos from left to right and a single action swing that causes $down_1$ (the leftmost domino falls) to be true, and $n-1$ axioms (state constraints) $down_i \Rightarrow down_{i+1}$ representing the fact that $down_{i+1}$ is true if $down_i$ is true. The goal is to have $down_n$ become true.

State constraints are usually dealt with by compiling them away. According to the compilation suggested in [33], for each axiom $down_i \Rightarrow down_{i+1}$, we introduce a new action $e_i$ whose effect is $down_{i+1}$ and whose precondition is $down_i$. Clearly, under this compilation, the plan to achieve the goal is the sequence of actions $[swing,e_1,\ldots ,e_{n-1}]$.

The main problem with this compilation is that the plan length increases with the number of objects. Even when it is only linear to the size of the original problem, it proves to be challenging for planners following this approach. Most planners have problem when plan length is greater than 500 (i.e., more than 500 dominos).     $\square$

The input language is the action language $\mathcal{A}^c$ (in [30, 31, 35]) and $\mathcal{A}_K^c$ (in [34]). Since $\mathcal{A}_K^c$ is an extension of $\mathcal{A}^c$ with sensing actions, we summarize the features of $\mathcal{A}_K^c$ below. An action theory in $\mathcal{A}_K^c$ is a collection of statements of the following forms:

$$\begin{aligned}&\,\, \mathbf {initially}(l) \end{aligned}$$

(2)

$$\begin{aligned}&\,\, \mathbf {executable\_if}(a,\psi ) \end{aligned}$$

(3)

$$\begin{aligned}&\,\, \mathbf {causes}(a,l,\phi ) \end{aligned}$$

(4)

$$\begin{aligned}&\,\, \mathbf {if}(l,\varphi ) \end{aligned}$$

(5)

$$\begin{aligned}&\,\, \mathbf {determines}(a,\theta ) \end{aligned}$$

(6)

where a is an action, l is a fluent literal, and $\psi ,\phi ,\varphi ,\theta$ are sets of literals⁵. (2) says that l holds in the initial situation. (3) says that a is executable in any situation in which $\psi$ holds (the precise meaning of hold will be given later). (4) represents a conditional effect of an action. It says that performing a in a situation in which $\phi$ holds causes l to hold in the successor situation. (5), called a static causal law, states that l holds in any situation in which $\varphi$ holds. (6) states that the values of literals in $\theta$, sometimes referred to as sensed-literals, will be known after a is executed.

The complete semantics of $\mathcal{A}_K^c$ can be found in [2]. It defines a transition function $\varPhi$ over pairs of actions and sets of belief states. The approximation semantics employed in the systems in [30, 31, 34, 35] defines a transition function $\varPhi _a$ over pairs of actions and approximation states where an approximation state is a set of consistent literals satisfying the static causal laws. $\varPhi _a$ can be defined in set theoretical terms [31, 34] or by logic program rules [35]. Its precise definition can be found in the aforementioned papers. $\varPhi _a$ can be used for conformant planning in ASP, in the same way that the transition function of the action language is used for planning as described in [16].

Given a planning problem instance $\mathcal{P}= (\mathcal{D},\mathcal{I},\mathcal{G})$, where $\mathcal{D}$ is a set of statements of the forms (3)–(6), $\mathcal{I}$ is a set of statements of the form (2), and $\mathcal{G}$ is a fluent formula. Let k be an integer denoting the maximal length of the desirable solutions. We solve $\mathcal{P}$ by translating it into a logic program $\pi _{k}(\mathcal{P})$ such that each answer set of $\pi _{k}(\mathcal{P})$ corresponds to a solution of at most k actions. Besides atoms defining the actions, fluents, literals, etc., $\pi _{k}(\mathcal{P})$ uses the following main predicates:

• holds(L, T): literal L holds at step T.

• poss(A, T): action A is executable at T.

• occ(A, T): action A occurs at T.

• pc(L, T): literal L may change at $T+1$.

• goal(T): the goal is satisfied at T.

The rules for encoding direct effects of actions in $\pi _{k}(\mathcal{P})$ are similar to the rules used for classical planning:

$$ holds(L, T+1) \leftarrow occ(A, T), causes(A, L, \varphi ), holds(\varphi , T). $$

The difference with classical planning lies in the rules defining pc(L, T) and the rule encoding of the inertial axiom:

$$ holds(L, T+1) \leftarrow holds(L, T), not \,pc(\lnot L, T+1). $$

Rules in $\pi _{k}(\mathcal{P})$ ensure that, for an answer set S of $\pi _{k}(\mathcal{P})$, if $\delta = \{l \mid holds(l, t)\in S\}$, $\delta ' = \{l \mid holds(l, t+1)\in S\}$, and $occ(a, t) \in S$ then (a) a is executable in $\delta$; and (b) $\delta ' = \varPhi _a(a, \delta )$.

As shown in Example 1, conformant plans are insufficient when sensing actions are needed. In this situation, conditional plans are required. Formally, a conditional plan is (i) [] is a conditional plan, denoting the empty plan, i.e., the plan containing no action; (ii) if a is a non-sensing action and p is a conditional plan then [a; p] is a conditional plan; (iii) if a is a sensing action with proposition (6), where $\theta = \{ g_1, \dots , g_n \}$, and $p_j$’s are conditional plans then $[a; \mathbf{cases}(\{g_j \rightarrow p_j\}_{j=1}^{n})]$ is a conditional plan; and (iv) Nothing else is a conditional plan.

To encode a conditional planning problem in ASP, we need to accommodate possible cases of a conditional plan. Let us observe that each conditional plan p corresponds to a labeled plan tree $T_p$ defined as below.

• If p = [] then $T_p$ is a tree with a single node.

• If $p = [a]$, where a is a non-sensing action, then $T_p$ is a tree with a single node and this node is labeled with a.

• If $p = [a;q]$, where a is a non-sensing action and q is a non-empty plan, then $T_p$ is a tree whose root is labeled with a and has only one subtree which is $T_q$. Furthermore, the link between a and $T_q$’s root is labeled with an empty string.

• If $p = [a;\mathbf{cases}(\{g_j \rightarrow p_j\}_{j=1}^n)]$, where a is a sensing action that determines $g_j$’s, then $T_p$ is a tree whose root is labeled with a and has n subtrees $\{T_{p_j} \mid j \in \{1,\dots ,n\}\}$. For each j, the link from a to the root of $T_{p_j}$ is labeled with $g_j$.

For instance, Fig. 1 shows the trees for the following four conditional plans in the domain of Example 1:

• (i) $p_1 = [push\_down;flip\_lock]$;

• (ii) $p_2 = check; \; \mathbf{cases}\left( \begin{array}{lll} open &{} \rightarrow &{} [] \\ closed &{} \rightarrow &{} [flip\_lock] \\ locked &{} \rightarrow &{} [] \end{array} \right)$;

• (iii) $p_3 = check; \; \mathbf{cases}\left( \begin{array}{lll} open &{} \rightarrow &{} [push\_down;flip\_lock] \\ closed &{} \rightarrow &{} [flip\_lock;flip\_lock;flip\_lock] \\ locked &{} \rightarrow &{} [] \end{array} \right) ; and$

• (iv) $p_4 = check; \; \mathbf{cases}\left( \begin{array}{lll} open &{} \rightarrow &{} [] \\ closed &{} \rightarrow &{} p_2 \\ locked &{} \rightarrow &{} [] \end{array} \right)$

Fig. 1.

Sample plan trees

Observe that each trajectory of the plan p corresponds to a path from the root to a leave of $T_p$. Furthermore, let $\alpha$ (or the width of $T_p$) be the number of leaves of $T_p$ and $\beta$ (or the height of $T_p$) be the number of nodes along the longest path from the root to the leaves of $T_p$. Let w and h be two integers such that $\alpha \le w$ and $\beta \le h$ and the leaves of $T_p$ be $x_1,\ldots ,x_{\alpha }$. We map each node y of $T_p$ to a pair of integers $n_y$ = ($t_y$,$p_y$), where $t_y$ is the number of nodes along the path from the root to y, and $p_y$ is defined in the following way.

• For each leaf $x_i$ of $T_p$, $p_{x_i}$ is an arbitrary integer between 1 and w such that (i) there exists a leaf x with $p_x = 1$, and (ii) $i \ne j$ implies $p_{x_i} \ne p_{x_j}$.

• For each interior node y of $T_p$ with children $y_1,\ldots ,y_r$, $p_y = \min \{p_{y_1},\ldots ,p_{y_r}\}$.

Fig. 2.

Possible mappings for $T_{p_i}$ ($i=1,2,3,4$) with $w=5$ and $h=4$

Figure 2 shows some possible mappings for the four trees in Fig. 1. It is easy to see that if $\alpha \le w$ and $\beta \le h$ then such a mapping always exists and (1, 1) is always assigned to the root. Furthermore, given a labeled tree $T_p$ whose nodes are numbered according to the about rules, the plan p can easily be reconstructed. This means that computing a solution p of a planing problem $\mathcal{P}= (\mathcal{D},\mathcal{I},\mathcal{G})$ is equivalent to identifying its tree $T_p$. This property allows for the encoding of $\mathcal{P}$ as a logic program $\pi _{h,w}(\mathcal{P})$ that generates labeled trees corresponding to solutions of $\mathcal{P}$ whose width and height are bounded by w and h, respectively. In addition to the usual predicates defining the actions, fluents, etc. $\pi _{h,w}(\mathcal{P})$ uses the following predicates:

• holds(L, T, P): literal L holds at node (T, P) (i.e., at step T of path P).

• poss(A, T, P): action A is executable at (T, P).

• occ(A, T, P): action A occurs at (T, P).

• pc(L, T, P): literal L may change at $(T+1,P)$.

• goal(T, P): the goal is satisfied at (T, P).

• $br(G,T,P,P_1)$: there exists a branch from (T, P) to $(T+1,P_1)$ labeled with G.

• used(T, P): (T, P) belongs to some extended trajectory of the constructed plan.

Observe that most of the predicates used in $\pi _{h,w}(\mathcal{P})$ are similar to those in $\pi _k(\mathcal{P})$ extended with the third parameter encoding branches of a conditional plan, the last two predicates are specific to $\pi _{h,w}(\mathcal{P})$. They encode the cases of the solution. The detail encoding of $\pi _{h,w}(\mathcal{P})$ and its soundness and completeness can be found in [34].

One disadvantage of the proposed approach is the incompleteness of the ASP based planners. To address this issue, we identified completeness condition of the approximation [35]. Saturation and meta-programming techniques (see Sect. 3) could be used for a complete ASP-based planner.

3 Answer Set Programming in Goal Recognition Design

Goal recognition, a special form of plan recognition, deals with online problems aiming at identifying the goal of an agent as quickly as possible given its behavior [9, 23]. For example, Fig. 3(a) shows an example gridworld application, where the agent starts at cell E3 and can move in any of the four cardinal directions. Its goal is one of three possible ones G1, G2, and G3. The traditional approach has been to find efficient algorithms that observe the trajectory of the agent and predict its actual goal [9, 23].

Fig. 3.

Example Problem

Goal recognition design (GRD) [12] aims at identifying possible changes to the environment in which the agents operate, typically by making a subset of feasible actions infeasible, so that agents are forced to reveal their goals as early as possible. For example, under the assumption that agents follow optimal plans to reach their goal, by making the action that moves the agent from cells E3 to D3 infeasible, the agent is forced to either move left to E2, which would immediately reveal that its goal is G1, or move right to E4, revealing that it is either G2 or G3. In [12], the authors introduced the notion of worst-case distinctiveness (wcd), as a goodness measure that assesses the ease of performing goal recognition within an environment. The wcd of a problem is the longest sequence of actions an agent can take without revealing its goal. The objective in GRD is then to find a subset of feasible actions to make infeasible such that the resulting wcd is minimized. We will next present two ASP-based solutions of the GRD problem. Abusing the notation, we represent a GRD problem $\mathcal{P}$ by the triple $(\mathcal{D},\mathcal{I},\mathcal{G})$ with the understanding that $\mathcal{G}$ is the set of possible goals of the agent. By $\mathtt {wcd}(\mathcal{P})$, we denote the wcd of $\mathcal{P}$.

3.1 A Saturation-Based Meta Encoding

The first encoding of the GRD problem in ASP utilizes meta-programming and saturation techniques. The saturation technique is an advanced guess and check methodology used in disjunctive ASP to check whether all possible guesses in a problem domain satisfy a certain property [4]. It can be used to encode $\varSigma ^P_2$-complete problems such as the satisfiability problem for $\exists \forall$-QBF. For instance, in a typical encoding for satisfiability of a $\exists \forall$-QBF the guess part uses disjunction to generate all possible truth values for the propositional atoms that are quantified by $\forall$ ($\forall$-atoms) and the check part checks the satisfiability of the formula for all valuations of the $\forall$-atoms (i.e., it checks whether the resulting formula after applying choices made for $\exists$-atoms is a tautology or not). To achieve this, the fact that answer sets are minimal w.r.t. the atoms defined by disjunctive rules is utilized. To this end, the saturation part of the program derives (saturates) all atoms defined in the guess part for generating the search space. It should be noted that the saturation technique puts syntactical restrictions on the program parts by forbidding the use of saturated atoms as default negation literals in a rule or as positive literals in a constraint [4, 15].

As it turns out, the wcd of a problem can be formulated as a $\exists \forall$-QBF formula as follows. Let $g \in \mathcal{G}$ and $\pi _g^*$ denote the minimal cost plan achieving g. Let vl(x, y, c) denote that c is the common prefix of minimal cost plans of $\pi _{x}^*$ and $\pi _{y}^*$. The wcd definition of $\mathcal{P}$ can be encoded by the following $\exists \forall$-QBF:

$$\begin{aligned} \exists x, y, c[ vl(x,y,c) \!\wedge \!\! [\forall x^\prime , y^\prime , c^\prime [vl(x^\prime , y^\prime , c^\prime ) {\rightarrow } |c| {\ge } |c^\prime |]] \end{aligned}$$

(7)

where, for the sake of simplicity, we omit some details such as $x, y, x^\prime , y^\prime \in \mathcal{G}$, and that c and $c^\prime$ correspond to sequences of actions that are the common prefix of cost-optimal plans $\pi _x^*$ and $\pi _y^*$, $\pi _{x^\prime }^*$ and $\pi _{y^\prime }^*$, respectively.

To compute the wcd using the saturation technique, we only need to encode the satisfiability of formula (7). Two possible implementations of the saturation techniques are detailed in [29]; one of them performs exceptionally well against the system developed by the inventor of the GRD problem.

3.2 A Multi-shot ASP Encoding

The second encoding of the GRD problem employs a hybrid implementation made possible by multi-shot ASP. Given a GRD $\mathcal{P}= (\mathcal{D}, \mathcal{I}, \mathcal{G})$, an integer k denoting the maximal number of actions that can be blocked for reducing the $\mathtt {wcd}$, and an integer max be denoting the maximal length of plans in $\mathcal{P}$. We develop a multi-shot ASP program $\varPi (\mathcal{P})$ for computing (i) $\mathtt {wcd}(\mathcal{P})$; and (ii) a solution of $\mathcal{P}$ wrt. k (a set of actions that should be blocked) to achieve $\mathtt {wcd}(\mathcal{P})$. Specifically, $\varPi (\mathcal{P})$ implements Algorithm 1 in multi-shot ASP and consists of a logic program $\pi (\mathcal{P})$ and a Python program $GRD(\mathcal{P}, k, max)$.

The program $\pi (\mathcal{P})$ consists of the following modules:

• Planning: A program encoding the domain information D of $\mathcal{P}$ and the rules for generating optimal plan for each $g \in \mathcal{G}$. This module is similar to the standard encoding in ASP planning [16] with an extension to allow for the generation of multiple plans for multiple goals at the same time (i.e., similar to that used in conditional planning in Sect. 2).

• Optimization: A set of rules for determining the longest prefix between two plans of two goals $g_I$ and $g_J$ on trajectories $I \ne J$ given a set of plans for the goals in $\mathcal{G}$. It also contains the optimization statement for selecting answer sets containing $\mathtt {wcd}(\mathcal{P})$.

• Blocking: A set of rules that interact with the Python program to block actions from the original problem.

The multi-shot ASP implementations of the GRD problem performs reasonably well against the system developed by the inventor of the GRD problem [29].

4 ASP in Multi-agent System

4.1 ASP and Distributed Constraint Optimization Problems

A distributed constraint optimization problem (DCOP) is defined by $\langle \mathcal {X, D, F, A, \,}\alpha \rangle$, where: $\mathcal {X} = \{x_1,\ldots ,x_n\}$ is a set of variables; $\mathcal {D} =\{D_1,\ldots ,D_n\}$ is a set of finite domains, where $D_i$ is the domain of variable $x_i$; $\mathcal {F} = \{f_1, \ldots , f_m\}$ is a set of constraints, where each $k_i$-ary constraint $f_i: D_{i_1} \times D_{i_2} \times \ldots \times D_{i_{k_i}} \mapsto \mathbb {N} \cup \{-\infty , 0\}$ specifies the utility of each combination of values of the variables in its scope, scope $(f_i)=\{x_{i_1},\ldots ,x_{i_{k_i}}\}$; $\mathcal {A} = \{a_1, \ldots , a_p\}$ is a set of agents; and $\alpha : \mathcal {X} \rightarrow \mathcal {A}$ maps each variable to one agent.

Figure 4(a,b) shows an example of a DCOP with three agents (see [14]), where each agent $a_i$ controls variable $x_i$ with domain $\{0,1\}$. Figure 4(a) shows its constraint graph and Fig. 4(b) shows the utility functions, assuming that all of the three constraints have the same function.

Fig. 4.

DCOP graph (a), utility table (b); DPOP graph (c), UTIL-Phase Computation Table (d, e)

A solution is a value assignment for all variables and its corresponding utility is the evaluation of all utility functions on such solution. The goal is to find a utility-maximal solution. Solutions of a DCOP can be computed in three steps  [22]: (i) constructing a pseudo-tree from the constraint graph (Fig. 4(c) for the example); (ii) UTIL-computation phase: each agent, starting from the leafs of the pseudo-tree, (ii.x) computes the optimal sum of utilities in its subtree for each value combination of variables in the set of variables owned by ancestor agents that are constrained with variables owned by the agents in the subtree (Fig. 4(d) shows the UTIL-computation of the agent $a_3$) and (ii.xx) sends the maximal value to its parent; and (iii) VALUE-propagation phase: each agent, starting from the root of the pseudo-tree, determines the optimal value for its variables upon receiving the VALUE message from its parent and sends to its children (Fig. 4(e) shows the VALUE-propagation of the agent $a_1$) in a VALUE message.

In [14], we presented an ASP-based system, ASP-DPOP, for computing solutions of DCOP. In this system, each agent consists of two modules, an ASP module and a controller. The ASP module is responsible for computing the UTIL and VALUE messages when the agent needs to do so. The controller, written in SICStus$^\copyright$ Prolog, is responsible for all communications between the agent and other agents. When an agent receives all UTIL messages from its children, the ASP module computes its UTIL-message and the controller sends the message to its parent. When an agent receives its parent’s VALUE message, the ASP module computes its own VALUE message and the controller sends the message to its children. The flexibility and expressiveness of ASP allows ASP-DPOP to work with agents who control multiple variables while state-of-the-art DCOP solvers assume that each agent controls only one variable. ASP-DPOP performs well against state-of-the-art DCOP solvers in several domains and has better performance, both in scalability and efficiency, in domains with hard constraints. The approach has been extended to deal with uncertainty in constraint utilities [13].

4.2 Multi-agent Planning

Multi-agent planning (MAP) is the problem of planning for multiple agents. The presence of multiple agents that can change the environment simultaneously brings about a number of issues:

• can the planning process be done centralized or must it be done distributed?

• what is the protocol for agents to communicate with each other?

• what types of actions are available for the agents (e.g., whether group actions are available? whether knowledge and/or belief changing actions are involved? etc.)?

• what are the representation languages used by individual agents?

For simplicity of the presentation, let us assume that all agents use the same representation language. The answer to the other questions depends on the degree of cooperativeness between agents.

Generally, a MAP for the agents $\{1,\ldots ,n\}$ can be represented by a tuple $(\mathcal{P}_1,\ldots ,\mathcal{P}_n)$ where $\mathcal{P}_i$ is a planning problem for agent i extended with information about other agents who can affect the view of the environment locally to i.

• When agents are fully cooperative and planning can be done by one single agent, the encoding for single-agent planning (e.g., in [16]) can be extended to deal with MAP by

  • creating the program $\pi _k(\mathcal{P}_i)$ for $\mathcal{P}_i$ ; and

  • adding constraints to eliminate conflicts that arise due to the (potentially) parallel execution of actions among agents

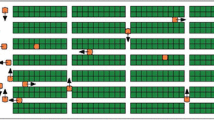
  A prototype of an ASP based MAP system was proposed in [28]. Recently, we extend this prototype to deal with an interesting application the Multi-Agent Path Finding (MAPF) problem that deals with teams of agents that need to find collision-free paths from their respective starting locations to their respective goal locations on a graph. This model has attracted a lot of attention due to the success of the autonomous warehouse systems [36]. In these systems (illustrated by Fig. 5), robots (in orange) navigate around a warehouse to pick up inventory pods from their storage locations (in green) and drop them off at designated inventory stations (in purple) in the warehouse.

  As it turns out, the ASP based system does not perform very well in this application comparing to state-of-the-art (e.g., [17]). The interesting part of this problem is that the basic ASP encoding is fairly simple. Yet, the problem quickly becomes unsolvable when its size increases.

  By adding domain-knowledge to the encoding and decomposing the problem into smaller sub-problems, the scalability of the system improves significantly [19]. For example, it is easy to see that by adding some designated locations to the map, a path can be seen as multiple segments among the designated locations. As such, a path can be generated in multiple steps. In the first step, segments of a path are generated using a simplified map. The final path is then obtained by generating the concrete path for each segment.

• For self-interested agents, solving an MAP requires that agents negotiate with each other and thus an integration of a negotiation framework with MAP will be necessary. As shown in [27], ASP can also be used effectively for the development of negotiation systems. It is worth noticing that any negotiation framework used for this purpose must consider the dynamic of the environment. In [26], we developed an ASP based prototype for planning with negotiation in a dynamic environment. While the underlying encoding for planning does not change, special attentions need to be made to deal with the “effects” of negotiations. We envision that this approach will be necessary for some future extensions of the MAPF problem that might require stronger interactions between agents. For example, an agent might request help from another agent to continue its job if it realizes that its battery will run out before it can complete its job.

Fig. 5.

Layout of an autonomous warehouse system [Wurman et al., 2008] (Color figure online)

5 Conclusions

In this paper, we describe the application of answer set programming in planning with incomplete information and sensing actions, goal recognition design, distributed constraint optimization problem, and various settings of multi-agent planning. We discuss the key techniques that contribute to the good performance of ASP based solutions and present a challenging application for ASP.